Hybrid ANFIS-PI-Based Optimization for Improved Power Conversion in DFIG Wind Turbine
Abstract
1. Introduction
1.1. Research Background
- Aerodynamic stage: This stage captures the wind’s dynamic energy and converts it into rotational motion through turbine blades. The blades are aerodynamically optimized to maximize power extraction under different atmospheric conditions.
- Mechanical stage: The rotational energy is transmitted through a gear mechanism that optimizes speed for generator efficiency.
- Electrical stage: The generated energy is converted and conditioned for grid integration using advanced power electronic components, including AC–DC–AC converters and filters.
- It can regulate real and reactive power, improving grid compatibility and electrical performance.
- It minimizes mechanical load on turbine parts, prolonging their lifespan.
- Its partial-scale power electronic converter design allows operation over a broad range of wind speeds, making it suitable for regions with moderate wind conditions.
- It provides a cost-effective balance between performance and production costs compared with other advanced generator systems [3].
- The rotor-side converter (RSC) controls the rotor current and manages reactive power.
- The grid-side converter (GSC) maintains the DC link voltage stability and ensures compliance with grid requirements [4].
1.2. Motivation for the Research
1.3. Literature Review
1.4. Problem Statement
1.5. Aim of the Research
1.6. Objectives of the Research
- Develop a hybrid ANFIS-PI controller to enhance power stability and grid compliance in DFIG-based WTSs.
- Reduce overshoot and improve settling time, ensuring better dynamic response under fluctuating wind speeds.
- Optimize RSC and GSC simultaneously, unlike previous works focusing on only one converter.
- Validate system performance by comparing it with conventional PI controllers and existing AI-based techniques.
1.7. Contribution
- Introduction of a novel hybrid ANFIS-PI controller, integrating fuzzy reasoning adaptability with neuro-computational learning.
- Dual converter optimization, enhancing both RSC and GSC control mechanisms, ensuring improved power stability and grid compliance.
- Reduction in computational complexity, minimizing the need for large training datasets while maintaining superior real-time adaptability.
- Validated performance improvements, demonstrating lower overshoot (20%) and improved settling time (50%) over traditional PI controllers.
1.8. Novelty and Advantages of the Proposed Method
- Hybrid control approach: The research introduced a novel adaptive neuro-fuzzy inference system (ANFIS)-PI hybrid controller for the rotor-side converter (RSC) and grid-side converter (GSC) in a doubly fed induction generator (DFIG)-based wind turbine system (WTS). Unlike traditional fixed-parameter controllers, this hybrid structure combined fuzzy logic inference with neural network adaptability, allowing dynamic parameter tuning.
- Improved system adaptability: Unlike conventional proportional-integral (PI) controllers, which struggle with real-time adaptation to fluctuating wind speeds and grid disturbances, the ANFIS-based controller dynamically learned from operational conditions and adjusted the control parameters accordingly.
- Optimized computational efficiency: The model achieved lower training errors (~0.034) in just 25 training epochs, compared with the conventional AI-based controllers requiring double the dataset size and 50 epochs for similar results. This highlights superior computational efficiency without compromising accuracy.
- Dual-converter optimization: Most previous studies optimized the RSC or the GSC. This research enhanced both converters, ensuring improved rotor current regulation, DC link voltage stability, and active/reactive power management for grid compliance.
- Real-time feasibility: Unlike meta-heuristic algorithms (such as genetic algorithms, particle swarm optimization, and ant colony optimization), which are computationally expensive and may suffer from slow convergence, ANFIS ensures fast and adaptive control decisions, making real-time applications more feasible.
2. Proposed System Configuration and Modeling of WTS Components
2.1. System Configuration
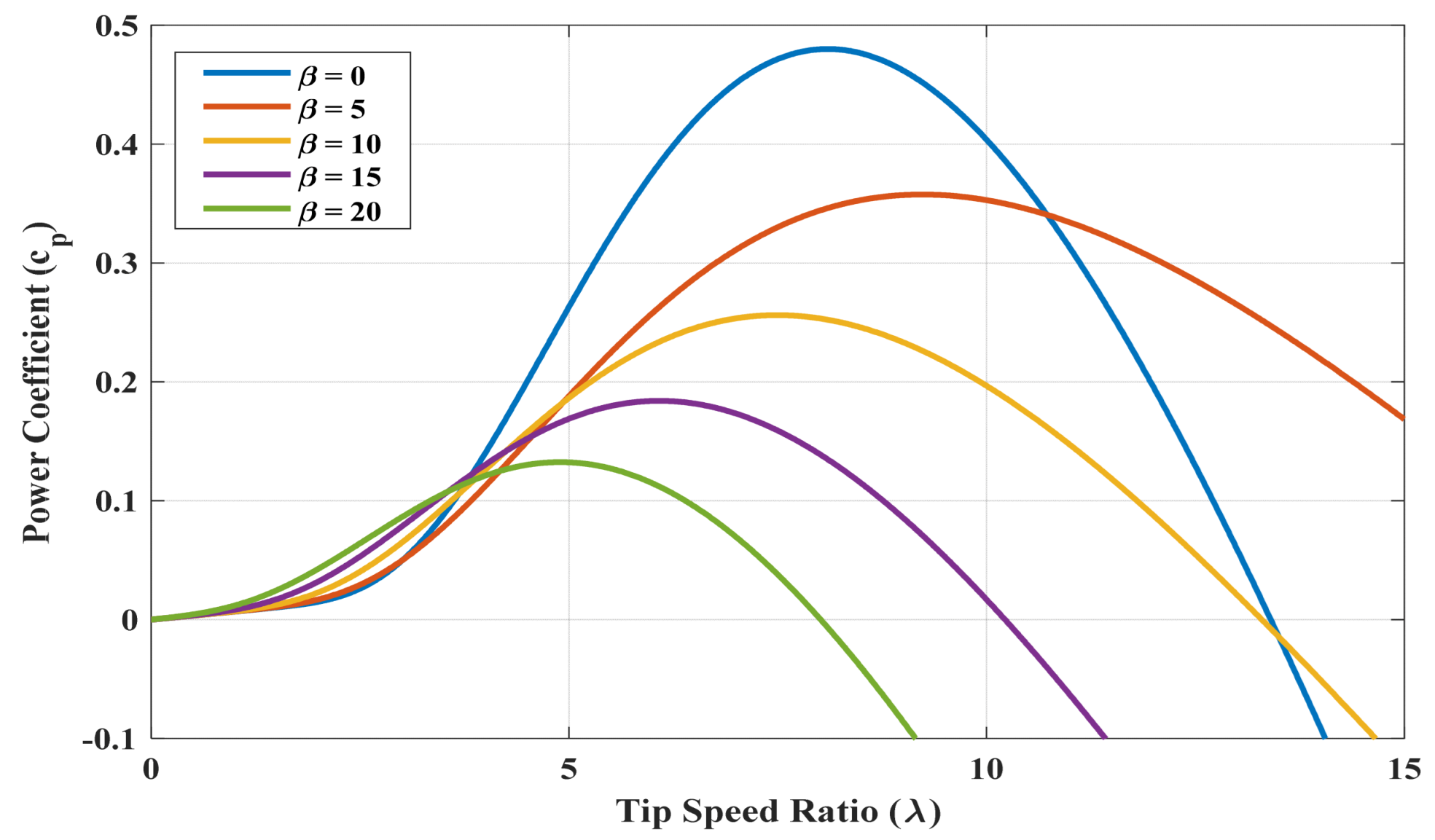
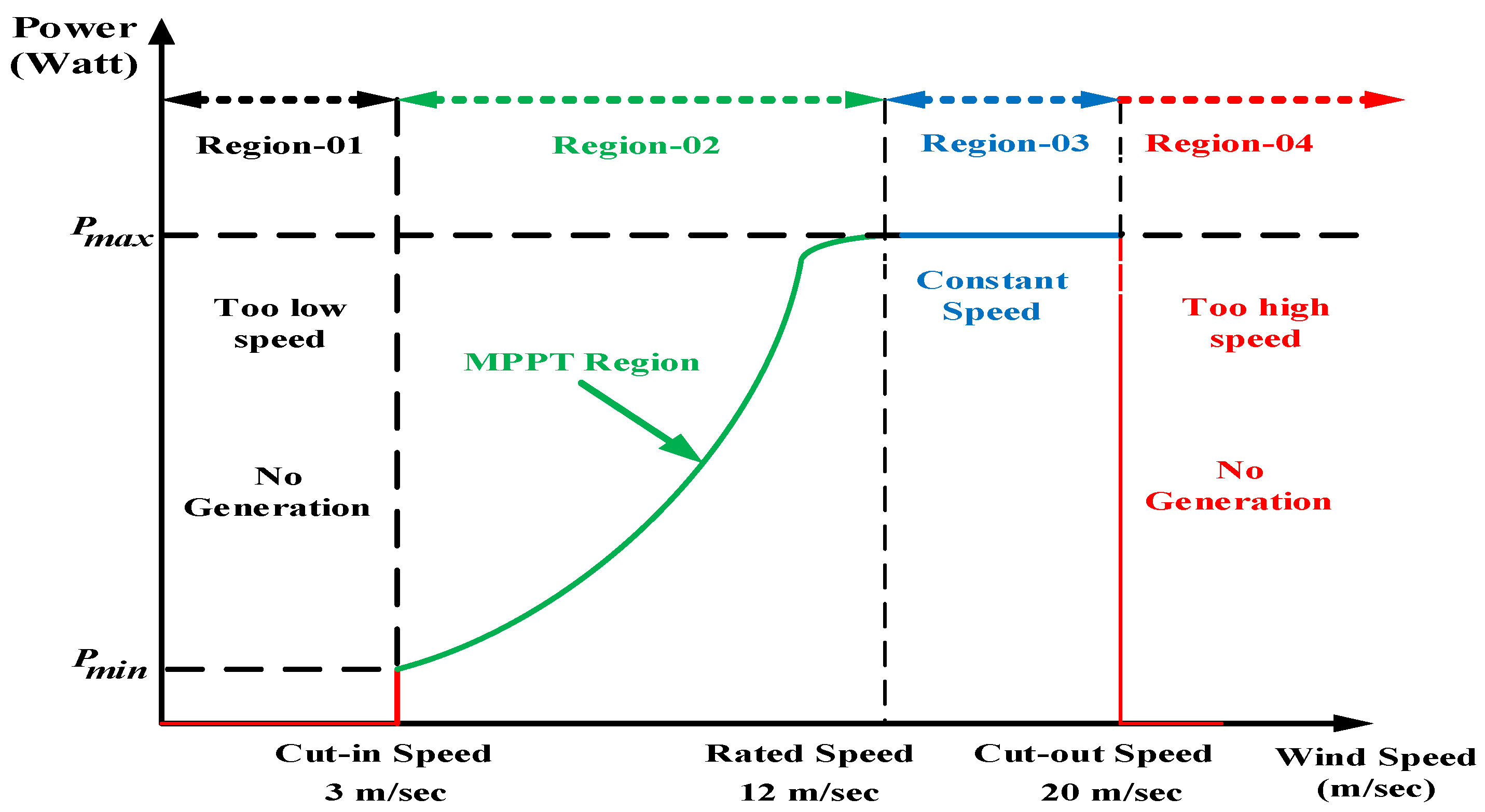
2.2. Mathematical Representation of Wind Turbine
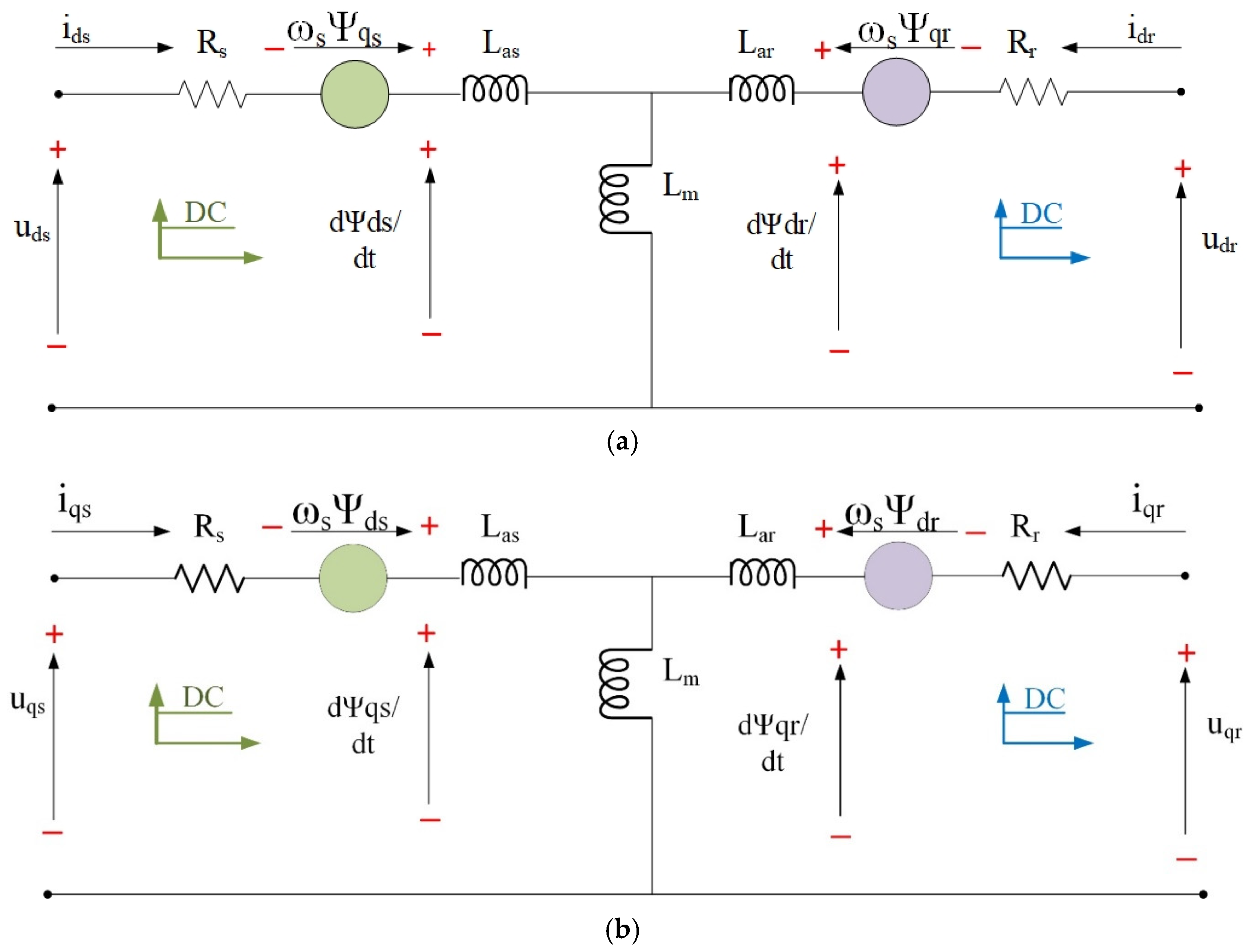
2.3. Mathematical Model of DFIG
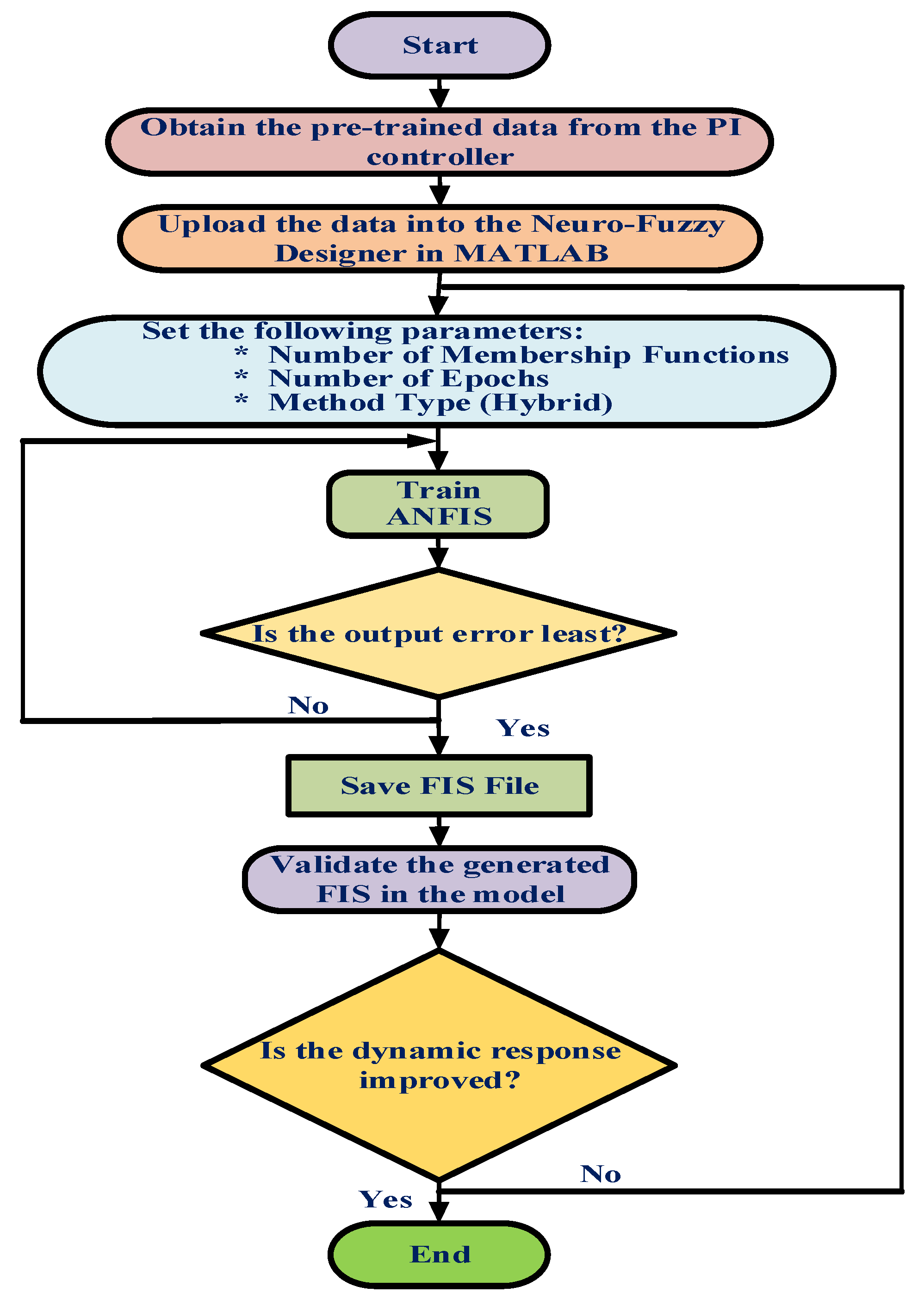
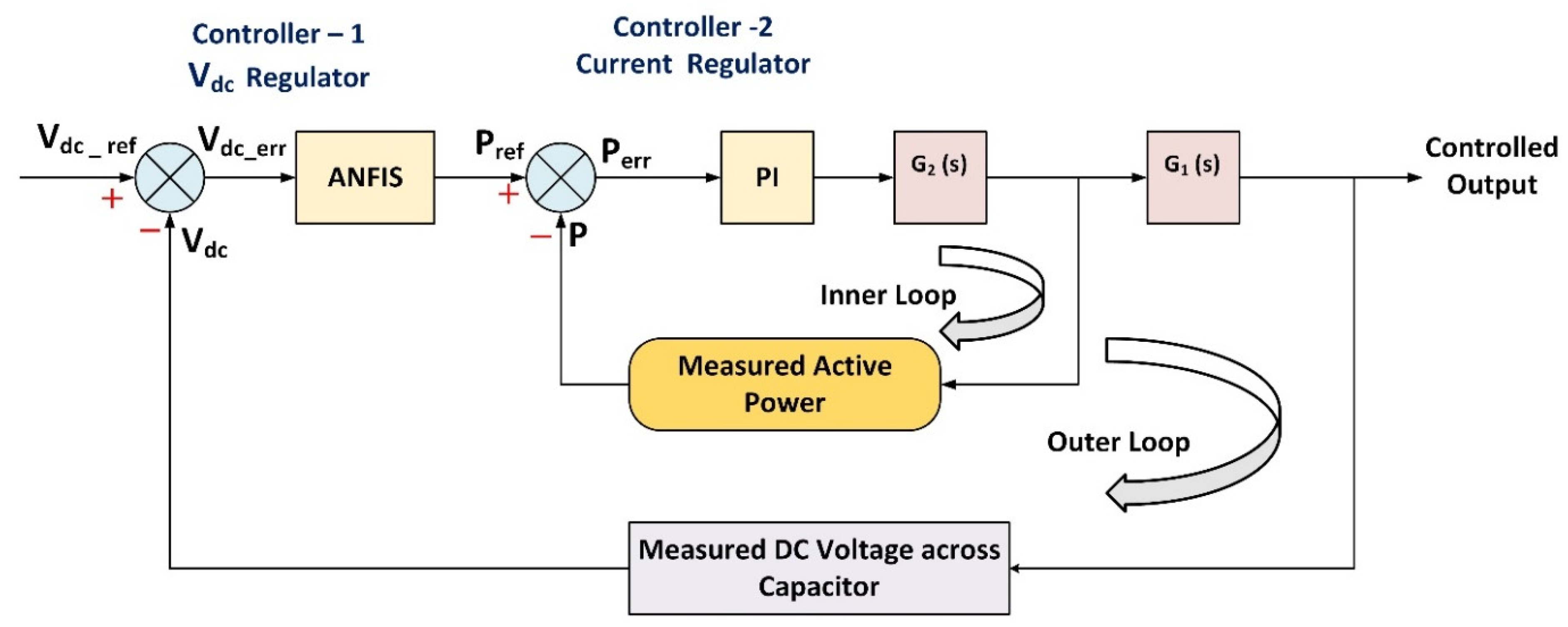
3. Proposed Hybrid ANFIS-PI Controller
Implementation of Proposed Hybrid Controller in WECS Model
4. Simulation Results and Discussion
- The training set (70%) was used for training the ANFIS model by adjusting membership functions and rule parameters.
- The validation set (15%) was applied for refinement and prevent overfitting, ensuring the model generalizes well.
- The testing set (15%) was used to assess the overall model accuracy and compare it against the PI controller for validation.
Limitations of the Proposed Method
- Initial training complexity: The ANFIS model requires an initial training phase, during which membership functions and rules must be optimized. Although it requires fewer training data than standalone ANN models, the training process still demands careful tuning to ensure stability and accuracy.
- Dependence on membership function design: The fuzzy logic component in ANFIS relies on well-defined membership functions. Suboptimal membership function selection can lead to degraded performance, requiring expert knowledge or additional optimization techniques for fine-tuning.
- Computational load during implementation: While ANFIS-PI is computationally more efficient than purely ANN-based or model predictive controllers, it still requires more processing power than traditional PI controllers. Implementing real-time control on low-cost embedded systems may require optimized hardware (e.g., DSP or FPGA) for efficient execution.
- Limited generalization for different wind turbine configurations: The proposed ANFIS-PI controller was designed for DFIG-based WTS, meaning its direct applicability to other types of wind turbines (e.g., PMSG-based systems) may require modifications in control strategies and parameter tuning.
- Additional computational cost for real-time adaptation: Since ANFIS continuously adapts control parameters, real-time adaptation in highly dynamic environments increases computational demand, potentially impacting performance in large-scale wind farms without adequate processing resources.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- GWEC’s Global Wind Report 2024. Available online: https://www.gwec.net/reports/globalwindreport (accessed on 4 March 2025).
- Ishaque, M.; Laghari, J.A.; Bhayo, M.A.; Chandio, S.; Mahariq, I. Hybrid ANFIS-PI-Based Robust Control of Wind Turbine Power Generation System. Int. Trans. Electr. Energy Syst. 2024, 2024, 2389751. [Google Scholar] [CrossRef]
- Ouhssain, S.; Chojaa, H.; Aljarhizi, Y.; Al Ibrahmi, E.; Maarif, A.; Mossa, M.A. Enhancing the Performance of a Wind Turbine Based DFIG Generation System Using an Effective ANFIS Control Technique. Int. J. Robot. Control Syst. 2024, 4, 1617–1640. [Google Scholar] [CrossRef]
- Martínez, J.C.; Rodríguez Amenedo, J.L.; Arnaltes Gómez, S.; Alonso-Martínez, J. Grid-forming control of doubly-fed induction generators based on the rotor flux orientation. Renew. Energy 2023, 207, 162–176. [Google Scholar] [CrossRef]
- Mossa, M.A.; Echeikh, H.; Iqbal, A. Enhanced control technique for a sensor-less wind driven doubly fed induction generator for energy conversion purpose. Energy Rep. 2021, 7, 5815–5833. [Google Scholar] [CrossRef]
- Boubzizi, S.; Abid, H.; El Hajjaji, A.; Chaabane, M. Comparative study of three types of controllers for DFIG in wind energy conversion system. Prot. Control Mod. Power Syst. 2018, 3, 21. [Google Scholar] [CrossRef]
- Chetouani, E.; Errami, Y.; Obbadi, A.; Sahnoun, S. Optimal tuning of PI controllers using adaptive particle swarm optimization for doubly-fed induction generator connected to the grid during a voltage dip. Bull. Electr. Eng. Inform. 2021, 10, 2367–2376. [Google Scholar] [CrossRef]
- Soomro, M.A.; Memon, Z.A.; Kumar, M.; Baloch, M.H. Wind energy integration: Dynamic modeling and control of DFIG based on super twisting fractional order terminal sliding mode controller. Energy Rep. 2021, 7, 6031–6043. [Google Scholar] [CrossRef]
- Sahito, G.M.; Korai, J.J.; Korai, M.B.; Shaikh, A.R.S. Design of PI Controller for Wind Energy Conversion System Using MATLAB/Simulink. Int. J. Electr. Eng. Emerg. Technol. 2022, 5, 6–10. [Google Scholar]
- Rodríguez, J.A.M. Metaheuristic Algorithm and Laser Projection for Adjusting the Model of the Last Lower Surface to a Footprint. Biomimetics 2024, 9, 699. [Google Scholar] [CrossRef]
- Alhato, M.M.; Bouallègue, S. Direct Power Control Optimization for Doubly Fed Induction Generator Based Wind Turbine Systems. Math. Comput. Appl. 2019, 24, 77. [Google Scholar] [CrossRef]
- Aguilar-Mejía, O.; Minor-Popocatl, H.; Tapia-Olvera, R. Comparison and Ranking of Metaheuristic Techniques for Optimization of PI Controllers in a Machine Drive System. Appl. Sci. 2020, 10, 6592. [Google Scholar] [CrossRef]
- Sunaina, S.; Shivahare, B.D.; Kumar, V.; Gupta, S.K.; Singh, P.; Diwakar, M. Metaheuristic Optimization Algorithms and recent applications: A comprehensive survey. In Proceedings of the 2023 International Conference on Computational Intelligence, Communication Technology and Networking (CICTN), Ghaziabad, India, 20–21 April 2023; pp. 506–511. [Google Scholar]
- Alwash, S.M.; Al-Thahab, O.Q.J.; Alwash, S.F. Modeling and Control Strategies for DFIG in Wind Turbines: A Comparative Analysis of SPWM, THIPWM, and SVPWM Techniques. J. Eur. Des Systèmes Autom. 2023, 56, 963–972. Available online: https://www.academia.edu/119271461/Modeling_and_Control_Strategies_for_DFIG_in_Wind_Turbines_A_Comparative_Analysis_of_SPWM_THIPWM_and_SVPWM_Techniques (accessed on 4 March 2025). [CrossRef]
- Nassef, A.M.; Abdelkareem, M.A.; Maghrabie, H.M.; Baroutaji, A. Review of Metaheuristic Optimization Algorithms for Power Systems Problems. Sustainability 2023, 15, 9434. [Google Scholar] [CrossRef]
- Tomar, V.; Bansal, M.; Singh, P. Metaheuristic Algorithms for Optimization: A Brief Review. Eng. Proc. 2024, 59, 238. [Google Scholar] [CrossRef]
- Zhou, J.; Lilhore, U.K.; Poongodi, M.; Hai, T.; Simaiya, S.; Jawawi, D.N.A.; Alsekait, D.M.; Ahuja, S.; Biamba, C.; Hamdi, M. Comparative analysis of metaheuristic load balancing algorithms for efficient load balancing in cloud computing. J. Cloud Comput. 2023, 12, 85. [Google Scholar] [CrossRef]
- Altay, E.V.; Altay, O.; Özçevik, Y. A Comparative Study of Metaheuristic Optimization Algorithms for Solving Real-World Engineering Design Problems. CMES Comput. Model. Eng. Sci. 2023, 139, 1039–1094. [Google Scholar] [CrossRef]
- Maafa, A.; Mellah, H.; Benaouicha, K.; Babes, B.; Yahiou, A.; Sahraoui, H. Fuzzy Logic-Based Smart Control of Wind Energy Conversion System Using Cascaded Doubly Fed Induction Generator. Sustainability 2024, 16, 9333. [Google Scholar] [CrossRef]
- Pandey, S.K.; Verma, K.; Kumar, S.; Agnihotri, P. Comparative Analysis of ANFIS and PI Based Control of DFIG for Wind Power Generation with Grid-Integration. In Proceedings of the 2023 9th IEEE India International Conference on Power Electronics (IICPE), Sonipat, India, 28–30 November 2023; pp. 1–7. [Google Scholar]
- Behara, R.K.; Saha, A.K. Neural Network Predictive Control for Improved Reliability of Grid-Tied DFIG-Based Wind Energy System under the Three-Phase Fault Condition. Energies 2023, 16, 4881. [Google Scholar] [CrossRef]
- Sayeh, K.F.; Tamalouzt, S.; Ziane, D.; Bekhiti, A.; Belkhier, Y. Utilizing Fuzzy Logic Control and Neural Networks Based on Artificial Intelligence Techniques to Improve Power Quality in Doubly Fed Induction Generator-Based Wind Turbine System. Int. J. Energy Res. 2025, 2025, 5985904. [Google Scholar] [CrossRef]
- Sayeh, K.F.; Tamalouzt, S.; Ziane, D.; Deffaf, B.; Belaid, S.L.; Belkhier, Y.; Bajaj, M.; Blazek, V. Fuzzy Logic-Enhanced Direct Power Control for Wind Turbines with Doubly Fed Induction Generators. Results Eng. 2024, 24, 103557. [Google Scholar] [CrossRef]
- Ouari, K.; Belkhier, Y. Model predictive direct torque algorithm for coordinated electrical grid operation of wind energy conversion system-based doubly fed induction generator. Int. J. Model. Simul. 2024, 1–14. [Google Scholar] [CrossRef]
- Chojaa, H.; Derouich, A.; Chehaidia, S.E.; Taoussi, M.; Zamzoum, O.; Mosaad, M.I.; Benbouhenni, H.; Yessef, M. Advanced Control Techniques for Doubly-Fed Induction Generators Based Wind Energy Conversion Systems. In Proceedings of the 2022 Global Energy Conference (GEC), Batman, Turkey, 26–29 October 2022; pp. 282–287. [Google Scholar]
- 5MW DFIG Wind Turbine with Variable Speed Operation Connected to a Grid—File Exchange—MATLAB Central. Available online: https://www.mathworks.com/matlabcentral/fileexchange/58202-1-5mw-dfig-wind-turbine-with-variable-speed-operation-connected-to-a-grid (accessed on 4 March 2025).
- Abad, G.; Lopez, J.; Rodriguez, M.; Marroyo, L.; Iwanski, G. Doubly Fed Induction Machine: Modeling and Control for Wind Energy Generation; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Hete, R.R.; Shrivastava, T.; Dash, R.; Anupallavi, L.; Fathima, M.; Reddy, K.J.; Dhanamjayalu, C.; Mohammad, F.; Khan, B. Design and development of PI controller for DFIG grid integration using neural tuning method ensembled with dense plexus terminals. Sci. Rep. 2024, 14, 7916. [Google Scholar] [CrossRef]
- Bhayo, M.A.; Mirsaeidi, S.; Koondhar, M.A.; Chandio, S.; Tunio, M.A.; Allasi, H.L.; Aziz, M.J.A.; Idris, N.R.N. An Experimental Hybrid Control Approach for Wind Turbine Emulator. IEEE Access 2023, 11, 58064–58077. [Google Scholar] [CrossRef]
- Liu, J.; Gao, Y.; Geng, S.; Wu, L. Nonlinear Control of Variable Speed Wind Turbines via Fuzzy Techniques. IEEE Access 2017, 5, 27–34. [Google Scholar] [CrossRef]
- Nasim, F.; Khatoon, S.; Ibraheem; Shahid, M. Implementation of crowbar protection in DFIG. In Advances in AI for Biomedical Instrumentation, Electronics and Computing; CRC Press: Boca Raton, FL, USA, 2024. [Google Scholar]
- Farrag, M.E.A.; Putrus, G.A. Design of an Adaptive Neurofuzzy Inference Control System for the Unified Power-Flow Controller. IEEE Trans. Power Deliv. 2012, 27, 53–61. [Google Scholar] [CrossRef]
- Htet, T.Z.; Zhao, Z.; Gu, Q. Design analysis of direct-driven PMSG in wind turbine application. In Proceedings of the 2016 International Conference on System Reliability and Science (ICSRS), Paris, France, 15–18 November 2016; pp. 7–11. [Google Scholar]
- Ukoba, K.; Onisuru, O.R.; Jen, T.-C. Harnessing machine learning for sustainable futures: Advancements in renewable energy and climate change mitigation. Bull. Natl. Res. Cent. 2024, 48, 99. [Google Scholar] [CrossRef]







| S# | Ref. | Control Technique Applied | Parameters Applied | Signal Applied | Merits | Demerits |
|---|---|---|---|---|---|---|
| 1 | [19] | PI controller | DC link voltage, wind turbine speed | Variable wind speed | Simple implementation, eliminates steady-state errors | Sudden overshoot, longer settling time |
| 2 | [3,4] | Particle swarm optimization (PSO) | Stator current, DC link voltage, active/reactive powers | Short circuit faults, variable wind speed | Enhances performance under faults, provides pitch angle regulation | High settling time, DC voltage instability under fluctuations |
| 3 | [5,6] | Genetic algorithm (GA) | Active/reactive powers | Rotor resistance variation | Smooth, reliable performance under variations | Difficulty in stopping criteria |
| 4 | [10] | Jellyfish search algorithm (JSA) | Power regulation parameters | Grid variations | Enhances stability, intense global search | High computational complexity |
| 5 | [11] | Grasshopper optimization algorithm (GOA) | DC link voltage, power factors | Grid variations | Fast execution, adaptive capabilities | Poor exploitation ability |
| 6 | [12] | Cuckoo search algorithm (CS) | Frequency and voltage control | Grid fluctuations | Strong global search ability | May get stuck in local optima |
| 7 | [13] | Grey wolf optimizer (GWO) | Power system stabilization | Grid disturbances | Adaptive behavior | Sensitive to initialization parameters |
| 8 | [14] | Whale optimization algorithm (WOA) | Reactive power optimization | Variable wind speed | Effective in multi-objective problems | Slower convergence |
| 9 | [15] | Bat algorithm (BA) | Stator and rotor control | Variable wind speed | Good exploration ability | High dependency on parameter tuning |
| 10 | [16] | Artificial fish-swarm algorithm (AFSA) | Grid synchronization parameters | Variable wind speed | Strong global optimization | Computational complexity |
| 11 | [22] | Fuzzy logic-based neural network | Power quality parameters | Grid disturbances | Handles nonlinearities, improves stability | Requires large datasets |
| 12 | [23] | Direct power control using fuzzy logic | Power control variables | Grid disturbances | Ensures grid stability | Longer response times |
| 13 | [24] | Model predictive direct torque control (MP-DTC) | Torque and flux parameters | Dynamic grid Variations | Improved torque precision | High computational demand |
| 14 | Proposed | Hybrid ANFIS-PI controller | RSC and GSC control parameters | Grid Variations | Superior adaptability with fuzzy learning and neural network-based optimization, reducing overshoot by 20% and improving settling time by 50% | Minimizes need for large datasets while maintaining real-time computational feasibility |
| Notation | Parameter | Magnitude and Unit |
|---|---|---|
| P | Nominal power | 1.5 MVA |
| V | Nominal L-L voltage | 575 |
| F | Grid frequency | 60 |
| p | No. of pole pairs | 40 |
| DC link voltage | 1.15 KV | |
| Line inductance | 0.31 pu | |
| Line resistance | 0.0032 pu |
| Parameters | Value |
|---|---|
| Proportion constant, Kp (RSC) | 2.25 |
| Integral constant, Ki (RSC) | 14 |
| Proportion constant, Kp (GSC) | 0.73 |
| Integral constant, Ki (GSC) | 2.85 |
| Dataset (input–output pairs) | 4,000,001 |
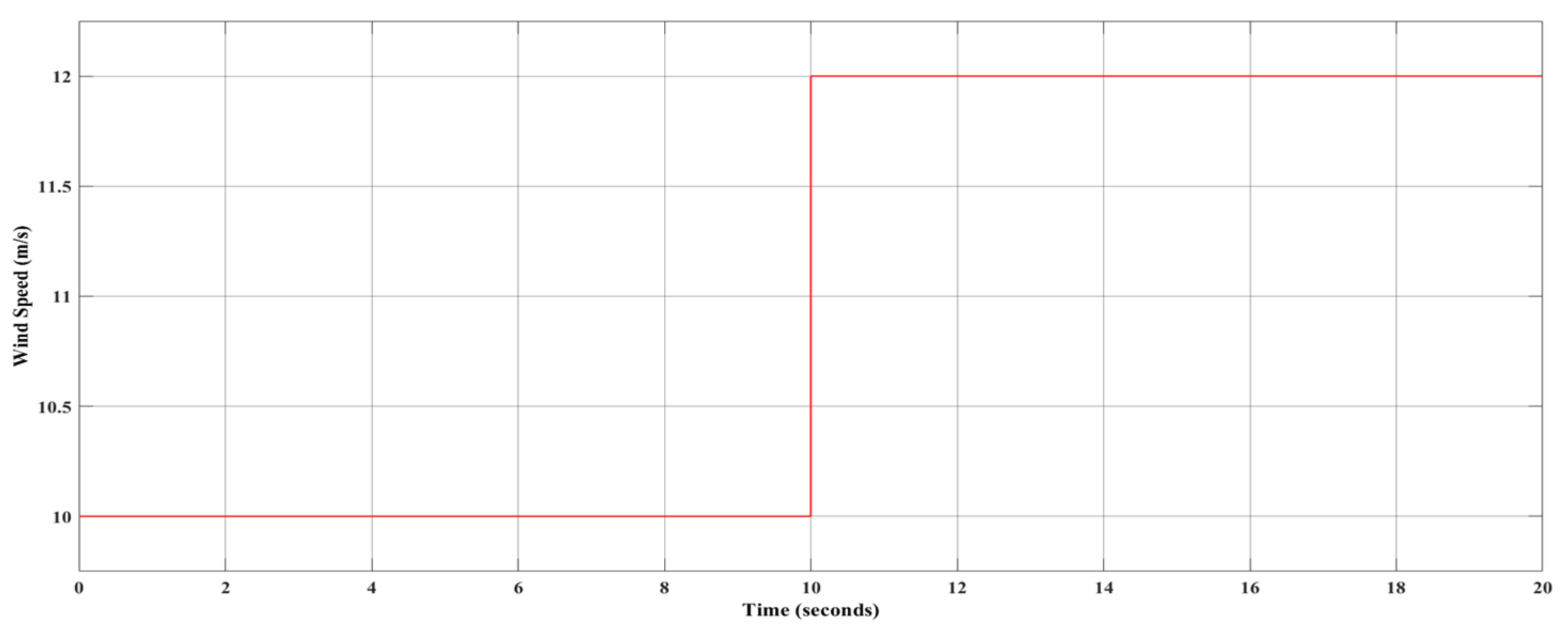
| Test signal applied (Vwind) at 10 s | From 10 m/s to 12 m/s |
| No. of inputs | 01 |
| No. of outputs | 01 |
| No. of membership functions | 08 |
| Type of membership functions | Constant |
| Nos. of epochs/iterations | 25 |
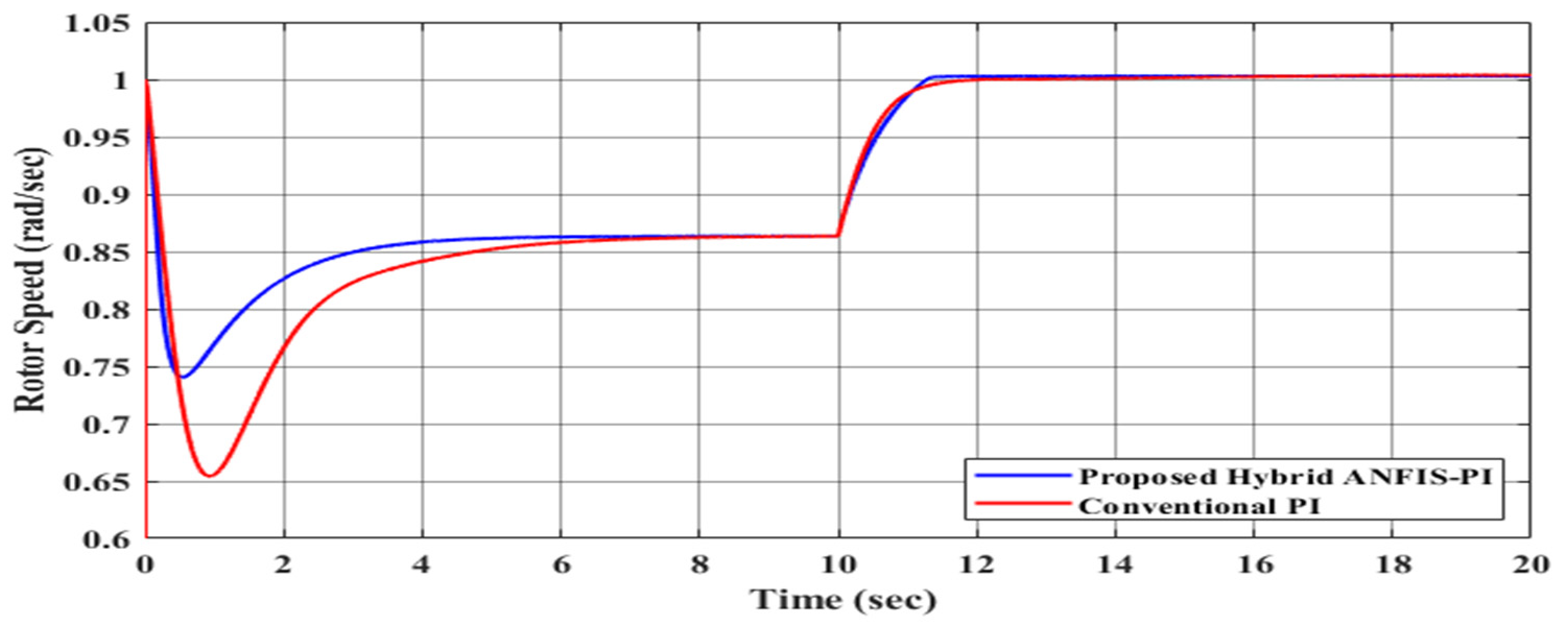
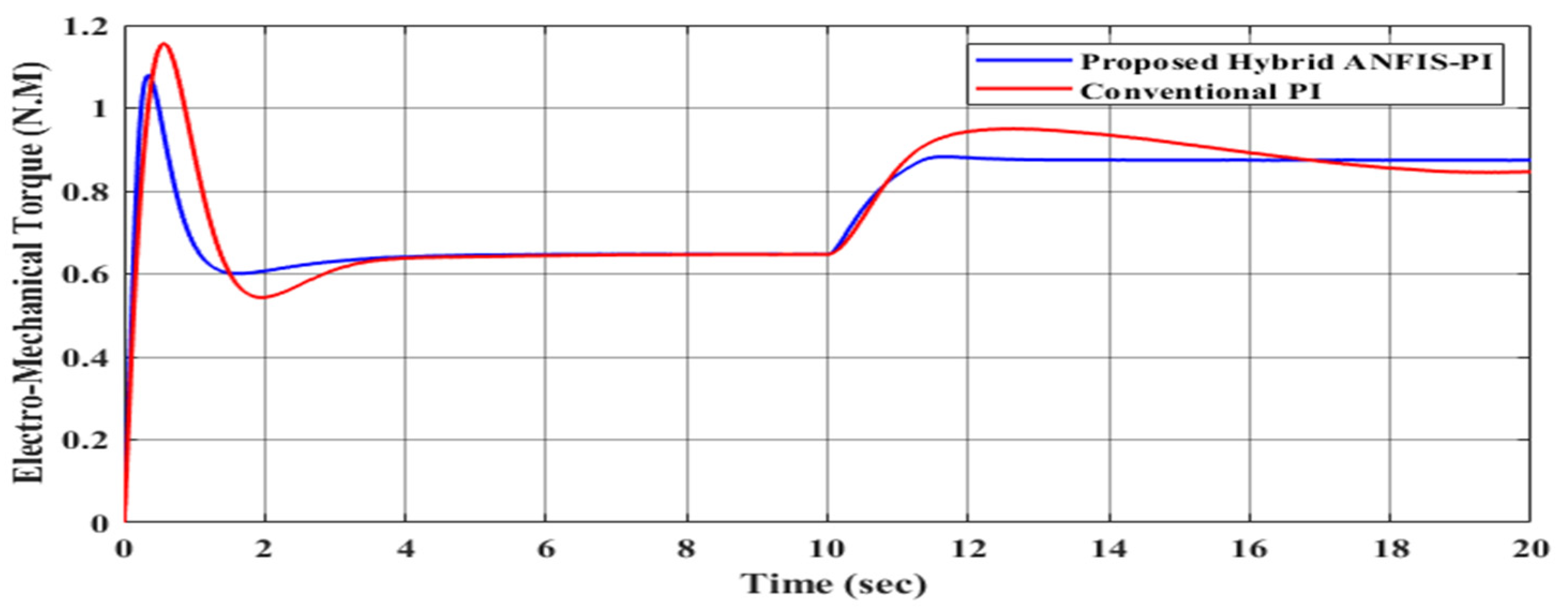
| S. No. | Parameters | Control Scheme | Rise Time (s) | Overshoot (%) | Settling Time (s) | Steady State Error |
|---|---|---|---|---|---|---|
| 1 | Rotor speed | PI | 1.2 | 5 | 2 | 0.88 |
| ANFIS-PI | 0.8 | 2 | 1 | 0 | ||
| 2 | Torque | PI | 1 | 43.75 | 4 | 0.9 |
| ANFIS-PI | 0.7 | 31.25 | 3 | 0 | ||
| 3 | Active power | PI | 0.56 | 9 | 4.5 | 0.83 |
| ANFIS-PI | 0.55 | 7 | 3 | 0 | ||
| 4 | DC bus Voltage | PI | 0.8 | 50 | 12 | 0.9 |
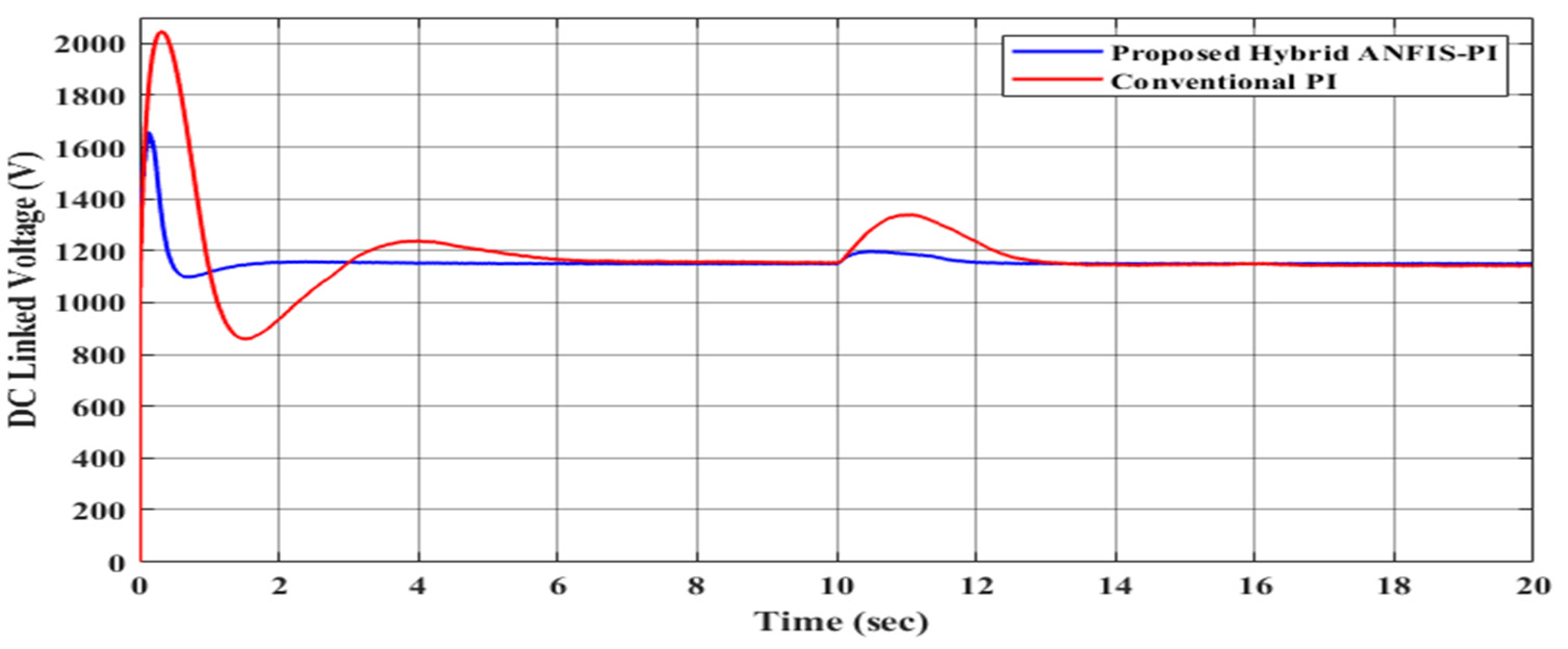
| ANFIS-PI | 0.7 | 30 | 10 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasim, F.; Khatoon, S.; Ibraheem; Urooj, S.; Shahid, M.; Ali, A.; Nasser, N. Hybrid ANFIS-PI-Based Optimization for Improved Power Conversion in DFIG Wind Turbine. Sustainability 2025, 17, 2454. https://doi.org/10.3390/su17062454
Nasim F, Khatoon S, Ibraheem, Urooj S, Shahid M, Ali A, Nasser N. Hybrid ANFIS-PI-Based Optimization for Improved Power Conversion in DFIG Wind Turbine. Sustainability. 2025; 17(6):2454. https://doi.org/10.3390/su17062454
Chicago/Turabian StyleNasim, Farhat, Shahida Khatoon, Ibraheem, Shabana Urooj, Mohammad Shahid, Asmaa Ali, and Nidal Nasser. 2025. "Hybrid ANFIS-PI-Based Optimization for Improved Power Conversion in DFIG Wind Turbine" Sustainability 17, no. 6: 2454. https://doi.org/10.3390/su17062454
APA StyleNasim, F., Khatoon, S., Ibraheem, Urooj, S., Shahid, M., Ali, A., & Nasser, N. (2025). Hybrid ANFIS-PI-Based Optimization for Improved Power Conversion in DFIG Wind Turbine. Sustainability, 17(6), 2454. https://doi.org/10.3390/su17062454








