Numerical Study on the Mechanism of Stoichiometric Combustion Knock in Marine Natural Gas Low-Carbon Engines in Rapid Compression Machine Combustion Chambers
Abstract
1. Introduction
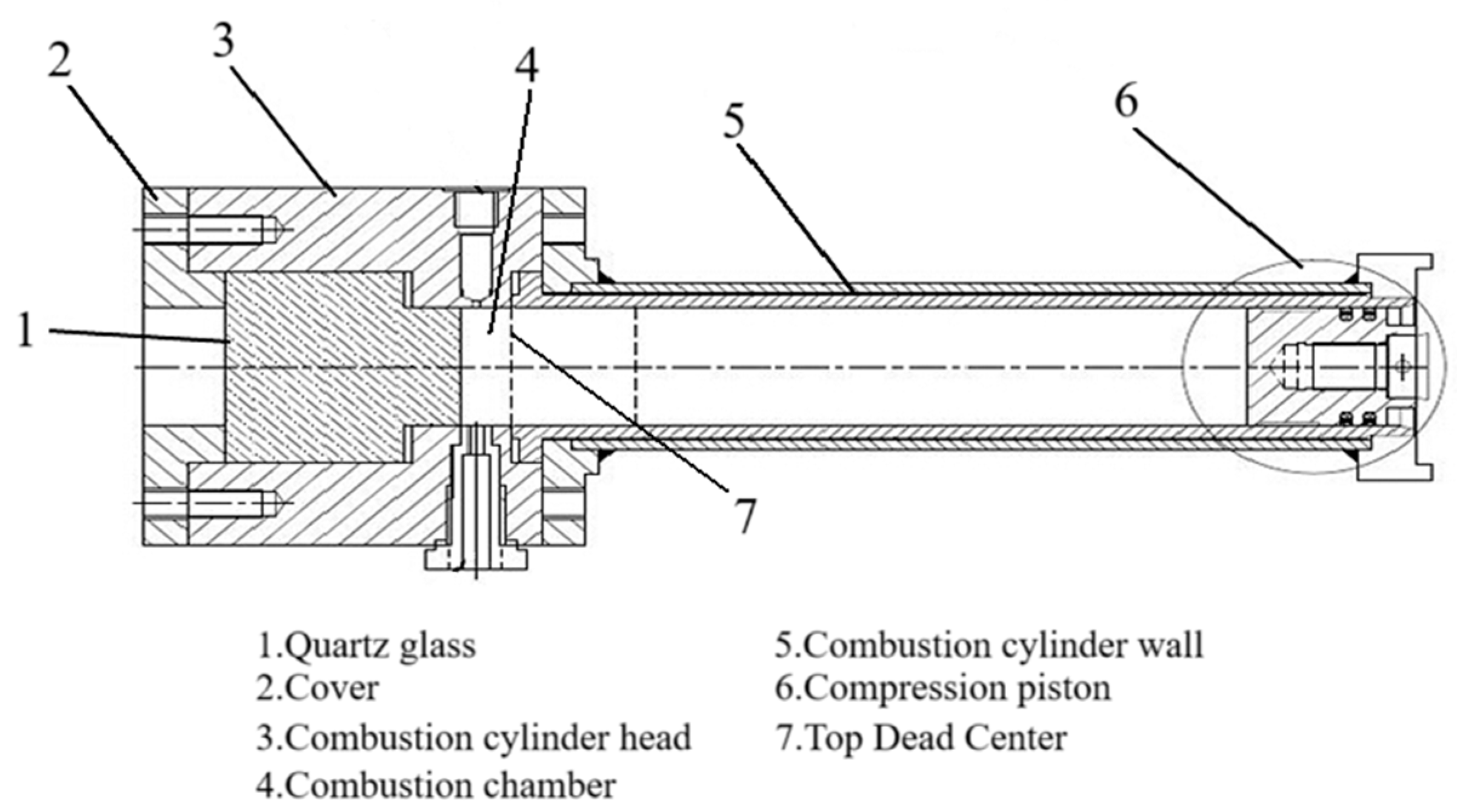
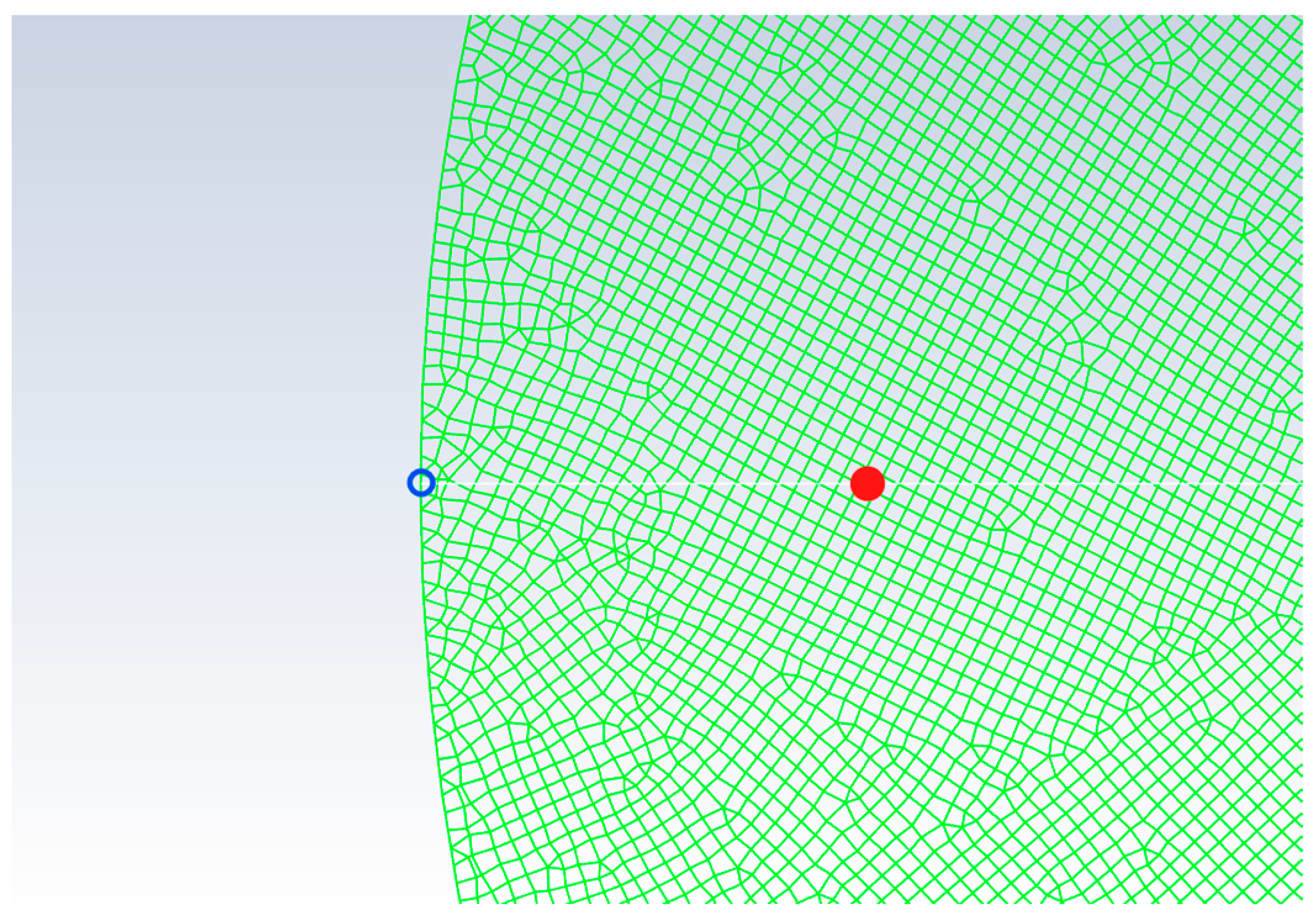
2. Establishment of the Model
3. Results and Discussion
3.1. Analyses of Combustion Characteristic Parameters
3.2. Auto-Ignition Modes and Combustion Modes When Knock Occurs
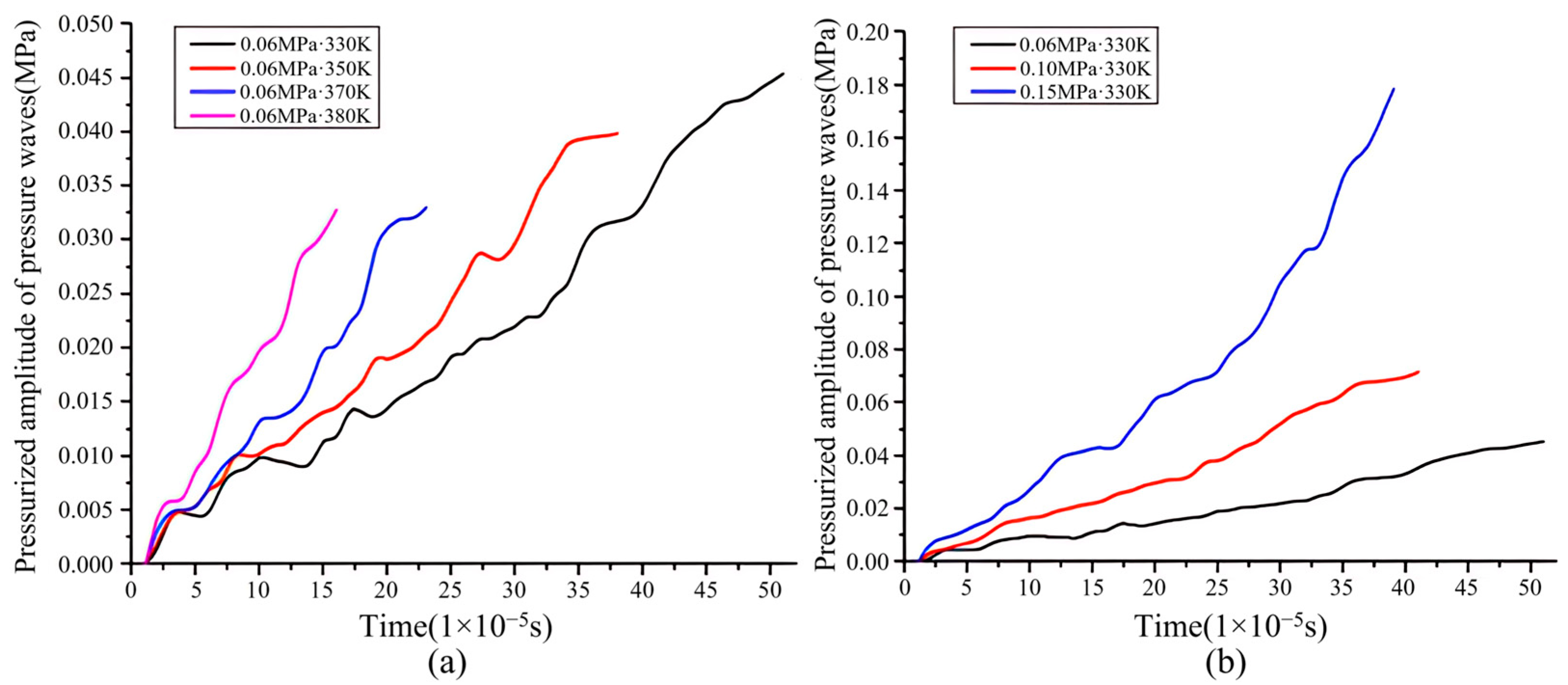
3.3. Change Rules of Pressurized Amplitude of Pressure Waves
- (a)
- The pressurized amplitude of the pressure waves increases continuously from low at each initial condition. The higher the initial temperature, the higher the pressurized amplitude and the growth rate. However, because the time of uniform pressure appearing in the unburned area is greatly shortened, the increase in the pressurized amplitude is lower, resulting in the highest pressurized amplitude being lower. The increase in the initial temperature inhibits the highest strength of pressure waves. The strength of pressure waves is not high enough to make auto-ignition occur in front of the flame.
- (b)
- The higher the initial pressure, the higher the pressurized amplitude and the growth rate. Auto-ignition occurs just slightly earlier. The increase in the pressurized amplitude is higher, resulting in the highest pressurized amplitude being higher. However, the time of combustion in the combustion chamber is very short. Even if the strength of the pressure waves increases and the time to increase the strength is prolonged, the strength of the pressure waves is not high enough to make auto-ignition occur in front of the flame. In addition, it is also related to the high ignition temperature of natural gas, which requires higher strength of pressure waves.
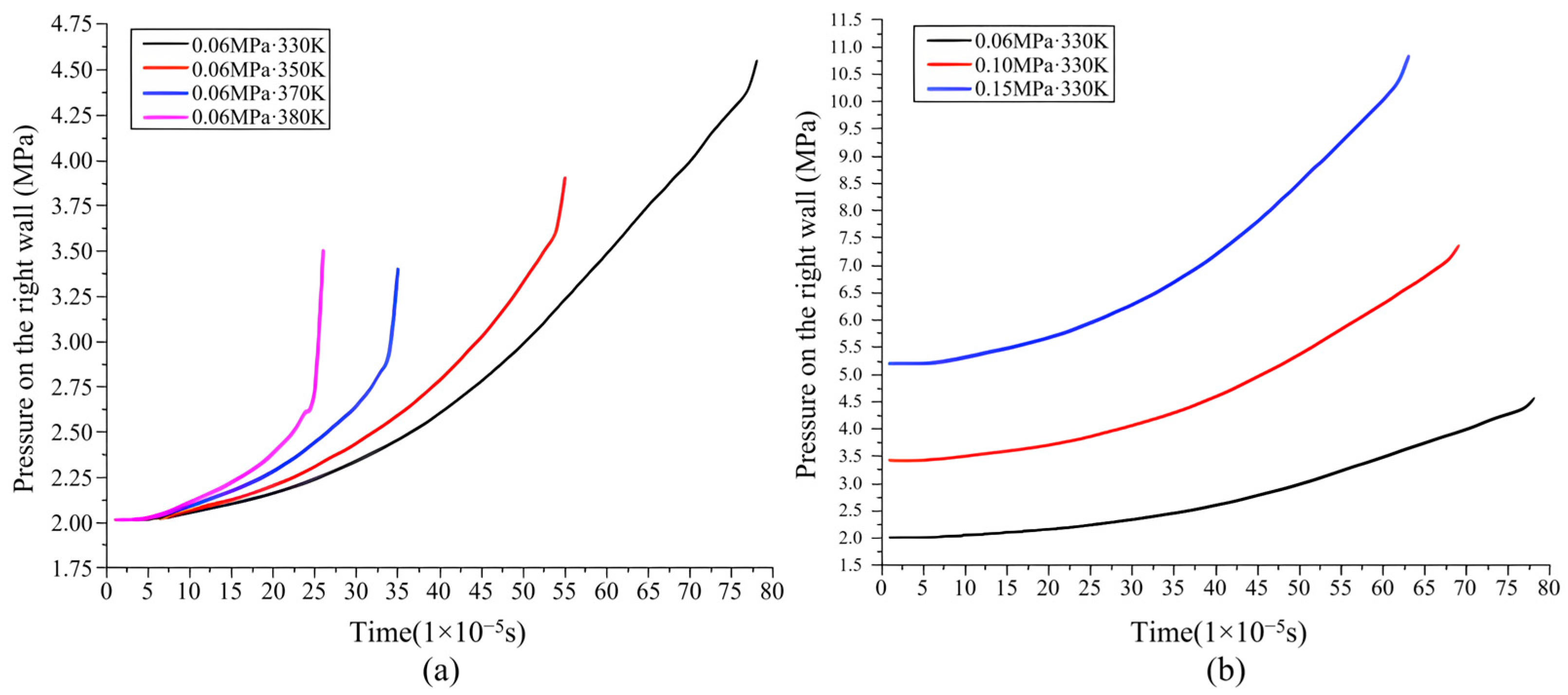
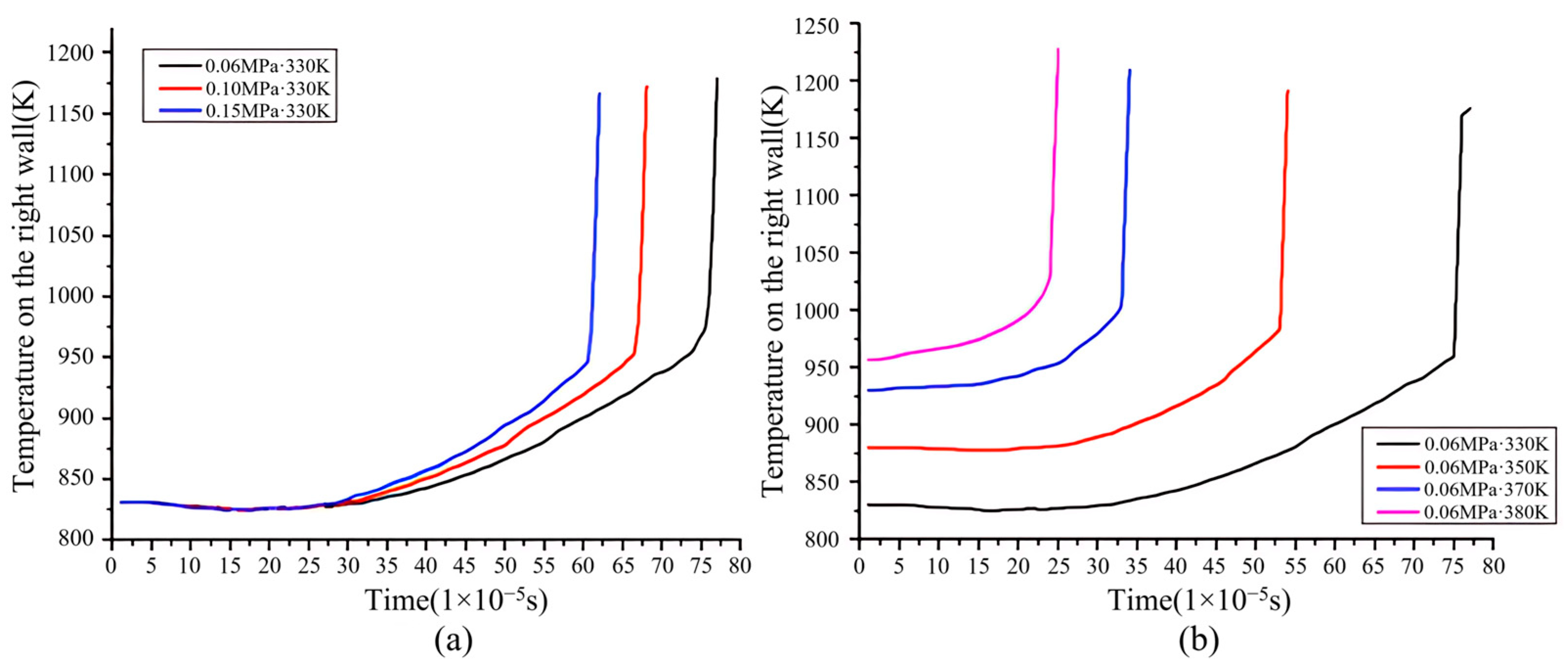
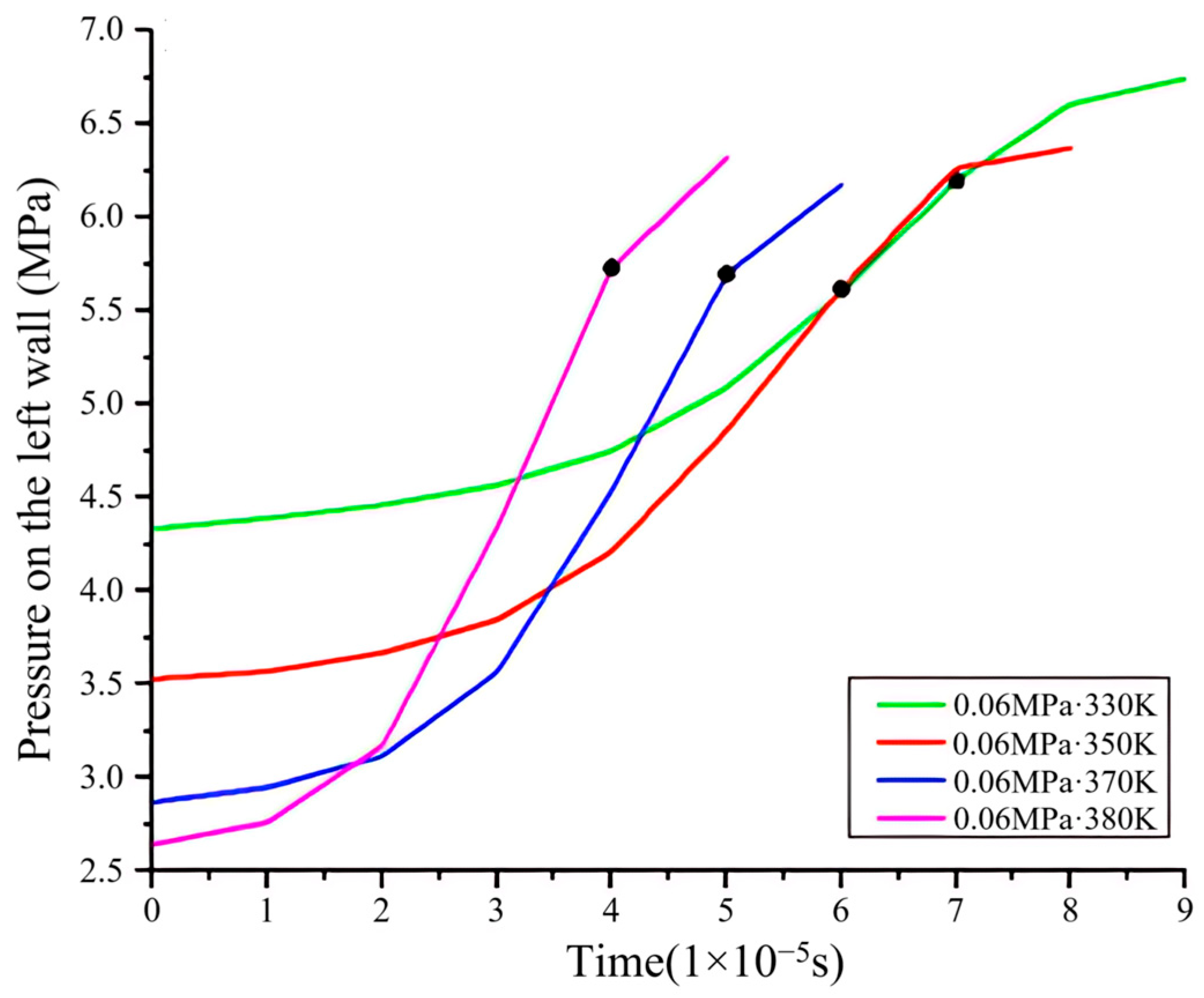
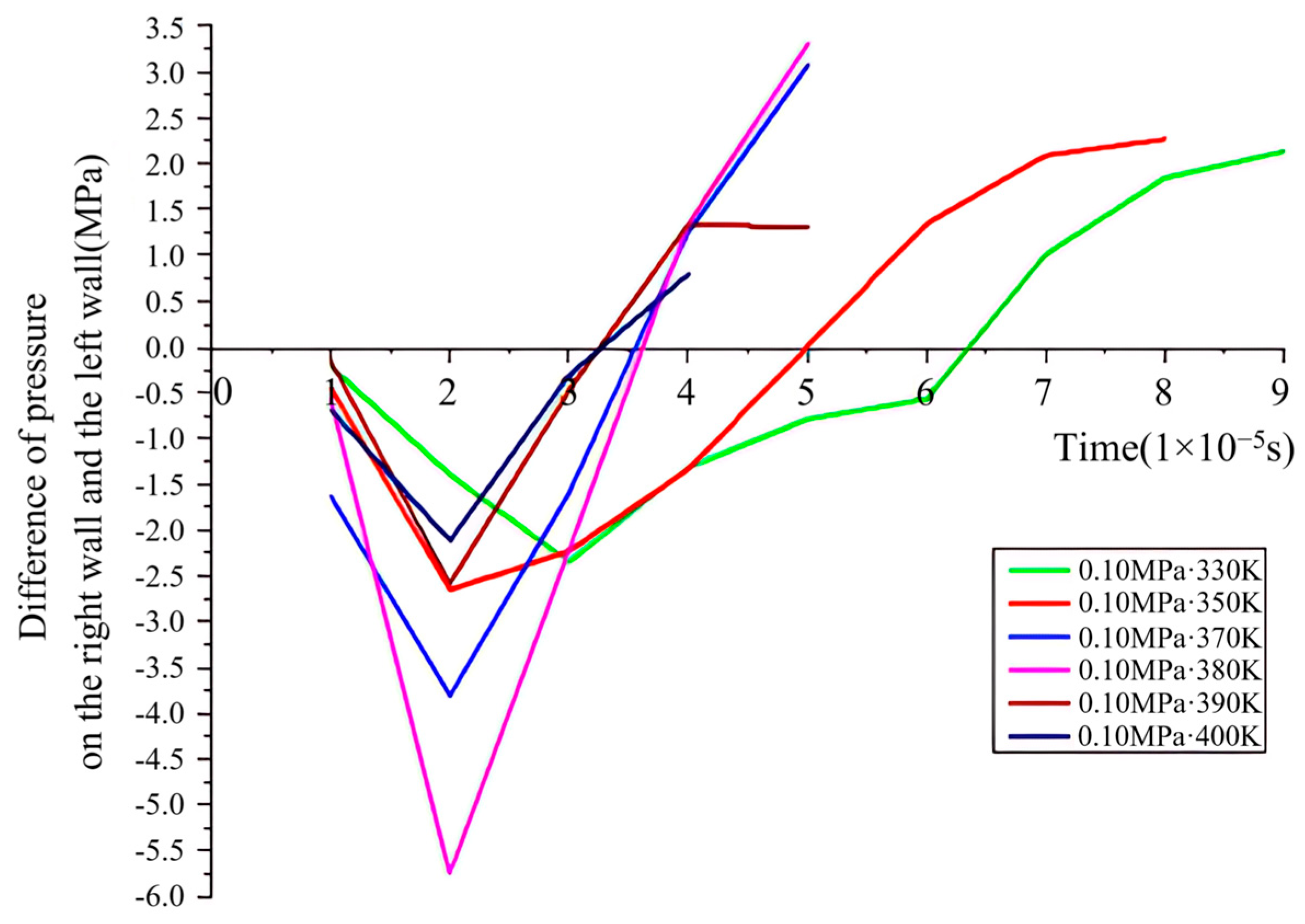
3.4. The Effects of Pressure Waves on Temperature and Pressure on the Wall
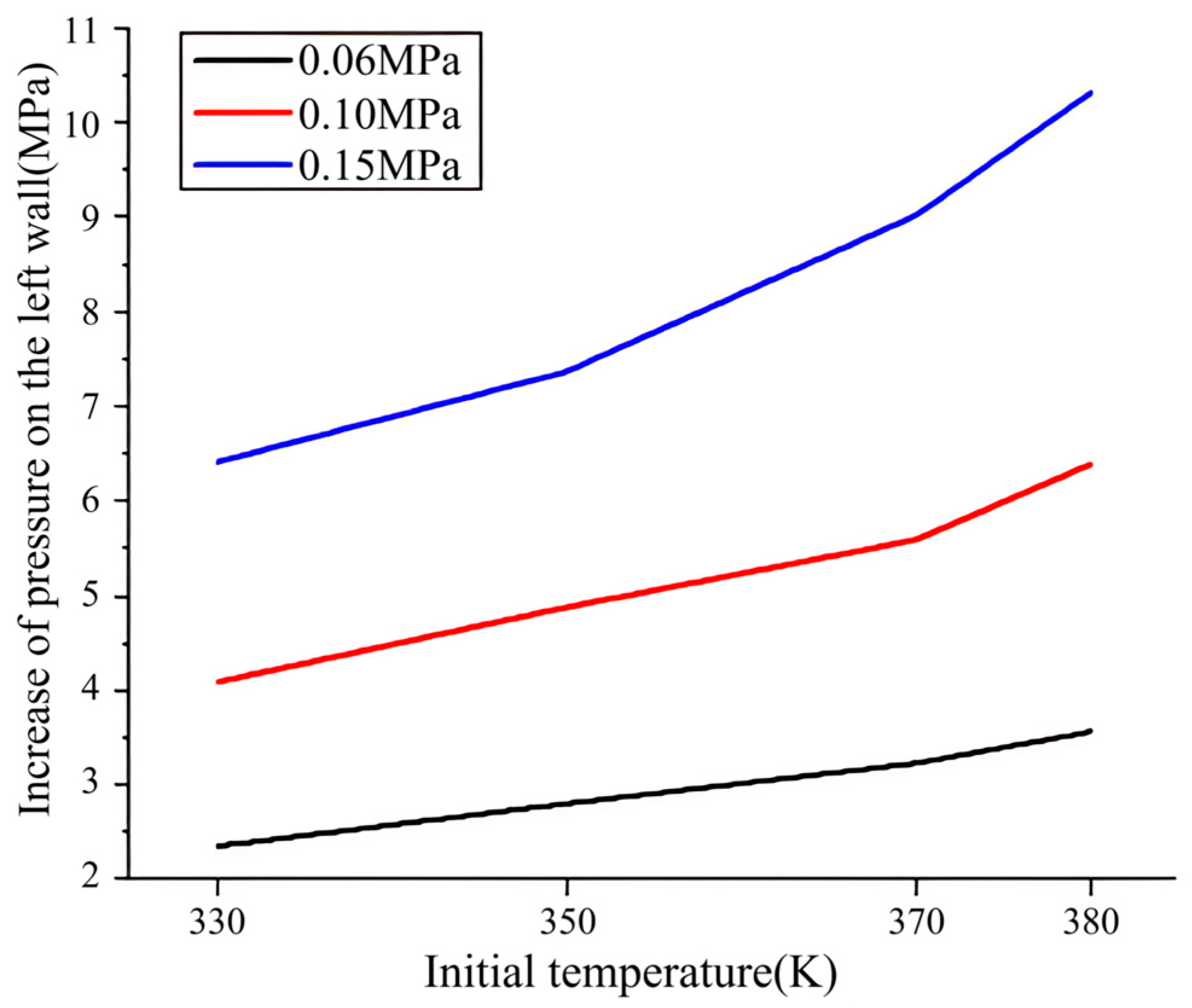
3.5. The Influence of Initial Conditions on Combustion Characteristic Parameters
3.6. Analyses of Combustion Characteristic Parameters at High Initial Temperature
3.6.1. Analyses of the Peak Pressure
3.6.2. Analyses of the Pressure Oscillation Amplitude
4. Conclusions
- Natural gas knock is still caused by the end-gas auto-ignition. The increase in the initial temperature will lead to the transformation of auto-ignition modes and combustion modes, and the increase in the unburned area is the main reason for the transformation. But the initial pressure has little effect on the size of the unburned area, auto-ignition modes, and combustion modes.
- The increase in the initial pressure and temperature will increase the pressurized amplitude of the pressure waves. But the increase in the initial temperature will decrease the highest strength of the pressure waves. The increase in the initial pressure will increase the highest strength of the pressure waves, but the time of combustion is very short, so the strength of pressure waves cannot increase high enough to make auto-ignition occur in front of the flame.
- With the increase in the initial pressure, the pressure of the end gas before auto-ignition increases which leads to the decrease in ignition temperature and the growth rate of temperature also increases, but the time of auto-ignition occurrence is slightly shortened. With the increase in the initial temperature, the pressure of the end gas before auto-ignition decreases which leads to the increase in the ignition temperature and the growth rate of temperature increases. The time of auto-ignition occurrence is significantly shortened. The main cause why auto-ignition occurs earlier is not the increase in the strength of pressure waves, but the decrease in the required increase in temperature to attain ignition temperature caused by the increase in initial temperature.
- Below the initial temperature of 380 K, the peak pressure is determined by the initial pressure on the left wall before auto-ignition and the increase in pressure on the left wall. The increase in the initial temperature can not only decrease the pressure on the left wall before auto-ignition, but also increases the pressure on the left wall to a greater extent. There is a competitive relationship between the two factors, leading to the trend of the peak pressure decreasing first and then increasing. The increase in the initial pressure can make the pressure of the end gas before auto-ignition and the increase in pressure on the left wall higher, so the peak pressure increases. The pressure oscillation amplitude is positively correlated to the increase in pressure on the left wall which is also positively correlated to initial temperature and pressure.
- Above the initial temperature of 380 K, constant volume combustion will occur as part of the initial pressure which makes the increase and decrease in pressure more uniform, so the pressure oscillation amplitude decreases. And the peak pressure sometimes appears in the constant volume combustion area. The competitive relationship between initial temperature and energy density makes constant volume combustion produce different increases in pressure at different initial conditions. Constant volume combustion will produce a high increase in pressure at the right initial conditions and the strength of pressure waves is very low, so the peak pressure will occur in the combustion area.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mueller, N.; Westerby, M.; Nieuwenhuijsen, M. Health impact assessments of shipping and port-sourced air pollution on a global scale: A scoping literature review. Environ. Res. 2023, 216, 114460. [Google Scholar]
- Deng, J.; Wang, X.; Wei, Z.; Wang, L.; Wang, C.; Chen, Z. A review of NOx and SOx emission reduction technologies for marine diesel engines and the potential evaluation of liquefied natural gas fuelled vessels. Sci. Total Environ. 2021, 766, 144319. [Google Scholar]
- International Maritime Organization (IMO). Greenhouse Gas Emissions; International Maritime Organization: London, UK, 2018. [Google Scholar]
- Ricardo, H.R. The High-Speed Internal-Combustion Engine; Blockne & Sons Ltd.: Glasgow, UK; London, UK, 1922. [Google Scholar]
- Miller, C.D.; Olsen, H.L.; Logan, W.O.; Osterstrom, G.E., Jr. Analysis of spark-ignition engine knock as seen in photographs taken at 200,000 frames per second. Natl. Advis. Comm. Aeronaut. 1946, TR857, 363–373. [Google Scholar]
- Male, T. Photographs at 500,000 frames per second of combustion and detonation in a reciprocating engine. Symp. Combust. Flame Explos. Phenom. 1948, 3, 721–726. [Google Scholar]
- Curry, S. A Three-Dimensional Study of Flame Propagation in a Spark Ignition Engine; SAE Paper: London, UK, 1963; pp. 628–650. [Google Scholar]
- Chen, R.; Zhang, P.; Pan, J.; Wei, H.; Shang, Y. Experimental study on the characteristics of auto-ignition of propane and the knock mechanism of propane. J. Tianjin Univ. 2018, 51, 1218–1222. [Google Scholar]
- Chen, L.; Zhang, R.; Wei, H.; Pan, J. Effect of flame speed on knocking characteristics for SI engine under critical knocking conditions. Fuel 2020, 282, 118846. [Google Scholar]
- Wu, Y.; Liu, L.; Liu, B.; Cao, E.; Xiong, Q. Investigation of rapid flame front controlled knock combustion and its suppression in natural gas dual-fuel marine engine. Energy 2023, 279, 128078. [Google Scholar]
- Zhang, Q.; Song, G.; Wang, X.; Li, M. Effects of injection strategy on the knocking behavior of a pilot ignited direct injection natural gas engine. Fuel 2022, 308, 121920. [Google Scholar] [CrossRef]
- Xu, H.; Ni, X.; Su, X.; Weng, C.; Yao, C. The effect of ignition intensity and in-cylinder pressure on the knock intensity and detonation formation in internal combustion engines. Appl. Therm. Eng. 2022, 200, 117690. [Google Scholar]
- Xian, K. A Study on the Knock Characteristics of Natural Gas Engine. Master’s Thesis, Shandong University, Jinan, China, 2015. [Google Scholar]
- Wu, C. A Study on the Knock of Natural Gas Engine with High Compression Ratio. Master’s Thesis, Hunan University, Changsha, China, 2017. [Google Scholar]
- Gao, D. A Study on the Flame-Shock Wave Interaction in Enclosed Space and Its Effect on Combustion Modes. Ph.D. Thesis, Tianjin University, Tianjin, China, 2017. [Google Scholar]
- Tao, K. Accelerated Flame Propagation in Constant Volume Combustion and Its Effects on End Gas Auto-Ignition. Master’s Thesis, Tianjin University, Tianjin, China, 2015. [Google Scholar]
- Ultiew, P.A.; Oppenheim, A.K. Experimental Observations of the Transition to Detonation in an Explosive Gas. Proc. R. Soc. Lond. 1966, A295, 13–28. [Google Scholar]
- Wei, H.; Qi, J.; Zhou, L.; Zhao, W.; Shu, G. Ignition characteristics of methane/n-heptane fuel blends under engine-like conditions. Energy Fuels 2018, 32, 6264–6277. [Google Scholar]
- Zou, F.; Zeng, H.; Wang, H.; Wang, X.X.; Xu, Z.X. Implementation and parameter analysis of the knock phenomenon of a marine dual-fuel engine based on a two-zone combustion model. Processes 2021, 9, 602. [Google Scholar] [CrossRef]
- Montoya, J.; Andrés AArrieta, A. Effect of the turbulence intensity on knocking tendency in a SI engine with high compression ratio using biogas and blends with natural gas, propane and hydrogen. Int. J. Hydrogen Energy 2022, 44, 18532–18544. [Google Scholar]
- Xiang, L.; Theotokatos, G.; Cui, H.; Xu, K.; Ben, H.; Ding, Y. Parametric Knocking Performance Investigation of Spark Ignition Natural Gas Engines and Dual Fuel Engines. J. Mar. Sci. Eng. 2020, 8, 459. [Google Scholar] [CrossRef]
- Zhou, W.; Xi, H.; Zhou, S.; Zhang, Z.; Shreka, M. Numerical study on knock characteristics and mechanism of a heavy duty natural gas/diesel RCCI engine. Int. J. Hydrogen Energy 2022, 47, 37072–37089. [Google Scholar]
- Guo, H.; Zhou, S.; Zou, J.; Shreka, M. A Numerical Study on the Pilot Injection Conditions of a Marine 2-Stroke Lean-Burn Dual Fuel Engine. Processes 2020, 8, 1396. [Google Scholar] [CrossRef]
- Kangbainietz, A.C. The Principle of Knock; Higher Education Press: Beijing, China, 1956; pp. 147–163. [Google Scholar]
- Lee, J.H.S.; Knystautas, R.; Yoshikawa, N. Photochemical initiation and gaseous detonations. Astronaut. Acta 1978, 5, 971–972. [Google Scholar] [CrossRef]
- Bradley, D.; Kalghatgi, G.T. Influence of auto-ignition delay time characteristics of different fuels on pressure waves and knock in reciprocating engines. Combust. Flame 2009, 156, 2307–2318. [Google Scholar] [CrossRef]
- ZelDovich, Y.B. Regime classification of an exothermic reaction with nonuniform initial conditions. Combust. Flame 1980, 39, 211–214. [Google Scholar] [CrossRef]
- Liu, H. Design and Experimental Research of Rapid Compression Machine. Master’s Thesis, Beijing University of Technology, Beijing, China, 2015. [Google Scholar]
- Zhang, H.; Shi, Z.; Lu, H.; Liu, H. A study on the ignition delay of methane based on the rapid compression machine. J. Beijing Univ. Technol. 2016, 42, 577–584. [Google Scholar]
- Zeldovich, Y.B.; Librovich, V.B.; Makhviladze, G.M.; Sivashinsky, G.I. On the development of detonation in a nonuniformly preheated gas. Astron Acta 1970, 15, 313. [Google Scholar]

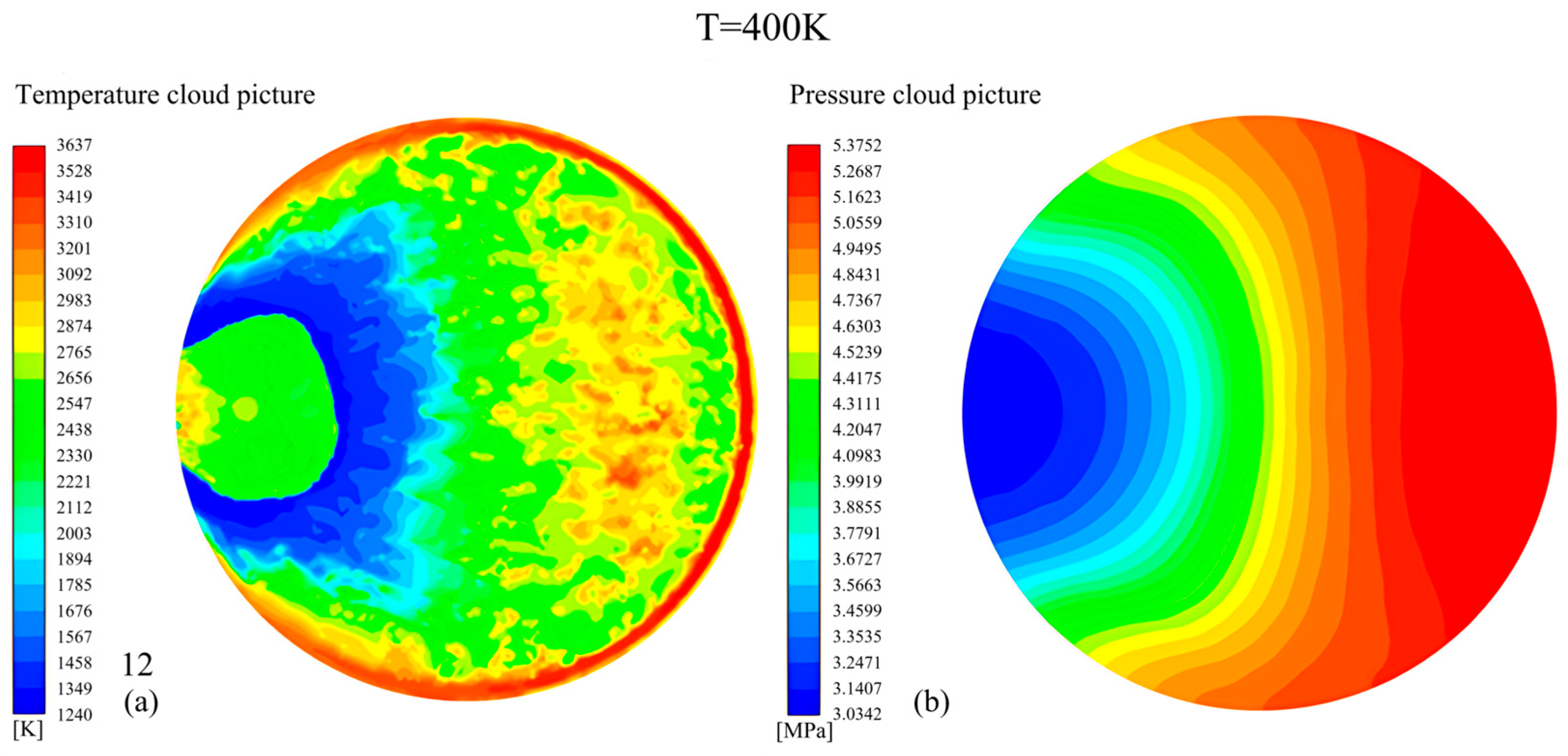

| Initial Conditions | Abnormal Combustion Modes | The Moment of Auto-Ignition Occurrence (1 × 10−5 s)/The Position of the Flame (m) | The Flame Propagation Velocity Generated by Auto-Ignition (m/s) | |
|---|---|---|---|---|
| Pressure (MPa) | Temperature (K) | |||
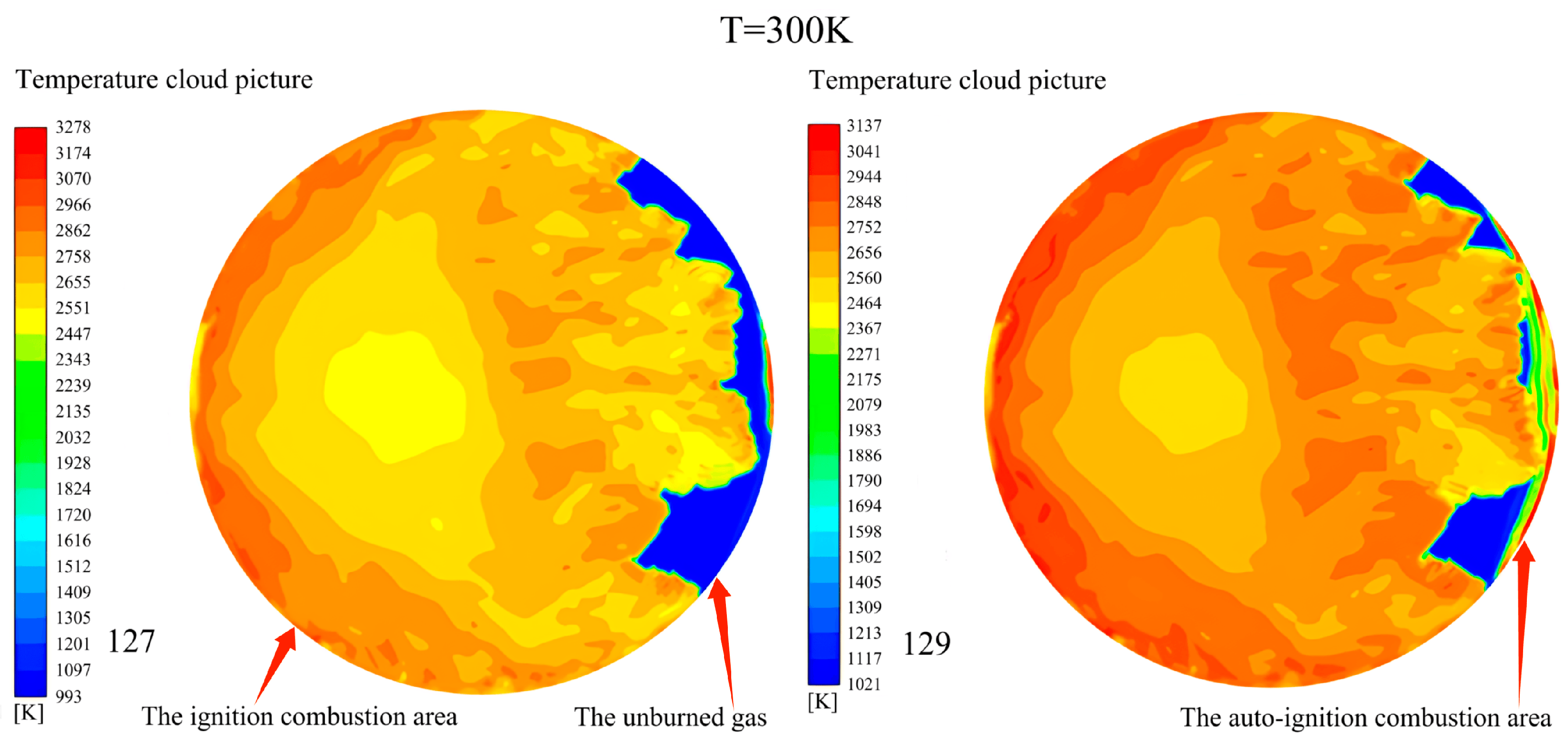
| 0.06 | 300 | Subsonic deflagration | 128/0.0240 | 50 |
| 330 | Subsonic deflagration | 79/0.0115 | 180 | |
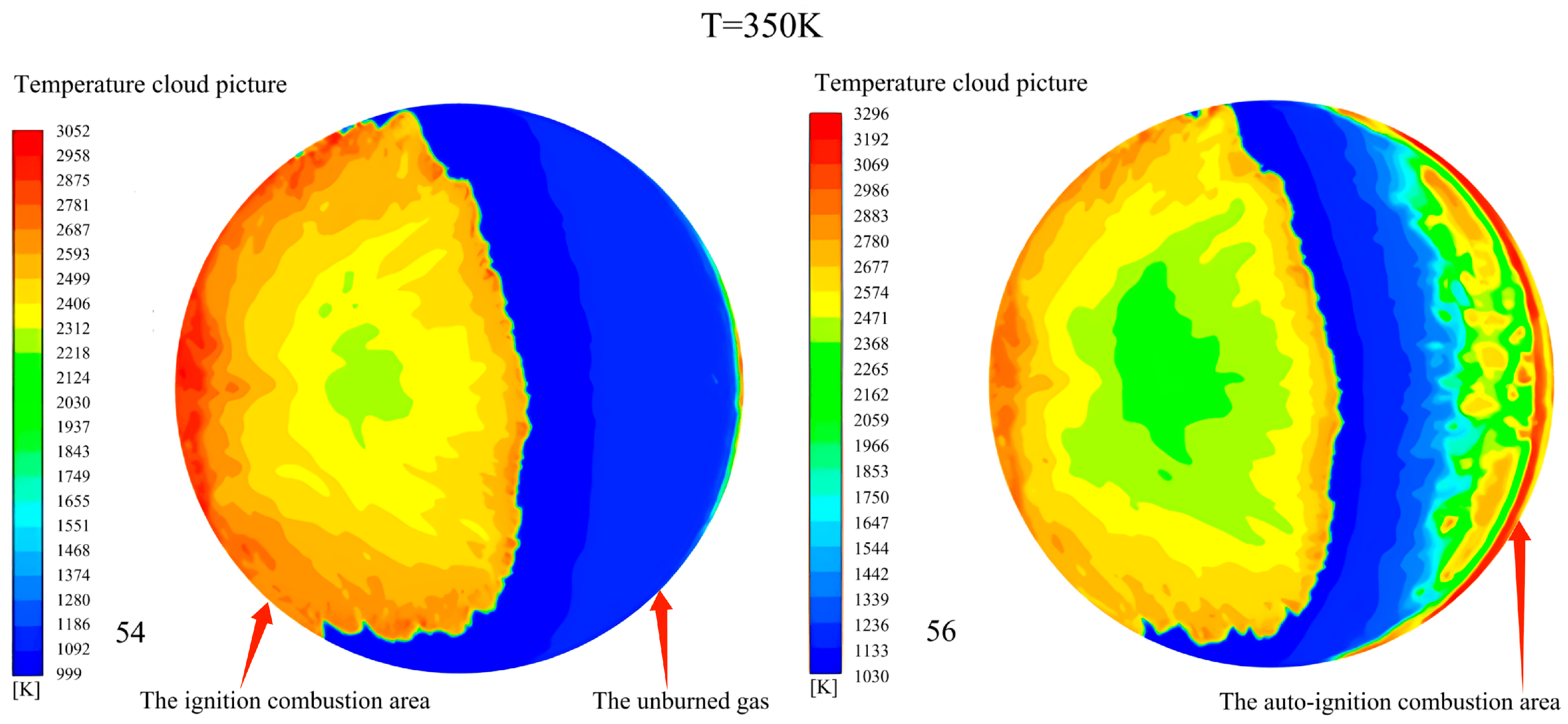
| 350 | Subsonic deflagration | 56/0.0060 | 500 | |
| 390 | Supersonic deflagration | 18/−0.0080 | 2400 | |
| 400 | Supersonic deflagration–Constant volume combustion | 13/−0.0120 | 3000 | |
| 0.10 | 300 | Subsonic deflagration | 112/0.0205 | 125 |
| 330 | Subsonic deflagration | 70/0.0120 | 200–350 | |
| 350 | Subsonic deflagration | 48/0.0050 | 500–700 | |
| 390 | Supersonic deflagration | 13/−0.0105 | 2700 | |
| 400 | Supersonic deflagration–Constant volume combustion | 10/−0.0125 | 3650 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Li, X.; Li, Z.; Xu, Y.; Zhao, G.; Yao, B. Numerical Study on the Mechanism of Stoichiometric Combustion Knock in Marine Natural Gas Low-Carbon Engines in Rapid Compression Machine Combustion Chambers. Sustainability 2025, 17, 3274. https://doi.org/10.3390/su17073274
Zhang Q, Li X, Li Z, Xu Y, Zhao G, Yao B. Numerical Study on the Mechanism of Stoichiometric Combustion Knock in Marine Natural Gas Low-Carbon Engines in Rapid Compression Machine Combustion Chambers. Sustainability. 2025; 17(7):3274. https://doi.org/10.3390/su17073274
Chicago/Turabian StyleZhang, Qiang, Xiangrong Li, Zhipeng Li, Yang Xu, Guohao Zhao, and Baofeng Yao. 2025. "Numerical Study on the Mechanism of Stoichiometric Combustion Knock in Marine Natural Gas Low-Carbon Engines in Rapid Compression Machine Combustion Chambers" Sustainability 17, no. 7: 3274. https://doi.org/10.3390/su17073274
APA StyleZhang, Q., Li, X., Li, Z., Xu, Y., Zhao, G., & Yao, B. (2025). Numerical Study on the Mechanism of Stoichiometric Combustion Knock in Marine Natural Gas Low-Carbon Engines in Rapid Compression Machine Combustion Chambers. Sustainability, 17(7), 3274. https://doi.org/10.3390/su17073274





