Advancing Sustainable Additive Manufacturing: Analyzing Parameter Influences and Machine Learning Approaches for CO2 Prediction
Abstract
1. Introduction and Motivation
- Impact of printing parameters: Analyze the influence of individual 3D printing parameters on the CO2 footprint, with a particular focus on material usage and energy consumption. The goal is to identify key parameters that serve as effective levers for reducing emissions.
- Prediction of CO2 footprint: Evaluate the effectiveness of different machine learning algorithms in predicting the CO2 footprint during fused deposition modeling (FDM), aming to determine the models with the highest predictive accuracy while requiring small training data.
2. Theoretical Foundations
2.1. Sustainability Science
2.2. AI-Driven Optimization
2.3. Industrial Engineering Framework
3. Related Works and Research Gap
3.1. Influence of Printing Parameters on Different Metrics
3.2. Prediction of Different Metrics Through AI Algorithms
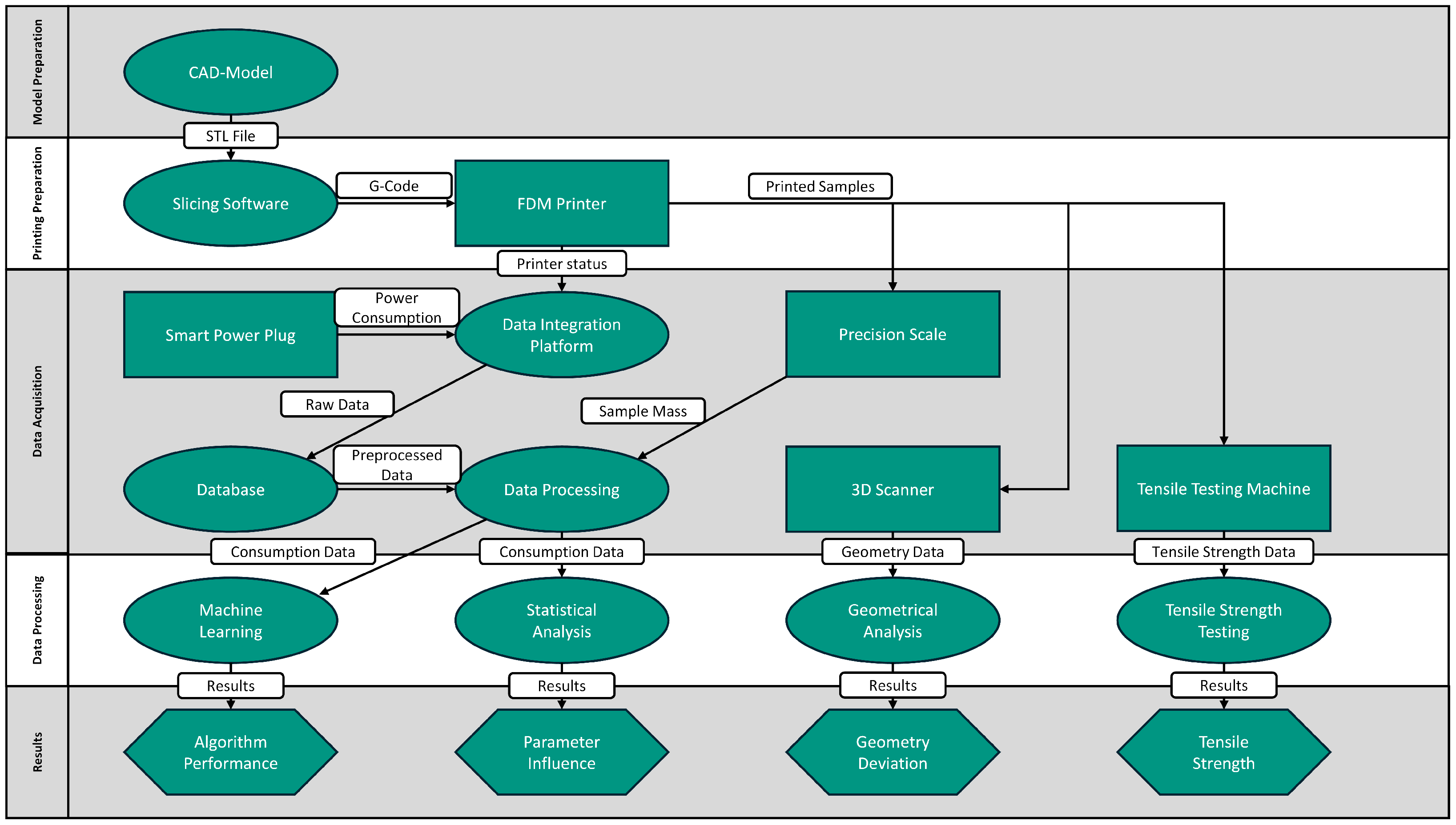
4. Materials and Methods
4.1. Experimental Setup and Design
4.2. Selection of Process Parameters and Sample Labeling
- 01: Minimum level (lowest parameter setting);
- 02: Intermediate level (median parameter setting);
- 03: Maximum level (highest parameter setting).
4.3. Materials
4.4. Quality Evaluation
4.5. Carbon Footprint Calculation
4.6. Data Analysis Procedure
4.6.1. Data Preprocessing
4.6.2. Statistical Analysis
- Analysis of Variance (ANOVA) [64]: If normal distribution is given, a one-way ANOVA is used to compare the means of the groups. The overall F-statistic is defined aswhere MSB (mean square between) is the variance between groups and MSW (mean square within) is the variance within groups.
- Kruskal–Wallis Test [65]: If the data are not normally distributed, the Kruskal–Wallis test is applied. Let be the rank sum for the i-th group and its sample size. The test statistic H is approximately chi-square distributed and is calculated aswhere is the total sample size and k is the number of groups.
4.6.3. Machine Learning Methods
Support Vector Machine (SVM)
TabTransformer
XGBoost (eXtreme Gradient Boosting)
Random Forest (RF)
Gaussian Process Regressor (GPR)
- is the mean prediction;
- is the variance (uncertainty) of the prediction;
- is the kernel matrix with entries ;
- is the vector of covariances between and the training inputs;
- is the noise variance.
4.6.4. Hyperparameter Optimization
4.6.5. Model Evaluation
- Coefficient of Determination ():which captures the proportion of variance in the target variable that is explained by the model;
- Root Mean Squared Error (RMSE):which quantifies the average magnitude of the errors;
- Mean Absolute Error (MAE):which measures the average absolute deviation from the actual values.
4.6.6. Model Interpretability
4.7. Error Analysis and Mathematical Considerations
5. Results
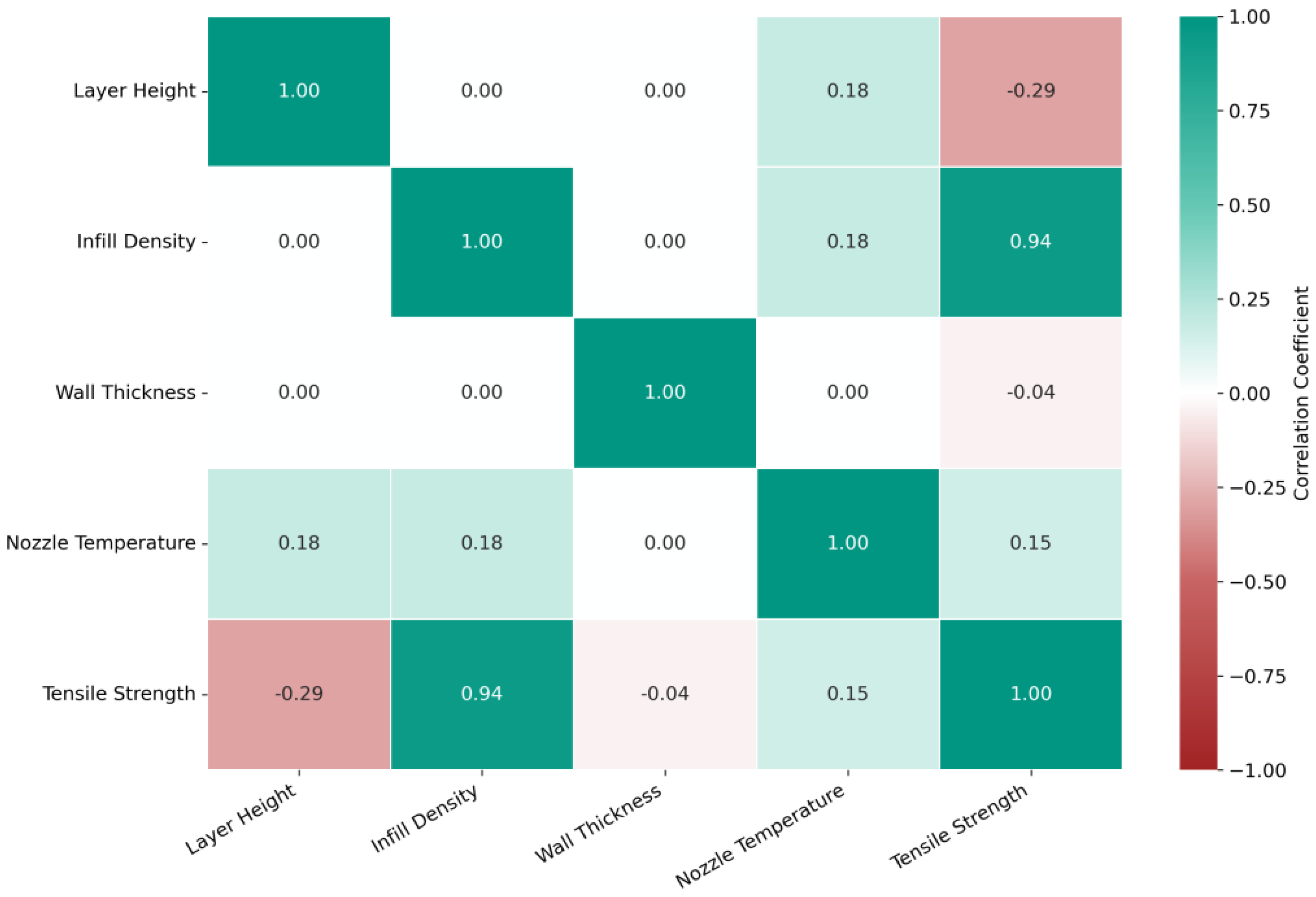
5.1. Influences of Printing Parameters
5.1.1. Statistical Analysis
5.1.2. Quality Evaluation
Visual Inspection of Printed Specimens
Mechanical Characterization via Tensile Testing
Geometrical Analysis via 3D Scanning
5.2. CO2 Prediction with ML Methods
5.2.1. Model Evaluation
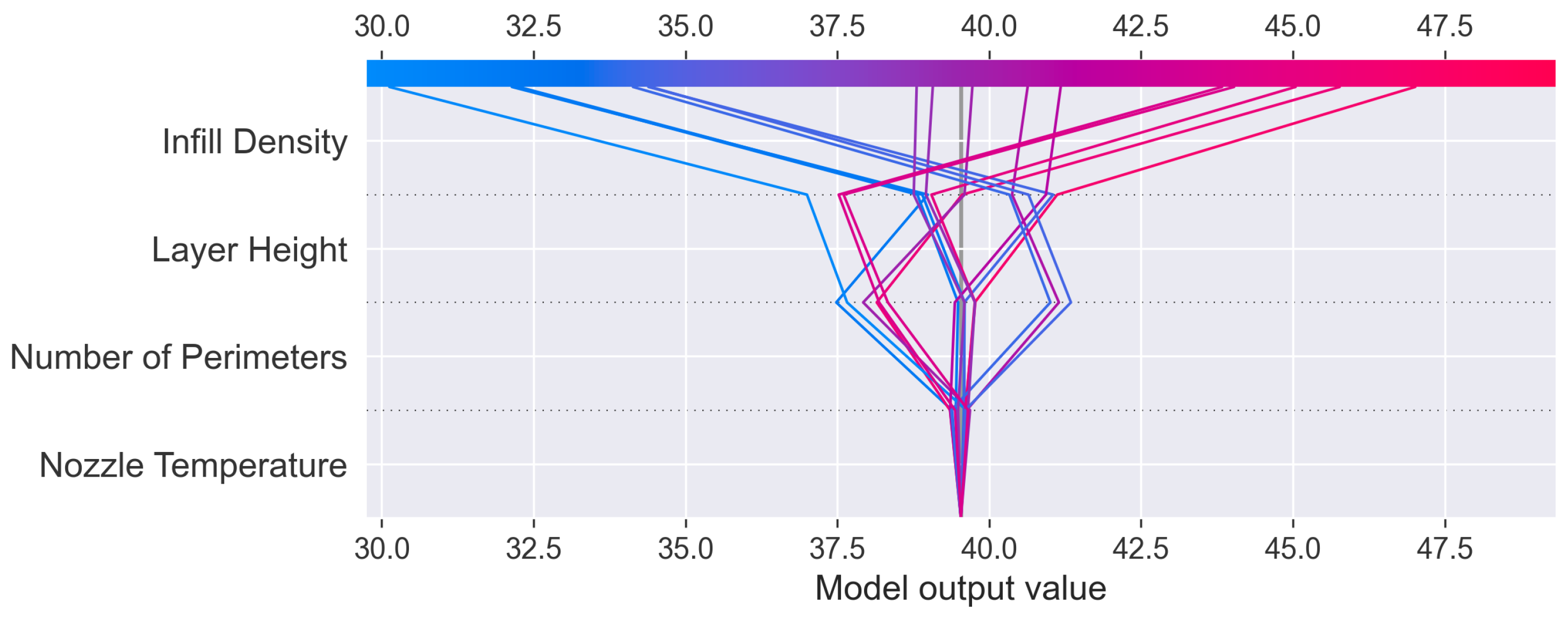
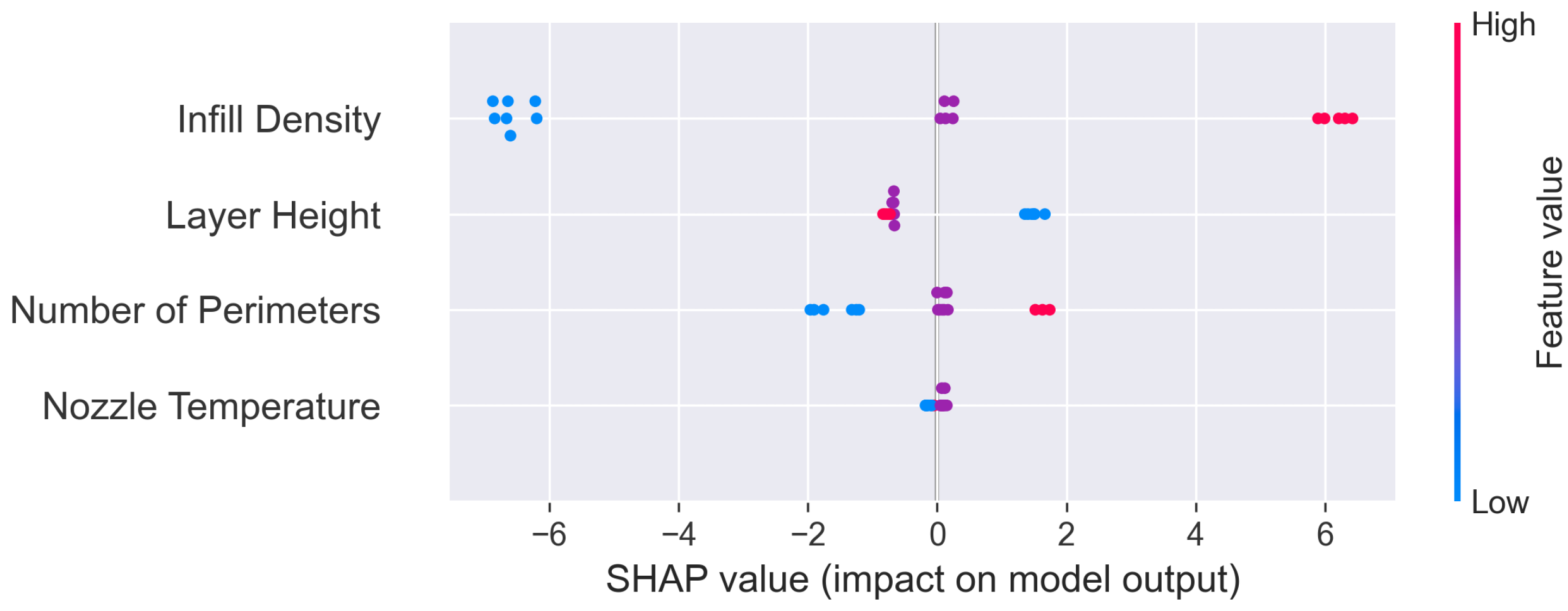
5.2.2. Model Interpretation
5.2.3. Edge Case Analyzes
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency (IEA). World Energy Outlook 2023; International Energy Agency (IEA): Paris, France, 2023. [Google Scholar]
- United Nations (UN). Paris Agreement; United Nations (UN): Bonn, Germany, 2015. [Google Scholar]
- Europäische Union (EU). Der Europäische Grüne Deal; Europäische Union (EU): Brussels, Belgium, 2019. [Google Scholar]
- European Union (EU). DIRECTIVE (EU) 2022/2464 OF THE EUROPEAN PARLIAMENT AND OF THE COUNCIL of 14 December 2022 Amending Regulation (EU) No 537/2014, Directive 2004/109/EC, Directive 2006/43/EC and Directive 2013/34/EU, as Regards Corporate Sustainability Reporting, 2022. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=CELEX%3A32022L2464 (accessed on 28 February 2025).
- Wiedmann, T.; Minx, J. A Definition of ‘Carbon Footprint’. Ecological Economics Research Trends; Nova Science Publisher: Hauppauge, NY, USA, 2008; pp. 1–11. [Google Scholar]
- World Resources Institute (WRI). Greenhouse Gas Protocol: A Corporate Accounting and Reporting Standard. World Resources Institute: Washington, DC, USA, 2004; Available online: https://ghgprotocol.org/corporate-standard (accessed on 28 February 2025).
- Ford, S.; Despeisse, M. Additive manufacturing and sustainability: An exploratory study of the advantages and challenges. J. Clean. Prod. 2016, 137, 1573–1587. [Google Scholar] [CrossRef]
- Mehrpouya, M.; Vosooghnia, A.; Dehghanghadikolaei, A.; Fotovvati, B. Chapter 2—The benefits of additive manufacturing for sustainable design and production. In Sustainable Manufacturing; Gupta, K., Salonitis, K., Eds.; Handbooks in Advanced Manufacturing; Elsevier: Amsterdam, The Netherlands, 2021; pp. 29–59. [Google Scholar] [CrossRef]
- Jung, S.; Kara, L.B.; Nie, Z.; Simpson, T.W.; Whitefoot, K.S. Is Additive Manufacturing an Environmentally and Economically Preferred Alternative for Mass Production? Environ. Sci. Technol. 2023, 57, 6373–6386. [Google Scholar] [CrossRef] [PubMed]
- Gebler, M.; Uiterkamp, A.J.S.; Visser, C. A global sustainability perspective on 3D printing technologies. Energy Policy 2014, 74, 158–167. [Google Scholar] [CrossRef]
- Qi, X.; Chen, G.; Li, Y.; Cheng, X.; Li, C. Applying Neural-Network-Based Machine Learning to Additive Manufacturing: Current Applications, Challenges, and Future Perspectives. Engineering 2019, 5, 721–729. [Google Scholar] [CrossRef]
- Ahmad, N.N.; Wong, Y.H.; Ghazali, N.N.N. A systematic review of fused deposition modeling process parameters. Soft Sci. 2022, 2, 11. [Google Scholar] [CrossRef]
- Enemuoh, E.U.; Duginski, S.; Feyen, C.; Menta, V.G. Effect of Process Parameters on Energy Consumption, Physical, and Mechanical Properties of Fused Deposition Modeling. Polymers 2021, 13, 2406. [Google Scholar] [CrossRef] [PubMed]
- Yu, S.; Liu, H.; Zhao, G.; Zhang, H.; Hou, F.; Xu, K. A code-based method for carbon emission prediction of 3D printing: A case study on the fused deposition modeling (FDM) 3D printing and comparison with conventional approach. J. Clean. Prod. 2024, 484, 144341. [Google Scholar] [CrossRef]
- Sood, A.; Ohdar, R.; Mahapatra, S. Parametric appraisal of fused deposition modelling process using the grey Taguchi method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2010, 224, 135–145. [Google Scholar] [CrossRef]
- Chia, H.Y.; Wu, J.; Yan, W. Process parameter optimization of metal additive manufacturing: A review and outlook. J. Mater. Inform. 2022, 2, 16. [Google Scholar] [CrossRef]
- Sing, S.L.; Kuo, C.N.; Shih, C.T.; Ho, C.C.; Chua, C.K. Perspectives of using machine learning in laser powder bed fusion for metal additive manufacturing. Virtual Phys. Prototyp. 2021, 16, 372–386. [Google Scholar] [CrossRef]
- Nikooharf, M.H.; Shirinbayan, M.; Arabkoohi, M.; Bahlouli, N.; Fitoussi, J.; Benfriha, K. Machine learning in polymer additive manufacturing: A review. Int. J. Mater. Form. 2024, 17, 52. [Google Scholar] [CrossRef]
- Zhang, X.; Li, J.; Wang, Y.; Liu, Y.; Zhang, H. Research on the formation mechanism of surface defects in 5182 aluminum alloy strip during hot rolling. Int. J. Miner. Metall. Mater. 2024, 31, 1–12. [Google Scholar] [CrossRef]
- Kumar, S.; Gopi, T.; Harikeerthana, N.; Gupta, M.K.; Gaur, V.; Krolczyk, G.M.; Wu, C. Machine learning techniques in additive manufacturing: A state of the art review on design, processes and production control. J. Intell. Manuf. 2023, 34, 21–55. [Google Scholar] [CrossRef]
- Wohlers, T.; Campbell, I.; Diegel, O.; Huff, J.; Kowen, R. Wohlers Report 2021: 3D Printing and Additive Manufacturing: State of the Industry, 26th ed.; Wohlers Associates: Fort Collins, CO, USA, 2021. [Google Scholar]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Additive Manufacturing Technologies; Springer International Publishing: Berlin/Heidelberg, Germany, 2021. [Google Scholar] [CrossRef]
- Elkington, J. Cannibals with Forks: The Triple Bottom Line of 21st Century Business; Capstone: Oxford, UK, 1997. [Google Scholar]
- Kates, R.W.; Clark, W.C.; Corell, R.; Hall, J.M.; Jaeger, C.C.; Lowe, I.; McCarthy, J.J.; Schellnhuber, H.J.; Bolin, B.; Dickson, N.M.; et al. Sustainability science. Science 2001, 292, 641–642. [Google Scholar] [CrossRef] [PubMed]
- Guinée, J.B.; Gorrée, M.; Heijungs, R.; Huppes, G.; Kleijn, R.; de Koning, A.; van Oers, L.; Wegener Sleeswijk, A.; Suh, S.; Udo de Haes, H.A.; et al. Life Cycle Assessment: An Operational Guide to the ISO Standards; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2002. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems; University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Greif, L.; Kimmig, A.; El Bobbou, S.; Jurisch, P.; Ovtcharova, J. Strategic view on the current role of AI in advancing environmental sustainability: A SWOT analysis. Discov. Artif. Intell. 2024, 4, 45. [Google Scholar] [CrossRef]
- Greif, L.; Röckel, F.; Kimmig, A.; Ovtcharova, J. A systematic review of current AI techniques used in the context of the SDGs. Int. J. Environ. Res. 2025, 19, 1. [Google Scholar] [CrossRef]
- Womack, J.P.; Jones, D.T. Lean Thinking: Banish Waste and Create Wealth in Your Corporation; Simon and Schuster: New York, NY, USA, 1996. [Google Scholar]
- Gibson, I.; Rosen, D.W.; Stucker, B. Additive Manufacturing Technologies: Rapid Prototyping to Direct Digital Manufacturing; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Rother, M.; Shook, J. Learning to See: Value-Stream Mapping to Add Value and Eliminate MUDA; Lean Enterprise Institute: Cambridge, MA, USA, 2009. [Google Scholar]
- Peng, T. Analysis of Energy Utilization in 3D Printing Processes. Procedia CIRP 2016, 40, 62–67. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, Q.; Zhang, Y.; Li, T.; Zhang, H.C. Sustainability of 3D Printing: A Critical Review and Recommendations. In Proceedings of the Volume 2: Materials; Biomanufacturing; Properties, Applications and Systems; Sustainable Manufacturing. American Society of Mechanical Engineers: New York, NY, USA, 2016; p. V002T05A004. [Google Scholar] [CrossRef]
- Hernandez, M.E.; Albajez, J.A.; Lamban, M.P.; Royo, J.; Santolaria, J.; Ng Corrales, L.C. Fused deposition modelling process environmental performance through the carbon footprint evaluation. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1193, 012127. [Google Scholar] [CrossRef]
- Peng, T.; Kellens, K.; Tang, R.; Chen, C.; Chen, G. Sustainability of additive manufacturing: An overview on its energy demand and environmental impact. Addit. Manuf. 2018, 21, 694–704. [Google Scholar] [CrossRef]
- Manford, D.; Budinoff, H.D. Predicting filament material extrusion energy consumption: A comparative study. Prog. Addit. Manuf. 2024, 10, 2653–2662. [Google Scholar] [CrossRef]
- Nikzad, M.H.; Heidari-Rarani, M.; Rasti, R. A novel systematically optimized tabular neural network (TabNet) algorithm for predicting the tensile modulus of additively manufactured PLA parts. Mater. Today Commun. 2024, 41, 110442. [Google Scholar] [CrossRef]
- Nikzad, M.H.; Heidari-Rarani, M.; Rasti, R.; Sareh, P. Machine learning-driven prediction of tensile strength in 3D-printed PLA parts. Expert Syst. Appl. 2025, 264, 125836. [Google Scholar] [CrossRef]
- Jayasudha, M.; Elangovan, M.; Mahdal, M.; Priyadarshini, J. Accurate Estimation of Tensile Strength of 3D Printed Parts Using Machine Learning Algorithms. Processes 2022, 10, 1158. [Google Scholar] [CrossRef]
- Afonso, J.A.; Alves, J.L.; Caldas, G.; Gouveia, B.P.; Santana, L.; Belinha, J. Influence of 3D printing process parameters on the mechanical properties and mass of PLA parts and predictive models. Rapid Prototyp. J. 2021, 27, 487–495. [Google Scholar] [CrossRef]
- Winter, S.; Osterod, J.O.; Schleich, B. Enabling Product Carbon Footprint Management in the Material Extrusion Process. Procedia CIRP 2024, 122, 31–36. [Google Scholar] [CrossRef]
- Yap, Y.F.; Yeong, W.Y. Machine Learning-Guided Three-Dimensional Printing of Tissue Engineering Scaffolds. Tissue Eng. Part A 2021, 27, 1168–1177. [Google Scholar] [CrossRef]
- Tatar, A.B. Predicting Three-Dimensional (3D) Printing Product Quality with Machine Learning-Based Regression Methods. Fırat Üniversitesi Deneysel ve Hesaplamalı Mühendislik Dergisi 2025, 4, 206–225. [Google Scholar] [CrossRef]
- Rooney, K.; Dong, Y.; Basak, A.K.; Pramanik, A. Prediction of Mechanical Properties of 3D Printed Particle-Reinforced Resin Composites. J. Compos. Sci. 2024, 8, 416. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Experimental investigation and empirical modelling of FDM process for compressive strength improvement. J. Adv. Res. 2012, 3, 81–90. [Google Scholar] [CrossRef]
- Murphy, C.; Meisel, N.; Simpson, T.W.; McComb, C. Predicting Part Mass, Required Support Material, and Build Time via Autoencoded Voxel Patterns. Preprints 2018. Available online: https://www.researchgate.net/publication/326159629_Predicting_Part_Mass_Required_Support_Material_and_Build_Time_via_Autoencoded_Voxel_Patterns (accessed on 28 February 2025).
- El youbi El idrissi, M.A.; Laaouina, L.; Jeghal, A.; Tairi, H.; Zaki, M. Energy consumption prediction for fused deposition modelling 3D printing using machine learning. Appl. Syst. Innov. 2022, 5, 86. [Google Scholar] [CrossRef]
- Junwen, C.; Gang, Z.; Hua, Z. Energy Consumption Prediction of Fused Deposition 3D Printer Based on Improved Regularized BP Neural Network. IOP Conf. Ser. Earth Environ. Sci. 2019, 295, 032001. [Google Scholar] [CrossRef]
- Kiran, R. The Importance of Data Quality and Quantity in Training Neural Networks. Artif. Intell. Rev. 2021, 55, 167–182. [Google Scholar] [CrossRef]
- Hasebe, T.; Katayama, E.; Yoshiteru, K. Deep CAD Shape Recognition for Carbon Footprint Estimation at the Design Stage. Procedia CIRP 2024, 122, 545–550. [Google Scholar] [CrossRef]
- ISO/ASTM 52900:2021; Additive Fertigung—Grundlagen—Terminologie. Deutsches Institut für Normung e.V.: Berlin, Germany, 2022.
- Khan, S.; Joshi, K.; Deshmukh, S. A comprehensive review on effect of printing parameters on mechanical properties of FDM printed parts. Mater. Today Proc. 2022, 50, 2119–2127. [Google Scholar] [CrossRef]
- Solomon, I.J.; Sevvel, P.; Gunasekaran, J. A review on the various processing parameters in FDM. Mater. Today Proc. 2021, 37, 509–514. [Google Scholar] [CrossRef]
- Mangla, S.K.; Kazancoglu, Y.; Sezer, M.D.; Top, N.; Sahin, I. Optimizing fused deposition modelling parameters based on the design for additive manufacturing to enhance product sustainability. Comput. Ind. 2022, 145, 103833. [Google Scholar] [CrossRef]
- Gao, G.; Xu, F.; Xu, J.; Tang, G.; Liu, Z. A Survey of the Influence of Process Parameters on Mechanical Properties of Fused Deposition Modeling Parts. Micromachines 2022, 13, 553. [Google Scholar] [CrossRef]
- Camposeco-Negrete, C. Optimization of printing parameters in fused deposition modeling for improving part quality and process sustainability. Int. J. Adv. Manuf. Technol. 2020, 108, 2131–2147. [Google Scholar] [CrossRef]
- IPCC. 2006 IPCC Guidelines for National Greenhouse Gas Inventories; Institute for Global Environmental Strategies (IGES): Kanagawa, Japan, 2006. [Google Scholar]
- Yang, H.; Ding, H. Carbon Emission Model Analysis of FDM Molding Process. IOSR J. Mech. Civ. Eng. (IOSR-JMCE) 2023, 20, 30–38. [Google Scholar] [CrossRef]
- Icha, P.; Lauf, T. Entwicklung der Spezifischen Treibhausgas-Emissionen des Deutschen Strommix in den Jahren 1990–2023; Umweltbundesamt: Dessau-Roßlau, Germany, 2024. [Google Scholar]
- Ecoinvent. Ecoinvent Database v3.9. 2024. Available online: https://www.ecoinvent.org (accessed on 28 February 2025).
- Razali, N.M.; Wah, Y.B. Power comparisons of shapiro-wilk, kolmogorov-smirnov, lilliefors and anderson-darling tests. J. Stat. Model. Anal. 2011, 2, 21–33. [Google Scholar]
- St, L.; Wold, S. Analysis of variance (ANOVA). Chemom. Intell. Lab. Syst. 1989, 6, 259–272. [Google Scholar]
- McKight, P.E.; Najab, J. Kruskal-wallis test. In The Corsini Encyclopedia of Psychology; Wiley: Hoboken, NJ, USA, 2010; p. 1. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Huang, X.; Khetan, A.; Cvitkovic, M.; Karnin, Z. Tabtransformer: Tabular data modeling using contextual embeddings. arXiv 2020, arXiv:2012.06678. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Segal, M.R. Machine Learning Benchmarks and Random Forest Regression; Technical Report; Center for Bioinformatics and Molecular Biostatistics, University of California: San Francisco, CA, USA, 2004. [Google Scholar]
- Williams, C.K.I.; Rasmussen, C.E. Gaussian Processes for Regression. In Advances in Neural Information Processing Systems 8; Touretzky, D.S., Mozer, M.C., Hasselmo, M.E., Eds.; MIT Press: Cambridge, MA, USA, 1996; pp. 514–520. Available online: https://papers.nips.cc/paper/1995/file/7cce53cf90577442771720a370c3c723-Paper.pdf (accessed on 4 April 2025).
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A next-generation hyperparameter optimization framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2623–2631. [Google Scholar]
- Wong, T.T.; Yeh, P.Y. Reliable accuracy estimates from k-fold cross validation. IEEE Trans. Knowl. Data Eng. 2019, 32, 1586–1594. [Google Scholar] [CrossRef]
- Parsa, A.B.; Movahedi, A.; Taghipour, H.; Derrible, S.; Mohammadian, A.K. Toward safer highways, application of XGBoost and SHAP for real-time accident detection and feature analysis. Accid. Anal. Prev. 2020, 136, 105405. [Google Scholar] [CrossRef]



| Experimental Settings | Analysis | Investigated Influences on… (Yes/No; If Yes: What Is the Influence?) | Source | |||||
|---|---|---|---|---|---|---|---|---|
| Material | Sample Size | Variable Printing Parameters | Parameter Links | CO2 Footprint | Energy Consumption | Material Consumption | Quality Regarding… | |
| PLA | 27 | Extrusion temperature; Layer height; Shell thickness; | yes | – | – | – | Tensile strength: pos. correlation with temperature; | [41] |
| PLA | 329 | Infill density; Raster orientation; Nozzle temperature; | yes | – | – | – | Tensile strength: pos. correlation with infill density and temperature neg. with raster orientation | [40] |
| PLA | 128 | Infill density; Raster orientation; Nozzle temperature; | yes | – | – | – | Elastic modulus: pos. correlation with infill density and temperature, neg. with raster orientation Infill density greatest effect; | [39] |
| PLA | – | Layer thickness; Print speed; Infill density; Build orientation; | yes | – | Greater layer thickness reduces energy consumption | – | Surface roughness: Greater layer thickness reduces surface quality; Mechanical strength | [12] |
| PLA | 27 | Infill density; Infill pattern; Layer thickness; Print speed; Shell thickness; | yes | – | Infill density, print speed, and layer thickness are significant for energy consumption | Higher infill densities lead to higher material consumption | Dimensional accuracy; Hardness | [13] |
| – | – | Hot-bed temperature; Nozzle temperature; Layer thickness; Printing speed; | – | Higher CO2: Higher temperature; Lower CO2: Higher layer thickness and speed; Nozzle temperature insignificant | – | – | Manufacturing quality: Only qualitative investigations | [14] |
| – | 27 | Layer thickness; Orientation; Raster angle; Raster width; Air gap; | yes | – | – | – | Dimensional accuracy: For length: layer thickness, orientation and raster angle are significant; For width and thickness: Layer thickness is most significant | [15] |
| Experimental Settings | Prediction with AI | Performance of AI Algorithm | Additional Analysis | Source | |||||
|---|---|---|---|---|---|---|---|---|---|
| Input Parameters | Sample Size | AI Algorithm | Prediction of… | Prediction Error | RSME | EVS | FIA/SHAP | ||
| – | 120 | 2 ML approaches; based on random forest | Part quality | – | – | – | – | – | [44] |
| Infill density, Nozzle temperature, Nozzle diameter, Layer thickness, Raster orientation, Printing speed | 128 | TabNet | Elastic modulus | 0.9685 | 10% | 0.193 | – | – | [39] |
| Printing direction | 120 | Various ML algorithms; KNN as most efficient | Elastic modulus | 0.95 | – | 5.2 | – | – | [46] |
| – | 32 | ANN | Compressive strength | 0.9977 | 1.2% | – | – | – | [47] |
| Infill density, Nozzle temperature, Nozzle diameter, Layer thickness, Raster orientation, Printing speed | 329 | 19 ML algorithms; CatBoost as most efficient | Tensile strength | 0.9446 | 10% | 1.803 | – | – | [40] |
| Extrusion temperature, Layer height, Shell thickness | 27 | 5 ML algorithms; XGBoost as most efficient | Tensile strength | 0.97 | – | – | – | – | [41] |
| Layer height, Wall thickness, Infill density, Infill pattern, Nozzle temperature, Bed temperature, Print speed, Fan speed | 120 | Various ML algorithms; GPR as most efficient | Roughness, Tensile strength, Elongation | 1 0.9 0.98 | – | 1.354 2.833 0.104 | – | – | [45] |
| Layer thickness | 27 | ANN | Dimensional accuracy | – | 0.12% | – | – | – | [15] |
| Experimental Settings | Prediction with AI | Performance of AI Algorithm | Additional Analysis | Source | |||||
|---|---|---|---|---|---|---|---|---|---|
| Input Parameters | Sample Size | AI-Algorithm | Prediction of… | Prediction Error | RSME | EVS | FIA /SHAP | ||
| Orientation | 7104 | DL algorithm | Part mass, Support material mass, Build time | 0.468 0.301 0.225 | - | - | - | – | [48] |
| – | – | DL algorithm with PSO | Energy consumption | – | – | – | – | – | [11] |
| Orientation | 184 | 12 ML algorithms; GPR as most efficient | Energy consumption | >0.99 | – | <5.8 | 0.99 | – | [49] |
| Layer thickness, Printing speed, Head temperature, Bed temperature | 27 | Improved regularized BP NNs; Standard BP NN | Energy consumption | – – | 1–2%; 10–16% | – – | – – | – | [50] |
| Level | Layer Height (L) | Infill Density (I) | Perimeters (P) | Nozzle Temp. (N) |
|---|---|---|---|---|
| 01 | 0.16 mm | 15% | 2 | 190 °C |
| 02 | 0.22 mm | 57.5% | 4 | 205 °C |
| 03 | 0.28 mm | 100% | 6 | 220 °C |
| Device | Manufacturer | Model Name | Error |
|---|---|---|---|
| Smart Plug | TP-Link | Tapo P110 | ±0.05 W |
| Precision Scale | Fousenuk | Fousenuk Precision Scale | ±0.01 g |
| Tensile Strength Testing Machine | Roell + Korthaus | Unknown | 1% |
| Parameter | Sum of Squares | df | F-Value | p-Value | Partial |
|---|---|---|---|---|---|
| Layer Height | 0.0004 | 2 | 314.24 | 0.250 | |
| Fill Density | 0.0006 | 2 | 511.88 | 0.352 | |
| Wall Count | 0.0001 | 2 | 75.36 | 0.074 | |
| Nozzle Temperature | 0.0000 | 2 | 3.07 | 0.056 | 0.003 |
| Parameter | H-Statistic | p-Value |
|---|---|---|
| Layer Height | 1.93 | 0.382 |
| Fill Density | 69.05 | |
| Wall Count | 3.57 | 0.168 |
| Nozzle Temperature | 0.34 | 0.843 |
| Parameter | H-Statistic | p-Value |
|---|---|---|
| Layer Height | 3.56 | 0.169 |
| Fill Density | 69.13 | |
| Wall Count | 4.60 | 0.100 |
| Nozzle Temperature | 0.13 | 0.937 |
| Test No. | Experiment No. | L | I | P | N | Tensile Strength [MPa] |
|---|---|---|---|---|---|---|
| 1 | 1 | 01 | 01 | 01 | 01 | 16.67 |
| 2 | 14 | 01 | 02 | 02 | 02 | 19.03 |
| 3 | 27 | 01 | 03 | 03 | 03 | 25.57 |
| 4 | 33 | 02 | 01 | 02 | 03 | 15.18 |
| 5 | 43 | 02 | 02 | 03 | 01 | 18.89 |
| 6 | 47 | 02 | 03 | 01 | 02 | 24.25 |
| 7 | 62 | 03 | 01 | 03 | 02 | 13.18 |
| 8 | 66 | 03 | 02 | 01 | 03 | 17.88 |
| 9 | 76 | 03 | 03 | 02 | 02 | 21.87 |
| Test No. | Exp. No. | L | I | P | N | Volume [mm3] | Deviation [%] |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 01 | 01 | 01 | 01 | 7781.722 | −0.38 |
| 2 | 5 | 01 | 01 | 02 | 02 | 7762.317 | −0.63 |
| 3 | 9 | 01 | 01 | 03 | 03 | 7796.831 | −0.18 |
| 4 | 37 | 02 | 02 | 01 | 01 | 7730.939 | −1.03 |
| 5 | 41 | 02 | 02 | 02 | 02 | 7780.962 | −0.39 |
| 6 | 45 | 02 | 02 | 03 | 03 | 7743.460 | −0.87 |
| 7 | 73 | 03 | 03 | 01 | 01 | 7762.873 | −0.62 |
| 8 | 77 | 03 | 03 | 02 | 02 | 7748.044 | −0.81 |
| 9 | 80 | 03 | 03 | 03 | 02 | 7750.204 | −0.78 |
| Reference | - | - | - | - | - | 7811.247 | 0.00 |
| Model | RMSE | MAE | |
|---|---|---|---|
| SVM | 1.0295 | 0.8902 | 0.9514 |
| TabTransformer | 1.1086 | 0.8452 | 0.9606 |
| XGBoost | 0.4816 | 0.3802 | 0.9922 |
| Random Forest | 1.4333 | 1.2131 | 0.9311 |
| Gaussian Process Regressor | 1.5640 | 1.1381 | 0.9173 |
| Index | L | I | P | N | y_true | y_pred | abs_error |
|---|---|---|---|---|---|---|---|
| 1 | 01 | 01 | 01 | 01 | 31.0563 | 32.1432 | 1.0869 |
| 14 | 03 | 02 | 02 | 03 | 39.8645 | 38.8058 | 1.0587 |
| 5 | 02 | 01 | 01 | 02 | 29.6249 | 30.1260 | 0.5011 |
| 13 | 02 | 01 | 03 | 03 | 34.9165 | 34.4288 | 0.4877 |
| 15 | 02 | 03 | 01 | 01 | 43.3545 | 43.8332 | 0.4787 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hauck, S.; Greif, L.; Benner, N.; Ovtcharova, J. Advancing Sustainable Additive Manufacturing: Analyzing Parameter Influences and Machine Learning Approaches for CO2 Prediction. Sustainability 2025, 17, 3804. https://doi.org/10.3390/su17093804
Hauck S, Greif L, Benner N, Ovtcharova J. Advancing Sustainable Additive Manufacturing: Analyzing Parameter Influences and Machine Learning Approaches for CO2 Prediction. Sustainability. 2025; 17(9):3804. https://doi.org/10.3390/su17093804
Chicago/Turabian StyleHauck, Svenja, Lucas Greif, Nils Benner, and Jivka Ovtcharova. 2025. "Advancing Sustainable Additive Manufacturing: Analyzing Parameter Influences and Machine Learning Approaches for CO2 Prediction" Sustainability 17, no. 9: 3804. https://doi.org/10.3390/su17093804
APA StyleHauck, S., Greif, L., Benner, N., & Ovtcharova, J. (2025). Advancing Sustainable Additive Manufacturing: Analyzing Parameter Influences and Machine Learning Approaches for CO2 Prediction. Sustainability, 17(9), 3804. https://doi.org/10.3390/su17093804






