Estimating the Aboveground Biomass for Planted Forests Based on Stand Age and Environmental Variables

Abstract

Measuring forest aboveground biomass (AGB) at local to regional scales is critical to understanding their role in regional and global carbon cycles. The Three-North Shelterbelt Forest Program (TNSFP) is the largest ecological restoration project in the world, and has been ongoing for over 40 years. In this study, we developed models to estimate the planted forest aboveground biomass (PF_AGB) for Yulin, a typical area in the project. Surface reflectances in the study area from 1978 to 2013 were obtained from Landsat series images, and integrated forest z-scores were constructed to measure afforestation and the stand age of planted forest. Normalized difference vegetation index (NDVI) was combined with stand age to develop an initial model to estimate PF_AGB. We then developed additional models that added environment variables to our initial model, including climatic factors (average temperature, total precipitation, and total sunshine duration) and a topography factor (slope). The model which combined the total precipitation and slope greatly improved the accuracy of PF_AGB estimation compared to the initial model, indicating that the environmental variables related to water distribution indirectly affected the growth of the planted forest and the resulting AGB. Afforestation in the study area occurred mainly in the early 1980s and early 21st century, and the PF_AGB in 2003 was 2.3 times than that of 1998, since the fourth term TNSFP started in 2000. The PF_AGB in 2013 was about 3.33 times of that in 2003 because many young trees matured. The leave-one-out cross-validation (LOOCV) approach showed that our estimated PF_AGB had a significant correlation with field-measured data (correlation coefficient (r) = 0.89, p < 0.001, root mean square error (RMSE) = 6.79 t/ha). Our studies provided a method to estimate long time series PF_AGB using satellite repetitive measures, particularly for arid or semi-arid areas.

1. Introduction

Forests not only play a key role in regional ecology, but also have a crucial impact on the global carbon cycle [1]. Forests’ carbon sequestration accounts for about 80% of the world’s aboveground and 40% of its belowground carbon stocks [2]. Moreover, trees have a long life cycle, and their canopy photosynthesis makes forests the largest carbon stock in terrestrial ecosystems [3]. Forest biomass refers to the accumulation of dry matter as a result of photosynthesis, and it is one of the most basic quantitative characteristics of forest ecosystems [4]. According to the 1994 International Forest Resources Monitoring Program published by Food and Agriculture Organization (FAO), forest biomass is an important component of forest resource monitoring [5]. Therefore, accurate estimating and monitoring of forest aboveground biomass (AGB) at local to regional scales is critical for understanding the role of forest AGB in regional and global carbon cycles [6].

China has implemented a series of ecological restoration projects, including the Three-North Shelter Forest Program (TNSFP), also known as the Green Great Wall [7,8], which was initiated in 1978 and remains the world’s largest ecological restoration project. The TNSFP is scheduled to continue until 2050 and aims to improve environmental conditions and ecosystem services of three northern regions of China (Northeast China, North China, and Northwest China) [9,10]. Considering the huge financial and material resources invested in this project, it is necessary to monitor its long-term progress before the project is completed [11]. It is difficult to make comprehensive and coordinated use of resources during project construction, which leads to the gradual decline or death of protected forests in arid areas. Previous studies have indicated that the biggest challenge to the TNSFP is that protected forests have decreased in the years following project implementation [12,13]. The ecosystems within TNSFP are still fragile, and the most prominent ecological cause of the decline has been damage due to sandstorms and soil erosion. The TNSFP covers 84% of the desertified land in China and 40% of areas experiencing soil erosion [14,15,16]. The reduction of protective forests will make these problems even more serious, resulting in a sharp decrease in protection efficiency. Quantifying and monitoring how forests and AGB change in the TNSFP region is of vital importance, so that management strategies can be adjusted as the forests change, thereby strengthening the ecological restoration benefits and increasing the rate of carbon sequestration.

Field studies of biomass estimation can be broadly divided into direct and indirect methods. The direct method obtains the biomass by drying and weighing individual components of the harvested trees [17], while indirect methods either use the volume of tree components multiplied by several factors [18] or apply empirical allometric equations to estimate tree biomass from parameters such as diameter at breast height (DBH) and tree height [19]. Both direct and indirect methods can accurately predict single-tree AGB, especially the allometric equations, which provide highly accurate and efficient estimates of forest AGB for field sites. Such methods provide the essential basis for expanding field measurements to larger scales [20]. However, these traditional methods are labor-intensive and can cause ecological damage when estimating large-scale forest.

Remote sensing techniques provide a fast, efficient, and comprehensive method for monitoring land cover change, revealing dynamic changes by providing macro-scale data about surface conditions and allowing for the detection and prediction of these changes [21,22]. Long-term data collection and high temporal resolution using remote sensing data are advantageous in capturing the dynamics of forest cover across large areas. The combination of sampled forest AGB and remote sensing data makes full use of the advantages of both allometric equations and remote sensing, representing an enormous potential for estimating regional forest AGB. In this study, the objective was to estimate AGB for planted forest in one typical area of the TNSFP. To achieve this in an efficient manner, time series Landsat data was used to estimate stand age at the pixel scale, and then AGB estimation models were developed based on stand age and environmental variables.

2. Data and Methods

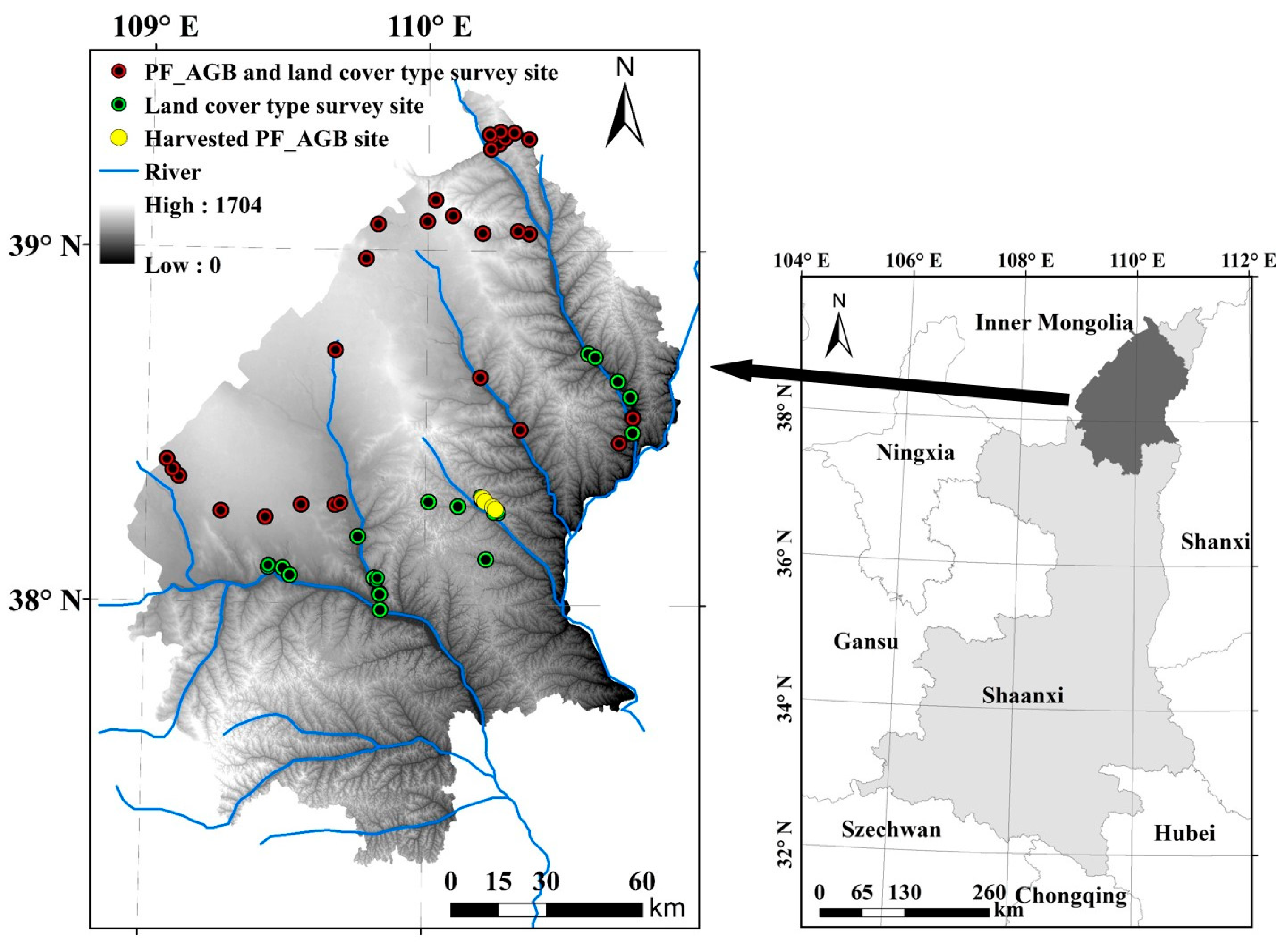
2.1. Study Area

Yulin is located in Shanxi province on the border between the loess plateau and the Inner Mongolian plateau (Figure 1). It is an ecologically fragile area in the TNSFP region with some of the worst instances of erosion in the world [14,15,16]. As a result, Yulin receives a lot of attention from the Chinese government and international societies [23]. Its special geographical environment means that Yulin is undergoing severe desertification and soil erosion, with soil loss rates exceeding 30 g/km² per year in some areas [24]. The ecological environment management objectives of TNSFP in Yulin are sand control and sand fixation. Yulin is also a useful case study for assessing the effectiveness of the TNSFP as a whole. Dynamic variation in the estimates of forest cover and forest biomass in Yulin can also reflect the effectiveness of the TNSFP. Primary land cover types in the study area include croplands, forest, grasslands, water bodies, urban and built-up, and barren or sparsely vegetated according to Moderate Resolution Imaging Spectroradiometer (MODIS) and other land cover type products [13,22]. Yulin’s climate is a temperate semi-arid continental monsoon climate with dry, windy conditions in spring; hot summers, when the majority of rainfall occurs; and dry, cold winters. Yulin has one of the highest sunshine durations in China, with not much precipitation. The annual total precipitation in the whole region is 310 mm to 510 mm, with most of the area receiving less than 450 mm. According to a field survey, the predominant tree species in the study area include Chinese pine (Pinus tabuliformis), poplar (Populus alba), and Chinese scholar (Styphnolobium japonicum).

2.2. Data

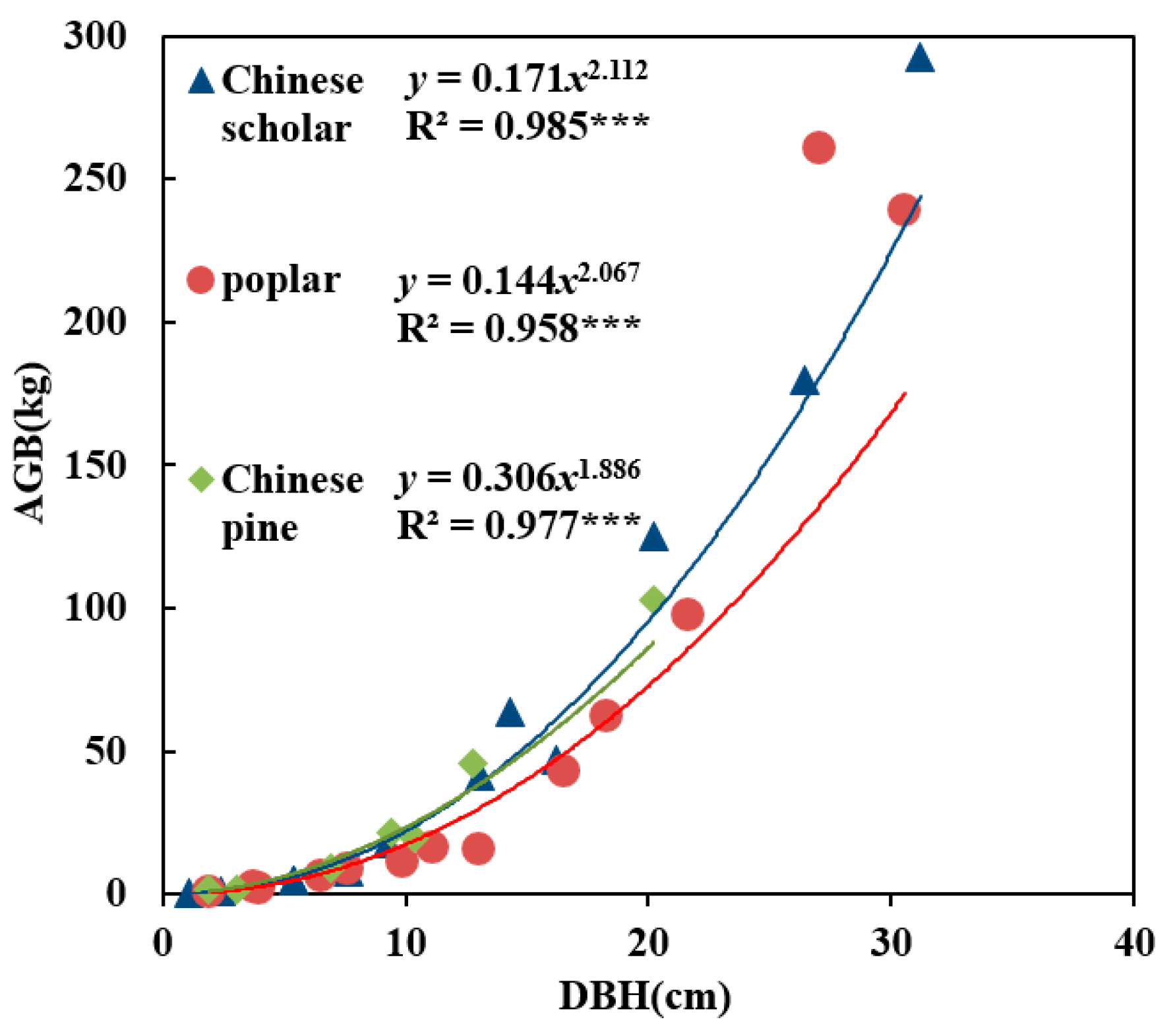
2.2.1. Field Data

Field observation data were first collected on 25–27 May, 2012. In total, 13 Chinese scholar trees (Styphnolobium japonicum), 14 poplar trees (Populus alba), and 7 Chinese pine trees (Pinus tabuliformis) were harvested in 7 plots (30 m × 30 m), and their stand age and DBH were measured. Harvested trees were taken to the laboratory for drying and calculating dry, aboveground biomass. The second field study was conducted on 11–14 October, 2013. In total, 28 plots (30 m × 30 m) were selected. Tree species, growth conditions, tree height, and DBH of all trees in each plot were measured (Figure 1). In addition, approximately 4700 points around 7 harvested PF_AGB sites, 28 PF_AGB survey sites, and another 26 sites (Figure 1) were surveyed to obtain land cover types, which were used to validate the detection of afforestation and forest loss in this study.

Allometric equations are a commonly used, reliable method for biomass estimation constructed from easily measurable variables (e.g., tree diameter). These equations have been developed to satisfy several forest ecological management studies [25,26,27]. In practice, DBH has been employed as the only independent variable in most allometric equations (Equation (1)) [27].

Biomass = a (DBH)^b

(1)

where a and b are constants. The relationships [7] between DBH and AGB for Chinese scholar, poplar, and Chinese pine developed for this study are shown in Figure 2.

The DBH was measured for all trees in each site in the second field study. The AGB for each tree was then estimated using allometric equations (Figure 2). We defined the site-level AGB as the sum of the AGB of all trees in the site. We used 28 site-level AGB values to validate the AGB derived from remote sensing images.

2.2.2. Remote Sensing Data

Landsat satellites have provided global observational data from 1972 to the present, and its continuity makes it suitable for studying long-term changes in forests and extracting stand age information [14,28]. Our study area covered two Landsat TM/ETM+ (path/row: 127/33, 127/34) images. Landsat MSS images in 1978 and Landsat TM/ETM+/OLI images from 1986 to 2013 were collected from the United States Geological Survey (glovis.usgs.gov). We selected 26 images, mainly from the growing season, with <10% cloud cover [7]. Specifically, images in 2000, 2001, and 2007 were obtained in May; images in 1993, 1995, 1996, 2009, and 2012 were obtained in June; images in 1987, 1992, 1998, 2005, 2010, and 2011 were obtained in July; images in 1986, 1990, 1994, 2002, and 2003, were obtained in August; and images in 1978, 1988, 1989, 2004, 2006, 2008, and 2013 were obtained in September. ASTER digital elevation model (DEM) data with a spatial resolution of 30 m was collected and used for terrain illumination correction based on the C-correction method [8]. We used the methods described in the study by Liu et al. [29] to apply the atmospheric correction based on the 6S radiative transfer model [30] to the Landsat TM images in 2000. The corrected images in 2000 were selected as the reference images for relative normalization of other Landsat images, and to obtain long time series Landsat surface reflectance data [30].

2.2.3. Meteorological Data

We collected monthly average temperature, monthly total precipitation, and monthly total sunshine duration for 18 meteorological stations around the study area from the Chinese National Meteorological Information Center (data.cma.cn) for March to October during 1978 to 2013 (growing season). Those meteorological data were used to develop estimation models for planted forest AGB (PF_AGB) in this study. A three-dimensional quadratic trend surface was constructed using stepwise regression in SPSS22 to get spatial gridded meteorological data, and the residuals were calculated by the subtraction of actual values and simulated values [31]. The inverse distance weighted (IDW) method [8] was used to spatially interpolate the residuals, and finally, to get monthly spatial meteorological data. Annual average temperature (T), total precipitation (ΣP), and total sunshine duration (ΣSD) for each year were calculated based on the monthly-gridded meteorological data [32].

2.3. Pixel-Level Stand Age Estimation

Vegetation change tracker (VCT) is a highly automated algorithm for determining forest cover change and detecting most forest disturbances using Landsat time series reflectance data [33]. In this algorithm, the integrated forest z-score (IFZ) was developed to distinguish forest and non-forest pixels using multi-spectral images. The forest z-score (FZ) indicates the coefficient of variation (CV) between a given pixel and a training forest pixel. As the FZ value decreases, the probability that the pixel is forested increases. The FZ value for a single band is defined as Equation (2).

$$F{Z}_i=\frac{\left|b_i-\overline{b_i}\right|}{S{D}_i}$$

(2)

where b_i represents the pixel value in the band i, $\overline{b_i}$ represents the average value for all training forest samples in this band, and SD_i represents the standard deviation of the pixel values for all training forest samples in this band. For multi-spectral images, the IFZ value of each pixel is defined as in Equation (3).

$$IFZ=\sqrt{\frac{1}{NB}{\displaystyle \sum _{i=1}^{NB}{(F{Z}_i)}^2}}$$

(3)

where NB is the number of the bands used. In this study, bands 3 (red), 5 (short-wave infrared band) and 7 (short-wave infrared band) were selected to calculate IFZ values [33] while bands 1, 2 and 4 were used to calculate IFZ value for Landsat MSS images [29].

Typical IFZ values for afforestation, forest loss and persisting forest from 1978 to 2013 are shown in Figure 3. Persisting forest areas showed stable low IFZ values of around 1.5. Values decreased gradually after afforestation in 1978, ending with a similar annual trend of IFZ as that of persisting forest. The IFZ values of forest loss had the opposite trend from afforestation: stable low IFZ values were observed before forest loss occurred in 2006, followed by increasing IFZ values. Based on these characteristics, we extracted all afforestation areas and calculated their corresponding stand ages.

2.4. Models for Forest Aboveground Biomass Estimation

Normalized difference vegetation index (NDVI) showed a significant linear correlation (r = 0.65, p < 0.001) with measured PF_AGB, and stand age showed an exponent significant relationship (r = 0.50, p < 0.001) with measured PF_AGB. As a result, NDVI was combined with the exponent transformation of the stand age to estimate forest AGB in this study.

We also found significant correlations between PF_AGB and several environment variables, including a topography factor (slope was selected in this study) and three climatic factors (i.e., annual average temperature (T), annual cumulative precipitation (ΣP), and annual cumulative precipitation (ΣSD)). For the growing season each year, the three climatic factors were averaged (temperature) or summed (total precipitation and total sunshine duration) to correspond with the stand age of this planted forest. This study area is characterized as the hilly and gully region based on the DEM distribution (Figure 1). Topography, especially slope, affects the distribution of water, which further affects forest growth. The PF_AGB decreased significantly with slope (r = 0.48, p < 0.01) and increased with total precipitation (r = 0.56, p < 0.01). Thus, total precipitation was combined with the power function transformation of slope and used as an indicator of PF_AGB.

In this study, we calculated PF_AGB in several ways. NDVI and the exponent transformation of the stand age was used as the base variable to estimate PF_AGB (Equation (4)). Total precipitation (combined with the power function transformation of slope), average temperature, and total sunshine duration were added to NDVI, respectively, in new models (Equations (5)–(7)). Finally, all factors were included in a single model (Equation (8)). Based on field observations, we got the coefficients of each function by the nonlinear regression analysis in the software of SPSS22, and assessed each model (Equations (4)–(8)) by determination coefficient (R²) and Akaike’s information criterion (AIC) [34]. AIC has been widely used as a criterion for model selection, it is calculated by the number of regressors, observations, and the residual sum of squares [34]. The model with the maximum R² value and the minimum AIC value was selected as the preferred model, and was used to estimate PF_AGB for our study area from 1978 to 2013.

$$PF\_AGB=f\left(\mathrm{NDVI},\mathrm{age}\right)=34.07\times \mathrm{NDVI}\times e^{0.033\times \mathrm{age}}-8.53$$

(4)

$$PF\_AGB=f\left(\mathrm{NDVI},\mathrm{age},\mathsf{\Sigma }\mathrm{P},\mathrm{slope}\right)=15.16\times \mathrm{NDVI}\times e^{0.012\times \mathrm{age}}\times \frac{e^{0.143\times \mathsf{\Sigma }\mathrm{P}}}{{\mathrm{slope}}^{0.498}}+0.79$$

(5)

$$PF\_AGB=f\left(\mathrm{NDVI},\mathrm{age},\mathrm{T}\right)=113.62\times \frac{\mathrm{NDVI}\times e^{0.029\times \mathrm{age}}}{ln\left(\mathrm{T}\right)}-11.01$$

(6)

$$PF\_AGB=f\left(\mathrm{NDVI},\mathrm{age},\mathsf{\Sigma }\mathrm{SD}\right)=1.11\times \mathrm{NDVI}\times e^{0.01\times \mathrm{age}}\times \mathsf{\Sigma }\mathrm{SD}-4.59$$

(7)

$$PF\_AGB=f\left(\mathrm{NDVI},\mathrm{age},\mathsf{\Sigma }\mathrm{P},\mathrm{slope},\mathrm{T},\mathsf{\Sigma }\mathrm{SD}\right)=1.44\times \mathrm{NDVI}\times e^{5.8\times {10}^{-5}\times \mathrm{age}}\times \frac{e^{0.108\times \mathsf{\Sigma }\mathrm{P}}}{{\mathrm{slope}}^{0.436}}\times \frac{1}{ln\left(\mathrm{T}\right)}\times \mathsf{\Sigma }\mathrm{SD}+2.6$$

(8)

where PF_AGB means the aboveground biomass of planted forest. T, ΣP, and ΣSD mean annual average temperature, annual cumulative precipitation, and annual cumulative precipitation, respectively.

3. Results

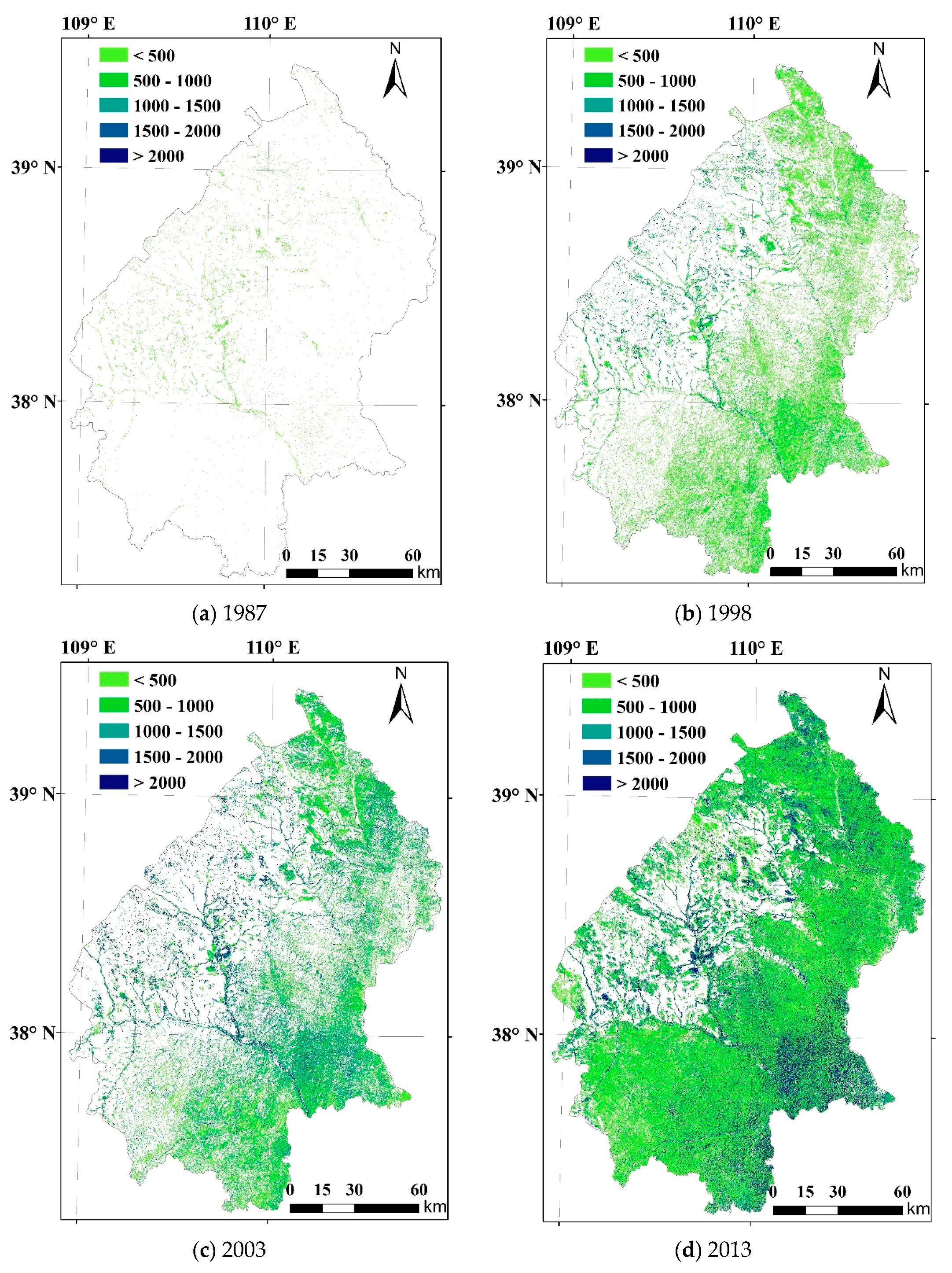
3.1. Afforestation Area and Stand Age

The area of afforestation was significantly larger during the early 1980s and the early 21st century than in other periods, especially during 2000 to 2003, when the afforested area was about 1249 km². Forest loss mainly happened several years after afforestation (i.e., during the mid-1980s and the mid-2000s), indicating that some forests did not survive, probably due to a lack of water. However, the area of forest loss was less than one percent of afforestation. Afforestation and forest loss area detection are essential steps needed to estimate the stand age for afforested areas. Approximately 4700 points of known land cover types were used to verify the accuracy of those area detections, and there was an overall accuracy of 90.95% with a kappa coefficient of 0.88. A previous study had also confirmed that vegetation cover in 1990s was increased compared with that in 1970s due to afforestation [14]. We collected statistical afforestation area from 2000 to 2013 and compared it with the afforested area detected in this study (Figure 4), and found that the interannual variation was generally consistent between the two methods.

We further validated the stand age of afforestation using field data and found that the absolute errors of 0-year, <1-year, <2-year, and <3-year accounted for 37.21%, 59.01%, 76.16%, and 83.72% of the survey sites, respectively. Afforestation verification was mainly conducted in the eastern study area, especially for valleys or stream sides (Figure 5a). The stand age in the eastern area was also greater than that of the western area. Most of the stand ages for afforested stands were found to be 27–35 years or 10–13 years, which accounted for about 14% and 60% of the afforestation area, respectively (Figure 5b). These two age groups corresponded to the key terms of TNSFP: the first term of TNSFP started in 1979 and the fourth term of TNSFP started in 2001. Since 2001, the Chinese government has increased financial input in TNSFP, and more afforestation efforts were conducted [35,36].

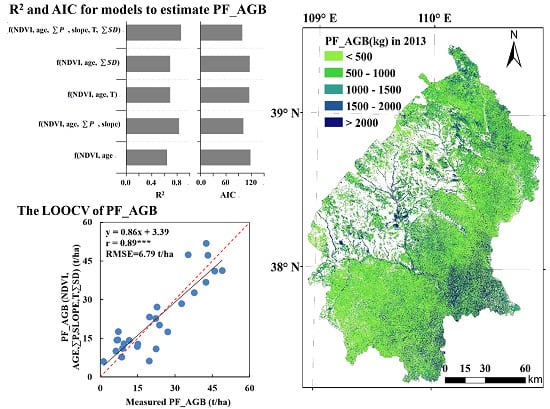
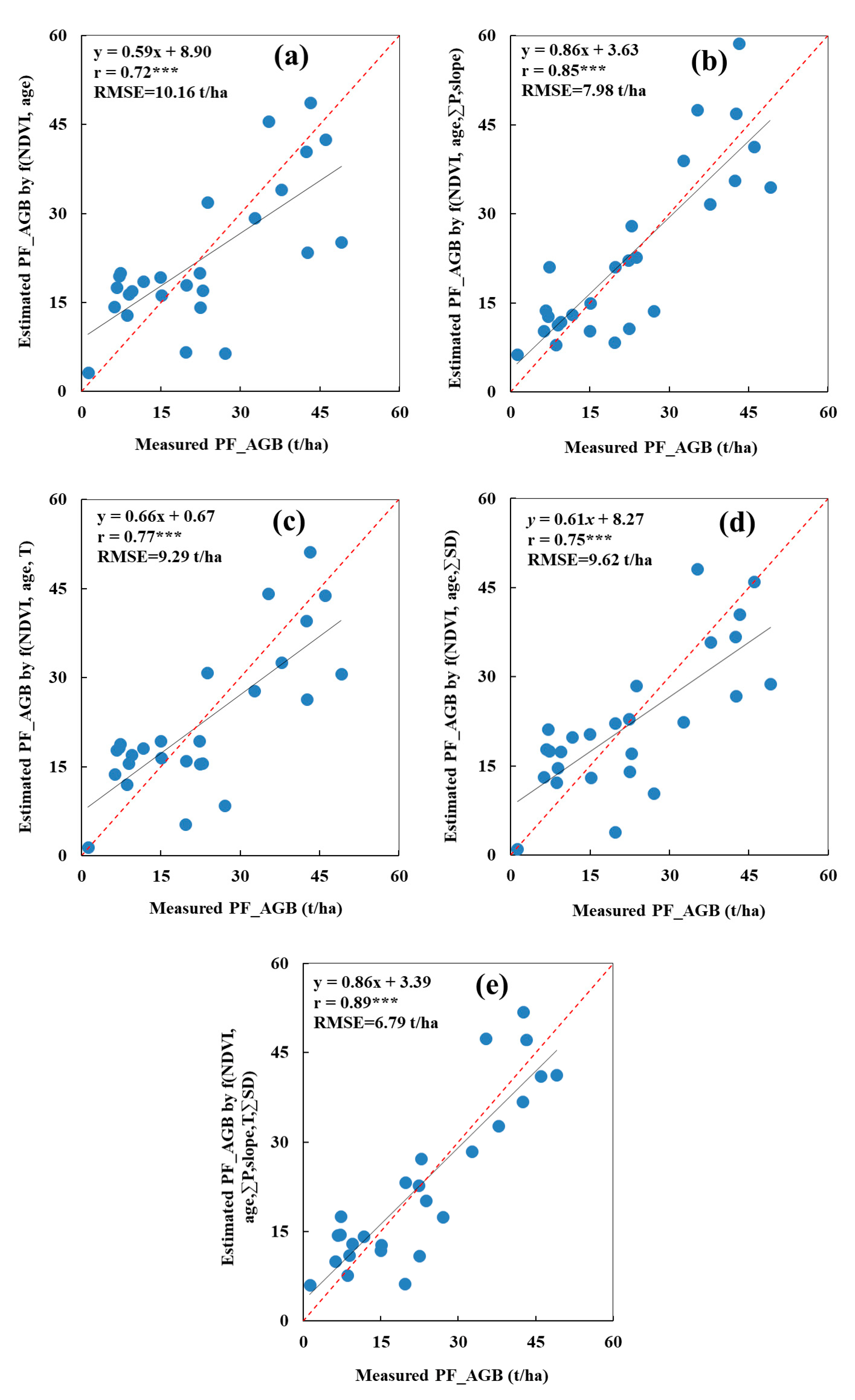
3.2. Planted Forest Aboveground Biomass Estimation and Validation

Figure 6 shows the determination coefficient (R²) and AIC for the five PF_AGB estimation by the models introduced in Section 2.4. NDVI and the exponent transformation of the stand age had a significant correlation with measured PF_AGB (R² = 0.64, p < 0.001), and this model’s AIC is 117.95. The correlation was more significant when considered with the addition of variables, especially total precipitation combined with the power function transformation of slope (f(NDVI, age, $\sum \mathrm{P}$, slope)), with the R² of 0.83 (p < 0.001) and an AIC of 101.04. The most significant correlation (R² = 0.86, p < 0.001) of measured PF_AGB was observed when NDVI and stand age were combined with all topographical and meteorological factors (f (NDVI, age, $\sum \mathrm{P}$, slope, T, $\sum \mathrm{SD}$)), resulting in the lowest AIC value of 98.56 (Figure 6).

Figure 4 shows that afforestation was mainly conducted in the early 1980s and again in the early 21st century, while afforestation was stable during the periods of 1988–1997 and 2003–2013 (Figure 4). The PF_AGBs in 1987, 1998, 2003, and 2013 were calculated using models that considered NDVI, stand age, topographic (slope), and meteorological factors (total precipitation, average temperature, and total sunshine duration); i.e., the model of f(NDVI, age, $\sum \mathrm{P}$, slope, T, $\sum \mathrm{SD}$). Results were mapped to represent interannual changes of PF_AGB. The PF_AGB was about 0.25 G kg in 1987, 0.8 G kg in 1998, 1.84 G kg in 2003, and 6.13 G kg in 2013 (Figure 7).

The leave-one-out cross-validation (LOOCV) approach, widely used for validation when the field observed samples are small, was employed. This method involves using one field observed value as a validation sample and the remaining field observed values as the training samples. This is repeated in all possible combinations to cut the original sample into a validation sample of one field observed value and a training sample [7,37]. Using the LOOCV approach, we validated PF_AGB based on the different models. We found that the estimated PF_AGB based on f(NDVI, age) had a correlation coefficient (r) of 0.72 (p < 0.001) and a root mean square error (RMSE) value of 10.16 t/ha. A marked increase in accuracy (r = 0.85, RMSE = 7.98 t/ha) was found when total precipitation combined with topographical factor (i.e., slope) were introduced. This combination was more accurate than the models of f(NDVI, age) combined with average temperature (f(NDVI, age, $\sum \mathrm{SD}$)) and total sunshine duration (f(NDVI, age, $\sum \mathrm{SD}$)) (Figure 8). The combination of all variables (f(NDVI, age, $\sum \mathrm{P}$, slope, T, $\sum \mathrm{SD}$)) showed the highest accuracy (r = 0.89, RMSE = 6.79 t/ha) when estimating PF_AGB.

4. Discussions

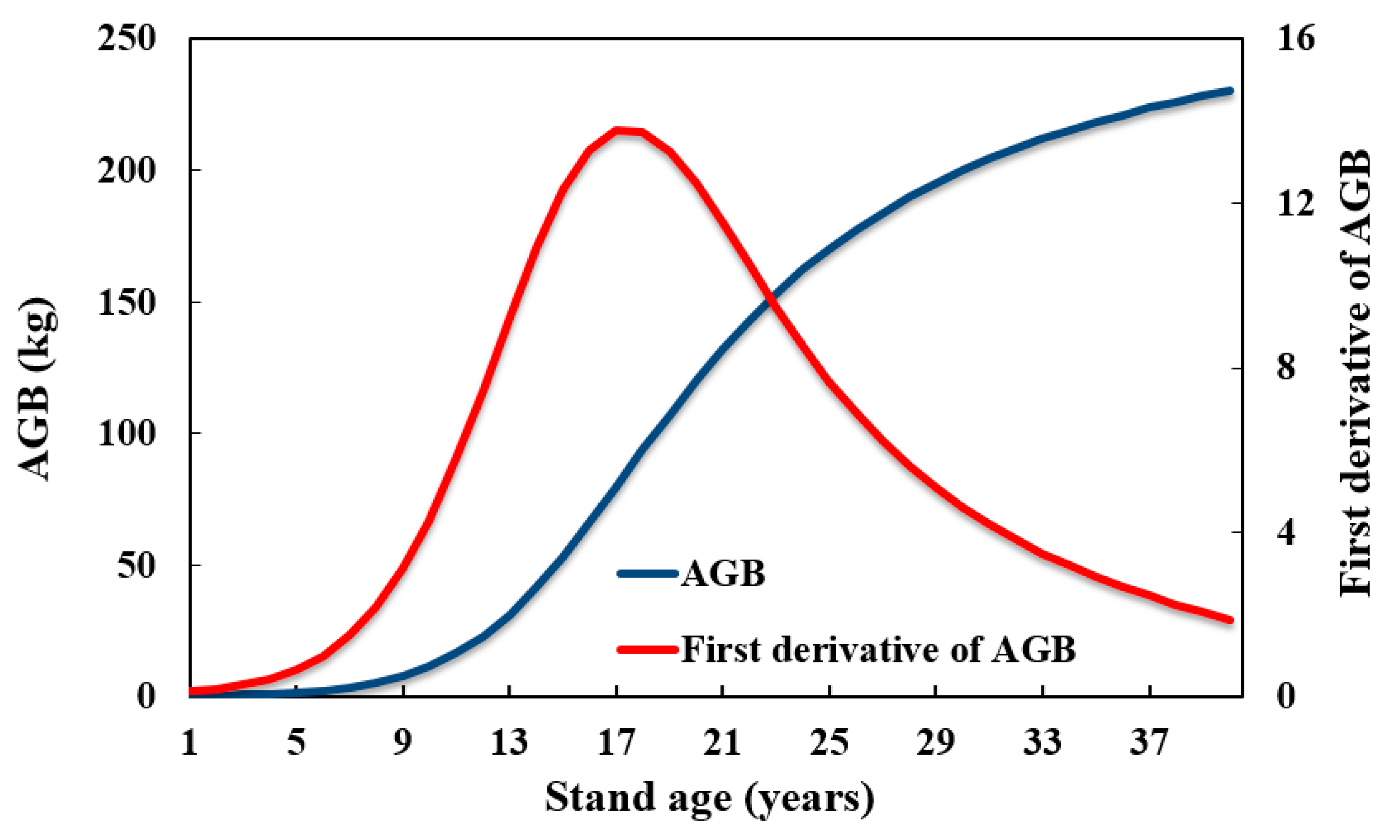
4.1. The Relationships of Vegetation Indices and Stand Age with Forest Biomass

Forest biomass correlates with the optical spectrum measurements, such as the shortwave infrared (SWIR) band [38] or near-infrared (NIR) band [39], and other various remotely sensed parameters, such as leaf area index (LAI) [40], normalized difference vegetation index (NDVI), enhanced vegetation Index (EVI), perpendicular vegetation Index (PVI), soil adjusted vegetation index (SAVI), and the simple ratio index (SR) [7,41]. They are usually used to build empirical models based on observations because there is no direct physical relationship between forest AGB and the reflectance value of the canopy in the optical and microwave ranges [42]. Previous studies have shown that remote sensing data are widely used in forest AGB estimation [43,44], but the relationship between forest AGB and optical spectrums or vegetation indices is different for different regions and periods [45]. NDVI is widely used to estimate leaf area index, biomass, chlorophyll concentration in leaves, plant productivity, fractional vegetation cover, and other vegetation biophysical and structural parameters [46,47]. A number of studies have shown that EVI has strong sensitivity in areas with middle and high LAI values [48,49]. Compared to NDVI, EVI’s calculation increases the blue band to avoid saturation of the red band caused by vegetation absorption. Therefore, replacing NDVI in forest AGB estimation models with EVI might have a better effect in densely forested areas. However, this study area is a semi-arid area with the sparse vegetation; the LAI is low even for the forest contained in the 30-m pixel. NDVI has high sensitivity in low and medium-LAI areas [50]. Therefore, NDVI is suitable for estimating AGB in our study area, as has been demonstrated in our previous study [7].

Stand age has been confirmed to be an important factor for estimating forest biomass or productivity [7,51]. The simulated relationship between our measured stand-age of poplar (Populus alba) and PF_AGB showed that PF_AGB increases rapidly with stand age when forests are young (Figure 9). The first derivative of forest biomass (Figure 9) indicates that peak forest growth occurs during a stand age of 15–17, after which it will gradually slow down. In the later stages of tree growth, therefore, forest biomass growth is slow, and the relationship between stand age and forest AGB is not a simple exponential function. The relationship between forest AGB (or productivity) and stand age is generally different after middle-age, and declining productivity is seen in many types of forests [51]. Due to the TNSFP initiated in 1978, the growth of the planted forest in our study area is mainly concentrated in the early stage, and changes of PF_AGB with the stand age are similar, mainly estimated using an exponential function. In addition, we found dynamic changes, such as afforestation, deforestation (or forest loss), restoration, or continued growth, demonstrating the need to update the stand age if deforestation (or forest loss) are observed after afforestation occurs [28,29]. The stand age used to estimate PF_AGB in this study was calculated according to latest afforestation event occurring in each pixel. In 1987, PF_AGB was much smaller than in other years because afforestation was conducted only a few years prior, while PF_AGB in 2003 had increased 2.5 times as compared to 1998 because the fourth term of TNSFP started in 2000. More afforestation was conducted in this term than any of the earlier three terms. In addition, a second project called “China’s Sloping Lands Conversion Project” was initiated in 2000. The sloping lands conversion project promoted the conversion of croplands in hilly areas to forests and also contributed to the afforestation of the study area [36]. By 2013, a large number of small trees had grown into forests, and the PF_AGB was about 4.6 times that in 2003.

4.2. The Influence of Environmental Variables on Tree Growth, Biomass, and Model Performance

As shown in our study, environmental variables play vital roles in model performance and biomass accumulation. This is also true in regard to the distributions of forest species. Evergreen tropical rainforest and broad-leaved forest are widely distributed in tropical and subtropical regions, which have high temperatures and precipitation; mixed forests and deciduous broad-leaf forests are distributed in temperate regions, which are wet and warm in summer and low-temperature in winter; and coniferous forest are located in cold areas [52,53]. The distribution of forest species is also restricted by local climate conditions. For example, in northern Mongolia P. obovata, a boreal tree species, is more sensitive to late spring and summer frost than Abies sibirica or Pinus sibirica, and as a result, P. obovate is mainly distributed in the area with the relatively high temperature [54,55]. The scots pine, a light-demanding species, is moderately drought resistant and has low nutritional requirements, thus can survive in the area with the nutrient poor soils [56,57]. However, in arid and semi-arid forests, water is the most important limiting factor [58], especially for seedlings [57,59]. For example, it was found that young birch trees are more sensitivity to water than older trees in the Altansumber study area of northern Mongolia [59].

Radiation, temperature, and water are the essential elements for vegetation growth [60]. Ollinger et al. [61] found that forest growth rates and carbon sequestration may accelerate due to rising temperatures, prolonged growing seasons, potential carbon-dioxide-driven growth in photosynthesis, and increased water use efficiency. Thompson et al. [62] conducted a simulation experiment and found that climate change contributes to 13.5% of forest AGB growth. Besides the macro-climate climate, topographical conditions (such as elevation, slope, and aspect) have proven to have a strong influence on the local climatic conditions [63,64,65]. For instance, P. sibirica and A. sibirica are water demanding species typically found at high elevations in the western Khentey, where the rainfall in the area is concentrated [54]. Temperatures and water have been found to be varied with slope [65], and as a result, few trees grow on the drier south-facing slopes of the steppe. Therefore, environmental variables, especially climate and topography, should be considered when modeling forest AGB. Our study area is typically arid or semi-arid, and the factors (i.e., precipitation and slope) that affect the spatial distribution of water directly affect the biomass (Figure 4) and the runoff from rainfall caused by topography may also influence forest growth [66]. Even within a small region, where the climate conditions are almost the same, the forest AGB can be completely different for the same forest species if planted on hillsides versus valleys. We were able to improve the accuracy of remote sensing biomass estimation by combining the forest AGB estimation models with meteorological and topographic data. Our results confirm that precipitation combined with slope had significant correlation with PF_AGB, and therefore, increase the accuracy of PF_AGB estimations in arid or semi-arid areas.

In the Three-North Shelter Forest Program area, deforestation is prohibited, and it is, therefore, impossible to harvest a large area of the forest to validate the results from this study. Some studies indicate that combining remote sensing data with structural parameters (such as tree height and crown width) can effectively improve the accuracy of biomass estimation, even in areas with complex forest structures [67,68,69,70]. While those structural parameters cannot be calculated from optical remote sensing data, especially at the 30 resolution of a Landsat image, LiDAR data can include metrics related to tree height or canopy density and can be used to estimate AGB [71,72,73]. However, airborne LiDAR data with high spatial resolution is not yet available for large areas, let alone for long time series monitoring of PF_AGB. Once operational, the Ice, Cloud and Land Elevation Satellite-2 (ICESat-2) will provide spatially continuous LiDAR data for global forest biomass estimation. We anticipate that the fusion of ICESat-2 LiDAR data and optical remote sensing data will further improve the accuracy for estimating vegetation biomass over large areas and provide a valuable resource for future afforestation projects [74].

5. Conclusions

In this study, we obtained Landsat time series surface reflectance data for Yulin from 1978 to 2013 and calculated the corresponding IFZs to retrieve pixel-level values for each year of afforestation. We then calculated the stand age for areas of afforestation. Field-measured planted forest AGBs and DBHs were used to construct allometric equations and calculate site-level (30 m × 30 m) AGBs. NDVI, stand age, climatic factors (average temperature, total precipitation, and total sunshine duration) and a topography factor (slope was selected in this study) were considered in models to estimate PF_AGB. The results demonstrated that the model based on NDVI combined with stand age and considering topographic and meteorological factors had the highest accuracy for estimating PF_AGB. The most important of these were the slope and total precipitation, which are the two main factors affecting the distribution of water, indirectly affecting the growth of forests in arid or semi-arid areas. Afforestation in the study area was mainly conducted in the early 1980s and early 21st century, and the PF_AGB in 2003 was 2.3 times that of 1998 since the fourth term TNSFP started in 2000. As a result, PF_AGB in 2013 was about 3.33 times that in 2003 because many young trees had grown up. The validation of PF_AGB by the LOOCV showed that our estimation had a R of 0.89, and a RMSE of 6.79 t/ha.