Next Article in Journal
Monitoring the Ice Phenology of Qinghai Lake from 1980 to 2018 Using Multisource Remote Sensing Data and Google Earth Engine
Previous Article in Journal
Analyzing the Effects of Sea Surface Temperature (SST) on Soil Moisture (SM) in Coastal Areas of Eastern China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 12
Issue 14
10.3390/rs12142213
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Random Forest Algorithm Improves Detection of Physiological Activity Embedded within Reflectance Spectra Using Stomatal Conductance as a Test Case

by
Snir Vitrack-Tamam
,
Lilach Holtzman
,
Reut Dagan
,
Shai Levi
,
Yuval Tadmor
,
Tamir Azizi
,
Onn Rabinovitz
,
Amos Naor
and
Oded Liran
*
Group of Agrophysics Studies, Migal Institute, Kiryat Shemona, Upper Galilee 11016, Israel
*
Author to whom correspondence should be addressed.
Remote Sens. 2020, 12(14), 2213; https://doi.org/10.3390/rs12142213
Submission received: 7 June 2020 / Revised: 6 July 2020 / Accepted: 7 July 2020 / Published: 10 July 2020
(This article belongs to the Section Remote Sensing in Agriculture and Vegetation)
Browse Figures
Versions Notes

Abstract

:
Plants transpire water through their tissues in order to move nutrients and water to the cells. Transpiration includes various mechanisms, primarily stomata movement, which controls the rate of CO2 and water vapor exchange between the tissues and the atmosphere. Assessment of stomatal conductance is available for gas exchange techniques at leaf level, yet these techniques are not scalable to the whole plant let alone a large vegetation area. Hyperspectral reflectance spectroscopy, which acquires hundreds of bands in a single scan, may capture a glimpse of the crop’s physiological activity and therefore meet the scalability challenge. In this study, classic chemometric analyses are used alongside advanced statistical learning algorithms in order to identify stomatal conductance cues in hyperspectral measurements of cotton plants experiencing a gradient of irrigation. Random forest of regression trees identified 23 wavelengths related to both structural properties of the plant as well as water content. Partial least squares regression succeeded in relating these wavelengths to stomatal conductance, but only partially (R2 < 0.2). An artificial neural network algorithm reported an R2 = 0.54 with an 89% error-free performance on the same data subset. This study discusses implementation of machine learning methodologies as a benchmark for deeper analysis of spectral information, such as required when searching for plant physiology-related attenuations embedded within reflectance spectra.

Graphical Abstract

1. Introduction

Transpiration is a physiological process within the plant that allows for water movement through tissues, starting at the root and exiting through specialized pores within the leaves, termed stomata [1]. Complex physiological and regulatory processes drive transpiration, the primary of which is stomatal conductance [2]. The stomata control the exchange of water vapor and CO2 between the leaf and the atmosphere by promptly changing the stomata aperture size according to the plant needs. Stomatal conductance reduces transpiration when plants experience water stress, therefore, it controls the water status of the plant and its tolerance to drought. Yet, this step reduces photosynthetic rates as well. Therefore, detecting this process on a global scale is a fundamental requirement to developing models for ecological resilience of crops during climate change, global ecology, and, in practice, irrigation management in agriculture [3]. Measuring gas exchange at leaf level through current techniques is not scalable to large vegetation areas due to the technical difficulties of sampling more than a handful of leaves each time. Therefore, remote sensing techniques that enable scanning of large areas in a short period can overcome these challenges and become the method of choice in environmental studies [4]. The most common remote sensing method for the detection of water status is infra-red thermography. The stomata closure increases the leaf temperature as a secondary effect, and it is the basis for the calculation of temperature-dependent Crop Water Stress Index (CWSI) [5]. Yet, thermal sensing is highly dependent on environmental parameters in the vicinity of leaves and measured canopies [6]. Another non-invasive remote sensing technique is reflectance spectroscopy [7,8]. Reflected sunlight carries information regarding biophysical and biochemical characteristics of the plant. This information can be retrieved with airborne platforms such as satellites, aircrafts, and drones. Penuellas et al. [9] introduced the usage of atmospheric properties in search for water status indices when they used the attenuation in the water absorption band located at 970 nm. In their seminal work, they mention that the index reacted well with plants that lost their cell wall elasticity during a period of water stress. Around the same time, Gao et al. (1996) found that, by taking into account the water absorption bands as a whole in the short wave infra-red (SWIR) region, water absorption bands can be also exploited to predict the water status of the plant [7]. Yet, this study was limited due to the index attenuation in view of different leaf area index between various crops. Working with computer simulations such as PROSPECT [10] enabled an added understanding of what exactly affects the electromagnetic spectrum when water status is being taken into account. For example, Ceccato et al. [11] explained why water status indices cannot be retrieved only from the Near Infra Red region within the electromagnetic spectrum (NIR) or the Short Wave Infra Red region (SWIR) alone but have to be combined. This happens due to attenuation in the SWIR region by leaf structure and dry weight. Transpiration is different than water status, because while water is a chemical quotient found within the plant tissues, transpiration is a complex physiological phenomenon encompassing several biochemical and biophysical mechanisms that affect the hydraulic conductances along the plant, and therefore it is more challenging to detect. There have been numerous studies that relate reflectance spectra characteristics and transpiration either directly by using established remote sensing indices (e.g., Marshall et al., 2016) [12] or indirectly by relating transpiration or (specifically) stomatal conductance to photosynthetic activity [13]. Reflectance-based indices are constructed from a limited number of wavelengths, usually two, which enable a fast acquisition and analysis but are limited in their ability to sense finer physiological changes. For example, the Normalized Differential Water Index (NDWI) is sensitive to water content at leaf level and only partially correlates to the same status when acquired at a distance from the plant due to severe dependency on leaf area index and crop geometry [13]. Hyperspectral reflectance spectroscopy expands the multispectral analysis, as it acquires hundreds of bands at a higher spectral resolution in a single acquisition and may better capture the physiological attenuations embedded within the spectrum [14].
Working with a large number of wavelengths will result, inevitably, in multicollinearity between various wavelengths and a low predictive capability of models. It is therefore crucial to lower the dimensions of the problem by reducing the number of wavelengths while retaining much of the information embedded within the spectrum. In this study, we combine both traditional chemometric analysis with more advanced supervised machine learning algorithms in order to isolate meaningful wavelengths that relate to stomatal conductance as a test case. We show that random forest of regression trees and artificial neural network algorithms are superior to traditional spectral analyses, contour-contour map and partial least squares regression.

2. Materials and Methods

2.1. Hyperspectral Technique Setup

Four-point microspectrometers (two units of STS + Flame, OceanInsight, Largo, FL, USA) were combined to cover a spectral range of 633–1659 nm and were mounted onto two home-made cages: ground and air [15]. Each spectrometer was radiometrically set with a calibrated light source (HL-2000-LL, OceanInsight, FL, USA) according to the manufacturer’s instructions. STS and FLAME spectrometers obtained an overlapping region in the spectral range of 936–1120 nm, and on this basis, each two acquired spectra were stitched together. Overall, there were 1222 wavelengths with 1 nm and 6 nm full width at height maximum (FWHM) spectral resolution for STS and FLAME spectrometers, respectively. The air unit was mounted on top of a trolley with a boom that situated the spectrometer pupil at a consistent 2.5 m above the sampled canopy. The ground unit was situated above a 94% reflectance white plate (Permaflect©; LabSphere, NH, USA). The spectrometers’ stitched spectra were spectrally calibrated according to the atmospheric water absorption band at 970 nm. Small deviations on the spectral range between STS and FLAME spectrometers were corrected according to Rascher et al. [16], and the radiometric deviations between the two units were corrected as well (when both were pointing at the reference plate). Thus, the water absorption band at 970 nm obtained the same magnitude and physical properties in both STS and FLAME spectrometers. Reflectance signatures were calculated and corrected for meteorological conditions according to Gordon and Wang’s study [17].

2.2. Stomatal Conductance Datasets

Various irrigation regimes on cotton plants were the basis for this study, aiming to maintain a wide range of the plants’ water status and stomatal conductance values. The irrigation experiments were conducted in 2018 and 2019 (Figure 1). The cotton plants were grown in 3.9 L pots filled with mixed ground (80:20 Peat soil:Clay, Kekkila BVB, Sweden). Four seeds were sown in each pot in a square geometry and, after emergence, the two weakest plants within each pot were removed. Every four pots within a quad were closely situated so that, early in the season, the canopies of adjacent pots were reducing the ground view. The pots were drip-irrigated with a fertigation solution, thus the fertilizer concentration was relative to the irrigation volume (Sheffer + 3 micro, ICL, Israel). There were 18 biological repeats per irrigation treatment times 4 technical repeats in each year for a total of 432 pots. Three cotton varieties—G. hirsutum, G. barbadense, and G. akalpi—were used in the study (they presented no difference in stomatal conductance within each irrigation treatment). Two irrigation experiments were performed: (a) irrigation volume gradient—four daily irrigation rates were applied at 4, 3, 2, and 1 L/pot, corresponding to midday water potentials of −1.4, −1.8, −2.0, and −2.5 MPa, respectively; water potential (Scholander bomb, MRC, Israel) measured at noon reflected the plant’s need for water; each repeat (irrigation treatment * variety) consisted of 18 pots, and each irrigation treatment * variety was replicated 6 times in random blocks; (b) irrigation shut-off experiment—all the quads received optimal irrigation volume, which was determined as 3 L per day (−1.8 MPa at noon); at t = 0, the irrigation was stopped for 24 h and resumed in an irrigation gradient with the same four volumes treatments as described above per day for a week. The 2019 experiment included a repeat on the volumetric gradient design part performed in 2018 on G. akalpi variety only. Measurements in all the experiments were conducted in the same phenological period.
Hyperspectral acquisition and abaxial stomatal conductance measurements (AP4, Delta-t, UK in 2018 and Licor 6800 photosynthesis system, Li-Cor Biosciences, IL, USA in 2019) were performed for two months covering vegetative growth, transfer to, and start of the reproductive growth stage. An AP4 porometer was calibrated with a calibration plate before the measurement sets according to the manufacturer’s instructions. In the case of Li-Cor 6800, an open chamber was used in order to receive sunlight at a natural intensity via a 3 × 3 cm window. Environmental conditions were as follows: the temperature and the relative humidity were set according to the meteorological station parameters (Table 1). CO2 level was always set to 400 ppm. Measurements were recorded when assimilation and conductance reached a plateau, approximately 30 s to 1 min after closing the chamber on the leaf. In each date, measurements were taken twice (once before noon and then again at noon), where ten measurements per pot quad were taken each season (Table 1 describes meteorological conditions during the measurements received from a local meteorological station). In both years, the meteorological station was about ~85 m southwest of the experimental plot.

2.3. Pre-Processing of Data for Important Features Selection

We followed Rinnan et al. [18] protocols to prepare the spectra for analysis (Figure 2). First, we used a box-car averaging technique in order to create an even, nominal pace between the two sides of the stitched spectra. That is, we eventually received 231 wavelengths of the 1222 total wavelengths of the raw data. Then, outlier spectra were identified by Cochran’s test [19] and removed from the data set, and a standard normal variate (SNV) test followed in order to correct for multiple scatter [20]. Next, spectra were corrected for their additive dispersion effect with a baseline correction and were normalized to the maximum peak within each spectrum. The procedure resulted in a negative local minimum at the water absorption band (between 1380–1450 nm). Therefore, these wavelengths were omitted from further usage and analysis. Finally, the spectra were mean-centered and standardized before performing further analysis on it. Stomatal conductance data was also curated for outliers per irrigation treatments, where if sample values were far from the average (as in, more than one standard deviation distance), the whole sample was omitted from the analysis.

2.4. Wavelength Selection

A Normalized Difference Index (NDI) combinations technique, also termed contour-contour map [21], was used as the first step to find a simple relationship between the spectra and the stomatal conductance. A coefficient of determination was the examined value. NDI formulations states:
N o r m a l i z e d   d i f f e r e n c e = a ρ i − b ρ j c ρ i + d ρ j
where ρi,j are the reflectance values at a designated wavelength i,j in units of the measurement (in our study nanometer (nm)), and a, b, c, d are rational number coefficients selected by the computer during minimization of sum of squares. The coefficient values (Equation (1)) were either set to “1” or were determined using the optimum minimize package in Python Software (Python, DE, USA) [22], operated with Constrained Optimization BY Linear Approximation process (COBYLA) [23]. A random forest ensemble method followed [24]; it allows the division of the dataset selected into nodes within a tree. Each node contains a subset of the original dataset. This subset comprises a subset of samples and a subset of the wavelengths. Each node is then averaged, and the number obtained is compared via root mean squared error (RMSE) to the measure stomatal conductance values. The target of the ensemble is to lower the RMSE as much as possible where important node dividers are flagged and kept. In this study, the divider was an arbitrary wavelength. Therefore, the selected architecture of the trees was the one with the lowest achieved RMSE and a set of dividers (wavelengths) that enabled this to occur. During the divisions into nodes, essentially deep in the tree, there could be left only one wavelength. In order to avoid it, pruning of the forest, i.e., stopping the tree from being developed [25], was performed in three levels: (a) numbers of trees in the forest (50, 100, 250, 500); (b) constant percentage of attributes within each branch split (10%, 20%, 30%, 40% of the attributes); (c) maximum depth of the regression tree (selected to be to two-thirds of an average maximum depth reached in preliminary iterations on the dataset).

2.5. Validation of Features Selected

The dataset was divided into 75% calibration sub-set and 25% testing sub-set. Initially, a standard multiple linear regression model was searched [26]. However, due to a violation of one of the model’s prerequisites, namely the inability to obtain a partial linear regression between each of the predictors and the predictand, a partial least square regression process was used instead [27]. This algorithm projects the original dataset into a latent structure where each of the new variables is independent of each other and therefore minimizes the co-linearity problem. It lowers the dimensionality of the problem, and the user has a greater chance to create a statistical model of spectra calculating stomatal conductance. In this study, the dimension of the problem was reduced from 23 selected features into a set of 4 new latent predictors. The model was cross-validated using a venetian blinds sub-sampling cross validation. With unimproved coefficient of determination, an artificial neural network (ANN) was used afterwards. This model accounts for the nonlinear relationship between the spectra and the physiological process [28]. The ANN architecture [29] included one hidden layer and a standard back-propagation process with Adam’s optimizer containing a loss function [30]. Performance of the ANN was validated as well, with a suite of statistical tests as suggested by Sousa et al. [28].

2.6. Statistical Packages

Dataset pre-processing, partial least squares regression, and k-means clustering were performed in UnscrumblerX software (Camo Analytics, AS, Norway). Data preparation for multiple linear regression was performed in SPSS (IBM SPSS, Armonk, NY, USA). Random forest of regression trees and artificial neural network were coded in Python programming language [22].

3. Results

The two most irrigated treatments had similar stomatal conductance (Figure 3A) and decreased with further reduction in water potential, as expected for plants experiencing water stress. For each stomatal conductance measurement, a spectral acquisition followed (Figure 3B–D). A portion of the short-wave infra-red (SWIR) region was removed from the analysis (see the region between 1380–1450 nm in Figure 2B) due to its negative appearance during pre-processing of the dataset. This happened because there was a strong absorption of the water band in this spectral region [31].
The only visible difference could be seen between the blue and the yellow colored curves: –2.5 and −1.4 MPa water potential, respectively. These were the two extreme conditions during the study: either over irrigating or wilting until it reached a very low water potential (−2.5 MPa) and 33% of the maximum stomatal conductance. When magnifying the spectral regions, it could also be seen that the trends in the reflectance values were very similar to the relations between the actual values of the stomatal conductance (Figure 3C,D compared to Figure 3A). The magnitude of the spectrum in the VISible-Near Infra Red (VIS-NIR) range increased with an increase in stomatal conductance. The spectra in the Short-Wave Infra-Red (SWIR) spectral range presented an opposite behavior to that in the VIS range (compare Figure 3C to Figure 3D). Here, the SWIR region was affected by water absorption bands, and therefore it was opposite because the plant retained more water within its tissues. As such, the water absorbed more light, and the reflectance in this region decreased. Finally, although there was a gradual decrease between the four irrigation treatments, it was visible that the extreme water stress (blue color) affected the spectrum more severely in the VIS region. Its magnitude was much smaller when compared to the other water treatments.
In the following sections, we discuss the wavelength selection process and the validation of that selection as a regression model between spectral and stomatal conductance measurements.

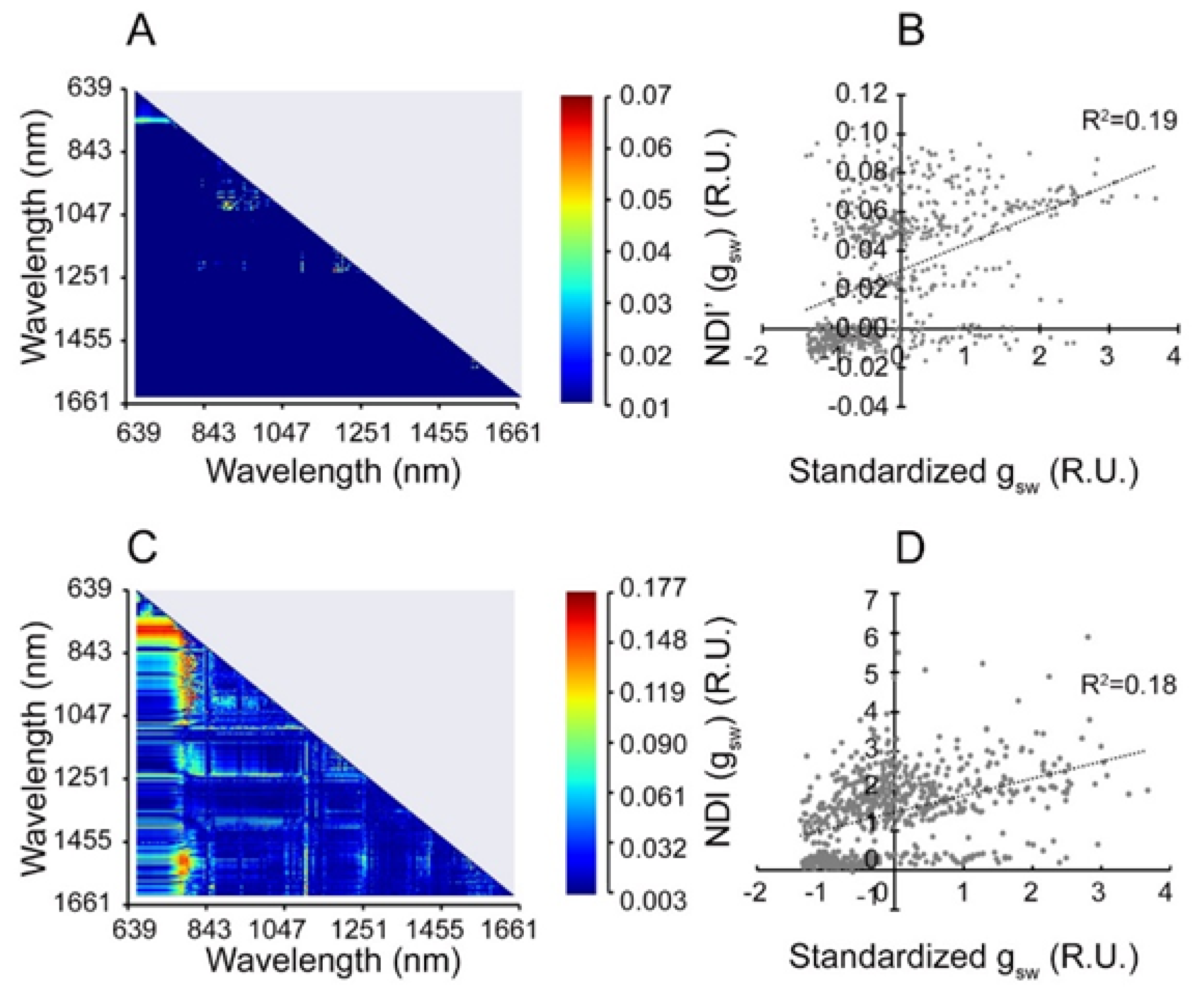
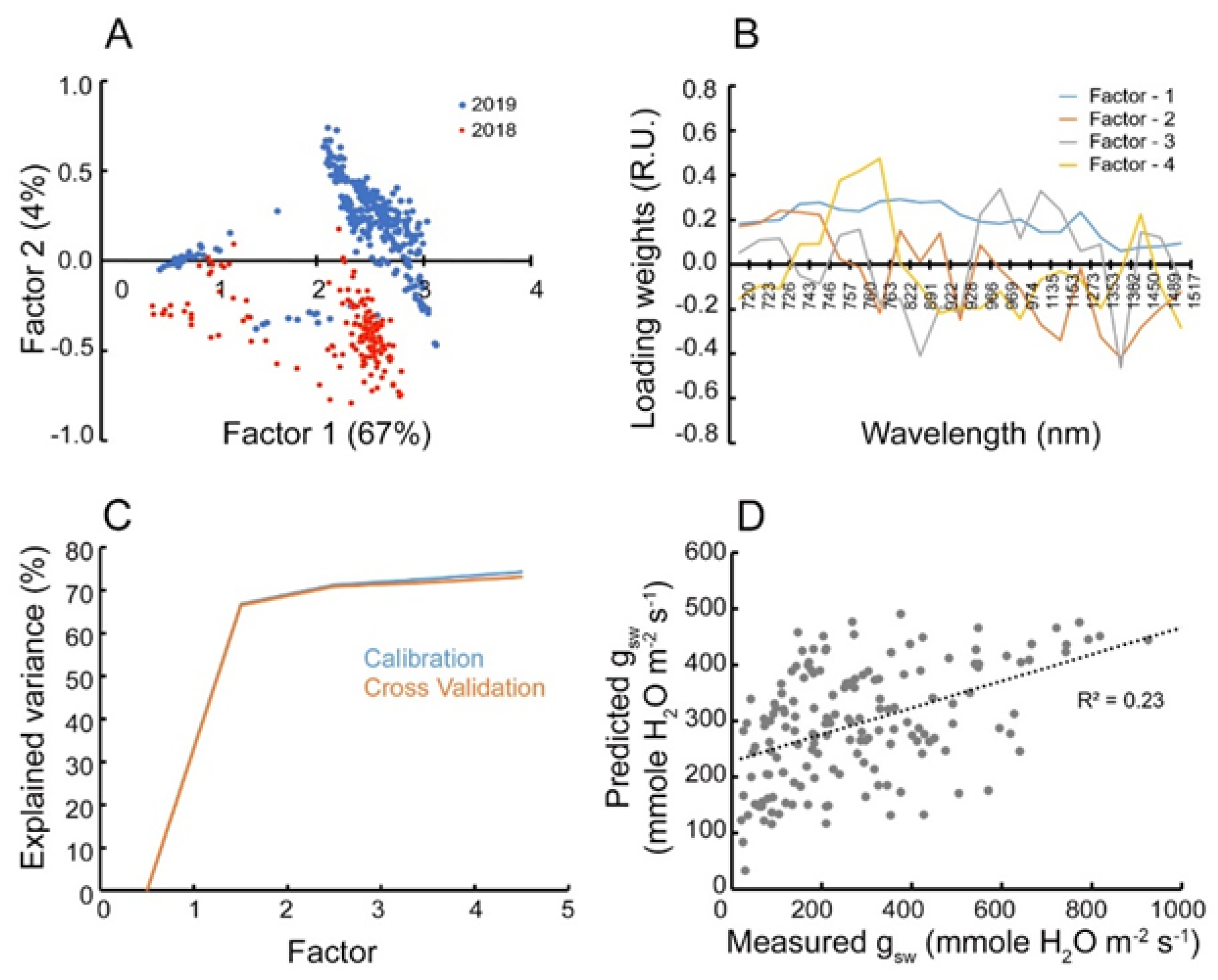
3.1. Wavelength Selection

Normalized Difference Index technique relates the chemical quotients of plants, such as nitrogen [32], water content [7], and photosynthetic pigments contents [33], to linear combinations of every two wavelengths within the acquired spectra [34]. Using this technique on 231 wavelengths in our dataset, we found four hot-spot regions that were more correlated to the stomatal conductance values than the rest of the wavelength combinations (Figure 4A): 693–703 nm, 780–890 nm, 1007–1120 nm, 1500–1560 nm.
However, the coefficient of determination was quite low (R2 < 0.2). NDI index was calculated with the combination that reached the highest R2—1094 nm and 1096 nm (Figure 4B). However, it was very poor due to natural clustering of the data within the correlation plot.
We therefore hypothesized that the detection of hot spot regions within the contour map could be improved if a generalization of the method were to take place. This means that coefficients a, b, c, and d in Equation (1) would receive an arbitrary rational number. In such a case, the NDI method shown in (Figure 4A) is a private case of the generalized equation, where all the coefficients equal one. Such a step increases the capability of the statistical process to minimize the RMSE and reach a higher coefficient of determination. This model was run on each of the 231 wavelength combinations. Using this approach, we found many more bi-wavelength combinations, which almost tripled the coefficient of determination values found in the private case of NDI (Figure 4C,D). The contour map in this setup revealed that the range between 634–843 nm related to stomatal conductance both within itself (parallel bold red line in Figure 4C) and within two main regions in the spectrum: 843–1047 nm and 1455–1661 nm. A maximum correlation was achieved for the two-wavelength combination of 734 nm and 830 nm with R2 = 0.19, as in the private case. Still, it was visible that the correlation to the actual regression line was poor (Figure 4D). The reason here is similar to the private case, where the generalization of the NDI technique managed to lower the number of natural clusters to two within the correlation plot.
We searched for a better and more advanced technique to correlate between spectra and stomatal conductance. Specifically, we searched for a technique that can isolate a lower number of features from the spectral range (one feature in this sense is one wavelength) and consider the non-linear relationship between the physiological phenomenon and the spectral information. This can be expected from researching biological activity such as stomatal conductance, which encompasses both chemical and structural attenuations of the sample measured. We selected a supervised machine learning algorithm random forest (RF) of regression trees [24] after the work of Abdel-Rahman and colleagues implementing RF for analysis of spectral measurements in general [35] (Figure 5). The algorithm performs an implicit feature selection (in this case, the features are the spectral wavelengths) and decides during the iterations which features are the best data selectors per a final dataset. In other words, the RF algorithm selects a subset of wavelengths and a subset of samples each time and compares the calculated stomatal conductance coming from the spectra to that of the measured stomatal conductance of that specific data subset (one regression node within one tree within the forest). Thus, it seeks to minimize an RMSE function between the two measures. The wavelengths that were able to obtain the lowest RMSE in each iteration over all the nodes and the trees in the forest are then flagged and regarded as “important” by the algorithm. This algorithm is highly resilient to over-fitting problems that may arise due to noise within the dataset by generating of a large number of data subsets (trees) [36].
RF was pruned on three different levels: the number of trees in the forest (colors of the curves (Figure 5), the percent number of features to consider in each branch split (Figure 5 the x-axis values), and the maximum depth to which a tree may divide the dataset (Figure 5 panels a–k), as suggested by [25]. Each point within the panels represented a different set of flagged wavelengths. The general behavior of the algorithm shows that, with an increase in branch number, the RMSE decreased in a logarithmic trend. Only after passing one-third of the total depth of the trees, the trend became noisy between the various numbers of trees within the forest (compare Figure 5E to Figure 5A). When the depth of the tree passed half of its maximum depth (especially in forests with the minimum number of trees, see the blue colored curves in Figure 5), the RMSE trend revealed a local minima and complete dispersion of the trend. For example, in Figure 5J, each trend obtained a different form with a local minima for each size of the forests. The lowest RMSE was not necessarily reached for the maximum number of trees, depth, and samples. Instead, the best architecture of the random forest was found to be at about two-thirds of the maximum depth, with 20 percent selection of attributes within each branch split and 250 trees in the forest (Figure 5G, bold black arrow).

3.2. Validation of Feature Selection

The random forest algorithm can predict parameters by its non-linear regression algorithm [37], yet, its prediction capability is limited to the calibrated dataset [38]. Therefore, in search of a viable equation or model that can relate actual stomatal conductance to the selected wavelengths, we first tried to build a multi-linear regression model (Supplementary Figure S1). The model could not be assembled due to a violation of the predominant assumption that each of the predictors obtains a partial linear relationship with the dependent variable. This was probably because some of the features selected by the RF mechanism were correlated. In order to neutralize that co-linearity, we projected the data into a latent structure and assembled a partial least squares regression [27] (Figure 6).
Partial least squares regression is a regularized regression method able to lower the dimensionality of the spectra through projection into a latent structure, where the new set of variables, each based on a combination of the original wavelengths, are now independent of each other. These latent variables preserve most of the variance of the original dataset. The data were divided into a 75:25 training/testing subset. During calibration of the model, the model presented a similar underlying representation of the stomatal conductance between the two years of experimentation—note the general shape of the red dots compared to the blue dots (Figure 6A). We tried to identify meaningful clusters within the scores plot by using the discrete dates during each year and water potentials (Supplementary Figure S2). However, we did not have success in associating either classification with stomatal conductance values. We did manage to divide the calibration set into four clusters using a squared Euclidian distance range within a k-means clusters technique, however, this was not correlated with any of our predictor classes. The optimum model was selected across four components, where both the calibration and the cross-validation tests reached about 80% of the explained variance at the fourth principal component (Figure 6C). However, the projected model only succeeded to predict at R2 = 0.23 of the behavior of the stomatal conductance in the test subset. Thus, it was not much better than the simpler method of NDI, but it did manage to cancel out the natural clustering seen in the NDI technique correlation plot. Specifically, the model had difficulties in predicting the stomatal conductance values at the range of 400–600 mmol H2O m−2 s−1. These were the treatments with a high stomatal conductance, where the cotton plant was adequately irrigated, and the explanation for this difficulty can be seen clearly upon inspecting Figure 3A. While the –1.4 MPa treatment should have been at least at the same level of the –1.8 MPa treatment, it declined, even if not statistically significant, and this was probably the reason for the failure of the predictive model. The PLS-R cannot decide which of the original features are the most important to the model, and thus we implemented an ANN instead (Figure 7). A standard ANN architecture consists of input nodes that receive the important wavelengths for prediction of stomatal conductance. They are then transferred towards a hidden layer where, along the way, they receive new values via a non-linear transfer function (usually a sigmoid function). Then, they are transferred again into the output node, this time with a linear function. Finally, the ANN calculates a value of stomatal conductance and compares it to the original value. The weight matrix that was created along the way is changed repeatedly until the bias term is minimized and the weights function is optimized [30]. The desired result should be a linear correlation between the spectral information and the stomatal conductance values.
We constructed a back-propagated one hidden layer standard architecture, which was proven in the past to correctly predict non-linear mathematical relations (Figure 7) [29]. The ANN algorithm succeeded in creating a linear relationship between 20 features out of the 23 features originally found by the RF algorithm. This model can reach stomatal conductance out of spectral information on the test-subset with R2 = 0.54 accuracy. We also checked the performance of the procedure with various statistical tests (Table 2) [28].
The ANN architecture correlates with a Pearson correlation at 0.7 between the measured and the predicted stomatal conductance. The “error-free” percentage of the model on the test set had 0.82 confidence, decreasing by 0.1 units from the calibration set, which implied the strength of such a model.

4. Discussion

The NDI technique pinpoints four regions that may be connected to stomatal conductance. The first region “red-edge” [39] has been long known to be related to plant stress spectral range and has been shown to relate to evapotranspiration in general [12]. It happens because this region in the spectrum is layered with both physiological and chemical processes. On one hand, it borders the absorption of the photosynthetic pigments Chl a and Chl b [40] and, on the other hand, it reflects the photosynthetic activity of the crop [41]. Therefore, it is expected that, with a higher wellbeing, the magnitude of the difference between two plateaus in the reflectance spectrum (Figure 3A) will increase [42].
The second range relates to the reflectance of the mesophyll tissue of the plant and encompasses many different remotely-sensed traits such as nitrogen concentration [43], pest response-related indices [44], and disease-related indices [45]. The third region relates to water content and cellular structures, such as lignin and cellulose, which are part of the water transfer vessel network [46]. The fourth region relates to starch molecules, which relate indirectly to transpiration, in that it is being synthesized as a transient product of photosynthesis within the leaf’s tissues. Thus, it can be argued that, with higher stomatal conductance, more starch is created and, hence, the relationship between spectral properties and chemical activity obtains an increased correlation [47,48]. When generalizing the NDI technique, the horizontal hot spot correlations was in the red-edge region, between 639 nm and 800 nm, with an additional vertical hot spot region spanning 740–1047 nm and 1455–1661 nm. This generalization corroborates the importance of the red-edge region as found in the private case of NDI when all coefficients equaled one.
When inspecting the optimal random forest architecture (Figure 5G, bold black arrow), the selected architecture included 23 flagged wavelengths (corresponds to 10% of the wavelengths in the dataset, (Table 3)) [49]. The Fraunhofer oxygen absorbance band O2A region was selected as the most important region to detect stomatal conductance in the spectra. This region overlaps the fluorescence emission during photosynthesis, which affects the magnitude of the reflected spectrum [41]. It corroborates the dependence of stomatal conductance on photosynthetic activity.
Interestingly, the RF algorithm also succeeded in pinpointing the fact that lignin is a very important feature for detection of stomatal conductance, even more than water absorption bands. Mutations in lignin-synthesizing enzymes have been shown to lower the turgor pressure of the plant and generally decrease stomatal conductance and transpiration, thus corroborating this finding as well [68]. Finally, the RF algorithm succeeded in eliciting diseases and pathogen response wavelengths, which are related to stomatal conductance activity. The relationship between plant–pathogen interaction and stomatal conductance was highlighted in past studies, e.g., downy mildew on cucumber leaves [69], carbon starvation in poplar stems caused by various fungi [70], and transpiration decrease in bean by anthracnose [56]. Although these studies corroborate our findings, it should be noted that the pathogen or the disease affected mostly photosynthesis within the plant, where attenuation in stomatal conductance is a secondary effect of the reaction of the plant to the stress in order to sustain photosynthetic activity.
In searching for a positive correlation between the important wavelengths and the actual stomatal conductance, a PLS-R model and an ANN were selected. In the PLS-R constructed model, each component was found to describe a different relation within the spectrum (Figure 6B), where: (a) factor 1 related to tissue structural wavelengths (76%); (b) factors 2–3 related to the water content in the plant (5%); (c) factor 4 related to the oxygen absorption band in the reflectance spectrum (2%). However, as the PLS-R model succeeded in relating the physiological phenomenon to the spectrum only moderately, it implies that a PLS-R model can be used to detect a stressed plant because it differentiates between the maximum and the minimum irrigation treatments well, but it cannot be used to detect more subtle attenuations in the data. Therefore, a more robust statistical engine is required in order to take into account the correlation between the various wavelengths isolated, a task which was eventually achieved by the ANN algorithm in this study.
There are two main sources of error in this study that need to be addressed in future studies. First, the ground truth technique for measurement of stomatal conductance differed in the two seasons (AP4, Delta-t, UK in 2018 and Licor 6800 photosynthesis system, Li-Cor Biosciences, IL, USA in 2019) (). The authors suggest creating a calibration factor between the two units on a pre-determined gradient irrigated plot where both units are used. Secondly, the two most irrigated treatments exhibited a mixed reaction in their stomatal conductance (Figure 4A). Although this behavior is expected, it affects the model’s construction by the artificial neural network, as it is sensitive to noise in the dataset [71]. It can explain the underestimation of stomatal conductance at the 400–600 mmole H2O m−2 s−1 (Figure 7). In order to avoid this in the future, the authors suggest a wider irrigation treatment gradient when calibrating a regression model. An additional step that can be taken is to use herbicides that attenuate the plant’s water budget artificially, thus a synthetic effect of stomatal conductance is achieved as well as better control of the physiological phenomenon.
While this study introduces advanced statistical algorithms to relate physiological activity such as stomatal conductance to spectral measurements, this study is limited to the meteorological conditions of Israel and cotton plants only. Several steps are needed in order to generalize the study and validate it in different meteorological conditions: (a) corroborate the measured behavior of the crop with radiative transfer models that account for atmosphere attenuation and its effect on the electromagnetic spectrum, for example, MODTRAN [72], 6S [73], and radiative transfer models of crops, e.g., PROSPECT, which returns a simulated reflectance profile that can be compared with the actual measurements [10], and SCOPE [74] for a simulation of photosynthesis in the given conditions; (b) develop additional formulation that takes into account the geometry of the crop such that, for example, the leaf angle distribution is taken into account [11]; and finally, (c) the authors suggest repeating this study on a large scale for various crops in different phenological stages in order to isolate important key features in the reflectance spectrum that are shared across species and that can improve prediction of stomatal conductance.
Being able to define stomatal conductance at 20 wavelengths is a promising step towards direct plant physiology assessment with remote sensing techniques. However, both the equipment needed for SWIR measurement, which is expensive, as well as the computer power, which is needed in order to compute a 20 wavelength model, render this study as purely academic. An additional analysis is required in order to construct a simpler model that relates fewer wavelengths to physiological activity.

5. Conclusions

This study introduced an improvement to current chemometric methodologies and intended to detect and extract physiological activity from reflectance spectra. Specifically, this study found the regions that responded mostly to irrigation treatments in cotton plants were photosynthesis and red-edge in the NIR and lignin and water-content in the SWIR spectral regions. When generalizing coefficient of determination contour maps and selecting bi-wavelengths indices, we showed that a three-fold improvement was achieved in correlating the spectral information to stomatal conductance when compared to the classic approach. However, only two wavelengths were not enough to relate spectral measurements to stomatal conductance due to the diverse biophysical and biochemical processes that affect the conductance. Random forest of regression trees isolated 23 out of the overall 231 wavelengths. These related to water vessel structural constituents, photosynthesis, and plant health wavelengths. These wavelengths revealed new traits that relate to stomatal conductance and are important in designing a remote sensing model. They also corroborated past findings about known wavelengths and their relation to stomatal conductance, hence a physiological activity. An artificial neural network succeeded in relating the spectral data within the 23 wavelengths to stomatal conductance at R2 = 0.54 with 82% error free confidence on the test sub-set, therefore validating the RF findings. While this study showed the advantage of using machine learning algorithms in identifying direct physiological activity such as stomatal conductance, it should be noted that this study was only the first step towards a robust general remote sensing model of stomatal conductance and plant physiological wellbeing. The examination of the effects of different crop varieties and types is needed in order to generalize the relationship between spectral and stomatal conductance measurements. It will contribute to the understanding of which wavelengths are related to all cases and why there are differences in spectral measurements when extracting information across species on stomatal conductance specifically and plant physiology in general.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/12/14/2213/s1, Figure S1: Multiple Linear Regression (MLR) partial correlations between each of the 24 wavelengths selected by the Random Forest algorithm and measured stomatal conductance., Figure S2: Representations of visual cluster analysis within the scores plot of the Partial Least Squares Regression algorithm during model construction on of stomatal index of a cotton plant.

Author Contributions

O.L. conceived the idea for the study; O.L., A.N., O.R., R.D., S.L., and T.A designed the experiments; R.D., S.L., Y.T., and T.A. performed the experiments; O.L., S.V.-T., and L.H. constructed the dataset; O.L., S.V.-T., L.H., and T.A. pre-processed the data; O.L., S.V.-T., L.H., R.D., S.L., and Y.T. analyzed the results, O.L., A.N., S.V.-T., and L.H. wrote the manuscript; O.L., A.N., O.R., S.V.-T., L.H., R.D., S.L., Y.T., and T.A. proofed and prepared the manuscript for publication. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the “Russell-Berrie Foundation––Making a Difference” grant number BG-1596-13.

Acknowledgments

The author would like to thank Yonatan Yerushalmi for his superior technical assistance and MIGAL for their logistics support for this project.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Collatz, G.J.; Ball, J.T.; Grivet, C.; Berry, J.A. Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: A model that includes a laminar boundary layer. Agric. For. Meteorol. 1991, 54, 107–136. [Google Scholar] [CrossRef]
  2. Buckley, T.N. Modeling Stomatal Conductance. Plant Physiol. 2017, 174, 572–582. [Google Scholar] [CrossRef] [PubMed]
  3. Carter, G.A. Reflectance Wavebands and Indices for Remote Estimation of Photosynthesis and Stomatal Conductance in Pine Canopies. Remote Sens. Environ. 1998, 63, 61–72. [Google Scholar] [CrossRef]
  4. Field, C.B.; Randerson, J.T.; Malmström, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ. 1995, 51, 74–88. [Google Scholar] [CrossRef] [Green Version]
  5. Jackson, R.D.; Idso, S.B.; Reginato, R.J.; Pinter, P.J., Jr. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar] [CrossRef]
  6. Jones, H.G.; Stoll, M.; Santos, T.; Sousa, C.D.; Chaves, M.M.; Grant, O.M. Use of infrared thermography for monitoring stomatal closure in the field: Application to grapevine. J. Exp. Bot. 2002, 53, 2249–2260. [Google Scholar] [CrossRef] [PubMed]
  7. Gao, B.-C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
  8. Penuelas, J.; Filella, I.; Gamon, J.A. Assessment of photosynthetic radiation-use efficiency with spectral reflectance. New Phytol. 1995, 131, 291–296. [Google Scholar] [CrossRef]
  9. Peñuelas, J.; Filella, I.; Biel, C.; Serrano, L.; Save, R. The reflectance at the 950–970 nm region as an indicator of plant water status. Int. J. Remote Sens. 1993, 14, 1887–1905. [Google Scholar] [CrossRef]
  10. Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
  11. Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.-M. Detecting vegetation leaf water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77, 22–33. [Google Scholar] [CrossRef]
  12. Marshall, M.; Thenkabail, P.; Biggs, T.; Post, K. Hyperspectral narrowband and multispectral broadband indices for remote sensing of crop evapotranspiration and its components (transpiration and soil evaporation). Agric. For. Meteorol. 2016, 218–219, 122–134. [Google Scholar] [CrossRef] [Green Version]
  13. Xiao, Y.; Zhao, W.; Zhou, D.; Gong, H. Sensitivity Analysis of Vegetation Reflectance to Biochemical and Biophysical Variables at Leaf, Canopy, and Regional Scales. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4014–4024. [Google Scholar] [CrossRef]
  14. Rodriguez, J.M.; Ustin, S.L.; Riaño, D. Contributions of imaging spectroscopy to improve estimates of evapotranspiration. Hydrol. Process. 2011, 25, 4069–4081. [Google Scholar] [CrossRef]
  15. Burkart, A.; Cogliati, S.; Schickling, A.; Rascher, U. A Novel UAV-Based Ultra-Light Weight Spectrometer for Field Spectroscopy. IEEE Sens. J. 2014, 14, 62–67. [Google Scholar] [CrossRef]
  16. Rascher, U.; Alonso, L.; Burkart, A.; Cilia, C.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M.; Guanter, L.; Hanus, J.; et al. Sun-induced fluorescence—A new probe of photosynthesis: First maps from the imaging spectrometer HyPlant. Glob. Chang. Biol. 2015, 21, 4673–4684. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  17. Gordon, H.R.; Wang, M. Influence of oceanic whitecaps on atmospheric correction of ocean-color sensors. Appl. Opt. AO 1994, 33, 7754–7763. [Google Scholar] [CrossRef]
  18. Rinnan, Å.; van den Berg, F.; Engelsen, S.B. Review of the most common pre-processing techniques for near-infrared spectra. Trac Trends Anal. Chem. 2009, 28, 1201–1222. [Google Scholar] [CrossRef]
  19. Cochran, W.G. The distribution of the largest of a set of estimated variances as a fraction of their total. Ann. Eugen. 1941, 11, 47–52. [Google Scholar] [CrossRef]
  20. Barnes, R.J.; Dhanoa, M.S.; Lister, S.J. Standard normal variate transformation and de-trending of near-infrared diffuse reflectance spectra. Appl. Spectrosc. 1989, 43, 772–777. [Google Scholar] [CrossRef]
  21. Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
  22. Van Rossum, G. Python Programming Language. In Proceedings of the USENIX Annual Technical Conference, Santa Clara, CA, USA, 17–22 June 2007; Volume 41, p. 36. [Google Scholar]
  23. Powell, M.J. A view of algorithms for optimization without derivatives. Math. Today-Bull. Inst. Math. Its Appl. 2007, 43, 170–174. [Google Scholar]
  24. Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
  25. Nan, F.; Wang, J.; Saligrama, V. Pruning random forests for prediction on a budget. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 2334–2342. [Google Scholar]
  26. Andrews, D.F. A robust method for multiple linear regression. Technometrics 1974, 16, 523–531. [Google Scholar] [CrossRef]
  27. Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
  28. Sousa, S.I.V.; Martins, F.G.; Alvim-Ferraz, M.C.M.; Pereira, M.C. Multiple linear regression and artificial neural networks based on principal components to predict ozone concentrations. Environ. Model. Softw. 2007, 22, 97–103. [Google Scholar] [CrossRef]
  29. Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
  30. Hecht-Nielsen, R. Theory of the backpropagation neural network. In Neural Networks for Perception; Elsevier: Amsterdam, The Netherlands, 1992; pp. 65–93. [Google Scholar]
  31. Jones, C.L.; Weckler, P.R.; Maness, N.O.; Stone, M.L.; Jayasekara, R. Estimating water stress in plants using hyperspectral sensing. In Proceedings of the 2004 ASAE Annual Meeting, Ottawa, ON, Canada, 1–4 August 2004; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2004; p. 1. [Google Scholar]
  32. Gamon, J.A.; Field, C.B.; Goulden, M.L.; Griffin, K.L.; Hartley, A.E.; Joel, G.; Peñuelas, J.; Valentini, R. Relationships between NDVI, canopy structure, and photosynthesis in three Californian vegetation types. Ecol. Appl. 1995, 5, 28–41. [Google Scholar] [CrossRef] [Green Version]
  33. Gamon, J.; Serrano, L.; Surfus, J.S. The photochemical reflectance index: An optical indicator of photosynthetic radiation use efficiency across species, functional types, and nutrient levels. Oecologia 1997, 112, 492–501. [Google Scholar] [CrossRef]
  34. Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
  35. Sellers, P.J. Canopy reflectance, photosynthesis, and transpiration, II. The role of biophysics in the linearity of their interdependence. Remote Sens. Environ. 1987, 21, 143–183. [Google Scholar] [CrossRef]
  36. Abdel-Rahman, E.M.; Ahmed, F.B.; Ismail, R. Random forest regression and spectral band selection for estimating sugarcane leaf nitrogen concentration using EO-1 Hyperion hyperspectral data. Int. J. Remote Sens. 2013, 34, 712–728. [Google Scholar] [CrossRef]
  37. Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
  38. Horning, N. Random Forests: An algorithm for image classification and generation of continuous fields data sets. In Proceedings of the International Conference on Geoinformatics for Spatial Infrastructure Development in Earth and Allied Sciences, Osaka, Japan, 9–11 December 2010. [Google Scholar]
  39. Smith, K.L.; Steven, M.D.; Colls, J.J. Use of hyperspectral derivative ratios in the red-edge region to identify plant stress responses to gas leaks. Remote Sens. Environ. 2004, 92, 207–217. [Google Scholar] [CrossRef]
  40. Gitelson, A.A.; Merzlyak, M.N. Remote sensing of chlorophyll concentration in higher plant leaves. Adv. Space Res. 1998, 22, 689–692. [Google Scholar] [CrossRef]
  41. Zarco-Tejada, P.J.; Pushnik, J.C.; Dobrowski, S.; Ustin, S.L. Steady-state chlorophyll a fluorescence detection from canopy derivative reflectance and double-peak red-edge effects. Remote Sens. Environ. 2003, 84, 283–294. [Google Scholar] [CrossRef]
  42. Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Proceedings of the Earth Resources Technology Satellite Symposium; NASA SP-351; NASA: Washington, DC, USA, 1973; Volume 1, pp. 309–317. [Google Scholar]
  43. Lee, Y.J.; Yang, C.M.; Chang, K.W.; Shen, Y. A simple spectral index using reflectance of 735 nm to assess nitrogen status of rice canopy. Agron. J. 2008, 100, 205–212. [Google Scholar] [CrossRef]
  44. Liu, Z.; Cheng, J.; Huang, W.; Li, C.; Xu, X.; Ding, X.; Shi, J.; Zhou, B. Hyperspectral discrimination and response characteristics of stressed rice leaves caused by rice leaf folder. In Proceedings of the International Conference on Computer and Computing Technologies in Agriculture, Beijing, China, 29–31 October 2011; Springer: Berlin, Germany, 2011; pp. 528–537. [Google Scholar]
  45. Zhao, J.; Zhang, D.; Luo, J.; Dong, Y.; Yang, H.; Huang, W. Characterization of the rice canopy infested with brown spot disease using field hyperspectral data. Wuhan Univ. J. Nat. Sci. 2012, 17, 86–92. [Google Scholar] [CrossRef]
  46. Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
  47. Mehrotra, R.; Siesler, H.W. Application of mid infrared/near infrared spectroscopy in sugar industry. Appl. Spectrosc. Rev. 2003, 38, 307–354. [Google Scholar] [CrossRef]
  48. Peet, M.M.; Huber, S.C.; Patterson, D.T. Acclimation to high CO2 in monoecious cucumbers: II. Carbon exchange rates, enzyme activities, and starch and nutrient concentrations. Plant Physiol. 1986, 80, 63–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  49. Menze, B.H.; Kelm, B.M.; Masuch, R.; Himmelreich, U.; Bachert, P.; Petrich, W.; Hamprecht, F.A. A comparison of random forest and its Gini importance with standard chemometric methods for the feature selection and classification of spectral data. BMC Bioinform. 2009, 10, 213. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  50. Singh, D.; Singh, S. Geospatial Modeling of Canopy Chlorophyll Content Using High Spectral Resolution Satellite Data in Himalayan Forests. Clim. Chang. Environ. Sustain. 2018, 6, 20–34. [Google Scholar] [CrossRef]
  51. Yang, C.-M.; Cheng, C.-H.; Chen, R.-K. Changes in spectral characteristics of rice canopy infested with brown planthopper and leaffolder. Crop Sci. 2007, 47, 329–335. [Google Scholar] [CrossRef]
  52. Yi, Q.; Huang, J.; Wang, F.; Wang, X. Quantifying biochemical variables of corn by hyperspectral reflectance at leaf scale. J. Zhejiang Univ. Sci. B 2008, 9, 378. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  53. Wang, Z.; Skidmore, A.K.; Darvishzadeh, R.; Wang, T. Mapping forest canopy nitrogen content by inversion of coupled leaf-canopy radiative transfer models from airborne hyperspectral imagery. Agric. For. Meteorol. 2018, 253, 247–260. [Google Scholar] [CrossRef]
  54. Deel, L.N. Assessing the cumulative impact of disturbance on canopy structure and chemistry in Appalachian forests. Master’s Thesis, West Virginia University, Morgantown, WV, USA, 2010. [Google Scholar]
  55. Dvořáček, V.; Štěrbová, L.; Matějová, E.; Bradová, J.; Hermuth, J. Reflectance Spectrometry as a Screening Tool for Prediction of Lutein Content in Diverse Wheat Species (Triticum spp.). Food Anal. Methods 2018, 11, 2579–2589. [Google Scholar] [CrossRef]
  56. Lobato, A.K.S.; Gonçalves-Vidigal, M.C.; Vidigal Filho, P.S.; Andrade, C.A.B.; Kvitschal, M.V.; Bonato, C.M. Relationships between leaf pigments and photosynthesis in common bean plants infected by anthracnose. N. Z. J. Crop Hortic. Sci. 2010, 38, 29–37. [Google Scholar] [CrossRef]
  57. Junhua, B.; Shaokun, L.; Keru, W. The response of canopy reflectance spectrum for the cotton LAI and LAI inversion. Sci. Agric. Sin. 2007, 40, 63–69. [Google Scholar]
  58. Kusumo, B.H.; Hedley, M.J.; Hedley, C.B.; Tuohy, M.P. Measuring carbon dynamics in field soils using soil spectral reflectance: Prediction of maize root density, soil organic carbon and nitrogen content. Plant Soil 2011, 338, 233–245. [Google Scholar] [CrossRef]
  59. Clevers, J.; Van der Heijden, G.; Verzakov, S.; Schaepman, M.E. Estimating grassland biomass using SVM band shaving of hyperspectral data. Photogramm. Eng. Remote Sens. 2007, 73, 1141–1148. [Google Scholar] [CrossRef] [Green Version]
  60. Rollin, E.M.; Milton, E.J. Processing of high spectral resolution reflectance data for the retrieval of canopy water content information. Remote Sens. Environ. 1998, 65, 86–92. [Google Scholar] [CrossRef]
  61. Chatani, E.; Tsuchisaka, Y.; Masuda, Y.; Tsenkova, R. Water molecular system dynamics associated with amyloidogenic nucleation as revealed by real time near infrared spectroscopy and aquaphotomics. PLoS ONE 2014, 9, e101997. [Google Scholar] [CrossRef] [PubMed]
  62. Somdatta, C.; Chakrabarti, S. Pre-processing of hyperspectral data: A case study of Henry and Lothian Islands in Sunderban Region, West Bengal, India. Int. J. Geomat. Geosci. 2011, 2, 490. [Google Scholar]
  63. Mullen, K.E. Early Detection of Mountain Pine Beetle Damage in Ponderosa Pine Forests of the Black Hills Using Hyperspectral and WorldView-2 Data. Master’s Thesis, Minnesota State University, Mankato, MN, USA, 2016. [Google Scholar]
  64. Liu, Z.-Y.; Huang, J.-F.; Tao, R.-X. Characterizing and estimating fungal disease severity of rice brown spot with hyperspectral reflectance data. Rice Sci. 2008, 15, 232–242. [Google Scholar] [CrossRef]
  65. Basayigit, L.; Albayrak, S. Reflectance measurement of N, P and K content of wollypod vetch under different N, P and K fertilization. Asian J. Chem. 2007, 19, 5609. [Google Scholar]
  66. Kuska, M.; Wahabzada, M.; Leucker, M.; Dehne, H.-W.; Kersting, K.; Oerke, E.-C.; Steiner, U.; Mahlein, A.-K. Hyperspectral phenotyping on the microscopic scale: Towards automated characterization of plant-pathogen interactions. Plant Methods 2015, 11, 28. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  67. Zhao, D.; Reddy, K.R.; Kakani, V.G.; Read, J.J.; Carter, G.A. Corn (Zea mays L.) growth, leaf pigment concentration, photosynthesis and leaf hyperspectral reflectance properties as affected by nitrogen supply. Plant Soil 2003, 257, 205–218. [Google Scholar] [CrossRef]
  68. Bonawitz, N.D.; Chapple, C. The Genetics of Lignin Biosynthesis: Connecting Genotype to Phenotype. Annu. Rev. Genet. 2010, 44, 337–363. [Google Scholar] [CrossRef] [PubMed]
  69. Lindenthal, M.; Steiner, U.; Dehne, H.-W.; Oerke, E.-C. Effect of Downy Mildew Development on Transpiration of Cucumber Leaves Visualized by Digital Infrared Thermography. Phytopathology 2005, 95, 233–240. [Google Scholar] [CrossRef] [Green Version]
  70. Li, P.; Liu, W.; Zhang, Y.; Xing, J.; Li, J.; Feng, J.; Su, X.; Zhao, J. Fungal canker pathogens trigger carbon starvation by inhibiting carbon metabolism in poplar stems. Sci. Rep. 2019, 9, 10111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  71. An, G. The effects of adding noise during backpropagation training on a generalization performance. Neural Comput. 1996, 8, 643–674. [Google Scholar] [CrossRef]
  72. Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN Cloud and Multiple Scattering Upgrades with Application to AVIRIS. Remote Sens. Environ. 1998, 65, 367–375. [Google Scholar] [CrossRef]
  73. Vermote, E.; Tanré, D.; Deuzé, J.L.; Herman, M.; Morcrette, J.J.; Kotchenova, S.Y. Second simulation of a satellite signal in the solar spectrum-vector (6SV). 6S User Guide Version 2006, 3, 1–55. [Google Scholar]
  74. Verrelst, J.; Rivera, J.P.; van der Tol, C.; Magnani, F.; Mohammed, G.; Moreno, J. Global sensitivity analysis of the SCOPE model: What drives simulated canopy-leaving sun-induced fluorescence? Remote Sens. Environ. 2015, 166, 8–21. [Google Scholar] [CrossRef]
Remotesensing 12 02213 g001 550
Figure 1. Setup of experiments in Gadash Farm, Hula Valley, Israel. (A,B) represent the plant pot experiments during 2018 and 2019, respectively.
Figure 1. Setup of experiments in Gadash Farm, Hula Valley, Israel. (A,B) represent the plant pot experiments during 2018 and 2019, respectively.
Remotesensing 12 02213 g001
Remotesensing 12 02213 g002 550
Figure 2. Strategy of chemometric analysis and stomatal conductance index construction. Acronyms used in this figure: SNV = standard normal variate; NDI = Normalized Differential Index; PLS-R = partial least square regression; ANN = artificial neural network.
Figure 2. Strategy of chemometric analysis and stomatal conductance index construction. Acronyms used in this figure: SNV = standard normal variate; NDI = Normalized Differential Index; PLS-R = partial least square regression; ANN = artificial neural network.
Remotesensing 12 02213 g002
Remotesensing 12 02213 g003 550
Figure 3. An example of data acquired in the study (in this example, 2 July 19 at 10:30). (A) Averaged values of stomatal conductance gsw in (mmol H2O m−2 s−1). N = at least four independent samples and error bars represent standard error of the mean. Color scheme in this figure corresponds to the four water potential treatments, where yellow, grey, light brown, and blue represent the water potential readings −1.4, −1.8, −2.0, −2.5 MPa. (B) Reflectance signature of cotton at four water potential treatments. (C,D) Magnification of spectral reflectance where there is a correlation between spectra magnitude and water potential treatments. Panels (B–D) were smooth-averaged with an 11-pace window for the qualitative purpose of presentation.
Figure 3. An example of data acquired in the study (in this example, 2 July 19 at 10:30). (A) Averaged values of stomatal conductance gsw in (mmol H2O m−2 s−1). N = at least four independent samples and error bars represent standard error of the mean. Color scheme in this figure corresponds to the four water potential treatments, where yellow, grey, light brown, and blue represent the water potential readings −1.4, −1.8, −2.0, −2.5 MPa. (B) Reflectance signature of cotton at four water potential treatments. (C,D) Magnification of spectral reflectance where there is a correlation between spectra magnitude and water potential treatments. Panels (B–D) were smooth-averaged with an 11-pace window for the qualitative purpose of presentation.
Remotesensing 12 02213 g003
Remotesensing 12 02213 g004 550
Figure 4. Normalized Differential Spectral Index (NDI) of spectral data collected over the two-year experiment with a cotton plant. (A,C) represent a 53,361 pixelated graph (for 231 × 231 wavelength combinations), where each pixel is colored by the coefficient of determination (r2) as is defined to the right of the graph. Only half of the pixels are shown, as the grey area is their mirror image. (B,D) represent the correlation between the calculated NDI with the maximum R2. Each grey dot represents a stomatal conductance measurement out of the 658 samples of the dataset.
Figure 4. Normalized Differential Spectral Index (NDI) of spectral data collected over the two-year experiment with a cotton plant. (A,C) represent a 53,361 pixelated graph (for 231 × 231 wavelength combinations), where each pixel is colored by the coefficient of determination (r2) as is defined to the right of the graph. Only half of the pixels are shown, as the grey area is their mirror image. (B,D) represent the correlation between the calculated NDI with the maximum R2. Each grey dot represents a stomatal conductance measurement out of the 658 samples of the dataset.
Remotesensing 12 02213 g004
Remotesensing 12 02213 g005 550
Figure 5. Presentation of all the random forest (RF) architectures root mean squared error (RMSE) grade in stomatal conductance experiment. Panels A–J represent a different depth (marked with a relative unit) of the regression tree, starting at 3 for Panel A and ending at 23 for Panel K. Parameter Mtry relates to the percent number of features to consider when looking for the best branch split; RMSE stands for the Root Mean Squared Rrror between the models’ selected samples average and the overall samples’ average. Curve colors represent the size of the RF where blue, red, green, and purple stand for 50, 100, 250, and 500 regression trees. Each point includes all the dataset (452 samples) repeated five times and averaged. Bold black arrow represents selected architecture for analysis.
Figure 5. Presentation of all the random forest (RF) architectures root mean squared error (RMSE) grade in stomatal conductance experiment. Panels A–J represent a different depth (marked with a relative unit) of the regression tree, starting at 3 for Panel A and ending at 23 for Panel K. Parameter Mtry relates to the percent number of features to consider when looking for the best branch split; RMSE stands for the Root Mean Squared Rrror between the models’ selected samples average and the overall samples’ average. Curve colors represent the size of the RF where blue, red, green, and purple stand for 50, 100, 250, and 500 regression trees. Each point includes all the dataset (452 samples) repeated five times and averaged. Bold black arrow represents selected architecture for analysis.
Remotesensing 12 02213 g005
Remotesensing 12 02213 g006 550
Figure 6. Construction of stomatal conductance index with partial least squares regression. (A–C) represent the model construction on 75% of the samples in the data (calibration—494), and (D) comparison between the predicted stomatal conductance by the model and the measured stomatal conductance on 25% of the samples (test—164). (A) Scores plot of the calibration subset. Only the first two principal components out of total of four are shown. Colors represent the years. (B) Loading weights plot of the calibration subset in each of the four principal components of the model and per wavelength selected by the RF algorithm. (C) Explained variance of the calibration subset together with a leave-one-out cross validation test on the same subset. (D) Coefficient of determination represents the correlation between the predicted and the measured stomatal conductance.
Figure 6. Construction of stomatal conductance index with partial least squares regression. (A–C) represent the model construction on 75% of the samples in the data (calibration—494), and (D) comparison between the predicted stomatal conductance by the model and the measured stomatal conductance on 25% of the samples (test—164). (A) Scores plot of the calibration subset. Only the first two principal components out of total of four are shown. Colors represent the years. (B) Loading weights plot of the calibration subset in each of the four principal components of the model and per wavelength selected by the RF algorithm. (C) Explained variance of the calibration subset together with a leave-one-out cross validation test on the same subset. (D) Coefficient of determination represents the correlation between the predicted and the measured stomatal conductance.
Remotesensing 12 02213 g006
Remotesensing 12 02213 g007 550
Figure 7. Results of stomatal conductance calculation by the ANN model compared to the actual acquired data.
Figure 7. Results of stomatal conductance calculation by the ANN model compared to the actual acquired data.
Remotesensing 12 02213 g007
Table
Table 1. Meteorological conditions during the experiment in cotton in 2018 and 2019.
Table 1. Meteorological conditions during the experiment in cotton in 2018 and 2019.
#YearDateTimeVPD Ϯ
(kPa)		Wind Speed
(ms−1)		Light
Intensity
(Wm−2)		RH †
(%)		Average
Air Temp.
(°C)
1201825.0611:002.88299439.932.1
12:303.263.7103036.633.4
226.0610:302.52299346.731.9
12:003.184.4104937.833.3
302.0710:302.371.0938.548.131.2
13:003.952.2100333.335.9
403.0710:302.511.697346.731.8
13:003.251.899740.534.4
509.0710:302.911.399042.733.2
12:003.631.41036.03635.2
610.0710:303.121.498838.333.1
11:303.682.9105131.634.2
716.0710:302.881.195242.132.8
13:003.922.398336.736.7
817.0710:302.531.89464932.7
13:003.093.799945.135
930.0710:302.533.1742.346.531.9
13:003.014.5102840.833.2
1009.0810:302.631.792049.633.7
11:303.431.895440.735.5
1201905.0810:301.771.482060.230.9
207.0810:302.381785.147.731.3
12:303.11.393041.433.9
314.0810:302.71.2735.744.332.4
415.0810:302.162.2766.252.731.3
12:302.894.190344.133.5
521.0810:302.672.3766.544.632.2
12:003.14.287539.333.3
626.0810:3021.2740.555.631
12:303.642.287438.235.8
728.0810:302.120.6695.65531.9
12:303.311.784642.335.4
802.0910:302.180.7739.552.331.3
12:304.143.987630.436
904.0910:301.830.573754.329
12:302.6183446.332.3
1009.0910:301.80.7704.357.630
12:302.85279544.233.3
† RH = relative humidity in percentage; Ϯ VPD = Vapor Pressure Deficit.
Table
Table 2. Artificial neural network (ANN) performance values on construction of stomatal conductance index.
Table 2. Artificial neural network (ANN) performance values on construction of stomatal conductance index.
Performance ParameterTrainTest
Correlation (R)0.750.71
Over/Under estimation of model (MBE Ϯ)0.020.03
Absolute Error (MAE †)0.430.59
RMSE ‡0.660.73
“Error-Free” results (d2 connectivity)0.930.82
Ϯ MBE = Mean Biased Error; † MAE = Mean Absolute Error; ‡ RMSE = Root Mean Squared Error.
Table
Table 3. Important wavelengths in the selected random forest architecture and their physiological meaning according to the literature. (R.U.) stands for Relative Units.
Table 3. Important wavelengths in the selected random forest architecture and their physiological meaning according to the literature. (R.U.) stands for Relative Units.
Feature (nm)Importance (R.U.) ‡MeaningReference
7573.13Chlorophyll content, pest related, atmospheric oxygen absorption feature[50,51]
[46]
7602.98Atmospheric oxygen absorption feature, chlorophyll content, nitrogen concentration[52]
7262.65Red-edge, chlorophyll content[45,53]
13532.29Biochemical process, lutein content, water content[54,55]
9222.06Moisture, potassium level, oil level[46]
7541.95Disease related band (anthracnose), atmospheric oxygen absorption feature[56]
8221.84Disease related band (brown spot disease in rice)[45]
7231.71Leaf Area Index, red-edge[57]
14551.43Lignin, water content[58]
11351.40Lignin, dry matter, chlorophyll content[59]
9741.29Water content[60]
13821.25Water content, water molecules[61]
15171.25Water vapor, protein, nitrogen[62]
11521.21Pest response related, lignin[63]
12731.14Water, lignin, cellulose[46]
7461.13Fungal disease response-related[64]
9681.12Water content[8,46]
8911.11Disease-related[31]
14891.04Cellulose, sugar[46]
7620.97Nitrogen level, fluorescence level[41,65]
7430.97Plant-pathogen interactions[66]
9280.92Oil[46]
14330.90Unknown
7210.89Chlorophyll related, nitrogen-related[67]
9660.87water, starch[46]
‡ R.U. = Relative Units.

Share and Cite

MDPI and ACS Style

Vitrack-Tamam, S.; Holtzman, L.; Dagan, R.; Levi, S.; Tadmor, Y.; Azizi, T.; Rabinovitz, O.; Naor, A.; Liran, O. Random Forest Algorithm Improves Detection of Physiological Activity Embedded within Reflectance Spectra Using Stomatal Conductance as a Test Case. Remote Sens. 2020, 12, 2213. https://doi.org/10.3390/rs12142213

AMA Style

Vitrack-Tamam S, Holtzman L, Dagan R, Levi S, Tadmor Y, Azizi T, Rabinovitz O, Naor A, Liran O. Random Forest Algorithm Improves Detection of Physiological Activity Embedded within Reflectance Spectra Using Stomatal Conductance as a Test Case. Remote Sensing. 2020; 12(14):2213. https://doi.org/10.3390/rs12142213

Chicago/Turabian Style

Vitrack-Tamam, Snir, Lilach Holtzman, Reut Dagan, Shai Levi, Yuval Tadmor, Tamir Azizi, Onn Rabinovitz, Amos Naor, and Oded Liran. 2020. "Random Forest Algorithm Improves Detection of Physiological Activity Embedded within Reflectance Spectra Using Stomatal Conductance as a Test Case" Remote Sensing 12, no. 14: 2213. https://doi.org/10.3390/rs12142213

APA Style

Vitrack-Tamam, S., Holtzman, L., Dagan, R., Levi, S., Tadmor, Y., Azizi, T., Rabinovitz, O., Naor, A., & Liran, O. (2020). Random Forest Algorithm Improves Detection of Physiological Activity Embedded within Reflectance Spectra Using Stomatal Conductance as a Test Case. Remote Sensing, 12(14), 2213. https://doi.org/10.3390/rs12142213

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop