Temporal-Spatial Frequency Rockfall Data from Open-Pit Highwalls Using a Low-Cost Monitoring System
Abstract
:1. Introduction
2. Materials and Methods
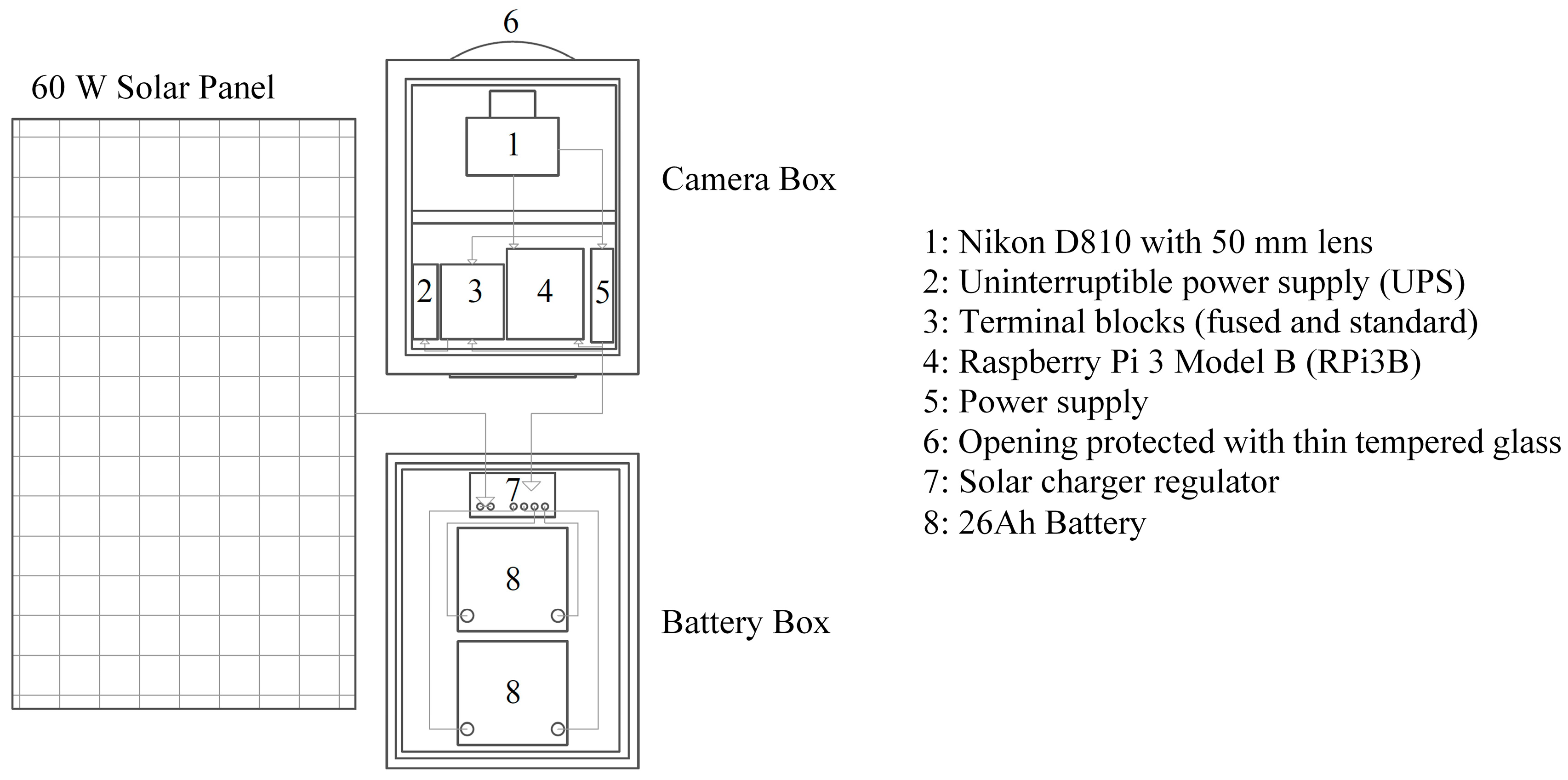
2.1. Photogrammetric Monitoring System
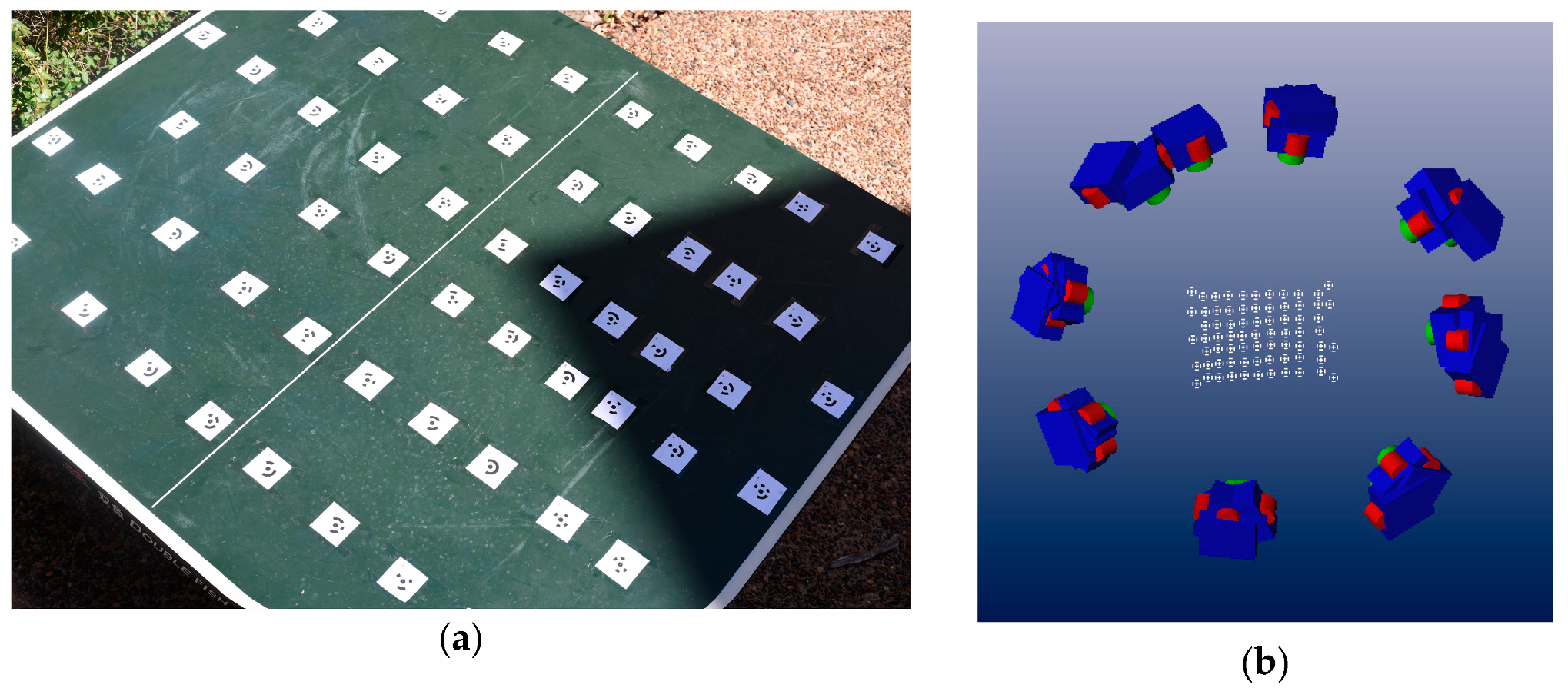
2.2. System Calibration and Installation
- Positioning of the mounting poles and bases in the desired locations.
- Mounting of the camera boxes on to the poles.
- Connection of the camera boxes to their power supply (solar panel and batteries).
- Trial set-up of the camera boxes towards the section of the rock wall to be monitored.
- Acquisition of preliminary images from each camera to check overlap and focus.
- Final fixing of the orientation of the cameras by locking the regulation screws on the mounting bracket.
- Determination of the position of the camera boxes using a retroreflective prism or GNSS antenna mounted on the camera boxes (Figure 4). If full georeferencing is required, at least one GCP on the rock wall must also be measured.
- Acquisition of an initial stereo-pair for subsequent offline estimation of the site-specific EO parameters.
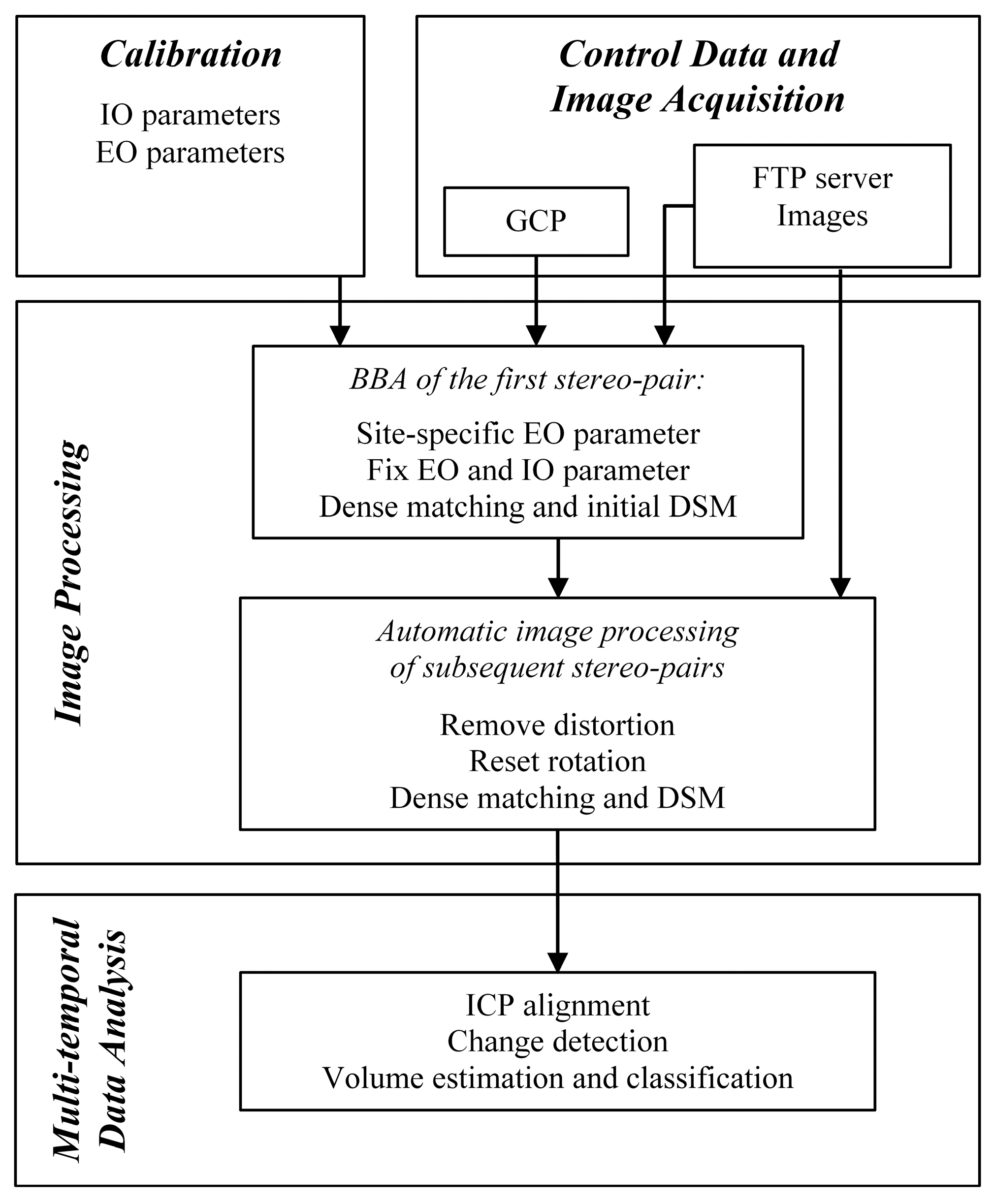
2.3. Image Processing
2.4. Multi-Temporal Data Analysis
3. System Validation
4. Application
4.1. Site Description
4.2. System Installation and Set-Up Validation
4.3. Multi-Temporal Data Analysis
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Giacomini, A.; Thoeni, K.; Lambert, C.; Booth, S.; Sloan, S.W. Experimental study on rockfall drapery systems for open pit highwalls. Int. J. Rock Mech. Min. Sci. 2012, 56, 171–181. [Google Scholar] [CrossRef]
- Ferrari, F.; Giacomini, A.; Thoeni, K. Qualitative Rockfall Hazard Assessment: A Comprehensive Review of Current Practices. Rock Mech. Rock Eng. 2016, 49, 2865–2922. [Google Scholar] [CrossRef]
- Royán, M.J.; Abellán, A.; Jaboyedoff, M.; Vilaplana, J.M.; Calvet, J. Spatio-temporal analysis of rockfall pre-failure deformation using Terrestrial LiDAR. Landslides 2014, 11, 697–709. [Google Scholar] [CrossRef]
- Macciotta, R.; Hendry, M.; Cruden, D.M.; Blais-Stevens, A.; Edwards, T. Quantifying rock fall probabilities and their temporal distribution associated with weather seasonality. Landslides 2017, 14, 2025–2039. [Google Scholar] [CrossRef]
- Terzaghi, K. Stability of steep slopes on hard unweathered rock. Geotechnique 1962, 12, 251–270. [Google Scholar] [CrossRef]
- Bjerrum, L.; Jørstad, F.A.; Jørstad, F.A. Stability of Rock Slopes in Norway; Norges Geotekniske Institute: Oslo, Norway, 1968. [Google Scholar]
- Peckover, F.L. Treatment of Rock Falls on Railway Lines; American Railway Engineering Association: Montreal, QC, Canada, 1972. [Google Scholar]
- Delonca, A.; Gunzburger, Y.; Verdel, T. Statistical correlation between meteorological and rockfall databases. Nat. Hazards Earth Syst. Sci. 2014, 14, 1953–1964. [Google Scholar] [CrossRef] [Green Version]
- Collins, B.D.; Stock, G.M. Rockfall triggering by cyclic thermal stressing of exfoliation fractures. Nat. Geosci. 2016, 9, 395–400. [Google Scholar] [CrossRef]
- Macciotta, R. Review and latest insights into rock fall temporal variability associated with weather. Proc. Inst. Civ. Eng. Geotech. Eng. 2019, 172, 556–568. [Google Scholar] [CrossRef]
- Krautblatter, M.; Moser, M. A nonlinear model coupling rockfall and rainfall intensity based on a four year measurement in a high Alpine rock wall (Reintal, German Alps). Nat. Hazards Earth Syst. Sci. 2009, 9, 1425–1432. [Google Scholar] [CrossRef] [Green Version]
- Macciotta, R.; Martin, C.D.; Edwards, T.; Cruden, D.M.; Keegan, T. Quantifying weather conditions for rock fall hazard management. Georisk 2015, 9, 171–186. [Google Scholar] [CrossRef]
- Jaboyedoff, M.; Oppikofer, T.; Abellán, A.; Derron, M.H.; Loye, A.; Metzger, R.; Pedrazzini, A. Use of LIDAR in landslide investigations: A review. Nat. Hazards 2012, 61, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Abellán, A.; Oppikofer, T.; Jaboyedoff, M.; Rosser, N.J.; Lim, M.; Lato, M.J. Terrestrial laser scanning of rock slope instabilities. Earth Surf. Process. Landf. 2014, 39, 80–97. [Google Scholar] [CrossRef]
- Scaioni, M.; Longoni, L.; Melillo, V.; Papini, M. Remote Sensing for Landslide Investigations: An Overview of Recent Achievements and Perspectives. Remote Sens. 2014, 6, 9600–9652. [Google Scholar] [CrossRef] [Green Version]
- Jaboyedoff, M.; Ornstein, P.; Rouiller, J.-D. Design of a geodetic database and associated tools for monitoring rock-slope movements: The example of the top of Randa rockfall scar. Nat. Hazards Earth Syst. Sci. 2004, 4, 187–196. [Google Scholar] [CrossRef] [Green Version]
- Bertacchini, E.; Capra, A.; Castagnetti, C.; Corsini, A. Atmospheric corrections for topographic monitoring systems in landslides. In Proceedings of the FIG Working Week 2011, Marrakesh, Morocco, 18–22 May 2011; pp. 1–15. [Google Scholar]
- Ferrero, A.M.; Forlani, G.; Roncella, R.; Voyat, H.I. Advanced Geostructural Survey Methods Applied to Rock Mass Characterization. Rock Mech. Rock Eng. 2009, 42, 631–665. [Google Scholar] [CrossRef]
- Delacourt, C.; Allemand, P.; Berthier, E.; Raucoules, D.; Casson, B.; Grandjean, P.; Pambrun, C.; Varel, E. Remote-sensing techniques for analysing landslide kinematics: A review. Bull. Soc. Geol. Fr. 2007, 178, 89–100. [Google Scholar] [CrossRef]
- Casagli, N.; Catani, F.; Del Ventisette, C.; Luzi, G. Monitoring, prediction, and early warning using ground-based radar interferometry. Landslides 2010, 7, 291–301. [Google Scholar] [CrossRef]
- Travelletti, J.; Delacourt, C.; Allemand, P.; Malet, J.P.; Schmittbuhl, J.; Toussaint, R.; Bastard, M. Correlation of multi-temporal ground-based optical images for landslide monitoring: Application, potential and limitations. ISPRS J. Photogramm. Remote Sens. 2012, 70, 39–55. [Google Scholar] [CrossRef]
- Casagli, N.; Frodella, W.; Morelli, S.; Tofani, V.; Ciampalini, A.; Intrieri, E.; Raspini, F.; Rossi, G.; Tanteri, L.; Lu, P. Spaceborne, UAV and ground-based remote sensing techniques for landslide mapping, monitoring and early warning. Geoenviron. Disasters 2017, 4, 1–23. [Google Scholar] [CrossRef]
- Michoud, C.; Bazin, S.; Blikra, L.H.; Derron, M.H.; Jaboyedoff, M. Experiences from site-specific landslide early warning systems. Nat. Hazards Earth Syst. Sci. 2013, 13, 2659–2673. [Google Scholar] [CrossRef] [Green Version]
- Sturzenegger, M.; Keegan, T.; Wen, A.; Willms, D.; Stead, D.; Edwards, T. LiDAR and discrete fracture network modeling for rockslide characterization and analysis. In Engineering Geology for Society and Territory; Springer: Berlin/Heidelberg, Germany, 2015; Volume 6, pp. 223–227. [Google Scholar]
- Guidelines for Slope Performance Monitoring; Sharon, R.; Eberhardt, E. (Eds.) CSIRO Publishing: Clayton, Australia, 2020; ISBN 9781486310999. [Google Scholar]
- Farina, P.; Leoni, L.; Babboni, F.; Coppi, F.; Mayer, L.; Ricci, P. IBIS-M, an Innovative Radar for Monitoring Slopes in Open-Pit Mines. In Proceedings of the Interrnational Symposium on Rock Slope Stability in Open Pit Mining and Civil Engineering, Vancouver, BC, Canada, 18–21 September 2011. [Google Scholar]
- Severin, J.; Eberhardt, E.; Leoni, L.; Fortin, S. Development and application of a pseudo-3D pit slope displacement map derived from ground-based radar. Eng. Geol. 2014, 181, 202–211. [Google Scholar] [CrossRef]
- Abellán, A.; Calvet, J.; Vilaplana, J.M.; Blanchard, J. Detection and spatial prediction of rockfalls by means of terrestrial laser scanner monitoring. Geomorphology 2010, 119, 162–171. [Google Scholar] [CrossRef]
- Ferrero, A.M.; Migliazza, M.; Roncella, R.; Segalini, A. Rock cliffs hazard analysis based on remote geostructural surveys: The Campione del Garda case study (Lake Garda, Northern Italy). Geomorphology 2011, 125, 457–471. [Google Scholar] [CrossRef] [Green Version]
- van Veen, M.; Hutchinson, D.J.; Kromer, R.; Lato, M.; Edwards, T. Effects of sampling interval on the frequency—magnitude relationship of rockfalls detected from terrestrial laser scanning using semi-automated methods. Landslides 2017, 14, 1579–1592. [Google Scholar] [CrossRef]
- Lato, M.; Diederichs, M.S.; Hutchinson, D.J.; Harrap, R. Optimization of LiDAR scanning and processing for automated structural evaluation of discontinuities in rockmasses. Int. J. Rock Mech. Min. Sci. 2009, 46, 194–199. [Google Scholar] [CrossRef]
- Oppikofer, T.; Jaboyedoff, M.; Pedrazzini, A.; Derron, M.H.; Blikra, L.H. Detailed DEM analysis of a rockslide scar to characterize the basal sliding surface of active rockslides. J. Geophys. Res. Earth Surf. 2011, 116, 1–22. [Google Scholar] [CrossRef]
- Klappstein, B.; Bonci, G.M.W.; Maston, W. Implementation of Real Time Geotechnical Monitoring at an Open Pit Mountain Coal Mine, Western Canada. In Proceedings of the International Multidisciplinary Symposium UNIVERSITARIA SIMPRO, Petrosani, Romania, 10–11 October 2014; pp. 250–262. [Google Scholar]
- Kromer, R.A.; Abellan, A.; Hutchinson, D.J.; Lato, M.; Chanut, M.-A.; Dubois, L.; Jaboyedoff, M. Automated Terrestrial Laser Scanning with Near Real-Time Change Detection—Monitoring of the Séchilienne Landslide. Earth Surf. Dyn. Discuss. 2017, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Kromer, R.A.; Rowe, E.; Hutchinson, J.; Lato, M.; Abellán, A. Rockfall risk management using a pre-failure deformation database. Landslides 2018, 15, 847–858. [Google Scholar] [CrossRef]
- Williams, J.G.; Rosser, N.J.; Hardy, R.J.; Brain, M.J.; Afana, A.A. Optimising 4-D surface change detection: An approach for capturing rockfall magnitude-frequency. Earth Surf. Dyn. 2018, 6, 101–119. [Google Scholar] [CrossRef] [Green Version]
- Casson, B.; Delacourt, C.; Baratoux, D.; Allemand, P. Seventeen years of the “La Clapière” landslide evolution analysed from ortho-rectified aerial photographs. Eng. Geol. 2003, 68, 123–139. [Google Scholar] [CrossRef]
- Liu, W.C.; Huang, W.C. Close range digital photogrammetry applied to topography and landslide measurements. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2016, 41, 875–880. [Google Scholar] [CrossRef]
- Thoeni, K.; Santise, M.; Guccione, D.E.; Fityus, S.; Roncella, R.; Giacomini, A. Use of low-cost terrestrial and aerial imaging sensors for geotechnical applications. Aust. Geomech. J. 2018, 53, 101–122. [Google Scholar]
- Sturzenegger, M.; Stead, D. Close-range terrestrial digital photogrammetry and terrestrial laser scanning for discontinuity characterization on rock cuts. Eng. Geol. 2009, 106, 163–182. [Google Scholar] [CrossRef]
- Lato, M.J.; Vöge, M. Automated mapping of rock discontinuities in 3D lidar and photogrammetry models. Int. J. Rock Mech. Min. Sci. 2012, 54, 150–158. [Google Scholar] [CrossRef]
- Thoeni, K.; Irschara, A.; Giacomini, A. Efficient photogrammetric reconstruction of highwalls in open pit coal mines. In Proceedings of the 16th Australasian Remote Sensing and Photogrammetry Conference Proceedings, Melbourne, Australia, 25 August–1 September 2012; pp. 85–90. [Google Scholar]
- Tannant, D. Review of Photogrammetry-Based Techniques for Characterization and Hazard Assessment of Rock Faces. Int. J. Geohazards Environ. 2015, 1, 76–87. [Google Scholar] [CrossRef] [Green Version]
- Travelletti, J.; Malet, J.-P.; Schmittbuhl, J.; Toussaint, R.; Bastard, M. Multi-temporal terrestrial photogrammetry for landslide monitoring. In Proceedings of the Mountain Risks International Conference, Firenze, Italy, 24–26 November 2010; pp. 183–191. [Google Scholar]
- Motta, M.; Gabrieli, F.; Corsini, A.; Manzi, V.; Ronchetti, F.; Cola, S. Landslide Displacement Monitoring from Multi-Temporal Terrestrial Digital Images: Case of the Valoria Landslide Site. In Landslide Science and Practice; Margottini, C., Canuti, P., Sassa, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 2, pp. 73–78. [Google Scholar]
- Roncella, R.; Forlani, G.; Fornari, M.; Diotri, F. Landslide monitoring by fixed-base terrestrial stereo-photogrammetry. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 2, 297–304. [Google Scholar] [CrossRef] [Green Version]
- James, M.R.; Robson, S. Mitigating systematic error in topographic models derived from UAV and ground-based image networks. Earth Surf. Process. Landforms 2014, 39, 1413–1420. [Google Scholar] [CrossRef] [Green Version]
- Eltner, A.; Kaiser, A.; Castillo, C.; Rock, G.; Neugirg, F.; Abellán, A. Image-based surface reconstruction in geomorphometry-merits, limits and developments. Earth Surf. Dyn. 2016, 4, 359–389. [Google Scholar] [CrossRef] [Green Version]
- Mallalieu, J.; Carrivick, J.L.; Quincey, D.J.; Smith, M.W.; James, W.H.M. An integrated Structure-from-Motion and time-lapse technique for quantifying ice-margin dynamics. J. Glaciol. 2017, 63, 937–949. [Google Scholar] [CrossRef] [Green Version]
- Parente, L.; Chandler, J.H.; Dixon, N. Optimising the quality of an SfM-MVS slope monitoring system using fixed cameras. Photogramm. Rec. 2019, 34, 408–427. [Google Scholar] [CrossRef]
- Kromer, R.; Walton, G.; Gray, B.; Lato, M.; Group, R. Development and optimization of an automated fixed-location time lapse photogrammetric rock slope monitoring system. Remote Sens. 2019, 11, 1890. [Google Scholar] [CrossRef] [Green Version]
- Blanch, X.; Abellan, A.; Guinau, M. Point Cloud Stacking: A Workflow to Enhance 3D Monitoring Capabilities Using Time-Lapse Cameras. Remote Sens. 2020, 12, 1240. [Google Scholar] [CrossRef]
- Santise, M.; Thoeni, K.; Roncella, R.; Diotri, F.; Giacomini, A. Analysis of low-light and night-time stereo-pair images for photogrammetric reconstruction. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.—ISPRS Arch. 2018, 42, 1015–1022. [Google Scholar] [CrossRef] [Green Version]
- Thoeni, K.; Guccione, D.E.; Santise, M.; Giacomini, A.; Roncella, R.; Forlani, G. The potential of low-cost RPAs for multi-view reconstruction of sub-vertical rock faces. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, XLI-B5, 909–916. [Google Scholar] [CrossRef]
- Brown, D.C. Close-Range Camera Calibration. Photogramm. Eng. Remote Sensing 1971, 37, 855–866. [Google Scholar]
- Forlani, G.; Pinto, L. GPS-assisted adjustment of terrestrial blocks. In Proceedings of the 5th International Symposium on Mobile Mapping Technology, Padua, Italy, 29–31 May 2007. [Google Scholar]
- Roncella, R.; Forlani, G. A fixed terrestrial photogrammetric system for landslide monitoring. In Modern Technologies for Landslide Monitoring and Prediction; Springer: Berlin/Heidelberg, Germany, 2015; pp. 43–67. [Google Scholar]
- Lucas, B.D.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of the 7th International Joint Conference on Artificial Intelligence, San Francisco, CA, USA, 24–28 August 1981; pp. 674–679. [Google Scholar]
- Dall’Asta, E.; Thoeni, K.; Santise, M.; Forlani, G.; Giacomini, A.; Roncella, R. Network Design and Quality Checks in Automatic Orientation of Close-Range Photogrammetric Blocks. Sensors 2015, 15, 7985–8008. [Google Scholar] [CrossRef]
- Agisoft Methashape 2020. Available online: https://www.agisoft.com/ (accessed on 1 June 2020).
- CloudCompare (Version 2.10.2) (GPL Software) 2020. Available online: https://www.danielgm.net/cc/ (accessed on 1 June 2020).
- Kraus, K.; Harley, I.A.; Kyle, S. Photogrammetry; De Gruyter: Berlin, Germany, 2011; ISBN 978-3-11-089287-1. [Google Scholar]
- Luhmann, T.; Robson, S.; Kyle, S.; Boehm, J. Close-Range Photogrammetry and 3d Imaging. In The Photogrammetric Record, 2nd ed.; De Gruyter: Berlin, Germany, 2014; Volume 29, pp. 125–127. [Google Scholar]
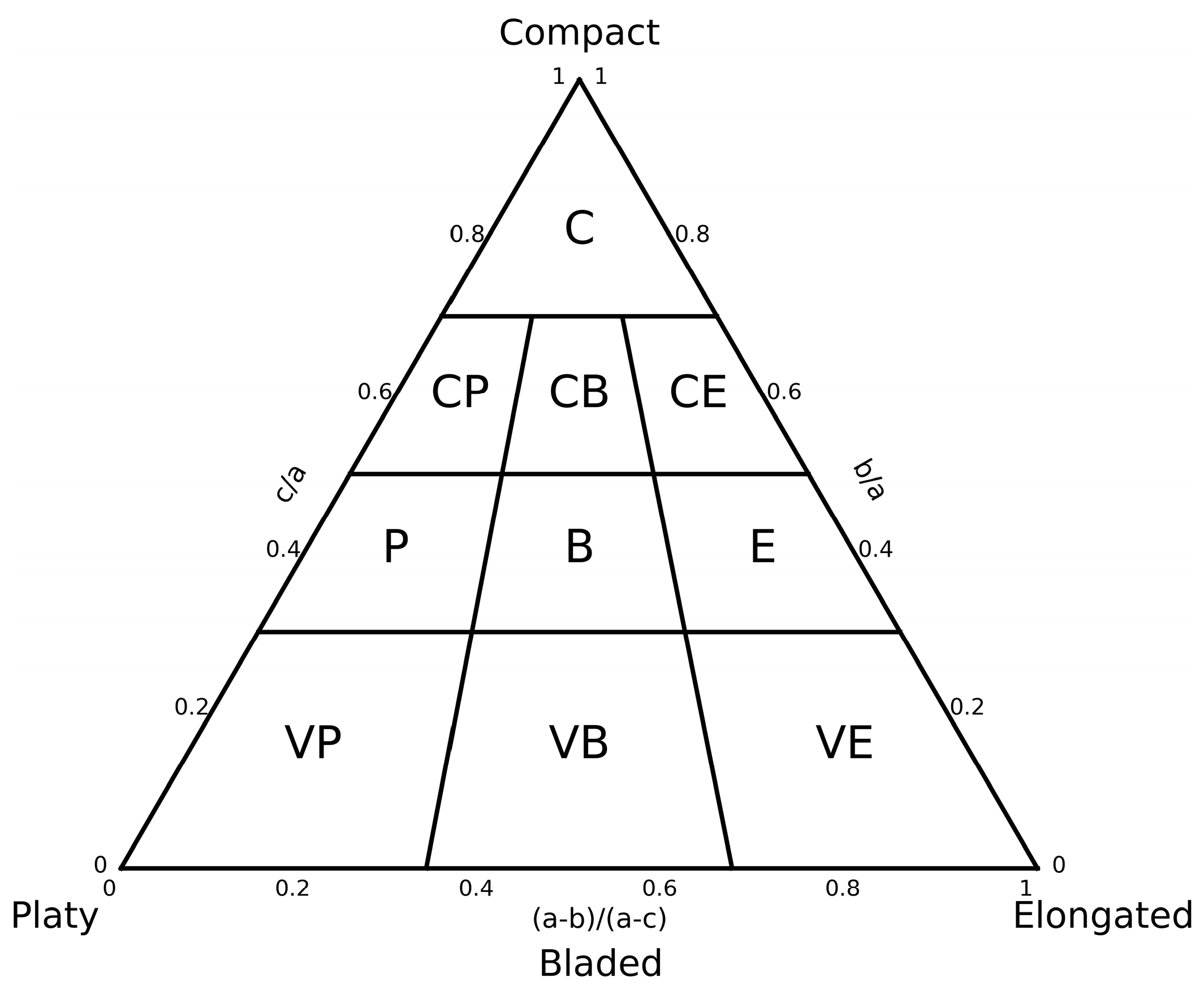
- Bonneau, D.A.; Jean Hutchinson, D.; DiFrancesco, P.M.; Coombs, M.; Sala, Z. Three-dimensional rockfall shape back analysis: Methods and implications. Nat. Hazards Earth Syst. Sci. 2019, 19, 2745–2765. [Google Scholar] [CrossRef] [Green Version]
- Sneed, E.D.; Folk, R.L. Pebbles in the Lower Colorado River, Texas a Study in Particle Morphogenesis. J. Geol. 1958, 66, 114–150. [Google Scholar] [CrossRef]
- Höhle, J.; Potuckova, M. Assessment of the Quality of Digital Terrain Medels; No. 60; European Spatial Data Research: Leuven, Belgium, 2011; p. 85. [Google Scholar]
- Diessel, C. Tuffs and Tonsteins in the Coal Measures of New South Wales, Australia. In Proceedings of the Dixieme Congres International de Stratigraphie et de Geologie du Carbonifere, Madrid, Spain, 12–17 September 1983; pp. 197–210. [Google Scholar]
- Seedsman, R. Claystones of the Newcastle Coal Measures; NERDDC Project C0902; NERDDC: Canberra, Australia, 1989; p. 749. [Google Scholar]
- Hajdarwish, A.; Shakoor, A.; Wells, N.A. Investigating statistical relationships among clay mineralogy, index engineering properties, and shear strength parameters of mudrocks. Eng. Geol. 2013, 159, 45–58. [Google Scholar] [CrossRef]
- Erguler, Z.A.; Ulusay, R. Assessment of physical disintegration characteristics of clay-bearing rocks: Disintegration index test and a new durability classification chart. Eng. Geol. 2009, 105, 11–19. [Google Scholar] [CrossRef]
- Van Eeckhout, E.M. The mechanisms of strength reduction due to moisture in coal mine shales. Int. J. Rock Mech. Min. Sci. Geomech. 1976, 13, 61–67. [Google Scholar] [CrossRef]
- Molinda, G.M.; Oyler, D.C.; Gurgenli, H. Identifying moisture sensitive roof rocks in coal mines. In Proceedings of the 25th International Conference Ground Control Mining, Morgantown, WY, USA, 1–3 August 2006; pp. 57–64. [Google Scholar]









| Comparison | SM RMSE [mm] | PS RMSE [mm] |
|---|---|---|
| TLS-3:50 pm | 4.8 (2.4 GSD) | 7.0 (3.5 GSD) |
| TLS-4:05 pm | 4.6 (2.4 GSD) | 7.0 (3.5 GSD) |
| TLS-4:20 pm | 4.5 (2.3 GSD) | 6.9 (3.5 GSD) |
| TLS-4:35 pm | 4.5 (2.3 GSD) | 7.0 (3.5 GSD) |
| TLS-4:50 pm | 4.5 (2.3 GSD) | 7.0 (3.5 GSD) |
| Comparison | SM RMSE [mm] | PS RMSE [mm] |
|---|---|---|
| 3:50 pm–4:05 pm | 1.5 (0.75 GSD) | 3.4 (1.75 GSD) |
| 3:50 pm–4:20 pm | 1.4 (0.73 GSD) | 3.6 (1.83 GSD) |
| 3:50 pm–4:35 pm | 1.7 (0.84 GSD) | 3.7 (1.90 GSD) |
| 3:50 pm–4:50 pm | 1.7 (0.84 GSD) | 3.8 (1.95 GSD) |
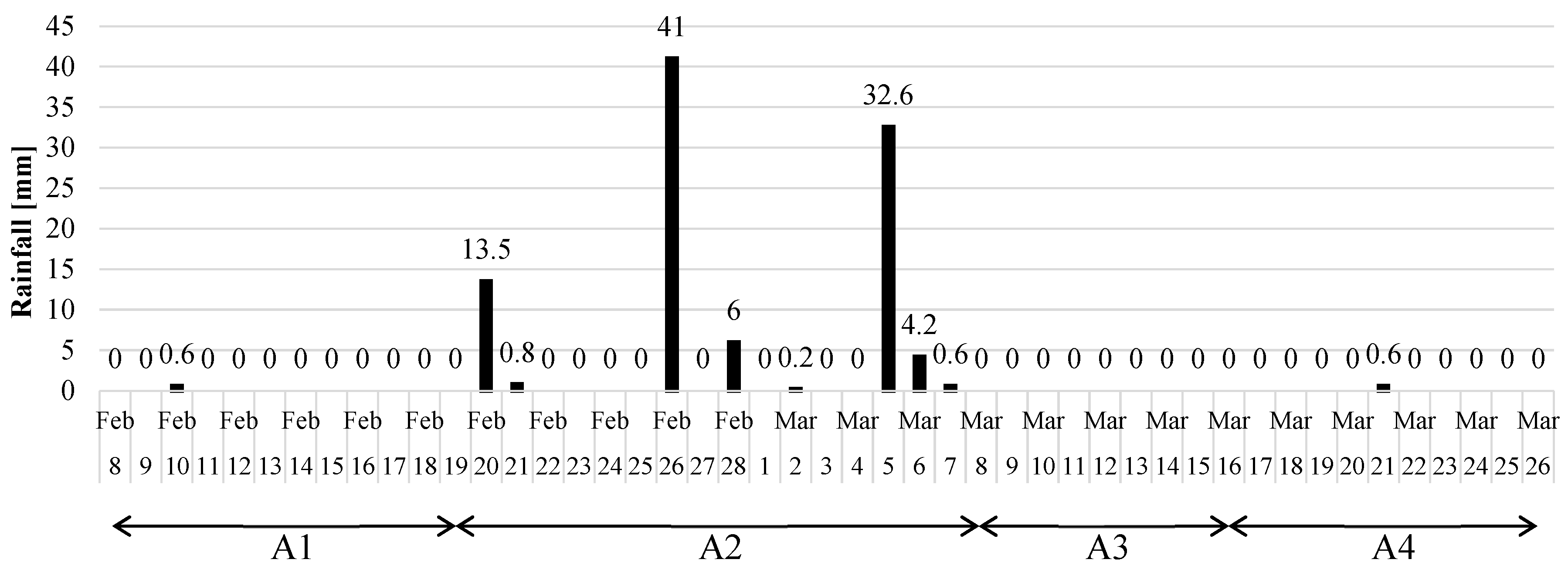
| Period | Date of Reference Model | Date of Comparison Model | Days within Period | Maximum Rainfall during Period [mm] | Total Rainfall during Period [mm] | Descriptor |
|---|---|---|---|---|---|---|
| A1 | 8 February 2018 | 19 February 2018 | 11 | 0.6 | 0.6 | dry |
| A2 | 19 February 2018 | 8 March 2018 | 17 | 41 | 98.9 | wet |
| A3 | 8 March 2018 | 16 March 2018 | 8 | 0 | 0 | short-term dry |
| A4 | 16 March 2018 | 26 March 2018 | 10 | 0.6 | 0.6 | long-term dry |
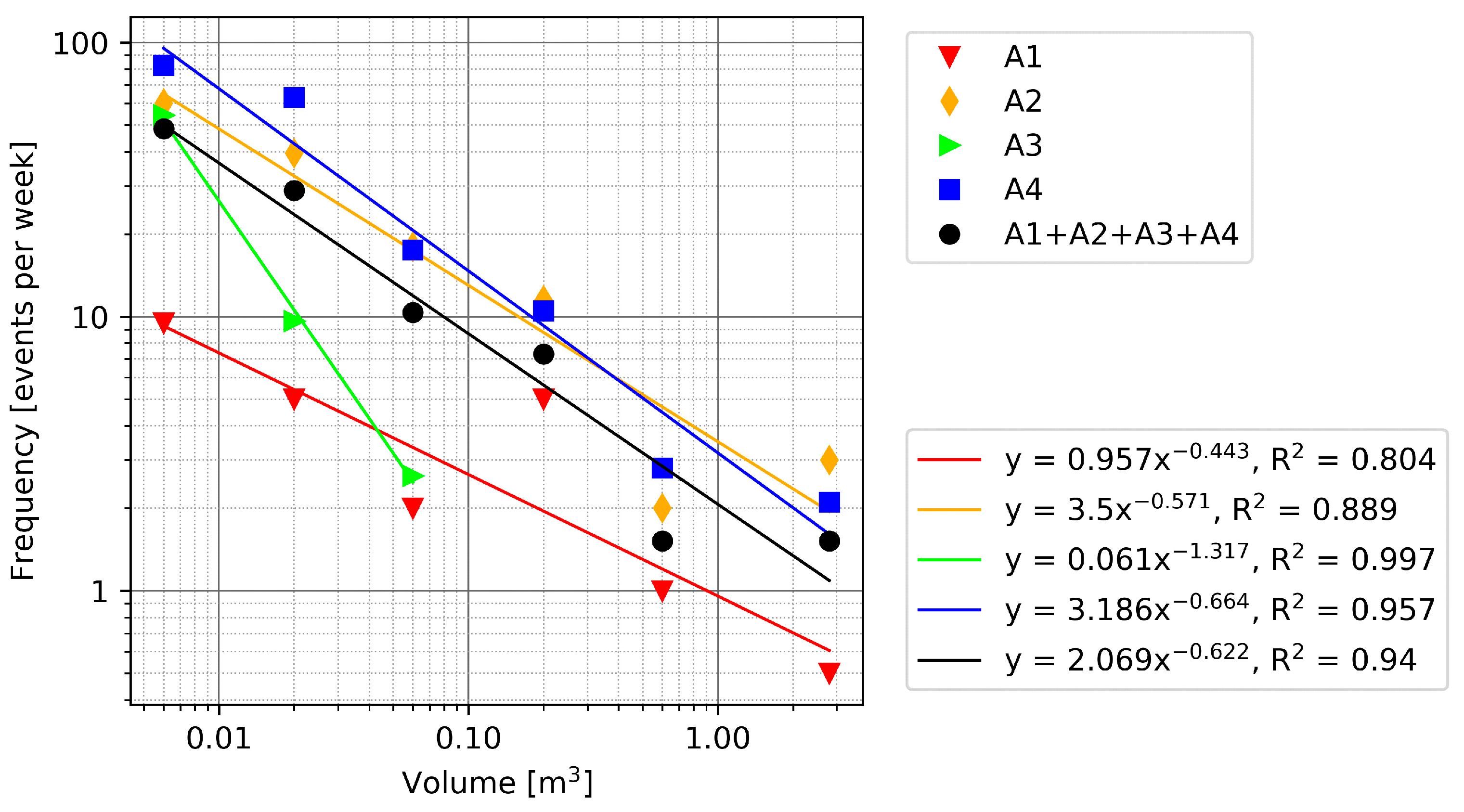
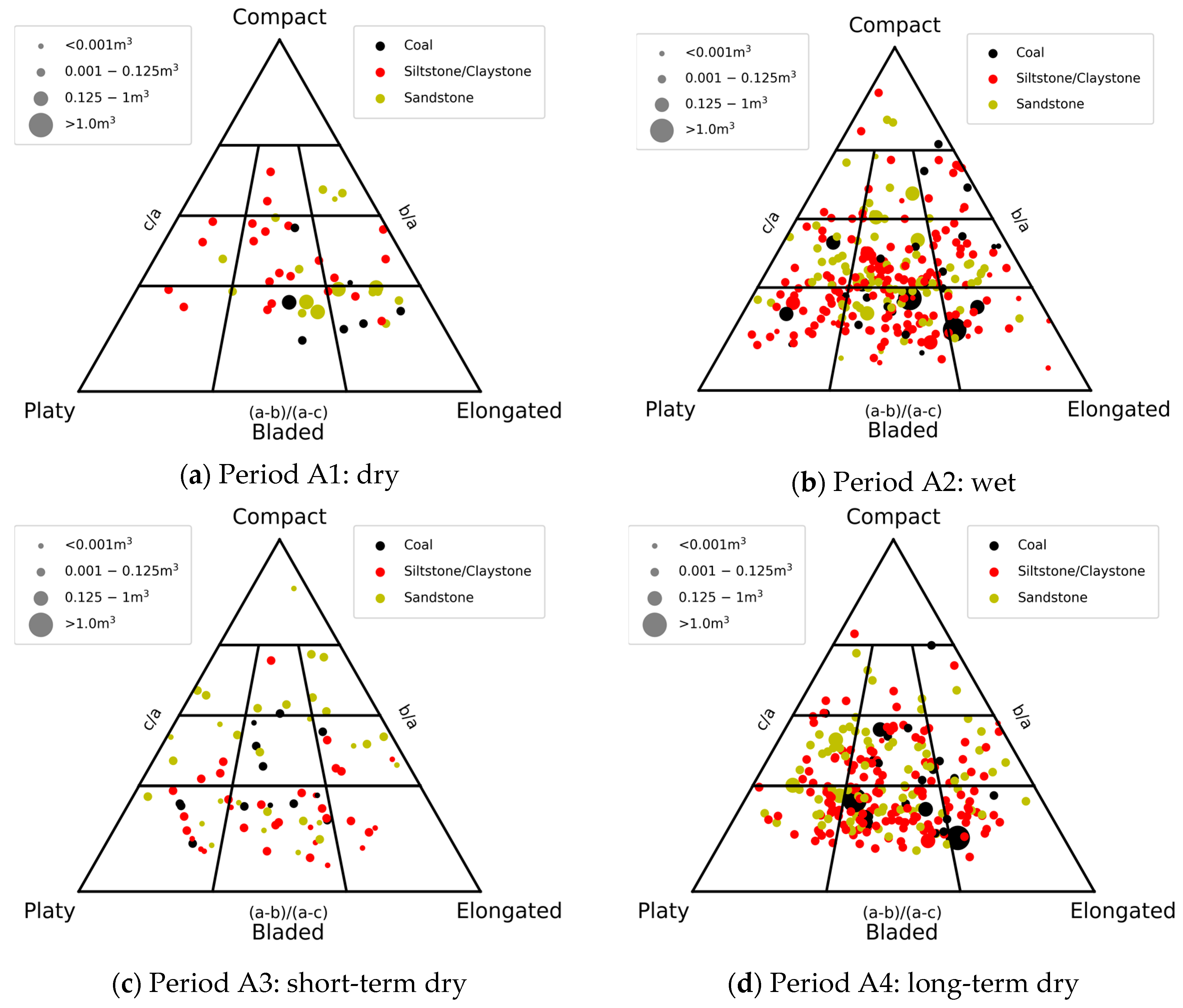
| Comparison | Layer | Number of Events during Period | Frequency [Events per Week] | Volume [m3] | |
|---|---|---|---|---|---|
| Min | Max | ||||
| A1 [dry] | Coal | 7 | 4.5 | 0.0002 | 0.4818 |
| [11 days] | Sandstone | 17 | 10.8 | 0.0001 | 0.6752 |
| [0.6 mm rainfall] | Siltstone/Claystone | 22 | 14.0 | 0.0011 | 0.0429 |
| All layers | 46 | 29.3 | 0.0001 | 0.6752 | |
| A2 [wet] | Coal | 26 | 10.7 | 0.0001 | 2.158 |
| [17 days] | Sandstone | 78 | 32.1 | 0.0001 | 0.642 |
| [99 mm rainfall] | Siltstone/Claystone | 164 | 67.5 | 0.0001 | 0.212 |
| All layers | 268 | 110.4 | 0.0001 | 2.158 | |
| A3 [short-term dry] | Coal | 13 | 11.4 | 0.0003 | 0.0578 |
| [8 days] | Sandstone | 30 | 26.3 | 0.0001 | 0.0262 |
| [0 mm rainfall] | Siltstone/Claystone | 33 | 28.9 | 0.0001 | 0.0205 |
| All layers | 76 | 66.5 | 0.0001 | 0.0578 | |
| A4 [long-term dry] | Coal | 23 | 16.1 | 0.0014 | 2.698 |
| [10 days] | Sandstone | 82 | 57.4 | 0.0013 | 0.4092 |
| [0.6 mm rainfall] | Siltstone/Claystone | 150 | 105.0 | 0.0001 | 0.1483 |
| All layers | 255 | 178.5 | 0.0001 | 2.698 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giacomini, A.; Thoeni, K.; Santise, M.; Diotri, F.; Booth, S.; Fityus, S.; Roncella, R. Temporal-Spatial Frequency Rockfall Data from Open-Pit Highwalls Using a Low-Cost Monitoring System. Remote Sens. 2020, 12, 2459. https://doi.org/10.3390/rs12152459
Giacomini A, Thoeni K, Santise M, Diotri F, Booth S, Fityus S, Roncella R. Temporal-Spatial Frequency Rockfall Data from Open-Pit Highwalls Using a Low-Cost Monitoring System. Remote Sensing. 2020; 12(15):2459. https://doi.org/10.3390/rs12152459
Chicago/Turabian StyleGiacomini, Anna, Klaus Thoeni, Marina Santise, Fabrizio Diotri, Shaun Booth, Stephen Fityus, and Riccardo Roncella. 2020. "Temporal-Spatial Frequency Rockfall Data from Open-Pit Highwalls Using a Low-Cost Monitoring System" Remote Sensing 12, no. 15: 2459. https://doi.org/10.3390/rs12152459
APA StyleGiacomini, A., Thoeni, K., Santise, M., Diotri, F., Booth, S., Fityus, S., & Roncella, R. (2020). Temporal-Spatial Frequency Rockfall Data from Open-Pit Highwalls Using a Low-Cost Monitoring System. Remote Sensing, 12(15), 2459. https://doi.org/10.3390/rs12152459









