Bias Correction of the Ratio of Total Column CH4 to CO2 Retrieved from GOSAT Spectra
Abstract
1. Introduction
2. Materials and Data Processing
2.1. GOSAT Data
2.2. Retrieval
2.3. Variables for Explaining the Bias in the Ratio Component
2.4. TCCON Data and Matching with GOSAT Data
3. Investigating the Bias in the Ratio Component
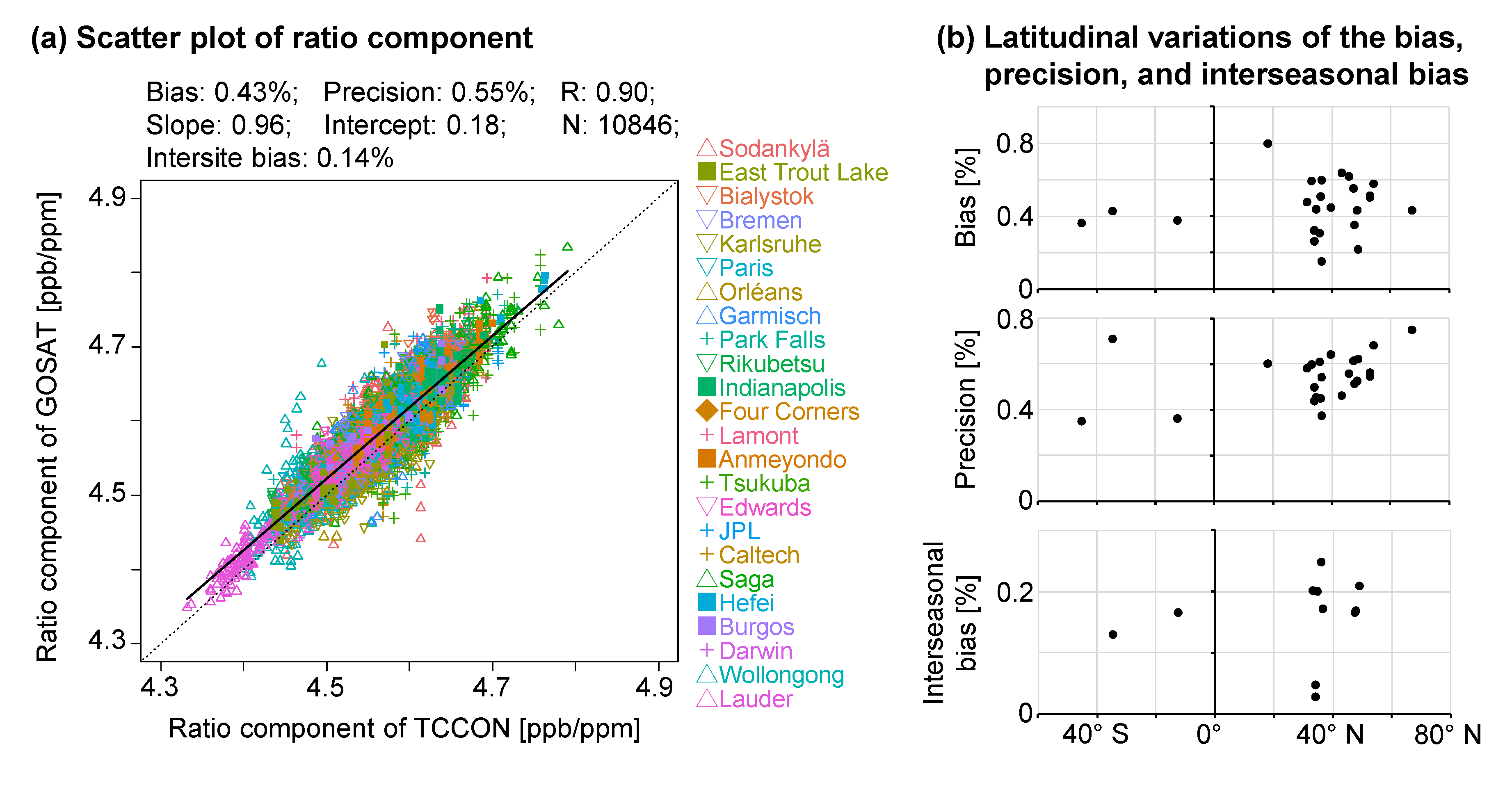
3.1. Comparison Between GOSAT and TCCON Under Cloud-Free Conditions
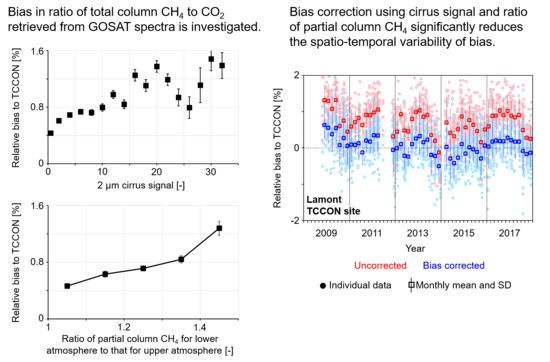
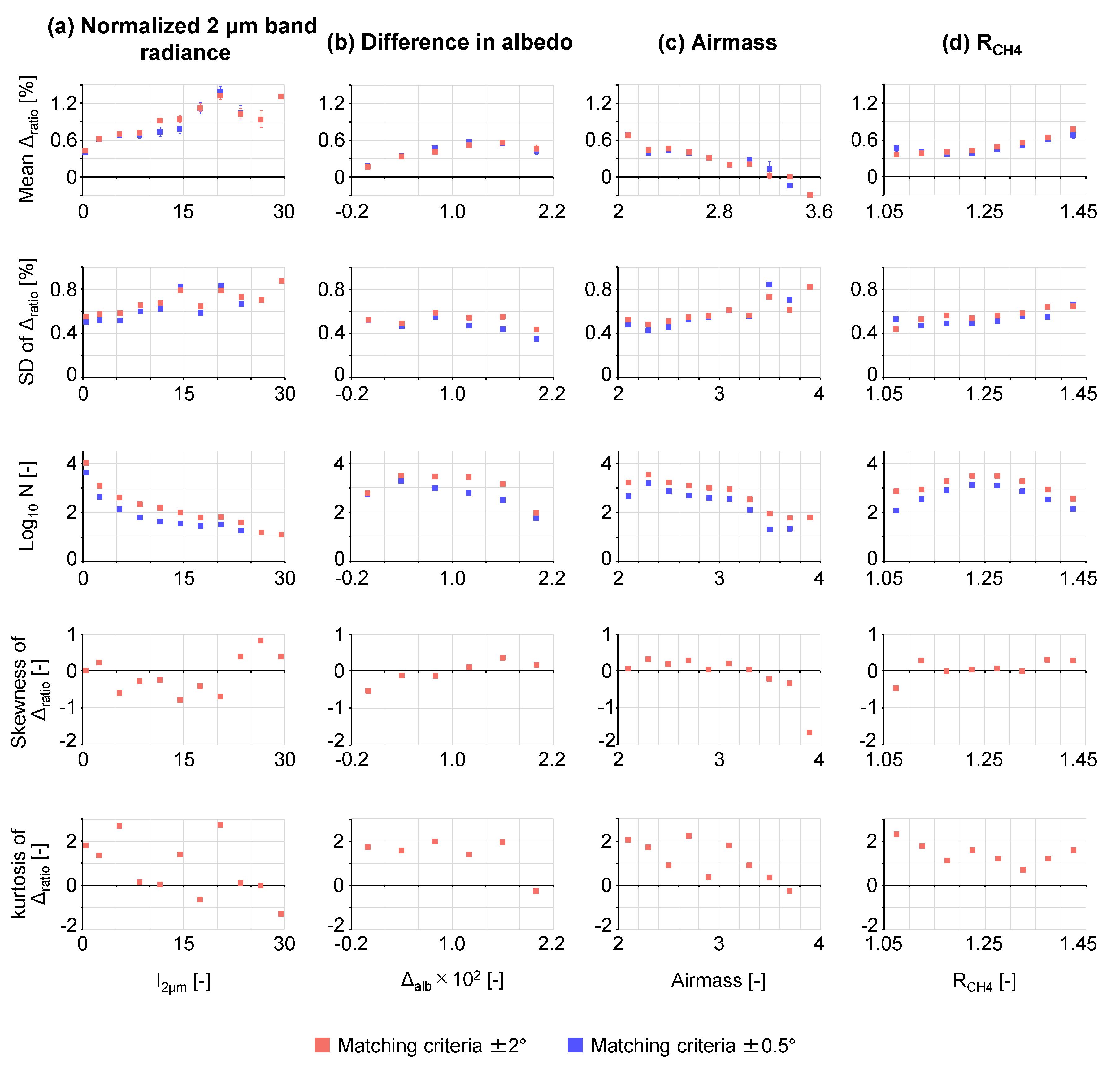
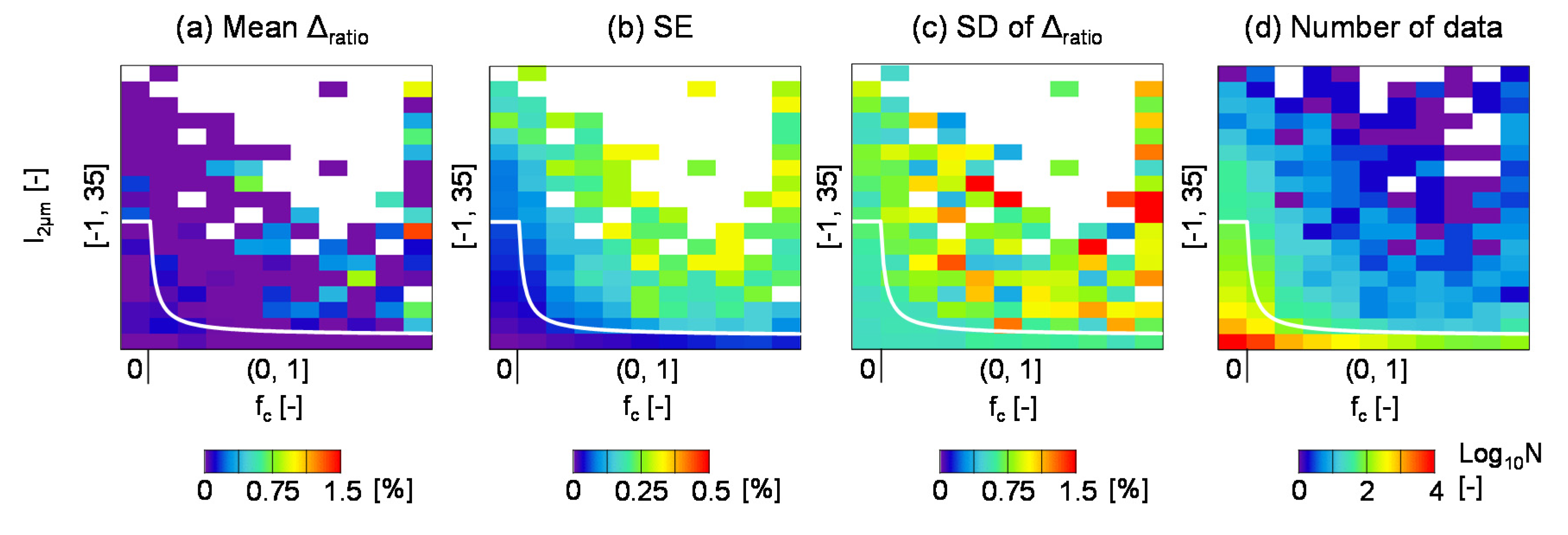
3.2. Relationship Between Bias and Related Variables
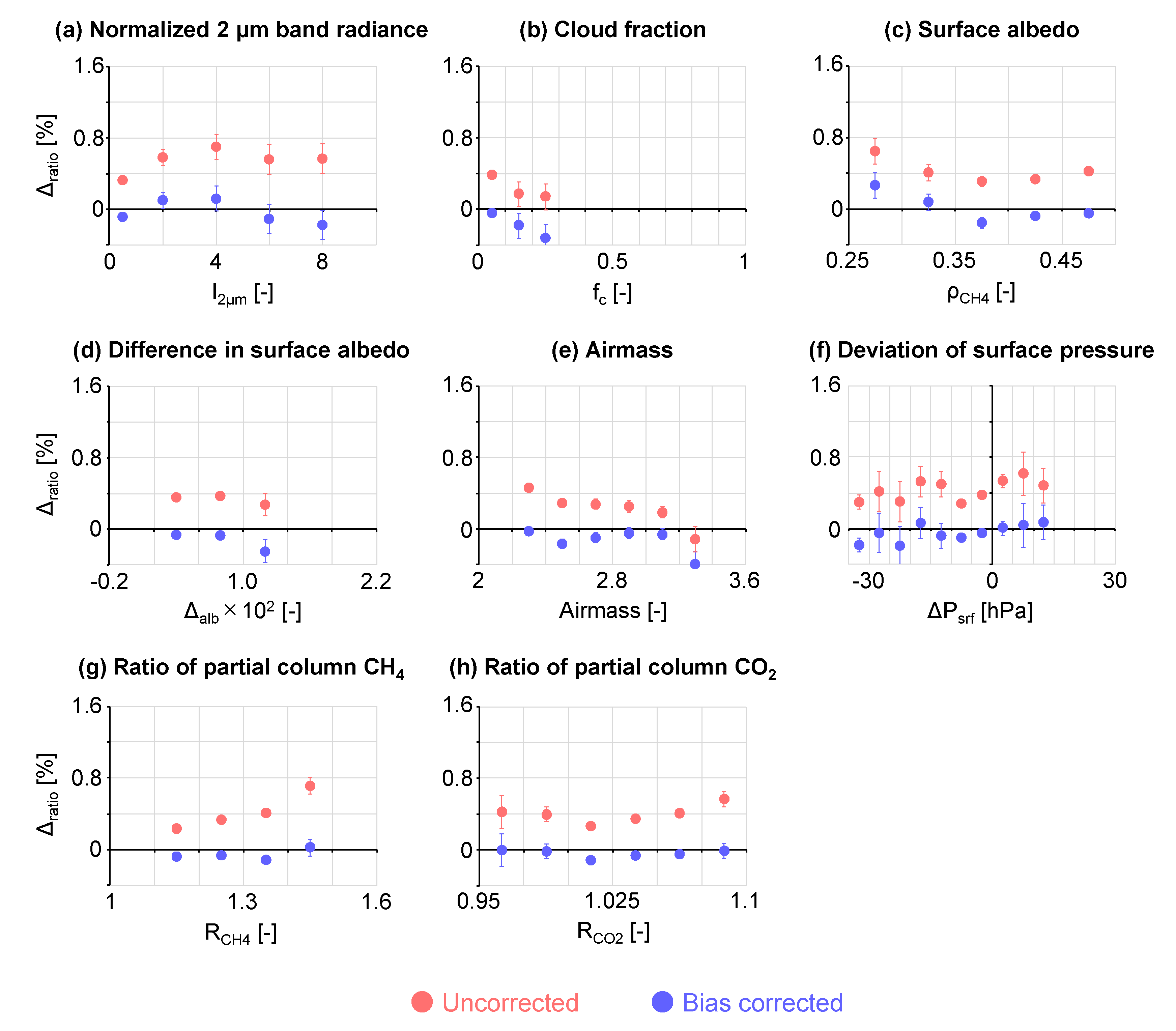
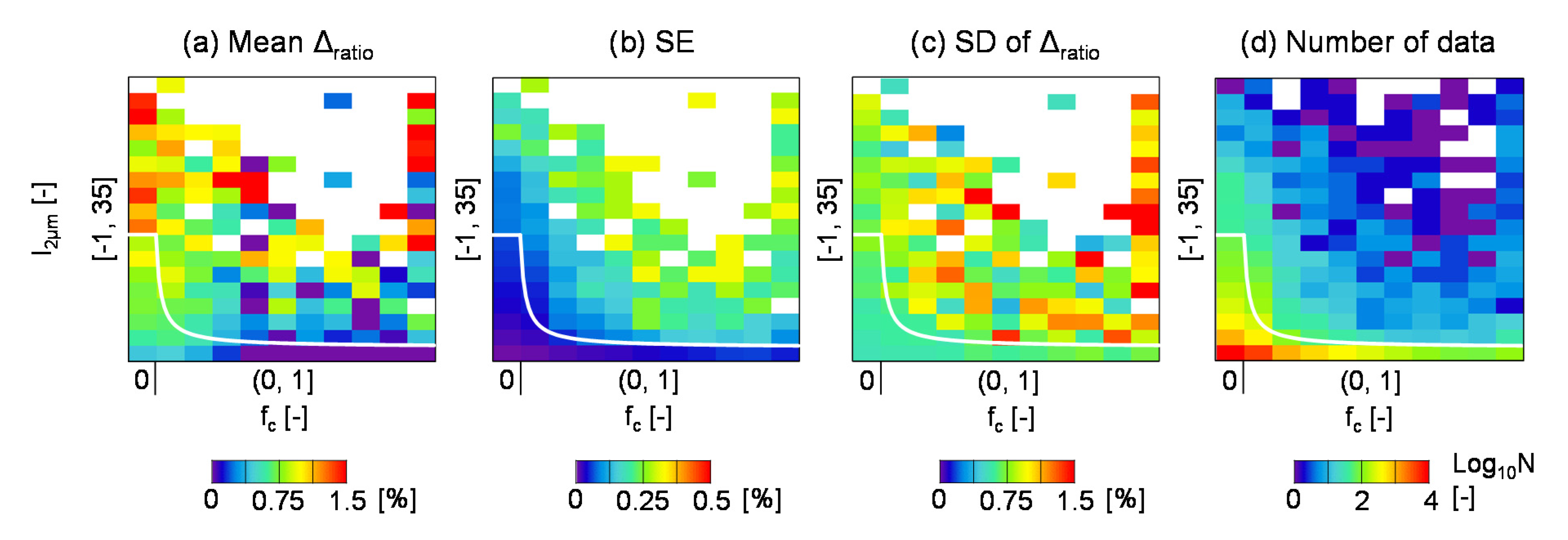
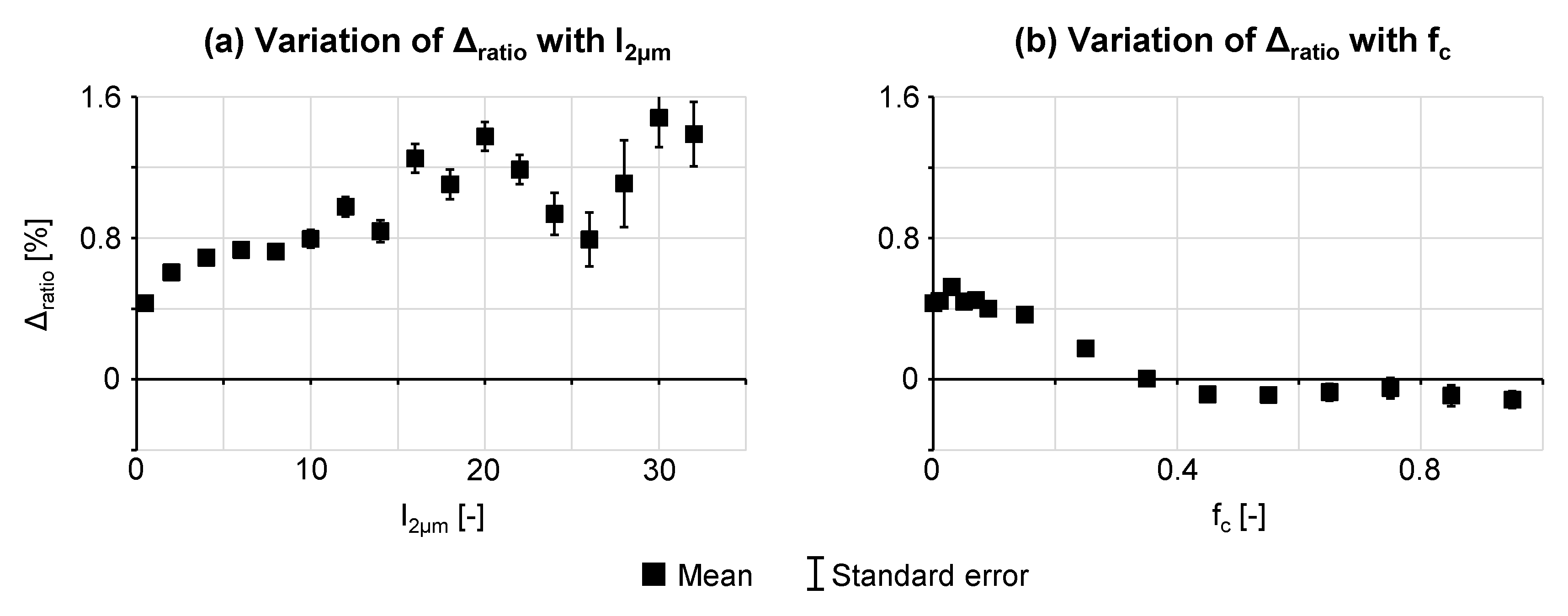
3.2.1. Cloud Fraction and Normalized 2 μm Band Radiance
3.2.2. Surface Albedo, Difference in Surface Albedo, Airmass, and Deviation of Surface Pressure
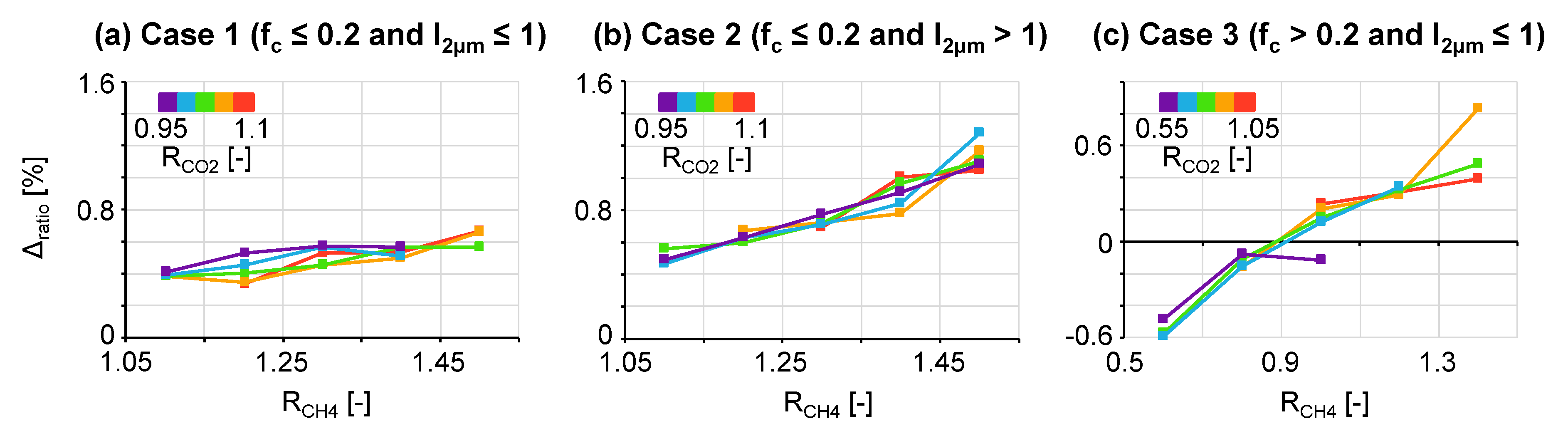
3.2.3. Vertical Profile of CH4 and CO2
4. Bias correction
4.1. Method
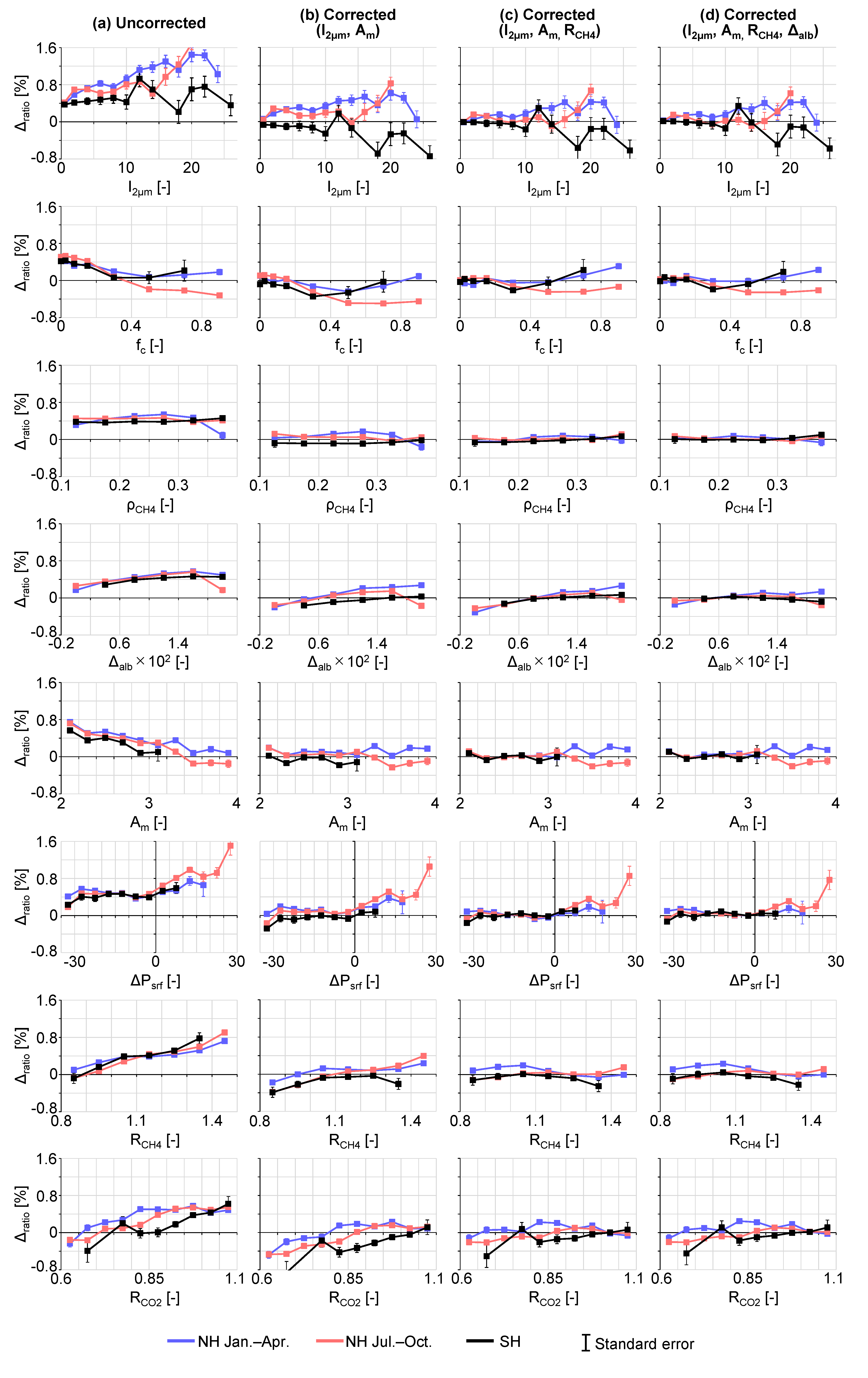
4.2. Selecting Explanatory Variables
4.3. Quality Control
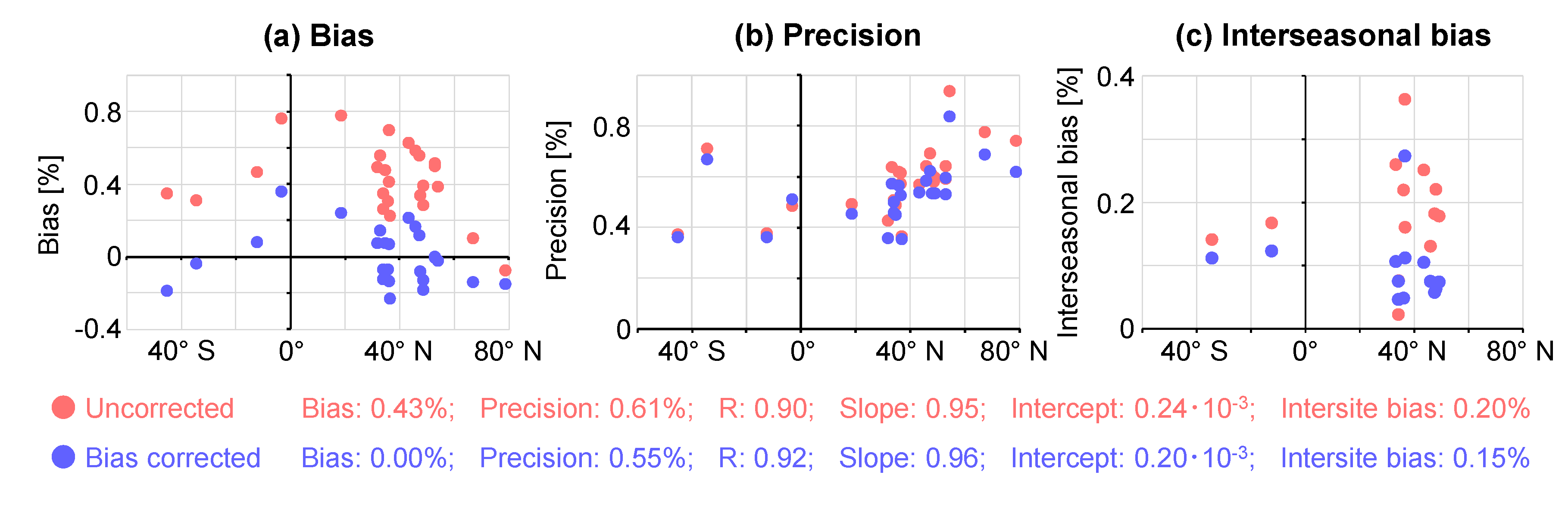
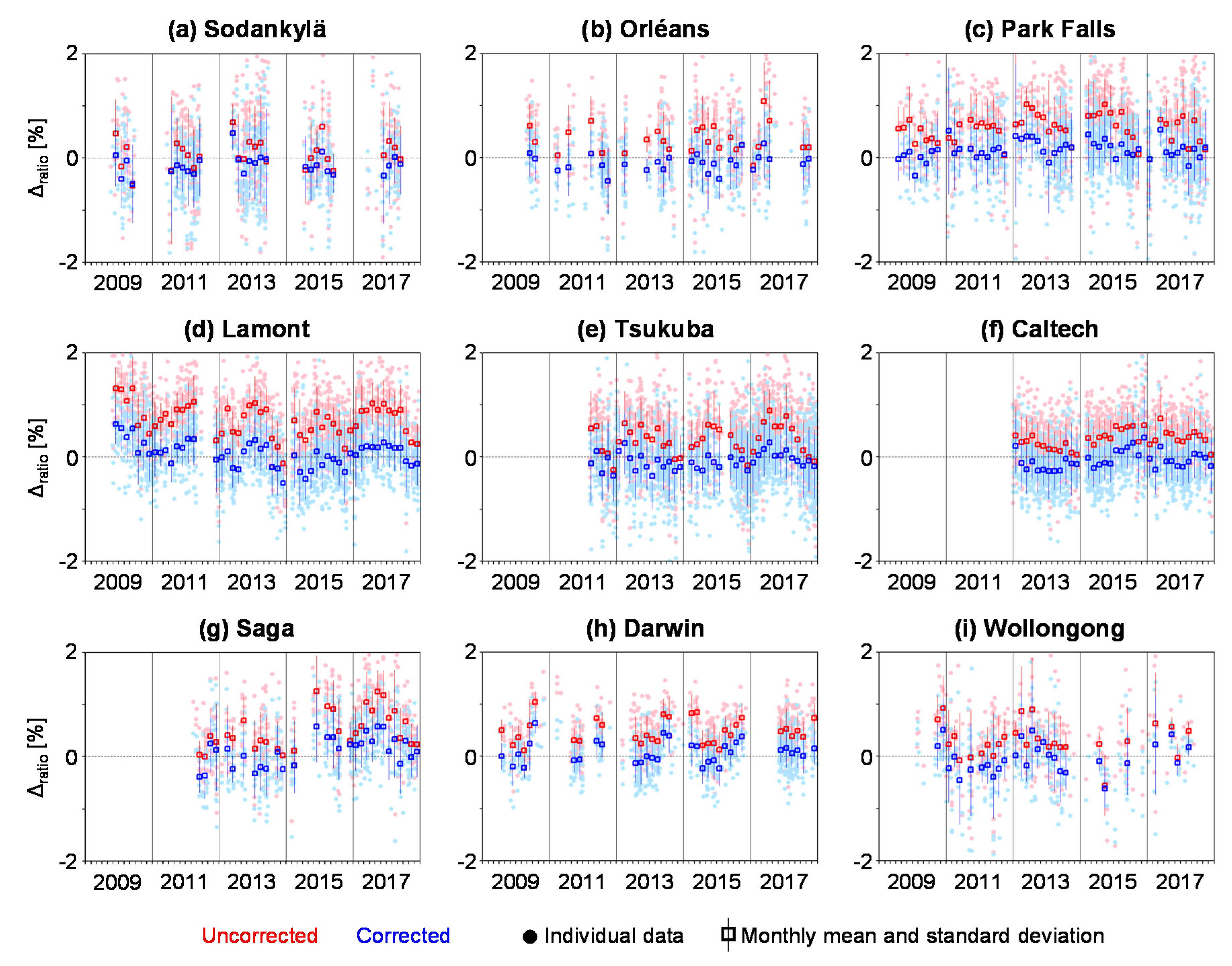
4.4. Evaluating the Corrected Results
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. TCCON Sites and the Influence of the Matching Criteria of GOSAT and TCCON

| Site | Country | Latitude (deg.) | Longitude (deg.) | Altitude(km) | Observation Period of the Data Used | Specific Characteristics |
|---|---|---|---|---|---|---|
| Ny Ålesund | Spitzbergen, Norway | 78.92N | 11.92E | 0.02 | 6 April 2014– 31 December 2018 | Useful data are not obtained during winter due to the high solar zenith angle. |
| Sodankylä | Finland | 67.37N | 26.63E | 0.19 | 16 May 2009– 31 December 2018 | Useful data are not obtained during winter due to the high solar zenith angle. |
| East Trout Lake | Canada | 54.35N | 104.99W | 0.50 | 7 October 2016– 31 December 2018 | |
| Bialystok | Poland | 53.23N | 23.03E | 0.18 | 23 April 2009– 1 October 2018 | |
| Bremen | Germany | 53.10N | 8.85E | 0.03 | 22 January 2010– 31 December 2018 | The site is in the middle-sized city (population ~550 000). |
| Karlsruhe | Germany | 49.10N | 8.44E | 0.12 | 19 April 2010– 31 December 2018 | The site is near the middle-sized city (population ~300 000). |
| Paris | France | 48.85N | 2.36E | 0.06 | 23 September 2014– 31 December 2018 | The site is in the large city (population ~2.15 million). |
| Orléans | France | 47.97N | 2.11E | 0.13 | 29 August 2009– 31 December 2018 | |
| Garmisch | Germany | 47.48N | 11.06E | 0.74 | 23 April 2009– 31 December 2018 | |
| Park Falls | USA | 45.95N | 90.27W | 0.44 | 23 April 2009– 31 December 2018 | |
| Rikubetsu | Japan | 43.46N | 143.77E | 0.38 | 16 November 2013– 31 December 2018 | |
| Indianapolis | USA | 39.86N | 86.00W | 0.27 | 23 August 2012– 1 December 2012 | The site is in the suburban area of a middle-sized city (population ~880 000). |
| Four Corners | USA | 36.80N | 108.48W | 1.64 | 16 March 2013– 4 October 2013 | The site is far from the city area but observes plant plumes and methane from mine shafts and fugitive leaks [74,75]. The observed total column peaks in the late morning. |
| Lamont | USA | 36.60N | 97.49W | 0.32 | 23 April 2009– 31 December 2018 | |
| Anmyeondo | Korea | 36.54N | 126.33E | 0.03 | 2 February 2015– 18 April 2018 | The site is located on the west coast of the Korean Peninsula. |
| Tsukuba | Japan | 36.05N | 140.12E | 0.03 | 4 August 2011– 31 December 2018 | The site is in the middle-sized city (population ~240 000). |
| Edwards | USA | 34.96N | 117.88W | 0.70 | 20 July 2013– 31 December 2018 | The site is adjacent to a very bright playa. |
| JPL | USA | 34.20N | 118.18W | 0.39 | 19 May 2011– 14 May 2018 | The site is near the large city (population ~17 million). |
| Caltech | USA | 34.14N | 118.13W | 0.23 | 20 September 2012– 31 December 2018 | The site is near the large city (population ~17 million). |
| Saga | Japan | 33.24N | 130.29E | 0.01 | 28 July 2011– 31 December 2018 | The site is in the middle-sized city (population ~230 000). |
| Hefei | China | 31.91N | 117.17E | 0.03 | 18 September 2015– 31 December 2016 | The site is near the large city (population ~5 million). |
| Burgos | Philippines | 18.53N | 120.65E | 0.04 | 3 March 2017– 31 December 2018 | The site is at the northernmost point of Luzon Island in the Philippines. |
| Manaus | Brazil | 3.21S | 60.60W | 0.05 | 1 October 2014– 24 June 2015 | |
| Darwin | Australia | 12.42S | 130.89E | 0.03 | 23 April 2009– 31 December 2018 | |
| Lauder | New Zealand | 45.04S | 169.68E | 0.37 | 23 April 2009– 31 December 2018 | The site is in the midst of rolling hills. |
| Wollongong | Australia | 34.41S | 150.88E | 0.03 | 23 April 2009– 31 December 2018 | The site is between the ocean and a sharp escarpment. |
| ±2° | ±1° | ±0.5° | ±0.1° | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Site | μ (%) | SD (%) | N | μ (%) | SD (%) | N | μ (%) | SD (%) | N | μ (%) | SD (%) | N |
| Sodankylä | 0.43 | 0.74 | 328 | 0.26 | 0.85 | 88 | ||||||
| East Trout Lake | 0.57 | 0.68 | 40 | |||||||||
| Bialystok | 0.50 | 0.56 | 263 | 0.46 | 0.51 | 87 | 0.53 | 0.45 | 50 | |||
| Bremen | 0.51 | 0.54 | 81 | |||||||||
| Karlsruhe | 0.22 | 0.62 | 267 | 0.19 | 0.57 | 102 | ||||||
| Paris | 0.43 | 0.52 | 102 | 0.50 | 0.50 | 59 | ||||||
| Orléans | 0.35 | 0.51 | 518 | 0.35 | 0.51 | 224 | 0.43 | 0.52 | 75 | |||
| Garmisch | 0.55 | 0.61 | 286 | 0.53 | 0.56 | 184 | 0.54 | 0.52 | 56 | |||
| Park Falls | 0.61 | 0.55 | 1017 | 0.61 | 0.55 | 728 | 0.59 | 0.55 | 575 | 0.60 | 0.55 | 536 |
| Rikubetsu | 0.63 | 0.46 | 135 | 0.73 | 0.44 | 56 | ||||||
| Indianapolis | 0.44 | 0.64 | 67 | |||||||||
| Lamont | 0.59 | 0.54 | 1949 | 0.59 | 0.51 | 855 | 0.61 | 0.45 | 461 | 0.62 | 0.45 | 305 |
| Anmeyondo | 0.51 | 0.45 | 50 | 0.52 | 0.37 | 33 | ||||||
| Tsukuba | 0.31 | 0.61 | 1407 | 0.31 | 0.59 | 1186 | 0.28 | 0.60 | 675 | 0.41 | 0.49 | 179 |
| Edwards | 0.43 | 0.45 | 126 | 0.60 | 0.45 | 59 | ||||||
| JPL | 0.26 | 0.49 | 609 | 0.27 | 0.43 | 490 | 0.24 | 0.39 | 438 | 0.25 | 0.38 | 103 |
| Caltech | 0.32 | 0.43 | 2067 | 0.32 | 0.43 | 1924 | 0.32 | 0.43 | 1412 | 0.31 | 0.43 | 853 |
| Saga | 0.59 | 0.59 | 438 | 0.58 | 0.55 | 288 | 0.65 | 0.53 | 222 | 0.72 | 0.52 | 66 |
| Darwin | 0.37 | 0.36 | 555 | 0.38 | 0.36 | 500 | 0.56 | 0.36 | 46 | 0.48 | 0.34 | 30 |
| Wollongong | 0.42 | 0.71 | 349 | 0.31 | 0.58 | 195 | 0.34 | 0.61 | 100 | |||
| Lauder | 0.36 | 0.35 | 124 | 0.35 | 0.34 | 121 | 0.37 | 0.31 | 92 | 0.36 | 0.30 | 85 |
| All sites | 0.43 | 0.55 | 10846 | 0.41 | 0.52 | 7263 | 0.40 | 0.51 | 4357 | 0.45 | 0.49 | 2249 |
| Intersite bias | 0.14 | 0.13 | 0.16 | 0.15 |

Appendix B. Bias Correction for the Data Acquired by Gain M

| Uncorrected | Bias-Corrected | |||||||
|---|---|---|---|---|---|---|---|---|
| Site | μ (%) | SD (%) | SSD (%) | N | μ (%) | SD (%) | SSD (%) | N |
| Edwards | 0.35 | 0.41 | 0.11 | 766 | −0.07 | 0.39 | 0.04 | 766 |
| JPL | 0.01 | 0.50 | 0.11 | 214 | −0.39 | 0.46 | 0.09 | 214 |
| Caltech | 0.04 | 0.35 | 15 | −0.40 | 0.34 | 15 | ||
References
- Buchwitz, M.; de Beek, R.; Burrows, J.P.; Bovensmann, H.; Warneke, T.; Notholt, J.; Meirink, J.F.; Goede, A.P.H.; Bergamaschi, P.; Körner, S.; et al. Atmospheric methane and carbon dioxide from SCIAMACHY satellite data: Initial comparison with chemistry and transport models. Atmos. Chem. Phys. 2005, 5, 941–962. [Google Scholar] [CrossRef]
- Frankenberg, C.; Meirink, J.F.; van Weele, M.; Platt, U.; Wagner, T. Assessing methane emissions from global space-borne observations. Science 2005, 308, 1010–1014. [Google Scholar] [CrossRef] [PubMed]
- Parker, R.; Boesch, H.; Cogan, A.; Fraser, A.; Feng, L.; Palmer, P.I.; Messerschmidt, J.; Deutscher, N.; Griffith, D.W.T.; Notholt, J.; et al. Methane observations from the Greenhouse Gases Observing SATellite: Comparison to ground-based TCCON data and model calculations. Geophys. Res. Lett. 2011, 38, L15807. [Google Scholar] [CrossRef]
- Butz, A.; Guerlet, S.; Hasekamp, O.; Schepers, D.; Galli, A.; Aben, I.; Frankenberg, C.; Hartmann, J.-M.; Tran, H.; Kuze, A.; et al. Toward accurate CO2 and CH4 observations from GOSAT. Geophys. Res. Lett. 2011, 38, L14812. [Google Scholar] [CrossRef]
- Yoshida, Y.; Ota, Y.; Eguchi, N.; Kikuchi, N.; Nobuta, K.; Tran, H.; Morino, I.; Yokota, T. Retrieval algorithm for CO2 and CH4 column abundances from short-wavelength infrared spectral observations by the Greenhouse gases observing satellite. Atmos. Meas. Tech. 2011, 4, 717–734. [Google Scholar] [CrossRef]
- Hu, H.; Landgraf, J.; Detmers, R.; Borsdorff, T.; de Brugh, J.A.; Aben, I.; Butz, A.; Hasekamp, O. Toward global mapping of methane with TROPOMI: First results and intersatellite comparison to GOSAT. Geophys. Res. Lett. 2018, 45, 3682–3689. [Google Scholar] [CrossRef]
- Bergamaschi, P.; Frankenberg, C.; Meirink, J.F.; Krol, M.; Dentener, F.; Wagner, T.; Platt, U.; Kaplan, J.O.; Körner, S.; Heimann, M.; et al. Satellite chartography of atmospheric CH4 from SCIAMACHY on board ENVISAT: 2. Evaluation based on inverse model simulations. J. Geophys. Res.-Atmos. 2007, 112, D02304. [Google Scholar] [CrossRef]
- Monteil, G.; Houweling, S.; Butz, A.; Guerlet, S.; Schepers, D.; Hasekamp, O.; Frankenberg, C.; Scheepmaker, R.; Aben, I.; Röckmann, T. Comparison of CH4 inversions based on 15 months of GOSAT and SCIAMACHY observations. J. Geophys. Res.-Atmos. 2013, 118, 11807–11823. [Google Scholar] [CrossRef]
- Cressot, C.; Chevallier, F.; Bousquet, P.; Crevoisier, C.; Dlugokencky, E.J.; Fortems-Cheiney, A.; Frankenberg, C.; Parker, R.; Pison, I.; Scheepmaker, R.A.; et al. On the consistency between global and regional methane emissions inferred from SCIAMACHY, TANSO-FTS, IASI and surface measurements. Atmos. Chem. Phys. 2014, 14, 577–592. [Google Scholar] [CrossRef]
- Alexe, M.; Bergamaschi, P.; Segers, A.; Detmers, R.; Butz, A.; Hasekamp, O.; Guerlet, S.; Parker, R.; Boesch, H.; Frankenberg, C.; et al. Inverse modelling of CH4 emissions for 2010–2011 using different satellite retrieval products from GOSAT and SCIAMACHY. Atmos. Chem. Phys. 2015, 15, 113–133. [Google Scholar] [CrossRef]
- Turner, A.J.; Jacob, D.J.; Wecht, K.J.; Maasakkers, J.D.; Lundgren, E.; Andrews, A.E.; Biraud, S.C.; Boesch, H.; Bowman, K.W.; Deutscher, N.M.; et al. Estimating global and North American methane emissions with high spatial resolution using GOSAT satellite data. Atmos. Chem. Phys. 2015, 15, 7049–7069. [Google Scholar] [CrossRef]
- Meirink, J.F.; Eskes, H.J.; Goede, A.P.H. Sensitivity analysis of methane emissions derived from SCIAMACHY observations through inverse modelling. Atmos. Chem. Phys. 2006, 6, 1275–1292. [Google Scholar] [CrossRef]
- GHG-CCI project team. User Requirements Document (URD) for the Essential Climate Variable (ECV) Greenhouse Gases (GHG), Version 2.1 (URDv2.1). 2016. Available online: http://cci.esa.int/sites/default/files/URDv2.1_GHG-CCI_Final.pdf (accessed on 15 May 2020).
- O’Brien, D.M.; Rayner, P.J. Global observations of the carbon budget 2. CO2 column from differential absorption of reflected sunlight in the 1.61 μm band of CO2. J. Geophys. Res.-Atmos. 2002, 107, 4354. [Google Scholar]
- Kuang, Z.; Margolis, J.; Toon, G.; Crisp, D.; Yung, Y. Spaceborne measurements of atmospheric CO2 by high-resolution NIR spectrometry of reflected sunlight: An introductory study. Geophys. Res. Lett. 2002, 29, 1716. [Google Scholar] [CrossRef]
- Dufour, E.; Bréon, F.-M. Spaceborne estimate of atmospheric CO2 column by use of the differential absorption method: Error analysis. Appl. Optics 2003, 42, 3595–3609. [Google Scholar] [CrossRef]
- Connor, B.J.; Boesch, H.; Toon, G.; Sen, B.; Miller, C.; Crisp, D. Orbiting Carbon Observatory: Inverse method and prospective error analysis. J. Geophys. Res.-Atmos. 2008, 113, D05305. [Google Scholar] [CrossRef]
- Butz, A.; Hasekamp, O.P.; Frankenberg, C.; Aben, I. Retrievals of atmospheric CO2 from simulated space-borne measurements of backscattered near-infrared sunlight: Accounting for aerosol effects. Appl. Opt. 2009, 48, 3322–3336. [Google Scholar] [CrossRef]
- Schepers, D.; Guerlet, S.; Butz, A.; Landgraf, J.; Frankenberg, C.; Hasekamp, O.; Blavier, J.-F.; Deutscher, N.M.; Griffith, D.W.T.; Hase, F.; et al. Methane retrievals from Greenhouse Gases Observing Satellite (GOSAT) shortwave infrared measurements: Performance comparison of proxy and physics retrieval algorithms. J. Geophys. Res.-Atmos. 2012, 117, D10307. [Google Scholar] [CrossRef]
- Cogan, A.J.; Boesch, H.; Parker, R.J.; Feng, L.; Palmer, P.I.; Blavier, J.-F.L.; Deutscher, N.M.; Macatangay, R.; Notholt, J.; Roehl, C.; et al. Atmospheric carbon dioxide retrieved from the Greenhouse gases Observing SATellite (GOSAT): Comparison with ground-based TCCON observations and GEOS-Chem model calculations. J. Geophys. Res.-Atmos. 2012, 117, D21301. [Google Scholar] [CrossRef]
- Yoshida, Y.; Kikuchi, N.; Morino, I.; Uchino, O.; Oshchepkov, S.; Bril, A.; Saeki, T.; Schutgens, N.; Toon, G.C.; Wunch, D.; et al. Improvement of the retrieval algorithm for GOSAT SWIR XCO2 and XCH4 and their validation using TCCON data. Atmos. Meas. Tech. 2013, 6, 1533–1547. [Google Scholar] [CrossRef]
- O’Dell, C.W.; Eldering, A.; Wennberg, P.O.; Crisp, D.; Gunson, M.R.; Fisher, B.; Frankenberg, C.; Kiel, M.; Lindqvist, H.; Mandrake, L.; et al. Improved retrievals of carbon dioxide from Orbiting Carbon Observatory-2 with the version 8 ACOS algorithm. Atmos. Meas. Tech. 2018, 11, 6539–6576. [Google Scholar] [CrossRef]
- Butz, A.; Hasekamp, O.P.; Frankenberg, C.; Vidot, J.; Aben, I. CH4 retrievals from space-based solar backscatter measurements: Performance evaluation against simulated aerosol and cirrus loaded scenes. J. Geophys. Res.-Atmos. 2010, 115, D24302. [Google Scholar] [CrossRef]
- Parker, R.J.; Boesch, H.; Byckling, K.; Webb, A.J.; Palmer, P.I.; Feng, L.; Bergamaschi, P.; Chevallier, F.; Notholt, J.; Deutscher, N.; et al. Assessing 5 years of GOSAT Proxy XCH4 data and associated uncertainties. Atmos. Meas. Tech. 2015, 8, 4785–4801. [Google Scholar] [CrossRef]
- Fraser, A.; Palmer, P.I.; Feng, L.; Bösch, H.; Parker, R.; Dlugokencky, E.J.; Krummel, P.B.; Langenfelds, R.L. Estimating regional fluxes of CO2 and CH4 using space-borne observations of XCH4: XCO2. Atmos. Chem. Phys. 2014, 14, 12883–12895. [Google Scholar] [CrossRef]
- Pandey, S.; Houweling, S.; Krol, M.; Aben, I.; Chevallier, F.; Dlugokencky, E.J.; Gatti, L.V.; Gloor, E.; Miller, J.B.; Detmers, R.; et al. Inverse modeling of GOSAT-retrieved ratios of total column CH4 and CO2 for 2009 and 2010. Atmos. Chem. Phys. 2016, 16, 5043–5062. [Google Scholar] [CrossRef]
- Feng, L.; Palmer, P.I.; Bösch, H.; Parker, R.J.; Webb, A.J.; Correia, C.S.C.; Deutscher, N.M.; Domingues, L.G.; Feist, D.G.; Gatti, L.V.; et al. Consistent regional fluxes of CH4 and CO2 inferred from GOSAT proxy XCH4: XCO2 retrievals, 2010–2014. Atmos. Chem. Phys. 2017, 17, 4781–4797. [Google Scholar] [CrossRef]
- GHG-CCI project team. Algorithm inter-comparison and error characterization & analysis report (AIECAR) of the GHG-CCI project of ESA’s Climate Change Initiative, Version 1 (AIECARv1). 2012. Available online: http://www.iup.uni-bremen.de/~buch/ghgcci_public/AIECARv1_GHG-CCI_Final.pdf (accessed on 15 May 2020).
- Parker, R.J.; Webb, A.; Boesch, H.; Somkuti, P.; Barrio Guillo, R.; Di Noia, A.; Kalaitzi, N.; Anand, J.; Bergamaschi, P.; Chevallier, F.; et al. A Decade of GOSAT Proxy Satellite CH4 Observations. Earth Syst. Sci. Data Discuss. 2020. in review. [Google Scholar]
- Detmers, R.; Hasekamp, O. Product User Guide (PUG) for the RemoTeC XCH4 PROXY GOSAT Data Product v2.3.8. 2016. Available online: ftp://ftp.sron.nl/pub/pub/RemoTeC/TEMIS/CRDP4/DOCS/PUGv4p1_CH4_GOS_SRPR.pdf (accessed on 8 March 2020).
- GHG-CCI project team. Product User Guide (PUGv4) for the University of Leicester Proxy XCH4 GOSAT Data Product (CH4_GOS_OCPR). 2016. Available online: https://catalogue.ceda.ac.uk/uuid/4774bc5719754c44add5c6f209fc25ae (accessed on 8 March 2020).
- Yoshida, Y.; Kikuchi, N.; Yokota, T. On-orbit radiometric calibration of SWIR bands of TANSO-FTS onboard GOSAT. Atmos. Meas. Tech. 2012, 5, 2515–2523. [Google Scholar] [CrossRef]
- Ishida, H.; Nakajima, T.Y. Development of an unbiased cloud detection algorithm for a spaceborne multispectral imager. J. Geophys. Res.-Atmos. 2009, 114, D07206. [Google Scholar] [CrossRef]
- Yoshida, Y.; Eguchi, N.; Ota, Y.; Kikuchi, N.; Nobuta, K.; Aoki, T.; Yokota, T. Algorithm theoretical basis document (ATBD) for CO2, CH4 and H2O column amounts retrieval from GOSAT TANSO-FTS SWIR. 2017. Available online: http://data2.gosat.nies.go.jp/doc/documents/ATBD_FTSSWIRL2_V2.0_en.pdf (accessed on 8 March 2020).
- Nakajima, T.; Nakajima, T.Y.; Higurashi, A.; Sano, I.; Takamura, T.; Ishida, H.; Schutgens, N. A study of aerosol and cloud information retrievals from CAI imager on board GOSAT satellite. J. Remote Sens. Soc. Japan. 2008, 28, 178–189, (in Japanese with English abstract and figure captions). [Google Scholar]
- Guerlet, S.; Butz, A.; Schepers, D.; Basu, S.; Hasekamp, O.P.; Kuze, A.; Yokota, T.; Blavier, J.-F.; Deutscher, N.M.; Griffith, D.W.T. Impact of aerosol and thin cirrus on retrieving and validating XCO2 from GOSAT shortwave infrared measurements. J. Geophys. Res.-Atmos. 2013, 118, 4887–4905. [Google Scholar] [CrossRef]
- Inoue, M.; Morino, I.; Uchino, O.; Nakatsuru, T.; Yoshida, Y.; Yokota, T.; Wunch, D.; Wennberg, P.O.; Roehl, C.M.; Griffith, D.W.T.; et al. Bias corrections of GOSAT SWIR XCO2 and XCH4 with TCCON data and their evaluation using aircraft measurement data. Atmos. Meas. Tech. 2016, 9, 3491–3512. [Google Scholar] [CrossRef]
- Christi, M.J.; Stephens, G.L. Retrieving profiles of atmospheric CO2 in clear sky and in the presence of thin cloud using spectroscopy from the near and thermal infrared: A preliminary case study. J. Geophys. Res.-Atmos. 2004, 109, D04316. [Google Scholar] [CrossRef]
- Wunch, D.; Wennberg, P.O.; Toon, G.C.; Connor, B.J.; Fisher, B.; Osterman, G.B.; Frankenberg, C.; Mandrake, L.; O’Dell, C.; Ahonen, P.; et al. A method for evaluating bias in global measurements of CO2 total columns from space. Atmos. Chem. Phys. 2011, 11, 12317–12337. [Google Scholar] [CrossRef]
- Taylor, T.E.; O’Dell, C.W.; O’Brien, D.M.; Kikuchi, N.; Yokota, T.; Nakajima, T.Y.; Ishida, H.; Crisp, D.; Nakajima, T. Comparison of cloud-screening methods applied to GOSAT near-infrared spectra. IEEE Trans. Geosci. Remote Sens. 2012, 50, 295–309. [Google Scholar] [CrossRef]
- Notholt, J.; Schrems, O.; Warneke, T.; Deutscher, N.; Weinzierl, C.; Palm, M.; Buschmann, M.; AWI-PEV Station Engineers. TCCON data from Ny Alesund, Spitzbergen, Norway, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/1289 (accessed on 8 March 2020).
- Kivi, R.; Heikkinen, P.; Kyro, E. TCCON data from Sodankyla, Finland, Release GGG2014R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/289 (accessed on 8 March 2020).
- Wunch, D.; Mendonca, J.; Colebatch, O.; Allen, N.; Blavier, J.-F.L.; Springett, S.; Worthy, D.; Kessler, R.; Strong, K. TCCON data from East Trout Lake, Canada, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/362 (accessed on 8 March 2020).
- Deutscher, N.; Notholt, J.; Messerschmidt, J.; Weinzierl, C.; Warneke, T.; Petri, C.; Grupe, P. TCCON data from Bialystok, Poland, Release GGG2014R2, TCCON Data Archive. Available online: https://data.caltech.edu/records/267 (accessed on 8 March 2020).
- Notholt, J.; Petri, C.; Warneke, T.; Deutscher, N.; Buschmann, M.; Weinzierl, C.; Macatangay, R.; Grupe, P. TCCON data from Bremen, Germany, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/268 (accessed on 8 March 2020).
- Hase, F.; Blumenstock, T.; Dohe, S.; Groß, J.; Kiel, M. TCCON data from Karlsruhe, Germany, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/278 (accessed on 8 March 2020).
- Té, Y.; Jeseck, P.; Janssen, C. TCCON data from Paris (FR), Release GGG2014.R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/284 (accessed on 8 March 2020).
- Warneke, T.; Messerschmidt, J.; Notholt, J.; Weinzierl, C.; Deutscher, N.; Petri, C.; Grupe, P.; Vuillemin, C.; Truong, F.; Schmidt, M.; et al. TCCON data from Orleans, France, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/283 (accessed on 8 March 2020).
- Sussmann, R.; Rettinger, M. TCCON data from Garmisch, Germany, Release GGG2014R2, TCCON Data Archive. Available online: https://data.caltech.edu/records/956 (accessed on 8 March 2020).
- Wennberg, P.O.; Roehl, C.; Wunch, D.; Toon, G.C.; Blavier, J.-F.; Washenfelder, R.; Keppel-Aleks, G.; Allen, N.; Ayers, J. TCCON data from Park Falls, Wisconsin, USA, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/295 (accessed on 8 March 2020).
- Morino, I.; Yokozeki, N.; Matzuzaki, T.; Horikawa, M. TCCON Data from Rikubetsu, Hokkaido, Japan, Release GGG2014R2, TCCON Data Archive. Available online: https://data.caltech.edu/records/957 (accessed on 8 March 2020).
- Iraci, L.; Podolske, J.; Hillyard, P.; Roehl, C.; Wennberg, P.O.; Blavier, J.-F.; Landeros, J.; Allen, N.; Wunch, D.; Zavaleta, J.; et al. TCCON data from Indianapolis, Indiana, USA, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/274 (accessed on 8 March 2020).
- Dubey, M.; Lindenmaier, R.; Henderson, B.; Green, D.; Allen, N.; Roehl, C.; Blavier, J.-F.; Butterfield, Z.; Love, S.; Hamelmann, J.; et al. TCCON data from Four Corners, NM, USA, Release GGG2014R0, TCCON data archive, TCCON Data Archive. Available online: https://data.caltech.edu/records/272 (accessed on 8 March 2020).
- Wennberg, P.O.; Wunch, D.; Roehl, C.; Blavier, J.-F.; Toon, G.C.; Allen, N.; Dowell, P.; Teske, K.; Martin, C.; Martin, J. TCCON data from Lamont, Oklahoma, USA, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/279 (accessed on 8 March 2020).
- Goo, T.-Y.; Oh, Y.-S.; Velazco, V.A. TCCON data from Anmeyondo, South Korea, Release GGG2014R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/266 (accessed on 8 March 2020).
- Morino, I.; Matsuzaki, T.; Horikawa, M. TCCON data from Tsukuba, Ibaraki, Japan, 125HR, Release GGG2014R2, TCCON Data Archive. Available online: https://data.caltech.edu/records/958 (accessed on 8 March 2020).
- Iraci, L.; Podolske, J.; Hillyard, P.; Roehl, C.; Wennberg, P.O.; Blavier, J.-F.; Landeros, J.; Allen, N.; Wunch, D.; Zavaleta, J.; et al. TCCON data from Armstrong Flight Research Center, Edwards, CA, USA, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/270 (accessed on 8 March 2020).
- Wennberg, P.O.; Roehl, C.; Blavier, J.-F.; Wunch, D.; Landeros, J.; Allen, N. TCCON data from Jet Propulsion Laboratory, Pasadena, California, USA, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/277 (accessed on 8 March 2020).
- Wennberg, P.O.; Wunch, D.; Roehl, C.; Blavier, J.-F.; Toon, G.C.; Allen, N. TCCON data from California Institute of Technology, Pasadena, California, USA, Release GGG2014R1, TCCON Data Archive. Available online: https://data.caltech.edu/records/285 (accessed on 8 March 2020).
- Kawakami, S.; Ohyama, H.; Arai, K.; Okumura, H.; Taura, C.; Fukamachi, T.; Sakashita, M. TCCON data from Saga, Japan, Release GGG2014R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/288 (accessed on 8 March 2020).
- Liu, C.; Wang, W.; Sun, Y. TCCON data from Hefei, China, Release GGG2014R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/1092 (accessed on 8 March 2020).
- Morino, I.; Velazco, V.A.; Hori, A.; Uchino, O.; Griffith, D.W.T. TCCON data from Burgos, Philippines, Release GGG2014R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/1090 (accessed on 8 March 2020).
- Dubey, M.; Henderson, B.; Green, D.; Butterfield, Z.; Keppel-Aleks, G.; Allen, N.; Blavier, J.-F.; Roehl, C.; Wunch, D.; Lindenmaier, R. TCCON data from Manaus, Brazil, Release GGG2014R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/282 (accessed on 8 March 2020).
- Griffith, D.W.T.; Deutscher, N.; Velazco, V.A.; Wennberg, P.O.; Yavin, Y.; Keppel Aleks, G.; Washenfelder, R.; Toon, G.C.; Blavier, J.-F.; Paton, W.C.; et al. TCCON data from Darwin, Australia, Release GGG2014R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/269 (accessed on 8 March 2020).
- Griffith, D.W.T.; Velazco, V.A.; Deutscher, N.; Paton, W.C.; Jones, N.; Wilson, S.; Macatangay, R.; Kettlewell, G.; Buchholz, R.R.; Riggenbach, M. TCCON data from Wollongong, Australia, Release GGG2014R0, TCCON Data Archive. 2017. Available online: https://data.caltech.edu/records/291 (accessed on 8 March 2020).
- Sherlock, V.; Connor, B.; Robinson, J.; Shiona, H.; Smale, D.; Pollard, D. TCCON data from Lauder, New Zealand, 120HR, Release GGG2014R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/280 (accessed on 8 March 2020).
- Sherlock, V.; Connor, B.; Robinson, J.; Shiona, H.; Smale, D.; Pollard, D. TCCON data from Lauder, New Zealand, 125HR, Release GGG2014R0, TCCON Data Archive. Available online: https://data.caltech.edu/records/281 (accessed on 8 March 2020).
- Dils, B.; Buchwitz, M.; Reuter, M.; Schneising, O.; Boesch, H.; Parker, R.; Guerlet, S.; Aben, I.; Blumenstock, T.; Burrows, J.P.; et al. The Greenhouse Gas Climate Change Initiative (GHG-CCI): Comparative validation of GHG-CCI SCIAMACHY/ENVISAT and TANSO-FTS/GOSAT CO2 and CH4 retrieval algorithm products with measurements from the TCCON. Atmos. Meas. Tech. 2014, 7, 1723–1744. [Google Scholar] [CrossRef]
- Wunch, D.; Toon, G.C.; Blavier, J.-F.L.; Washenfelder, R.A.; Notholt, J.; Connor, B.J.; Griffith, D.W.T.; Sherlock, V.; Wennberg, P.O. The Total Carbon Column Observing Network. Phil. Trans. R. Soc. A 2011, 369, 2087–2112. [Google Scholar] [CrossRef]
- Deutscher, N.M.; Griffith, D.W.T.; Bryant, G.W.; Wennberg, P.O.; Toon, G.C.; Washenfelder, R.A.; Keppel-Aleks, G.; Wunch, D.; Yavin, Y.; Allen, N.T.; et al. Total column CO2 measurements at Darwin, Australia—Site description and calibration against in situ aircraft profiles. Atmos. Meas. Tech. 2010, 3, 947–958. [Google Scholar] [CrossRef]
- Mendonca, J.; Strong, K.; Wunch, D.; Toon, G.C.; Long, D.A.; Hodges, J.T.; Sironneau, V.T.; Franklin, J.E. Using a speed-dependent Voigt line shape to retrieve O2 from Total Carbon Column Observing Network solar spectra to improve measurements of XCO2. Atmos. Meas. Tech. 2019, 12, 35–50. [Google Scholar] [CrossRef]
- Schneising, O.; Heymann, J.; Buchwitz, M.; Reuter, M.; Bovensmann, H.; Burrows, J.P. Anthropogenic carbon dioxide source areas observed from space: Assessment of regional enhancements and trends. Atmos. Chem. Phys. 2013, 13, 2445–2454. [Google Scholar] [CrossRef]
- Kivi, R.; Heikkinen, P. Fourier transform spectrometer measurements of column CO2 at Sodankylä, Finland. Geosci. Instrum. Method. Data Syst. 2016, 5, 271–279. [Google Scholar] [CrossRef]
- Lindenmaier, R.; Dubey, M.K.; Henderson, B.G.; Butterfield, Z.T.; Herman, J.R.; Rahn, T.; Lee, S.-H. Multiscale observations of CO2, 13CO2, and pollutants at Four Corners for emission verification and attribution. Proc. Natl. Acad. Sci. USA 2014, 111, 8386–8391. [Google Scholar] [CrossRef] [PubMed]
- Kort, E.A.; Frankenberg, C.; Costigan, K.R.; Lindenmaier, R.; Dubey, M.K.; Wunch, D. Four corners: The largest US methane anomaly viewed from space. Geophys. Res. Lett. 2014, 41, 6898–6903. [Google Scholar] [CrossRef]
- Kuze, A.; Suto, H.; Shiomi, K.; Urabe, T.; Nakajima, M.; Yoshida, J.; Kawashima, T.; Yamamoto, Y.; Kataoka, F.; Buijs, H. Level 1 algorithms for TANSO on GOSAT: Processing and on-orbit calibrations. Atmos. Meas. Tech. 2012, 5, 2447–2467. [Google Scholar] [CrossRef]



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oshio, H.; Yoshida, Y.; Matsunaga, T.; Deutscher, N.M.; Dubey, M.; Griffith, D.W.T.; Hase, F.; Iraci, L.T.; Kivi, R.; Liu, C.; et al. Bias Correction of the Ratio of Total Column CH4 to CO2 Retrieved from GOSAT Spectra. Remote Sens. 2020, 12, 3155. https://doi.org/10.3390/rs12193155
Oshio H, Yoshida Y, Matsunaga T, Deutscher NM, Dubey M, Griffith DWT, Hase F, Iraci LT, Kivi R, Liu C, et al. Bias Correction of the Ratio of Total Column CH4 to CO2 Retrieved from GOSAT Spectra. Remote Sensing. 2020; 12(19):3155. https://doi.org/10.3390/rs12193155
Chicago/Turabian StyleOshio, Haruki, Yukio Yoshida, Tsuneo Matsunaga, Nicholas M. Deutscher, Manvendra Dubey, David W. T. Griffith, Frank Hase, Laura T. Iraci, Rigel Kivi, Cheng Liu, and et al. 2020. "Bias Correction of the Ratio of Total Column CH4 to CO2 Retrieved from GOSAT Spectra" Remote Sensing 12, no. 19: 3155. https://doi.org/10.3390/rs12193155
APA StyleOshio, H., Yoshida, Y., Matsunaga, T., Deutscher, N. M., Dubey, M., Griffith, D. W. T., Hase, F., Iraci, L. T., Kivi, R., Liu, C., Morino, I., Notholt, J., Oh, Y.-S., Ohyama, H., Petri, C., Pollard, D. F., Roehl, C., Shiomi, K., Sussmann, R., ... Wunch, D. (2020). Bias Correction of the Ratio of Total Column CH4 to CO2 Retrieved from GOSAT Spectra. Remote Sensing, 12(19), 3155. https://doi.org/10.3390/rs12193155