Geodetic Measurements and Numerical Models of Deformation at Coso Geothermal Field, California, USA, 2004–2016
Abstract
:1. Introduction
2. Data
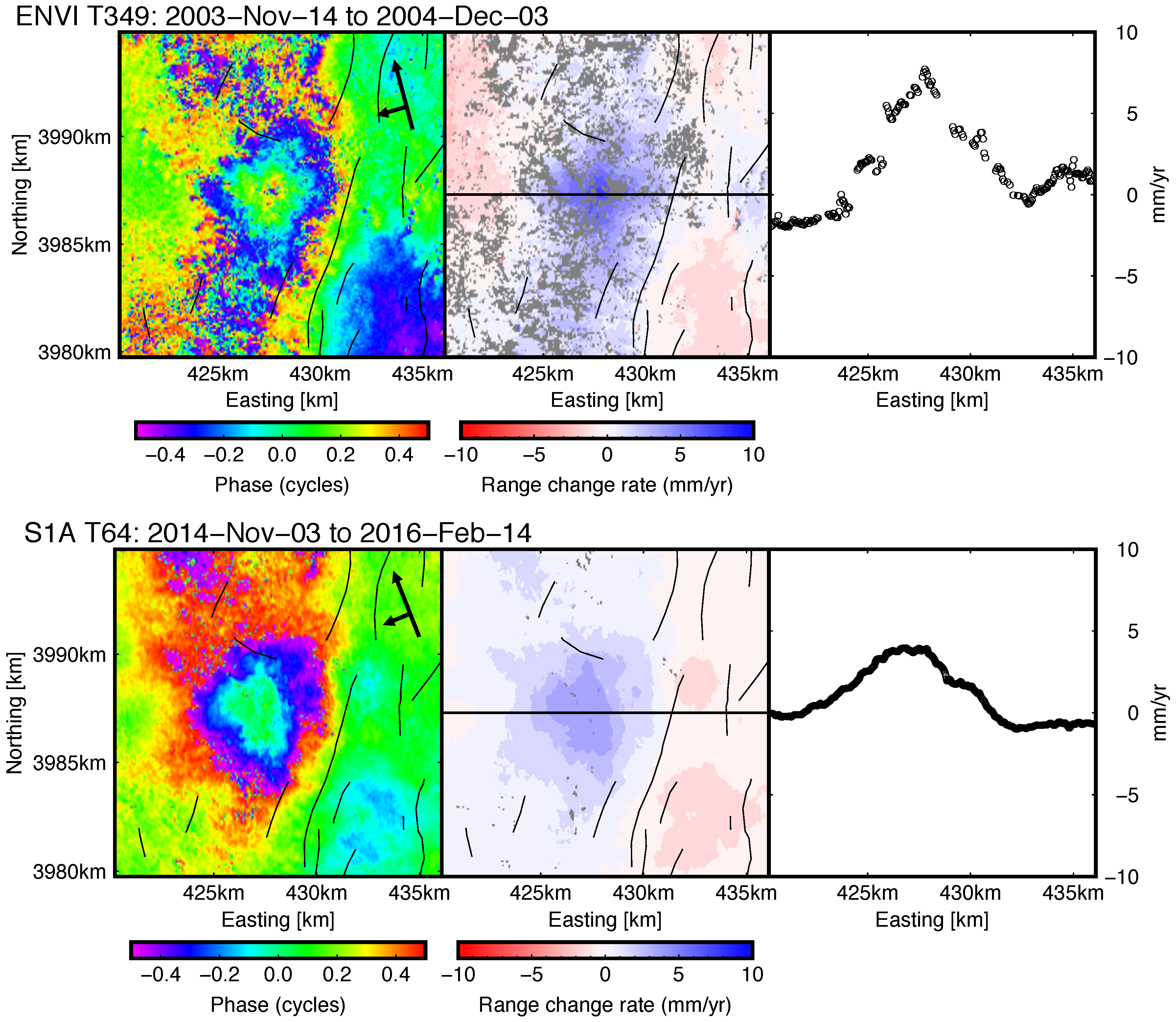
2.1. Interferometric Synthetic Aperture Radar (InSAR)
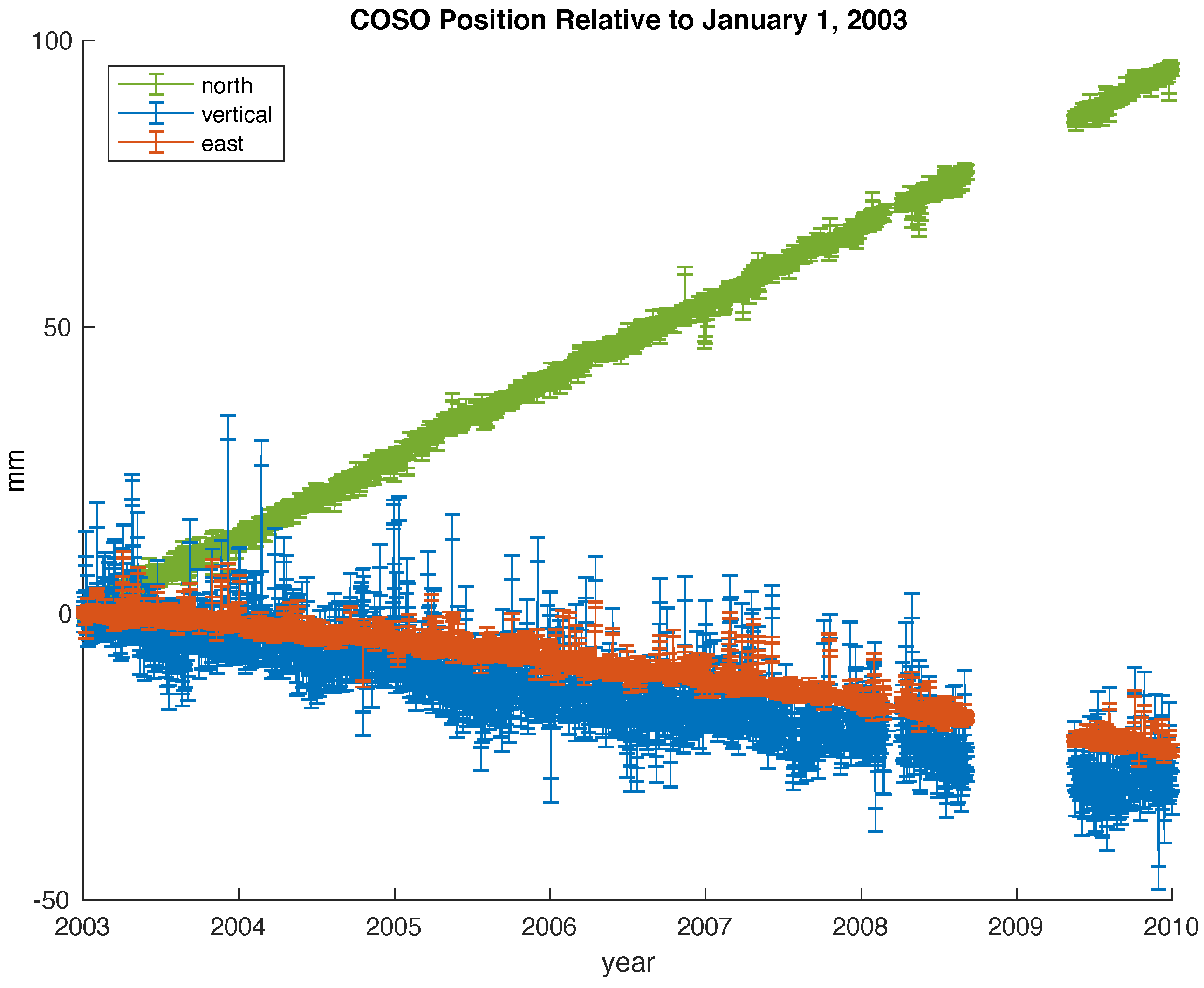
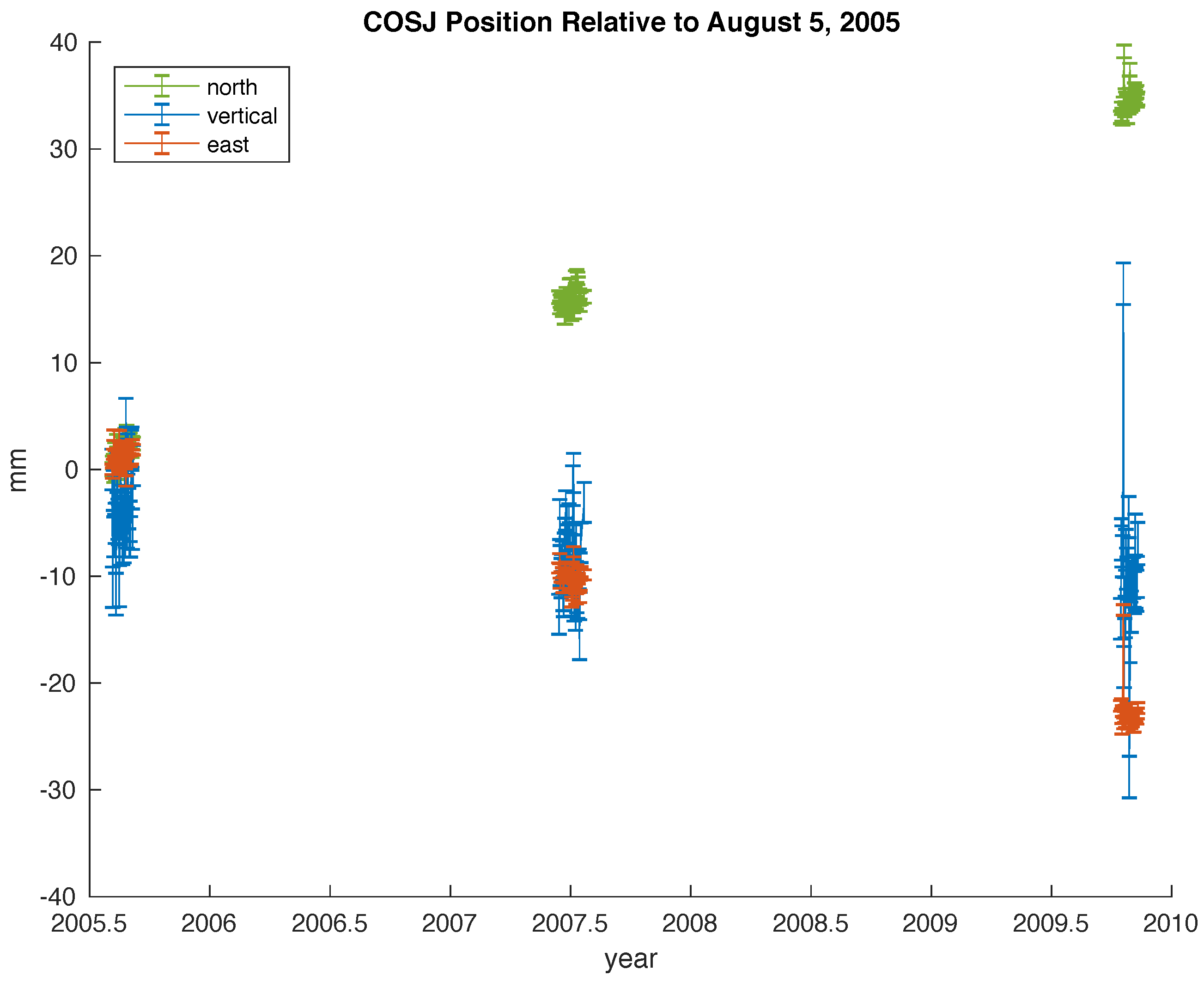
2.2. Global Positioning System (GPS)
2.3. Seismic Catalog
2.4. Pumping Records
3. Methods
3.1. Accuracy
3.2. Estimating Volume Change of The Reservoir
3.3. Time Series
4. Results
4.1. Deformation Modeling
4.2. Time-Series Analysis
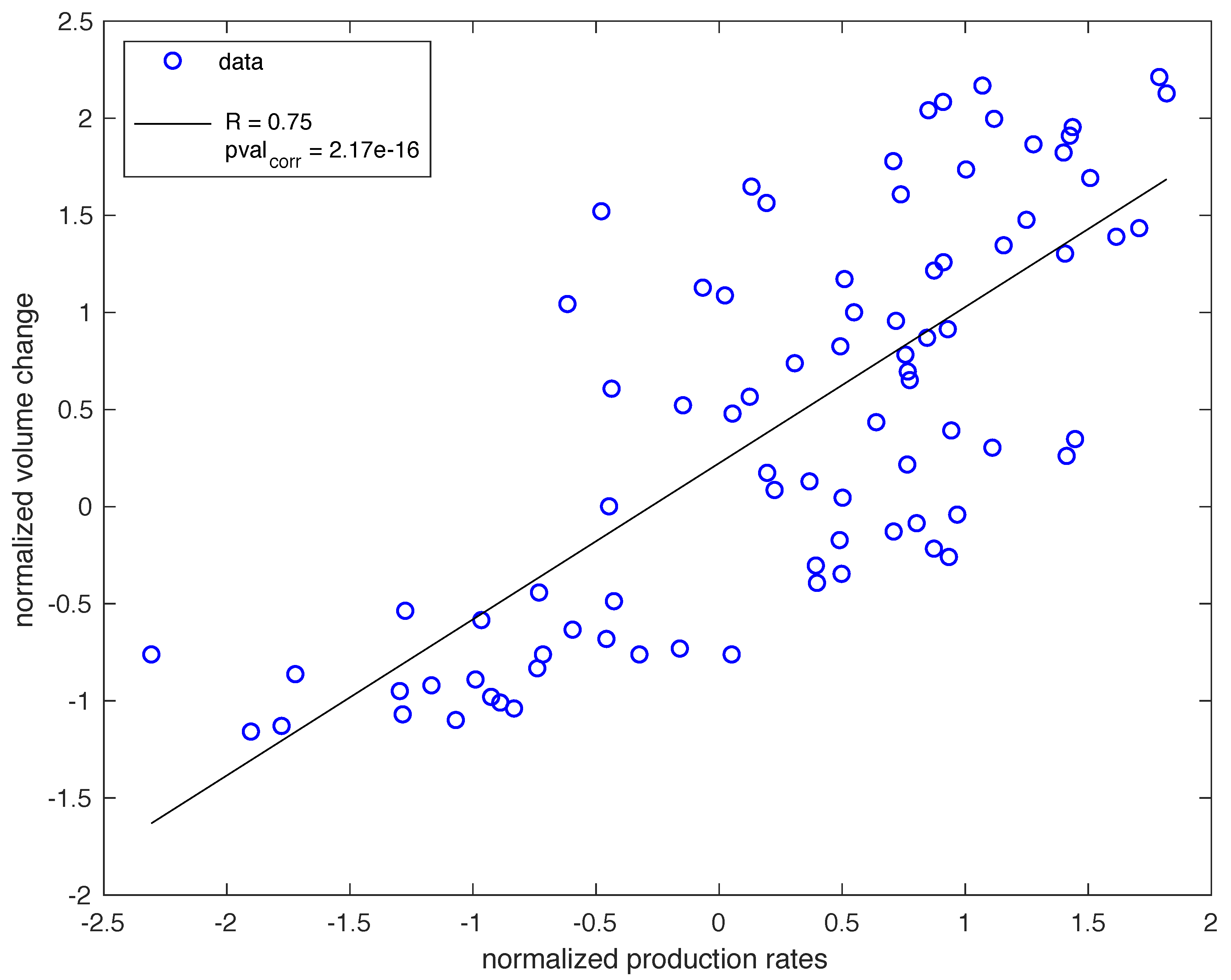
4.3. Correlation Test
4.4. Identifying a Driving Mechanism for the Observed Subsidence
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Unruh, J.R.; Hauksson, E.; Monastero, F.C.; Twiss, R.J.; Lewis, J.C. Seismotectonics of the Coso Range–Indian Wells Valley region, California: Transtensional deformation along the southeastern margin of the Sierran microplate. Geol. Evol. Mojave Desert Southwest. Basin Range Geol. Soc. Am. Mem. 2002, 195, 277–294. [Google Scholar]
- Monastero, F.; Katzenstein, A.; Miller, J.; Unruh, J.; Adams, M.; Richards-Dinger, K. The Coso geothermal field: A nascent metamorphic core complex. Geol. Soc. Am. Bull. 2005, 117, 1534–1553. [Google Scholar] [CrossRef] [Green Version]
- Fournier, R.; Thompson, J.; Austin, C. Interpretation of chemical analyses of waters collected from two geothermal wells at Coso, California. J. Geophys. Res. Solid Earth 1980, 85, 2405–2410. [Google Scholar] [CrossRef]
- Davatzes, N.C.; Hickman, S.H. The feedback between stress, faulting, and fluid flow: Lessons from the Coso Geothermal Field, CA, USA. In Proceedings of the World Geothermal Congress 2010, Bali, Indonesia, 25–29 April 2010; pp. 1–14. [Google Scholar]
- Division of Oil, Gas, and Geothermal Resources. Monthly Records of Production and Injection for Geothermal Resources. Available online: ftp://ftp.consrv.ca.gov/pub/oil/geothermal/Coso.xls (accessed on 22 September 2016).
- TEAM Engineering & Management, Inc. Hay Ranch Project Conditional Use Permit Hydrologic Monitoring Report: Fourth Quarter 2017 Inyo County, California. Technical Report. TEAM, 2018. Available online: http://www.inyowater.org/wp-content/uploads/legacy/INDEX_DOCS/Coso%20Hay%20Ranch_FEIR_Dec_30_08.pdf (accessed on 26 January 2019).
- OpenEI. Coso Geothermal Area. Available online: https://openei.org/wiki/Coso_Geothermal_Area (accessed on 2 October 2018).
- Fialko, Y.; Simons, M. Deformation and seismicity in the Coso geothermal area, Inyo County, California: Observations and modeling using satellite radar interferometry. J. Geophys. Res. Solid Earth 2000, 105, 21781–21793. [Google Scholar] [CrossRef] [Green Version]
- Bhattacharyya, J.; Lees, J.M. Seismicity and seismic stress in the Coso Range, Coso geothermal field, and Indian Wells Valley region, southeast-central California. Mem. Geol. Soc. Am 2002, 195, 243–257. [Google Scholar]
- Kaven, J.O.; Hickman, S.H.; Davatzes, N.C. Micro-seismicity, fault structure and hydraulic compartmentalization within the Coso gethermal field, California. In Proceedings of the Thirty-Sixth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 31 January–2 February 2011. [Google Scholar]
- Kaven, J.O.; Hickman, S.H.; Davatzes, N.C. Using micro-seismicity and seismic velocities to map subsurface geologic and hydrologic structure within the Coso geothermal field, California. In Proceedings of the Thirty-Seventh Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 30 January–1 February 2012. [Google Scholar]
- Kaven, J.O.; Hickman, S.H.; Davatzes, N.C. Micro-seismicity within the Coso geothermal field, California, from 1996–2012. In Proceedings of the Thirty-Eighth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 11–13 February 2013. [Google Scholar]
- Schoenball, M.; Glen, J.M.; Davatzes, N.C. Analysis and interpretation of stress indicators in deviated wells of the Coso geothermal field. In Proceedings of the Forty-First Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 22–24 February 2016; pp. 1169–1180. [Google Scholar]
- Majer, E.L.; Baria, R.; Stark, M.; Oates, S.; Bommer, J.; Smith, B.; Asanuma, H. Induced seismicity associated with enhanced geothermal systems. Geothermics 2007, 36, 185–222. [Google Scholar] [CrossRef]
- Brodsky, E.E.; Lajoie, L.J. Anthropogenic seismicity rates and operational parameters at the Salton Sea Geothermal Field. Science 2013, 341, 543–546. [Google Scholar] [CrossRef]
- Ellsworth, W.L. Injection-induced earthquakes. Science 2013, 341, 142. [Google Scholar] [CrossRef]
- Mazzoldi, A.; Borgia, A.; Ripepe, M.; Marchetti, E.; Ulivieri, G.; della Schiava, M.; Allocca, C. Faults strengthening and seismicity induced by geothermal exploitation on a spreading volcano, Mt. Amiata, Italia. J. Volcanol. Geotherm. Res. 2015, 301, 159–168. [Google Scholar] [CrossRef]
- Cardiff, M.; Lim, D.D.; Akerley, J.R.P.J.; Spielman, P.; Lopeman, J.; Walsh, P.; Singh, A.; Foxall, W.; Wang, H.F.; Lord, N.E.; et al. Geothermal production and reduced seismicity: Correlation and proposed mechanism. Earth Planet. Sci. Lett. 2017, 482, 470–477. [Google Scholar] [CrossRef]
- Warren, I.; Gasperikova, E.; Pullammanappallil, S.; Grealy, M. Mapping Geothermal Permeability Using Passive Seismic Emission Tomography Constrained by Cooperative Inversion of Active Seismic and Electromagnetic Data. In Proceedings of the 43rd Stanford Workshop on Geothermal Reservoir Engineering, Palo Alto, CA, USA, 12–14 February 2018. [Google Scholar]
- McLeod, I.H.; Cumming, I.G.; Seymour, M.S. ENVISAT ASAR data reduction: Impact on SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 589–602. [Google Scholar] [CrossRef]
- Geudtner, D.; Torres, R.; Snoeij, P.; Davidson, M.; Rommen, B. Sentinel-1 system capabilities and applications. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 1457–1460. [Google Scholar]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. Open radar interferometry software for mapping surface deformation. Eos. Trans. Am. Geophys. Union 2011, 92, 234. [Google Scholar] [CrossRef] [Green Version]
- Sandwell, D.; Mellors, R.; Tong, X.; Wei, M.; Wessel, P. GMTSAR: An InSAR Processing System Based on Generic Mapping Tools; Scripps Institution of Oceanography: San Diego, CA, USA, 2011; Available online: http://escholarship.org/uc/item/8zq2c02m (accessed on 3 September 2017).
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.W.; Zebker, H.A. Network approaches to two-dimensional phase unwrapping: intractability and two new algorithms. JOSA A 2000, 17, 401–414. [Google Scholar] [CrossRef] [PubMed]
- Reinisch, E.C.; Cardiff, M.; Feigl, K.L. Graph theory for analyzing pair-wise data: Application to geophysical model parameters estimated from interferometric synthetic aperture radar data at Okmok volcano, Alaska. J. Geod. 2017, 91, 9–24. [Google Scholar] [CrossRef] [Green Version]
- Ali, S.T.; Akerley, J.; Baluyut, E.C.; Davatzes, N.C.; Lopeman, J.; Moore, J.; Plummer, M.; Spielman, P.; Warren, I.; Feigl, K.L. Geodetic measurements and numerical models of deformation: Examples from geothermal fields in the western United States. In Proceedings of the Forty-First Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 22–24 February 2016. [Google Scholar]
- Snyder, J.P. Map Projections–A Working Manual; US Government Printing Office: Washington, DC, USA, 1987; Volume 1395. [Google Scholar]
- Reinisch, E.C.; Feigl, K.L. Envisat Track 349 and Sentinel-1A Track 64 Interferometric Synthetic Aperture Radar Data of Coso Geothermal Field, California, USA, 2004–2016; Technical Report, DOE Geothermal Data Repository; University of Wisconsin: Madison, WI, USA, 2019; Available online: http://gdr.openei.org/submissions/1145 (accessed on 26 June 2019).
- Jennings, P. Fault Map of California With Volcanoes, Thermal Springs and Thermal Wells at 1:750,000 Scale. Geological Data Map, Map No. 1. 1975. Available online: https://searchworks.stanford.edu/view/510979 (accessed on 25 September 2018).
- Jennings, C.; Saucedo, G.; Dart, R.; Machette, M.; Burns, D.; Faneros, G.; Little, J.; Davis, J. Digital database of faults from the fault activity map of California and adjacent areas. Calif. Div. Mines Geol. 2000, 6, 2000. Available online: https://searchworks.stanford.edu/view/4463334 (accessed on 25 September 2018).
- Blewitt, G.; Hammond, W.; Kreemer, C. Harnessing the GPS data explosion for interdisciplinary science. Eos 2018, 99. [Google Scholar] [CrossRef]
- Blewitt, G. Nevada Geodetic Laboratory Station ID: COSO. Available online: http://geodesy.unr.edu/NGLStationPages/stations/COSO.sta (accessed on 20 September 2018).
- Blewitt, G. Nevada Geodetic Laboratory Station ID: COSJ. Available online: http://geodesy.unr.edu/NGLStationPages/stations/COSJ.sta (accessed on 20 September 2018).
- Lindseth, R.O. Synthetic sonic logs—A process for stratigraphic interpretation. Geophysics 1979, 44, 3–26. [Google Scholar] [CrossRef]
- Feighner, M.; Goldstein, N. A gravity model for the Coso geothermal area, California. In Proceedings of the Annual Meeting of the Geothermal Resources Council and International Symposium on Geothermal Energy, Kailua-Kona, HI, USA, 20–24 August 1990. [Google Scholar]
- Wackerly, D.; Mendenhall, W.; Scheaffer, R. Mathematical Statistics with Applications; Cengage Learning: Boston, MA, USA, 2007; p. 944. [Google Scholar]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Feigl, K.L.; Thurber, C.H. A method for modelling radar interferograms without phase unwrapping: Application to the M 5 Fawnskin, California earthquake of 1992 December 4. Geophys. J. Int. 2009, 176, 491–504. [Google Scholar] [CrossRef] [Green Version]
- Reinisch, E.C.; Cardiff, M.; Feigl, K.L. Characterizing volumetric strain at Brady Hot Springs, Nevada, USA using geodetic data, numerical models, and prior information. Geophys. J. Int. 2018, 215, 1501–1513. [Google Scholar] [CrossRef] [Green Version]
- Ali, S.; Davatzes, N.; Mellors, R.; Foxall, W.; Drakos, P.; Zemach, E.; Kreemer, C.; Wang, H.; Feigl, K. InSAR measurements and numerical models of deformation at Brady Hot Springs geothermal field (Nevada), 1995–2012. In Proceedings of the Thirty-Ninth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24–26 February 2014. [Google Scholar]
- Eneva, M.; Barbour, A.; Adams, D.; Hsiao, V.; Blake, K.; Falorni, G.; Locatelli, R. Satellite observations of surface deformation at the Coso geothermal field, California. GRC Trans. 2018, 42, 1383–1401. [Google Scholar]
- Patterson, J.R.; Cardiff, M.; Coleman, T.; Wang, H.; Feigl, K.L.; Akerley, J.; Spielman, P. Geothermal reservoir characterization using distributed temperature sensing at Brady Geothermal Field, Nevada. Lead. Edge 2017, 36, 1024a1–1024a7. [Google Scholar] [CrossRef] [Green Version]
- Patterson, J.R. Understanding Constraints on Geothermal Sustainability Through Reservoir Characterization at Brady Geothermal Field, Nevada. Master’s Thesis, University of Wisconsin, Madison, WI, USA, 2018. [Google Scholar]
- Strang, G.; Borre, K. Linear Algebra, Geodesy, and GPS; SIAM: Philadelphia, PA, USA, 1997; p. 624. [Google Scholar]
- Rose, P.E. Creation of an Enhanced Geothermal System Through Hydraulic And Thermal Stimulation; Technical Report; Energy and Geoscience Institute at the University of Utah: Salt Lake City, UT, USA, 2013. [Google Scholar]
- Spane Jr, F.A. Hydrogeologic Investigation of Coso Hot Springs, Inyo County, California; Technical Report; Hydro-Search Inc.: Reno, NV, USA, 1978. [Google Scholar]
- Austin, C.F.; Moore, J. Structural Interpretation of the Coso Geothermal Field; Technical Report; Naval Weapons Center: China Lake, CA, USA, 1987. [Google Scholar]
- Wang, H. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology; Princeton Series in Geophysics; Princeton University Press: Princeton, NJ, USA, 2000; p. 301. [Google Scholar]
- Blankenship, D. West Flank Coso, CA FORGE: Well 48-11TCH Temperature, Pressure, Directional, Well History, Well Bore Schematic; Technical Report, DOE Geothermal Data Repository; Sandia National Laboratories: Albuquerque, NM, USA, 2016. [Google Scholar] [CrossRef]
- Mossop, A.; Segall, P. Subsidence at The Geysers geothermal field, N. California from a comparison of GPS and leveling surveys. Geophys. Res. Lett. 1997, 24, 1839–1842. [Google Scholar] [CrossRef] [Green Version]
- Mossop, A.; Segall, P. Volume strain within The Geysers geothermal field. J. Geophys. Res. Solid Earth 1999, 104, 29113–29131. [Google Scholar] [CrossRef]
- Nygren, A.J. Geomechanics Applied to Reservoir Development in the Coso Geothermal Field. Ph.D. Thesis, University of North Dakota, Grand Forks, ND, USA, 2005. [Google Scholar]
- Rutqvist, J.; Dobson, P.F.; Garcia, J.; Hartline, C.; Jeanne, P.; Oldenburg, C.M.; Vasco, D.W.; Walters, M. The northwest Geysers EGS demonstration project, California: Pre-stimulation modeling and interpretation of the stimulation. Math. Geosci. 2015, 47, 3–29. [Google Scholar] [CrossRef] [Green Version]
- Reinisch, E.C. Spatio-Temporal Characterization of Geothermal Fields by Inverse Modeling. Ph.D. Thesis, University of Wisconsin, Madison, WI, USA, 2019. [Google Scholar]
- Segall, P. Stress and subsidence resulting from subsurface fluid withdrawal in the epicentral region of the 1983 Coalinga earthquake. J. Geophys. Res. Solid Earth 1985, 90, 6801–6816. [Google Scholar] [CrossRef]
- Deng, K.; Liu, Y.; Harrington, R.M. Poroelastic stress triggering of the December 2013 Crooked Lake, Alberta, induced seismicity sequence. Geophys. Res. Lett. 2016, 43, 8482–8491. [Google Scholar] [CrossRef]
- Zencher, F.; Bonafede, M.; Stefansson, R. Near-lithostatic pore pressure at seismogenic depths: A thermoporoelastic model. Geophys. J. Int. 2006, 166, 1318–1334. [Google Scholar] [CrossRef] [Green Version]
- Barbour, A.J.; Evans, E.L.; Hickman, S.H.; Eneva, M. Subsidence rates at the southern Salton Sea consistent with reservoir depletion. J. Geophys. Res. Solid Earth 2016, 121, 5308–5327. [Google Scholar] [CrossRef] [Green Version]
- Wessel, P.; Smith, W.H.; Scharroo, R.; Luis, J.; Wobbe, F. Generic Mapping Tools: Improved version released. Eos. Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef] [Green Version]
- Feigl, K.L.; Reinisch, E.C.; Ali, S.T.; Thurber, C.H.; Powell, L.; Sobol, P.; Masters, A. General Inversion of Phase Technique (GIPhT) Software Repository—Coso Branch; Technical Report; GitHub Inc.: San Francisco, CA, USA, 2019; Available online: https://github.com/feigl/gipht/tree/Coso (accessed on 6 June 2019).










| Parameter Name | Best-Fitting Estimate | Uncertainty |
|---|---|---|
| Easting in m | 428,651.3 | 1000 |
| Northing in m | 3,987,538.4 | 1000 |
| Reservoir depth in m | 2366.6 | 250 |
| Reservoir half thickness in m | 2053.1 | 250 |
| Reservoir half length in m | 3027.2 | 500 |
| Young’s Modulus in GPa | 25 | 0 |
| Poisson’s Ratio | 0.25 | 0 |
| Pressure Change in MPa | 0 | |
| Biot’s Coefficient | 1 | 0 |
| Parameter Name | Best-Fitting Estimate | Uncertainty |
|---|---|---|
| Easting gradient | 6.78 | 2.19 |
| Northing gradient | −9.93 | 1.86 |
| Upwards gradient | −9.97 | 9.67 |
| Offset in cycles | −0.5 | 0.8 |
| Poisson ratio | 0.21 | 0 |
| Volume change rate | −2.02 | 2.81 |
| Centroid Easting E in m | 428,580.4 | 531.3 |
| Centroid Northing N in m | 3,987,509.0 | 250.0 |
| Centroid Depth in m | 2418.2 | 531.3 |
| Cuboid L in m | 3.07 | 3.23 |
| Cuboid W in m | 2.28 | 2.25 |
| Cuboid H in m | 1.95 | 2.42 |
| Parameter Name | Best-Fitting Estimate | Uncertainty |
|---|---|---|
| Easting gradient | 1.64 | 6.25 |
| Northing gradient | −1.39 | 9.38 |
| Upwards gradient | 6.73 | 2.19 |
| Offset in cycles | −0.5 | 0.6 |
| Poisson ratio | 0.21 | 0 |
| Volume change rate | −1.07 | 2.25 |
| Centroid Easting E in m | 428,870.4 | 48.4 |
| Centroid Northing N in m | 3,986,482.0 | 46.9 |
| Centroid Depth in m | 3098.7 | 195.3 |
| Cuboid L in m | 3.12 | 4.84 |
| Cuboid W in m | 2.34 | 4.84 |
| Cuboid H in m | 1.93 | 4.84 |
| Start of Break 1 | Start of Break 2 | Rate 1 [m3/year] | Rate 2 [m3/year] | Test Value | Critical Value | Result | |
|---|---|---|---|---|---|---|---|
| 20031114 | 20100101 | 78 | 3.95 | 1.99 | reject | ||
| 20031114 | 20141102 | 76 | −25.16 | 1.99 | reject | ||
| 20100101 | 20141102 | 16 | −4.67 | 2.12 | reject |
| Pre-2010 Rate m3/year | Post-2010 Rate m3/year | Test Value | Critical Value | Result | |
|---|---|---|---|---|---|
| 3638 | −843.22 | 1.96 | reject |
| Data Source | [L/s] |
|---|---|
| Gross injection [5] | |
| Gross production [5] | |
| Net production [5] | |
| Cuboid sink estimated from InSAR data from 2005 to 2010 | |
| Cuboid sink from InSAR data from 2014 to 2016 | |
| Cuboid sink estimated from GPS data from 2005 to 2010 | |
| Cuboid sink from GPS data from 2014 to 2016 | |
| Average recharge [47,48] | 130 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reinisch, E.C.; Ali, S.T.; Cardiff, M.; Kaven, J.O.; Feigl, K.L. Geodetic Measurements and Numerical Models of Deformation at Coso Geothermal Field, California, USA, 2004–2016. Remote Sens. 2020, 12, 225. https://doi.org/10.3390/rs12020225
Reinisch EC, Ali ST, Cardiff M, Kaven JO, Feigl KL. Geodetic Measurements and Numerical Models of Deformation at Coso Geothermal Field, California, USA, 2004–2016. Remote Sensing. 2020; 12(2):225. https://doi.org/10.3390/rs12020225
Chicago/Turabian StyleReinisch, Elena C., S. Tabrez Ali, Michael Cardiff, J. Ole Kaven, and Kurt L. Feigl. 2020. "Geodetic Measurements and Numerical Models of Deformation at Coso Geothermal Field, California, USA, 2004–2016" Remote Sensing 12, no. 2: 225. https://doi.org/10.3390/rs12020225
APA StyleReinisch, E. C., Ali, S. T., Cardiff, M., Kaven, J. O., & Feigl, K. L. (2020). Geodetic Measurements and Numerical Models of Deformation at Coso Geothermal Field, California, USA, 2004–2016. Remote Sensing, 12(2), 225. https://doi.org/10.3390/rs12020225






