Precise Orbit Determination for Climate Applications of GNSS Radio Occultation including Uncertainty Estimation
Abstract
:1. Introduction
2. Missions and Spacecraft Payload
3. Processing Setup and Description
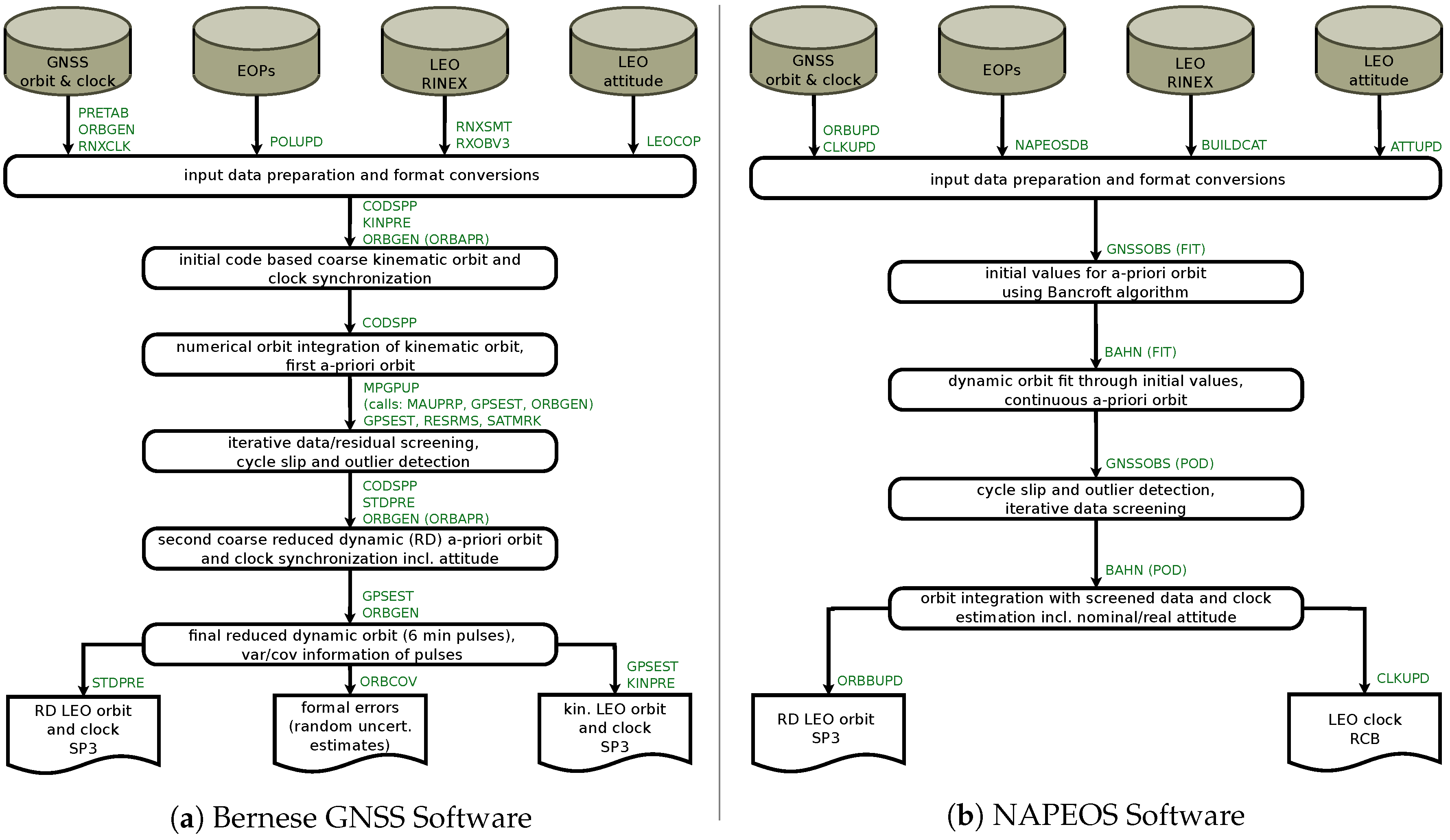
3.1. Data and Tools
3.2. Precise Orbit Determination
3.3. Orbit Solutions
- WEGC-BC: The orbit solution selected for the following RO data processing. The calculation is based on Bernese and the GNSS orbit and clock data from the CODE reprocessing in 2015; referred to as primary solution hereafter.
- WEGC-BI: Same Bernese setup as for WEGC-BC above but employing GNSS orbit and clocks from JPL (as part of IGS repro2).
- WEGC-NC: This solution is calculated using NAPEOS, introducing the GNSS orbit and clock products from CODE as for WEGC-BC.
3.4. Satellite Laser Ranging
3.5. Uncertainty Modeling
3.5.1. LEO Systematic Uncertainty Estimates
- (a)
- WEGC-BC vs. WEGC-NC difference (LEO POD cross-check):Based on GNSS orbit input from CODE the orbit differences are driven by computational setup and model considerations of the different LEO POD software packages employed.
- (b)
- WEGC-BC vs. WEGC-BI difference (GNSS input sanity-check):The orbit computations are carried out by Bernese with different GNSS orbit, clock, and EOP data and might reveal deficiencies in the transmitter orbit modeling.
- (c)
- WEGC-BC vs. SLR difference (SLR validation cross-check):Analysis of SLR residuals for missions equipped with an LRR. This validation represents snapshots because of the limited number of available SLR measurement sequences per day.
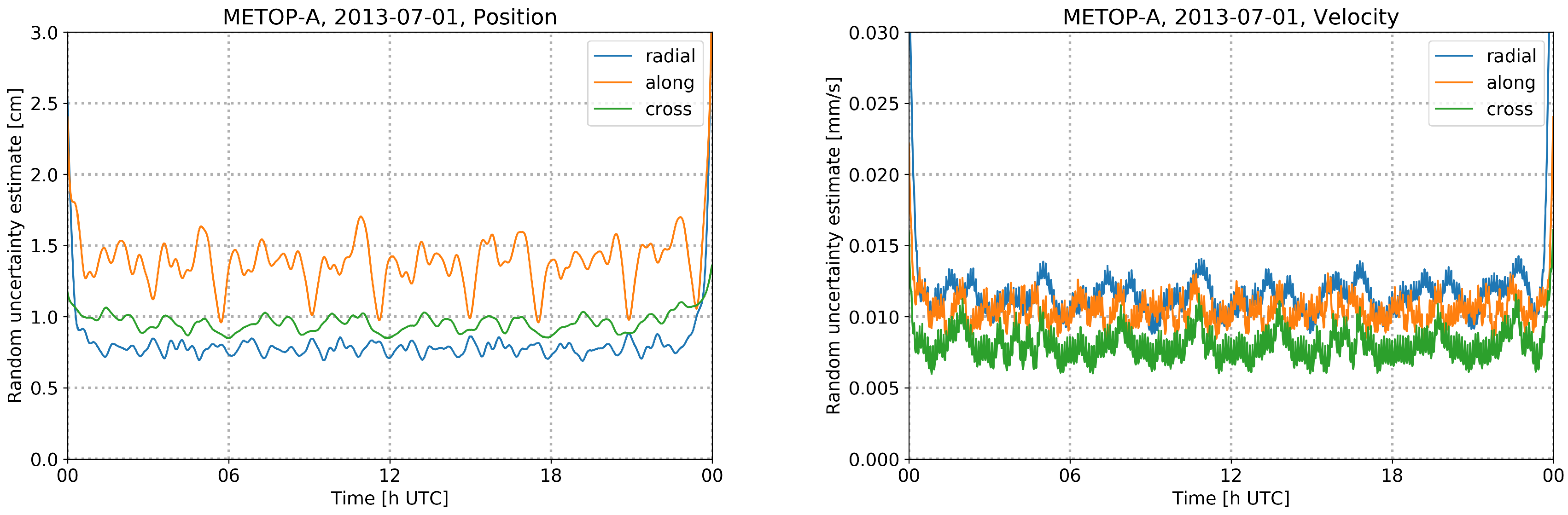
3.5.2. LEO Random Uncertainty Estimates
3.5.3. GNSS Uncertainty Estimates
4. Results and Discussion
4.1. Orbit Comparison
4.2. Satellite Laser Ranging Validation
4.3. Uncertainty Estimation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AC | Analysis Center |
| ASC | Advanced Star Camera |
| CB | Conservative Bound |
| CDAAC | COSMIC Data Analysis and Archive Center |
| CHAMP | CHAllenging Minisatellite Payload |
| CODE | Center for Orbit Determination in Europe |
| DSM | Daily System Modeling |
| DLR | German Aerospace Center |
| DTU | Technical University of Denmark |
| ECOM | Empirical CODE Orbit Model |
| ECV | Essential Climate Variable |
| EOP | Earth Orientation Parameter |
| ESA | European Space Agency |
| ESOC | European Space Operations Centre |
| EUMETSAT | European Organization for the Exploitation of Meteorological Satellites |
| FCDR | Fundamental Climate Data Record |
| GNSS | Global Navigation Satellite System |
| GFZ | German Research Centre for Geosciences |
| GPS | Global Positioning System |
| GRACE | Gravity And Climate Experiment |
| GRAS | GNSS Receiver for Atmospheric Sounding |
| IERS | International Earth Rotation and Reference Systems Service |
| ILRS | International Laser Ranging Service |
| IGS | International GNSS Service |
| IR | Infrared |
| ITRF | International Terrestrial Reference Frame |
| JCGM | Joint Committee for Guides in Metrology |
| JPL | Jet Propulsion Laboratory |
| LEO | Low Earth Orbit |
| LRR | Laser Retroreflector |
| Metop | Meteorological Operational |
| NASA | National Aeronautics and Space Administration |
| ODP | Occultation Data Processing |
| PCO | Phase Center Offset |
| PCV | Phase Center Variation |
| POD | Precise Orbit Determination |
| RCB | Receiver Clock Bias file format |
| RINEX | Receiver Independent Exchange Format |
| RO | Radio Occultation |
| rOPS | Reference Occultation Processing System |
| RTN | Radial-Transverse-Normal |
| SLR | Satellite Laser Ranging |
| SP3 | Standard Product 3 orbit file format |
| UCAR | University Corporation for Atmospheric Research |
Appendix A
References
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems; Springer: Wien, NY, USA, 2008. [Google Scholar]
- Teunissen, P.J.; Montenbruck, O. Springer Handbook of Global Navigation Satellite Systems; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Kursinski, E.R.; Hajj, G.A.; Schofield, J.T.; Linfield, R.P.; Hardy, K.R. Observing Earth’s atmosphere with radio occultation measurements using the Global Positioning System. J. Geophys. Res. 1997, 102, 23429–23465. [Google Scholar] [CrossRef]
- Syndergaard, S. Retrieval Analysis and Methodologies in Atmospheric Limb Sounding Using the GNSS Radio Occultation Technique. Ph.D. Thesis, Danish Meteorological Institute, Copenhagen, Denmark, 1999. [Google Scholar]
- Hajj, G.A.; Kursinski, E.R.; Romans, L.J.; Bertiger, W.I.; Leroy, S.S. A technical description of atmospheric sounding by GPS occultation. J. Atmos. Solar-Terr. Phys. 2002, 64, 451–469. [Google Scholar] [CrossRef]
- Anthes, R.A. Exploring Earth’s atmosphere with radio occultation: Contributions to weather, climate, and space weather. Atmos. Meas. Tech. 2011, 4, 1077–1103. [Google Scholar] [CrossRef] [Green Version]
- Steiner, A.K.; Lackner, B.C.; Ladstädter, F.; Scherllin-Pirscher, B.; Foelsche, U.; Kirchengast, G. GPS radio occultation for climate monitoring and change detection. Radio Sci. 2011, 46. [Google Scholar] [CrossRef] [Green Version]
- Leroy, S.S.; Dykema, J.A.; Anderson, J.G. Climate benchmarking using GNSS occultation. In Atmosphere and Climate: Studies by Occultation Methods; Foelsche, U., Kirchengast, G., Steiner, A.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 287–301. [Google Scholar] [CrossRef]
- Foelsche, U.; Scherllin-Pirscher, B.; Ladstädter, F.; Steiner, A.K.; Kirchengast, G. Refractivity and temperature climate records from multiple radio occultation satellites consistent within 0.05%. Atmos. Meas. Tech. 2011, 4, 2007–2018. [Google Scholar] [CrossRef] [Green Version]
- Steiner, A.K.; Ladstädter, F.; Ao, C.O.; Gleisner, H.; Ho, S.P.; Hunt, D.; Schmidt, T.; Foelsche, U.; Kirchengast, G.; Kuo, Y.H.; et al. Consistency and structural uncertainty of multi-mission GPS radio occultation records. Atmos. Meas. Tech. Discuss. 2019. [Google Scholar] [CrossRef]
- Bojinski, S.; Verstraete, M.; Peterson, T.C.; Richter, C.; Simmons, A.; Zemp, M. The concept of Essential Climate Variables in support of climate research, applications, and policy. Bull. Am. Meteor. Soc. 2014, 95, 1431–1443. [Google Scholar] [CrossRef]
- National Research Council. Earth Science and Applications from Space: National Imperatives for the Next Decade and Beyond (Decadal Survey); The National Academies Press: Washington, DC, USA, 2007. [CrossRef]
- GCOS. Status of the Global Observing System for Climate—Full Report; GCOS-195; WMO: Geneva, Switzerland, 2015. [Google Scholar]
- Scherllin-Pirscher, B.; Steiner, A.K.; Kirchengast, G.; Kuo, Y.H.; Foelsche, U. Empirical analysis and modeling of errors of atmospheric profiles from GPS radio occultation. Atmos. Meas. Tech. 2011, 4, 1875–1890. [Google Scholar] [CrossRef] [Green Version]
- Scherllin-Pirscher, B.; Kirchengast, G.; Steiner, A.K.; Kuo, Y.H.; Foelsche, U. Quantifying uncertainty in climatological fields from GPS radio occultation: An empirical-analytical error model. Atmos. Meas. Tech. 2011, 4, 2019–2034. [Google Scholar] [CrossRef] [Green Version]
- Angerer, B.; Ladstädter, F.; Scherllin-Pirscher, B.; Schwärz, M.; Steiner, A.K.; Foelsche, U.; Kirchengast, G. Quality aspects of the WEGC multi-satellite GPS radio occultation record OPSv5.6. Atmos. Meas. Tech. 2017, 10, 4845–4863. [Google Scholar] [CrossRef] [Green Version]
- Ho, S.P.; Hunt, D.; Steiner, A.K.; Mannucci, A.J.; Kirchengast, G.; Gleisner, H.; Heise, S.; von Engeln, A.; Marquardt, C.; Sokolovskiy, S.; et al. Reproducibility of GPS radio occultation data for climate monitoring: Profile-to-profile inter-comparison of CHAMP climate records 2002 to 2008 from six data centers. J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef]
- Steiner, A.K.; Hunt, D.; Ho, S.P.; Kirchengast, G.; Mannucci, A.J.; Scherllin-Pirscher, B.; Gleisner, H.; von Engeln, A.; Schmidt, T.; Ao, C.; et al. Quantification of structural uncertainty in climate data records from GPS radio occultation. Atmos. Chem. Phys. 2013, 13, 1469–1484. [Google Scholar] [CrossRef] [Green Version]
- Kirchengast, G.; Schwärz, M.; Schwarz, J.; Scherllin-Pirscher, B.; Pock, C.; Innerkofler, J.; Proschek, V.; Steiner, A.K.; Danzer, J.; Ladstädter, F.; et al. The reference occultation processing system approach to interpret GNSS radio occultation as SI-traceable planetary system refractometer. Presented at the OPAC-IROWG International Workshop, Seggau/Leibnitz, Austria, 8–14 September 2016; Available online: http://wegcwww.uni-graz.at/opacirowg2016 (accessed on 23 March 2020).
- Kirchengast, G.; Schwärz, M.; Angerer, B.; Schwarz, J.; Innerkofler, J.; Proschek, V.; Ramsauer, J.; Fritzer, J.; Scherllin-Pirscher, B.; Rieckh, T. Reference OPS DAD—Reference Occultation Processing System (rOPS) Detailed Algorithm Description; Tech. Rep. for ESA and FFG No. 1/2018, Doc-Id: WEGC–rOPS–2018–TR01, Issue 2.0; Wegener Center, Univ. of Graz: Graz, Austria, 2018. [Google Scholar]
- Schwarz, J.C.; Kirchengast, G.; Schwaerz, M. Integrating uncertainty propagation in GNSS radio occultation retrieval: From bending angle to dry-air atmospheric profiles. Earth Space Sci. 2017, 4, 200–228. [Google Scholar] [CrossRef] [Green Version]
- Schwarz, J.C.; Kirchengast, G.; Schwaerz, M. Integrating uncertainty propagation in GNSS radio occultation retrieval: From excess phase to atmospheric bending angle profiles. Atmos. Meas. Tech. 2018, 11, 2601–2631. [Google Scholar] [CrossRef] [Green Version]
- Innerkofler, J.; Pock, C.; Kirchengast, G.; Schwärz, M.; Jäggi, A.; Andres, Y.; Marquardt, C.; Schwarz, J. Multi-Mission Multi-Center Level 1 Data Inter-Validation towards Wegener Center Reference Occultation System Reprocessing. Presented at the EUMETSAT ROM SAF-IROWG International Workshop, Helsingør, Denmark, 19–25 September 2019; Available online: https://www.romsaf.org/romsaf-irowg-2019/en/content/21/program-agenda-by-day (accessed on 23 March 2020).
- Rocken, C.; Anthes, R.; Exner, M.; Hunt, D.; Sokolovskiy, S.; Ware, R.; Gorbunov, M.; Schreiner, W.; Feng, D.; Herman, B.; et al. Analysis and validation of GPS/MET data in the neutral atmosphere. J. Geophys. Res. 1997, 102, 29849–29866. [Google Scholar] [CrossRef]
- Wickert, J.; Galas, R.; Beyerle, G.; König, R.; Reigber, C. GPS ground station data for CHAMP radio occultation measurements. Phys. Chem. Earth 2001, 26, 503–511. [Google Scholar] [CrossRef]
- Wickert, J. Das CHAMP-Radiooccultationsexperiment: Algorithmen, Prozessierungssystem und erste Ergebnisse. Ph.D. Thesis, GeoForschungsZentrum Potsdam, Potsdam, Germany, 2002. Scientific Tech. Rep. STR02/07. [Google Scholar]
- Wickert, J.; Schmidt, T.; Michalak, G.; Heise, S.; Arras, C.; Beyerle, G.; Falck, C.; König, R.; Pingel, D.; Rothacher, M. GPS radio occultation with CHAMP, GRACE-A, SAC-C, TerraSAR-X, and FORMOSAT-3/COSMIC: Brief review of results from GFZ. In New Horizons in Occultation Research: Studies in Atmosphere and Climate; Steiner, A.K., Pirscher, B., Foelsche, U., Kirchengast, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 3–16. [Google Scholar]
- Montenbruck, O.; Andres, Y.; Bock, H.; van Helleputte, T.; van den Ijssel, J.; Loiselet, M.; Marquardt, C.; Silvestrin, P.; Visser, P.; Yoon, Y. Tracking and orbit determination performance of the GRAS instrument on MetOp-A. GPS Solut. 2008, 12, 289–299. [Google Scholar] [CrossRef] [Green Version]
- Montenbruck, O.; Hauschild, A.; Andres, Y.; von Engeln, A.; Marquardt, C. (Near-)real-time orbit determination for GNSS radio occultation processing. GPS Solut. 2013, 17, 199–209. [Google Scholar] [CrossRef]
- Dach, R.; Andritsch, F.; Arnold, D.; Bertone, S.; Fridez, P.; Jäggi, A.; Jean, Y.; Maier, A.; Mervart, L.; Meyer, U.; et al. Bernese GNSS Software Version 5.2, User Manual; Astron. Inst., Univ. of Bern: Bern, Switzerland, 2015. [Google Scholar] [CrossRef]
- Springer, T.A. NAPEOS—Mathematical Models and Algorithms; DOPS-SYS-TN-0100-OPS-GN; European Space Operation Centre, European Space Agency: Darmstadt, Germany, 2009. [Google Scholar]
- Jean, Y.; Dach, R. International GNSS Service Technical Report 2015; IGS Annual Report; IGS Central Bureau and University of Bern: Bern, Switzerland, 2016. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The International GNSS Service in a changing landscape of Global Navigation Satellite Systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Wickert, J.; Beyerle, G.; König, R.; Heise, S.; Grunwaldt, L.; Michalak, G.; Reigber, C.; Schmidt, T. GPS radio occultation with CHAMP and GRACE: A first look at a new and promising satellite configuration for global atmospheric sounding. Ann. Geophys. 2005, 23, 653–658. [Google Scholar] [CrossRef] [Green Version]
- Klaes, D.; Lugert, M.; Bojkov, B.; Ackermann, J.; Borde, R.; Coppens, D.; Guedj, S.; Linow, S.; August, T.; Marquardt, C.; et al. Metop Science Update and the Metop-C Mission of the Eumetsat Polar System (EPS). Presented at the AMS 2019 Joint Satellite Conference, Boston, MA, USA, 28 September–4 October 2019; Available online: https://ams.confex.com/ams/JOINTSATMET/meetingapp.cgi/Paper/359586 (accessed on 23 March 2020).
- Reigber, C.; Lühr, H.; Schwintzer, P. Status of the CHAMP Mission. In Towards an Integrated Global Geodetic Observing System (IGGOS); Rummel, R., Drewes, H., Bosch, W., Hornik, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2000; pp. 63–65. [Google Scholar]
- Montenbruck, O.; Kroes, R. In-flight performance analysis of the CHAMP BlackJack GPS Receiver. GPS Solut. 2003, 7, 74–86. [Google Scholar] [CrossRef]
- Beutler, G.; Jäggi, A.; Hugentobler, U.; Mervart, L. Efficient satellite orbit modelling using pseudo-stochastic parameters. J. Geod. 2006, 80, 353–372. [Google Scholar] [CrossRef] [Green Version]
- Wickert, J.; Reigber, C.; Beyerle, G.; König, R.; Marquardt, C.; Schmidt, T.; Grunwaldt, L.; Galas, R.; Meehan, T.; Melbourne, W.; et al. Atmosphere sounding by GPS radio occultation: First results from CHAMP. Geophys. Res. Lett. 2001, 28, 3263–3266. [Google Scholar] [CrossRef] [Green Version]
- Jørgensen, J.L. In Orbit Performance of a Fully Autonomous Star Tracker. In ESA 4th Symposion on Spacecraft Guidance Navigation and Control; ESTEC, European Space Agency: Noordwijk, Netherlands, 1999. [Google Scholar]
- Jørgensen, P.S.; Jørgensen, J.L.; Denver, T.; Betto, M. In-flight quality and accuracy of attitude measurements from the CHAMP advanced stellar compass. Acta Astron. 2005, 56, 181–186. [Google Scholar] [CrossRef] [Green Version]
- Neubert, R.; Grunwaldt, L.; Neubert, J. The Retro-Reflector for the CHAMP Satellite: Final Design and Realization. In Proceedings of the 11th International Workshop on Laser Ranging, Deggendorf, Germany, 21–25 September 1998; pp. 260–270. [Google Scholar]
- Grunwaldt, L.; Neubert, R. First Results of Laser Ranging to the CHAMP Retroreflector. In Proceedings of the 12th International Workshop on Laser Ranging, Matera, Italy, 13–17 November 2000. [Google Scholar]
- Arnold, D.; Montenbruck, O.; Hackel, S.; Sośnica, K. Satellite laser ranging to low Earth orbiters: Orbit and network validation. J. Geodesy 2018. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.; Watkins, M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.; Landerer, F.; Chambers, D.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 5. [Google Scholar] [CrossRef]
- Kim, J.; Lee, S.W. Flight performance analysis of GRACE K-band ranging instrument with simulation data. Acta Astron. 2009, 65, 1571–1581. [Google Scholar] [CrossRef]
- Dunn, C.; Bertiger, W.; Franklin, G.; Harris, I.; Kruizinga, G.; Meehan, T. The instrument on NASA’s GRACE mission: Augmentation of GPS to achieve unprecedented gravity field measurements. In Proceedings of the 15th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS 2002), Portland, Oregon, 24–27 September 2002; pp. 724–730. [Google Scholar]
- Beyerle, G.; Schmidt, T.; Michalak, G.; Heise, S.; Wickert, J.; Reigber, C. GPS radio occultation with GRACE: Atmospheric profiling utilizing the zero difference technique. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef] [Green Version]
- Flechtner, F.; Morton, P.; Watkins, M.; Webb, F. Status of the GRACE Follow-On Mission. In Gravity, Geoid and Height Systems; Marti, U., Ed.; Springer International Publishing: Cham, Switzerland, 2014; pp. 117–121. [Google Scholar] [CrossRef]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M.; Gath, P.F.; Bettadpur, S. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Klaes, K.D.; Cohen, M.; Buhler, Y.; Schlüssel, P.; Munro, R.; Luntama, J.P.; von Engeln, A.; Clérigh, E.Ó.; Bonekamp, H.; Ackermann, J.; et al. An Introduction to the EUMETSAT Polar system. Bull. Am. Meteor. Soc. 2007, 88, 1085–1096. [Google Scholar] [CrossRef]
- Loiselet, M.; Stricker, N.; Menard, Y.; Luntama, J.P. GRAS—MetOp’s GPS-based atmospheric sounder. ESA Bull. 2000, 102, 38–44. [Google Scholar]
- Silvestrin, P.; Bagge, R.; Bonnedal, M.; Carlström, A.; Christensen, J.; Hägg, M.; Lindgren, T. Spaceborne GNSS Radio Occultation Instrumentation for Operational Applications. In Proceedings of the 13th ION-GPS Meeting, Salt Lake City, UT, USA, 19–22 September 2000. [Google Scholar]
- Bonnedal, M.; Christensen, J.; Carlström, A.; Berg, A. Metop-GRAS in-orbit instrument performance. GPS Solut. 2010, 14, 109–120. [Google Scholar] [CrossRef]
- von Engeln, A.; Healy, S.; Marquardt, C.; Andres, Y.; Sancho, F. Validation of operational GRAS radio occultation data. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Pearlman, M.; Degnan, J.; Bosworth, J. The International Laser Ranging Service. Adv. Space Res. 2002, 30, 135–143. [Google Scholar] [CrossRef]
- Pearlman, M.R.; Noll, C.E.; Pavlis, E.C.; Lemoine, F.G.; Combrink, L.; Degnan, J.J.; Kirchner, G.; Schreiber, U. The ILRS: Approaching 20 years and planning for the future. J. Geodesy 2019. [Google Scholar] [CrossRef]
- Susnik, A.; Dach, R.; Villiger, A.; Maier, A.; Arnold, D.; Schaer, S.; Jäggi, A. CODE Reprocessing Product Series; Astronomical Institute, University of Bern: Bern, Switzerland, 2016. [Google Scholar] [CrossRef]
- Griffiths, J.; Ray, J. On the precision and accuracy of IGS orbits. J. Geod. 2009, 83. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to Using International GNSS Service (IGS) Products; Technical Report; IGS: Pasadena, CA, USA, 2009. [Google Scholar]
- Ray, J. Precision, Accuracy, and Consistency of GNSS Products. In Encyclopedia of Geodesy; Grafarend, E., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Griffiths, J. Combined orbits and clocks from IGS second reprocessing. J. Geod. 2019, 93, 177–195. [Google Scholar] [CrossRef] [Green Version]
- Bock, H.; Dach, R.; Jäggi, A.; Beutler, G. High-rate GPS clock corrections from CODE: Support of 1 Hz applications. J. Geod. 2009, 83, 1083–1094. [Google Scholar] [CrossRef] [Green Version]
- Arnold, D.; Meindl, M.; Beutler, G.; Dach, R.; Schaer, S.; Lutz, S.; Prange, L.; Sośnica, K.; Mervart, L.; Jäggi, A. CODE’s new solar radiation pressure model for GNSS orbit determination. J. Geod. 2015, 89. [Google Scholar] [CrossRef] [Green Version]
- Gurtner, W. RINEX: The Receiver Independent Exchange Format. GPS World 1994, 5, 48–52. [Google Scholar]
- Case, K.; Kruizinga, G.; Wu, S.C. GRACE Level 1B Data Product User Handbook; D-22027; JPL: Pasadena, CA, USA, 2010.
- Jäggi, A.; Hugentobler, U.; Beutler, G. Pseudo-Stochastic Orbit Modeling Techniques for Low-Earth Orbiters. J. Geod. 2006, 80, 47–60. [Google Scholar] [CrossRef] [Green Version]
- Jäggi, A. Pseudo-Stochastic Orbit Modeling of Low Earth Satellites Using the Global Positioning System. Ph.D. Thesis, Schweizerische Geodätische Kommission/Swiss Geodetic Commission, Zürich, Switzerland, 2007. [Google Scholar]
- Švehla, D.; Rothacher, M. Kinematic Orbit Determination of LEOs Based on Zero or Double-difference Algorithms Using Simulated and Real SST GPS Data. In Vistas for Geodesy in the New Millennium; Ádám, J., Schwarz, K.P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; pp. 322–328. [Google Scholar]
- Zehentner, N.; Mayer-Gürr, T. Precise orbit determination based on raw GPS measurements. J. Geod. 2016, 90, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Švehla, D.; Rothacher, M. Kinematic Precise Orbit Determination for Gravity Field Determination. In A Window on the Future of Geodesy; Sansò, F., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 181–188. [Google Scholar]
- Schutz, B.E.; Tapley, B.D.; Abusali, P.A.M.; Rim, H.J. Dynamic orbit determination using GPS measurements from TOPEX/POSEIDON. Geophys. Res. Lett. 1994, 21, 2179–2182. [Google Scholar] [CrossRef]
- Wu, S.C.W.; Yunck, T.P.; Thornton, C.L. Reduced-dynamic technique for precise orbit determination of low earth satellites. J. Guid. Control Dynam. 1991, 14, 24–30. [Google Scholar] [CrossRef]
- Yunck, T.P.; Bertiger, W.I.; Wu, S.C.; Bar-Sever, Y.E.; Christensen, E.J.; Haines, B.J.; Lichten, S.M.; Muellerschoen, R.J.; Vigue, Y.; Willis, P. First assessment of GPS-based reduced dynamic orbit determination on TOPEX/Poseidon. Geophys. Res. Lett. 1994, 21, 541–544. [Google Scholar] [CrossRef]
- Montenbruck, O.; van Helleputte, T.; Kroes, R.; Gill, E. Reduced dynamic orbit determination using GPS code and carrier measurements. Aerosp. Sci. Technol. 2005, 9, 261–271. [Google Scholar] [CrossRef]
- Peter, H.; Jäggi, A.; Fernández, J.; Escobar, D.; Ayuga, F.; Arnold, D.; Wermuth, M.; Hackel, S.; Otten, M.; Simons, W.; et al. Sentinel-1A—First precise orbit determination results. Adv. Space Res. 2017, 60, 879–892. [Google Scholar] [CrossRef]
- Bancroft, S. An Algebraic Solution of the GPS Equations. IEEE Trans. Aerosp. Electron. Syst. 1985, AES-21, 56–59. [Google Scholar] [CrossRef]
- Jäggi, A.; Beutler, G.; Hugentobler, U. Efficient Stochastic Orbit Modeling Techniques using Least Squares Estimators. In A Window on the Future of Geodesy; Sansò, F., Ed.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 175–180. [Google Scholar]
- IERS. IERS Conventions (2010). In International Earth Rotation and Reference Systems Service; IERS technical note no. 36; Gérard Petit and Brain Luzum, Ed.; IERS: Frankfurt am Main, Germany, 2010. [Google Scholar]
- IERS. IERS Conventions (2003). In International Earth Rotation and Reference Systems Service; IERS Technical note no. 32; McCarthy, D.D., Petit, G., Eds.; IERS: Frankfurt am Main, Germany, 2004. [Google Scholar]
- Altamimi, Z.; Collilieux, X.; Métivier, L. ITRF2008: An improved solution of the international terrestrial reference frame. J. Geod. 2011, 85, 457–473. [Google Scholar] [CrossRef] [Green Version]
- Schmid, R.; Dach, R.; Collilieux, X.; Jäggi, A.; Schmitz, M.; Dilssner, F. Absolute IGS antenna phase center model igs08.atx: Status and potential improvements. J. Geod. 2016, 90, 343–364. [Google Scholar] [CrossRef] [Green Version]
- Pavlis, N.K.; Holmes, S.A.; Kenyon, S.C.; Factor, J.K. The development and evaluation of the Earth Gravitational Model 2008 (EGM2008). J. Geophys. Res. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Rudenko, S.; Dettmering, D.; Esselborn, S.; Schöne, T.; Förste, C.; Lemoine, J.M.; Ablain, M.; Alexandre, D.; Neumayer, K.H. Influence of time variable geopotential models on precise orbits of altimetry satellites, global and regional mean sea level trends. Adv. Space Res. 2014, 54, 92–118. [Google Scholar] [CrossRef] [Green Version]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dynam. 2006, 56, 394–415. [Google Scholar] [CrossRef]
- Standish, E.M. JPL Planetary and Lunar Ephemerides; DE405/LE405. Interoffice Memorandum (IOM), 98, 048; Jet Propulsion Laboratory: Pasadena, CA, USA, 1998.
- Hedin, A.E. Extension of the MSIS thermosphere model into the middle and lower atmosphere. J. Geophys. Res. 1991, 96, 1159–1172. [Google Scholar] [CrossRef]
- Hwang, C.; Tseng, T.P.; Lin, T.; Švehla, D.; Schreiner, B. Precise orbit determination for the FORMOSAT-3/COSMIC satellite mission using GPS. J. Geod. 2009, 83, 477–489. [Google Scholar] [CrossRef]
- Schreiner, W.S.; Rocken, C.; Sokolovskiy, S.; Hunt, D. Quality assessment of COSMIC/FORMOSAT-3 GPS radio occultation data derived from single- and double-difference atmospheric excess phase processing. GPS Solut. 2010, 14, 13–22. [Google Scholar] [CrossRef]
- EUMETSAT. GRAS Level 1B Bending Angle Climate Data Record Release 1—Metop-A; European Organisation for the Exploitation of Meteorological Satellites: Darmstadt, Germany, 2017. [Google Scholar] [CrossRef]
- Prange, L.; Jäggi, A.; Dach, R.; Bock, H.; Beutler, G.; Mervart, L. AIUB-CHAMP02S: The influence of GNSS model changes on gravity field recovery using spaceborne GPS. Adv. Space Res. 2010, 45, 215–224. [Google Scholar] [CrossRef]
- Jäggi, A.; Dach, R.; Montenbruck, O.; Hugentobler, U.; Peter, H.; Beutler, G. Phase center modeling for LEO GPS receiver antennas and its impact on precise orbit determination. J. Geod. 2009, 83, 1145–1162. [Google Scholar] [CrossRef] [Green Version]
- Pock, C. Low Earth Orbit Determination for GNSS Radio Occultation with Aspects of Uncertainty Estimation. Master’s Thesis, Wegener Center Verlag Graz, Graz, Austria, 2015. Sci. Rep. 66-2015. [Google Scholar]
- Combrinck, L. Satellite Laser Ranging. In Sciences of Geodesy - I: Advances and Future Directions; Xu, G., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 301–338. [Google Scholar] [CrossRef]
- Wilkinson, M.; Schreiber, K.; Prochazka, I.; Moore, C.; Degnan, J.; Kirchner, G.; Zhongping, Z.; Dunn, P.; Shargorodskiy, V.; Sadovnikov, M.; et al. The next generation of satellite laser ranging systems. J. Geodesy 2018. [Google Scholar] [CrossRef]
- Strugarek, D.; Sośnica, K.; Jäggi, A. Characteristics of GOCE orbits based on Satellite Laser Ranging. Adv. Space Res. 2019, 63, 417–431. [Google Scholar] [CrossRef]
- JCGM. Evaluation of Measurement Data—Guide to the Expression of Uncertainty in Measurement; Rep. JCGM 100:2008; Joint Committee for Guides in Metrology, Office BIPM: Paris, France, 2008. [Google Scholar]
- Schwarz, J.C. Benchmark Quality Processing of Radio Occultation Data with Integrated Uncertainty Propagation. Ph.D. Thesis, Wegener Center Verlag Graz, Graz, Austria, 2018. Sci. Rep. 77-2018. [Google Scholar]
- Scaramuzza, S.; Dach, R.; Beutler, G.; Arnold, D.; Sušnik, A.; Jäggi, A. Dependency of geodynamic parameters on the GNSS constellation. J. Geod. 2018, 92, 93–104. [Google Scholar] [CrossRef] [Green Version]
- Urschl, C.; Gurtner, W.; Hugentobler, U.; Schaer, S.; Beutler, G. Validation of GNSS orbits using SLR observations. Adv. Space Res. 2005, 36, 412–417. [Google Scholar] [CrossRef]
- Sośnica, K.; Thaller, D.; Dach, R.; Steigenberger, P.; Beutler, G.; Arnold, D.; Jäggi, A. Satellite laser ranging to GPS and GLONASS. J. Geod. 2015, 89, 725–743. [Google Scholar] [CrossRef] [Green Version]
- Anthes, R.A.; Bernhardt, P.A.; Chen, Y.; Cucurull, L.; Dymond, K.F.; Ector, D.; Healy, S.B.; Ho, S.P.; Hunt, D.C.; Kuo, Y.H.; et al. The COSMIC/FORMOSAT-3 mission: Early results. Bull. Am. Meteor. Soc. 2008, 89, 313–333. [Google Scholar] [CrossRef]
- Sun, Y.; Bai, W.; Liu, C.; Liu, Y.; Du, Q.; Wang, X.; Yang, G.; Liao, M.; Yang, Z.; Zhang, X.; et al. The FengYun-3C radio occultation sounder GNOS: A review of the mission and its early results and science applications. Atmos. Meas. Tech. 2018, 11, 5797–5811. [Google Scholar] [CrossRef] [Green Version]
- Masters, D.; Irisov, V.; Nguyen, V.; Duly, T.; Nogués-Correig, O.; Tan, L.; Yuasa, T.; Ringer, J.; Sikarin, R.; Gorbunov, M.; et al. Status and plans for Spire’s commercial constellation of GNSS science CubeSats, 2019. Presented at the EUMETSAT ROM SAF-IROWG International Workshop, Helsingør, Denmark, 19–25 September 2019; Available online: https://www.romsaf.org/romsaf-irowg-2019/en/content/21/program-agenda-by-day (accessed on 23 March 2020).
- Schreiner, B.; Sokolovskiy, S.; Weiss, J.; Braun, J.; Anthes, R.; Kuo, Y.H.; Hunt, D.; Zeng, Z.; Wee, T.K.; VanHove, T.; et al. Performance Assessment and Requirement Verification of COSMIC-2 Neutral Atmospheric Radio Occultation Data, 2019. Presented at the EUMETSAT ROM SAF-IROWG International Workshop, Helsingør, Denmark, 19–25 September 2019; Available online: https://www.romsaf.org/romsaf-irowg-2019/en/content/21/program-agenda-by-day (accessed on 23 March 2020).





| Bernese GNSS Software v5.2 | NAPEOS v3.3.1 | |
|---|---|---|
| Reference system | ||
| Polar motion and UT1 | IERS C04 08 | IERS finals2000A.data |
| Polar model | IERS 2010 Conventions [80] | IERS 2003 Conventions [81] |
| Precision/Nutation | IERS 2010 Conventions | IERS 2003 Conventions |
| Reference frame | ITRF 2008 [82] | ITRF 2008 |
| GPS measurement characteristics | ||
| Observations | undifferenced ionosphere corrected | undifferenced ionosphere corrected |
| code and phase | code and phase | |
| Sampling | 30 s | 30 s |
| Elevation angle cut-off | 5 degrees | 5 degrees |
| GPS antenna PCO/PCV | igs08.atx [83] | igs08.atx |
| Antenna phase wind-up | applied [61] | applied |
| Relativity | applied | applied |
| GPS parameters | ||
| GPS orbits | CODE repro2015 (15 min) / IGS repro2 (15 min) | CODE repro2 (15 min) |
| GPS clocks | CODE repro2015 (5 s/30 s) / IGS repro2 (30 s) | CODE repro2 (5 s/30 s) |
| Gravitational forces | ||
| Gravity field model (static) | EGM2008 (120 × 120) [84] | EIGEN-6S2 (120 × 120) [85] |
| Solid Earth tides | applied (IERS2010) | applied (IERS2003) |
| Ocean tide model | FES2004 (50 × 50) [86] | FES2004 (50 × 50) |
| Planetary ephemeris | DE-405 [87] | DE-405 |
| Earth pole tide | IERS2010 | IERS2003 |
| Ocean pole tide | IERS2010 | IERS2003 |
| Non-gravitational forces | ||
| Atmospheric density model | n/a | MSISE-90 [88] |
| Atmospheric drag | n/a | constant area (10/24 h) |
| Radiation pressure model | n/a | constant area |
| Earth Radiation | n/a | NAPEOS model for Albedo and IR |
| 1/rev empiricals | n/a | 1/12 h (along- and cross-track) |
| Other empiricals | piece-wise constant accelerations in RTN | n/a |
| (every 6 min); constraints: 0.5 | ||
| Arc cut | ||
| Arc lengths | 24 h | 24 h |
| Maneuvers | n/a | n/a |
| Handle of data gaps | yes | yes |
| Estimation | ||
| Estimation | batch least squares | batch least squares |
| Solution Identifier | Analysis Center | Software | GNSS Data | Remark |
|---|---|---|---|---|
| Internal Solutions | ||||
| WEGC-BC | WEGC | Bernese 5.2 | CODE | primary solution |
| WEGC-BI | WEGC | Bernese 5.2 | IGS-JPL | control run |
| WEGC-NC | WEGC | NAPEOS 3.3.1 | CODE | control run |
| External Solutions | ||||
| UCAR | UCAR | Bernese | https://cdaac-www.cosmic.ucar.edu | |
| EUM | EUMETSAT | NAPEOS | https://eoportal.eumetsat.int | |
| AIUB | AIUB | Bernese | http://ftp.aiub.unibe.ch | |
| ID | Position (cm) | Velocity (mm/s) | ||||||
|---|---|---|---|---|---|---|---|---|
| Radial | Along | Cross | 3D | Radial | Along | Cross | 3D | |
| CHAMP: vs. WEGC-BC | ||||||||
| WEGC-BI | ||||||||
| WEGC-NC | ||||||||
| UCAR | ||||||||
| EUM | ||||||||
| AIUB | ||||||||
| GRACE-A: vs. WEGC-BC | ||||||||
| WEGC-BI | ||||||||
| WEGC-NC | ||||||||
| UCAR | ||||||||
| AIUB | ||||||||
| Metop-A: vs. WEGC-BC | ||||||||
| WEGC-BI | ||||||||
| WEGC-NC | ||||||||
| UCAR | ||||||||
| EUM | ||||||||
| Metop-B: vs. WEGC-BC | ||||||||
| WEGC-BI | ||||||||
| WEGC-NC | ||||||||
| UCAR | ||||||||
| EUM | ||||||||
| Solution | CHAMP | GRACE-A | ||
|---|---|---|---|---|
| All Stations | HQ Stations | All Stations | HQ Stations | |
| WEGC-BC | ||||
| WEGC-BI | ||||
| WEGC-NC | ||||
| UCAR | ||||
| EUMETSAT | n/a | n/a | ||
| AIUB | ||||
| Satellite | Random (cm) | Systematic (cm) | ||||||
|---|---|---|---|---|---|---|---|---|
| 3D | Radial | Along | Cross | 3D | Radial | Along | Cross | |
| CHAMP | ||||||||
| GRACE-A | ||||||||
| Metop-A | ||||||||
| Metop-B | ||||||||
| GPS-23 | ||||||||
| GPS-24 | ||||||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Innerkofler, J.; Kirchengast, G.; Schwärz, M.; Pock, C.; Jäggi, A.; Andres, Y.; Marquardt, C. Precise Orbit Determination for Climate Applications of GNSS Radio Occultation including Uncertainty Estimation. Remote Sens. 2020, 12, 1180. https://doi.org/10.3390/rs12071180
Innerkofler J, Kirchengast G, Schwärz M, Pock C, Jäggi A, Andres Y, Marquardt C. Precise Orbit Determination for Climate Applications of GNSS Radio Occultation including Uncertainty Estimation. Remote Sensing. 2020; 12(7):1180. https://doi.org/10.3390/rs12071180
Chicago/Turabian StyleInnerkofler, Josef, Gottfried Kirchengast, Marc Schwärz, Christian Pock, Adrian Jäggi, Yago Andres, and Christian Marquardt. 2020. "Precise Orbit Determination for Climate Applications of GNSS Radio Occultation including Uncertainty Estimation" Remote Sensing 12, no. 7: 1180. https://doi.org/10.3390/rs12071180
APA StyleInnerkofler, J., Kirchengast, G., Schwärz, M., Pock, C., Jäggi, A., Andres, Y., & Marquardt, C. (2020). Precise Orbit Determination for Climate Applications of GNSS Radio Occultation including Uncertainty Estimation. Remote Sensing, 12(7), 1180. https://doi.org/10.3390/rs12071180






