Analysis and Prediction of Gap Dynamics in a Secondary Deciduous Broadleaf Forest of Central Japan Using Airborne Multi-LiDAR Observations
Abstract
:1. Introduction
2. Materials and Methods
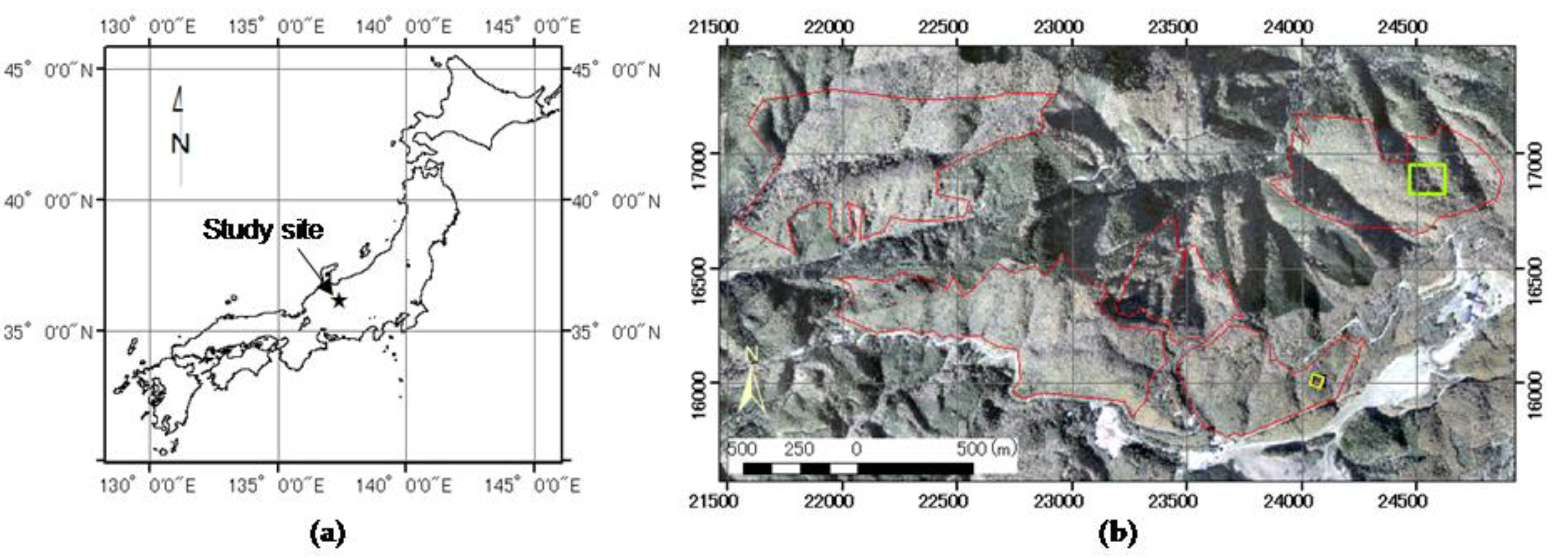
2.1. Study Site
2.2. Data
2.2.1. LiDAR Data
2.2.2. Aerial Photos Taken by Unmanned Aerial Vehicle (UAV)
2.2.3. Forest Type Maps and Aerial Photos
2.3. Field Survey and Data Processing
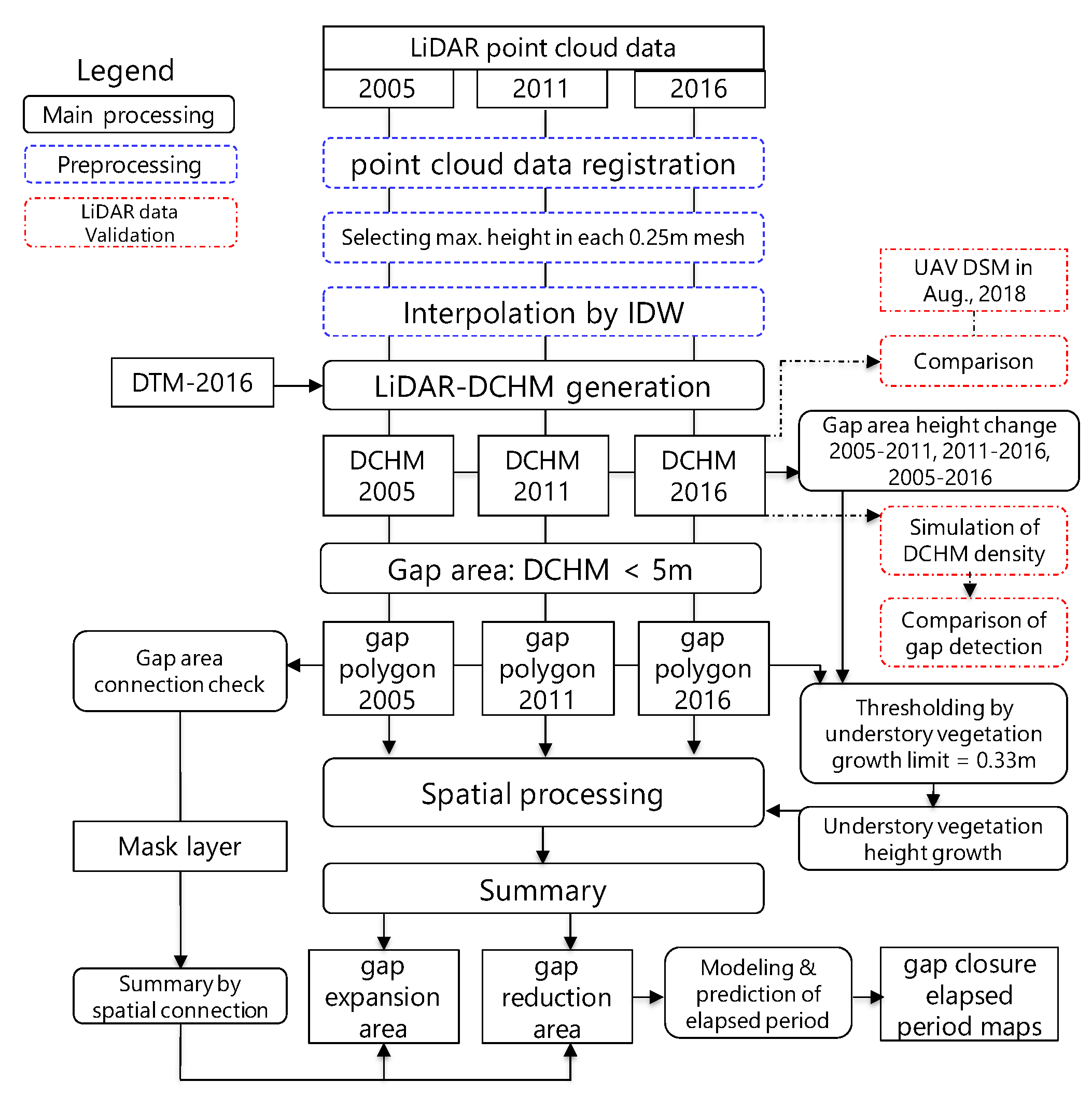
2.3.1. Generating DCHMs and Extracting Gaps from LiDAR Data
2.3.2. Compatibility Validation of Generated DSMs
2.3.3. Time-Series Tracking of Gap Generation and Canopy Closure
2.3.4. Modeling Gap Reduction and Lifespan
3. Results
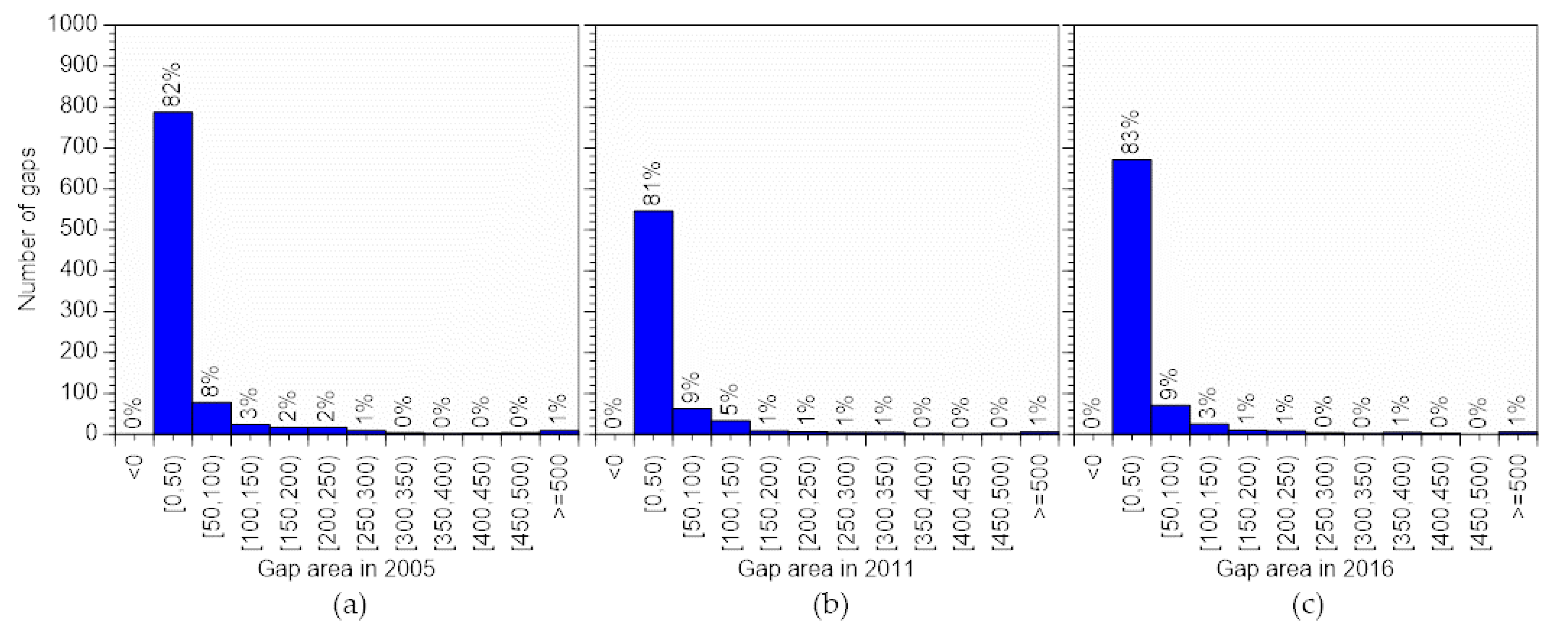
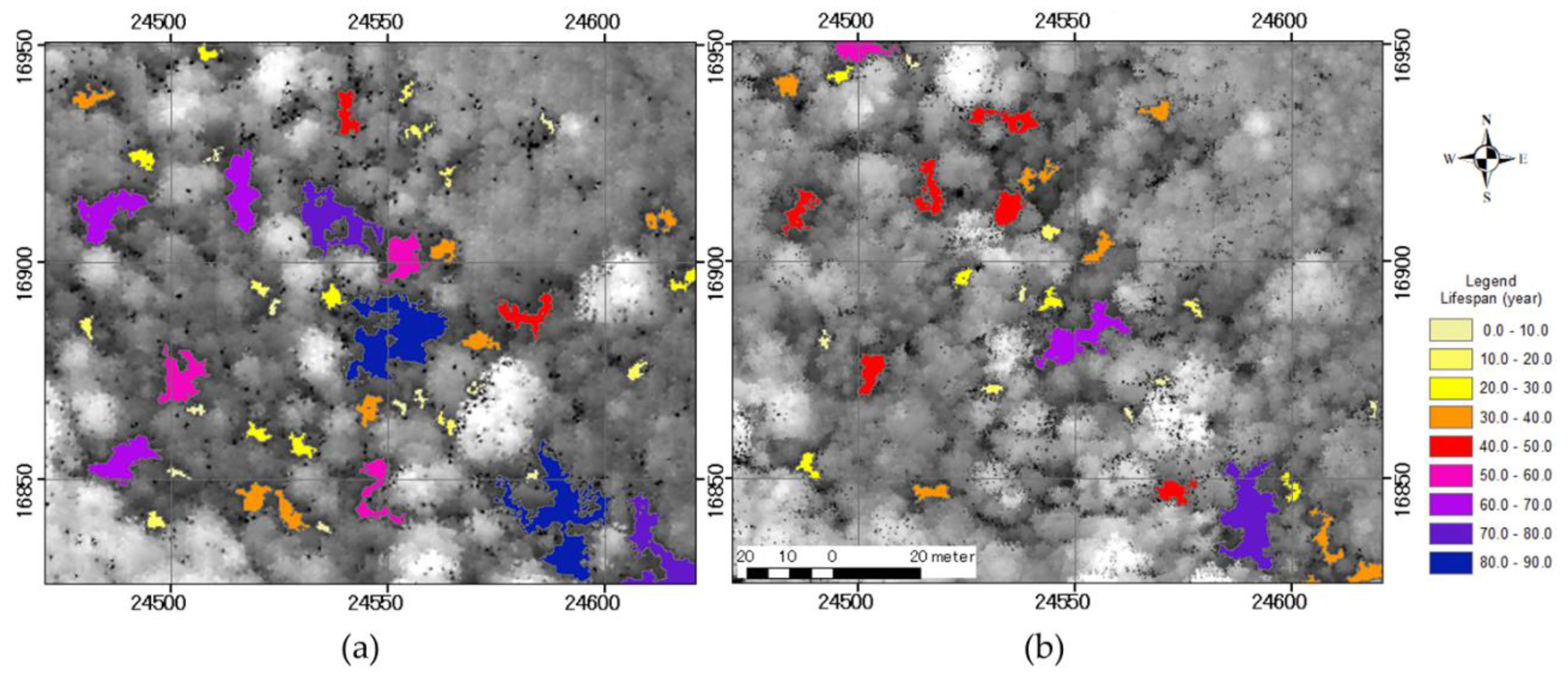
3.1. Generating DCHMs and Extracting Gaps from LiDAR Data
3.2. Compatibility Validation of Generated DSMs
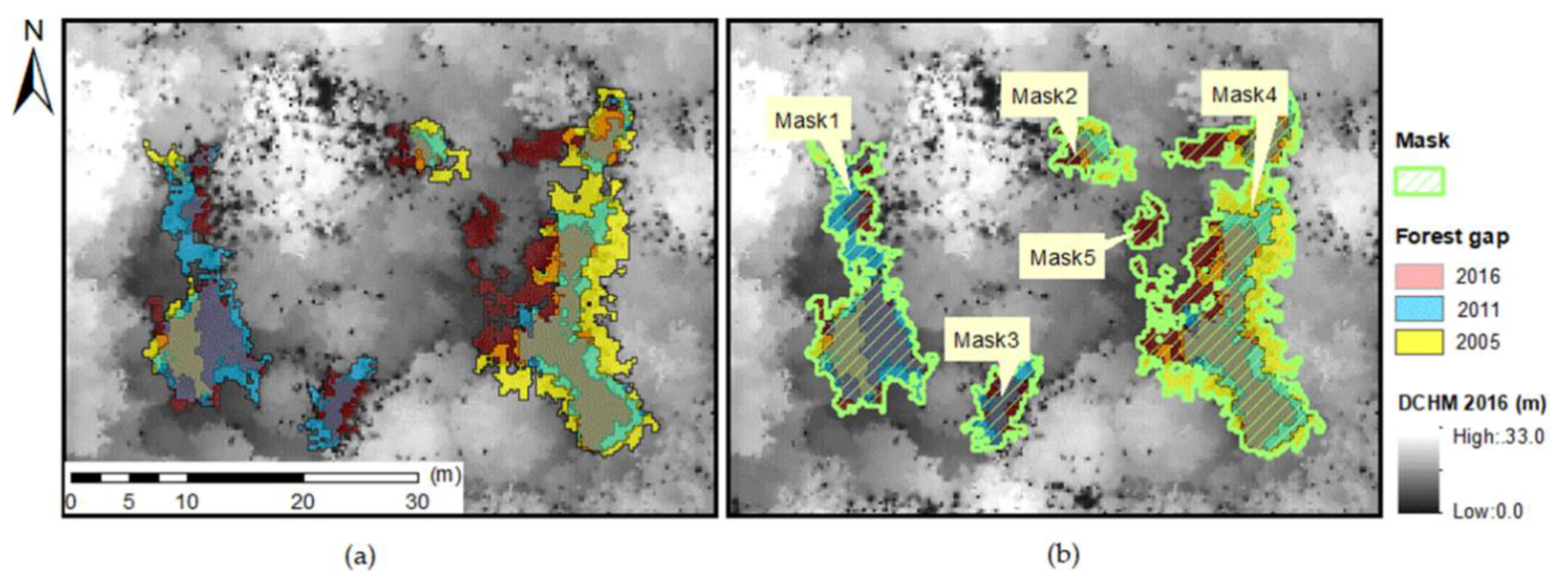
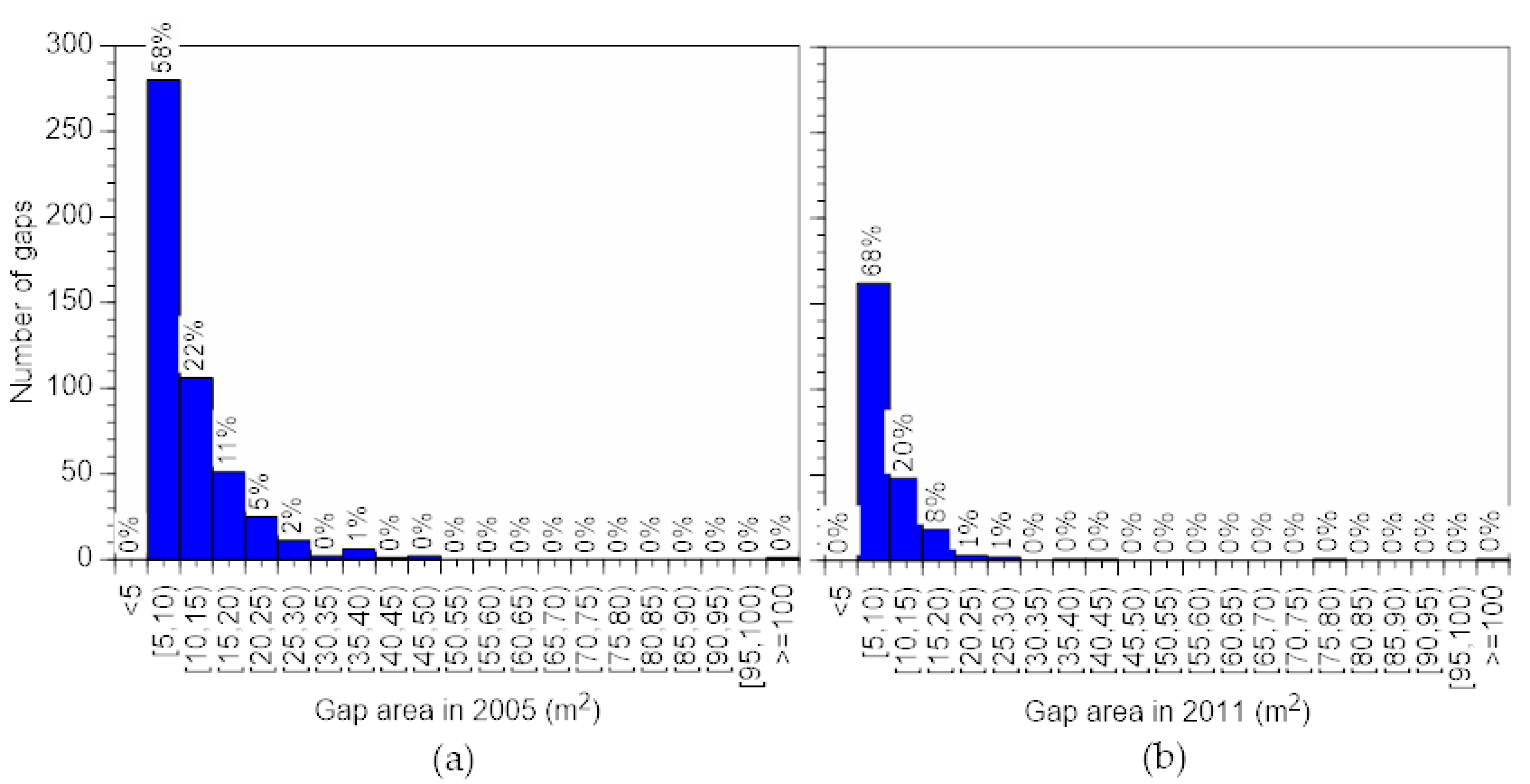
3.3. Time-Series Tracking of Gap Generation and Canopy Closure
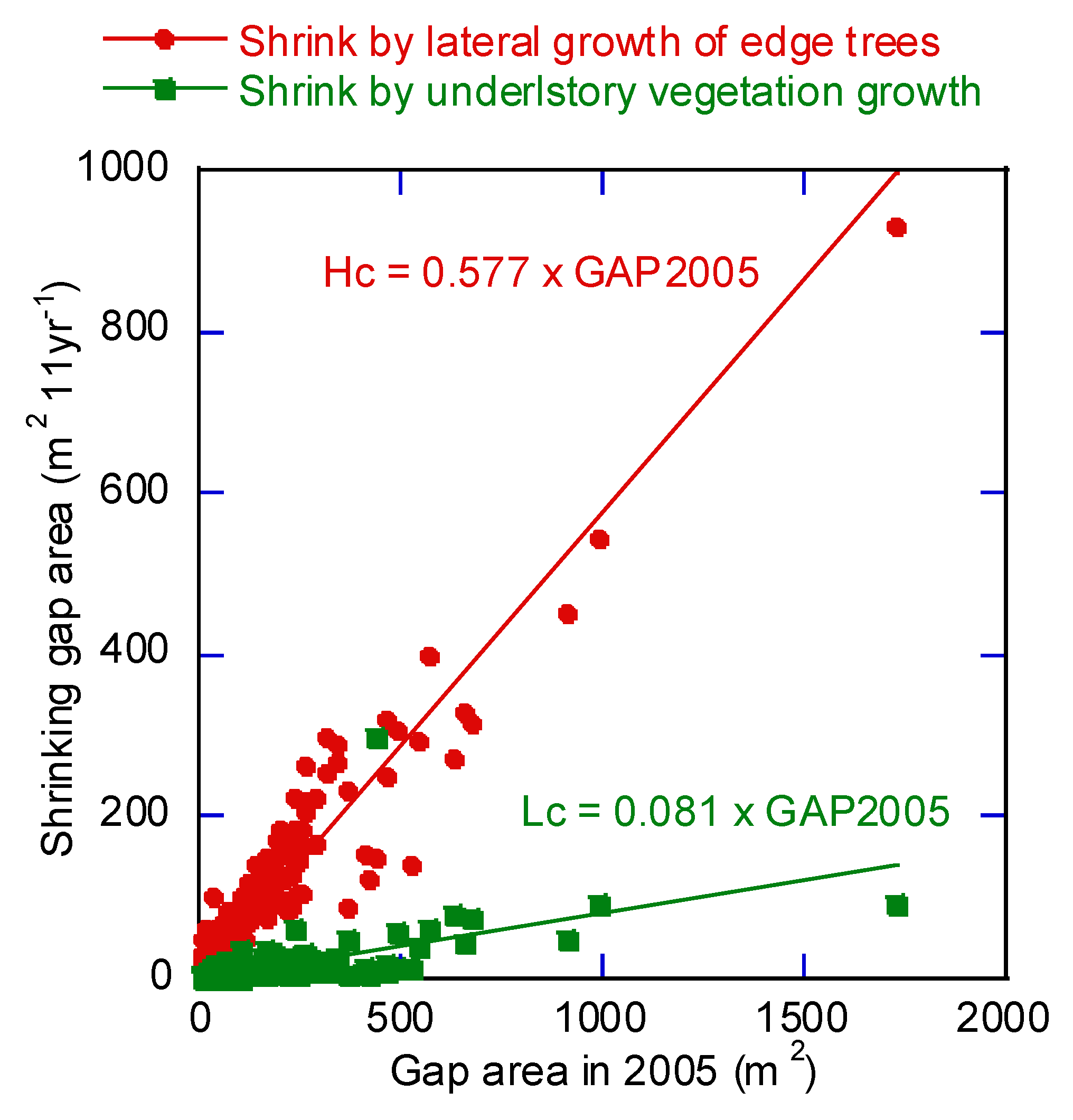
3.4. Modeling of Gap Reduction and Predicting Gap Lifespan
- (1)
- Case for period C with a duration k of 11 years
- (2)
- Case for period B with a duration k of 5 years for existing gaps
- (3)
- Case for period B with a duration k of 5 years for new gaps
4. Discussion
4.1. Generating DCHMs and Extracting Gaps from LiDAR Data
4.2. Validation of Compatibility of Generated DSMs
4.3. Time-Series Tracking of Gap Generation and Canopy Closure
4.4. Modeling of Gap Reduction and Predicting Gap Lifespan
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nakashizuka, T.; Iida, S. Composition, dynamics and disturbance regime of temperate deciduous forests in Monsoon Asia. Vegetatio 1995, 121, 23–30. [Google Scholar] [CrossRef]
- Yamamoto, S. Forest Gap Dynamics and Tree Regeneration. J. Res. 2000, 5, 223–229. [Google Scholar] [CrossRef]
- Marks, P.L. The role of pin cherry (Prunus pensylvancia l.) in the maintenance of stability in northern hardwood ecosystems. Ecol. Monogr. 1974, 44, 73–88. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, S. Gap characteristics and gap regeneration in subalpine old-growth coniferous forests, central Japan. Ecol. Res. 1995, 10, 31–39. [Google Scholar] [CrossRef]
- Ishizuka, M.; Ochiai, Y.; Utsugi, G. Micro-environment and growth in gaps. In Diversity and Interaction in a Temperate Forest Community: Ogawa Forest Reserve of Japan; Nakashizuka, T., Matumoto, Y., Eds.; Ecological Studies; Springer: Tokyo, Japan, 2002; Volume 158, pp. 229–244. [Google Scholar]
- Sumita, A. Spatial structure of hardwood forest communities-individual based approaches. Jpn. J. Ecol. 1996, 46, 31–44, (In Japanese with English Summary). [Google Scholar]
- Ishida, M. Height distribution types and regeneration traits of main tree species in Quercus serrata-Pinus densiflora secondary forest. J. Jpn. For. Soc. 1996, 78, 410–418, (In Japanese with English Summary). [Google Scholar]
- Yamamoto, S.; Nishimura, N. Canopy gap formation and replacement pattern of major tree species among developmental stages of beech (Fagus crenata) stands, Japan. Plant Ecol. 1999, 140, 167–176. [Google Scholar] [CrossRef]
- Gendreau-Berthiaume, B.; Kneeshaw, D. Influence of Gap Size and Position within Gaps on Light Levels. Int. J. For. Res. 2009. [Google Scholar] [CrossRef] [Green Version]
- Miura, M.; Manabe, T.; Nishimura, N.; Yamamoto, S. Forest canopy and community dynamics in a temperate old-growth evergreen broad-leaved forest, south-western Japan: A 7-year study of a 4-ha plot. J. Ecol. 2001, 89, 841–849. [Google Scholar] [CrossRef] [Green Version]
- Tanouchi, H.; Yamamoto, S. Structure and regeneration of canopy species in an old-growth evergreen broad-leaved forest in Aya district, southwestern Japan. Vegetatio 1995, 117, 51–60. [Google Scholar] [CrossRef]
- Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. For. Res. 2010, 129, 749–770. [Google Scholar] [CrossRef]
- Wulder, M.A.; White, J.C.; Nelson, R.F.; Næsset, E.; Ole Ørka, H.; Coops, N.C.; Hilker, T.; Bater, C.W.; Gobakken, T. Lidar sampling for large-area forest characterization: A review. Remote Sens. Environ. 2012, 121, 196–209. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, H.; Nakashizuka, T. Fifteen years of canopy dynamics analyzed by aerial photographs in a temperate deciduous forest, Japan. Ecology 1997, 78, 612–620. [Google Scholar] [CrossRef]
- Fujita, T.; Itaya, A.; Miura, M.; Manabe, T.; Yamamoto, S. Long-term canopy dynamics analyzed by aerial photographs in a temperate old-growth evergreen broad-leaved forest. J. Ecol. 2003, 91, 686–693. [Google Scholar] [CrossRef]
- Taguchi, H.; Furukawa, K.; Endo, T.; Sawada, H.; Yasuoka, Y. Monitoring of forest canopy using digital canopy models generated by multi-temporal aerial photographs. J. Jpn. Soc. Photogramm. Remote Sens. 2009, 48, 4–14, (In Japanese with English Summary). [Google Scholar]
- Torimaru, T.; Itaya, A.; Yamamoto, S. Quantification of repeated gap formation events and their spatial patterns in three types of old-growth forests: Analysis of long-term canopy dynamics using aerial photographs and digital surface models. For. Ecol. Manag. 2012, 284, 1–11. [Google Scholar] [CrossRef]
- Vepakomma, U.; St-Onge, B.; Kneeshaw, D. Spatially explicit characterization of boreal forest gap dynamics using multi-temporal lidar data. Remote Sens. Environ. 2008, 112, 2326–2340. [Google Scholar] [CrossRef]
- Kato, A.; Ishii, H.; Enoki, T.; Kobayashi, T.; Umeki, K.; Sakai, T.; Matsue, K. Application of laser remote sensing to forest ecological research. J. Jpn. For. Soc. 2014, 96, 168–181, (In Japanese with English Summary). [Google Scholar] [CrossRef] [Green Version]
- Lefsky, M.A.; Cohen, W.B. Selection of Remotely Sensed Data. In Remote Sensing of Forest Environments: Concepts and Case Studies; Wulder, M.A., Franklin, S.E., Eds.; Kluwer Academic Publishers: Norwell, MA, USA, 2003; pp. 13–46. [Google Scholar]
- Awaya, Y.; Tanaka, N.; Tanaka, K.; Takao, G.; Kodani, E.; Tsuyuki, S. Stand parameter estimation of artificial evergreen conifer forests using airborne images: An evaluation of seasonal difference on accuracy and best wavelength. J. For. Res. 2000, 5, 247–258. [Google Scholar] [CrossRef]
- Franklin, S.E.; Hall, R.J.; Smith, L.; Gerylo, G.R. Discrimination of conifer height, age and crown closure classes using Landsat-5 TM imagery in the Canadian Northwest Territories. Int. J. Remote Sens. 2003, 24, 1823–1834. [Google Scholar] [CrossRef]
- Awaya, Y.; Takahashi, T.; Kiyono, Y.; Saito, H.; Shimada, M.; Sato, T.; Toriyama, J.; Monda, Y.I.; Nengah, S.J.M.; Buce, S.; et al. Monitoring of peat swamp forest using PALSAR data-A trial of double bounce correction. J. For. Plann. 2014, 18, 117–126. [Google Scholar]
- Soja, M.; Persson, H.; Ulander, L. Estimation of forest height and canopy density from a single InSAR correlation coefficient. IEEE Geosci. Remote Sens. Lett. 2015, 12, 646–650. [Google Scholar] [CrossRef] [Green Version]
- Beraldin, J.; Blais, F.; Lohr, U. Laser Scanning Technology. In Airborne and Terrestrial Laser Scanning; Vosselman, G., Mass, H., Eds.; Whittles Publishing: Scotland, UK, 2010; pp. 19–30. [Google Scholar]
- Vepakomma, U.; Kneeshaw, D.; Fortin, M.J. Spatial contiguity and continuity of canopy gaps in mixed wood boreal forests: Persistence, expansion, shrinkage and displacement. J. Ecol. 2012, 100, 1257–1268. [Google Scholar] [CrossRef]
- Vepakomma, U.; St-Onge, B.; Kneeshaw, D. Response of a boreal forest to canopy opening: Assessing vertical and lateral tree growth with multi-temporal lidar data. Ecol. Appl. 2011, 21, 99–121. [Google Scholar] [CrossRef]
- Vepakomma, U.; Kneeshaw, D.; St-Onge, B. Interactions of multiple disturbances in shaping boreal forest dynamics: A spatially explicit analysis using multi-temporal lidar data and high-resolution imagery. J. Ecol. 2010, 98, 526–539. [Google Scholar] [CrossRef]
- Schreier, H.; Lougheed, J.; Tucker, C.; Leckie, D. Automated measurements of terrain reflection and height variations using an airborne infrared laser system. Int. J. Remote Sens. 1985, 6, 101–113. [Google Scholar] [CrossRef]
- Hirata, Y. Relationship between Tree Height and Topography in a Chamaecyparis obtusa Stand Derived from Airborne Laser Scanner Data. J. Jpn. For. Soc. 2005, 87, 497–503, (In Japanese with English Summary). [Google Scholar] [CrossRef] [Green Version]
- Nelson, R.; Krabill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ. 1988, 24, 247–267. [Google Scholar] [CrossRef]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ. 1997, 61, 246–253. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.; Cohen, W.B.; Parker, G.; Shugart, H.H. Surface lidar remote sensing of basal area and biomass in deciduous forests of eastern Maryland, USA. Remote Sens. Environ. 1999, 67, 83–98. [Google Scholar] [CrossRef]
- Maltamo, M.; Eerikäinenn, K.; Pitkänen, J.; Hyyppä, J.; Vehmas, M. Estimation of timber volume and stem density based on scanning laser altimetry and expected tree size distribution functions. Remote Sens. Environ. 2004, 90, 319–330. [Google Scholar] [CrossRef]
- Itoh, T.; Matsue, K.; Naito, K. Estimating forest resources using airborne LiDAR-Application of model for estimating the stem volume of Sugi (Cryptomeria japonica D. Don) and Hinoki (Chamaecyparis obtusa Endl.) by the tree height and the parameter of crown. J. Jpn. Soc. Photogramm. 2008, 47, 26–35, (In Japanese with English Summary). [Google Scholar]
- Takahashi, T.; Awaya, Y.; Hirata, Y.; Furuya, N.; Sakai, T.; Sakai, A. Stand volume estimation by combining low laser-sampling density LiDAR data with QuickBird panchromatic imagery in closed-canopy Japanese cedar (Cryptomeria japonica) plantations. Int. J. Remote Sens. 2010, 31, 1281–1301. [Google Scholar] [CrossRef]
- Awaya, Y.; Takahashi, T. Evaluating the differences in modeling biophysical attributes between deciduous broadleaved and evergreen conifer forests using low-density small-footprint LiDAR data. Remote Sens. 2017, 9, 572. [Google Scholar] [CrossRef] [Green Version]
- Ko, C.; Sohn, G.; Remmel, T.K.; Miller, J. Hybrid Ensemble Classification of Tree Genera Using Airborne LiDAR Data. Remote Sens. 2014, 6, 11225–11243. [Google Scholar] [CrossRef]
- Hovi, A.; Korhonen, L.; Vauhkonen, J.; Korpela, I. LiDAR waveform features for tree species classification and their sensitivity to tree- and acquisition related parameters. Remote Sens. Environ. 2016, 173, 224–237. [Google Scholar] [CrossRef]
- Awaya, Y.; Kameta, C.; Gotoh, S.; Miyasaka, S.; Unome, S. Classification of Sugi and Hinoki using high density airborne LiDAR data and two canopy shape parameters. Jpn. J. For. Plann. 2017, 51, 9–18, (In Japanese with English Summary). [Google Scholar]
- Nakatake, S.; Yamamoto, K.; Yoshida, N.; Yamaguchi, A.; Unome, S. Development of a single tree classification method using airborne LiDAR. J. Jpn. For. Soc. 2018, 100, 149–157, (In Japanese with English Summary). [Google Scholar] [CrossRef] [Green Version]
- Zhang, K. Identification of gaps in mangrove forests with airborne LIDAR. Remote Sens. Environ. 2008, 112, 2309–2325. [Google Scholar] [CrossRef]
- Choi, H.; Song, Y.; Jang, Y. Urban Forest Growth and Gap Dynamics Detected by Yearly Repeated Airborne Light Detection and Ranging (LiDAR): A Case Study of Cheonan, South Korea. Remote Sens. 2019, 11, 1551. [Google Scholar] [CrossRef] [Green Version]
- Gifu Prefecture Government Typhoon No 23 in 2004. Available online: https://www.pref.gifu.lg.jp/kurashi/bosai/shizen-saigai/11115/siryou/H16-taifuu23.html (accessed on 12 July 2020). (In Japanese).
- Snow and Ice Research Center (NIED) Snow Damage Survey in Hida area, Gifu Prefecture in December 2014–Flash News. Available online: https://www.bosai.go.jp/seppyo/kenkyu_naiyou/seppyousaigai/2015/quick%20report20150114gifu.pdf (accessed on 12 July 2020). (In Japanese).
- Fukuda, N.; Awaya, Y.; Kojima, T. Classification of forest vegetation types using LiDAR data and Quickbird images-Case study of the Daihachiga River Basin in Takayama city. J. JASS 2010, 28, 115–122, (In Japanese with English Summary). [Google Scholar]
- Masaharu, H. Map Projections-Technique on Geospatial Information; Asakura Publishing Co. Ltd.: Tokyo, Japan, 2011; pp. 19–26. (In Japanese) [Google Scholar]
- Campbell, J.B.; Wynne, R.H. Introduction to Remote Sensing, 5th ed.; The Guilford Press: New York, NY, USA, 2011; pp. 321–324. [Google Scholar]
- Watson, D.F.; Philip, G.M. A refinement of inverse distance weighted interpolation. Geo-Processing 1985, 2, 315–327. [Google Scholar]
- Abe, S.; Masaki, T.; Nakashizuka, T. Factors influencing sapling composition in canopy gaps of a temperate deciduous forest. Vegetatio 1995, 120, 21–32. [Google Scholar]




| Observation Date | Contractor | Scanner Manufacturer | Pulse Divergence (m Rad) | Wave-Length (nm) | Flight Altitude AGL (m) | Footprint Size (m) | FOV (∘) | Pulse Density *1 (Pulse m−2) | Plat-Form | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Aver-Age | SD *2 | Max. | Min. | |||||||||
| 25 July 2005 | Nakanihon Air Service Co., Nagoya, Japan | ALTM 2050DC Teledyne Optech, Ontario, Canada | 0.19 | 1064 | 1200 | 0.24 | ±22 | 1.54 | 1.05 | 7 | 0 | Fixed wing air-craft |
| 28 August 2011 | Nakanihon Air Service Co., Nagoya, Japan | LMS-Q560 RIEGL, Horn, Austria | 0.50 | 1550 | 600 | 0.30 | ±26 | 4.83 | 3.08 | 16 | 0 | Heli-copter |
| 24 October 2016 | Asia Air Survey Co., Tokyo, Japan | ALS70 Leica Geosystems, Heerbrug, Switzerland | 0.22 | 1064 | 1600 | 0.35 | ±15 | 5.91 | 1.64 | 13 | 1 | Fixed wing air-craft |
| Year | Number of Canopy Openings | |||
|---|---|---|---|---|
| All | <1 m2 | ≥1 m2 and <5 m2 | ≥5 m2 | |
| 2005 | 139,628 | 133,752 | 4749 | 1127 |
| 2011 | 263,817 | 260,886 | 1994 | 937 |
| 2016 | 112,217 | 109,280 | 1934 | 1003 |
| Year | 2005 | 2005 Recount | 2011 | 2011 Recount | 2016 | 2016 Recount | |
|---|---|---|---|---|---|---|---|
| No. of gaps | 1127 | 954 | 937 | 678 | 1003 | 805 | |
| Gap area (m2) | Minimum | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 | 5.00 |
| Maximum | 1058.13 | 1724.44 | 608.75 | 1071.50 | 549.44 | 1029.00 | |
| Average | 39.01 | 44.46 | 32.42 | 42.98 | 31.59 | 38.01 | |
| Median | 14.00 | 14.50 | 13.81 | 15.44 | 12.50 | 12.69 | |
| Standard Deviation | 83.83 | 104.10 | 58.77 | 88.02 | 56.90 | 83.44 | |
| Total | 43,963.01 | 42,415.82 | 30,375.87 | 29,139.53 | 31,685.34 | 30,598.70 |
| (a) Period A (2005–2011) | ||||||
| Gap Type | New Gap | Expanding Gap | Closing Gap | Shrinking Gap by Edge Trees | Shrinking Gap by Undergrowth | |
| No. of gaps | 209 | 674 | 485 | 954 | 908 | |
| Gap area (m2) | Minimum | 5.0 | 0.06 | 5.0 | 0.50 | 0.06 |
| Maximum | 98.75 | 285.19 | 231.81 | 723.44 | 269.38 | |
| Average | 12.49 | 15.32 | 11.67 | 24.74 | 3.13 | |
| Median | 8.69 | 7.25 | 9.06 | 11.81 | 1.06 | |
| Standard Deviation | 10.47 | 24.93 | 12.07 | 45.03 | 10.70 | |
| Total | 2611.18 | 10,329.03 | 5659.72 | 23,603.39 | 2842.25 | |
| (b) Period B (2011–2016) | ||||||
| Gap Type | New Gap | Expanding Gap | Closing Gap | Shrinking Gap by Edge Trees | Shrinking Gap by Undergrowth | |
| No. of gaps | 364 | 802 | 237 | 678 | 584 | |
| Gap area (m2) | Minimum | 5.00 | 0.06 | 5.00 | 0.31 | 0.12 |
| Maximum | 170.50 | 330.37 | 230.31 | 298.99 | 28.44 | |
| Average | 13.70 | 18.19 | 10.52 | 19.10 | 1.98 | |
| Median | 8.66 | 8.50 | 7.69 | 10.09 | 0.81 | |
| Standard Deviation | 16.72 | 33.20 | 15.79 | 27.82 | 3.50 | |
| Total | 4986.38 | 14,588.46 | 2493.19 | 12,950.59 | 1155.97 | |
| (c) Period C (2005–2016) | ||||||
| Gap type | New Gap | Expanding Gap | Closing Gap | Shrinking Gap by Edge Trees | Shrinking Gap by Undergrowth | |
| No. of gaps | 414 | 799 | 563 | 953 | 791 | |
| Gap area (m2) | Minimum | 5.00 | 0.06 | 5.00 | 0.37 | 0.12 |
| Maximum | 170.50 | 350.95 | 264.38 | 791.66 | 360.0 | |
| Average | 14.95 | 20.84 | 14.71 | 29.78 | 5.97 | |
| Median | 9.19 | 9.31 | 9.94 | 12.56 | 1.56 | |
| Standard Deviation | 17.96 | 35.82 | 16.24 | 54.94 | 17.62 | |
| Total | 6190.93 | 16,652.20 | 8284.53 | 28,376.01 | 4723.10 | |
| Gap Area Class in 2005 (m2) | Growth Speed of Understory Vegetation (m year−1) | Growth of Understory Vegetation in Period C (m) |
|---|---|---|
| <15 | 0.117 | 1.285 |
| <50 | 0.154 | 1.699 |
| <100 | 0.164 | 1.809 |
| ≧100 | 0.155 | 1.704 |
| Gap Type | Period | Relationship (Initial and Shrining Gap Area) | Validation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Group | Number of Samples | slope a | t Value *2 | RMSE *3 | Group | Number of Samples | Slope b | t Value *2 | RMSE *3 | ||
| all gaps | Period C 2005–2016 | 0,1,2 | 254 | 0.400 | 40.25 | 30.56 | 3 | 84 | 0.828 | 24.69 | 23.58 |
| 0,1,3 | 253 | 0.415 | 43.73 | 46.98 | 2 | 85 | 0.914 | 19.23 | 32.04 | ||
| 0,2,3 *1 | 253 | 0.402 | 35.23 | 30.35 | 1 | 85 | 0.911 | 32.36 | 26.25 | ||
| 1,2,3 | 254 | 0.402 | 43.76 | 28.96 | 0 | 84 | 0.771 | 18.36 | 27.40 | ||
| existing gaps | Period B 2011–2016 | 0,1,2 | 254 | 0.286 | 40.57 | 15.85 | 3 | 84 | 0.895 | 20.58 | 14.67 |
| 0,1,3 | 253 | 0.274 | 38.76 | 15.63 | 2 | 85 | 0.778 | 24.76 | 12.66 | ||
| 0,2,3 *1 | 253 | 0.292 | 37.27 | 15.87 | 1 | 85 | 0.993 | 27.31 | 15.34 | ||
| 1,2,3 | 254 | 0.279 | 41.45 | 15.18 | 0 | 84 | 0.771 | 19.80 | 14.41 | ||
| new gaps | Period B 2011–2016 | 0,1,2 | 77 | 0.422 | 19.66 | 4.11 | 3 | 26 | 0.809 | 13.81 | 2.74 |
| 0,1,3 *1 | 77 | 0.429 | 18.77 | 4.27 | 2 | 26 | 0.920 | 17.73 | 2.42 | ||
| 0,2,3 | 77 | 0.491 | 24.31 | 3.39 | 1 | 26 | 1.233 | 11.05 | 5.37 | ||
| 1,2,3 | 78 | 0.391 | 21.76 | 3.48 | 0 | 25 | 0.590 | 15.11 | 2.25 | ||
| Shrinking gap area = a × Initial gap area | Predicted shrinking area = b × Observed shrinking area | ||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Araki, K.; Awaya, Y. Analysis and Prediction of Gap Dynamics in a Secondary Deciduous Broadleaf Forest of Central Japan Using Airborne Multi-LiDAR Observations. Remote Sens. 2021, 13, 100. https://doi.org/10.3390/rs13010100
Araki K, Awaya Y. Analysis and Prediction of Gap Dynamics in a Secondary Deciduous Broadleaf Forest of Central Japan Using Airborne Multi-LiDAR Observations. Remote Sensing. 2021; 13(1):100. https://doi.org/10.3390/rs13010100
Chicago/Turabian StyleAraki, Kazuho, and Yoshio Awaya. 2021. "Analysis and Prediction of Gap Dynamics in a Secondary Deciduous Broadleaf Forest of Central Japan Using Airborne Multi-LiDAR Observations" Remote Sensing 13, no. 1: 100. https://doi.org/10.3390/rs13010100
APA StyleAraki, K., & Awaya, Y. (2021). Analysis and Prediction of Gap Dynamics in a Secondary Deciduous Broadleaf Forest of Central Japan Using Airborne Multi-LiDAR Observations. Remote Sensing, 13(1), 100. https://doi.org/10.3390/rs13010100






