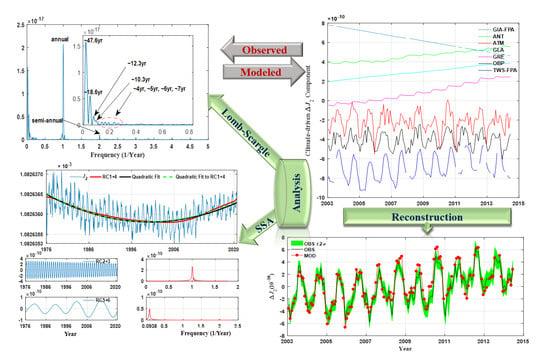
Geophysical Signal Detection in the Earth’s Oblateness Variation and Its Climate-Driven Source Analysis
Abstract
:1. Introduction
2. Analysis Methods
2.1. Singular Spectrum Analysis
2.2. Lomb-Scargle Periodogram Analysis
3. Geophysical Signal Detection from ΔJ2 Time Series
3.1. Geophysical Signals Detected by Singular Spectral Analysis
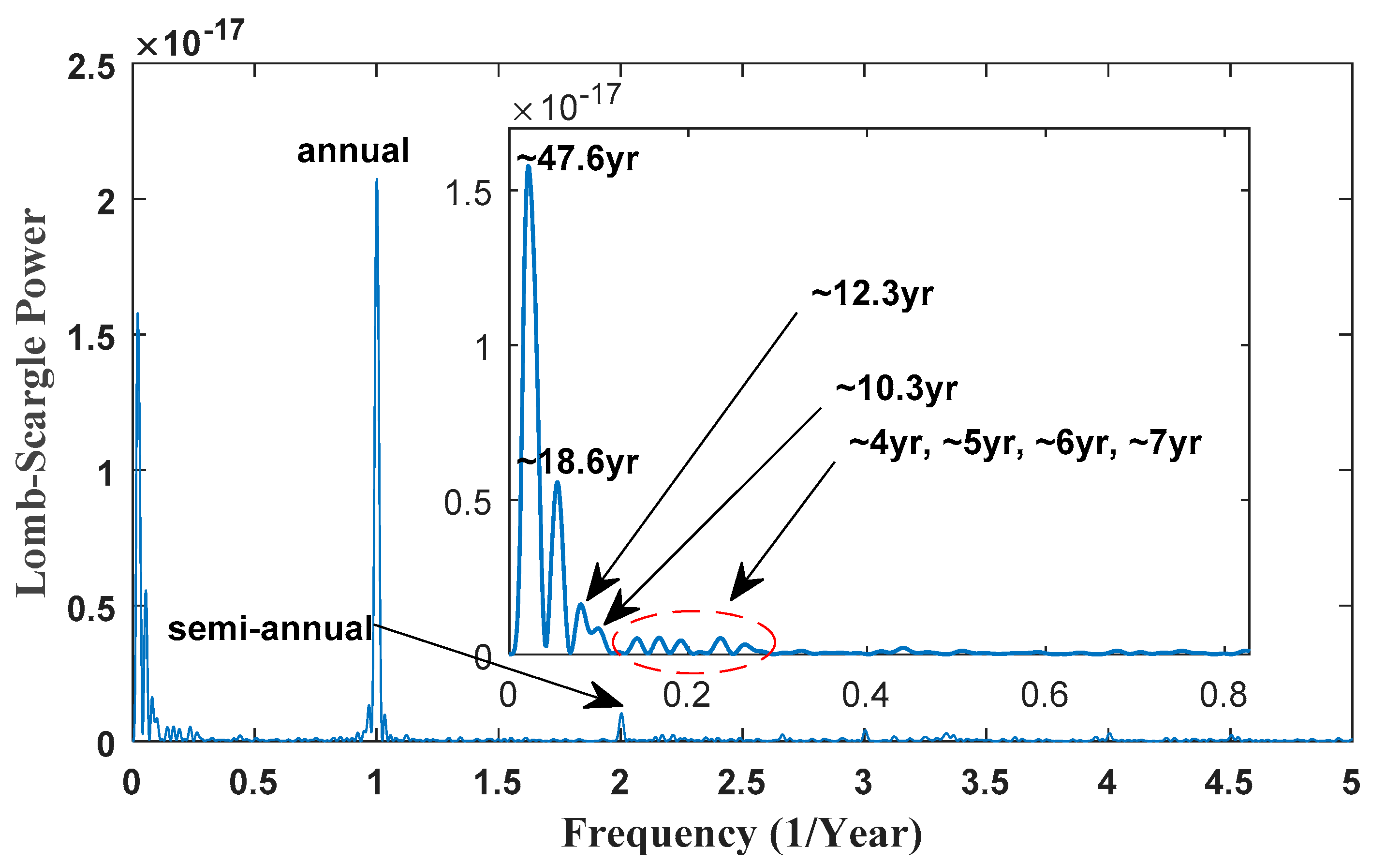
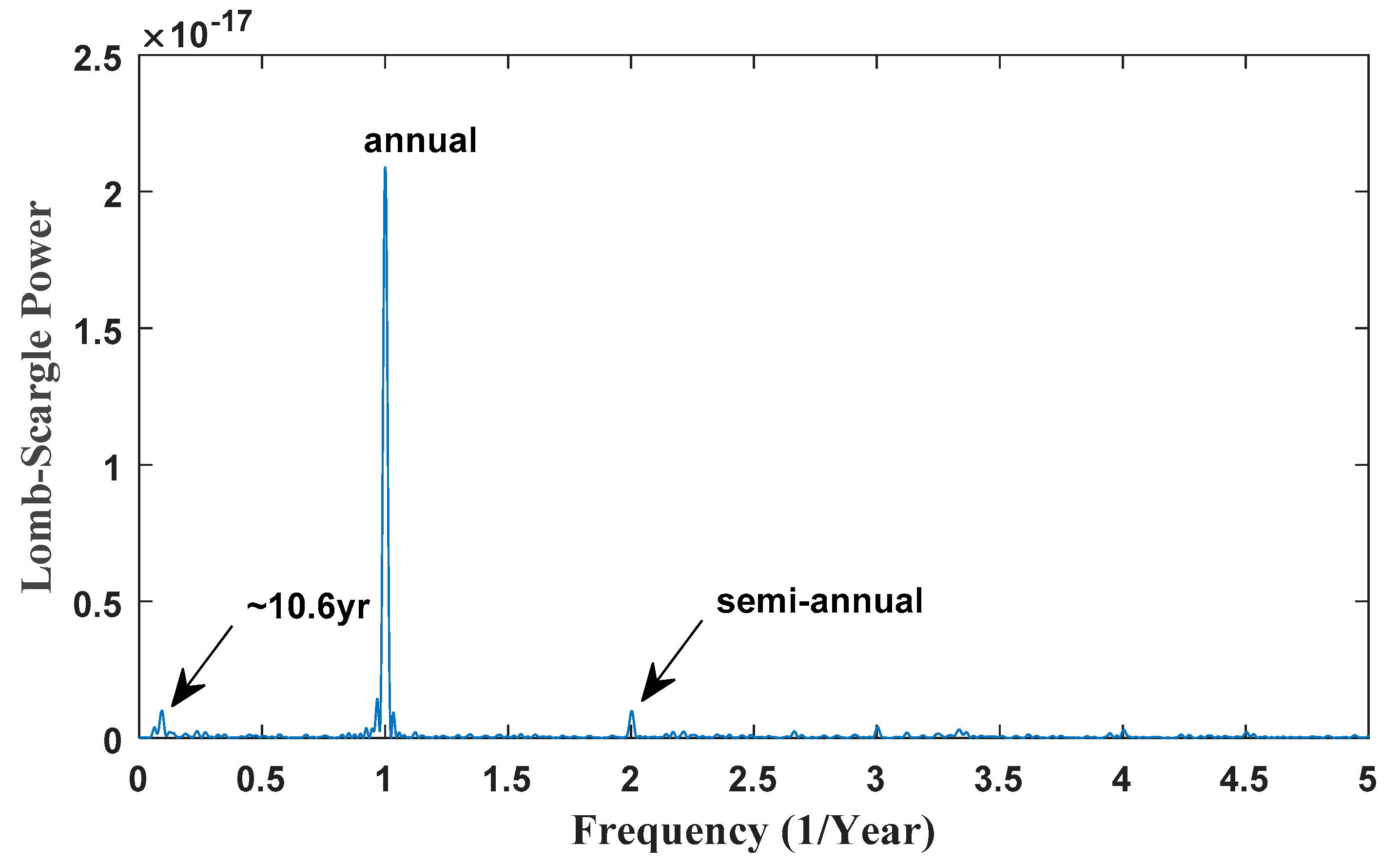
3.2. Geophysical Signals Detected by Lomb-Scargle Periodogram
3.3. Discussions
4. Reconstruction and Interpretation of the Variations in the Earth’s Oblateness
4.1. ΔJ2 Reconstruction with Climate-Driven Sources
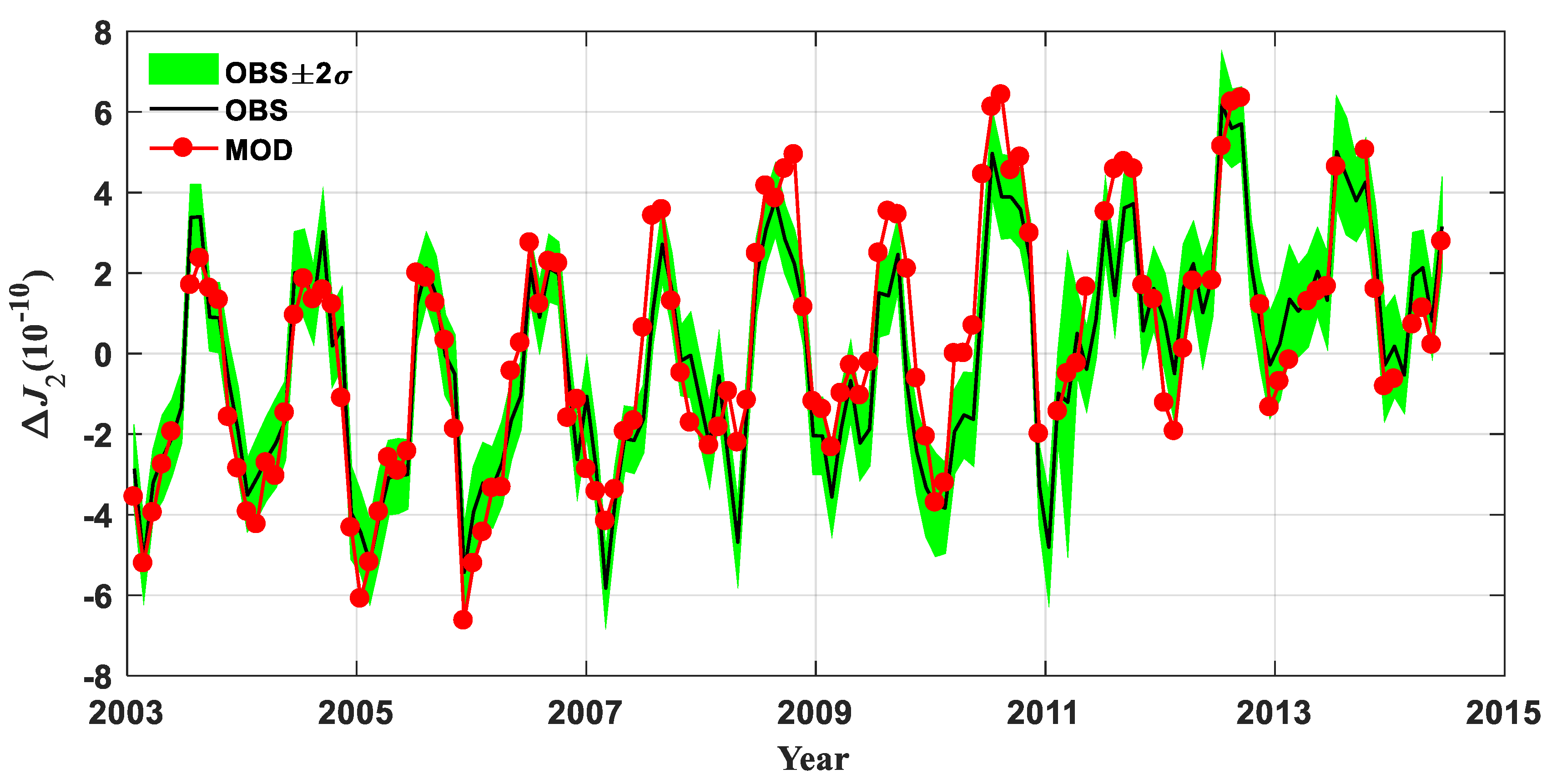
4.2. Comparison and Interpretation of Reconstructed and Observed ΔJ2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Cheng, M.; Tapley, B.D.; Ries, J.C. Deceleration in the Earth’s oblateness. J. Geophys. Res. Solid Earth 2013, 118, 740–747. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C. Decadal Variation in Earth’s Oblateness (J2) from Satellite Laser Ranging Data. Geophys. J. Int. 2018, 212, 1218–1224. [Google Scholar] [CrossRef]
- Sośnica, K.; Jäggi, A.; Meyer, U.; Thaller, D.; Beutler, G.; Arnold, D.; Dach, R. Time Variable Earth’s Gravity Field from SLR Satellites. J. Geod. 2015, 89, 945–960. [Google Scholar] [CrossRef] [Green Version]
- Bloßfeld, M.; Müller, H.; Gerstl, M.; Štefka, V.; Bouman, J.; Göttl, F.; Horwath, M. Second-Degree Stokes Coefficients from Multi-Satellite SLR. J. Geod. 2015, 89, 857–871. [Google Scholar] [CrossRef]
- Loomis, B.D.; Rachlin, K.E.; Luthcke, S.B. Improved Earth Oblateness Rate Reveals Increased Ice Sheet Losses and Mass-Driven Sea Level Rise. Geophys. Res. Lett. 2019, 46, 6910–6917. [Google Scholar] [CrossRef]
- Lemoine, J.M.; Bourgogne, S.; Biancale, R.; Bruinsma, S. RL04 Monthly Gravity Field Solutions from CNES/GRGS. In Proceedings of the GRACE/GRACE-FO Science Team Meeting, Potsdam, Germany, 9–11 October 2018; Available online: http://presentations.copernicus.org/GSTM-2018-42_presentation.pdf (accessed on 11 January 2021).
- Cheng, M.; Ries, J. The Unexpected Signal in GRACE Estimates of C20. J. Geod. 2017, 91, 897–914. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from satellite laser ranging and GRACE. J. Geophys. Res. Space Phys. 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Chao, B.F.; Yu, Y.; Chung, C.H. Variation of Earth’s Oblateness J 2 on Interannual-to-Decadal Timescales. J. Geophys. Res. Solid Earth 2020, 125, e2020JB019421. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Variations in the Earth’s oblateness during the past 28 years. J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef]
- Dickey, J.O.; Marcus, S.L.; De Viron, O.; Fukumori, I. Recent Earth Oblateness Variations: Unraveling Climate and Postglacial Rebound Effects. Science 2002, 298, 1975–1977. [Google Scholar] [CrossRef] [PubMed]
- Yoder, C.F.; Williams, J.G.; Dickey, J.O.; Schutz, B.E.; Eanes, R.J.; Tapley, B.D. Secular Variation of Earth’s Gravitational Harmonic J2 Coefficient from Lageos and Nontidal Acceleration of Earth Rotation. Nat. Cell Biol. 1983, 303, 757–762. [Google Scholar] [CrossRef]
- Seo, K.-W.; Chen, J.; Wilson, C.R.; Lee, C.-K. Decadal and Quadratic Variations of Earth’s Oblateness and Polar Ice Mass Balance from 1979 to 2010. Geophys. J. Int. 2015, 203, 475–481. [Google Scholar] [CrossRef]
- Mitrovica, J.X.; Peltier, W.R. Present-Day Secular Variations in the Zonal Harmonics of Earth’s Geopotential. J. Geophys. Res. Space Phys. 1993, 98, 4509–4526. [Google Scholar] [CrossRef]
- Cox, C.M.; Chao, B.F. Detection of a Large-Scale Mass Redistribution in the Terrestrial System since 1998. Science 2002, 297, 831–833. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.K.; Eanes, R.J.; Shum, C.K.; Schutz, B.E.; Tapley, B.D. Temporal Variations in Low Degree Zonal Harmonics from Starlette Orbit Analysis. Geophys. Res. Lett. 1989, 16, 393–396. [Google Scholar] [CrossRef]
- Cheng, M.; Tapley, B.D. Seasonal Variations in Low Degree Zonal Harmonics of the Earth’s Gravity Field from Satellite Laser Ranging Observations. J. Geophys. Res. Space Phys. 1999, 104, 2667–2681. [Google Scholar] [CrossRef]
- Ivins, E.R.; Sammis, C.G.; Yoder, C.F. Deep Mantle Viscous Structure with Prior Estimate and Satellite Constraint. J. Geophys. Res. Space Phys. 1993, 98, 4579–4609. [Google Scholar] [CrossRef]
- Jacob, T.; Wahr, J.M.; Pfeffer, W.T.; Swenson, S.C. Recent Contributions of Glaciers and Ice Caps to Sea Level Rise. Nat. Cell Biol. 2012, 482, 514–518. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.Y.; Chao, B.F. Seismic Effects on the Secular Drift of the Earth’s Rotational Pole. J. Geophys. Res. Solid Earth 2019, 124, 6092–6100. [Google Scholar] [CrossRef]
- Chao, B.F.; Ding, H. Global Geodynamic Changes Induced by All Major Earthquakes, 1976–2015. J. Geophys. Res. Solid Earth 2016, 121, 8987–8999. [Google Scholar] [CrossRef]
- Chao, B.F. Anthropogenic Impact on Global Geodynamics Due to Reservoir Water Impoundment. Geophys. Res. Lett. 1995, 22, 3529–3532. [Google Scholar] [CrossRef] [Green Version]
- Chao, B.F.; O’Connor, W.P.; Chang, A.T.C.; Hall, D.K.; Foster, J.L. Snow Load Effect on the Earth’s Rotation and Gravitational Field, 1979–1985. J. Geophys. Res. Space Phys. 1987, 92, 9415–9422. [Google Scholar] [CrossRef] [Green Version]
- Cheng, M.K.; Shum, C.K.; Tapley, B.D. Determination of Long-Term Changes in the Earth’s Gravity Field from Satellite Laser Ranging Observations. J. Geophys. Res. Space Phys. 1997, 102, 22377–22390. [Google Scholar] [CrossRef]
- Marcus, S.L.; Dickey, J.O.; Willis, J.K.; Seitz, F. Earth Oblateness Changes Reveal Land Ice Contribution to Interannual Sea Level Variability. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Ding, H.; Chao, B.F. Application of Stabilized AR-z Spectrum in Harmonic Analysis for Geophysics. J. Geophys. Res. Solid Earth 2018, 123, 8249–8259. [Google Scholar] [CrossRef]
- Colebrook, J.M. Continuous Plankton Records-Zooplankton and Environment, Northeast Atlantic and North-Sea, 1948–1975. Oceanol. Acta 1978, 1, 9–23. [Google Scholar]
- Fraedrich, K. Estimating the Dimensions of Weather and Climate Attractors. J. Atmos. Sci. 1986, 43, 419–432. [Google Scholar] [CrossRef]
- Hassani, H. Singular Spectrum Analysis: Methodology and Comparison. J. Data Sci. 2007, 5, 239–257. [Google Scholar]
- Shen, Y.; Guo, J.; Liu, X.; Kong, Q.; Guo, L.; Li, W. Long-Term Prediction of Polar Motion Using a Combined SSA and ARMA model. J. Geod. 2018, 92, 333–343. [Google Scholar] [CrossRef]
- Guo, J.Y.; Gao, W.Z.; Yu, H.J.; Liu, X.; Kong, Q.L.; Chen, X.D. Gravity Tides Extracted from Relative Gravimetric Data with Singular Spectrum Analysis. Chin. J. Geophys. 2018, 61, 3889–3902. [Google Scholar] [CrossRef]
- Shen, Y.; Peng, F.; Li, B. Improved Singular Spectrum Analysis for Time Series with Missing Data. Nonlinear Process. Geophys. 2015, 22, 371–376. [Google Scholar] [CrossRef] [Green Version]
- Wang, F.; Shen, Y.; Chen, T.; Chen, Q.; Li, W. Improved Multichannel Singular Spectrum Analysis for Post-Processing Grace Monthly Gravity Field Models. Geophys. J. Int. 2020, 223, 825–839. [Google Scholar] [CrossRef]
- Vautard, R.; Ghil, M. Singular Spectrum Analysis in Nonlinear Dynamics, with Applications to Paleoclimatic Time Series. Phys. D Nonlinear Phenom. 1989, 35, 395–424. [Google Scholar] [CrossRef]
- VanderPlas, J.T. Understanding the Lomb-Scargle Periodogram. Astrophys. J. Suppl. Ser. 2018, 236. Available online: https://iopscience.iop.org/article/10.3847/1538-4365/aab766/pdf (accessed on 25 November 2020). [CrossRef]
- Reimann, J.D. Frequency Estimation Using Unequally-Spaced Astronomical Data; University of California: Berkeley, CA, USA, 1994. [Google Scholar]
- Bretthorst, G.L. Bayesian Spectrum Analysis and Parameter Estimation. Lecture Notes in Statistics 48; Springer: Berlin, Germany, 1988. [Google Scholar]
- Swingler, D.N. A Comparison of the Fourier, Jurkevich, and Stellingwerf Methods of Period Estimation. Astron. J. 1989, 97, 280. [Google Scholar] [CrossRef]
- Sun, Y.; Riva, R.; Ditmar, P.; Rietbroek, R. Using GRACE to Explain Variations in the Earth’s Oblateness. Geophys. Res. Lett. 2019, 46, 158–168. [Google Scholar] [CrossRef] [Green Version]
- Kondrashov, D.; Shprits, Y.; Ghil, M. Gap Filling of Solar Wind Data by Singular Spectrum Analysis. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef] [Green Version]
- Lomb, N.R. Least-Squares Frequency Analysis of Unequally Spaced Data. Astrophys. Space Sci. 1976, 39, 447–462. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. II-Statistical aspects of spectral analysis of unevenly spaced data. Astron. J. 1982, 263, 835–853. [Google Scholar] [CrossRef]
- Zechmeister, M.; Kürster, M. The Generalised Lomb-Scargle Periodogram-a New Formalism for the Floating-Mean and Keplerian Periodograms. Astron. Astrophys. 2009, 496, 577–584. [Google Scholar] [CrossRef]
- Gottlieb, E.W.; Wright, E.L.; Liller, W. Optical Studies of UHURU Sources. XI. A Probable Period for Scorpius X-1= V818 Scorpii. Astrophys. J. 1975, 195, L33–L35. [Google Scholar] [CrossRef]
- Nerem, R.S.; Wahr, J. Recent Changes in the Earth’s Oblateness Driven by Greenland and Antarctic Ice Mass Loss. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Matsuo, K.; Chao, B.F.; Otsubo, T.; Heki, K. Accelerated Ice Mass Depletion Revealed by Low-Degree Gravity Field from Satellite Laser Ranging: Greenland, 1991–2011. Geophys. Res. Lett. 2013, 40, 4662–4667. [Google Scholar] [CrossRef] [Green Version]
- Reegen, P. SigSpec. Astron. Astrophys. 2007, 467, 1353–1371. [Google Scholar] [CrossRef] [Green Version]
- Kovács, G. Frequency Shift in Fourier Analysis. Astrophys. Space Sci. 1981, 78, 175–188. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, Y. Climate-Driven Seasonal Geocenter Motion during the GRACE Period. Acta Geophys. 2018, 66, 223–232. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Riva, R.; Ditmar, P. Optimizing Estimates of Annual Variations and Trends in Geocenter Motion and J 2 from a Combination of GRACE Data and Geophysical Models. J. Geophys. Res. Solid Earth 2016, 121, 8352–8370. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Ditmar, P.; Riva, R. Observed Changes in the Earth’s Dynamic Oblateness from GRACE Data and Geophysical Models. J. Geod. 2016, 90, 81–89. [Google Scholar] [CrossRef] [Green Version]
- Sun, Y.; Ditmar, P.; Riva, R. Statistically Optimal Estimation of Degree-1 and C20 Coefficients Based on GRACE Data and an Ocean Bottom Pressure Model. Geophys. J. Int. 2017, 210, 1305–1322. [Google Scholar] [CrossRef] [Green Version]
- Rietbroek, R.; Brunnabend, S.-E.; Kusche, J.; Schröter, J. Resolving Sea Level Contributions by Identifying Fingerprints in Time-Variable Gravity and Altimetry. J. Geodyn. 2012, 59–60, 72–81. [Google Scholar] [CrossRef]
- Peltier, W.R. Constraint on Deep Mantle Viscosity from Lageos Acceleration Data. Nat. Cell Biol. 1983, 304, 434–436. [Google Scholar] [CrossRef]
- Rignot, E.; Box, J.E.; Burgess, E.; Hanna, E. Mass Balance of the Greenland Ice Sheet from 1958 to 2007. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef] [Green Version]
- Zwally, H.J.; Giovinetto, M.B.; Li, J.; Cornejo, H.G.; Beckley, M.A.; Brenner, A.C.; Saba, J.L.; Yi, D. Mass Changes of the Greenland and Antarctic Ice Sheets and Shelves and Contributions to Sea-Level Rise: 1992–2002. J. Glaciol. 2005, 51, 509–527. [Google Scholar] [CrossRef] [Green Version]
- Frederikse, T.; Riva, R.; Kleinherenbrink, M.; Wada, Y.; Broeke, M.V.D.; Marzeion, B. Closing the Sea Level Budget on a Regional Scale: Trends and Variability on the Northwestern European continental Shelf. Geophys. Res. Lett. 2016, 43, 10864–10872. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van de Berg, W.J.; Medley, B. Brief Communication: Upper-Air Relaxation in RACMO2 Significantly Improves Modelled Interannual Surface Mass Balance Variability in Antarctica. Cryosphere 2016, 10, 459–463. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rignot, E.; Velicogna, I.; Broeke, M.R.V.D.; Monaghan, A.; Lenaerts, J.T.M. Acceleration of the Contribution of the Greenland and Antarctic Ice Sheets to Sea Level Rise. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef] [Green Version]
- Marzeion, B.; Leclercq, P.W.; Cogley, J.G.; Jarosch, A.H. Brief Communication: Global Reconstructions of Glacier Mass Change during the 20th Century are Consistent. Cryosphere 2015, 9, 2399–2404. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Thomas, M. Ocean Induced Variations of Earths Rotation–Results from a Simultaneous Model of Global Circulation and Tides. Ph.D. Thesis, University of Hamburg, Hamburg, Germany, 2002; p. 129. [Google Scholar]
- Tamisiea, M.E.; Hill, E.M.; Ponte, R.M.; Davis, J.L.; Velicogna, I.; Vinogradova, N.T. Impact of Self-Attraction and Loading on the Annual Cycle in Sea Level. J. Geophys. Res. Space Phys. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
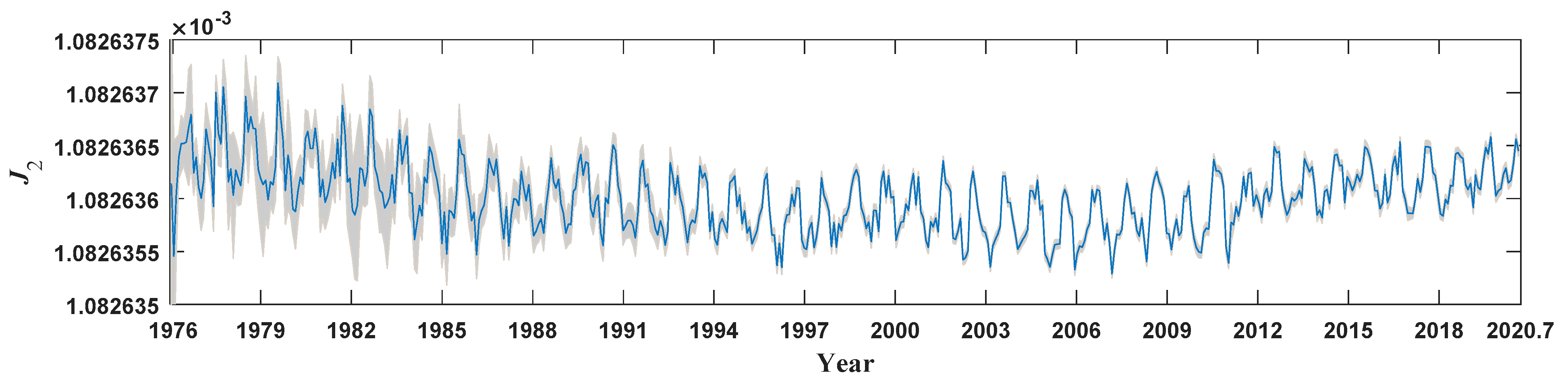
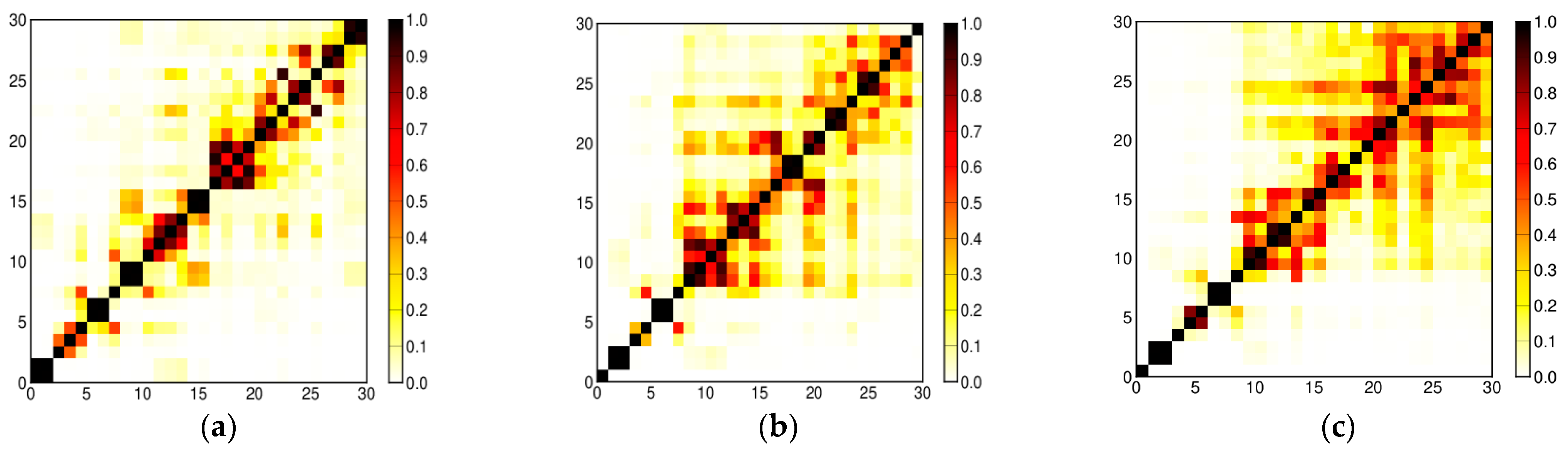
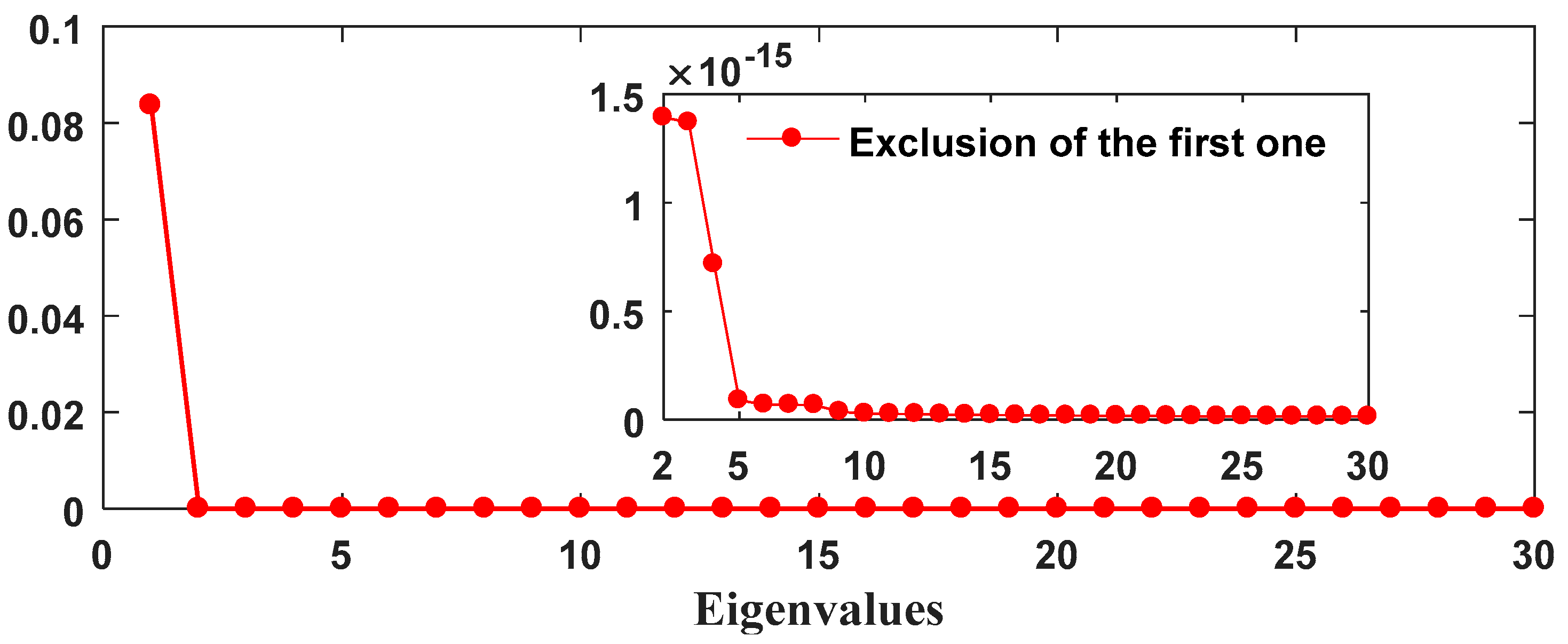



| RC-Index | Linear Trend Term | Quadratic Term | Time Span |
|---|---|---|---|
| RC (1,4) | (−5.80 ± 0.08) × 10−11/yr | (2.38 ± 0.02) × 10−12/yr2 | 1976.01~2020.09 |
| Quadratic Fit | (−5.64 ± 0.66) × 10−11/yr | (2.29 ± 0.14) × 10−12/yr2 | 1976.01~2020.09 |
| Cheng et al. (2013) | −5.90 × 10−11/yr | 1.80 × 10−12/yr2 | 1976.01~2011.01 |
| RC-Index | Period | Frequency (1/year) | Amplitude |
|---|---|---|---|
| RC (2 + 3) | annual | 1 | 2.67 × 10−10 |
| RC (5 + 6) | 10.6-year | 0.0938 | 5.01 × 10−11 |
| RC (7 + 8) | Semi-annual | 2 | 5.56 × 10−11 |
| Linear Trend | Annual | Semi-Annual | Correlation | |||
|---|---|---|---|---|---|---|
| Amplitude | Phase | Amplitude | Phase | |||
| OBS | (3.81 ± 0.75) × 10−11/yr | (2.79 ± 0.36) × 10−10 | 204.6 ± 7.4 | 92% | ||
| MOD | (3.34 ± 0.65) × 10−11/yr | (2.91 ± 0.31) × 10−10 | 202.1 ± 6.1 | |||
| GIA | (−2.78 ± 0.00) × 10−11/yr | |||||
| ANT | (1.62 ± 0.04) × 10−11/yr | |||||
| GLA | (1.69 ± 0.01) × 10−11/yr | |||||
| GRE | (2.80 ± 0.07) × 10−11/yr | |||||
| TWS | (1.07 ± 0.40) × 10−11/yr | (1.01 ± 0.19) × 10−10 | 203.2 ± 10.8 | (3.75 ± 0.90) × 10−11 | 206.0 ± 14.3 | |
| ATM | (0.89 ± 0.20) × 10−10 | 199.0 ± 13.0 | (1.61 ± 0.49) × 10−11 | 188.1 ± 17.8 | ||
| OBP | (0.83 ± 0.14) × 10−10 | 201.3 ± 9.8 | (1.51 ± 0.41) × 10−11 | 186.2 ± 16.0 | ||
| Sources | Total | ANT | ATM | GLA | GRE | OBP | TWS |
|---|---|---|---|---|---|---|---|
| V (%) | 81.5 | 11.0 | 40.1 | 13.5 | 22.6 | 26.3 | 31.9 |
| V (%, Annual) | 30.1 | 25.4 | 30.8 | ||||
| V (%, Semi-annual) | 1.6 | 0.7 | 1.0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, H.; Chen, Q.; Sun, Y.; Sosnica, K. Geophysical Signal Detection in the Earth’s Oblateness Variation and Its Climate-Driven Source Analysis. Remote Sens. 2021, 13, 2004. https://doi.org/10.3390/rs13102004
Yu H, Chen Q, Sun Y, Sosnica K. Geophysical Signal Detection in the Earth’s Oblateness Variation and Its Climate-Driven Source Analysis. Remote Sensing. 2021; 13(10):2004. https://doi.org/10.3390/rs13102004
Chicago/Turabian StyleYu, Hongjuan, Qiujie Chen, Yu Sun, and Krzysztof Sosnica. 2021. "Geophysical Signal Detection in the Earth’s Oblateness Variation and Its Climate-Driven Source Analysis" Remote Sensing 13, no. 10: 2004. https://doi.org/10.3390/rs13102004
APA StyleYu, H., Chen, Q., Sun, Y., & Sosnica, K. (2021). Geophysical Signal Detection in the Earth’s Oblateness Variation and Its Climate-Driven Source Analysis. Remote Sensing, 13(10), 2004. https://doi.org/10.3390/rs13102004