Retrieval of Summer Sea Ice Concentration in the Pacific Arctic Ocean from AMSR2 Observations and Numerical Weather Data Using Random Forest Regression
Abstract
:1. Introduction
2. Materials
2.1. AMSR2 Data
2.2. SAR-Derived Ice/Water Maps
2.3. ERA-5 Reanalysis Data
2.4. BT and ASI Sea Ice Concentration Products
2.5. Landsat-8 OLI Images
3. Methodology
3.1. Construction of Reference Dataset and Input Variables for Machine Learning
3.2. Random Forest Regression for SIC Retrieval
4. Results and Discussion
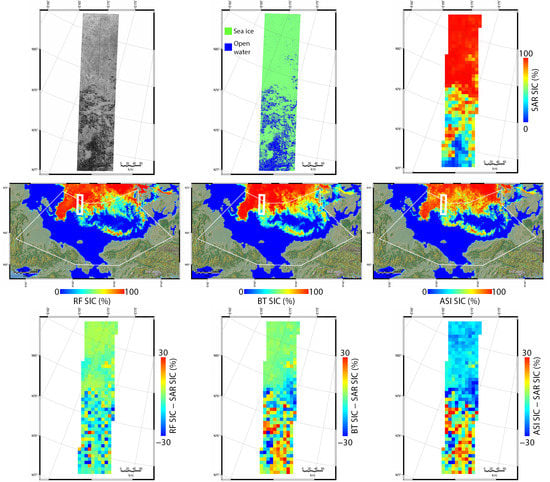
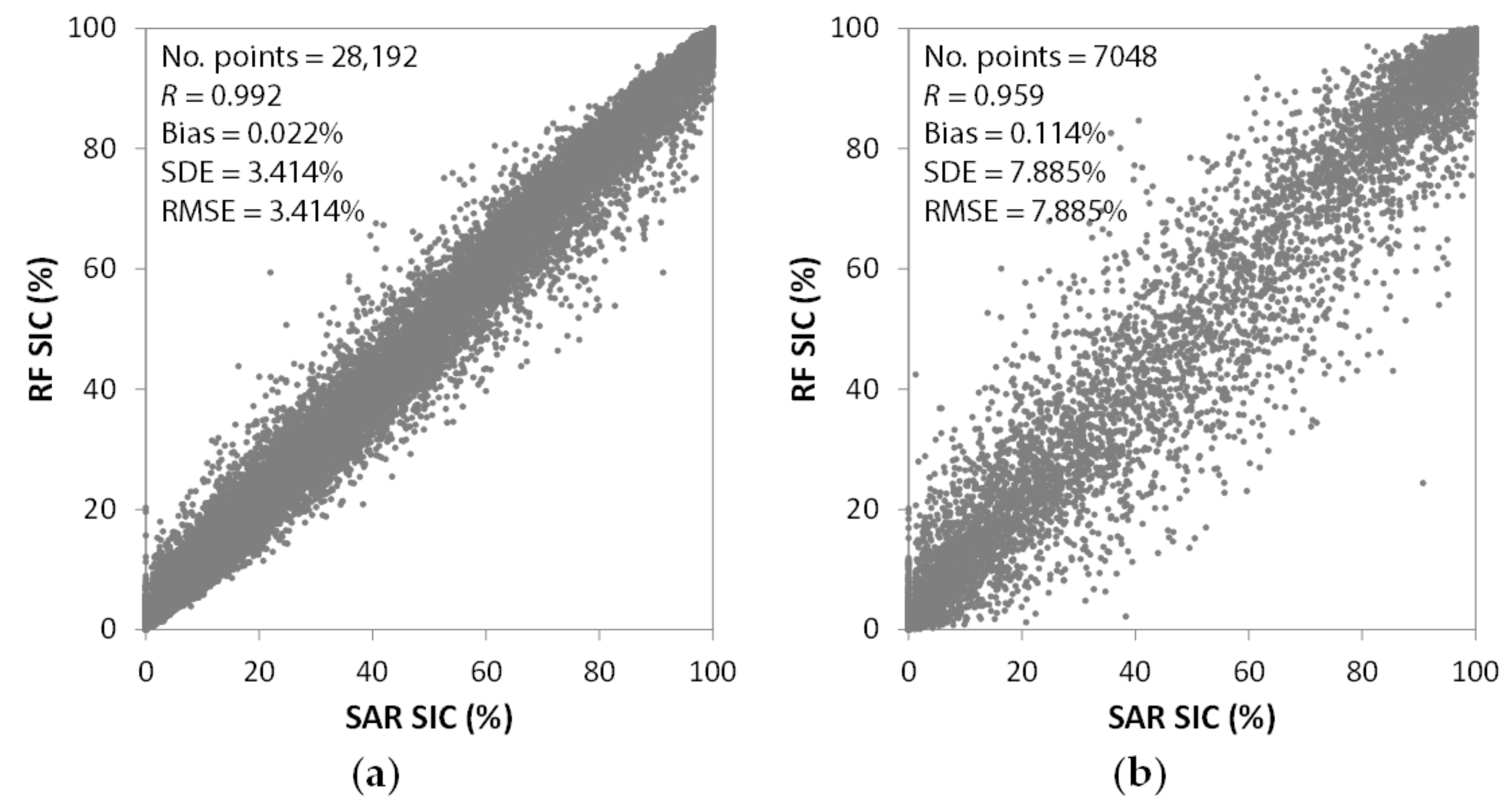
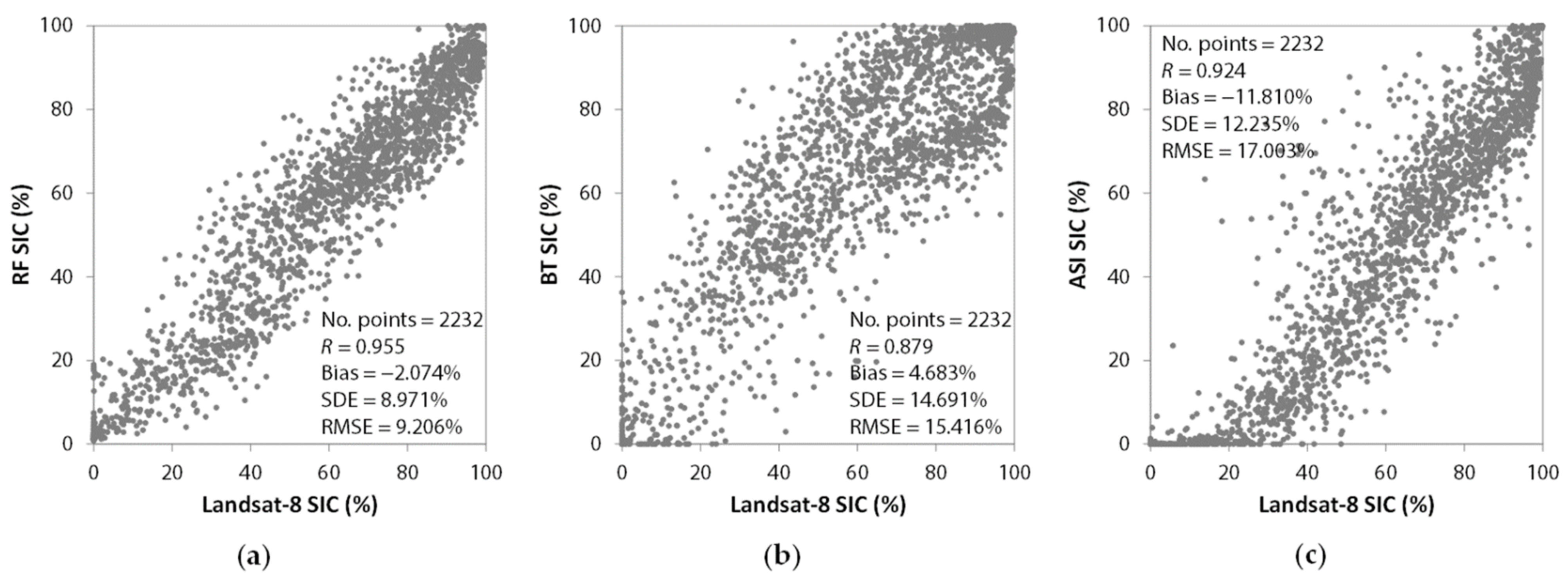
4.1. Performance of Summer SIC Retrieval Model Based on RF Regression
4.2. Variable Importance of the RF Model
4.3. Implications for the Machine Learning Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Comiso, J.C.; Cavalieri, D.J.; Parkinson, C.L.; Gloersen, P. Passive microwave algorithms for sea ice concentration: A comparison of two techniques. Remote Sens. Environ. 1997, 60, 357–384. [Google Scholar] [CrossRef]
- Johannessen, O.M.; Bengtsson, L.; Miles, M.W.; Kuzmina, S.I.; Semenov, V.A.; Alekseev, G.V.; Nagurnyi, A.P.; Zakharov, V.F.; Bobylev, L.P.; Pettersson, L.H.; et al. Arctic climate change: Observed and modelled temperature and sea-ice variability. Tellus A 2004, 56, 328–341. [Google Scholar] [CrossRef]
- Sun, L.; Alexander, M.; Deser, C. Evolution of the global coupled climate response to Arctic sea ice loss during 1990–2090 and its contribution to climate change. J. Clim. 2018, 31, 7823–7843. [Google Scholar] [CrossRef]
- Ogawa, F.; Keenlyside, N.; Gao, Y.; Koenigk, T.; Yang, S.; Suo, L.; Wang, T.; Gastineau, G.; Nakamura, T.; Cheung, H.N.; et al. Evaluating impacts of recent Arctic sea ice loss on the northern hemisphere winter climate change. Geophys. Res. Lett. 2018, 45, 3255–3263. [Google Scholar] [CrossRef]
- Vinnikov, K.Y.; Robock, A.; Stouffer, R.J.; Walsh, J.E.; Parkinson, C.L.; Cavalieri, D.J.; Mitchell, J.F.B.; Garrett, D.; Zakharov, V.F. Global warming and northern hemisphere sea ice extent. Science 1999, 286, 1934–1937. [Google Scholar] [CrossRef] [PubMed]
- Kay, J.E.; Holland, M.M.; Jahn, A. Inter-annual to multi-decadal Arctic sea ice extent trends in a warming world. Geophys. Res. Lett. 2011, 38, L15708. [Google Scholar] [CrossRef] [Green Version]
- Yadav, J.; Kumar, A.; Mohan, R. Dramatic decline of Arctic sea ice linked to global warming. Nat. Hazards 2020, 103, 2617–2621. [Google Scholar] [CrossRef]
- Pörtner, H.O.; Roberts, D.C.; Masson-Delmotte, V.; Zhai, P.; Tignor, M.; Poloczanska, E.; Mintenbeck, K.; Nicolai, M.; Okem, A.; Petzold, J.; et al. IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; IPCC Intergovernmental Panel on Climate Change (IPCC): Geneva, Switzerland, 2019; in press. [Google Scholar]
- Arrigo, K.R.; van Dijken, G.; Pabi, S. Impact of a shrinking Arctic ice cover on marine primary production. Geophys. Res. Lett. 2008, 35, L19603. [Google Scholar] [CrossRef]
- Kovacs, K.M.; Lydersen, C.; Overland, J.E.; Moore, S.E. Impacts of changing sea-ice conditions on Arctic marine mammals. Mar. Biodivers. 2011, 41, 181–194. [Google Scholar] [CrossRef]
- Inoue, J.; Yamazaki, A.; Ono, J.; Dethloff, K.; Maturilli, M.; Neuber, R.; Edwards, P.; Yamaguchi, H. Additional Arctic observations improve weather and sea-ice forecasts for the Northern Sea Route. Sci. Rep. 2015, 5, 16868. [Google Scholar] [CrossRef] [Green Version]
- Boé, J.; Hall, A.; Qu, X. September sea-ice cover in the Arctic Ocean projected to vanish by 2100. Nat. Geosci. 2009, 2, 341–343. [Google Scholar] [CrossRef]
- Overland, J.E.; Wang, M. When will the summer Arctic be nearly sea ice free? Geophys. Res. Lett. 2013, 40, 2097–2101. [Google Scholar] [CrossRef]
- Notz, D.; Stroeve, J. Observed Arctic sea-ice loss directly follows anthropogenic CO2 emission. Science 2016, 354, 747–750. [Google Scholar] [CrossRef] [Green Version]
- Rogelj, J.; den Elzen, M.; Höhne, N.; Fransen, T.; Fekete, H.; Winkler, H.; Schaeffer, R.; Sha, F.; Riahi, K.; Meinshausen, M. Paris Agreement climate proposals need a boost to keep warming well below 2 °C. Nature 2016, 534, 631–639. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ivanova, N.; Johannessen, O.M.; Pedersen, L.T.; Tonboe, R.T. Retrieval of Arctic sea ice parameters by satellite passive microwave sensors: A comparison of eleven sea ice concentration algorithms. IEEE Trans. Geosci. Remote Sens. 2014, 52, 7233–7246. [Google Scholar] [CrossRef]
- Kunkee, D.B.; Swadley, S.D.; Poe, G.A.; Hong, Y.; Werner, M.F. Special Sensor Microwave Imager Sounder (SSMIS) radiometric calibration anomalies—Part I: Identification and characterization. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1017–1033. [Google Scholar] [CrossRef]
- Imaoka, K.; Kachi, M.; Fujii, H.; Murakami, H.; Hori, M.; Ono, A.; Igarashi, T.; Nakagawa, K.; Oki, T.; Honda, Y.; et al. Global Change Observation Mission (GCOM) for monitoring carbon, water cycles, and climate change. Proc. IEEE 2010, 98, 717–734. [Google Scholar] [CrossRef]
- Okuyama, A.; Imaoka, K. Intercalibration of Advanced Microwave Scanning Radiometer-2 (AMSR2) brightness temperature. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4568–4577. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Gloersen, P.; Campbell, W.J. Determination of sea ice parameters with the Nimbus 7 SMMR. J. Geophys. Res. 1984, 89, 5355–5369. [Google Scholar] [CrossRef]
- Comiso, J.C. Characteristics of Arctic winter sea ice from satellite multispectral microwave observations. J. Geophys. Res. 1986, 91, 975–994. [Google Scholar] [CrossRef]
- Spreen, G.; Kaleschke, L.; Heygster, G. Sea ice remote sensing using AMSR-E 89-GHz channels. J. Geophys. Res. 2008, 113, C02S03. [Google Scholar] [CrossRef] [Green Version]
- Ivanova, N.; Pedersen, L.T.; Tonboe, R.T.; Kern, S.; Heygster, G.; Lavergne, T.; Sørensen, A.; Saldo, R.; Dybkjær, G.; Brucker, L.; et al. Inter-comparison and evaluation of sea ice algorithms: Towards further identification of challenges and optimal approach using passive microwave observations. Cryosphere 2015, 9, 1797–1817. [Google Scholar] [CrossRef] [Green Version]
- Tonboe, R.T.; Eastwood, S.; Lavergne, T.; Sørensen, A.M.; Rathmann, N.; Dybkjær, G.; Pedersen, L.T.; Høyer, J.L.; Kern, S. The EUMETSAT sea ice concentration climate data record. Cryosphere 2016, 10, 2275–2290. [Google Scholar] [CrossRef] [Green Version]
- Andersen, S.; Tonboe, R.; Kern, S.; Schyberg, H. Improved retrieval of sea ice total concentration from spaceborne passive microwave observations using numerical weather prediction model fields: An intercomparison of nine algorithms. Remote Sens. Environ. 2006, 104, 374–392. [Google Scholar] [CrossRef]
- Han, H.; Kim, H.-C. Evaluation of summer passive microwave sea ice concentrations in the Chukchi Sea based on KOMPSAT-5 SAR and numerical weather prediction data. Remote Sens. Environ. 2018, 209, 343–362. [Google Scholar] [CrossRef]
- Shin, D.-B.; Chiu, L.S.; Clemente-Colon, P. Effects of atmospheric water and surface wind on passive microwave retrievals of sea ice concentration: A simulation study. Int. J. Remote Sens. 2008, 29, 5717–5731. [Google Scholar] [CrossRef]
- Meier, W.N. Comparison of passive microwave ice concentration algorithm retrievals with AVHRR imagery in Arctic peripheral seas. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1324–1337. [Google Scholar] [CrossRef]
- Meier, W.; Notz, D. A note on the accuracy and reliability of satellite-derived passive microwave estimates of sea-ice extent. In Clic Arctic Sea Ice Working Group Consensus Document; World Climate Research Program: Geneva, Switzerland, 2010. [Google Scholar]
- Cavalieri, D.J.; Germain, K.M.S.; Swift, C.T. Reduction of weather effects in the calculation of sea-ice concentration with the DMSP SSM/I. J. Glaciol. 1995, 41, 455–464. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Scott, K.A.; Xu, L.; Clausi, D.A. Sea ice concentration estimation during melt from dual-pol SAR scenes using deep convolutional neural networks: A case study. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4524–4533. [Google Scholar] [CrossRef]
- Karvonen, J. Baltic sea ice concentration estimation using SENTINEL-1 SAR and AMSR2 microwave radiometer data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2871–2883. [Google Scholar] [CrossRef]
- Wang, L.; Scott, K.A.; Clausi, D.A. Sea ice concentration estimation during freeze-up from SAR imagery using a convolutional neural network. Remote Sens. 2017, 9, 408. [Google Scholar] [CrossRef]
- Chi, J.; Kim, H.-C.; Lee, S.; Crawford, M.M. Deep learning based retrieval algorithm for Arctic sea ice concentration from AMSR2 passive microwave and MODIS optical data. Remote Sens. Environ. 2019, 231, 111204. [Google Scholar] [CrossRef]
- Fritzner, S.; Graversen, R.; Christensen, K.H. Assessment of high-resolution dynamical and machine learning models for prediction of sea ice concentration in a regional application. J. Geophys. Res. 2020, 125, e2020JC016277. [Google Scholar] [CrossRef]
- Kim, Y.J.; Kim, H.-C.; Han, D.; Lee, S.; Im, J. Prediction of monthly Arctic sea ice concentrations using satellite and reanalysis data based on convolutional neural networks. Cryosphere 2020, 14, 1083–1104. [Google Scholar] [CrossRef] [Green Version]
- Han, H.; Hong, S.-H.; Kim, H.-c.; Chae, T.-B.; Choi, H.-J. A study of the feasibility of using KOMPSAT-5 SAR data to map sea ice in the Chukchi Sea in late summer. Remote Sens. Lett. 2017, 8, 468–477. [Google Scholar] [CrossRef]
- Woodgate, R.A.; Weingartner, T.; Lindsay, R. The 2007 Bering Strait oceanic heat flux and anomalous Arctic sea-ice retreat. Geophys. Res. Lett. 2010, 37, L01602. [Google Scholar] [CrossRef] [Green Version]
- Stroeve, J.C.; Markus, T.; Boisvert, L.; Miller, J.; Barrett, A. Changes in Arctic melt season and implications for sea ice loss. Geophys. Res. Lett. 2014, 41, 1216–1225. [Google Scholar] [CrossRef]
- Meier, W.N.; Stroeve, J.; Fetterer, F. Whither Arctic sea ice? A clear signal of decline regionally, seasonally and extending beyond the satellite record. Ann. Glaciol. 2007, 46, 428–434. [Google Scholar] [CrossRef] [Green Version]
- Maeda, T.; Taniguchi, Y.; Imaoka, K. GCOM-W1 AMSR2 level 1R product: Dataset of brightness temperature modified using the antenna pattern matching technique. IEEE Trans. Geosci. Remote Sens. 2015, 54, 770–782. [Google Scholar] [CrossRef]
- Hersbach, H.; de Rosnay, P.; Bell, B.; Schepers, D.; Simmons, A.; Soci, C.; Abdalla, S.; Alonso-Balmaseda, M.; Balsamo, G.; Bechtold, P.; et al. Operational Global Reanalysis: Progress, Future Directions and Synergies with NWP. ECMWF Re-Anal. Proj. Rep. Ser. 2018, 27, 1–63. [Google Scholar]
- Serreze, M.C.; Crawford, A.D.; Stroeve, J.C.; Barrett, A.P.; Woodgate, R.A. Variability, trends, and predictability of seasonal sea ice retreat and advance in the Chukchi Sea. J. Geophys. Res. 2016, 121, 7308–7325. [Google Scholar] [CrossRef]
- Markus, T.; Dokken, S.T. Evaluation of late summer passive microwave Arctic sea ice retrievals. IEEE Trans. Geosci. Remote Sens. 2002, 40, 348–356. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Belgiu, M.; Drăguţ, L. Random forest in remote sensing: A review of applications and future directions. ISPRS J. Photogramm. Remote Sens. 2016, 114, 24–31. [Google Scholar] [CrossRef]
- Han, H.; Im, J.; Kim, M.; Sim, S.; Kim, J.; Kim, D.-J.; Kang, S.-H. Retrieval of melt ponds on arctic multiyear sea ice in summer from terrasar-x dual-polarization data using machine learning approaches: A case study in the Chukchi Sea with mid-incidence angle data. Remote Sens. 2016, 8, 57. [Google Scholar] [CrossRef] [Green Version]
- Kim, M.; Im, J.; Han, H.; Kim, J.; Lee, S.; Shin, M.; Kim, H.-C. Landfast sea ice monitoring using multisensor fusion in the Antarctic. GIScience Remote Sens. 2015, 52, 239–256. [Google Scholar] [CrossRef]
- Shen, X.; Zhang, J.; Zhang, X.; Meng, J.; Ke, C. Sea ice classification using Cryosat-2 altimeter data by optimal classifier–feature assembly. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1948–1952. [Google Scholar] [CrossRef]
- Kim, M.; Kim, H.-C.; Im, J.; Lee, S.; Han, H. Object-based landfast sea ice detection over West Antarctica using time series ALOS PALSAR data. Remote Sens. Environ. 2020, 242, 111782. [Google Scholar] [CrossRef]
- Lee, S.; Im, J.; Kim, J.; Kim, M.; Shin, M.; Kim, H.-C.; Quackenbush, L.J. Arctic sea ice thickness estimation from CryoSat-2 satellite data using machine learning-based lead detection. Remote Sens. 2016, 8, 698. [Google Scholar] [CrossRef] [Green Version]
- Murashkin, D.; Spreen, G.; Huntemann, M.; Dierking, W. Method for detection of leads from Sentinel-1 SAR images. Ann. Glaciol. 2018, 59, 124–136. [Google Scholar] [CrossRef] [Green Version]
- Cavalieri, D.J.; Markus, T.; Hall, D.K.; Gasiewski, A.J.; Klein, M.; Ivanoff, A. Assessment of EOS Aqua AMSR-E Arctic sea ice concentrations using Landsat-7 and airborne microwave imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 3057–3069. [Google Scholar] [CrossRef]
- Cavalieri, D.J.; Markus, T.; Hall, D.K.; Ivanoff, A.; Glick, E. Assessment of AMSR-E Antarctic winter sea-ice concentrations using Aqua MODIS. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3331–3339. [Google Scholar] [CrossRef]
- Liang, S.; Strahler, A.; Walthall, C. Retrieval of land surface albedo from satellite observations: A simulation study. In Proceedings of the 1998 IEEE International Geoscience and Remote Sensing Symposium IGARSS ‘98, Seattle, WA, USA, 6–10 July 1998; Volume 1283, pp. 1286–1288. [Google Scholar]
- Brandt, R.E.; Warren, S.G.; Worby, A.P.; Grenfell, T.C. Surface albedo of the Antarctic sea ice zone. J. Clim. 2005, 18, 3606–3622. [Google Scholar] [CrossRef] [Green Version]
- Radhakrishnan, R.; Scott, A.; Clausi, D.A. Sea ice concentration estimation: Using passive microwave and SAR data with a U-net and curriculum learning. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2021. [Google Scholar] [CrossRef]
- Kern, S.; Rösel, A.; Pedersen, L.T.; Ivanova, N.; Saldo, R.; Tonboe, R.T. The impact of melt ponds on summertime microwave brightness temperatures and sea-ice concentrations. Cryosphere 2016, 10, 2217–2239. [Google Scholar] [CrossRef] [Green Version]
- Meier, W.N.; Ivanoff, A. Intercalibration of AMSR2 NASA Team 2 algorithm sea ice concentrations with AMSR-E slow rotation data. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2017, 10, 3923–3933. [Google Scholar] [CrossRef]
- Wang, C.; Graham, R.M.; Wang, K.; Gerland, S.; Granskog, M.A. Comparison of ERA5 and ERA-Interim near-surface air temperature, snowfall and precipitation over Arctic sea ice: Effects on sea ice thermodynamics and evolution. Cryosphere 2019, 13, 1661–1679. [Google Scholar] [CrossRef] [Green Version]
- Di Napoli, C.; Barnard, C.; Prudhomme, C.; Cloke, H.L.; Pappenberger, F. ERA5-HEAT: A global gridded historical dataset of human thermal comfort indices from climate reanalysis. Geosci. Data J. 2020, 1–9. [Google Scholar] [CrossRef]



| Date | Path | Row |
|---|---|---|
| 12 July 2013 | 77 | 10 |
| 11 August 2014 | 90 | 6 |
| 11 August 2014 | 90 | 8 |
| 6 September 2014 | 105 | 8 |
| 8 July 2015 | 87 | 6 |
| 13 July 2018 | 82 | 10 |
| 27 July 2018 | 173 | 239 |
| 9 August 2018 | 168 | 240 |
| Statistics | Mean | Median | Std. | Min. | Max. | Q1 | Q3 | |
|---|---|---|---|---|---|---|---|---|
| Variable | ||||||||
| TB 6H (K) | 168.23 | 171.34 | 38.94 | 87.87 | 241.45 | 133.82 | 200.65 | |
| TB 6V (K) | 218.23 | 222.73 | 24.40 | 165.68 | 259.93 | 196.63 | 238.40 | |
| TB 10H (K) | 173.73 | 178.11 | 37.72 | 96.00 | 240.02 | 140.25 | 206.11 | |
| TB 10V (K) | 223.53 | 228.48 | 22.42 | 175.06 | 259.60 | 203.72 | 242.84 | |
| TB 18H (K) | 183.35 | 189.06 | 32.29 | 113.03 | 241.38 | 155.61 | 211.49 | |
| TB 18V (K) | 230.08 | 234.0 | 17.11 | 190.47 | 258.33 | 215.35 | 245.09 | |
| TB 23H (K) | 198.75 | 203.93 | 26.33 | 131.93 | 250.18 | 176.80 | 220.52 | |
| TB 23V (K) | 236.13 | 237.41 | 13.70 | 202.38 | 263.07 | 224.65 | 248.38 | |
| TB 36H (K) | 195.44 | 198.90 | 24.23 | 141.35 | 250.18 | 175.15 | 215.40 | |
| TB 36V (K) | 232.28 | 231.83 | 12.73 | 194.31 | 262.47 | 222.15 | 242.47 | |
| TB 89H (K) | 220.86 | 218.88 | 16.06 | 179.16 | 268.38 | 209.31 | 231.33 | |
| TB 89V (K) | 243.05 | 243.66 | 12.18 | 194.90 | 272.15 | 236.61 | 250.06 | |
| PR18 | 1.12 | 1.11 | 0.06 | 1.03 | 1.26 | 1.07 | 1.16 | |
| GR(36V18V) | 1.01 | 1.01 | 0.02 | 0.91 | 1.06 | 0.99 | 1.02 | |
| GR(23V18V) | 1.01 | 1.01 | 0.01 | 0.98 | 1.05 | 1.00 | 1.02 | |
| GR(89H18H) | 2.07 | 2.06 | 0.03 | 2.00 | 2.17 | 2.04 | 2.10 | |
| GR(89V18V) | 1.10 | 1.09 | 0.08 | 0.92 | 1.29 | 1.04 | 1.16 | |
| 1.03 | 1.03 | 0.05 | 0.88 | 1.13 | 0.99 | 1.07 | ||
| TCWV (kg/m2) | 11.99 | 11.35 | 3.45 | 3.83 | 29.28 | 9.98 | 13.34 | |
| Wind speed (m/s) | 4.88 | 4.68 | 2.44 | 0.04 | 13.09 | 2.94 | 6.24 | |
| 2 m air temperature (°C) | −0.28 | −0.12 | 1.73 | −10.81 | 6.78 | −0.81 | 0.70 | |
| 925 hPa air temperature (°C) | −0.32 | −0.58 | 4.25 | −10.98 | 12.98 | −3.10 | 2.08 | |
| 30-day average of 2 m air temperature (°C) | 0.63 | 0.69 | 1.02 | −3.88 | 5.57 | 0.10 | 1.30 | |
| 30-day average of 925 hPa air temperature (°C) | 1.07 | 0.31 | 3.01 | −5.87 | 8.11 | −1.22 | 3.72 | |
| Reference SIC (%) | 61.06 | 71.13 | 34.95 | 0.00 | 100.00 | 26.44 | 95.36 | |
| Statistics | Mean | Median | Std. | Min. | Max. | Q1 | Q3 | |
|---|---|---|---|---|---|---|---|---|
| Variable | ||||||||
| TCWV (kg/m2) | 14.19 | 13.99 | 3.07 | 10.54 | 26.02 | 11.01 | 16.15 | |
| Wind speed (m/s) | 5.67 | 5.76 | 1.26 | 3.03 | 8.39 | 4.84 | 6.60 | |
| 2 m air temperature (°C) | 0.65 | 0.58 | 0.49 | −0.28 | 4.05 | 0.26 | 0.9 | |
| 925 hPa air temperature (°C) | 3.84 | 5.44 | 3.42 | −3.54 | 7.74 | 0.88 | 6.19 | |
| 30 days average of 2 m air temperature (°C) | 1.09 | 0.75 | 0.87 | −0.09 | 7.62 | 0.55 | 1.46 | |
| 30 days average of 925 hPa air temperature (°C) | 2.43 | 2.01 | 2.71 | −1.06 | 9.96 | −0.09 | 3.25 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Lee, S.; Kim, H.-C.; Kim, M. Retrieval of Summer Sea Ice Concentration in the Pacific Arctic Ocean from AMSR2 Observations and Numerical Weather Data Using Random Forest Regression. Remote Sens. 2021, 13, 2283. https://doi.org/10.3390/rs13122283
Han H, Lee S, Kim H-C, Kim M. Retrieval of Summer Sea Ice Concentration in the Pacific Arctic Ocean from AMSR2 Observations and Numerical Weather Data Using Random Forest Regression. Remote Sensing. 2021; 13(12):2283. https://doi.org/10.3390/rs13122283
Chicago/Turabian StyleHan, Hyangsun, Sungjae Lee, Hyun-Cheol Kim, and Miae Kim. 2021. "Retrieval of Summer Sea Ice Concentration in the Pacific Arctic Ocean from AMSR2 Observations and Numerical Weather Data Using Random Forest Regression" Remote Sensing 13, no. 12: 2283. https://doi.org/10.3390/rs13122283
APA StyleHan, H., Lee, S., Kim, H.-C., & Kim, M. (2021). Retrieval of Summer Sea Ice Concentration in the Pacific Arctic Ocean from AMSR2 Observations and Numerical Weather Data Using Random Forest Regression. Remote Sensing, 13(12), 2283. https://doi.org/10.3390/rs13122283