Cereal Yield Forecasting with Satellite Drought-Based Indices, Weather Data and Regional Climate Indices Using Machine Learning in Morocco
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Yield Data
2.3. Satellite-Based Drought Indices
2.4. Weather Data
2.5. Climate Data
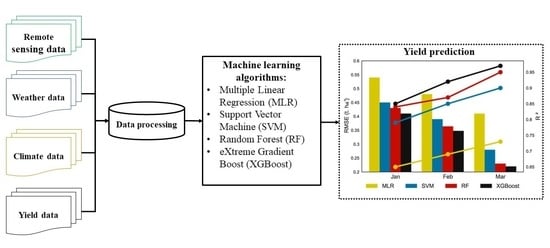
2.6. Machine Learning Methods for Cereal Yield Forecasting
2.6.1. Multiple Linear Regression
2.6.2. Random Forest (RF)
2.6.3. Support Vector Machine (SVM)
2.6.4. eXtreme Gradient Boost (XGBoost)
2.7. Model Evaluation
2.8. Experiment Design
3. Results
3.1. Choice of Input Data Sets
3.2. Model Performance as a Function of Lead Time before Harvest
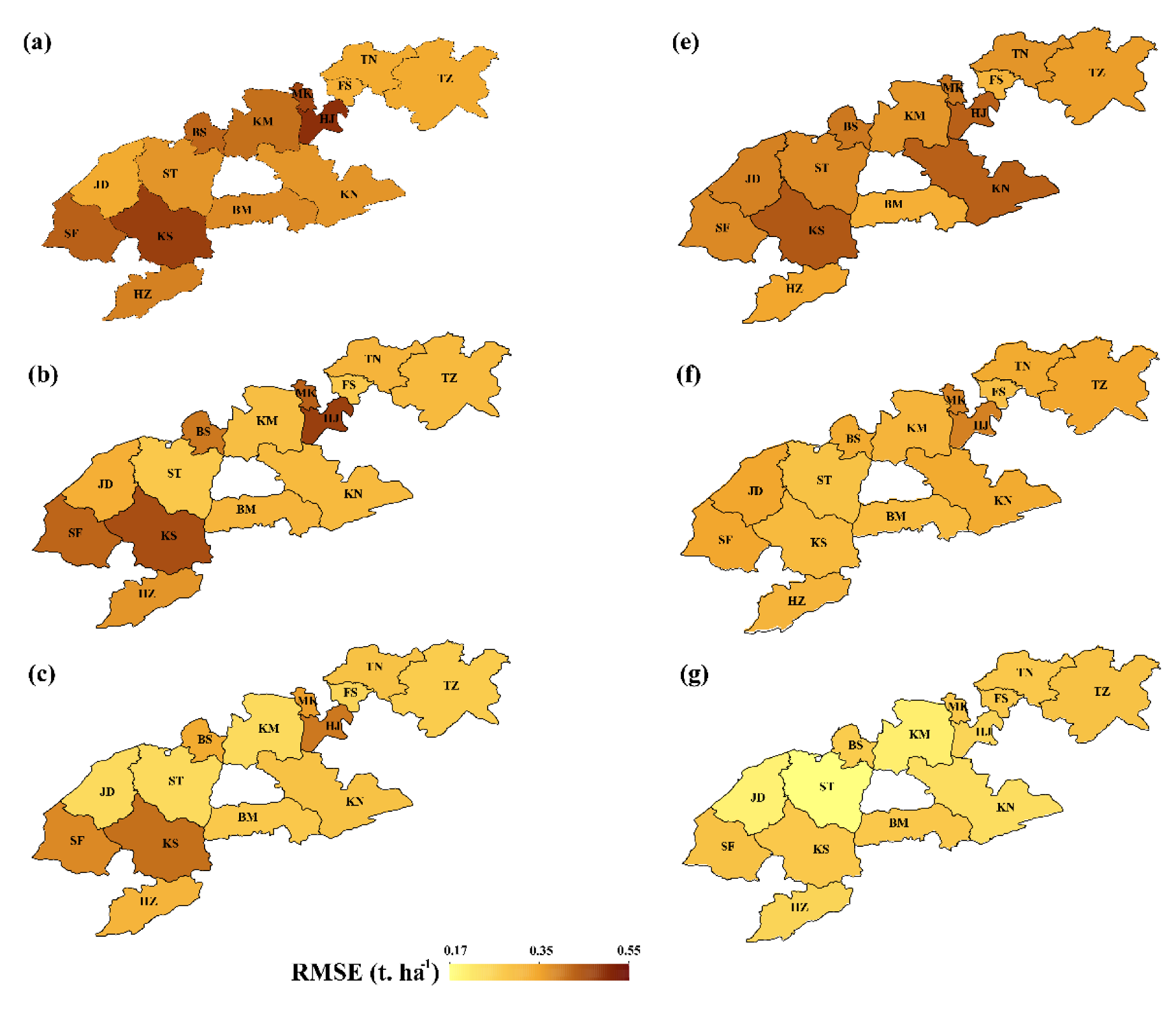
3.3. Model Performance at a Regional Scale
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Asseng, S.; Ewert, F.; Martre, P.; Rötter, R.; Lobell, D.; Cammarano, D.; Kimball, B.A.; Ottman, M.J.; Wall, G.W.; White, J.W.; et al. Rising temperatures reduce global wheat production. Nat. Clim. Chang. 2015, 5, 143–147. [Google Scholar] [CrossRef]
- FAO. Climate Change and Food Security: Risks and Responses; Food and Agriculture Organization of The United Nations: Rome, Italy, 2016; ISBN 9789251089989. [Google Scholar]
- Giorgi, F. Climate change hot-spots. Geophys. Res. Lett. 2006, 33, 101029. [Google Scholar] [CrossRef]
- Lionello, P.; Scarascia, L. The relation between climate change in the Mediterranean region and global warming. Reg. Environ. Chang. 2018, 18, 1481–1493. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Quiring, S.M.; Peña-Gallardo, M.; Yuan, S.; Domínguez-Castro, F. A review of environmental droughts: Increased risk under global warming? Earth Sci. Rev. 2020, 201, 1–23. [Google Scholar] [CrossRef]
- Kogan, F.; Guo, W.; Yang, W. Drought and food security prediction from NOAA new generation of operational satellites. Geomat. Nat. Hazards Risk 2019, 10, 651–666. [Google Scholar] [CrossRef] [Green Version]
- Schilling, J.; Hertig, E.; Tramblay, Y.; Scheffran, J. Climate change vulnerability, water resources and social implications in North Africa. Reg. Environ. Chang. 2020, 20, 1–15. [Google Scholar] [CrossRef] [Green Version]
- UN General Assembly. Transforming Our World: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2015. [Google Scholar]
- Bouras, E.; Jarlan, L.; Khabba, S.; Er-Raki, S.; Dezetter, A.; Sghir, F.; Tramblay, Y. Assessing the impact of global climate changes on irrigated wheat yields and water requirements in a semi-arid environment of Morocco. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef]
- Bouras, E.H.; Jarlan, L.; Er-Raki, S.; Albergel, C.; Richard, B.; Balaghi, R.; Khabba, S. Linkages between rainfed cereal production and agricultural drought through remote sensing indices and a land data assimilation system: A case study in Morocco. Remote Sens. 2020, 12, 4018. [Google Scholar] [CrossRef]
- Jarlan, L.; Abaoui, J.; Duchemin, B.; Ouldbba, A.; Tourre, Y.M.; Khabba, S.; Le Page, M.; Balaghi, R.; Mokssit, A.; Chehbouni, G. Linkages between common wheat yields and climate in Morocco (1982–2008). Int. J. Biometeorol. 2014, 58, 1489–1502. [Google Scholar] [CrossRef]
- Balaghi, R.; Tychon, B.; Eerens, H.; Jlibene, M. Empirical regression models using NDVI, rainfall and temperature data for the early prediction of wheat grain yields in Morocco. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 438–452. [Google Scholar] [CrossRef] [Green Version]
- Lobell, D.B.; Burke, M.B.; Tebaldi, C.; Mastrandrea, M.D.; Falcon, W.P.; Naylor, R.L. Prioritizing climate change adaptation needs for food security in 2030. Science 2008, 319, 607–610. [Google Scholar] [CrossRef]
- Sacks, W.J.; Kucharik, C.J. Crop management and phenology trends in the U.S. Corn Belt: Impacts on yields, evapotranspiration and energy balance. Agric. For. Meteorol. 2011, 151, 882–894. [Google Scholar] [CrossRef]
- Basso, B.; Liu, L. Seasonal crop yield forecast: Methods, applications, and accuracies. Adv. Agron. 2019, 54, 201–255. [Google Scholar]
- Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Toward a new generation of agricultural system data, models, and knowledge products: State of agricultural systems science. Agric. Syst. 2017, 155, 269–288. [Google Scholar] [CrossRef]
- Lawless, C.; Semenov, M.A. Assessing lead-time for predicting wheat growth using a crop simulation model. Agric. For. Meteorol. 2005, 135, 302–313. [Google Scholar] [CrossRef]
- Wang, X.; Zhao, C.; Li, C.; Liu, L.; Huang, W.; Wang, P. Use of Ceres-wheat model for wheat yield forecast in Beijing. In Proceedings of the IFIP Advances in Information and Communication Technology; Springer: Boston, MA, USA, 2009. [Google Scholar]
- Li, Z.; Song, M.; Feng, H.; Zhao, Y. Within-season yield prediction with different nitrogen inputs under rain-fed condition using CERES-Wheat model in the northwest of China. J. Sci. Food Agric. 2016, 96, 2906–2916. [Google Scholar] [CrossRef]
- Dumont, B.; Leemans, V.; Ferrandis, S.; Bodson, B.; Destain, J.P.; Destain, M.F. Assessing the potential of an algorithm based on mean climatic data to predict wheat yield. Precis. Agric. 2014, 15, 255–272. [Google Scholar] [CrossRef] [Green Version]
- Hansen, J.W.; Indeje, M. Linking dynamic seasonal climate forecasts with crop simulation for maize yield prediction in semi-arid Kenya. Agric. For. Meteorol. 2004, 125, 143–157. [Google Scholar] [CrossRef]
- Mishra, A.; Hansen, J.W.; Dingkuhn, M.; Baron, C.; Traoré, S.B.; Ndiaye, O.; Ward, M.N. Sorghum yield prediction from seasonal rainfall forecasts in Burkina Faso. Agric. For. Meteorol. 2008, 148, 1798–1814. [Google Scholar] [CrossRef]
- Kogan, F.; Yang, B.; Guo, W.; Pei, Z.; Jiao, X. Modelling corn production in China using AVHRR-based vegetation health indices. Int. J. Remote Sens. 2005, 26, 2325–2336. [Google Scholar] [CrossRef]
- Kogan, F.; Kussul, N.; Adamenko, T.; Skakun, S.; Kravchenko, O.; Kryvobok, O.; Shelestov, A.; Kolotii, A.; Kussul, O.; Lavrenyuk, A. Winter wheat yield forecasting in Ukraine based on Earth observation, meteorologicaldata and biophysical models. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 192–203. [Google Scholar] [CrossRef]
- Johnson, D.M. An assessment of pre- and within-season remotely sensed variables for forecasting corn and soybean yields in the United States. Remote Sens. Environ. 2014, 141, 116–128. [Google Scholar] [CrossRef]
- Meroni, M.; Fasbender, D.; Balaghi, R.; Dali, M.; Haffani, M.; Haythem, I.; Hooker, J.; Lahlou, M.; Lopez-Lozano, R.; Mahyou, H.; et al. Evaluating NDVI Data Continuity Between SPOT-VEGETATION and PROBA-V Missions for Operational Yield Forecasting in North African Countries. IEEE Trans. Geosci. Remote Sens. 2016, 54, 795–804. [Google Scholar] [CrossRef]
- Mathieu, J.A.; Aires, F. Assessment of the agro-climatic indices to improve crop yield forecasting. Agric. For. Meteorol. 2018, 253–254, 15–30. [Google Scholar] [CrossRef]
- Dumont, B.; Basso, B.; Leemans, V.; Bodson, B.; Destain, J.P.; Destain, M.F. A comparison of within-season yield prediction algorithms based on crop model behaviour analysis. Agric. For. Meteorol. 2015, 204, 10–21. [Google Scholar] [CrossRef]
- Basso, B.; Cammarano, D.; Carfagna, E. Review of Crop Yield Forecasting Methods and Early Warning Systems. In Proceedings of the First Meeting of the Scientific Advisory Committee of the Global Strategy to Improve Agricultural and Rural Statistics, Rome, Italy, 18–19 July 2013. [Google Scholar]
- Sierra, E.M.; Brynsztein, S.M. Wheat yield variability in the S.E. of the Province of Buenos Aires. Agric. For. Meteorol. 1990, 49, 281–290. [Google Scholar] [CrossRef]
- Giri, A.K.; Bhan, M.; Agrawal, K.K. Districtwise wheat and rice yield predictions using meteorological variables in eastern Madhya Pradesh. J. Agrometeorol. 2017, 9, 366–368. [Google Scholar]
- Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using low resolution satellite imagery for yield prediction and yield anomaly detection. Remote Sens. 2013, 1, 5572–5573. [Google Scholar] [CrossRef] [Green Version]
- Anderson, M.C.; Zolin, C.A.; Sentelhas, P.C.; Hain, C.R.; Semmens, K.; Tugrul Yilmaz, M.; Gao, F.; Otkin, J.A.; Tetrault, R. The Evaporative Stress Index as an indicator of agricultural drought in Brazil: An assessment based on crop yield impacts. Remote Sens. Environ. 2016, 174, 82–99. [Google Scholar] [CrossRef]
- Salazar, L.; Kogan, F.; Roytman, L. Use of remote sensing data for estimation of winter wheat yield in the United States. Int. J. Remote Sens. 2007, 28, 3795–3811. [Google Scholar] [CrossRef]
- Wang, M.; Tao, F.L.; Shi, W.J. Corn yield forecasting in northeast china using remotely sensed spectral indices and crop phenology metrics. J. Integr. Agric. 2014, 13, 1538–1545. [Google Scholar] [CrossRef]
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens. Environ. 2010, 114, 1312–1323. [Google Scholar] [CrossRef]
- Liu, W.T.; Kogan, F. Monitoring Brazilian soybean production using NOAA/AVHRR based vegetation condition indices. Int. J. Remote Sens. 2002, 23, 1161–1179. [Google Scholar] [CrossRef]
- García-León, D.; Contreras, S.; Hunink, J. Comparison of meteorological and satellite-based drought indices as yield predictors of Spanish cereals. Agric. Water Manag. 2019, 213, 388–396. [Google Scholar] [CrossRef]
- Nguyen-Huy, T.; Deo, R.C.; An-Vo, D.A.; Mushtaq, S.; Khan, S. Copula-statistical precipitation forecasting model in Australia’s agro-ecological zones. Agric. Water Manag. 2017, 191, 153–172. [Google Scholar] [CrossRef]
- Ceglar, A.; Turco, M.; Toreti, A.; Doblas-Reyes, F.J. Linking crop yield anomalies to large-scale atmospheric circulation in Europe. Agric. For. Meteorol. 2017, 240–241, 35–45. [Google Scholar] [CrossRef]
- Wang, B.; Feng, P.; Waters, C.; Cleverly, J.; Liu, D.L.; Yu, Q. Quantifying the impacts of pre-occurred ENSO signals on wheat yield variation using machine learning in Australia. Agric. For. Meteorol. 2020, 291, 108043. [Google Scholar] [CrossRef]
- Knippertz, P.; Christoph, M.; Speth, P. Long-term precipitation variability in Morocco and the link to the large-scale circulation in recent and future climates. Meteorol. Atmos. Phys. 2003, 83, 67–88. [Google Scholar] [CrossRef]
- Podestá, G.; Letson, D.; Messina, C.; Royce, F.; Ferreyra, R.A.; Jones, J.; Hansen, J.; Llovet, I.; Grondona, M.; O’Brien, J.J. Use of ENSO-related climate information in agricultural decision making in Argentina: A pilot experience. Agric. Syst. 2002, 74, 371–392. [Google Scholar] [CrossRef]
- Martinez, C.J.; Baigorria, G.A.; Jones, J.W. Use of climate indices to predict corn yields in southeast USA. Int. J. Climatol. 2009, 29, 1680–1691. [Google Scholar] [CrossRef]
- Lehmann, J.; Kretschmer, M.; Schauberger, B.; Wechsung, F. Potential for Early Forecast of Moroccan Wheat Yields Based on Climatic Drivers. Geophys. Res. Lett. 2020, 41, 1–10. [Google Scholar] [CrossRef]
- Cai, X.L.; Sharma, B.R. Integrating remote sensing, census and weather data for an assessment of rice yield, water consumption and water productivity in the Indo-Gangetic river basin. Agric. Water Manag. 2010, 97, 309–316. [Google Scholar] [CrossRef]
- Van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Abbas, F.; Afzaal, H.; Farooque, A.A.; Tang, S. Crop yield prediction through proximal sensing and machine learning algorithms. Agronomy 2020, 10, 1046. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Z.; Tao, F.; Zhang, L.; Luo, Y.; Han, J.; Li, Z. Identifying the contributions of multi-source data for winter wheat yield prediction in China. Remote Sens. 2020, 12, 750. [Google Scholar] [CrossRef] [Green Version]
- Feng, P.; Wang, B.; Liu, D.L.; Waters, C.; Xiao, D.; Shi, L.; Yu, Q. Dynamic wheat yield forecasts are improved by a hybrid approach using a biophysical model and machine learning technique. Agric. For. Meteorol. 2020, 285–286, 107922. [Google Scholar] [CrossRef]
- Kamir, E.; Waldner, F.; Hochman, Z. Estimating wheat yields in Australia using climate records, satellite image time series and machine learning methods. ISPRS J. Photogramm. Remote Sens. 2020, 160, 124–135. [Google Scholar] [CrossRef]
- Kang, Y.; Ozdogan, M.; Zhu, X.; Ye, Z.; Hain, C.; Anderson, M. Comparative assessment of environmental variables and machine learning algorithms for maize yield prediction in the US Midwest. Environ. Res. Lett. 2020, 15, 064005. [Google Scholar] [CrossRef]
- Mateo-Sanchis, A.; Piles, M.; Muñoz-Marí, J.; Adsuara, J.E.; Pérez-Suay, A.; Camps-Valls, G. Synergistic integration of optical and microwave satellite data for crop yield estimation. Remote Sens. Environ. 2019, 234, 111460. [Google Scholar] [CrossRef]
- Han, J.; Zhang, Z.; Cao, J.; Luo, Y.; Zhang, L.; Li, Z.; Zhang, J. Prediction of winter wheat yield based on multi-source data and machine learning in China. Remote Sens. 2020, 12, 236. [Google Scholar] [CrossRef] [Green Version]
- Schwalbert, R.A.; Amado, T.; Corassa, G.; Pott, L.P.; Prasad, P.V.V.; Ciampitti, I.A. Satellite-based soybean yield forecast: Integrating machine learning and weather data for improving crop yield prediction in southern Brazil. Agric. For. Meteorol. 2020, 284, 107886. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L.; et al. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Driouech, F.; Déqué, M.; Mokssit, A. Numerical simulation of the probability distribution function of precipitation over Morocco. Clim. Dyn. 2009, 2, 1055–1063. [Google Scholar] [CrossRef]
- Kaufman, L.; Rousseeuw, P.J. Finding Groups in Data: An. Introduction to Cluster Analysis; Wiley Series in Probability and Statistics; Wiley: Hoboken, NJ, USA, 1990; ISBN 0471735787. [Google Scholar]
- West, H.; Quinn, N.; Horswell, M. Remote sensing for drought monitoring & impact assessment: Progress, past challenges and future opportunities. Remote Sens. Environ. 2019, 232, 111291. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- Zhang, A.; Jia, G. Monitoring meteorological drought in semiarid regions using multi-sensor microwave remote sensing data. Remote Sens. Environ. 2013, 134, 12–23. [Google Scholar] [CrossRef]
- Jiao, W.; Tian, C.; Chang, Q.; Novick, K.A.; Wang, L. A new multi-sensor integrated index for drought monitoring. Agric. For. Meteorol. 2019, 268, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Bento, V.A.; Trigo, I.F.; Gouveia, C.M.; DaCamara, C.C. Contribution of Land Surface Temperature (TCI) to Vegetation Health Index: A comparative study using clear sky and all-weather climate data records. Remote Sens. 2018, 10, 1324. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for improved Earth system understanding: State-of-the art and future directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Heng, L.K.; Asseng, S.; Mejahed, K.; Rusan, M. Optimizing wheat productivity in two rain-fed environments of the West Asia-North Africa region using a simulation model. Eur. J. Agron. 2007, 26, 121–129. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Barnston, A.G.; Livezey, R.E. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Henry, N.W.; Cohen, J.; Cohen, P. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences. Contemp. Sociol. 1977, 6, 320. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Sain, S.R.; Vapnik, V.N. The Nature of Statistical Learning Theory. Technometrics 1996, 38, 409. [Google Scholar] [CrossRef]
- Gunn, S. Support Vector Machines for classification and regression. Analyst 1998, 135, 230–267. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Kuter, S. Completing the machine learning saga in fractional snow cover estimation from MODIS Terra reflectance data: Random forests versus support vector regression. Remote Sens. Environ. 2021, 255, 112294. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A scalable tree boosting system. In Proceedings of the ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Song, Y.; Liu, X.; Zhang, L.; Jiao, X.; Qiang, Y.; Qiao, Y.; Liu, Z. Prediction of double-high biochemical indicators based on lightGBM and XGBoost. In Proceedings of the ACM International Conference Proceeding Series, Wuhan, China, 12–13 July 2019. [Google Scholar]
- Kaneko, H.; Funatsu, K. Fast optimization of hyperparameters for support vector regression models with highly predictive ability. Chemom. Intell. Lab. Syst. 2015, 142, 64–69. [Google Scholar] [CrossRef] [Green Version]
- Picard, R.R.; Cook, R.D. Cross-validation of regression models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Kohavi, R. A Study of Cross-Validation and Bootstrap for Accuracy Estimation and Model Selection. Int. Jt. Conf. Artif. Intell. 1995, 2, 1137–1143. [Google Scholar]
- Arlot, S.; Celisse, A. A survey of cross-validation procedures for model selection. Stat. Surv. 2010, 4, 40–79. [Google Scholar] [CrossRef]
- Baumann, K. Cross-validation as the objective function for variable-selection techniques. TrAC Trends Anal. Chem. 2003, 22, 395–406. [Google Scholar] [CrossRef]
- Faroux, S.; Kaptué Tchuenté, A.T.; Roujean, J.-L.; Masson, V.; Martin, E.; Le Moigne, P. ECOCLIMAP-II/Europe: A twofold database of ecosystems and surface parameters at 1 km resolution based on satellite information for use in land surface, meteorological and climate models. Geosci. Model. Dev. 2013, 6, 563–582. [Google Scholar] [CrossRef] [Green Version]
- ESA. Land Cover CCI Product User Guide Version 2.0; ESA: Paris, France, 2017; Available online: http://maps.elie.ucl.ac.be/CCI/viewer/download/ESACCI-LC-Ph2-PUGv2_2.0.pdf (accessed on 31 July 2021).
- Rasouli, K.; Hsieh, W.W.; Cannon, A.J. Daily streamflow forecasting by machine learning methods with weather and climate inputs. J. Hydrol. 2012, 414–415, 284–293. [Google Scholar] [CrossRef]
- Genovese, G.P.; Fritz, S.; Bettio, M. A comparison and evaluation of performances among crop yield forecasting models based on remote sensing: Results from the geoland observatory of food monitoring. Int. Arch. Photogramm. Remote Sens. Spacial Inf. Sci. 2006, 36, 71–77. [Google Scholar]
- Belaqziz, S.; Khabba, S.; Er-Raki, S.; Jarlan, L.; Le Page, M.; Kharrou, M.H.; Adnani, M.E.; Chehbouni, A. A new irrigation priority index based on remote sensing data for assessing the networks irrigation scheduling. Agric. Water Manag. 2013, 119, 1–9. [Google Scholar] [CrossRef]
- Satir, O.; Berberoglu, S. Crop yield prediction under soil salinity using satellite derived vegetation indices. Field Crop. Res. 2016, 192, 134–143. [Google Scholar] [CrossRef]
- Hengl, T.; De Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [Green Version]
- El Hajj, M.; Baghdadi, N.; Zribi, M.; Belaud, G.; Cheviron, B.; Courault, D.; Charron, F. Soil moisture retrieval over irrigated grassland using X-band SAR data. Remote Sens. Environ. 2016, 176, 202–218. [Google Scholar] [CrossRef] [Green Version]
- Ouaadi, N.; Jarlan, L.; Ezzahar, J.; Zribi, M.; Khabba, S.; Bouras, E.; Bousbih, S.; Frison, P.-L. Monitoring of wheat crops using the backscattering coefficient and the interferometric coherence derived from Sentinel-1 in semi-arid areas. Remote Sens. Environ. 2020, 251, 112050. [Google Scholar] [CrossRef]
- Zhang, Z.; Jin, Y.; Chen, B.; Brown, P. California almond yield prediction at the orchard level with a machine learning approach. Front. Plant. Sci. 2019, 10, 809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tramblay, Y.; El Adlouni, S.; Servat, E. Trends and variability in extreme precipitation indices over maghreb countries. Nat. Hazards Earth Syst. Sci. 2013, 13, 3235–3248. [Google Scholar] [CrossRef] [Green Version]
- Conte, M.; Giuffrida, A.; Tedesco, S. The Mediterranean Oscillation. Impact on Precipitation and Hydrology in Italy Climate Water; Academy of Finland: Helsinki, Fenland, 1989. [Google Scholar]
- Ouachani, R.; Bargaoui, Z.; Ouarda, T. Power of teleconnection patterns on precipitation and streamflow variability of upper Medjerda Basin. Int. J. Climatol. 2013, 33, 58–76. [Google Scholar] [CrossRef]
- Kang, S.; Shi, W.; Zhang, J. An improved water-use efficiency for maize grown under regulated deficit irrigation. Field Crop. Res. 2000, 67, 207–214. [Google Scholar] [CrossRef]
- Song, L.; Jin, J.; He, J. Effects of severe water stress on maize growth processes in the field. Sustainability 2019, 11, 5086. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.H.; Hsu, C.S.; Huang, P.C. Developing crop price forecasting service using open data from Taiwan markets. In Proceedings of the TAAI 2015—2015 Conference on Technologies and Applications of Artificial Intelligence, Tainan, Taiwan, 20–22 November 2015. [Google Scholar]





| Category | Product | Variable | Spatial Resolution | Temporal Resolution | Source of Data |
|---|---|---|---|---|---|
| Crop Yield | Crop yield | Province level | Yearly | Ministry of agriculture of Morocco | |
| Remote sensing | MOD13A2 | NDVI | 1 km | 16-Day | https://lpdaac.usgs.gov (accessed on 31 July 2021) |
| LST | 1 km | Daily | |||
| MOD11A1 | |||||
| ESA CCI SM COMBINED | SM | 25 km | Daily | https://www.esa-soilmoisture-cci.org (accessed on 31 July 2021) | |
| Weather | ERA5 | Rainfall, Air temperature | 30 km | Daily | https://www.ecmwf.int/en/forecasts/dataset/reanalysis-datasets/era5 (accessed on 31 July 2021) |
| Climate | NAO, SCA, SST | Monthly | https://psl.noaa.gov/data/ climateindices/ (accessed on 31 July 2021) |
| Predictor Variables | Raw Products | Time Span of the Year | Publication |
|---|---|---|---|
| VCI | NDVI | February–April | [10,11,12] |
| TCI | LST | January–February | [10] |
| SMCI | SM | October–November | [10] |
| Air temperature | ERA5 air temperature | December | [11,12] |
| Rainfall | ERA5 rainfall | October–November and January–March | [11,12] |
| NAO | Northern Hemispheric Teleconnection Patterns | December | [11] |
| SCA | Northern Hemispheric Teleconnection Patterns | January | [11] |
| Atlantic Tripole | SST | February | [11] |
| Atlantic Niño | SST | October | [11] |
| Input Data | Models | RMSE (t. ha−1) | MAE (t. ha−1) | R2 |
| Satellite-based drought indices only | MLR | 0.66 | 0.57 | 0.67 |
| SVM | 0.54 | 0.43 | 0.78 | |
| RF | 0.46 | 0.35 | 0.80 | |
| XGBoost | 0.45 | 0.34 | 0.81 | |
| Satellite-based drought indices and weather data | MLR | 0.46 | 0.39 | 0.72 |
| SVM | 0.40 | 0.31 | 0.80 | |
| RF | 0.34 | 0.24 | 0.84 | |
| XGBoost | 0.37 | 0.25 | 0.86 | |
| Satellite-based drought indices, weather data and climate indices | MLR | 0.41 | 0.31 | 0.75 |
| SVM | 0.25 | 0.21 | 0.88 | |
| RF | 0.22 | 0.19 | 0.92 | |
| XGBoost | 0.20 | 0.16 | 0.95 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouras, E.h.; Jarlan, L.; Er-Raki, S.; Balaghi, R.; Amazirh, A.; Richard, B.; Khabba, S. Cereal Yield Forecasting with Satellite Drought-Based Indices, Weather Data and Regional Climate Indices Using Machine Learning in Morocco. Remote Sens. 2021, 13, 3101. https://doi.org/10.3390/rs13163101
Bouras Eh, Jarlan L, Er-Raki S, Balaghi R, Amazirh A, Richard B, Khabba S. Cereal Yield Forecasting with Satellite Drought-Based Indices, Weather Data and Regional Climate Indices Using Machine Learning in Morocco. Remote Sensing. 2021; 13(16):3101. https://doi.org/10.3390/rs13163101
Chicago/Turabian StyleBouras, El houssaine, Lionel Jarlan, Salah Er-Raki, Riad Balaghi, Abdelhakim Amazirh, Bastien Richard, and Saïd Khabba. 2021. "Cereal Yield Forecasting with Satellite Drought-Based Indices, Weather Data and Regional Climate Indices Using Machine Learning in Morocco" Remote Sensing 13, no. 16: 3101. https://doi.org/10.3390/rs13163101
APA StyleBouras, E. h., Jarlan, L., Er-Raki, S., Balaghi, R., Amazirh, A., Richard, B., & Khabba, S. (2021). Cereal Yield Forecasting with Satellite Drought-Based Indices, Weather Data and Regional Climate Indices Using Machine Learning in Morocco. Remote Sensing, 13(16), 3101. https://doi.org/10.3390/rs13163101