Machine Learning to Estimate Surface Roughness from Satellite Images
Abstract
:1. Introduction
2. Site Characteristics
3. Material and Method
3.1. Satellite Data
3.2. In-Situ Measurement
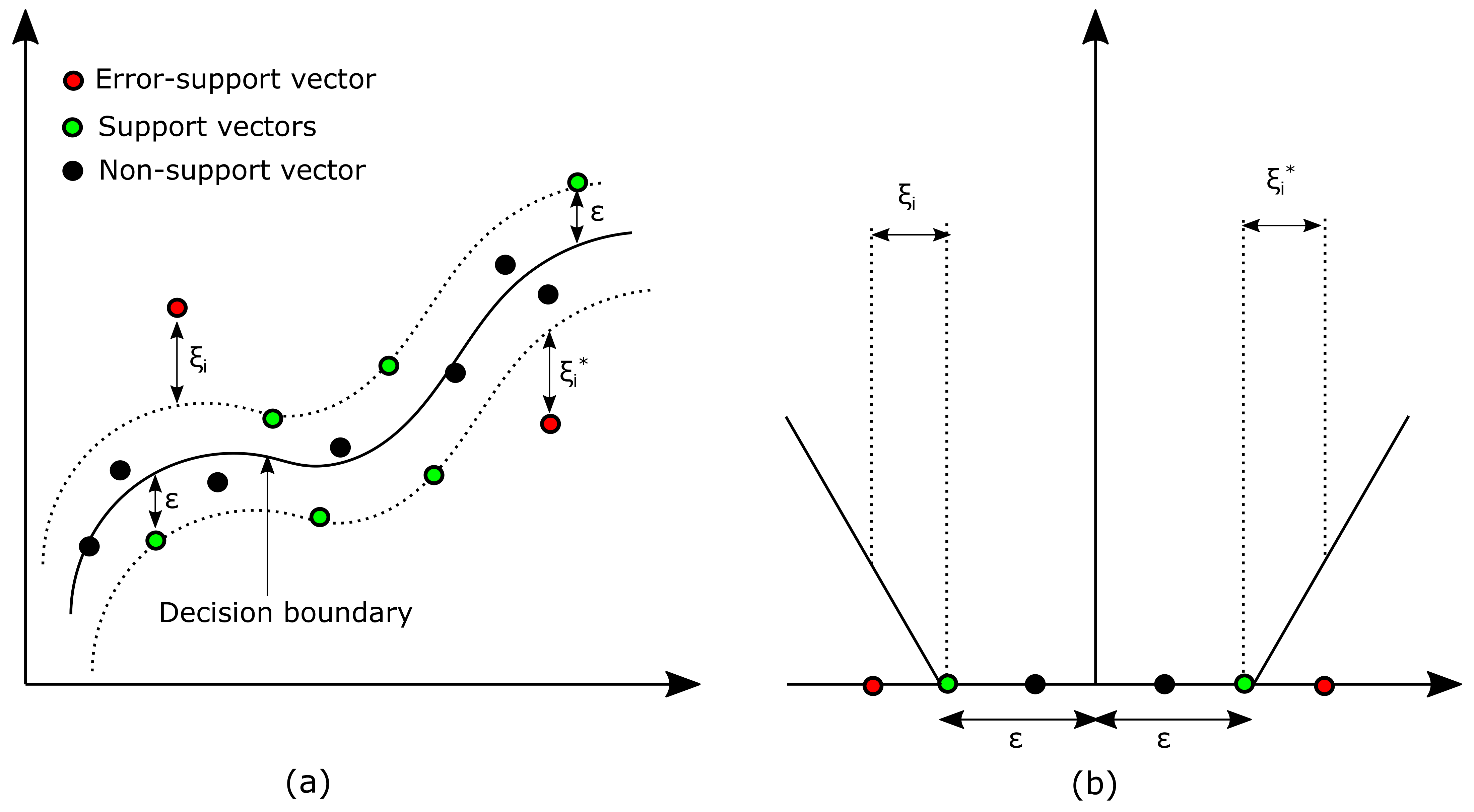
3.3. Support Vector Regression
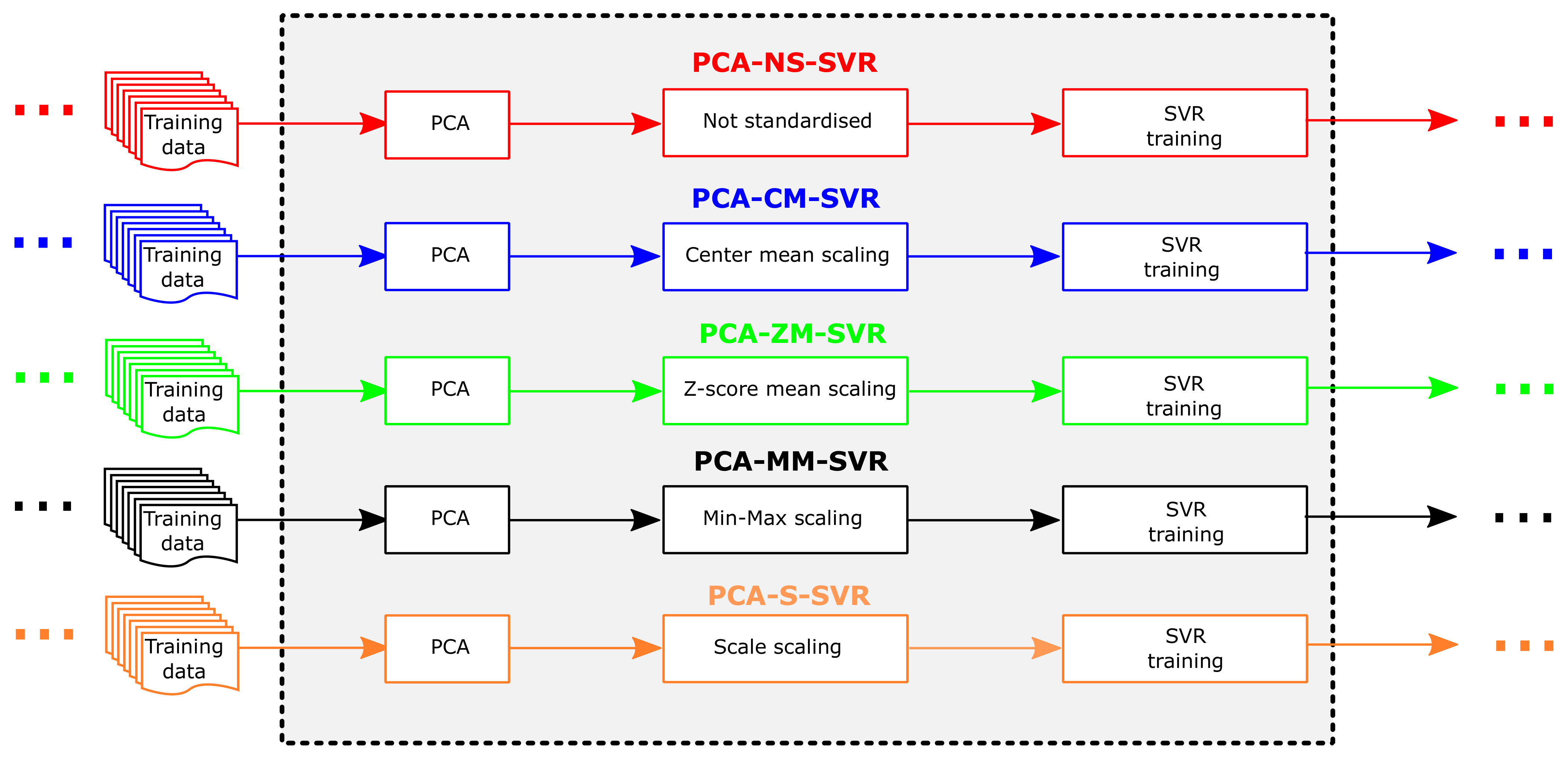
3.3.1. Model Setup
3.3.2. Hyperparameter Optimisation
4. Result
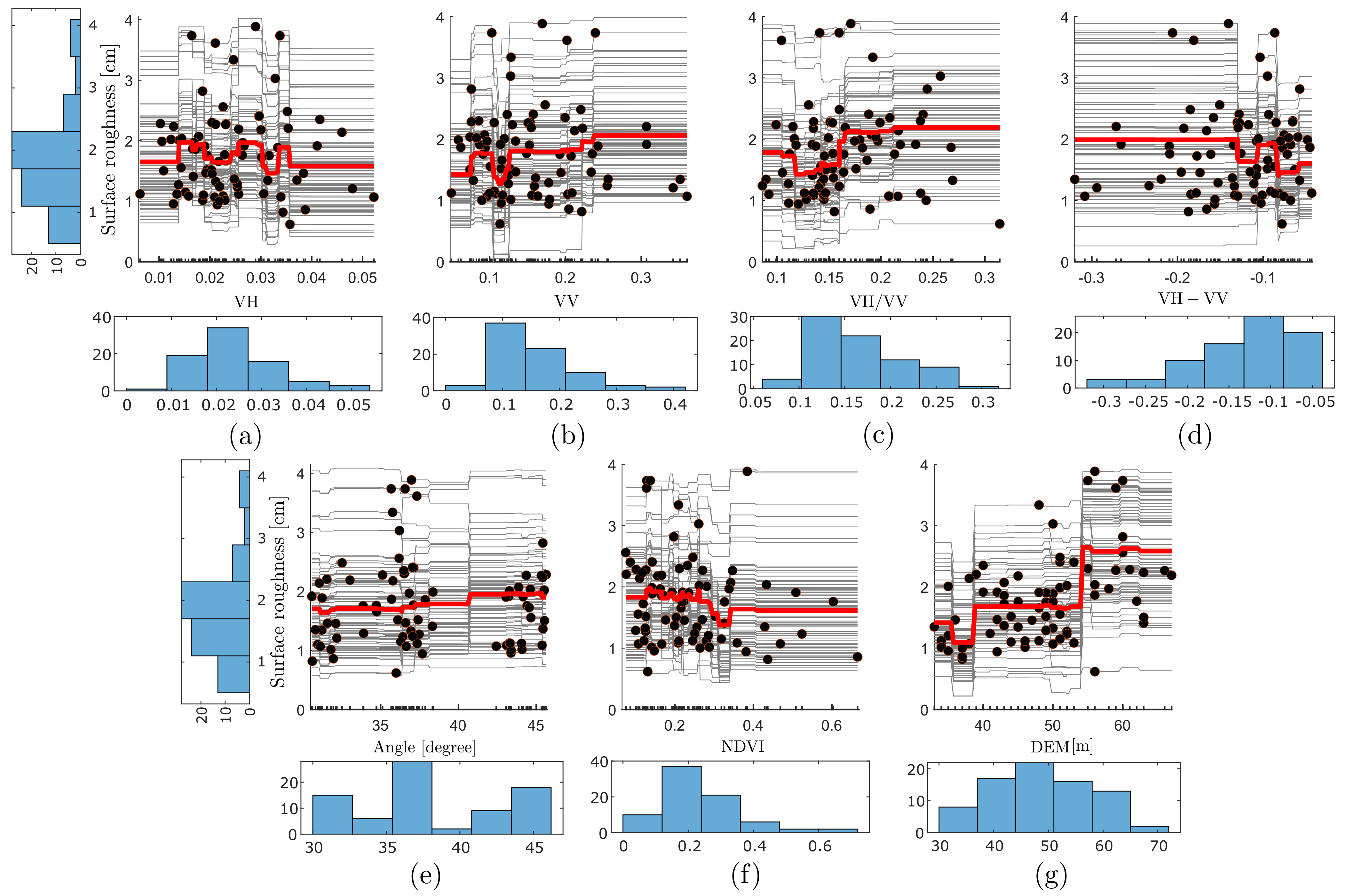
4.1. Feature Importance
4.2. Feature Sensitivity
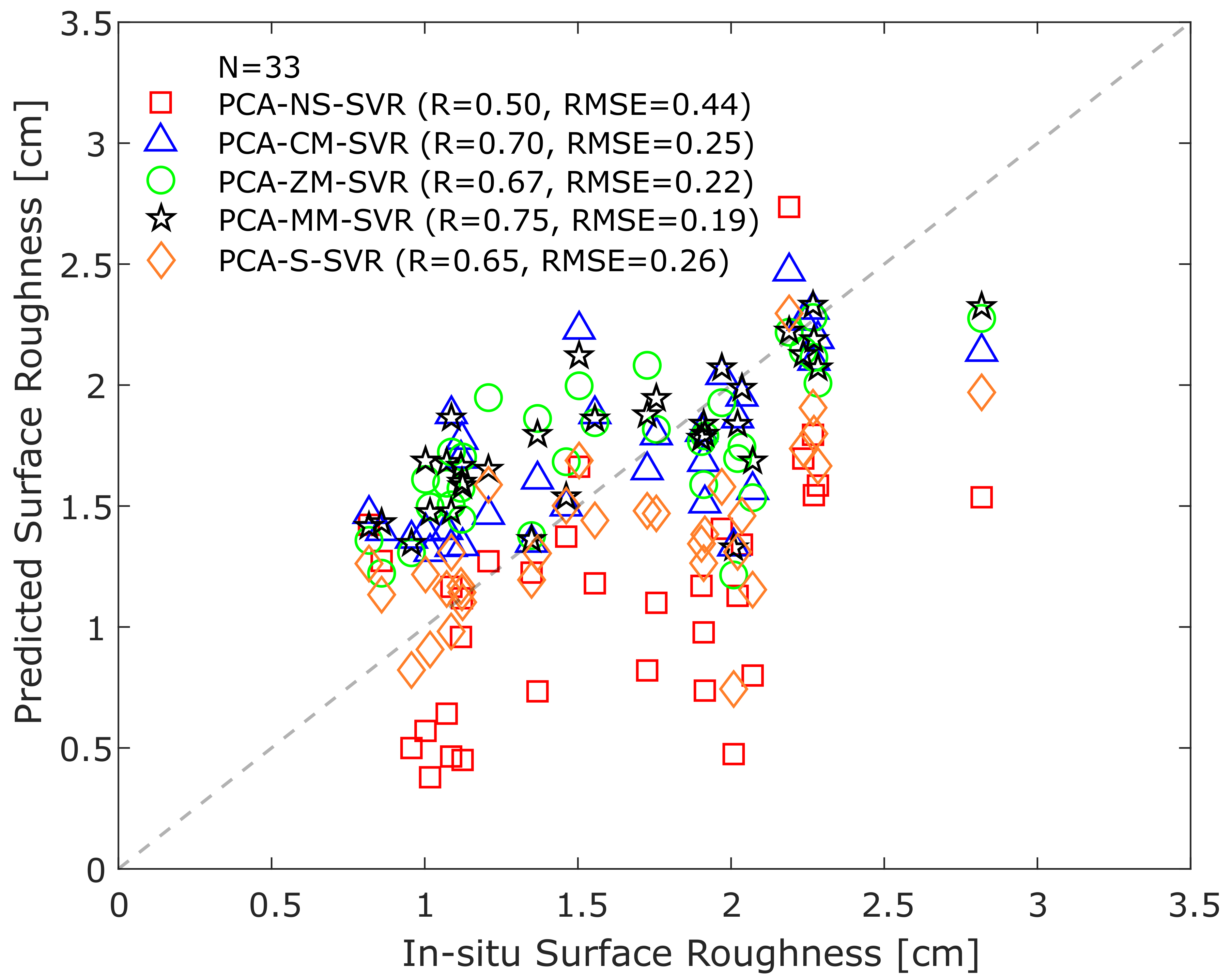
4.3. Surface Roughness
5. Discussion
5.1. Comparison with the Benchmark Machine Learning Models
5.2. Comparison with Backscatter Models
5.3. Surface Roughness of the Kosi Fan
5.4. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Site ID | Longitude | Latitude | Date dd-mm-yyyy) | Mission Identifier | Surface Roughness (cm) | Lobe | Direction | Soil Temperature (°C) | Landuse | Training/Testing |
|---|---|---|---|---|---|---|---|---|---|---|
| 01 | 86.63923 | 26.13257 | 11 December 2019 | S1A | 2.4029 | I | NE | 21 | Uncultivated bare land (Ploughed) | Training |
| 02 | 86.64361 | 26.10979 | 11 December 2019 | S1A | 1.2736 | I | NE | 22 | Uncultivated bare land (Harrowed) | Training |
| 03 | 86.62364 | 26.09691 | 11 December 2019 | S1A | 2.4072 | I | SW | 20 | Uncultivated bare land (Ploughed) | Training |
| 04 | 86.62604 | 26.0954 | 11 December 2019 | S1A | 1.5181 | I | NE | 16 | Uncultivated bare land (Harrowed) | Training |
| 05 | 86.62061 | 26.0632 | 11 December 2019 | S1A | 3.0288 | I | NE | 16 | Uncultivated bare land (Ploughed) | Training |
| 06 | 86.566 | 26.0243 | 11 December 2019 | S1A | 1.5175 | I | NE | 18 | Uncultivated bare land (Harrowed) | Training |
| 07 | 86.57533 | 25.97547 | 11 December 2019 | S1A | 1.1172 | I | NE | 19 | Uncultivated bare land (Harrowed) | Training |
| 08 | 86.64431 | 25.99772 | 11 December 2019 | S1A | 1.9886 | I | NE | 23 | Harrowed + wheat sowed | Training |
| 09 | 86.64072 | 26.03379 | 11 December 2019 | S1A | 1.3282 | I | SW | 24 | Uncultivated bare land (Harrowed) | Training |
| 10 | 86.62675 | 26.15357 | 11 December 2019 | S1A | 3.7350 | I | SW | 17 | Furrow field | Training |
| 11 | 86.66584 | 26.19629 | 11 December 2019 | S1A | 3.8858 | I | NE | 19 | Furrow field | Training |
| 12 | 86.6998 | 26.21087 | 11 December 2019 | S1A | 1.9685 | I | NE | 20 | Uncultivated bare land (Harrowed) | Training |
| 13 | 86.73994 | 26.22444 | 11 December 2019 | S1A | 1.7677 | I | NE | 20 | Harrowed + wheat sowed | Training |
| 14 | 86.75186 | 26.23693 | 11 December 2019 | S1A | 1.8670 | I | NE | 21 | Uncultivated bare land (Harrowed) | Training |
| 15 | 86.78488 | 26.24503 | 11 December 2019 | S1A | 2.2774 | I | NE | 19 | Uncultivated bare land (Ploughed) | Training |
| 16 | 86.79723 | 26.26185 | 11 December 2019 | S1A | 2.5599 | I | SW | 20 | Uncultivated bare land (Ploughed) | Training |
| 17 | 86.80273 | 26.2389 | 11 December 2019 | S1A | 1.4094 | I | NE | 21 | Uncultivated bare land (Harrowed) | Training |
| 18 | 86.79795 | 26.20753 | 11 December 2019 | S1A | 3.6128 | I | SW | 20 | Furrow field | Training |
| 19 | 86.79031 | 26.18241 | 11 December 2019 | S1A | 3.7361 | I | NE | 20 | Furrow field | Training |
| 20 | 86.76803 | 26.1514 | 11 December 2019 | S1A | 2.3002 | I | NE | 20 | Uncultivated bare land (Ploughed) | Training |
| 21 | 86.65507 | 26.11443 | 11 December 2019 | S1A | 1.2325 | I | NE | 18 | Harrowed + wheat sowed | Training |
| 22 | 86.70612 | 26.06255 | 11 December 2019 | S1A | 1.1504 | I | NE | 21 | Harrowed + wheat sowed | Training |
| 23 | 86.73248 | 26.04625 | 11 December 2019 | S1A | 0.6181 | I | NE | 21 | Direct stubble seeding | Training |
| 24 | 86.71229 | 26.03606 | 11 December 2019 | S1A | 1.0680 | I | NE | 20 | Uncultivated bare land (Harrowed) | Training |
| 25 | 86.75741 | 26.02952 | 11 December 2019 | S1A | 3.3369 | I | NE | 20 | Uncultivated bare land (Ploughed) | Training |
| 26 | 86.75144 | 25.91161 | 11 December 2019 | S1A | 1.6568 | I | NE | 20 | Uncultivated bare land (Harrowed) | Training |
| 27 | 86.66203 | 25.86703 | 15 December 2019 | S1A | 1.0155 | I | SE | 18 | Uncultivated bare land (Harrowed) | Training |
| 28 | 86.68053 | 25.82926 | 15 December 2019 | S1A | 1.1016 | I | SE | 18 | Uncultivated bare land (Harrowed) | Training |
| 29 | 86.68639 | 25.78836 | 15 December 2019 | S1A | 1.9144 | I | NW | 18 | Uncultivated bare land (Harrowed) | Training |
| 30 | 86.6876 | 25.74611 | 15 December 2019 | S1A | 1.3448 | II | NW | 19 | Harrowed + maize sowed | Training |
| 31 | 86.71125 | 25.6878 | 15 December 2019 | S1A | 1.0688 | II | NW | 18 | Uncultivated bare land (Harrowed) | Training |
| 32 | 86.69384 | 25.70237 | 15 December 2019 | S1A | 2.2058 | I | NW | 21 | Ploughed + wheat sowed | Training |
| 33 | 86.65567 | 25.72331 | 15 December 2019 | S1A | 2.1397 | I | NW | 20 | Uncultivated bare land (Ploughed) | Training |
| 34 | 86.80625 | 25.91648 | 15 December 2019 | S1A | 1.4551 | II | NW | 18 | Harrowed + wheat sowed | Training |
| 35 | 86.93388 | 25.89581 | 15 December 2019 | S1A | 1.8875 | II | NW | 17 | Harrowed + maize sowed | Training |
| 36 | 87.00225 | 25.90533 | 15 December 2019 | S1A | 2.4824 | II | NW | 20 | Uncultivated bare land (Ploughed) | Training |
| 37 | 87.06107 | 25.90827 | 15 December 2019 | S1A | 1.2896 | II | SE | 20 | Uncultivated bare land (Harrowed) | Training |
| 38 | 87.09836 | 25.92137 | 15 December 2019 | S1A | 1.7548 | II | SE | 22 | Uncultivated bare land (Harrowed) | Training |
| 39 | 87.21534 | 25.88781 | 15 December 2019 | S1A | 1.7604 | II | SE | 22 | Uncultivated bare land (Harrowed) | Training |
| 40 | 86.6099 | 25.72783 | 17 December 2019 | S1B | 2.3510 | I | NW | 20 | Uncultivated bare land (Ploughed) | Training |
| 41 | 86.57812 | 25.7314 | 17 December 2019 | S1B | 0.9426 | I | NW | 21 | Direct stubble seeding | Training |
| 42 | 86.54615 | 25.77154 | 17 December 2019 | S1B | 1.2406 | I | NW | 20 | Uncultivated bare land (Harrowed) | Training |
| 43 | 86.52457 | 25.80515 | 17 December 2019 | S1B | 1.4675 | I | NW | 20 | Uncultivated bare land (Harrowed) | Training |
| 44 | 86.53774 | 25.85775 | 17 December 2019 | S1B | 2.1787 | I | SE | 19 | Uncultivated bare land (Ploughed) | Training |
| 45 | 86.56369 | 25.8713 | 17 December 2019 | S1B | 1.8584 | I | NW | 20 | Uncultivated bare land (Harrowed) | Training |
| 46 | 87.46254 | 25.72741 | 17 December 2019 | S1B | 0.8180 | III | NE | 17 | Direct stubble seeding | Testing |
| 47 | 87.42014 | 25.6838 | 17 December 2019 | S1B | 0.8593 | III | NE | 17 | Direct stubble seeding | Testing |
| 48 | 87.39914 | 25.64069 | 17 December 2019 | S1B | 1.2080 | III | SW | 18 | Uncultivated bare land (Harrowed) | Testing |
| 49 | 87.39871 | 25.60628 | 17 December 2019 | S1B | 1.4618 | III | NE | 21 | Uncultivated bare land (Harrowed) | Testing |
| 50 | 87.42513 | 25.61369 | 17 December 2019 | S1B | 1.3488 | III | NE | 21 | Uncultivated bare land (Harrowed) | Testing |
| 51 | 87.034 | 26.29657 | 17 December 2019 | S1B | 2.1895 | II | NE | 15 | Uncultivated bare land (Ploughed) | Testing |
| 52 | 87.475 | 25.60035 | 18 December 2019 | S1A | 1.0862 | III | SW | 20 | Uncultivated bare land (Harrowed) | Testing |
| 53 | 87.48171 | 25.59672 | 18 December 2019 | S1A | 1.1235 | III | SW | 22 | Uncultivated bare land (Harrowed) | Testing |
| 54 | 87.55177 | 25.60905 | 18 December 2019 | S1A | 1.0174 | III | SW | 20 | Uncultivated bare land (Harrowed) | Testing |
| 55 | 87.54285 | 25.62759 | 18 December 2019 | S1A | 0.9566 | III | SW | 21 | Direct stubble seeding | Testing |
| 56 | 87.53111 | 25.65317 | 18 December 2019 | S1A | 1.0716 | III | NE | 22 | Uncultivated bare land (Harrowed) | Testing |
| 57 | 87.52139 | 25.67509 | 18 December 2019 | S1A | 1.0026 | III | SW | 21 | Uncultivated bare land (Harrowed) | Testing |
| 58 | 87.51138 | 25.70004 | 18 December 2019 | S1A | 2.0085 | III | SW | 21 | Uncultivated bare land (Ploughed) | Testing |
| 59 | 87.51614 | 25.81319 | 18 December 2019 | S1A | 2.0704 | III | NE | 17 | Uncultivated bare land (Ploughed) | Testing |
| 60 | 87.52789 | 25.82046 | 18 December 2019 | S1A | 1.9143 | III | SW | 17 | Uncultivated bare land (Harrowed) | Testing |
| 61 | 87.54014 | 25.91021 | 18 December 2019 | S1A | 1.9034 | III | NE | 18 | Uncultivated bare land (Harrowed) | Testing |
| 62 | 87.51805 | 25.99278 | 18 December 2019 | S1A | 1.9106 | III | SW | 18 | Uncultivated bare land (Harrowed) | Testing |
| 63 | 87.50936 | 26.00962 | 18 December 2019 | S1A | 1.1215 | III | SW | 18 | Uncultivated bare land (Harrowed) | Testing |
| 64 | 87.46062 | 26.12101 | 18 December 2019 | S1A | 1.5554 | III | SW | 19 | Uncultivated bare land (Harrowed) | Testing |
| 65 | 87.29737 | 26.22082 | 18 December 2019 | S1A | 1.9698 | III | SW | 17 | Uncultivated bare land (Harrowed) | Testing |
| 66 | 87.27813 | 26.24172 | 18 December 2019 | S1A | 2.2836 | III | SW | 18 | Uncultivated bare land (Ploughed) | Testing |
| 67 | 87.23487 | 26.27511 | 18 December 2019 | S1A | 2.2357 | III | SW | 19 | Uncultivated bare land (Ploughed) | Testing |
| 68 | 87.2269 | 26.24339 | 18 December 2019 | S1A | 1.5040 | III | SW | 20 | Uncultivated bare land (Harrowed) | Testing |
| 69 | 87.2321 | 26.20331 | 18 December 2019 | S1A | 2.2703 | III | SW | 18 | Uncultivated bare land (Ploughed) | Testing |
| 70 | 87.23437 | 26.17834 | 18 December 2019 | S1A | 2.0355 | III | NE | 19 | Ploughed + wheat sowed | Testing |
| 71 | 87.23401 | 26.13083 | 18 December 2019 | S1A | 1.0870 | III | NE | 18 | Harrowed + wheat sowed | Testing |
| 72 | 87.25929 | 26.01328 | 18 December 2019 | S1A | 1.7560 | II | SW | 18 | Uncultivated bare land (Harrowed) | Testing |
| 73 | 87.30746 | 25.93218 | 18 December 2019 | S1A | 1.1182 | III | NE | 17 | Harrowed + maize sowed | Testing |
| 74 | 87.20622 | 26.326 | 18 December 2019 | S1A | 2.2675 | III | SW | 15 | Uncultivated bare land (Ploughed) | Testing |
| 75 | 87.00787 | 26.17258 | 20 December 2019 | S1A | 2.8180 | II | NE | 16 | Uncultivated bare land (Ploughed) | Testing |
| 76 | 86.99307 | 26.05495 | 20 December 2019 | S1A | 2.0213 | II | NE | 17 | Uncultivated bare land (Ploughed) | Testing |
| 77 | 86.97813 | 25.77722 | 20 December 2019 | S1A | 1.7262 | II | SW | 18 | Uncultivated bare land (Harrowed) | Testing |
| 78 | 86.96597 | 25.71033 | 20 December 2019 | S1A | 1.3681 | II | NE | 18 | Uncultivated bare land (Harrowed) | Testing |
Appendix B
Appendix C
References
- McColl, K.A.; Alemohammad, S.H.; Akbar, R.; Konings, A.G.; Yueh, S.; Entekhabi, D. The global distribution and dynamics of surface soil moisture. Nat. Geosci. 2017, 10, 100–104. [Google Scholar] [CrossRef]
- Helming, K.; Römkens, M.; Prasad, S. Surface roughness related processes of runoff and soil loss: A flume study. Soil Sci. Soc. Am. J. 1998, 62, 243–250. [Google Scholar] [CrossRef]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.C.; Bizzarri, B.; Wigneron, J.P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Baghdadi, N.; El Hajj, M.; Choker, M.; Zribi, M.; Bazzi, H.; Vaudour, E.; Gilliot, J.M.; Ebengo, D.M. Potential of Sentinel-1 images for estimating the soil roughness over bare agricultural soils. Water 2018, 10, 131. [Google Scholar] [CrossRef] [Green Version]
- Alexakis, D.D.; Mexis, F.D.K.; Vozinaki, A.E.K.; Daliakopoulos, I.N.; Tsanis, I.K. Soil moisture content estimation based on Sentinel-1 and auxiliary earth observation products. A hydrological approach. Sensors 2017, 17, 1455. [Google Scholar] [CrossRef] [Green Version]
- Verhoest, N.E.; Lievens, H.; Wagner, W.; Álvarez-Mozos, J.; Moran, M.S.; Mattia, F. On the soil roughness parameterization problem in soil moisture retrieval of bare surfaces from synthetic aperture radar. Sensors 2008, 8, 4213–4248. [Google Scholar] [CrossRef] [Green Version]
- Romkens, M.; Wang, J. Effect of tillage on surface roughness. Trans. ASAE 1986, 29, 429–0433. [Google Scholar] [CrossRef]
- Govers, G.; Takken, I.; Helming, K. Soil roughness and overland flow. Agronomie 2000, 20, 131–146. [Google Scholar] [CrossRef]
- Snapir, B.; Hobbs, S.; Waine, T. Roughness measurements over an agricultural soil surface with Structure from Motion. ISPRS J. Photogramm. Remote Sens. 2014, 96, 210–223. [Google Scholar] [CrossRef]
- Turner, R.; Panciera, R.; Tanase, M.A.; Lowell, K.; Hacker, J.M.; Walker, J.P. Estimation of soil surface roughness of agricultural soils using airborne LiDAR. Remote Sens. Environ. 2014, 140, 107–117. [Google Scholar] [CrossRef]
- Hamze, M.; Baghdadi, N.; El Hajj, M.M.; Zribi, M.; Bazzi, H.; Cheviron, B.; Faour, G. Integration of L-Band Derived Soil Roughness into a Bare Soil Moisture Retrieval Approach from C-Band SAR Data. Remote Sens. 2021, 13, 2102. [Google Scholar] [CrossRef]
- Thomsen, L.; Baartman, J.; Barneveld, R.; Starkloff, T.; Stolte, J. Soil surface roughness: Comparing old and new measuring methods and application in a soil erosion model. Soil 2015, 1, 399–410. [Google Scholar] [CrossRef] [Green Version]
- Saleh, A. Soil roughness measurement: Chain method. J. Soil Water Conserv. 1993, 48, 527–529. [Google Scholar]
- Hajnsek, I.; Pottier, E.; Cloude, S.R. Inversion of surface parameters from polarimetric SAR. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 727–744. [Google Scholar] [CrossRef]
- Merzouki, A.; McNairn, H.; Pacheco, A. Mapping soil moisture using RADARSAT-2 data and local autocorrelation statistics. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2011, 4, 128–137. [Google Scholar] [CrossRef]
- Le Morvan, A.; Zribi, M.; Baghdadi, N.; Chanzy, A. Soil moisture profile effect on radar signal measurement. Sensors 2008, 8, 256–270. [Google Scholar] [CrossRef] [Green Version]
- Zheng, X.; Li, L.; Chen, S.; Jiang, T.; Li, X.; Zhao, K. Temporal evolution characteristics and prediction methods of spatial correlation function shape of rough soil surfaces. Soil Tillage Res. 2019, 195, 104417. [Google Scholar] [CrossRef]
- Alijani, Z.; Lindsay, J.; Chabot, M.; Rowlandson, T.; Berg, A. Sensitivity of C-Band SAR Polarimetric Variables to the Directionality of Surface Roughness Parameters. Remote Sens. 2021, 13, 2210. [Google Scholar] [CrossRef]
- Gharechelou, S.; Tateishi, R.; A Johnson, B. A Simple Method for the Parameterization of Surface Roughness from Microwave Remote Sensing. Remote Sens. 2018, 10, 1711. [Google Scholar] [CrossRef] [Green Version]
- Jester, W.; Klik, A. Soil surface roughness measurement—Methods, applicability, and surface representation. Catena 2005, 64, 174–192. [Google Scholar] [CrossRef]
- Peng, J.; Albergel, C.; Balenzano, A.; Brocca, L.; Cartus, O.; Cosh, M.H.; Crow, W.T.; Dabrowska-Zielinska, K.; Dadson, S.; Davidson, M.W.; et al. A roadmap for high-resolution satellite soil moisture applications—Confronting product characteristics with user requirements. Remote Sens. Environ. 2020, 252, 112162. [Google Scholar] [CrossRef]
- Le Page, M.; Jarlan, L.; El Hajj, M.M.; Zribi, M.; Baghdadi, N.; Boone, A. Potential for the detection of irrigation events on maize plots using sentinel-1 soil moisture products. Remote Sens. 2020, 12, 1621. [Google Scholar] [CrossRef]
- Fersch, B.; Jagdhuber, T.; Schrön, M.; Völksch, I.; Jäger, M. Synergies for soil moisture retrieval across scales from airborne polarimetric SAR, cosmic ray neutron roving, and an in situ sensor network. Water Resour. Res. 2018, 54, 9364–9383. [Google Scholar] [CrossRef]
- Marzahn, P.; Rieke-Zapp, D.; Ludwig, R. Assessment of soil surface roughness statistics for microwave remote sensing applications using a simple photogrammetric acquisition system. ISPRS J. Photogramm. Remote Sens. 2012, 72, 80–89. [Google Scholar] [CrossRef]
- Panciera, R.; Walker, J.P.; Merlin, O. Improved understanding of soil surface roughness parameterization for L-band passive microwave soil moisture retrieval. IEEE Geosci. Remote Sens. Lett. 2009, 6, 625–629. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 1992, 30, 370–381. [Google Scholar] [CrossRef]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An inversion algorithm for retrieving soil moisture and surface roughness from polarimetric radar observation. In Proceedings of the IGARSS’94-1994 IEEE International Geoscience and Remote Sensing Symposium, Pasadena, CA, USA, 8–12 August 1994; Volume 3, pp. 1582–1584. [Google Scholar]
- Dubois, P.C.; Van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens. 1995, 33, 915–926. [Google Scholar] [CrossRef] [Green Version]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. Semi-empirical model of the ensemble-averaged differential Mueller matrix for microwave backscattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1348–1355. [Google Scholar] [CrossRef] [Green Version]
- Oh, Y. Quantitative retrieval of soil moisture content and surface roughness from multipolarized radar observations of bare soil surfaces. IEEE Trans. Geosci. Remote Sens. 2004, 42, 596–601. [Google Scholar] [CrossRef]
- Attema, E.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci. 1978, 13, 357–364. [Google Scholar] [CrossRef]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens. 1992, 30, 356–369. [Google Scholar] [CrossRef]
- Fung, A.K. Microwave Scattering and Emission Models and Their Applications; Artech House: Norwood, MA, USA, 1994. [Google Scholar]
- Shi, J.; Wang, J.; Hsu, A.; O’Neili, P.; Engman, E.T. Estimation of soil moisture and surface roughness parameters using L-band SAR measurements. In Proceedings of the 1995 International Geoscience and Remote Sensing Symposium, IGARSS’95. Quantitative Remote Sensing for Science and Applications, Firenze, Italy, 10–14 July 1995; Volume 1, pp. 507–509. [Google Scholar]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’Neill, P.E.; Engman, E.T. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1254–1266. [Google Scholar]
- Baghdadi, N.; King, C.; Bourguignon, A.; Remond, A. Potential of ERS and RADARSAT data for surface roughness monitoring over bare agricultural fields: Application to catchments in Northern France. Int. J. Remote Sens. 2002, 23, 3427–3442. [Google Scholar] [CrossRef]
- Zribi, M.; Baghdadi, N.; Guérin, C. Analysis of surface roughness heterogeneity and scattering behavior for radar measurements. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2438–2444. [Google Scholar] [CrossRef]
- Rahman, M.; Moran, M.; Thoma, D.; Bryant, R.; Collins, C.H.; Jackson, T.; Orr, B.; Tischler, M. Mapping surface roughness and soil moisture using multi-angle radar imagery without ancillary data. Remote Sens. Environ. 2008, 112, 391–402. [Google Scholar] [CrossRef]
- Baghdadi, N.; Cresson, R.; Hajj, M.E.; Ludwig, R.; Jeunesse, I.L. Estimation of soil parameters over bare agriculture areas from C-band polarimetric SAR data using neural networks. Hydrol. Earth Syst. Sci. 2012, 16, 1607–1621. [Google Scholar] [CrossRef] [Green Version]
- Sawada, Y.; Koike, T.; Aida, K.; Toride, K.; Walker, J.P. Fusing microwave and optical satellite observations to simultaneously retrieve surface soil moisture, vegetation water content, and surface soil roughness. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6195–6206. [Google Scholar] [CrossRef]
- Mirmazloumi, S.M.; Sahebi, M.R.; Amani, M. New empirical backscattering models for estimating bare soil surface parameters. Int. J. Remote Sens. 2021, 42, 1928–1947. [Google Scholar] [CrossRef]
- Zribi, M.; Dechambre, M. A new empirical model to retrieve soil moisture and roughness from C-band radar data. Remote Sens. Environ. 2003, 84, 42–52. [Google Scholar] [CrossRef]
- Srivastava, H.; Patel, P.; Navalgund, R.; Sharma, Y. Retrieval of surface roughness using multi-polarized Envisat-1 ASAR data. Geocarto Int. 2008, 23, 67–77. [Google Scholar] [CrossRef]
- Ullmann, T.; Stauch, G. Surface Roughness Estimation in the Orog Nuur Basin (Southern Mongolia) Using Sentinel-1 SAR Time Series and Ground-Based Photogrammetry. Remote Sens. 2020, 12, 3200. [Google Scholar] [CrossRef]
- Azizi, A.; Abbaspour-Gilandeh, Y.; Mesri-Gundoshmian, T.; Farooque, A.A.; Afzaal, H. Estimation of soil surface roughness using stereo vision approach. Sensors 2021, 21, 4386. [Google Scholar] [CrossRef]
- Hsieh, C.Y.; Fung, A.K.; Nesti, G.; Sieber, A.J.; Coppo, P. A further study of the IEM surface scattering model. IEEE Trans. Geosci. Remote Sens. 1997, 35, 901–909. [Google Scholar] [CrossRef]
- Mancini, M.; Hoeben, R.; Troch, P.A. Multifrequency radar observations of bare surface soil moisture content: A laboratory experiment. Water Resour. Res. 1999, 35, 1827–1838. [Google Scholar] [CrossRef]
- Wells, N.A.; Dorr, J.A., Jr. Shifting of the Kosi river, northern India. Geology 1987, 15, 204–207. [Google Scholar] [CrossRef]
- Sinha, R. The great avulsion of Kosi on 18 August 2008. Curr. Sci. 2009, 97, 429–433. [Google Scholar]
- Sinha, R. The Kosi Megafan: The best-known Himalayan megafan. In Landscapes and Landforms of India; Springer: Dordrecht, The Netherlands, 2014; pp. 151–156. [Google Scholar]
- Gaurav, K.; Métivier, F.; Devauchelle, O.; Sinha, R.; Chauvet, H.; Houssais, M.; Bouquerel, H. Morphology of the Kosi megafan channels. Earth Surface Dyn. 2015, 3, 321–331. [Google Scholar] [CrossRef] [Green Version]
- Gaurav, K.; Tandon, S.; Devauchelle, O.; Sinha, R.; Métivier, F. A single width—Discharge regime relationship for individual threads of braided and meandering rivers from the Himalayan Foreland. Geomorphology 2017, 295, 126–133. [Google Scholar] [CrossRef] [Green Version]
- NRSC. District and Category Wise Distribution of Land Use and Land Cover in Bihar (2015–2016). ISRO; 2017. Available online: https://bhuvan.nrsc.gov.in/home/index.php (accessed on 25 March 2021).
- Singh, A.; Meena, G.K.; Kumar, S.; Gaurav, K. Analysis of the effect of incidence angle and moisture content on the penetration depth of L- and S-band SAR signals into the ground surface. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 4, 197–202. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Meena, G.K.; Kumar, S.; Gaurav, K. Evaluation of the Penetration Depth of L-and S-Band (NISAR mission) Microwave SAR Signals into Ground. In Proceedings of the 2019 URSI Asia-Pacific Radio Science Conference (AP-RASC), New Delhi, India, 9–15 March 2019; p. 1. [Google Scholar] [CrossRef]
- Singh, A.; Gaurav, K.; Meena, G.K.; Kumar, S. Estimation of soil moisture applying modified dubois model to Sentinel-1; a regional study from central India. Remote Sens. 2020, 12, 2266. [Google Scholar] [CrossRef]
- DeVries, B.; Huang, C.; Armston, J.; Huang, W.; Jones, J.W.; Lang, M.W. Rapid and robust monitoring of flood events using Sentinel-1 and Landsat data on the Google Earth Engine. Remote Sens. Environ. 2020, 240, 111664. [Google Scholar] [CrossRef]
- Martins, V.S.; Barbosa, C.C.F.; De Carvalho, L.A.S.; Jorge, D.S.F.; Lobo, F.d.L.; Novo, E.M.L.d.M. Assessment of atmospheric correction methods for Sentinel-2 MSI images applied to Amazon floodplain lakes. Remote Sens. 2017, 9, 322. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Roy, D.P. A global analysis of Sentinel-2A, Sentinel-2B and Landsat-8 data revisit intervals and implications for terrestrial monitoring. Remote Sens. 2017, 9, 902. [Google Scholar] [CrossRef] [Green Version]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective, 2nd ed.; Prentice-Hall Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Werner, M. Shuttle radar topography mission (SRTM) mission overview. Frequenz 2001, 55, 75–79. [Google Scholar] [CrossRef]
- Farr, T.G.; Kobrick, M. Shuttle Radar Topography Mission produces a wealth of data. Eos Trans. Am. Geophys. Union 2000, 81, 583–585. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The shuttle radar topography mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef] [Green Version]
- Ryan, J.; Hubbard, A.; Irvine-Fynn, T.D.; Doyle, S.H.; Cook, J.; Stibal, M.; Box, J. How robust are in situ observations for validating satellite-derived albedo over the dark zone of the Greenland Ice Sheet? Geophys. Res. Lett. 2017, 44, 6218–6225. [Google Scholar] [CrossRef] [Green Version]
- Thakur, K.K.; Vanderstichel, R.; Barrell, J.; Stryhn, H.; Patanasatienkul, T.; Revie, C.W. Comparison of remotely-sensed sea surface temperature and salinity products with in situ measurements from British Columbia, Canada. Front. Mar. Sci. 2018, 5, 121. [Google Scholar] [CrossRef] [Green Version]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [Green Version]
- Murdoch, W.J.; Singh, C.; Kumbier, K.; Abbasi-Asl, R.; Yu, B. Definitions, methods, and applications in interpretable machine learning. Proc. Natl. Acad. Sci. USA 2019, 116, 22071–22080. [Google Scholar] [CrossRef] [Green Version]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Yu, P.S.; Chen, S.T.; Chang, I.F. Support vector regression for real-time flood stage forecasting. J. Hydrol. 2006, 328, 704–716. [Google Scholar] [CrossRef]
- Xiao, X.; Zhang, T.; Zhong, X.; Shao, W.; Li, X. Support vector regression snow-depth retrieval algorithm using passive microwave remote sensing data. Remote Sens. Environ. 2018, 210, 48–64. [Google Scholar] [CrossRef]
- Kuter, S. Completing the machine learning saga in fractional snow cover estimation from MODIS Terra reflectance data: Random forests versus support vector regression. Remote Sens. Environ. 2021, 255, 112294. [Google Scholar] [CrossRef]
- Ge, J.; Meng, B.; Liang, T.; Feng, Q.; Gao, J.; Yang, S.; Huang, X.; Xie, H. Modeling alpine grassland cover based on MODIS data and support vector machine regression in the headwater region of the Huanghe River, China. Remote Sens. Environ. 2018, 218, 162–173. [Google Scholar] [CrossRef]
- Xie, X.; Liu, W.T.; Tang, B. Spacebased estimation of moisture transport in marine atmosphere using support vector regression. Remote Sens. Environ. 2008, 112, 1846–1855. [Google Scholar] [CrossRef]
- Okujeni, A.; van der Linden, S.; Tits, L.; Somers, B.; Hostert, P. Support vector regression and synthetically mixed training data for quantifying urban land cover. Remote Sens. Environ. 2013, 137, 184–197. [Google Scholar] [CrossRef]
- Su, H.; Wu, X.; Yan, X.H.; Kidwell, A. Estimation of subsurface temperature anomaly in the Indian Ocean during recent global surface warming hiatus from satellite measurements: A support vector machine approach. Remote Sens. Environ. 2015, 160, 63–71. [Google Scholar] [CrossRef]
- Malik, A.; Tikhamarine, Y.; Souag-Gamane, D.; Rai, P.; Sammen, S.S.; Kisi, O. Support vector regression integrated with novel meta-heuristic algorithms for meteorological drought prediction. Meteorol. Atmos. Phys. 2021, 133, 891–909. [Google Scholar] [CrossRef]
- Jebadurai, J.; Peter, J.D. SK-SVR: Sigmoid kernel support vector regression based in-scale single image super-resolution. Pattern Recognit. Lett. 2017, 94, 144–153. [Google Scholar] [CrossRef]
- Ni, K.S.; Nguyen, T.Q. Image superresolution using support vector regression. IEEE Trans. Image Process. 2007, 16, 1596–1610. [Google Scholar] [CrossRef]
- Peng, Y.; Albuquerque, P.H.M.; de Sá, J.M.C.; Padula, A.J.A.; Montenegro, M.R. The best of two worlds: Forecasting high frequency volatility for cryptocurrencies and traditional currencies with Support Vector Regression. Expert Syst. Appl. 2018, 97, 177–192. [Google Scholar] [CrossRef]
- Ghanem, K.; Aparicio-Navarro, F.J.; Kyriakopoulos, K.G.; Lambotharan, S.; Chambers, J.A. Support vector machine for network intrusion and cyber-attack detection. In Proceedings of the 2017 Sensor Signal Processing for Defence Conference (SSPD), London, UK, 6–7 December 2017; pp. 1–5. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. In Advances in Neural Information Processing Systems; Denver, CO, USA, December 1997; pp. 155–161. Available online: https://papers.nips.cc/paper/1996/file/d38901788c533e8286cb6400b40b386d-Paper.pdf (accessed on 13 July 2021).
- Ittner, A.; Schlosser, M. Discovery of Relevant New Features by Generating Non-Linear Decision Trees. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 108–113. [Google Scholar]
- Toloşi, L.; Lengauer, T. Classification with correlated features: Unreliability of feature ranking and solutions. Bioinformatics 2011, 27, 1986–1994. [Google Scholar] [CrossRef] [PubMed]
- Reed, R.; MarksII, R.J. Neural Smithing: Supervised Learning in Feedforward Artificial Neural Networks; MIT Press: Cambridge, MA, USA, 1999. [Google Scholar]
- Tuv, E.; Borisov, A.; Runger, G.; Torkkola, K. Feature selection with ensembles, artificial variables, and redundancy elimination. J. Mach. Learn. Res. 2009, 10, 1341–1366. [Google Scholar]
- Kohavi, R.; Sommerfield, D. Feature Subset Selection Using the Wrapper Method: Overfitting and Dynamic Search Space Topology. 1995, pp. 192–197. Available online: https://www.aaai.org/Papers/KDD/1995/KDD95-049.pdf (accessed on 13 July 2021).
- John, G.H.; Kohavi, R.; Pfleger, K. Irrelevant features and the subset selection problem. In Machine Learning Proceedings 1994; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1994; pp. 121–129. [Google Scholar]
- Kohavi, R.; John, G.H. Wrappers for feature subset selection. Artif. Intell. 1997, 97, 273–324. [Google Scholar] [CrossRef] [Green Version]
- Mao, K.Z. Orthogonal forward selection and backward elimination algorithms for feature subset selection. IEEE Trans. Syst. Man Cybern. Part B (Cybernetics) 2004, 34, 629–634. [Google Scholar] [CrossRef]
- Pham, B.T.; Nguyen-Thoi, T.; Ly, H.B.; Nguyen, M.D.; Al-Ansari, N.; Tran, V.Q.; Le, T.T. Extreme learning machine based prediction of soil shear strength: A sensitivity analysis using Monte Carlo simulations and feature backward elimination. Sustainability 2020, 12, 2339. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Goldstein, A.; Kapelner, A.; Bleich, J.; Pitkin, E. Peeking inside the black box: Visualizing statistical learning with plots of individual conditional expectation. J. Comput. Graph. Stat. 2015, 24, 44–65. [Google Scholar] [CrossRef]
- Ly, H.B.; Le, T.T.; Vu, H.L.T.; Tran, V.Q.; Le, L.M.; Pham, B.T. Computational hybrid machine learning based prediction of shear capacity for steel fiber reinforced concrete beams. Sustainability 2020, 12, 2709. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.; Kotiyal, V.; Sharma, S.; Nagar, J.; Lee, C.C. A machine learning approach to predict the average localization error with applications to wireless sensor networks. IEEE Access 2020, 8, 208253–208263. [Google Scholar] [CrossRef]
- Singh, A.; Nagar, J.; Sharma, S.; Kotiyal, V. A Gaussian process regression approach to predict the k-barrier coverage probability for intrusion detection in wireless sensor networks. Expert Syst. Appl. 2021, 172, 114603. [Google Scholar] [CrossRef]
- He, X.; Zhao, K.; Chu, X. AutoML: A Survey of the State-of-the-Art. Knowl. Based Syst. 2021, 212, 106622. [Google Scholar] [CrossRef]
- Neill, S.P.; Hashemi, M.R. Fundamentals of Ocean Renewable Energy: Generating Electricity from the Sea; Academic Press; Elsevier Ltd., 2018; Available online: https://www.elsevier.com/books/fundamentals-of-ocean-renewable-energy/neill/978-0-12-810448-4 (accessed on 13 July 2021).
- Botchkarev, A. Performance metrics (error measures) in machine learning regression, forecasting and prognostics: Properties and typology. arXiv 2018, arXiv:1809.03006. [Google Scholar]
- Yang, Y.; Ye, Z.; Su, Y.; Zhao, Q.; Li, X.; Ouyang, D. Deep learning for in vitro prediction of pharmaceutical formulations. Acta Pharm. Sin. B 2019, 9, 177–185. [Google Scholar] [CrossRef]
- Pham, H. A new criterion for model selection. Mathematics 2019, 7, 1215. [Google Scholar] [CrossRef] [Green Version]
- Vrieze, S.I. Model selection and psychological theory: A discussion of the differences between the Akaike information criterion (AIC) and the Bayesian information criterion (BIC). Psychol. Methods 2012, 17, 228. [Google Scholar] [CrossRef] [Green Version]
- Claeskens, G.; Hjort, N.L. Model Selection and Model Averaging, Cambridge Books; Cambridge University Press: Cambridge, UK, 2008; number 9780521852258, 1-312; Available online: https://ideas.repec.org/b/cup/cbooks/9780521852258.html (accessed on 13 July 2021).
- Rao, S.S.; Das, S.; Nagaraju, M.; Venugopal, M.; Rajankar, P.; Laghate, P.; Reddy, M.S.; Joshi, A.; Sharma, J. Modified Dubois model for estimating soil moisture with dual polarized SAR data. J. Indian Soc. Remote Sens. 2013, 41, 865–872. [Google Scholar]
- Choker, M.; Baghdadi, N.; Zribi, M.; El Hajj, M.; Paloscia, S.; Verhoest, N.E.; Lievens, H.; Mattia, F. Evaluation of the Oh, Dubois and IEM backscatter models using a large dataset of SAR data and experimental soil measurements. Water 2017, 9, 38. [Google Scholar] [CrossRef]
- Zhu, L.; Walker, J.P.; Ye, N.; Rüdiger, C. Roughness and vegetation change detection: A pre-processing for soil moisture retrieval from multi-temporal SAR imagery. Remote Sens. Environ. 2019, 225, 93–106. [Google Scholar] [CrossRef]






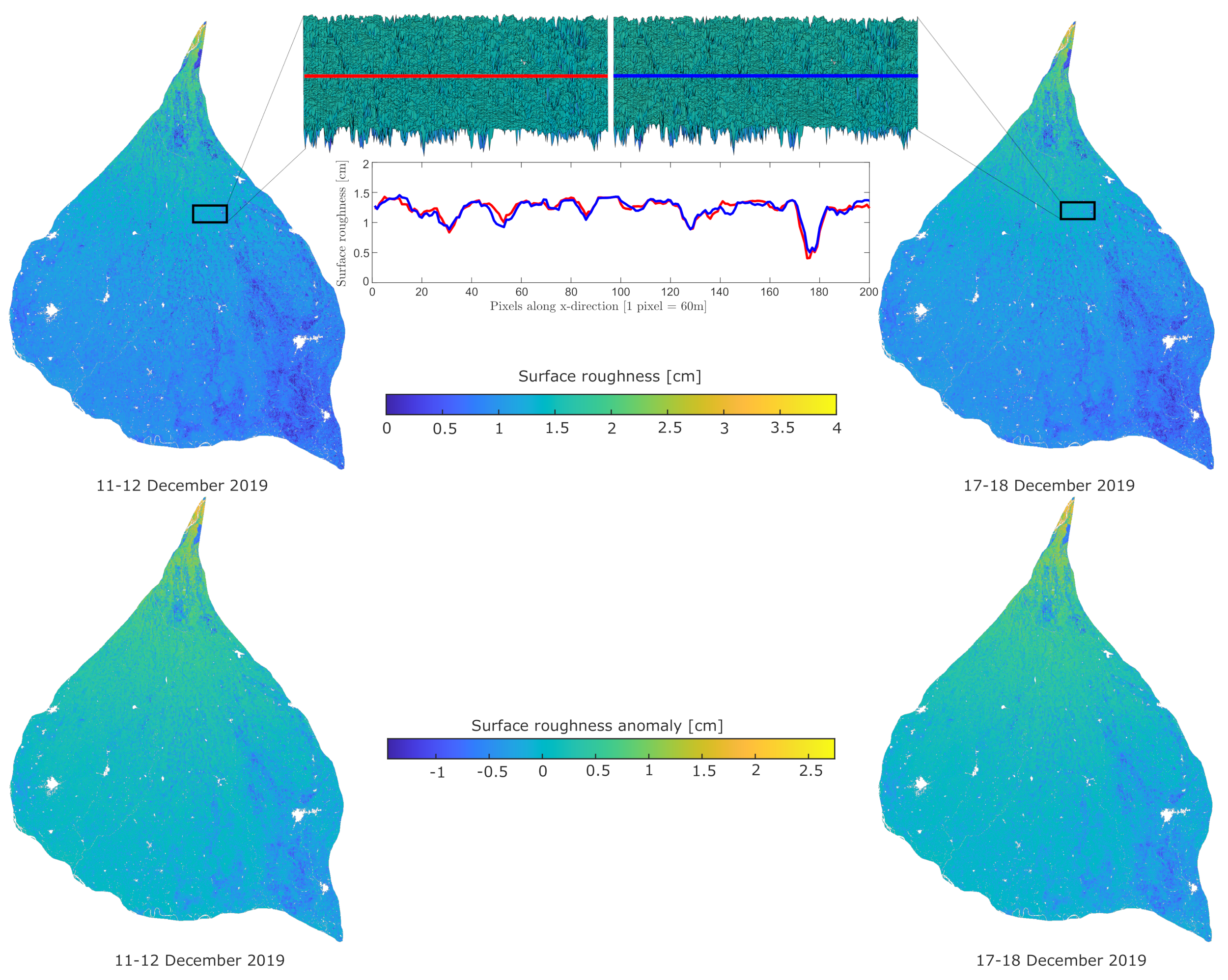
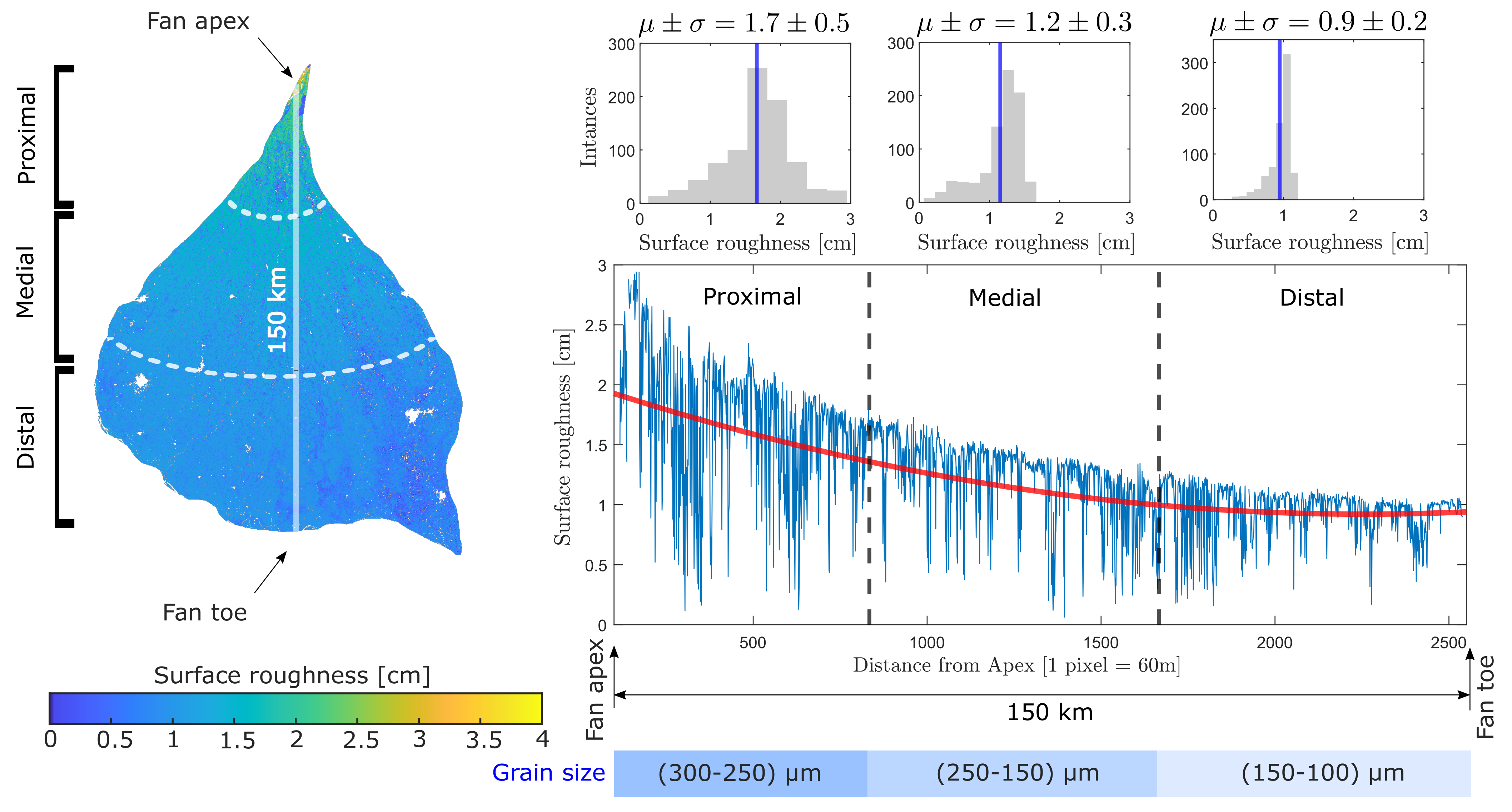

| Sentinel-1 | ||||
| Date | Polarization | Incidence Angle () | Pixel Size (m) | Direction |
| 11 December 2019 | (VH, VV) | 38.6 | 10 × 10 | NE |
| 15 December 2019 | (VH, VV) | 38.5 | 10 × 10 | NW |
| 17 December 2019 | (VH, VV) | 38.4 | 10 × 10 | NE |
| 18 December 2019 | (VH, VV) | 38.5 | 10 × 10 | NE |
| 20 December 2019 | (VH, VV) | 38.5 | 10 × 10 | NW |
| Sentinel-2 | ||||
| Date | Orbit number and direction | Band | Wavelength (nm) | Spatial Resolution (m) |
| 9 December 2019 | 76, Descending | 4 | 646–685 | 10 |
| 9 December 2019 | 76, Descending | 8 | 774–907 | 10 |
| Standardisation Method | Formulation | Description |
|---|---|---|
| Not Standardised | Same as input | |
| Center Mean | Features are centered with zero mean. | |
| Z-score Mean | It converts the features to a common scale with zero mean and unit standard deviation. It has same skewness and kurtosis as that of original data. | |
| Min-Max | It converts the features to an identical range [0, 1]. The extreme values has strong influence on the final output. | |
| Scale | Features are scaled by the standard deviation. |
| Parameters | Values |
|---|---|
| Penalty factor (C) | 0.1–0.5 |
| Epsilon () | 0.1 |
| Kernel | Homogeneous Polynomial |
| Polynomial degree (d) | 1 |
| Gamma () | 1 |
| Methods | Parameters | ||||||
|---|---|---|---|---|---|---|---|
| R | RMSE (cm) | MSE (cm2) | AIC | AICc | BIC | Time (s) | |
| SVR | |||||||
| PCA-NS-SVR | 0.50 | 0.44 | 0.19 | −87.01 | −39.42 | −83.39 | 0.95 |
| PCA-CM-SVR | 0.70 | 0.25 | 0.06 | −138.53 | −90.95 | −134.92 | 0.26 |
| PCA-ZM-SVR | 0.67 | 0.22 | 0.05 | −147.12 | −99.53 | −143.51 | 0.12 |
| PCA-MM-SVR | 0.75 * | 0.19 * | 0.04 * | −160.32 * | −112.74 | −156.71 * | 0.08 * |
| PCA-S-SVR | 0.65 | 0.26 | 0.07 | −133.70 | −86.14 | −130.09 | 0.18 |
| GPR | |||||||
| PCA-NS-GPR | 0.30 | 0.21 | 0.04 | −152.97 | −105.38 | −149.35 | 1.09 |
| PCA-CM-GPR | 0.23 | 0.24 | 0.06 | −139.93 | −92.35 | −136.32 | 0.25 |
| PCA-ZM-GPR | 0.44 | 0.32 | 0.10 | −116.37 | −68.78 | −112.75 | 0.16 |
| PCA-MM-GPR | 0.29 | 0.24 | 0.06 | −140.10 | −92.51 | −136.48 | 0.11 |
| PCA-S-GPR | 0.46 | 0.27 | 0.07 | −131.36 | −83.77 | −127.75 | 0.30 |
| GRNN | |||||||
| PCA-NS-GRNN | 0.11 | 0.63 | 0.40 | 752.17 | −113.76 | 1483.87 | 1.68 |
| PCA-CM-GRNN | 0.25 | 0.55 | 0.31 | 740.11 | −125.82 | 1471.81 | 0.36 |
| PCA-ZM-GRNN | 0.51 | 0.28 | 0.08 | 680.14 | −185.80 | 1411.84 | 0.23 |
| PCA-MM-GRNN | 0.67 | 0.04 | 0.00 | 509.29 | −356.65 * | 1241.00 | 0.17 |
| PCA-S-GRNN | 0.51 | 0.21 | 0.05 | 653.93 | −212.01 | 1385.63 | 0.45 |
| BDT | |||||||
| PCA-NS-BDT | 0.22 | 0.54 | 0.29 | −65.80 | −17.80 | −60.38 | 1.09 |
| PCA-CM-BDT | 0.41 | 0.54 | 0.29 | −65.95 | −17.95 | −60.53 | 0.19 |
| PCA-ZM-BDT | 0.36 | 0.55 | 0.30 | −64.95 | −16.95 | −59.53 | 0.10 |
| PCA-MM-BDT | 0.19 | 0.61 | 0.37 | −55.17 | −7.17 | −49.75 | 0.08 |
| PCA-S-BDT | 0.24 | 0.53 | 0.28 | −67.32 | −19.32 | −61.90 | 0.26 |
| Bagging EL (Random Forest) | |||||||
| PCA-NS-BAGG | 0.44 | 0.24 | 0.06 | 55.36 | −263.51 | 245.06 | 3.07 |
| PCA-CM-BAGG | 0.56 | 0.24 | 0.06 | 65.61 | −253.27 | 255.31 | 1.16 |
| PCA-ZM-BAGG | 0.58 | 0.24 | 0.06 | 63.44 | −255.43 | 253.14 | 0.82 |
| PCA-MM-BAGG | 0.50 | 0.22 | 0.05 | 55.36 | −263.51 | 245.06 | 0.71 |
| PCA-S-BAGG | 0.46 | 0.20 | 0.04 | 46.46 | −272.41 | 236.16 | 1.05 |
| Boosting EL (LSBoost) | |||||||
| PCA-NS-BOOST | 0.31 | 0.69 | 0.47 | 160.17 | −158.70 | 349.87 | 1.48 |
| PCA-CM-BOOST | 0.38 | 0.61 | 0.37 | 148.03 | −170.83 | 337.73 | 0.54 |
| PCA-ZM-BOOST | 0.50 | 0.57 | 0.32 | 142.60 | −176.26 | 332.30 | 0.38 |
| PCA-MM-BOOST | 0.20 | 0.65 | 0.42 | 154.23 | −164.65 | 343.93 | 0.36 |
| PCA-S-BOOST | 0.36 | 0.60 | 0.36 | 146.92 | −171.95 | 336.61 | 0.51 |
| AutoML | |||||||
| PCA-NS-AutoML | 0.44 | 0.19 | 0.04 | 284.17 | −232.59 | 690.68 | 5.82 |
| PCA-CM-AutoML | 0.59 | 0.21 | 0.04 | 292.12 | −224.64 | 698.62 | 3.98 |
| PCA-ZM-AutoML | 0.59 | 0.20 | 0.04 | 291.05 | −225.70 | 697.55 | 3.87 |
| PCA-MM-AutoML | 0.32 | 0.21 | 0.05 | 337.79 | −220.62 | 784.04 | 3.79 |
| PCA-S-AutoML | 0.38 | 0.20 | 0.04 | 288.57 | −228.18 | 695.07 | 4.32 |
| Parameters | Methods | ||||
|---|---|---|---|---|---|
| Modified Dubois | Modified Oh, 2002 | Modified Oh, 2004 | Srivastava, 2008 | PCA-MM-SVR | |
| R | 0.34 | 0.08 | 0.07 | 0.11 | 0.75 |
| ubRMSE (cm) | 1.25 | 0.86 | 1.35 | 0.07 | 0.08 |
| MSE (cm) | 0.60 | 0.31 | 1.23 | 0.23 | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, A.; Gaurav, K.; Rai, A.K.; Beg, Z. Machine Learning to Estimate Surface Roughness from Satellite Images. Remote Sens. 2021, 13, 3794. https://doi.org/10.3390/rs13193794
Singh A, Gaurav K, Rai AK, Beg Z. Machine Learning to Estimate Surface Roughness from Satellite Images. Remote Sensing. 2021; 13(19):3794. https://doi.org/10.3390/rs13193794
Chicago/Turabian StyleSingh, Abhilash, Kumar Gaurav, Atul Kumar Rai, and Zafar Beg. 2021. "Machine Learning to Estimate Surface Roughness from Satellite Images" Remote Sensing 13, no. 19: 3794. https://doi.org/10.3390/rs13193794
APA StyleSingh, A., Gaurav, K., Rai, A. K., & Beg, Z. (2021). Machine Learning to Estimate Surface Roughness from Satellite Images. Remote Sensing, 13(19), 3794. https://doi.org/10.3390/rs13193794








