Estimation of Salinity Content in Different Saline-Alkali Zones Based on Machine Learning Model Using FOD Pretreatment Method
Abstract
:1. Introduction
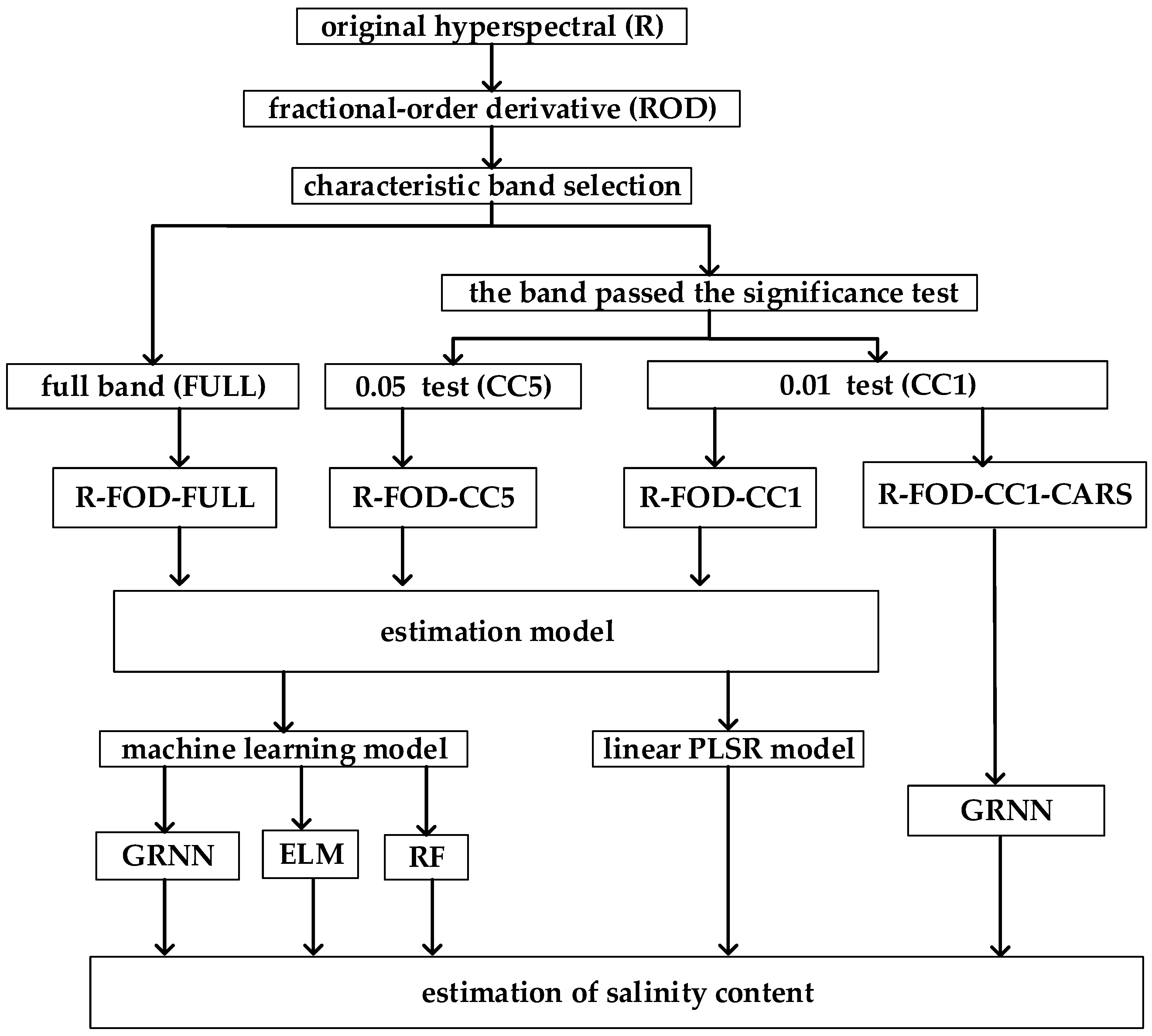
2. Materials and Methods
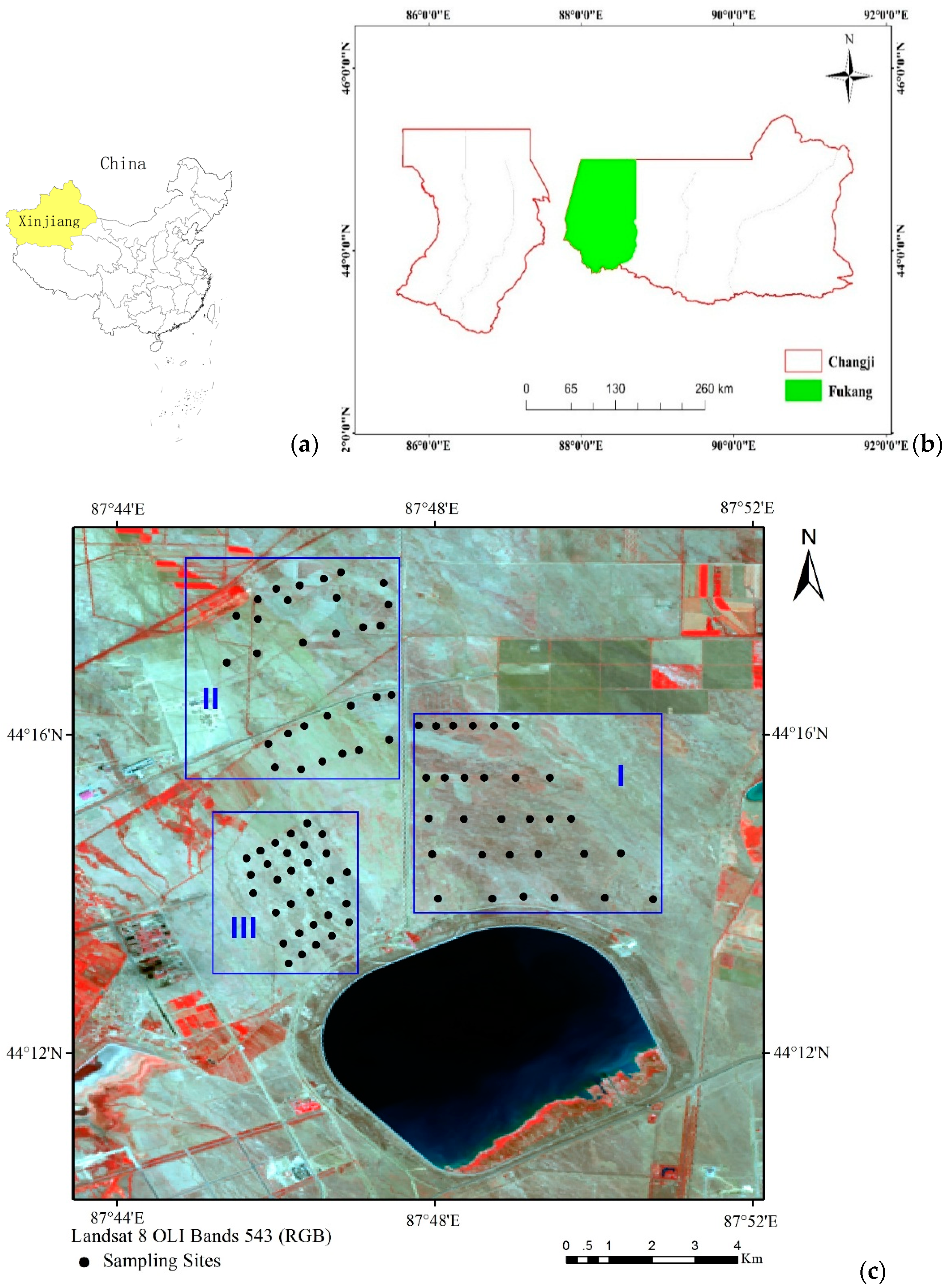
2.1. Study Zone
2.2. Data Collection and Preprocessing
2.3. Machine Learning Model
2.3.1. General Regression Neural Network
2.3.2. Extreme Learning Machine
2.3.3. Random Forest
2.4. Linear PLSR Model
2.5. Characteristic Band Selections
2.5.1. Correlation Coefficient
2.5.2. Competitive Adaptive Reweighted Sampling
2.6. Model Evaluation Indicator
3. Simulation Results
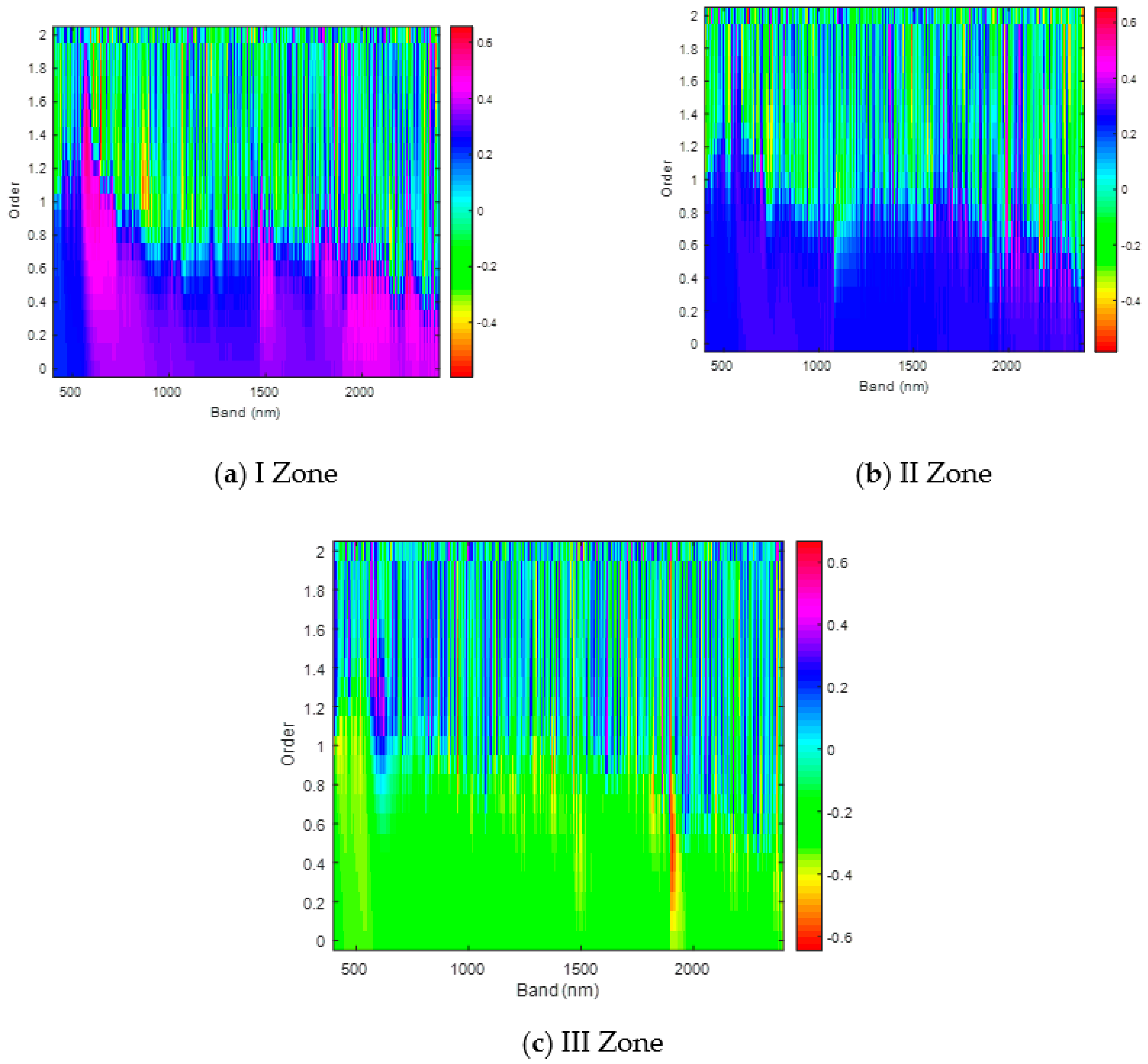
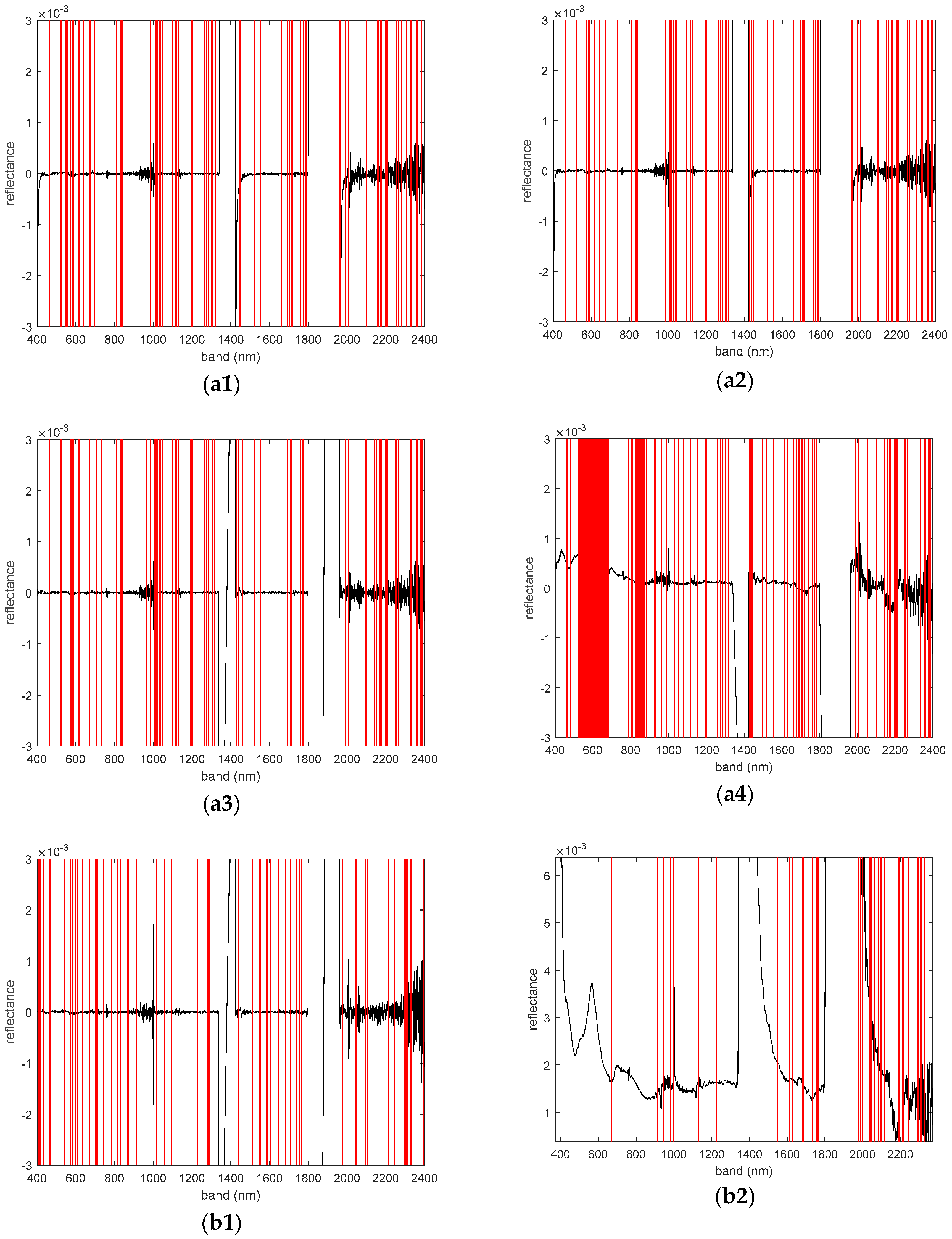
3.1. Correlation Coefficient Matrix Heat Map between Spectra and Salinity Based on Fractional-Order Derivative
3.2. Estimation of Salinity Based on Full Band
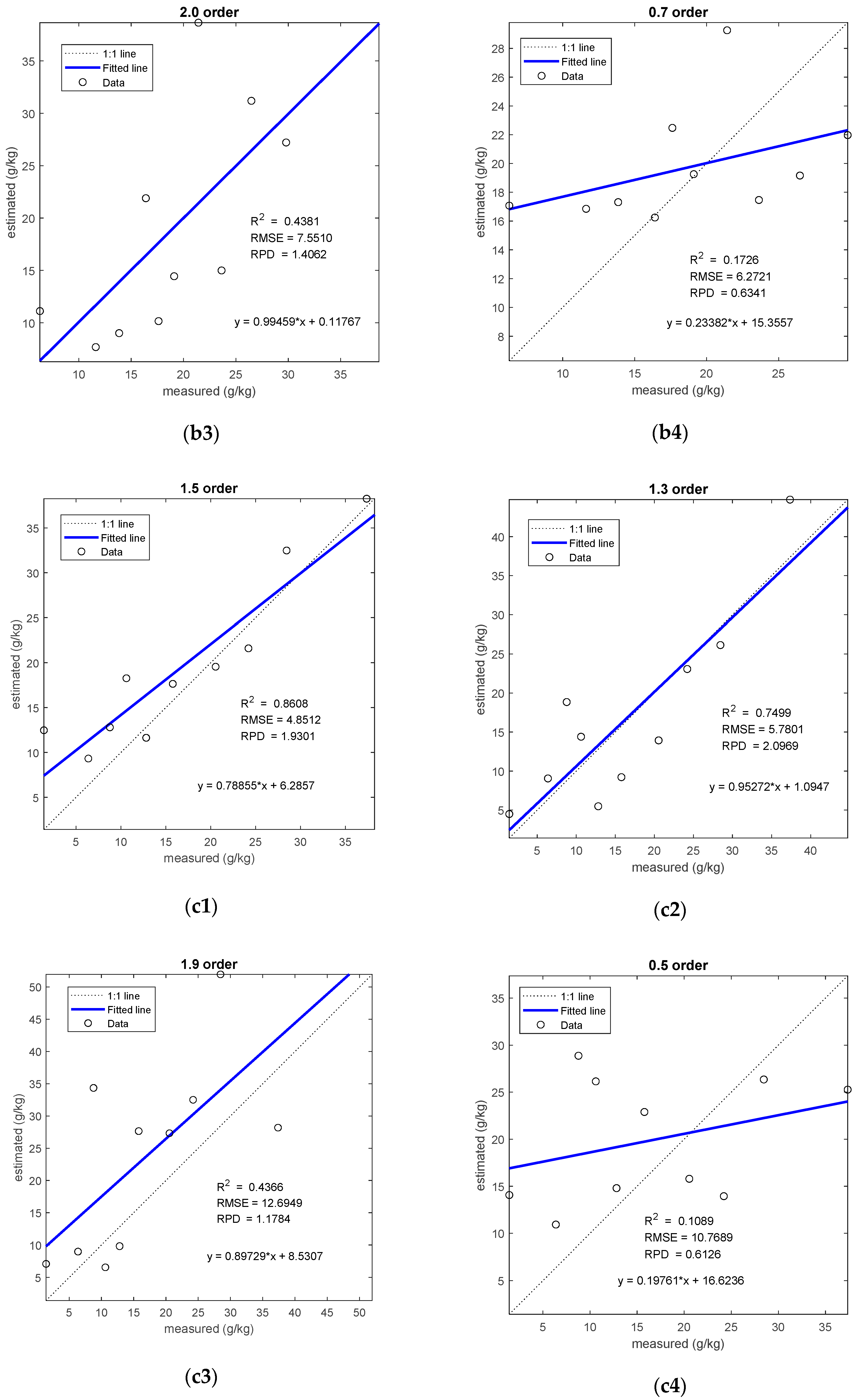
3.3. Estimation of Salinity Based on a Characteristic Band Model with a Significance Level of 0.05
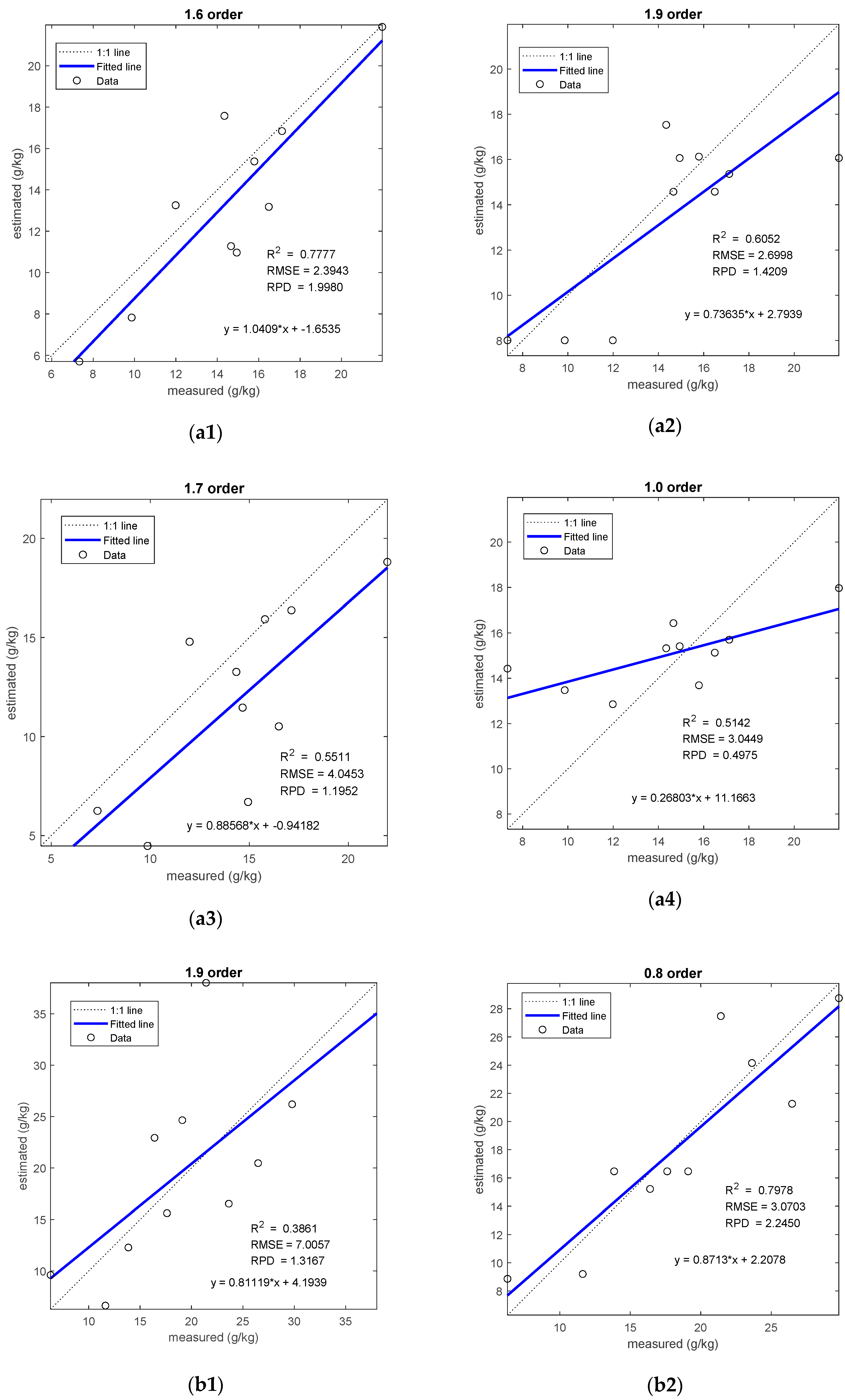
3.3.1. Performance Analysis for Estimating Salinity
3.3.2. Test Results of Different Models
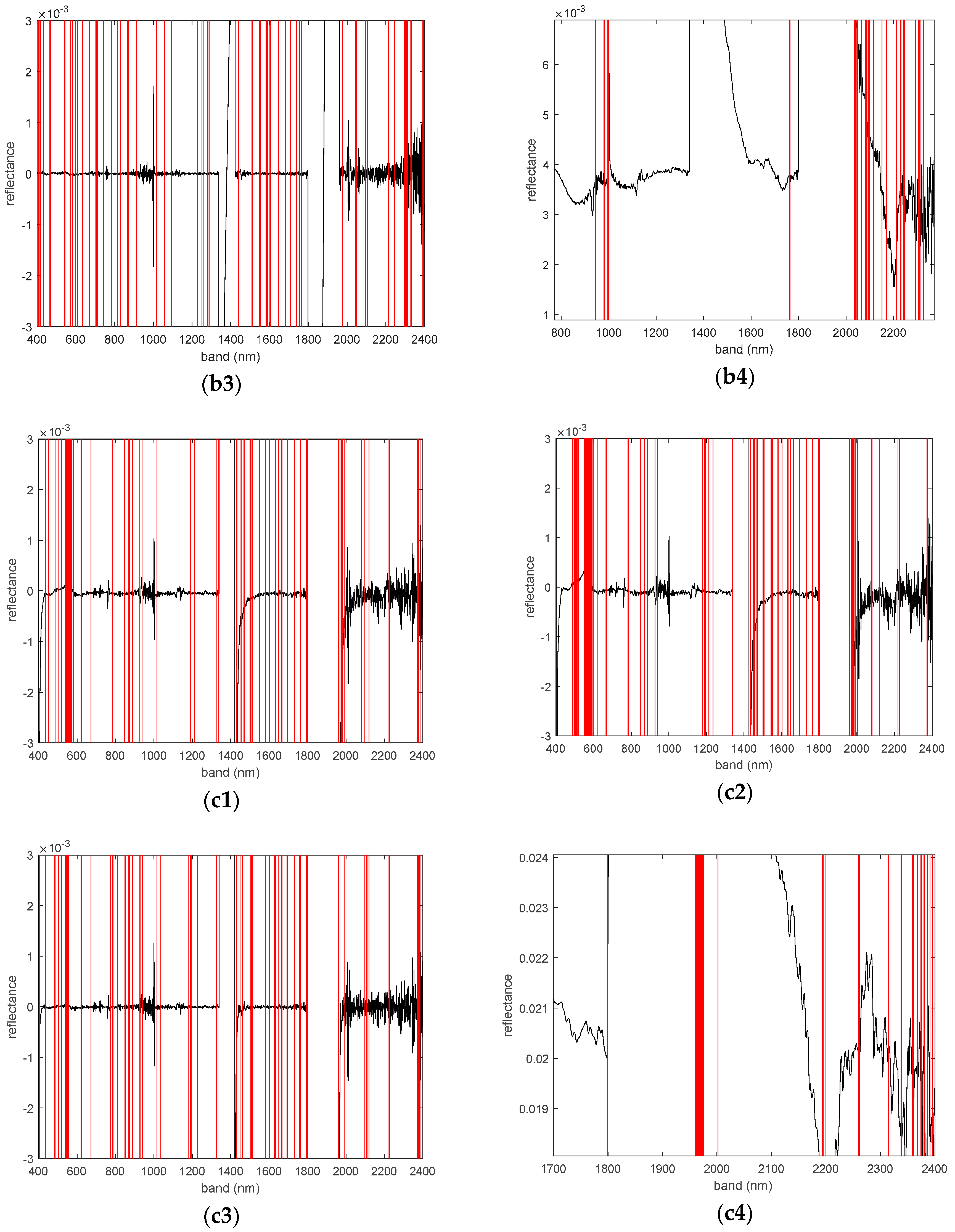
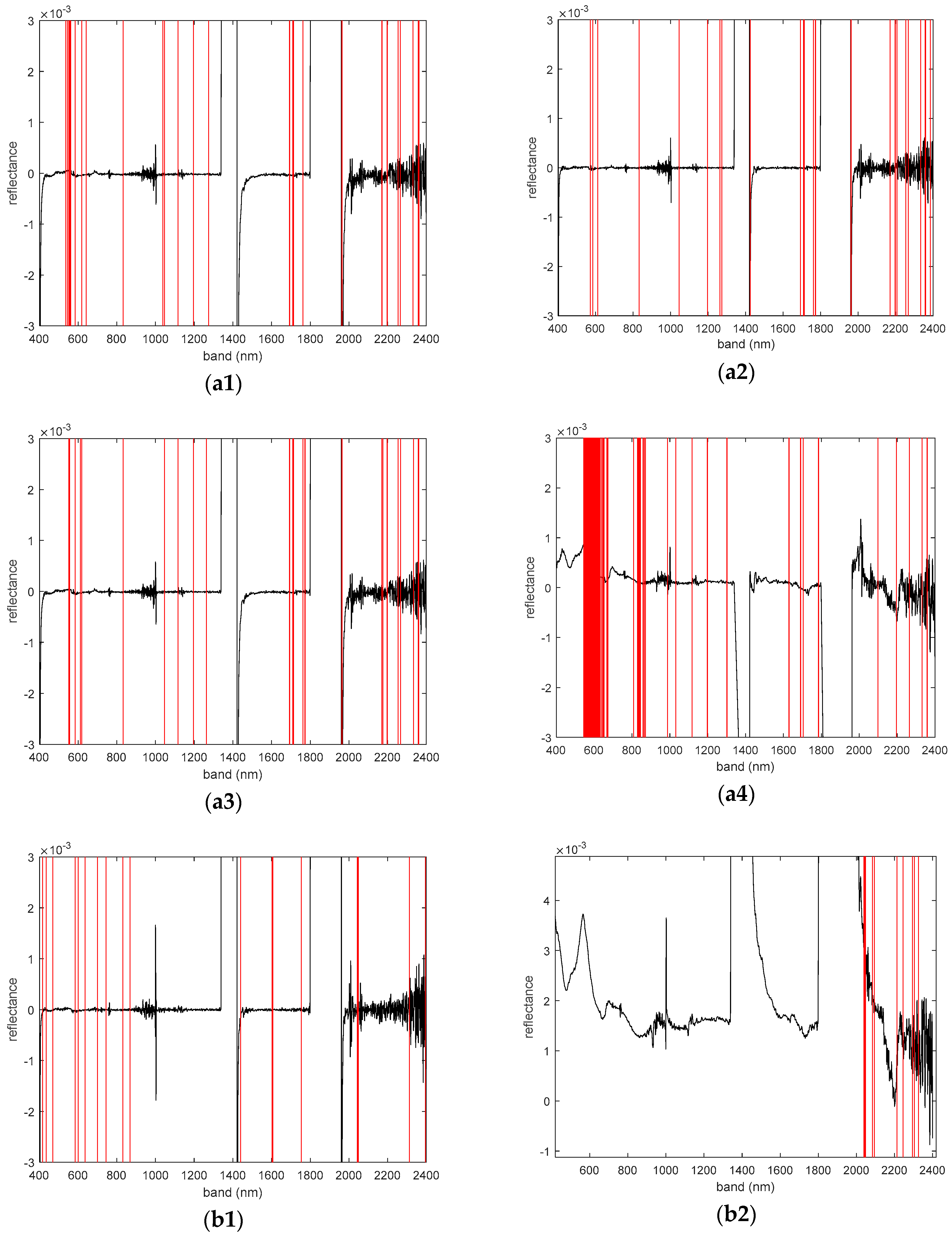
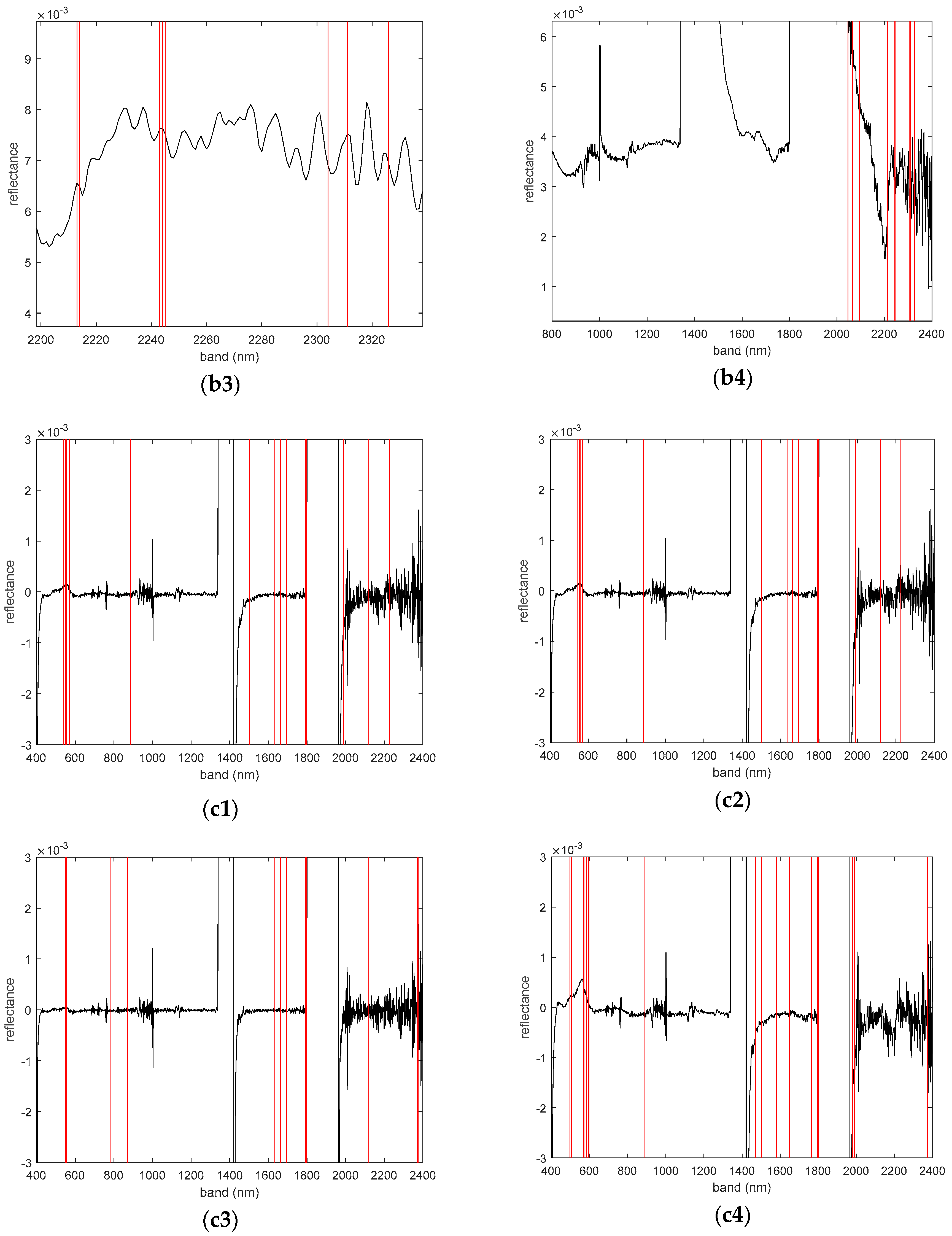
3.3.3. Characteristic Bands Selected by Different Models
3.4. Estimation of Salinity Based on a Characteristic Band Model with a Significance Level of 0.01
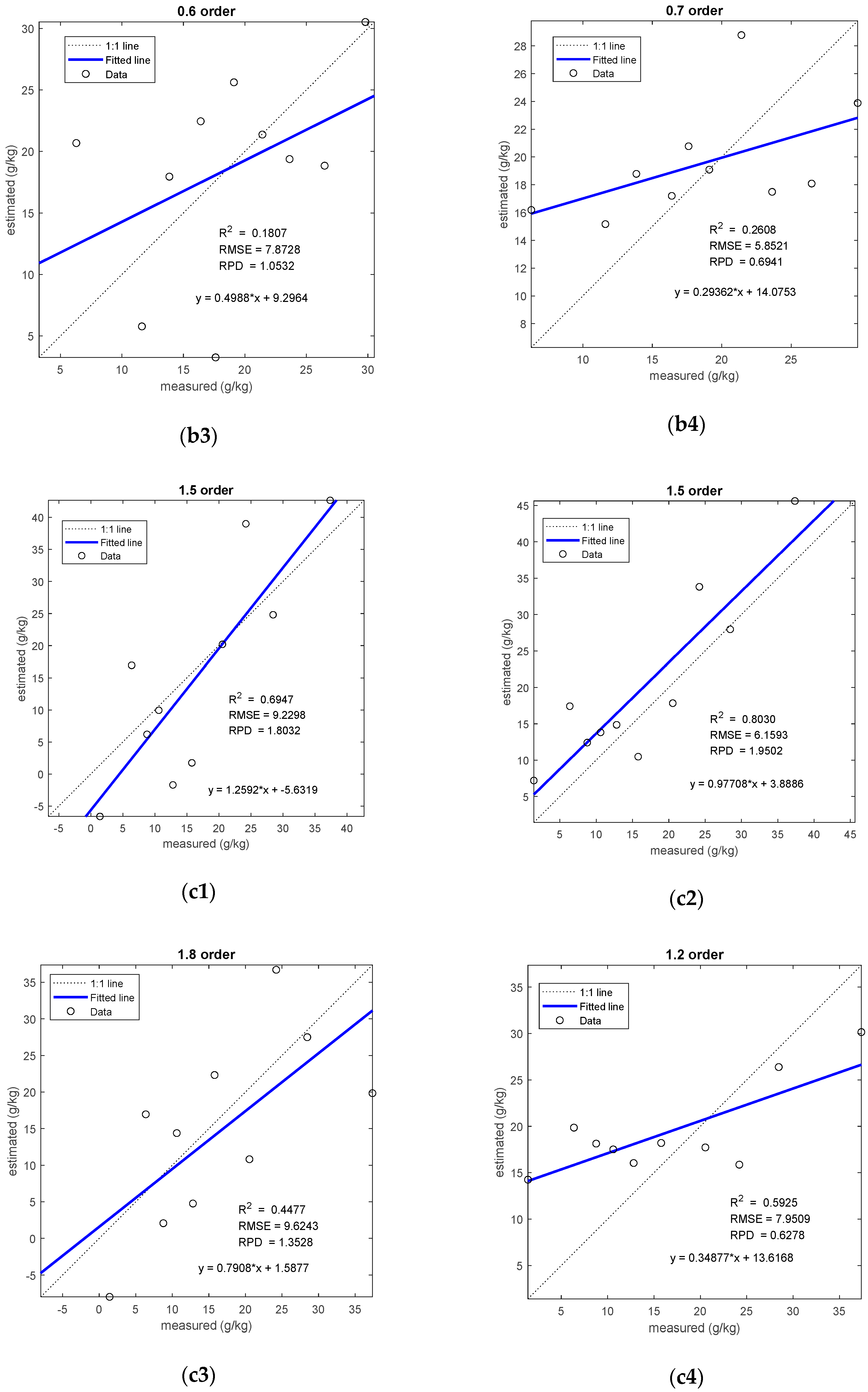
3.4.1. Accuracy Comparison of Salt Estimation
3.4.2. Validation of Optimal Salt Model
3.4.3. The Characteristic Band of the Optimal Model
3.5. Estimation of Salinity Based on R-FOD-CC1-CARS-GRNN Model
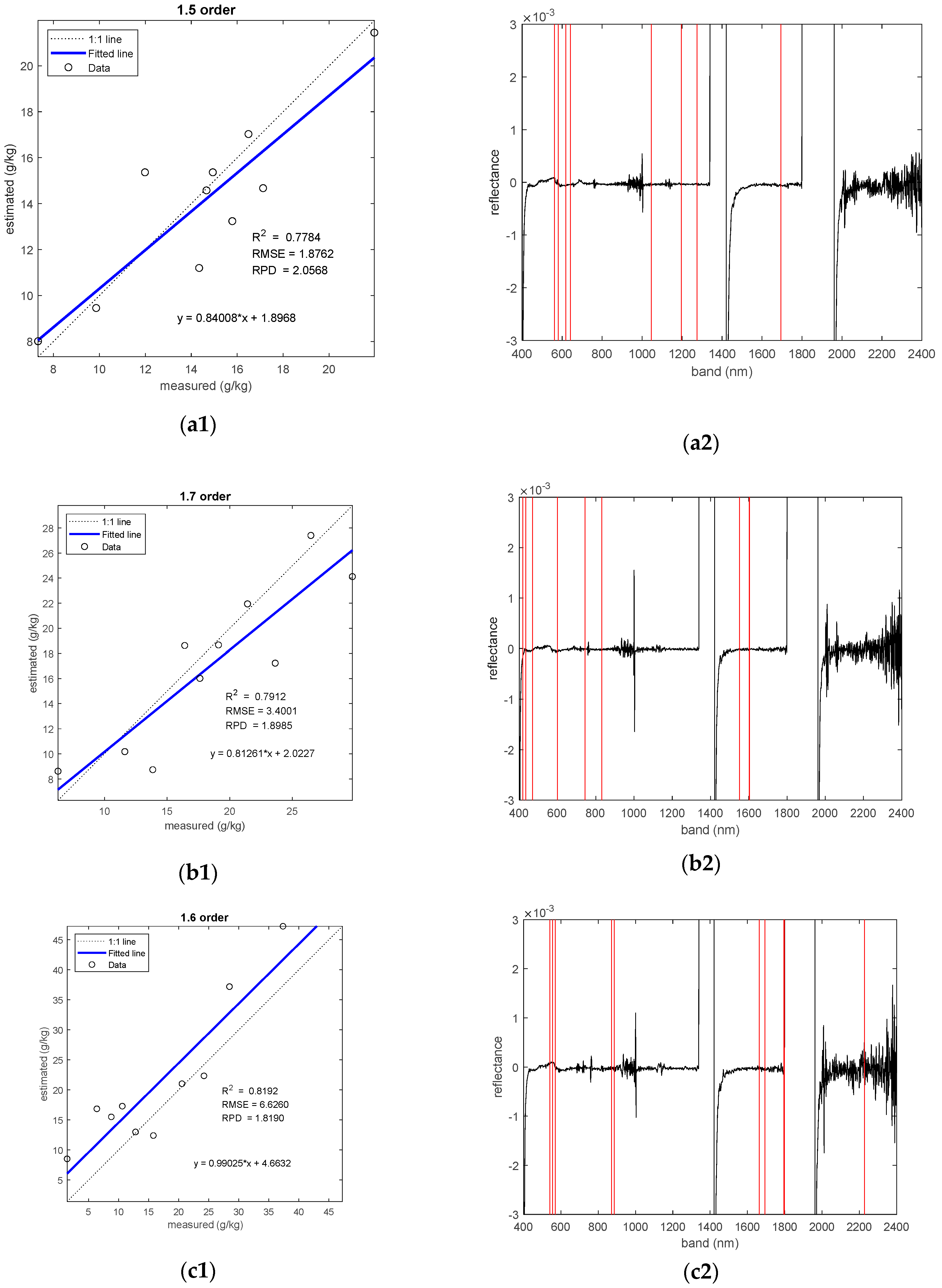
3.5.1. Inversion Results of Salt Estimation
3.5.2. Validation Result and Feature Band of the Best Model
4. Discussion
4.1. Comparison of Estimation Accuracy between Linear Model and Nonlinear Model
4.2. Comparison of Model Estimation Results Based on Different Characteristic Band Methods
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ding, J.; Yang, S.; Shi, Q.; Wei, Y.; Wang, F. Using Apparent Electrical Conductivity as Indicator for Investigating Potential Spatial Variation of Soil Salinity across Seven Oases along Tarim River in Southern Xinjiang, China. Remote Sens. 2020, 12, 2601. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Yu, D.; Teng, D.; He, B.; Chen, X.; Ge, X.; Zhang, Z.; Wang, Y.; Yang, X.; et al. Machine learning-based detection of soil salinity in an arid desert region, Northwest China: A comparison between Landsat-8 OLI and Sentinel-2 MSI. Sci. Total Environ. 2020, 707, 136092. [Google Scholar] [CrossRef] [PubMed]
- Tian, A.; Fu, C.; Yao, H.; Su, X.; Xiong, H. A New Methodology of Soil Salinization Degree Classification by Probability Neural Network Model based on Centroid of Fractional Lorenz Chaos Self-Synchronization Error Dynamics. IEEE Trans. Geosci. Remote Sens. 2020, 58, 799–810. [Google Scholar] [CrossRef]
- Yang, X.; Yu, Y. Estimating soil salinity under various moisture conditions: An experimental study. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2525–2533. [Google Scholar] [CrossRef]
- Nawar, S.; Munnaf, M.A.; Mouazen, A.M. Machine Learning Based On-Line Prediction of Soil Organic Carbon after Removal of Soil Moisture Effect. Remote Sens. 2020, 12, 1308. [Google Scholar] [CrossRef] [Green Version]
- Xiao, D.; Vu, Q.H.; Le, B.T. Salt content in saline-alkali soil detection using visible-near infrared spectroscopy and a 2D deep learning. Microchem. J. 2021, 165, 106182. [Google Scholar] [CrossRef]
- Xu, H.; Xu, D.; Chen, S.; Ma, W.; Shi, Z. Rapid Determination of Soil Class Based on Visible-Near Infrared, Mid-Infrared Spectroscopy and Data Fusion. Remote Sens. 2020, 12, 1512. [Google Scholar] [CrossRef]
- Askari, M.S.; O’Rourke, S.M.; Holden, N.M. A comparison of point and imaging visible-near infrared spectroscopy for determining soil organic carbon. J. Near Infrared Spectrosc. 2018, 26, 133–146. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Yan, J.; Li, Z.; Leng, P.; Duan, Q.Y. Hyperspectral Estimation of Soil Organic Matter Content using Different Spectral Preprocessing Techniques and PLSR Method. Remote Sens. 2020, 12, 1206. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Zhang, B.; Shen, Q.; Yao, Y.; Zhang, S.; Wei, H.; Yao, R.; Zhang, Y. Estimation of Soil Salt and Ion Contents Based on Hyperspectral Remote Sensing Data: A Case Study of Baidunzi Basin, China. Water 2021, 13, 559. [Google Scholar] [CrossRef]
- Kahaer, Y.; Tashpolat, N.; Shi, Q.; Liu, S. Possibility of Zhuhai-1 Hyperspectral Imagery for Monitoring Salinized Soil Moisture Content Using Fractional Order Differentially Optimized Spectral Indices. Water 2020, 12, 3360. [Google Scholar] [CrossRef]
- An, D.; Zhao, G.; Chang, C.; Wang, Z.; Li, P.; Zhang, T.; Jia, J. Hyperspectral field estimation and remote-sensing inversion of salt content in coastal saline soils of the Yellow River Delta. Int. J. Remote Sens. 2016, 37, 455–470. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Ding, J.; Kung, H.; Latif, A.; Johnson, V.C. Estimation of soil salt content (SSC) in the Ebinur LakeWetland National Nature Reserve (ELWNNR), Northwest China, based on a Bootstrap-BP neural network model and optimal spectral indices. Sci. Total Environ. 2018, 615, 918–930. [Google Scholar] [CrossRef] [PubMed]
- Ben-Dor, E.; Granot, A.; Notesco, G. A simple apparatus to measure soil spectral information in the field under stable conditions. Geoderma 2017, 306, 73–80. [Google Scholar] [CrossRef]
- Tang, Y.; Chen, Z. Soil pH Prediction Based on Convelution Neural Network and Near Infrared Spectrpscopy. Spectrosc. Spectr. Anal. 2021, 41, 892–897. [Google Scholar]
- Yuan, Z.; Wei, L.; Zhang, Y.; Yu, M.; Yan, X. Hyperspectral Inversion and Analysis of Heavy Metal Arsenic Content in Farmland Soil Based on Optimizing CARS Combined with PSO-SVM Algorithm. Spectrosc. Spectr. Anal. 2020, 40, 567–573. [Google Scholar]
- Sourav, B.; Vasit, S.; Maitiniyazi, M.; Matthew, M.; Maria, N.; Nadia, S.; Todd, C.M. Quantifying Leaf Chlorophyll Concentration of Sorghum from Hyperspectral Data Using Derivative Calculus and Machine Learning. Remote Sens. 2020, 12, 2082. [Google Scholar]
- Meng, X.; Bao, Y.; Ye, Q.; Liu, H.; Zhang, X.; Tang, H.; Zhang, X. Soil Organic Matter Prediction Model with Satellite Hyperspectral Image Based on Optimized Denoising Method. Remote Sens. 2021, 13, 2273. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, X.; Zhang, F.; Chan, N.; Kunge, H.; Liu, S.; Deng, L. Estimation of soil salt content using machine learning techniques based on remote-sensing fractional derivatives, a case study in the Ebinur Lake Wetland National Nature Reserve, Northwest China. Ecol. Indic. 2020, 119, 106869. [Google Scholar] [CrossRef]
- Chen, L.; Lai, J.; Tan, K.; Wang, X.; Chen, Y.; Ding, J. Development of a soil heavy metal estimation method based on a spectral index: Combining fractional-order derivative pretreatment and the absorption mechanism. Sci. Total Environ. 2021, 11, 151882. [Google Scholar] [CrossRef]
- Abulaiti, Y.; Sawut, M.; Maimaitiaili, B.; Chunyue, M. A possible fractional order derivative and optimized spectral indices for assessing total nitrogen content in cotton. Comput. Electron. Agric. 2020, 171, 105275. [Google Scholar] [CrossRef]
- Hong, Y.; Liua, Y.; Chen, Y.; Liu, Y.; Yu, L.; Liu, Y.; Cheng, H. Application of fractional-order derivative in the quantitative estimation of soil organic matter content through visible and near-infrared spectroscopy. Geoderma 2019, 337, 758–769. [Google Scholar] [CrossRef]
- Zhang, B.; Li, W.; Li, X.; See-Kiong, N. Intelligent Fault Diagnosis Under Varying Working Conditions Based on Domain Adaptive Convolutional Neural Networks. IEEE Access 2018, 6, 66367–66384. [Google Scholar] [CrossRef]
- Chen, Z.; Yang, Y.; Jiang, C.; Hao, J.; Zhang, L. Light Sensor Based Occupancy Estimation via Bayes Filter With Neural Networks. IEEE Trans. Ind. Electron. 2020, 67, 5787–5797. [Google Scholar] [CrossRef]
- Tian, A.; Zhao, J.; Tang, B.; Zhu, D.; Fu, C.; Xiong, H. Hyperspectral Prediction of Soil Total Salt Content by Different Disturbance Degree under a Fractional-Order Differential Model with Differing Spectral Transformations. Remote Sens. 2021, 13, 4283. [Google Scholar] [CrossRef]
- Tian, A.; Zhao, J.; Tang, B.; Zhu, D.; Fu, C.; Xiong, H. Study on the Pretreatment of Soil Hyperspectral and Na+ Ion Data under Different Degrees of Human Activity Stress by Fractional-Order Derivatives. Remote Sens. 2021, 13, 3974. [Google Scholar] [CrossRef]
- Pano-Azucena, A.D.; Ovilla-Martinez, B.; Tlelo-Cuautle, E.; Muñoz-Pacheco, J.M.; la Fraga, L.G. FPGA-based implementation of different families of fractional-order chaotic oscillators applying Grünwald–Letnikov method. Commun. Nonlinear Sci. Numer. Simul. 2019, 72, 516–527. [Google Scholar] [CrossRef]
- Chen, H.; Holland, F.; Stynes, M. An analysis of the Grünwald–Letnikov scheme for initial-value problems with weakly singular solutions. Appl. Numer. Math. 2019, 139, 52–61. [Google Scholar] [CrossRef]
- Sadeghi, F.; Yu, Y.; Zhu, X.; Li, J. Damage identification of steel-concrete composite beams based on modal strain energy changes through general regression neural network. Eng. Struct. 2021, 244, 112824. [Google Scholar] [CrossRef]
- Mirzaei, S.; Moradi, S.; Ehzari, H.; Farhadian, N.; Shahlaei, M. Application of general regression neural network and central composite design in fabrication and performance of magnetite (Fe3O4) modified carbon paste electrode for the electrochemical detection of Clomiphene. Microchem. J. 2019, 147, 1028–1037. [Google Scholar] [CrossRef]
- Tian, X.; Jiao, W.; Liu, T.; Ren, L.; Song, B. Leakage detection of low-pressure gas distribution pipeline system based on linear fitting and extreme learning machine. Int. J. Press. Vessel. Pip. 2021, 194, 104553. [Google Scholar] [CrossRef]
- Duan, M.; Li, K.L.; Liao, X.; Li, K.Q. A Parallel Multiclassification Algorithm for Big Data Using an Extreme Learning Machine. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 2337–2351. [Google Scholar] [CrossRef] [PubMed]
- Shah, S.H.; Angel, Y.; Houborg, R.; Ali, S.; McCabe, M.F. A Random Forest Machine Learning Approach for the Retrieval of Leaf Chlorophyll Content in Wheat. Remote Sens. 2019, 11, 920. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Yang, W.; Zhang, M.; Feng, M.; Xiao, L.; Ding, G. Estimation of water content in corn leaves using hyperspectral data based on fractional order Savitzky-Golay derivation coupled with wavelength selection. Comput. Electron. Agric. 2021, 182, 05989. [Google Scholar] [CrossRef]
- Biney, J.K.M.; Borůvka, L.; Agyeman, P.C.; Němeček, K.; Klement, A. Comparison of Field and Laboratory Wet Soil Spectra in the Vis-NIR Range for Soil Organic Carbon Prediction in the Absence of Laboratory Dry Measurements. Remote Sens. 2020, 12, 3082. [Google Scholar] [CrossRef]
- Guo, P.; Li, M.; Luo, W.; Cha, Z. Estimation of foliar nitrogen of rubber trees using hyperspectral reflectance with feature bands. Infrared Phys. Technol. 2019, 102, 103021. [Google Scholar] [CrossRef]
- Gao, L.; Zhu, X.; Han, Z.; Wang, L.; Zhao, G.; Jiang, Y. Spectroscopy-Based Soil Organic Matter Estimation in Brown Forest Soil Areas of the Shandong Peninsula, China. Pedosphere 2019, 29, 810–818. [Google Scholar] [CrossRef]
- Li, Q.; Xie, J.; Zhang, J.; Yan, H.; Xiong, Y.; Liu, W.; Min, S. A global model for the determination of prohibited addition in pesticide formulations by near infrared spectroscopy. Infrared Phys. Technol. 2020, 105, 103191. [Google Scholar] [CrossRef]
- Xing, Z.; Du, C.; Shen, Y.; Ma, F.; Zhou, J. A method combining FTIR-ATR and Raman spectroscopy to determine soil organic matter: Improvement of prediction accuracy using competitive adaptive reweighted sampling (CARS). Comput. Electron. Agric. 2021, 191, 106549. [Google Scholar] [CrossRef]
- Kumar, K. Competitive adaptive reweighted sampling assisted partial least square analysis of excitation-emission matrix fluorescence spectroscopic data sets of certain polycyclic aromatic hydrocarbons. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 244, 118874. [Google Scholar] [CrossRef]
- Peng, J.; Biswas, A.; Jiang, Q.; Zhao, R.; Hu, J.; Hu, B.; Shi, Z. Estimating soil salinity from remote sensing and terrain data in southern Xinjiang Province, China. Geoderma 2019, 337, 1309–1319. [Google Scholar] [CrossRef]
- Cezar, E.; Nanni, M.R.; Crusiol, L.G.T.; Sun, L.; Chicati, M.S.; Furlanetto, R.H.; Rodrigues, M.; Sibaldelli, R.N.R.; Silva, G.F.C.; de Oliveira, K.M.; et al. Strategies for the Development of Spectral Models for Soil Organic Matter Estimation. Remote Sens. 2021, 13, 1376. [Google Scholar] [CrossRef]
- Wang, N.; Xue, J.; Peng, J.; Biswas, A.; He, Y.; Shi, Z. Integrating Remote Sensing and Landscape Characteristics to Estimate Soil Salinity Using Machine Learning Methods: A Case Study from Southern Xinjiang, China. Remote Sens. 2020, 12, 4118. [Google Scholar] [CrossRef]
- Wang, J.; Hu, X.; Shi, T.; He, L.; Hu, W.; Wu, G. Assessing toxic metal chromium in the soil in coal mining areas via proximal sensing: Prerequisites for land rehabilitation and sustainable development. Geoderma 2021, 405, 115399. [Google Scholar] [CrossRef]
- Hong, Y.; Chen, S.; Liu, Y.; Zhang, Y.; Yu, L.; Chen, Y.; Liu, Y.; Cheng, H.; Liu, L. Combination of fractional order derivative and memory-based learning algorithm to improve the estimation accuracy of soil organic matter by visible and near-infrared spectroscopy. Catena 2019, 174, 104–116. [Google Scholar] [CrossRef]
- Duan, P.; Xiong, H.; Li, R.; Zhang, L. A quantitative analysis of the reflectance of the saline soil under different disturbance extent. Sepctrosc. Spectr. Anal. 2017, 37, 571–576. [Google Scholar]
- Fu, C.; Gan, S.; Yuan, X.; Xiong, H.; Tian, A. Pretreatment of Total Phosphorus Content in Saline Soil in Arid Area by Fractional Differential Algorithm. Sens. Mater. 2018, 30, 2469–2477. [Google Scholar] [CrossRef]
- Tian, A.; Fu, C.; Xiong, H.; Yau, H.-T. Innovative Intelligent Methodology for the Classification of Soil Salinization Degree Using a Fractional-Order Master-Slave Chaotic System. Int. J. Bifurc. Chaos 2019, 29, 1950026. [Google Scholar] [CrossRef]
- Xu, X.; Chen, S.; Ren, L.; Han, C.; Lv, D.; Zhang, Y.; Ai, F. Estimation of Heavy Metals in Agricultural Soils Using Vis-NIR Spectroscopy with Fractional-Order Derivative and Generalized Regression Neural Network. Remote Sens. 2021, 13, 2718. [Google Scholar] [CrossRef]
- Yin, F.; Wu, M.; Liu, L.; Zhu, Y.; Feng, J.; Yin, D.; Yin, C.; Yin, C. Predicting the abundance of copper in soil using reflectance spectroscopy and GF5 hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102420. [Google Scholar] [CrossRef]
- Nowkandeh, S.M.; Noroozi, A.A.; Homaeec, M. Estimating soil organic matter content from Hyperion reflectance images using PLSR, PCR, MinR and SWR models in semi-arid regions of Iran. Environ. Dev. 2018, 25, 23–32. [Google Scholar] [CrossRef]
- Hong, Y.; Shen, R.; Cheng, H.; Chen, Y.; Zhang, Y.; Liu, Y.; Zhou, M.; Yu, L.; Liu, Y.; Liu, Y. Estimating lead and zinc concentrations in peri-urban agricultural soils through reflectance spectroscopy: Effects of fractional-order derivative and random forest. Sci. Total Environ. 2019, 651, 1969–1982. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Abulimiti, A.; Cai, L. Quantitative estimation of soil salinity by means of different modeling methods and visible-near infrared (VIS-NIR) spectroscopy, Ebinur Lake Wetland, Northwest China. PeerJ 2018, 6, e4703. [Google Scholar] [CrossRef] [Green Version]
- Lao, C.; Chen, J.; Zhang, Z.; Chen, Y.; Ma, Y.; Chen, H.; Gu, X.; Ning, J.; Jin, J.; Li, X. Predicting the contents of soil salt and major water-soluble ions with fractional-order derivative spectral indices and variable selection. Comput. Electron. Agric. 2021, 182, 106031. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Wang, J.; Ge, X. Prediction of soil organic matter in northwestern China using fractional order derivative spectroscopy and modified normalized difference indices. Catena 2020, 185, 104257. [Google Scholar] [CrossRef]
- Zhang, D.; Tiyip, T.; Ding, J.; Zhang, F.; Nurmemet, I.; Kelimu, A.; Wang, J. Quantitative Estimating Salt Content of Saline Soil Using Laboratory Hyperspectral Data Treated by Fractional Derivative. J. Spectrosc. 2016, 2016, 1081674. [Google Scholar] [CrossRef]
- Chen, K.; Li, C.; Tang, R. Estimation of the nitrogen concentration of rubber tree using fractional calculus augmented NIR spectra. Ind. Crops Prod. 2017, 108, 831–839. [Google Scholar] [CrossRef]
- Bao, Y.; Meng, X.; Ustin, S.; Wang, X.; Zhang, X.; Liu, H.; Tang, H. Vis-SWIR spectral prediction model for soil organic matter with different grouping strategies. Catena 2020, 195, 104703. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Y.; Wang, M.; Shi, X. Determination of rice root density from Vis–NIR spectroscopy by support vector machine regression and spectral variable selection techniques. Catena 2017, 157, 12–23. [Google Scholar] [CrossRef]
- Huang, Y.; Du, G.; Ma, Y.; Zhou, J. Predicting heavy metals in dark sun-cured tobacco by near-infrared spectroscopy modeling based on the optimized variable selections. Ind. Crops Prod. 2021, 172, 114003. [Google Scholar] [CrossRef]



| Zone | Models | Band Numbers | Order | Validation Set | ||
|---|---|---|---|---|---|---|
| R2 | RMSE | RPD | ||||
| I | R-FOD-FULL-PLSR | 1759 | 0.9 | 0.0049 | 4.6408 | 0.5322 |
| R-FOD-FULL-GRNN | 1759 | 0.5 | 0.0759 | 4.1106 | 0.7279 | |
| R-FOD-FULL-ELM | 1759 | 1.3 | 0.1407 | 7.5471 | 0.4889 | |
| R-FOD-FULL-RF | 1759 | 0.0 | 0.1312 | 4.6246 | 0.3445 | |
| II | R-FOD-FULL-PLSR | 1759 | 0.7 | 0.0027 | 10.5566 | 0.6757 |
| R-FOD-FULL-GRNN | 1759 | 0.6 | 0.0378 | 13.2326 | 0.7622 | |
| R-FOD-FULL-ELM | 1759 | 1.9 | 0.4799 | 20.3946 | 0.7796 | |
| R-FOD-FULL-RF | 1759 | 0.5 | 0.0050 | 7.6970 | 0.5349 | |
| III | R-FOD-FULL-PLSR | 1759 | 0.7 | 0.0805 | 13.0614 | 0.7121 |
| R-FOD-FULL-GRNN | 1759 | 0.0 | 0.6933 | 5.8371 | 1.6998 | |
| R-FOD-FULL-ELM | 1759 | 0.8 | 0.0037 | 35.4817 | 0.9357 | |
| R-FOD-FULL-RF | 1759 | 0.4 | 0.0061 | 12.3467 | 0.5793 | |
| Zone | Models | Band Numbers | Percentage | Order | Validation Set | ||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | RPD | |||||
| I | R-FOD-CC5-PLSR | 112 | 6.37% | 1.8 | 0.8556 | 1.7313 | 1.6595 |
| R-FOD-CC5-GRNN | 111 | 6.31% | 1.9 | 0.6025 | 2.5151 | 1.4608 | |
| R-FOD-CC5-ELM | 107 | 6.08% | 2.0 | 0.0933 | 4.1783 | 0.4900 | |
| R-FOD-CC5-RF | 277 | 15.75% | 1.0 | 0.5189 | 3.1324 | 0.3970 | |
| II | R-FOD-CC5-PLSR | 80 | 4.55% | 2.0 | 0.7071 | 4.0899 | 1.8402 |
| R-FOD-CC5-GRNN | 62 | 3.52% | 0.8 | 0.6549 | 5.1665 | 1.6786 | |
| R-FOD-CC5-ELM | 80 | 4.55% | 2.0 | 0.4381 | 7.5510 | 1.4062 | |
| R-FOD-CC5-RF | 48 | 2.73% | 0.7 | 0.1726 | 6.2721 | 0.6341 | |
| III | R-FOD-CC5-PLSR | 82 | 4.66% | 1.5 | 0.8608 | 4.8512 | 1.9301 |
| R-FOD-CC5-GRNN | 103 | 5.86% | 1.3 | 0.7499 | 5.7801 | 2.0969 | |
| R-FOD-CC5-ELM | 76 | 4.32% | 1.9 | 0.4366 | 12.6949 | 1.1784 | |
| R-FOD-CC5-RF | 40 | 2.27% | 0.5 | 0.1089 | 10.7689 | 0.6126 | |
| Zone | Models | Band Numbers | Percentage | Order | Validation Set | ||
|---|---|---|---|---|---|---|---|
| R2 | RMSE | RPD | |||||
| I | R-FOD-CC1-PLSR | 33 | 1.88% | 1.6 | 0.7777 | 2.3943 | 1.9980 |
| R-FOD-CC1-GRNN | 25 | 1.42% | 1.9 | 0.6052 | 2.6998 | 1.4209 | |
| R-FOD-CC1-ELM | 25 | 1.42% | 1.7 | 0.5511 | 4.0453 | 1.1952 | |
| R-FOD-CC1-RF | 112 | 6.37% | 1.0 | 0.5142 | 3.0449 | 0.4975 | |
| II | R-FOD-CC1-PLSR | 18 | 1.02% | 1.9 | 0.3861 | 7.0057 | 1.3167 |
| R-FOD-CC1-GRNN | 13 | 0.74% | 0.8 | 0.7978 | 3.0703 | 2.2450 | |
| R-FOD-CC1-ELM | 8 | 0.45% | 0.6 | 0.1807 | 7.8728 | 1.0532 | |
| R-FOD-CC1-RF | 12 | 0.68% | 0.7 | 0.2608 | 5.8521 | 0.6941 | |
| III | R-FOD-CC1-PLSR | 18 | 1.02% | 1.5 | 0.6947 | 9.2298 | 1.8032 |
| R-FOD-CC1-GRNN | 18 | 1.02% | 1.5 | 0.8030 | 6.1593 | 1.9502 | |
| R-FOD-CC1-ELM | 12 | 0.68% | 1.8 | 0.4477 | 9.6243 | 1.3528 | |
| R-FOD-CC1-RF | 22 | 1.25% | 1.2 | 0.5925 | 7.9509 | 0.6278 | |
| Zone | Models | Band Numbers | Percentage | Band Variable | Order | Validation Set | ||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | RPD | ||||||
| I | R-FOD-CC1-CARS-GRNN | 8 | 0.45% | 562, 581, 618, 641, 1046, 1197, 1275, 1694 nm | 1.5 | 0.7784 | 1.8762 | 2.0568 |
| R-FOD-CC1-GRNN | 25 | 1.42% | 572, 585, 612, 832, 1046,1197, 1263, 1274, 1426, 1693, 1710, 1713, 1762, 1773, 1963, 2170, 2197, 2198, 2208, 2254, 2267, 2334, 2358, 2361, 2385 nm | 1.9 | 0.6052 | 2.6998 | 1.4209 | |
| R-FOD-CC1-PLSR | 33 | 1.88% | 536, 545, 552, 556, 557, 559, 560, 561, 562, 585, 618, 641, 832, 1038, 1046, 1116, 1197, 1275, 1693, 1694, 1710, 1713, 1762, 1964, 2170, 2171, 2197, 2198, 2254, 2265, 2331, 2358, 2362 nm | 1.6 | 0.7777 | 2.3943 | 1.9980 | |
| II | R-FOD-CC1-CARS-GRNN | 9 | 0.51% | 418, 434, 469, 600, 744, 831, 1551, 1603, 1604 nm | 1.7 | 0.7912 | 3.4001 | 1.8985 |
| R-FOD-CC1-GRNN | 13 | 0.74% | 2039, 2040, 2045, 2046, 2047, 2084, 2094, 2212, 2213, 2244, 2293, 2304, 2326 nm | 0.8 | 0.7978 | 3.0703 | 2.2450 | |
| R-FOD-CC1-PLSR | 18 | 1.02% | 416, 434, 469, 584, 600, 636, 700, 744, 831, 868, 1440, 1603, 1606, 1754, 2044, 2048, 2312, 2396 nm | 1.9 | 0.3861 | 7.0057 | 1.3167 | |
| III | R-FOD-CC1-CARS-GRNN | 11 | 0.63% | 541, 555, 556, 570, 872, 886, 1663, 1694, 1795, 1799, 2227 nm | 1.6 | 0.8192 | 6.6260 | 1.8190 |
| R-FOD-CC1-GRNN | 18 | 1.02% | 541, 551, 555, 556, 569, 570, 886, 1502, 1634, 1663, 1694, 1794, 1795, 1798, 1799, 1990, 2120, 2227 nm | 1.5 | 0.8030 | 6.1593 | 1.9502 | |
| R-FOD-CC1-PLSR | 18 | 1.02% | 541, 551, 555, 556, 569, 570, 886, 1502, 1634, 1663, 1694, 1794, 1795, 1798, 1799, 1990, 2120, 2227 nm | 1.5 | 0.6947 | 9.2298 | 1.8032 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, C.; Tian, A.; Zhu, D.; Zhao, J.; Xiong, H. Estimation of Salinity Content in Different Saline-Alkali Zones Based on Machine Learning Model Using FOD Pretreatment Method. Remote Sens. 2021, 13, 5140. https://doi.org/10.3390/rs13245140
Fu C, Tian A, Zhu D, Zhao J, Xiong H. Estimation of Salinity Content in Different Saline-Alkali Zones Based on Machine Learning Model Using FOD Pretreatment Method. Remote Sensing. 2021; 13(24):5140. https://doi.org/10.3390/rs13245140
Chicago/Turabian StyleFu, Chengbiao, Anhong Tian, Daming Zhu, Junsan Zhao, and Heigang Xiong. 2021. "Estimation of Salinity Content in Different Saline-Alkali Zones Based on Machine Learning Model Using FOD Pretreatment Method" Remote Sensing 13, no. 24: 5140. https://doi.org/10.3390/rs13245140
APA StyleFu, C., Tian, A., Zhu, D., Zhao, J., & Xiong, H. (2021). Estimation of Salinity Content in Different Saline-Alkali Zones Based on Machine Learning Model Using FOD Pretreatment Method. Remote Sensing, 13(24), 5140. https://doi.org/10.3390/rs13245140







