Fractal and Multifractal Characteristics of Lineaments in the Qianhe Graben and Its Tectonic Significance Using Remote Sensing Images
Abstract
:1. Introduction
- to extract and evaluate the geological lineaments in the Qianhe Graben using various algorithms;
- to estimate the dimension and distribution characteristics of the lineaments using fractal and multifractal analysis;
- to reveal the tectonic significance of lineaments in this area.
2. Geological Background
3. Methods
3.1. Lineament Extraction
3.1.1. Segment Tracing Algorithm (STA)
3.1.2. LINE Algorithm in PCI Software
3.1.3. Tensor Voting (TV)
3.2. Fractal and Multifractal Analysis
3.2.1. Fractal Characteristics
3.2.2. Multifractal Characteristics
4. Results
4.1. Lineament Extraction and Validation
4.1.1. Lineament Extraction Results
4.1.2. Accuracy of Lineament Algorithm
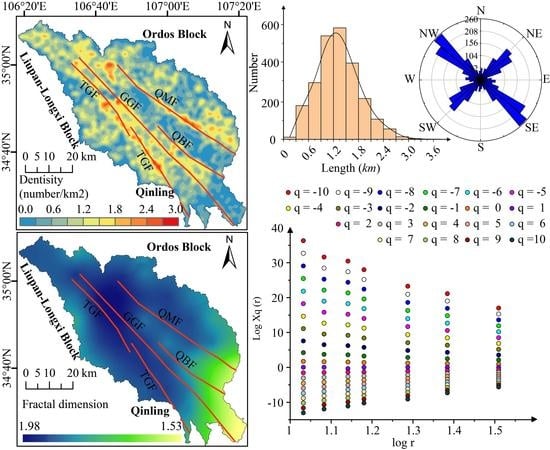
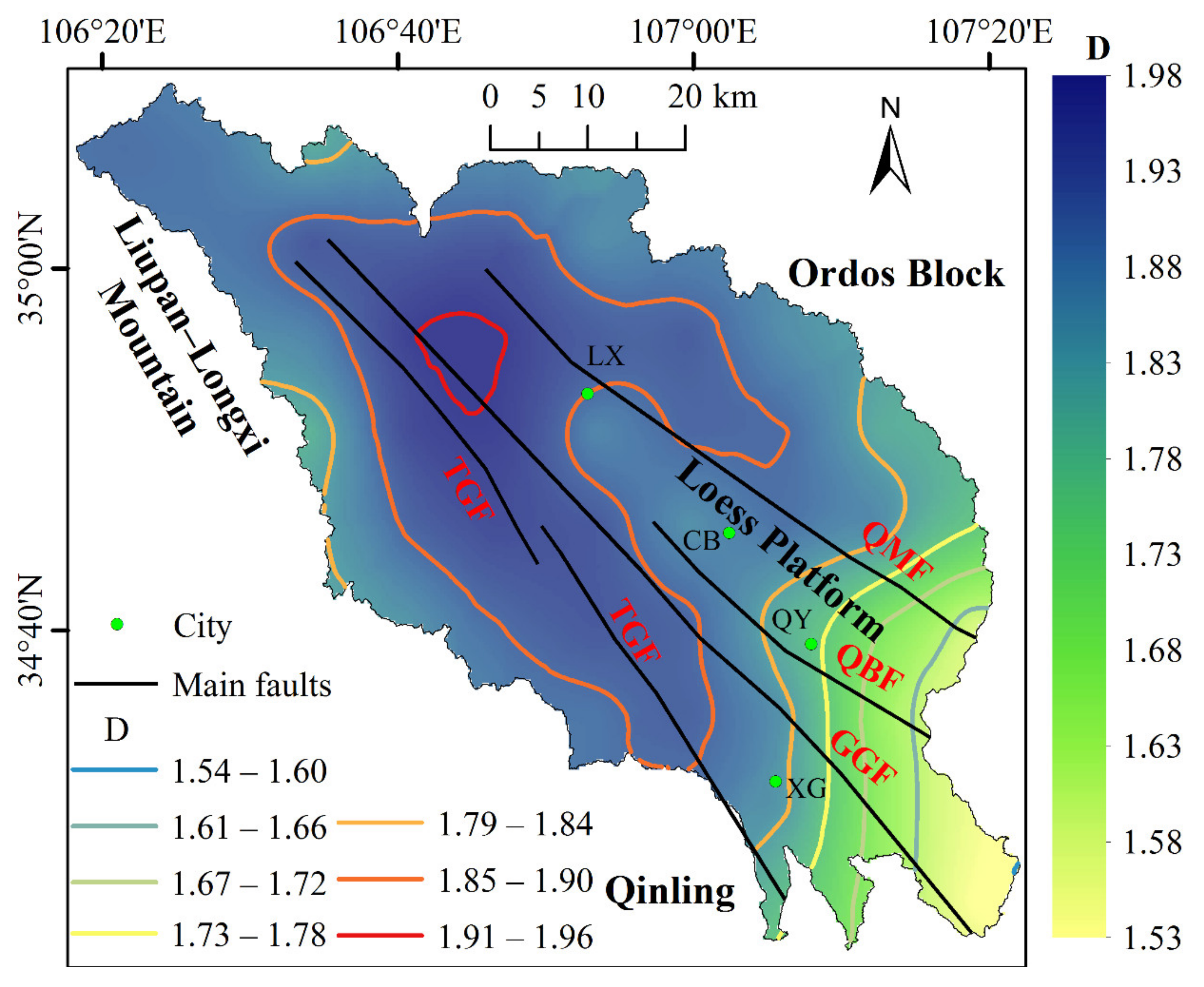
4.2. Fractal Characteristics
4.3. Multifractal Characteristics
5. Discussion
5.1. Why Do the Lineaments Have Fractal and Multifractal Characteristics?
5.2. Analysis of the Fractal Dimension and Multifractal Characteristics in the Qianhe Graben
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Clark, C.D.; Wilson, C. Spatial analysis of lineaments. Comput. Geosci. 1994, 20, 1237–1258. [Google Scholar] [CrossRef]
- Gabrielsen, R.H.; Braathen, A. Models of fracture lineaments—Joint swarms, fracture corridors and faults in crystalline rocks, and their genetic relations. Tectonophysics 2014, 628, 26–44. [Google Scholar] [CrossRef]
- Ni, C.; Zhang, S.; Chen, Z.; Yan, Y.; Li, Y. Mapping the Spatial Distribution and Characteristics of Lineaments Using Fractal and Multifractal Models: A Case Study from Northeastern Yunnan Province, China. Sci. Rep. 2017, 7, 10511. [Google Scholar] [CrossRef] [PubMed]
- He, H.; An, L.; Liu, W.; Yang, X.; Gao, Y.; Yang, L.; Suo, Y. Fractal characteristics of fault systems and their geological significance in the Hutouya poly-metallic orefield of Qimantage, East Kunlun, China. Geol. J. 2017, 52, 419–424. [Google Scholar] [CrossRef]
- Wang, N.; Liu, Y.; Peng, N.; Wu, C.; Liu, N.; Nie, B.; Yang, X. Fractal Characteristics of Fault Structures and Their Use for Mapping Ore-prospecting Potential in the Qitianling Area, Southern Hunan Province, China. Acta Geol. Sin. 2015, 89, 121–132. [Google Scholar]
- Bernardinetti, S.; Pieruccioni, D.; Mugnaioli, E.; Talarico, F.M.; Trotta, M.; Harroud, A.; Tufarolo, E. A pilot study to test the reliability of the ERT method in the identification of mixed sulphides bearing dykes: The example of Sidi Flah mine (Anti-Atlas, Morocco). Ore Geol. Rev. 2018, 101, 819–838. [Google Scholar] [CrossRef]
- Fridovsky, V.Y.; Polufuntikova, L.I.; Goryachev, N.A.; Kudrin, M.V. Ore-controlling thrust faults at the Bazovskoe gold-ore deposit (Eastern Yakutia). Dokl. Earth Sci. 2017, 474, 617–619. [Google Scholar] [CrossRef]
- Nouri, R.; Jafari, M.R.; Arian, M.; Feizi, F.; Afzal, P. Correlation between Cu mineralization and major faults using multifractal modelling in the Tarom area (NW Iran). Geol. Carpathica 2013, 64, 409–416. [Google Scholar] [CrossRef] [Green Version]
- Adib, A.; Afzal, P.; Mirzaei Ilani, S.; Aliyari, F. Determination of the relationship between major fault and zinc mineralization using fractal modeling in the Behabad fault zone, central Iran. J. Afr. Earth Sci. 2017, 134, 308–319. [Google Scholar] [CrossRef]
- Mirzaie, A.; Bafti, S.S.; Derakhshani, R. Fault control on Cu mineralization in the Kerman porphyry copper belt, SE Iran: A fractal analysis. Ore Geol. Rev. 2015, 71, 237–247. [Google Scholar] [CrossRef]
- Han, L.; Liu, Z.; Ning, Y.; Zhao, Z. Extraction and analysis of geological lineaments combining a DEM and remote sensing images from the northern Baoji loess area. Adv. Space Res. 2018, 62, 2480–2493. [Google Scholar] [CrossRef]
- Mallast, U.; Gloaguen, R.; Geyer, S.; Rödiger, T.; Siebert, C. Derivation of groundwater flow-paths based on semi-automatic extraction of lineaments from remote sensing data. Hydrol. Earth Syst. Sci. 2011, 15, 2665–2678. [Google Scholar] [CrossRef] [Green Version]
- Jun, D.; Yun, F.; Liqiang, Y.; Junchen, Y.; Zhongshi, S.; Jianping, W.; Shijiang, D.; Qingfei, W. Numerical Modelling of Ore-forming Dynamics of Fractal Dispersive Fluid Systems. Acta Geol. Sin. 2001, 75, 220–232. [Google Scholar] [CrossRef]
- Sheikhrahimi, A.; Pour, A.B.; Pradhan, B.; Zoheir, B. Mapping hydrothermal alteration zones and lineaments associated with orogenic gold mineralization using ASTER data: A case study from the Sanandaj-Sirjan Zone, Iran. Adv. Space Res. 2019, 63, 3315–3332. [Google Scholar] [CrossRef]
- Ramli, M.F.; Yusof, N.; Yusoff, M.K.; Juahir, H.; Shafri, H.Z.M. Lineament mapping and its application in landslide hazard assessment: A review. Bull. Eng. Geol. Environ. 2010, 69, 215–233. [Google Scholar] [CrossRef]
- Koike, K.; Nagano, S.; Ohmi, M. Lineament analysis of satellite images using a Segment Tracing Algorithm (STA). Comput. Geosci. 1995, 21, 1091–1104. [Google Scholar] [CrossRef]
- Karnieli, A.; Meisels, A.; Fisher, L.; Arkin, Y. Automatic extraction and evaluation of geological linear features from digital remote sensing data using a Hough transform. Photogramm. Eng. Remote Sens. 1996, 62, 525–531. [Google Scholar] [CrossRef]
- Elmahdy, S.I.; Ali, T.A.; Mohamed, M.M.; Yahia, M. Topographically and hydrologically signatures express subsurface geological structures in an arid region: A modified integrated approach using remote sensing and GIS. Geocarto Int. 2020, 1–21. [Google Scholar] [CrossRef]
- Hashim, M.; Ahmad, S.; Johari, M.A.M.; Pour, A.B. Automatic lineament extraction in a heavily vegetated region using Landsat Enhanced Thematic Mapper (ETM+) imagery. Adv. Space Res. 2013, 51, 874–890. [Google Scholar] [CrossRef]
- Alhirmizy, S.M. Automatic Mapping of Lineaments Using Shaded Relief Images Derived From Digital Elevation Model (DEM) in Kirkuk northeast Iraq. Int. J. Sci. Res. 2015, 4, 2319–7064. [Google Scholar]
- Vasuki, Y.; Holden, E.-J.; Kovesi, P.; Micklethwaite, S. Semi-automatic mapping of geological Structures using UAV-based photogrammetric data: An image analysis approach. Comput. Geosci. 2014, 69, 22–32. [Google Scholar] [CrossRef]
- Bisdom, K.; Nick, H.M.; Bertotti, G. An integrated workflow for stress and flow modelling using outcrop-derived discrete fracture networks. Comput. Geosci. 2017, 103, 21–35. [Google Scholar] [CrossRef] [Green Version]
- Thiele, S.T.; Grose, L.; Samsu, A.; Micklethwaite, S.; Vollgger, S.A.; Cruden, A.R. Rapid, semi-automatic fracture and contact mapping for point clouds, images and geophysical data. Solid Earth 2017, 8, 1241–1253. [Google Scholar] [CrossRef] [Green Version]
- Martínez, M.F.; Guirao, J.L.G.; Sánchez-Granero, M.Á.; Segovia, J.E.T. Fractal Dimension for Fractal Structures. Topol. Appl. 2019, 163, 93–111. [Google Scholar] [CrossRef]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Barton, C.C.; La Pointe, P.R. Fractals in Petroleum Geology and Earth Processes; Plenum Publishing Corp.: New York, NY, USA, 1995. [Google Scholar]
- Zhang, S.; Yang, S.; Cheng, J.; Zhang, B.; Lu, C. Study on Relationships between Coal Fractal Characteristics and Coal and Gas Outburst. Procedia Eng. 2011, 26, 327–334. [Google Scholar] [CrossRef] [Green Version]
- Cello, G.; Malamud, B.D. Fractal Analysis for Natural Hazards; Geological Society of London: London, UK, 2006. [Google Scholar]
- Xiaohua, Z.; Yunlong, C.; Xiuchun, Y. On Fractal Dimensions of China’s Coastlines. Math. Geol. 2004, 36, 447–461. [Google Scholar] [CrossRef]
- Klinkenberg, B. Fractals and morphometric measures: Is there a relationship? Geomorphology 1992, 5, 5–20. [Google Scholar] [CrossRef]
- Donadio, C.; Paliaga, G.; Radke, J.D. Tsunamis and rapid coastal remodeling: Linking energy and fractal dimension. Prog. Phys. Geogr. Earth Environ. 2019, 44, 550–571. [Google Scholar] [CrossRef]
- Paliaga, G. Erosion Triangular Facets as Markers of Order in an Open Dissipative System. Pure Appl. Geophys. 2014, 172, 1985–1997. [Google Scholar] [CrossRef]
- Zhong, X.; Yu, P.; Chen, S. Fractal properties of shoreline changes on a storm-exposed island. Sci. Rep. 2017, 7, 8274. [Google Scholar] [CrossRef] [Green Version]
- Mabee, S.B.; Curry, P.J.; Hardcastle, K.C. Correlation of Lineaments to Ground Water Inflows in a Bedrock Tunnel. Groundwater 2002, 40, 37–43. [Google Scholar] [CrossRef]
- Gonçalves, M.A.; Mateus, A.; Pinto, F.; Vieira, R. Using multifractal modelling, singularity mapping, and geochemical indexes for targeting buried mineralization: Application to the W-Sn Panasqueira ore-system, Portugal. J. Geochem. Explor. 2018, 189, 42–53. [Google Scholar] [CrossRef]
- Kaixuan, T.; Yanshi, X. Multifractal Mechanism of Faults Controlling Hydrothermal Deposits in Altay, Xinjiang, China. Geotecton. Et Metallog. 2010, 34, 32–39. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, S.; Zuo, R.; Carranza, E.J.M. Mapping complexity of spatial distribution of faults using fractal and multifractal models: Vectoring towards exploration targets. Comput. Geosci. 2011, 37, 1958–1966. [Google Scholar] [CrossRef]
- Guarnieri, P. Regional strain derived from fractal analysis applied to strike-slip fault systems in NW Sicily. Chaos Solitons Fractals 2002, 14, 71–76. [Google Scholar] [CrossRef]
- Liu, Z.; Han, L.; Boulton, S.J.; Wu, T.; Guo, J. Quantifying the transient landscape response to active faulting using fluvial geomorphic analysis in the Qianhe Graben on the southwest margin of Ordos, China. Geomorphology 2020, 351, 106974. [Google Scholar] [CrossRef]
- Xiang, J.; Xu, Y.; Yuan, J.; Wang, Q.; Wang, J.; Deng, X. Multifractal Analysis of River Networks in an Urban Catchment on the Taihu Plain, China. Water 2019, 11, 2283. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Qu, G.; JACOBI, R.D. Fractal and Multifractal Properties of the Spatial Distribution of Natural Fractures—Analyses and Applications. Acta Geol. Sin. 1999, 73, 477–487. [Google Scholar]
- Li, W. Multifractal characteristics of various metallogenic elements in Damoqujia ore deposit, Shandong province. Acta Petrol. Sin. 2007, 23, 1211–1216. [Google Scholar]
- Wang, Q.; Deng, J.; Wan, L.; Zhao, J.; Gong, Q.; Yang, L.; Zhou, L.; Zhang, Z. Multifractal Analysis of Element Distribution in Skarn-type Deposits in the Shizishan Orefield, Tongling Area, Anhui Province, China. Acta Geol. Sin. 2008, 82, 896–905. [Google Scholar]
- Zhang, T.; Fan, S.; Chen, S.; Li, S.; Lu, Y. Geomorphic evolution and neotectonics of the Qianhe River Basin on the southwest margin of the Ordos Block, North China. J. Asian Earth Sci. 2019, 176, 184–195. [Google Scholar] [CrossRef]
- Chen, S.; Fan, S.; Wang, X.; Wang, R.; Liu, Y.; Yang, L.; Ning, X.; Li, R. Neotectonic movement in the southern margin of the Ordos Block inferred from the Qianhe River terraces near the north of the Qinghai-Tibet Plateau. Geol. J. 2018, 53, 274–281. [Google Scholar] [CrossRef]
- Lin, A.; Rao, G.; Yan, B. Flexural fold structures and active faults in the northern–western Weihe Graben, central China. J. Asian Earth Sci. 2015, 114, 226–241. [Google Scholar] [CrossRef] [Green Version]
- Zheng, W.; Yuan, D.; Zhang, P.; Yu, J.; Lei, Q.; Wang, W.; Zheng, D.; Zhang, H.; Li, X.; Li, C.; et al. Tectonic geometry and kinematic dissipation of the active faults in the northeastern Tibetan Plateau and their implications for understanding northeastward growth of the plateau. Quat. Sci. 2016, 36, 775–788. [Google Scholar] [CrossRef]
- Shi, X.; Yang, Z.; Dong, Y.; Wang, S.; He, D.; Zhou, B.; Somerville, I.D. Longitudinal profile of the Upper Weihe River: Evidence for the late Cenozoic uplift of the northeastern Tibetan Plateau. Geol. J. 2018, 53, 364–378. [Google Scholar] [CrossRef]
- Fan, S.; Li, R.; Wang, R. The 1:50,000 Geological Mapping in the Loess-Coveredregion with the Map Sheets: Caobizhen (I48E008021), Liangting (I48E008022), Zhaoxian (I48E008023), Qianyang (I48E009021), Fengxiang (I48E009022), and Yaojiagou (I48E009023) in Shaanxi Province, China; Chang’an University: Xi’an, China, 2016. [Google Scholar]
- Fan, S.; Li, Q.; Han, L.; Liang, J.; Chen, S.; Zhang, T.; Ma, J.; Liu, Z. The 1:50,000 Geological Mapping in the Loess-Covered Region in Shaanxi Province, China; Chang’an University: Xi’an, China, 2020. [Google Scholar]
- Shi, W. The Analysis of the Development Characteristics and Activity about Fault Zone of Longxian-Baoji; Chang’an University: Xi’an, China, 2011. [Google Scholar]
- Li, W.; Dong, Y.; Guo, A.; Liu, X.; Zhou, D. Chronology and tectonic significance of Cenozoic faults in the Liupanshan Arcuate Tectonic Belt at the northeastern margin of the Qinghai–Tibet Plateau. J. Asian Earth Sci. 2013, 73, 103–113. [Google Scholar] [CrossRef]
- Lin, X.; Chen, H.; Wyrwoll, K.-H.; Batt, G.E.; Liao, L.; Xiao, J. The Uplift History of the Haiyuan-Liupan Shan Region Northeast of the Present Tibetan Plateau: Integrated Constraint from Stratigraphy and Thermochronology. J. Geol. 2011, 119, 372–393. [Google Scholar] [CrossRef]
- Liang, M.; Wang, Z.; Zhou, S.; Zong, K.; Hu, Z. The provenance of Gansu Group in Longxi region and implications for tectonics and paleoclimate. Sci. China Earth Sci. 2014, 57, 1221–1228. [Google Scholar] [CrossRef]
- Shi, X. Tectonic Geomorphology in Qinling-Daba Mountains and Its Geodynamic Implications; Northwest University: Kirkland, WA, USA, 2018. [Google Scholar]
- Fan, S.; Zhang, T.; Chen, S.e.; Li, R. New findings regarding the Fen-Wei Graben on the southeastern margin of the Ordos Block: Evidence from the Cenozoic sedimentary record from the borehole. Geol. J. 2020, 55, 7581–7593. [Google Scholar] [CrossRef]
- Qari, M.H.T. Lineament extraction from multi-resolution satellite imagery: A pilot study on Wadi Bani Malik, Jeddah, Kingdom of Saudi Arabia. Arab. J. Geosci. 2011, 4, 1363–1371. [Google Scholar] [CrossRef]
- Ni, C.Z.; Zhang, S.T.; Liu, C.X.; Yan, Y.F.; Li, Y.J. Lineament Length and Density Analyses Based on the Segment Tracing Algorithm: A Case Study of the Gaosong Field in Gejiu Tin Mine, China. Math. Probl. Eng. 2016, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Saepuloh, A.; Heriawan, M.N.; Kubo, T. Identification of linear features at geothermal field based on Segment Tracing Algorithm (STA) of the ALOS PALSAR data. IOP Conf. Ser. Earth Environ. Sci. 2016, 42, 012003. [Google Scholar]
- Liu, C.; Ni, C.; Yan, Y.; Tan, L. Automatically extraction of lineaments from DEM. Remote Sens. Technol. Appl. 2014, 29, 273–277. [Google Scholar] [CrossRef]
- Salui, C.L. Methodological Validation for Automated Lineament Extraction by LINE Method in PCI Geomatica and MATLAB based Hough Transformation. J. Geol. Soc. India 2018, 92, 321–328. [Google Scholar] [CrossRef]
- Chao, H.; Kerwin, W.S.; Hatsukami, T.S.; Jenq-Neng, H.; Chun, Y. Detecting objects in image sequences using rule-based control in an active contour model. IEEE Trans. Biomed. Eng. 2003, 50, 705–710. [Google Scholar] [CrossRef]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 3rd ed.; Prentice-Hall Inc.: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Tam, V.T.; De Smedt, F.; Batelaan, O.; Dassargues, A. Study on the relationship between lineaments and borehole specific capacity in a fractured and karstified limestone area in Vietnam. Hydrogeol. J. 2004, 12, 662–673. [Google Scholar] [CrossRef] [Green Version]
- Rahnama, M.; Gloaguen, R. TecLines: A MATLAB-Based Toolbox for Tectonic Lineament Analysis from Satellite Images and DEMs, Part 1: Line Segment Detection and Extraction. Remote Sens. 2014, 6, 5938–5958. [Google Scholar] [CrossRef] [Green Version]
- Rahnama, M.; Gloaguen, R. TecLines: A MATLAB-Based Toolbox for Tectonic Lineament Analysis from Satellite Images and DEMs, Part 2: Line Segments Linking and Merging. Remote Sens. 2014, 6, 11468–11493. [Google Scholar] [CrossRef] [Green Version]
- Goren, L.; Fox, M.; Willett, S.D. Tectonics from fluvial topography using formal linear inversion: Theory and applications to the Inyo Mountains, California. J. Geophys. Res. Earth Surf. 2014, 119, 1651–1681. [Google Scholar] [CrossRef]
- Maboudi, M.; Amini, J.; Hahn, M.; Saati, M. Road Network Extraction from VHR Satellite Images Using Context Aware Object Feature Integration and Tensor Voting. Remote Sens. 2016, 8, 637. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Zhang, B.; Liu, D.; Yang, T.; Song, W.; Li, F. Durface crack detection algorithm based on double threshold and tensor voting. Laser Optoelectron. Prog. 2018, 55, 167–174. [Google Scholar] [CrossRef]
- Wen, P.; Huang, J.; Ning, R.; Wu, X. Boundary extraction of active contour based on tensor voting. Comput. Eng. 2012, 38, 216–218. [Google Scholar] [CrossRef]
- Cross, A.M. Detection of circular geological features using the Hough transform. Int. J. Remote Sens. 1988, 9, 1519–1528. [Google Scholar] [CrossRef]
- Lyngsie, S.B.; Thybo, H.; Rasmussen, T.M. Regional geological and tectonic structures of the North Sea area from potential field modelling. Tectonophysics 2006, 413, 147–170. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature. Am. J. Phys. 1998, 51, 468. [Google Scholar] [CrossRef]
- Sun, T.; Li, H.; Wu, K.; Chen, L.; Liu, W.; Hu, Z. Fractal and Multifractal Characteristics of Regional Fractures in Tongling Metallogenic Area. Nonferr. Met. Eng. 2018, 8, 111–115. [Google Scholar] [CrossRef]
- Wu, C. Fractal characteristcs of lineaments in Fozichong lead-zine district. China Min. Mag. 2017, 26, 233–236. [Google Scholar]
- Cheng, Q. Singularity-Generalized Self-Similarity-Fractal Spectrum (3S) Models. Earth Sci. J. China Univ. Geosci. 2006, 31, 337–348. [Google Scholar]
- Cao, J.; Fang, X.; Na, J.; Tang, G. Study on the characteristics of the topographic relief of shoulder line of different geomorphic types in Loess Plateau based on multi-fractal. Geogr. Geo-Inf. Sci. 2017, 33, 51–56. [Google Scholar] [CrossRef]
- Zhao, J.; Lei, L.; Pu, X. Fractal Theory and Its Application in Signal Processing; Tsinghua University Press: Beijing, China, 2008. [Google Scholar]
- Li, S.; Yu, H.; Luo, Q.; Liu, Y.; He, J.; Lin, Y.; Wang, D.; Li, J. Variation characteristics of soil particle composition and multifractal analysis of natural recovery forestland after damage under the disturbance of flood induced disasters. J. Beijing For. Univ. 2020, 4, 112–121. [Google Scholar] [CrossRef]
- Yang, X.; Han, J.; Qin, H. Analysis of Multifractual of Lava’s Extension Fracture on the West of Laoheishan Volcano, Wudalianchi. J. Cap. Norm. Univ. 2012, 33, 62–66. [Google Scholar] [CrossRef]
- Chen, G. Identifying Weak but Complex Geophysical and Geochemical Anomalies Caused by Buried Ore Bodies Using Fractal and Wavelet Methods; China University of Geosciences (Wuhan): Wuhan, China, 2016. [Google Scholar]
- Chen, P.; Peng, S.; Wang, P.; Chen, X.; Yang, T.; Liu, Y. Fractal and multifractal characteristics of geological faults in coal mine area and their control on outburst. Coal Sci. Technol. 2019, 47, 47–52. [Google Scholar] [CrossRef]
- Qu, W.; Lu, Z.; Zhang, Q.; Wang, Q.; Hao, M.; Zhu, W.; Qu, F. Crustal deformation and strain fields of the Weihe Basin and surrounding area of central China based on GPS observations and kinematic models. J. Geodyn. 2018, 120, 1–10. [Google Scholar] [CrossRef]
- Qu, W.; Lu, Z.; Zhang, Q.; Li, Z.; Peng, J.; Wang, Q.; Drummond, J.; Zhang, M. Kinematic model of crustal deformation of Fenwei basin, China based on GPS observations. J. Geodyn. 2014, 75, 1–8. [Google Scholar] [CrossRef]
- Wang, F.; Peng, J.; Lu, Q.; Cheng, Y.; Meng, Z.; Qiao, J. Mechanism of Fuping ground fissure in the Weihe Basin of northwest China: Fault and rainfall. Environ. Earth Sci. 2019, 78. [Google Scholar] [CrossRef]
- Telesca, L.; Lapenna, V.; Macchiato, M. Mono- and multi-fractal investigation of scaling properties in temporal patterns of seismic sequences. Chaos Solitons Fractals 2004, 19, 1–15. [Google Scholar] [CrossRef]
- Mao, H.; Zhang, M.; Jiang, R.; Li, B.; Xu, J.; Xu, N. Study on deformation pre-warning of rock slopes based on multi-fractal characteristics of microseismic signals. Chin. J. Rock Mech. Eng. 2020, 39, 560–571. [Google Scholar]
- Zhang, Y.; Ma, Y.; Yang, N.; Shi, W.; Dong, S. Cenozoic extensional stress evolution in North China. J. Geodyn. 2003, 36, 591–613. [Google Scholar] [CrossRef]
- Bai, D.; Unsworth, M.J.; Meju, M.A.; Ma, X.; Teng, J.; Kong, X.; Sun, Y.; Sun, J.; Wang, L.; Jiang, C.; et al. Crustal deformation of the eastern Tibetan plateau revealed by magnetotelluric imaging. Nat. Geosci. 2010, 3, 358–362. [Google Scholar] [CrossRef]
- Lei, T.; Cui, F.; Yu, F.; Xu, H. Study on Fractal Feature of Fault Structure and Its Geological Implications Based on Remote Sensing—A Case Study of Jiuyi Mountain Area, Southern Hunan. Geol. Rev. 2012, 58, 594–600. [Google Scholar] [CrossRef]
- Yu, M.; Wen, X.; Zhu, A.; Xu, J.; Li, C.; Min, G. Application of Fractal Statistics of Remote Sensing Linear Structure in Maoping Lead-Zinc Deposit. In Proceedings of the 2015 Conference of Geological Society of China, Xi’an, China, 23–29 November 2015; pp. 324–336. [Google Scholar]
- Lyu, C.; Cheng, Q.; Zuo, R.; Wang, X. Mapping spatial distribution characteristics of lineaments extracted from remote sensing image using fractal and multifractal models. J. Earth Sci. 2017, 28, 207–515. [Google Scholar] [CrossRef]
- Fan, C.; Qin, Q.; Hu, D.; Wang, X.; Zhu, M.; Huang, W.; Li, Y.; Ashraf, M.A. Fractal characteristics of reservoir structural fracture: A case study of Xujiahe Formation in central Yuanba area, Sichuan Basin. Earth Sci. Res. J. 2018, 22, 113–118. [Google Scholar] [CrossRef]
- Pavičić, I.; Dragičević, I.; Vlahović, T.; Grgasović, T. Fractal Analysis of Fracture Systems in Upper Triassic Dolomites in Žumberak Mountain, Croatia. Rud. Geološko Naft. Zb. 2017, 32, 1–13. [Google Scholar] [CrossRef]
- Kong, F.; Ding, G. The implications of the fractal dimension values of lineaments. Earthquake 1991, 10, 33–37. [Google Scholar]







| Region | Manually | STA | PCI | Tensor Voting |
|---|---|---|---|---|
| (a) | 65 | 213 | 183 | 185 |
| (b) | 58 | 146 | 123 | 114 |
| (c) | 55 | 205 | 128 | 147 |
| (d) | 55 | 206 | 238 | 140 |
| Region | Methods | TP (km) | FP (km) | FN (km) | A (%) | P (%) | R (%) | F1 |
|---|---|---|---|---|---|---|---|---|
| (a) | STA | 125.19 | 41.24 | 39.07 | 68.47 | 75.22 | 76.21 | 0.76 |
| PCI | 114.32 | 45.02 | 49.69 | 62.06 | 71.75 | 69.70 | 0.71 | |
| TV | 146.19 | 29.59 | 21.43 | 81.45 | 83.17 | 87.22 | 0.85 | |
| (b) | STA | 130.19 | 32.40 | 25.32 | 78.52 | 80.07 | 83.72 | 0.82 |
| PCI | 111.67 | 30.21 | 38.64 | 68.56 | 78.71 | 74.29 | 0.76 | |
| TV | 131.50 | 28.90 | 23.72 | 80.03 | 81.98 | 84.72 | 0.83 | |
| (c) | STA | 98.61 | 29.68 | 23.45 | 74.35 | 76.86 | 80.79 | 0.79 |
| PCI | 102.27 | 22.68 | 19.24 | 78.87 | 81.85 | 84.17 | 0.83 | |
| TV | 109.34 | 24.49 | 13.34 | 83.56 | 81.70 | 89.13 | 0.85 | |
| (d) | STA | 90.69 | 27.09 | 20.97 | 72.11 | 77.00 | 81.22 | 0.79 |
| PCI | 94.33 | 28.69 | 17.74 | 74.52 | 76.68 | 84.17 | 0.80 | |
| TV | 107.12 | 20.11 | 7.59 | 86.31 | 84.19 | 93.38 | 0.89 |
| No. | Region | Δα | References |
|---|---|---|---|
| 1 | Fault zone of Jiaozuo mining area in Henan, China | 0.3–2.0 | [82] |
| 2 | Altay, Xinjiang, China | 0.81 | [36] |
| 3 | Tongling metallogenic area, China | 1.35 | [74] |
| 4 | Northeastern Yunnan Pb–Zn metallogenic belt, China | 1.60 | [3] |
| No. | Region | Box Dimensions | References |
|---|---|---|---|
| 1 | Polymetallic ore field in Hutouya, China | 1.09 | [4] |
| 2 | Jiuyi Mountain fault zone in southern Hunan, China | 1.12 | [90] |
| 3 | Maoping Pb–Zn Mine in Zhaotong, Yunnan, China | 1.28 | [91] |
| 4 | Metallogenic area in Tongling, China | 1.29 | [74] |
| 5 | Shanghang–Yunxiao metallogenic belt, China | 1.36 | [92] |
| 6 | Central Sichuan Basin fault zone, China | 1.53 | [93] |
| 7 | Pb–Zn district in Fozichong, China | 1.53 | [75] |
| 8 | Croatia Zumberak Mountain fault zone, Croatia | 1.69–1.78 | [94] |
| 9 | Pb–Zn metallogenic belt in Northeastern Yunnan, China | 1.98 | [3] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Han, L.; Du, C.; Cao, H.; Guo, J.; Wang, H. Fractal and Multifractal Characteristics of Lineaments in the Qianhe Graben and Its Tectonic Significance Using Remote Sensing Images. Remote Sens. 2021, 13, 587. https://doi.org/10.3390/rs13040587
Liu Z, Han L, Du C, Cao H, Guo J, Wang H. Fractal and Multifractal Characteristics of Lineaments in the Qianhe Graben and Its Tectonic Significance Using Remote Sensing Images. Remote Sensing. 2021; 13(4):587. https://doi.org/10.3390/rs13040587
Chicago/Turabian StyleLiu, Zhiheng, Ling Han, Chengyan Du, Hongye Cao, Jianhua Guo, and Haiyang Wang. 2021. "Fractal and Multifractal Characteristics of Lineaments in the Qianhe Graben and Its Tectonic Significance Using Remote Sensing Images" Remote Sensing 13, no. 4: 587. https://doi.org/10.3390/rs13040587
APA StyleLiu, Z., Han, L., Du, C., Cao, H., Guo, J., & Wang, H. (2021). Fractal and Multifractal Characteristics of Lineaments in the Qianhe Graben and Its Tectonic Significance Using Remote Sensing Images. Remote Sensing, 13(4), 587. https://doi.org/10.3390/rs13040587