Next Article in Journal
Geomorphological and Spatial Characteristics of Underwater Volcanoes in the Easternmost Australian-Antarctic Ridge
Next Article in Special Issue
Sea Ice Concentration and Sea Ice Extent Mapping with L-Band Microwave Radiometry and GNSS-R Data from the FFSCat Mission Using Neural Networks
Previous Article in Journal
Improved Mekong Basin Runoff Estimate and Its Error Characteristics Using Pure Remotely Sensed Data Products
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 13
Issue 5
10.3390/rs13050994
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Soil Moisture Estimation Synergy Using GNSS-R and L-Band Microwave Radiometry Data from FSSCat/FMPL-2

by
Joan Francesc Munoz-Martin
1,*,
David Llaveria
1,
Christoph Herbert
1,
Miriam Pablos
2,3,
Hyuk Park
1 and
Adriano Camps
1
1
CommSensLab—UPC, Universitat Politècnica de Catalunya—BarcelonaTech and IEEC/CTE-UPC, 08034 Barcelona, Spain
2
Physical and Technological Oceanography Group, Institut de Ciències del Mar, Consejo Superior de Investigaciones Científicas (ICM-CSIC), Centre of Excellence Severo Ochoa, Passeig Marítim de la Barceloneta 37-49, 08003 Barcelona, Spain
3
Barcelona Expert Center on Remote Sensing (BEC), Passeig Marítim de la Barceloneta 37-49, 08003 Barcelona, Spain
*
Author to whom correspondence should be addressed.
Remote Sens. 2021, 13(5), 994; https://doi.org/10.3390/rs13050994
Submission received: 4 February 2021 / Revised: 28 February 2021 / Accepted: 2 March 2021 / Published: 5 March 2021
(This article belongs to the Special Issue Applications of GNSS Reflectometry for Earth Observation II)
Browse Figures
Versions Notes

Abstract

:
The Federated Satellite System mission (FSSCat) was the winner of the 2017 Copernicus Masters Competition and the first Copernicus third-party mission based on CubeSats. One of FSSCat’s objectives is to provide coarse Soil Moisture (SM) estimations by means of passive microwave measurements collected by Flexible Microwave Payload-2 (FMPL-2). This payload is a novel CubeSat based instrument combining an L1/E1 Global Navigation Satellite Systems-Reflectometer (GNSS-R) and an L-band Microwave Radiometer (MWR) using software-defined radio. This work presents the first results over land of the first two months of operations after the commissioning phase, from 1 October to 4 December 2020. Four neural network algorithms are implemented and analyzed in terms of different sets of input features to yield maps of SM content over the Northern Hemisphere (latitudes above 45° N). The first algorithm uses the surface skin temperature from the European Centre of Medium-Range Weather Forecast (ECMWF) in conjunction with the 16 day averaged Normalized Difference Vegetation Index (NDVI) from the Moderate Resolution Imaging Spectroradiometer (MODIS) to estimate SM and to use it as a comparison dataset for evaluating the additional models. A second approach is implemented to retrieve SM, which complements the first model using FMPL-2 L-band MWR antenna temperature measurements, showing a better performance than in the first case. The error standard deviation of this model referred to the Soil Moisture and Ocean Salinity (SMOS) SM product gridded at 36 km is 0.074 m 3 / m 3 . The third algorithm proposes a new approach to retrieve SM using FMPL-2 GNSS-R data. The mean and standard deviation of the GNSS-R reflectivity are obtained by averaging consecutive observations based on a sliding window and are further included as additional input features to the network. The model output shows an accurate SM estimation compared to a 9 km SMOS SM product, with an error of 0.087 m 3 / m 3 . Finally, a fourth model combines MWR and GNSS-R data and outperforms the previous approaches, with an error of just 0.063 m 3 / m 3 . These results demonstrate the capabilities of FMPL-2 to provide SM estimates over land with a good agreement with respect to SMOS SM.

Graphical Abstract

1. Introduction

Soil Moisture (SM) is one of the Essential Climate Variables (ECVs) [1] needed to better understand the water cycle. The soil is a natural water reservoir, and it is used by plants as a nutrient carrier. The amount of SM has great relevance in dividing incoming radiation over land into latent and sensible heat fluxes through evaporation and transpiration and in partitioning precipitation into runoff, subsurface flow, and infiltration. The risk of flooding [2] and erosion [3], the deployment of sustainable irrigation policies, the prevention of forest fires, the assessment of vegetation senescence, and the comprehensive understanding of land-atmosphere feedback loops in a changing climate require constant SM monitoring [4].
There are several methods to measure SM, each of them having different spatio-temporal resolutions. First, in situ probes are able to provide continuous and accurate measurements at a single point, but they have limited spatial coverage, so they are not feasible to intensively monitor large areas. Second, proximal soil sensing technologies, such as electromagnetic induction and ground-penetrating radar, are increasingly being used to sense SM in many field experiments. This technology provides good accuracy and better coverage as compared to probes, but with lower temporal resolution [5,6,7]. Finally, remote sensing techniques, including airborne and spaceborne platforms, have been broadly used over extended regions, allowing sensing SM at a global scale.
Focusing on satellite remote sensing, currently, there are different sensors to retrieve the surface SM (i.e., the water content within the first centimeters of the soil) [8]. Their penetration depth mainly depends on the frequency of operation, decreasing with the frequency and the SM conditions, being higher for dry soils than for wet soils. Optical based sensors, as those acquiring reflectances or thermal infrared data [9,10,11], have been used to retrieve SM due to their high spatial resolution, but they are limited by the vegetation cover and the cloud conditions and cannot acquire during night time. Passive microwave based sensors are neither affected by clouds, nor Sun illumination. In this regard, two L-band radiometers, as the Microwave Imaging Radiometer using Aperture Synthesis (MIRAS) instrument onboard the Soil Moisture and Ocean Salinity (SMOS) mission from the European Space Agency (ESA) [12], and the one onboard the Soil Moisture Active Passive (SMAP) mission from the National Aeronautics and Space Administration (NASA) [13], are currently providing surface SM measurements with global coverage with an average revisit time of ~3 days and a spatial resolution of ~40 km. Moreover, active microwave based sensors (radars), such as scatterometers (e.g., Neiami et al. [14]) or Synthetic Aperture Radars (SAR) (e.g., Hegarat et al. [15], Pathe et al. [16], Srivastava et al. [17], Paloscia et al. [18], or Gorrab et al. [19]) have also been used to retrieve near-surface SM indices from space. Recently, a multi-static radar approach based on Global Navigation Satellite System-Reflectometry (GNSS-R) has also been proven to allow SM retrievals from space [20,21,22]. Observations provided by the TechDemoSat-1 (TDS-1) mission have proven to be sensitive to SM [23,24], indicating that GNSS-R is capable of estimating SM. However, the large dispersion in the reflectivity produced by the surface roughness [20,25] makes a single-pass retrieval from GNSS-R data a titanic task [26].
Thanks to the large amount of data collected by the Cyclone GNSS (CyGNSS) constellation [27,28] and by the evolution of data-driven and machine learning algorithms, promising results have been achieved in the last few years, as they are able to recognize “hidden” patterns in large amounts of data. Several algorithms have been applied to retrieve SM using Artificial Neural Networks (ANNs) [21,29,30]. These algorithms can easily solve complex non-linear problems, which traditional approaches often fail to address adequately. Prior to the model training, GNSS-R observations can be combined differently in terms of preceding averaging, gridding, and time-series processing. In previous research studies, multiple GNSS-R observables were combined in different ways, such as performing multiple averages into a 36 km grid [29,31], computing spatio-temporal averages to finer grids (achieving a resolution of 22 km), or by means of time-series analysis [32].
Aside from CyGNSS, several missions carrying a GNSS-R instrument have been launched, such as the BuFeng-1 A/B [33] mission, the two GNSS-R CubeSats from Spire [34], or the Federated Satellite System mission (FSSCat).
The FSSCat mission was the 2017 ESA S⌃3Challenge and the 2017 Copernicus Master overall winner [35]. Even due to the delays produced by the explosion of Vega VV15and the 2020 COVID-19 pandemic, the mission has been designed, implemented, tested, and operated in record time. The FSSCat mission is the first ESA third-party mission based on CubeSats contributing to the Copernicus system [36]. The mission is composed of two 6-unitCubeSats, the 3 Cat-5/A and the 3 Cat-5/B.
Flexible Microwave Payload-2 (FMPL-2) is the main payload of the 3 Cat-5/A satellite. It is a dual passive microwave remote sensing instrument, consisting of a GNSS-R receiver at L1/E1 and an L-band Microwave Radiometer (MWR) working as a total power radiometer with frequent internal calibration, with an antenna footprint of ~350 × 500 km 2 . The instrument design and characteristics were described in detail in Munoz-Martin et al. [37], and the in-orbit validation was presented in Munoz-Martin et al. [38]. FMPL-2 is simultaneously retrieving GNSS-R and L-band MWR measurements at a rate of 2 Hz. The instrument uses a dual-band antenna to receive the GNSS-R L1 reflected signals and the L-band antenna temperature. Regarding the GNSS-R part, as compared to the CyGNSS or TDS-1 instruments, FMPL-2 uses a very short integration time of 40 ms to maximize the spatial resolution and minimize the blurring (40 ms correspond roughly to the size of the first Fresnel zone divided by the sub-satellite point speed, and it also is a multiple of 1 ms and 4 ms, the lengths of the GPSL1 C/A and Galileo E1 OScodes). Besides, it also allows for frequent internal noise calibration of the MWR using an internal matched load and an active cold load.
This work presents the first SM retrievals using FSSCat/FMPL-2 data. The performance of four ANN implementations using different combinations of FMPL-2 data is addressed. Since FMPL-2 is a dual sensor, the goal of this research is to investigate how the combination of GNSS-R and MWR data improves the SM estimation accuracy compared to the selected ground truth SM, which is used for model training and validation. This paper is organized as follows: Section 2 describes the different input features, including the data collected by FMPL-2, other ancillary products, and the “ground truth” selected to implement the data-driven algorithms. Section 3 presents the four ANN topologies designed to retrieve SM from NDVI/skin temperature data; from the combination of these two together with the FMPL-2 L-band MWR data; using the FMPL-2 GNSS-R data; finally from the combination of the FMPL-2 MWR and GNSS-R data sets. Section 4 discusses the way forward to provide an improved-quality SM product using GNSS-R data. Finally, the main conclusions that arose from this study are summarized in Section 5.

2. Data Description

FMPL-2 was commissioned in less than three weeks after launch. As part of its primary scientific objective (sea-ice monitoring), the FMPL-2 instrument was collecting data over the poles on a weekly basis, as described in Munoz-Martin et al. [38]. This notwithstanding, the mission also pursues to provide SM estimates over land as a secondary scientific objective. For this reason, the FMPL-2 performs acquisitions over the North Pole (down to 45° N). The data used in this study correspond to the period from 1 October 2020 to 4 December 2020.

2.1. Ancillary Data

A global SM dataset was needed as a reference for training the ANNs. In this regard, two products of SMOS were selected. The nominal accuracy of SMOS SM is 0.04 m 3 /m 3 . The error standard deviation (std) obtained when validating the ESA SMOS Level 2 SM against in situ SM observations ranged between 0.04 and 0.07 m 3 /m 3 [39]. In this study, the Barcelona Expert Center on Remote Sensing (BEC) [40] provided two dedicated SMOS SM data on a daily basis at two different spatial resolutions: 36 km and 9 km [41]. The accuracy of the products was assessed in previous studies over areas with different environmental characteristics. It is important to remark that the product used in this work shows a dry bias with respect to in situ SM data found in many sites and an unbiased root mean squared error around ~0.04–0.08 m 3 /m 3 [42,43,44]. Note that the requirement of 0.04 m 3 /m 3 for the SMOS SM accuracy is defined over non-forested areas with low to medium topography and without snow or frozen soil. In general, validations of SMOS SM were carried out in non-forested regions. Only a few of them were conducted over forests. For instance, the ESA SMOS L2 SM was assessed over boreal forests in Saskatchewan, Canada, obtaining an un-biased root-mean-square error (ubRMSE)of 0.15–0.18 m 3 /m 3 [45], and over temperate forests in the Continental U.S., showing an ubRMSE of 0.03–0.11 m 3 /m 3 [46]. However, most recent SMOS SM processor versions (V650, released in 2017) already include validation stations in boreal forest areas that have been used to enhance the SM estimations [47].
In this paper, the SMOS SM at 36 km is used to train and validate a data-driven algorithm implemented using FMPL-2 radiometry measurements, and the one at 9 km is used for the FMPL-2 GNSS-R measurements. The 9 km product is used to validate the combined MWR/GNSS-R SM product. The ground truth product is shown in Figure 1, the dynamic change could be seen in the Video S1. Note that the projection of all maps presented in this manuscript is the global Equal-Area Scalable Earth (EASE) Grid 2.0 [48].
As the FMPL-2 pixel is ~10 times larger than the SMOS one, other data sources were used to down-scale the original FMPL-2 pixel to 36 km. The ancillary data used to down-scale those measurements were a re-gridded version of the 16 day average Normalized Difference Vegetation Index (NDVI) from MODIS [49] and the daily skin temperature from ECMWF [50], also gridded at 36 km. In addition, a land cover mask derived from MODIS was also used, gridded at 36 km. The two products are shown in Figure 2.

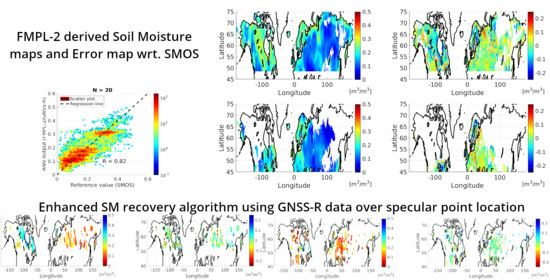
2.2. FMPL-2 Data

The calibration procedures of both the MWR and GNSS-R sensors were explained in Munoz-Martin et al. [37], and the FMPL-2 performance was analyzed in Munoz-Martin et al. [38]. The FMPL-2 data are sampled at 2 Hz, together with the spacecraft telemetry. Once downloaded, the measurements were geo-located using the spacecraft position and pointing. This process was based on a Nearest Neighbor Interpolation (NNI), which was described in detail in Munoz-Martin et al. [38], but using a global EASE Grid 2.0 projection at 36 km, instead of a polar EASE2 grid. The algorithm geo-locates each MWR antenna temperature (T A ) measurement into a single 36 km. Then, all T A measurements with a time-span of five days are averaged into a single map, followed by a triangulation based natural neighbor interpolation. Finally, an antenna pattern compensation was performed based on 2D moving window filtering, using a circular window representing the same area of the antenna footprint. In this way, an entire map out of five days of measurements was generated. Thanks to this technique, there were no gaps in the antenna temperature data, which lately has helped collocate GNSS-R and MWR measurements to provide the combined MWR/GNSS-R SM estimation. Figure 3 illustrates the results of the NNI algorithm. This method allows detecting the coastline borders with a finer resolution than the one given by the antenna footprint (350 × 500 km 2 ), as can be seen over Greenland (see Figure 3). For example, the ocean area at the top of Canada, where it seems there is no land-water transition, is completely covered by sea-ice; thus, there is “jump” in the measured antenna temperature values, as the entire region is covered by sea-ice, which has a larger apparent brightness temperature than the ocean [51].
Finally, Figure 4 shows the reflectivity of the collected (a) GNSS reflections over land, (b) the associated incidence angles, and (c) the estimated SM values interpolated from the SMOS SM product. The reflectivity is calculated as shown in [37], and as explained in [38], all the GNSS-R tracks were pre-processed to filter out reflections with poor SNR or with inconsistent absolute Doppler frequencies. Moreover, only reflection points that had a time-collocated SMOS SM measurement were used in this study. After filtering, the resulting amount of specular reflections was 12,585. The collocation of the SMOS SM product was performed by interpolating the SMOS SM values to the reflection points’ location using a nearest neighbor 2D linear interpolation, producing scattered SM values over the specular points.

3. Soil Moisture Retrieval Using ANN

As ANNs show a great potential to solve non-linear problems, these algorithms have also been applied to soil moisture retrieval. The ECMWF is assimilating real-time Level 2 SM derived from SMOS using ANN [52], and several other SM retrieval algorithms using CyGNSS GNSS-R data are also using ANNs [29,53]. However, ANNs have several challenges: to select the correct ground truth (known as the algorithm “target”) to train the algorithm, to correctly pre-filter and collocate the input data set and to avoid network over-fitting [54].
All previous ANN algorithms using GNSS-R to retrieve SM used either SMAP or in situ probes as the ground truth. However, there is a large collocation error when the CyGNSS observable, with a native resolution ~0.5 × 6.5 km 2 [28], is collocated with an SMAP cell of 36 km. In all previous cases, multiple averages were used to finally provide a good agreement between the resulting network and the target values (see Table 1 and Figure 13 from [29]). Moreover, algorithms using in situ probes as the ground truth (e.g., [30,55]) compare the CyGNSS reflectivity with single point measurements. Thus, it is necessary to apply either an averaging of different in situ probes or a statistical estimation of the SM of the equivalent GNSS-R pixel under study. In this case, using erroneous targets may introduce a bias in the algorithm and network over-fitting (i.e., the ANN does not perform well out of the training set).
The aim of this work is to investigate different ANN algorithms to retrieve SM using FMPL-2 MWR and GNSS-R data. For that reason, different ANNs are proposed to validate the performance of the MWR and the GNSS-R data separately. Each of the ANNs used in this study was dimensioned to avoid network over-fitting [54]. The amount of neurons in each of the layers was always less than two times the number of inputs. Each neuron used the sigmoid function as the transfer function, and the training process was stopped at an early stage to prevent noise over-fitting, as suggested in [54]. Finally, the trained networks were always pruned after training [56].
Table 1 details the different data-driven algorithms studied in this section, indicating the input data for each algorithm and the “ground truth” used for training each ANN.

3.1. Using Optical Data

L-band MWR data were used to recover SM, but several algorithms have also been proposed using optical data only, as NDVI and Land Surface Temperature (LST) measurements (e.g., [10]). In [11] (pp. 47–72), other methods based on optical data were summarized. Although it is possible to retrieve SM from optical data, errors are larger than if L-band MWR is built into the model. The two following main objectives are pursued in this section. First is to show the capabilities of an ANN based algorithm to provide SM estimates just using optical data, and second is to serve as a validation base of the down-scaling algorithm from FMPL-2 MWR data provided in Section 3.2.
The first approach is based on the aforementioned skin temperatures and NDVI datasets. The ANN used here was a three hidden layer network with six neurons per layer. The data were divided into 15% for training, 5% for validation, and 80% for testing, and the network “ground truth” was the SMOS-derived SM product gridded at 36 km. The input data were the following:
  • NDVI from MODIS [49],
  • Skin temperature from ECMWF [50], and
  • Land cover mask from MODIS [49].
Results are shown in Figure 5. As can be seen, the Pearson correlation coefficient R was 0.56, and the Standard Deviation of the Error (STD(Err)) was 0.084 m 3 / m 3 . Note that the scatter-density plot shows many pixels with an SM value of ~0.2 m 3 / m 3 in order to minimize the error. The shortcoming of this methods becomes clear as the network is missing the valuable information coming from the L-band MWR.

3.2. Using L-Band Microwave Radiometry Data

In this second approach, the FMPL-2 MWR data were added to the skin temperature and to the NDVI data sets to improve the SM estimation. The five day averaged FMPL-2 MWR data presented in Figure 3 were combined with the daily skin temperature and the 16 day averaged NDVI data. This produced a daily product that can be compared to the daily SMOS SM product gridded at 36 km.
The same network topology using three hidden layers was used here, but with 10 neurons per layer. In this case, the number of neurons was increased as more inputs were used in the model. Then, the data were divided again into 15% for training, 5% for validation, and 80% for testing. In this case, additional low resolution data inputs were used (see Figure 6) in addition to the FMPL-2 MWR data. The inputs of the network were:
  • FMPL-2 antenna temperature,
  • FMPL-2 standard deviation of the antenna temperature in the along-track measurement,
  • NDVI from MODIS [49],
  • Low resolution NDVI from MODIS [49],
  • Skin temperature from ECMWF [50],
  • Low resolution skin temperature from ECMWF [50],
  • Land cover mask from MODIS [49], and
  • Low resolution land cover mask from MODIS [49].
The objective of this second approach was to down-scale the coarse footprint measurement of the FMPL-2 radiometer to a “higher resolution” pixel by using the NDVI and the skin temperature gridded at 36 km. Pixel down-scaling with L-band MWR data is a known technique [41,57], where optical datasets are usually complemented with coarse-scale radiometry observations to achieve higher resolved images. However, to the authors’ knowledge, this is the first implementation of a down-scaling algorithm using ANNs. The idea behind the network architecture is similar to the one conceived of in [41], but here, the ANN algorithm takes the NDVI, the skin temperature, the land cover mask, and the antenna temperature at a coarse resolution, and then, with the help of higher resolution NDVI, skin temperature, and land cover maps, it down-scales the original antenna temperature to provide a down-scaled SM product. An example of the skin temperature after “blurring” is provided in Figure 6a for illustration purposes. Moreover, the standard deviation of the antenna temperature measured in the along-track direction was also used as a proxy to correct the edge transitions (i.e., land-water transitions, as highlighted in Figure 6b).
Figure 7 shows the scatter-density plot and the error histogram of the ANN used to provide the down-scaled FMPL-2 soil moisture at 36 km. As compared to the previous case, adding the FMPL-2 MWR data resulted in more accurate SM estimations. The R increased from R = 0.56 to R = 0.69, and the STD(Err) decreased from 0.084 to 0.074 m 3 / m 3 , showing a negligible bias in both cases. This result validates that the five day averaged FMPL-2 antenna temperature data enhances the SM retrieval algorithm. Therefore, even at a coarse resolution, the FMPL-2 MWR data can be used to estimate SM. It is important to remark that studies comparing different remote sensing SM products (i.e., from the Advanced Microwave Scanning Radiometer, SMAP, or SMOS) to ground truth sensor networks [58] showed similar errors to the ones presented in this section (i.e., root mean squared differences of ~0.076 m 3 / m 3 and unbiased root mean squared difference of ~0.056 m 3 / m 3 ).
Figure 8 shows the estimated SM maps using the FMPL-2 MWR data and the errors with respect to the SMOS SM estimations. In this case, high resolution ancillary data contain the relevant information to obtain SM maps at full coverage. The first remarkable aspect is that the map corresponding to the latest period (Figure 8d) includes lower latitudes due to a change in the spacecraft execution scheduling, which started acquiring data above 45° Latitude North, as explained in Section 2. The error maps present many areas with errors lower than 0.1 m 3 / m 3 (i.e., color scale around yellow, green, and light-blue). Note that, as the FMPL-2 antenna temperature measurements used in this algorithm were built from the average of five days in order to provide a full-coverage map, SM estimations on areas with strong rain events occurring after FMPL-2 measurements will exhibit larger errors. To solve this problem in future missions, additional data sets could be used in the algorithm: for example, a constellation of multiple satellites including FMPL-2 sensors would provide a finer temporal resolution. Thus, if 5-8 satellites are used in different orbital planes, the required amount of time averages would decrease from five days to just one day, making it possible to provide a daily full coverage SM map above 45° N.

3.3. Using GNSS-R Data

Since the launch of CyGNSS, several data-driven algorithms have shown their potential to estimate SM from their measurements [59]. However, the GNSS-R data retrieved by the SGR-ReSi receiver [60] used in the TDS-1 and CyGNSS missions are configured with long integration times (i.e., 0.5 or 1 s incoherent integration time), as the main objective of these missions is to study the ocean.
In FMPL-2, the integration time of the GNSS-R processor is set to 40 ms in order to enhance the spatial resolution and to avoid waveform blurring. As seen in [61], the ground-track displacement in 40 ms from a spacecraft orbiting at ~550 km is equivalent to the size of the first Fresnel zone (i.e., 7.5 km/s · 40 ms = 300 m) of the GNSS signal reflection.
In this section, an ANN approach based on [62] is proposed to retrieve SM from GNSS-R measurements. The method uses the moving average (movmean) and the moving standard deviation (movstd) of the reflectivity (computed in linear units and then converted to dB) to infer the SM values. As discussed in Munoz-Martin et al. [62], the movmean and the movstd parameters are used by the ANN as a proxy to correct for the surface roughness effects.
In this case, a very simple network is proposed, using just two hidden layers, with six neurons per layer. The ANN target is the SMOS 9 km SM product. However, as introduced in Section 2.2, instead of gridding the GNSS-R data into the 9 km SMOS grid, the SMOS SM product is interpolated over the specular point location using a 2D linear interpolation algorithm. As the data set (see Figure 4) contains fewer points as compared to the MWR case, enough data should be used to train the algorithm to prevent over-fitting. Thus, the data were randomly divided into 60% for training, 10% for validation, and 30% for testing. The input data of this network were the following:
  • Incidence angle θ i n c ,
  • Moving average of the reflectivity (movmean( Γ )) over N samples,
  • Moving standard deviation of the reflectivity (movstd( Γ )) over N samples, as a proxy to correct the surface roughness and speckle noise effects, and
  • Moving average of the SNR (movmean(SNR)) over N samples.
where N is the number of samples used in the movmean and movstd operations. Note that, four different N values are proposed: 3, 5, 10, and 20. By instrument design, the length of a GNSS track produced by FMPL-2 is up to 90 samples successively (i.e., 45 s of data sampled at 2 Hz).
Figure 9 presents the density-scatter plot and the error histogram of the ANN output developed to estimate SM using GNSS-R data from FMPL-2 with respect to the collocated SMOS SM from BEC [40]. By looking at the shape of the density-scatter plot and the error histograms, in general, the ANN algorithm does not provide accurate results for low SM values (<0.15 m 3 / m 3 ), showing a large dispersion in this range. Similar results were discussed in [63], as due to the very low reflectivity of dry soils, GNSS-R loses sensitivity. Thus, the ANN algorithm over-estimates low SM values and under-estimates larger SM values.
The Pearson correlation coefficient (R) and the STD(Err) were computed for each integration time used to evaluate the algorithm performance for different averaging (N). As can be seen, as the averaging time increases, the correlation coefficient increases, and the STD(Err) decreases. For the shortest integration time ( N = 3 ), the correlation coefficient was R = 0.52 , and the STD(Err) was 0.094 m 3 / m 3 . For longer integration times, the R increased, and the STD(Err) decreased. For N = 5 , the correlation coefficient grew up to R = 0.56 , and the STD(Err) decreased down to 0.091 m 3 / m 3 . As more samples were used in the “moving” operation, the R increased even more, up to R = 0.61 and R = 0.62 , for N = 10 and N = 20 , respectively. The STD(Err) was also reduced to 0.087 m 3 / m 3 for both cases. It is important to remark that the bias was negligible (< 0.001 m 3 / m 3 ) in all presented cases.
This result is in agreement with the error graph presented in Figure 13 from [29], where the larger error was linked to areas where fewer samples were used to average the GNSS-R reflectivities. As discussed in [62], the effect of these “moving” operations is to smooth the surface roughness and to reduce speckle noise effects. When the averaging is large enough (i.e., N = 20 ), the correlation coefficient is maximized, and the error with respect to the SMOS SM product is minimized.
The increased average (i.e., larger N) produces a degradation of the spatial resolution, as more samples are required to derive a single measurement. In this case, taking into account the sampling rate (2 Hz) and the ground-track velocity ( v t r a c k ~6.5 km/s), a N = 3 means that the spacecraft has moved ~9.75 km during moving window computation; thus, the equivalent spatial resolution following this technique would be ~9.75 km for N = 3 , 16.25 km for N = 10 , 32.5 km for N = 10 , and 65 km for N = 20 . This phenomenon is a clear example of the remote sensing trade-off, which implies that maximizing the spatial and the radiometric resolution at the same time is not possible, and one is usually sacrificed for the benefit of the other. These results are in agreement with other studies using CyGNSS data [29,53]. It is shown that a large number of averages is required to retrieve accurate SM values from GNSS-R, showing similar errors to other algorithms developed using CyGNSS data.
Finally, Figure 10 presents the geo-located specular points with the estimated SM values and their computed errors with respect to the SMOS SM estimates, for two time periods, from 1–31 October 2020 and from 1 November to 4 December 2020.
The error maps are defined as the network output minus the ground truth. Thus, a negative error means that the ANN algorithm estimates a lower SM than the actual ground truth (under-estimation), and a positive error means that the algorithm estimates a larger SM value than the actual ground truth (over-estimation). By looking at the first data period, it can be seen that larger errors were found in the area at the top of Canada (65° N, 100° W). In this case, most errors were under-estimations of SM for areas with moderate-low moisture content, as also identified in the scatter plots in Figure 9. Furthermore, the SM retrieved over Russia showed, in general, a good accuracy, with errors around ±0.1 m 3 /m 3 and a few SM points containing a slight over-estimation on low-moderate SM values (~0.1 0.2 m 3 /m 3 ).
For the second period, focusing on the area at the top of Canada, the algorithm now presented SM over-estimations. In this case, the area contains several points over very dry areas (see Figure 4), and some others that are very wet, at the southern side of Hudson Bay. As expected from the scatter-density plots, dry areas were over-estimated, and wet areas were under-estimated.
Retrieving soil moisture using single-pass GNSS-R is a complex task [26]. In many cases, the surface roughness, and its dependence on SM, make SM recovery difficult. In our case, the training process of the ANN algorithm became biased because of the large dispersion of the GNSS-R reflectivity values due to this effect. For this reason, additional data must be used to develop a more accurate model, even using movstd( Γ ) as a proxy to correct the surface roughness effects.

3.4. Using Combined GNSS-R and Radiometry Data

In order to correct the fitting errors produced by lower SM values, which then causes this “bias” for larger SM values, the L-band MWR data from FMPL-2 were used. Brightness temperature data are the complementary magnitude of the reflectivity [64]. Thus, even at a very low resolution, FMPL-2 data may contain meaningful and valid information to enhance the SM recovery when combined with GNSS-R.
The algorithm proposed in this section combines both measurements to provide a more accurate SM estimation. As is seen in Equation (12) from [65], the reflectivity of a given area is linked to its brightness temperature. In our example, the coarse resolution MWR data were used as ancillary data to improve the SM retrieval algorithm using the high resolution GNSS-R data. The network proposed here was the same as in the GNSS-R example: two hidden layers with six neurons per layer, using the same train/validation/test division. The target output was the same as in the previous case, and the input set now included the MWR radiometry data as follows:
  • FMPL-2 antenna temperature,
  • FMPL-2 standard deviation of the antenna temperature in the along-track measurement,
  • Incidence angle θ i n c ,
  • Moving average of the reflectivity (movmean( Γ )) over N samples,
  • Moving standard deviation of the reflectivity (movstd( Γ )) over N samples, and
  • Moving average of the SNR (movmean(SNR)) over N samples.
In this case, the same approach to collocate the target output was used to collocate the FMPL-2 measurements. Therefore, a 2D linear interpolation was used to generate the scattered data from the 36 km FMPL-2 gridded data. In this case, the standard deviation of the antenna temperature was also used as a proxy to correct the edge transitions (i.e., land-water transitions).
Figure 11 shows the scatter-density plot and error histogram of the new ANN algorithm to derive SM from the combined MWR and GNSS-R data, as compared to the SMOS SM. In this last case, the resulting network showed a significant improvement with respect to the GNSS-R-only case. For lower SM values, the algorithm was more accurate, presenting, in general, a lower dispersion.
This is also reflected in the Pearson correlation coefficient and in STD(Err). The R was boosted from 0.52 to 0.79 for N = 3 , from 0.56 to 0.80 for N = 5 , from 0.61 to 0.81 for N = 10 , and from 0.62 to 0.82 for N = 20 . In the four cases, the bias was also negligible, and the STD(Err) also decreased from 0.094 m 3 / m 3 to 0.067 m 3 / m 3 , from 0.091 m 3 / m 3 to 0.066 m 3 / m 3 , from 0.087 m 3 / m 3 to 0.064 m 3 / m 3 , and from 0.087 m 3 /m 3 to 0.063 m 3 /m 3 , for the four N cases: 3, 5, 10, and 20, respectively. The use of the FMPL-2 MWR data contributed to decreasing the overall error with respect to SMOS SM at 9 km, even for small values of N. The error difference between the shorter integration time and the largest integration time was 0.04 m 3 /m 3 .
Finally, Figure 12 presents the geo-located specular points as in the previous section, but with this new ANN algorithm that uses the MWR and GNSS-R data. As compared to the previous case, most of the errors previously analyzed in Figure 10 were now lower than 0.1 m 3 / m 3 . As compared to the previous case (using only GNSS-R data), the errors produced in the northern part of Canada were now drastically reduced. Drier areas were better detected thanks to the use of the MWR data, which is the complementary magnitude of the reflectivity. Thus, when the GNSS-R reflectivity is low, the antenna temperature retrieved by FMPL-2 MWR is high, and vice versa. This synergy allows solving the uncertainty for the surface roughness attenuation, which produces low reflectivity values for high SM values. Thanks to the MWR data, low reflectivity values that are collocated with a low antenna temperature corresponds to wet soils, but the reflection is affected by the surface roughness. Analogously, low reflectivity values collocated with a large antenna temperature correspond to drier soils.

4. Discussion

Machine learning works as a data-driven approach, and data from different sources must be introduced as input data to deliver quality results. Different space-borne approaches have been presented in the last few years using ANN to estimate SM from GNSS-R measurements, as seen in Table 1 from [29]. As summarized in Table 2, four ANN based models were implemented to infer SM from a different combination of input features.
The use of movstd on a set of consecutive samples proposed in [62] was used to correct the speckle noise and surface roughness effects, and it was validated for SM retrieval using spaceborne GNSS-R data. In Figure 13, the error of the airborne algorithm presented in [62] is compared to the error achieved using FMPL-2 GNSS-R data. As can be seen, both error curves follow the same trend, where a large number of measurements or Fresnel zones are required to provide a lower error. Note that this effect was also studied in Figure 13 of [29], where a large number of samples within a grid were required to achieve a lower error. Moreover, there is an almost constant “gap” between both curves of ~0.03 m 3 / m 3 , which in this case might be due to the difference in directivity between the airborne GNSS-R instrument (i.e., ~21 dB [66]) and FMPL-2 (i.e., ~12 dB [37]). However, the best results were achieved when combining the GNSS-R and the L-band MWR data retrieved by FMPL-2. The intrinsic synergy of GNSS-R with L-band MWR allows for more accurate SM retrievals, with a finer spatial resolution over the specular reflection points.
In both the airborne case in [62] and in the methodology described in this paper (Section 3.4), the use of combined data decreases the SM estimation error with respect to the SMOS SM target. However, this is not the case for other algorithms (i.e., Table 1 from [29]), where the efforts are focused on decreasing the amount of ancillary data used to retrieve SM from GNSS-R data, at the expense of using large spatial and temporal averages. However, this is not how a data-driven (and machine learning) algorithms works. Proper inputs shall be strategically selected to retrieve SM at larger spatial and radiometric resolutions. Thus, combining data from different sensors is key to retrieve a higher quality product.
CubeSats have a great potential for Earth observation. As is shown in this work, even a CubeSat based instrument can be used to retrieve SM measurements with good accuracy, although not as good as with traditional larger satellites, such as SMOS or SMAP. FMPL-2 has shown its potential to infer an enhanced resolution SM by means of combined MWR and GNSS-R measurements, in addition to the down-scaling algorithm using optical multi-spectral data used to derive vegetation indices and LST. In addition, a CubeSat based constellation with eight satellites embarking FMPL-2 as the payload would allow entirely covering all latitudes above +45° N every single day, with enough footprint oversampling to retrieve daily SM products (FMPL-2 MWR on board 3 Cat-5/A requires up to 3–5 days, depending on the downlink scheduling, to cover all latitudes above 45° N and 5–8 days to cover all latitudes above 35° N).
The more sensors in orbit, the more data will be available to implement data-driven algorithms like those presented in this work. This is the idea behind the CubeSat philosophy. Therefore, this hypothetical constellation of CubeSats embarking FMPL-2 among other optical sensors would allow high-quality Earth observation products, with improved revisit times, radiometric accuracy, and spatial resolution, as compared to the product currently available. The way to beat the trade-off between spatial and radiometric resolutions is to add extra information and to benefit from data-driven and data fusion algorithms, such as ANN.

5. Conclusions

This work presents the first SM retrievals using FMPL-2 data, showing the potential of CubeSats to produce quality science products for land monitoring applications. Four different algorithms based on ANNs are presented. The first algorithm serves as validation of the initial ECMWF skin temperature and MODIS NDVI data to retrieve SM. The second algorithm presents an ANN based pixel down-scaling technique, which takes the FMPL-2 MWR data along with MODIS NDVI data and ECMWF skin temperature to produce down-scaled SM measurements at 36 km resolution from an initial MWR pixel of 350 × 500 km 2 . The effect of adding FMPL-2 data to the ANN is validated, showing a performance improvement when the FMPL-2 antenna temperature is used.
The third algorithm presents an ANN using GNSS-R data from FMPL-2 to estimate SM content, without using any ancillary data. The proposed ANN takes movmean and the movstd of N consecutive samples together with the incidence angle and compares them to a down-scaled SMOS SM product at 9 km resolution. As expected from other SM studies using GNSS-R, the larger the N samples used to produce a measurement, the smaller the error is. In this case, by just utilizing GNSS-R data, the algorithm shows a standard deviation of the error of 0.079 m 3 / m 3 at N = 20 samples.
Finally, a fourth algorithm that combines FMPL-2 MWR and GNSS-R data is presented. It is shown that the combination of L-band antenna temperature measurements with GNSS-R reflectivity data significantly enhances the retrieval algorithm performance. In this case, the error is decreased by ~ 27.5%, with a standard deviation of the error of 0.067–0.063 m 3 / m 3 , for N = 3 to N = 20 , respectively. In conclusion, the combination of collocated MWR and GNSS-R data from FMPL-2 produces a higher accuracy in the soil moisture estimation.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/13/5/994/s1, Video S1: Soil Moisture and Ocean Salinity (SMOS)-derived Soil Moisture (SM) from [40] projected on a 36 km Equal-Area Scalable Earth (EASE) grid.

Author Contributions

Conceptualization, J.F.M.-M. and A.C.; methodology, J.F.M.-M. and A.C.; software, J.F.M.-M., D.L., M.P., and C.H.; validation, M.P. and A.C.; formal analysis, J.F.M.-M. and A.C.; investigation, J.F.M.-M., H.P., and A.C.; resources M.P. and A.C.; data curation J.F.M.-M., D.L., C.H., M.P., and A.C.; visualization J.F.M.-M.; supervision A.C.; project administration A.C.; funding acquisition, A.C.; writing—original draft preparation, J.F.M.-M. and A.C.; writing—review and editing, J.F.M.-M., C.H., H.P., and A.C. All authors read and agreed to the published version of the manuscript.

Funding

This work was supported by the 2017 ESA S3 challenge and Copernicus Masters overall winner award (“FSSCat” project). This work was (partially) sponsored by project SPOT: Sensing with Pioneering Opportunistic Techniques grant RTI2018-099008-B-C21 / AEI / 10.13039/501100011033, and by the Unidad de Excelencia Maria de Maeztu MDM-2016-0600. This work was also (partially) sponsored by the Spanish Ministry of Science and Innovation through the project ESP2017-89463-C3, by the Centro de Excelencia Severo Ochoa (CEX2019-000928-S), and by the CSIC Plataforma Temática Interdisciplinar de Teledetección (PTI-Teledetect). Joan Francesc Munoz-Martin received support from the grant for the recruitment of early-stage research staff FI-DGR 2018 of the AGAUR - Generalitat de Catalunya (FEDER), Spain; Christoph Herbert received the support of a fellowship from “la Caixa” Foundation (ID 100010434) with the fellowship code LCF/BQ/DI18/11660050 and funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie Grant Agreement No. 713673; David Llavería received support from an FPU fellowship from the Spanish Ministry of Education FPU18/06107.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data used in this study will be publicly and freely available for everyone at the Copernicus system as part of the FSSCat mission.

Acknowledgments

The authors would like to thank all NanoSat-Lab members who made possible the development and testing of the FMPL-2 payload, as well as the support to build the Montsec S-band ground station used to download FMPL-2 data. The authors would like to thank Balamis S.L. employees Roger Jové, Adrià Amezaga, and Ricard Gonzálvez who designed and manufactured the RF front-end board of FMPL-2 with the internal calibrators and the FSSCat consortium, especially the Tyvak operations team, the Deimos DPGS team, and the Golbriak OU team for their support during the mission operations. Finally, the authors would like to give special thanks to Bernardo Carnicero and Massimiliano Pastena (ESA/ESTEC) for their continued technical support and advice during the whole project.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. GCOS. What are Essential Climate Variables? Available online: https://gcos.wmo.int/en/essential-climate-variables/abouth (accessed on 18 January 2021).
  2. Wasko, C.; Nathan, R. Influence of changes in rainfall and soil moisture on trends in flooding. J. Hydrol. 2019, 575, 432–441. [Google Scholar] [CrossRef]
  3. Wei, L.; Zhang, B.; Wang, M. Effects of antecedent soil moisture on runoff and soil erosion in alley cropping systems. Agric. Water Manag. 2007, 94, 54–62. [Google Scholar] [CrossRef]
  4. Miralles, D.G.; Gentine, P.; Seneviratne, S.I.; Teuling, A.J. Land-atmospheric feedbacks during droughts and heatwaves: State of the science and current challenges. Ann. N. Y. Acad. Sci. 2018, 1436, 19–35. [Google Scholar] [CrossRef]
  5. Badewa, E.; Unc, A.; Cheema, M.; Kavanagh, V.; Galagedara, L. Soil Moisture Mapping Using Multi-Frequency and Multi-Coil Electromagnetic Induction Sensors on Managed Podzols. Agronomy 2018, 8, 224. [Google Scholar] [CrossRef] [Green Version]
  6. Klotzsche, A.; Jonard, F.; Looms, M.; van der Kruk, J.; Huisman, J. Measuring Soil Water Content with Ground Penetrating Radar: A Decade of Progress. Vadose Zone J. 2018, 17, 180052. [Google Scholar] [CrossRef] [Green Version]
  7. Wu, K.; Rodriguez, G.A.; Zajc, M.; Jacquemin, E.; Clément, M.; Coster, A.D.; Lambot, S. A new drone-borne GPR for soil moisture mapping. Remote Sens. Environ. 2019, 235, 111456. [Google Scholar] [CrossRef]
  8. Petropoulos, G.P.; Ireland, G.; Barrett, B. Surface soil moisture retrievals from remote sensing: Current status, products & future trends. Phys. Chem. Earth Parts A/B/C 2015, 83–84, 36–56. [Google Scholar] [CrossRef]
  9. Jackson, R.D. Soil Moisture Inferences from Thermal-Infrared Measurements of Vegetation Temperatures. IEEE Trans. Geosci. Remote Sens. 1982, GE-20, 282–286. [Google Scholar] [CrossRef]
  10. Moran, M.; Clarke, T.; Inoue, Y.; Vidal, A. Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sens. Environ. 1994, 49, 246–263. [Google Scholar] [CrossRef]
  11. Rahimzadeh-Bajgiran, P.; Berg, A. Soil Moisture Retrievals Using Optical/TIR Methods. In Satellite Soil Moisture Retrieval; Elsevier: Amsterdam, The Netherlands, 2016; pp. 47–72. [Google Scholar] [CrossRef]
  12. Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS Mission: New Tool for Monitoring Key Elements of the Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef] [Green Version]
  13. Entekhabi, D.; Njoku, E.G.; O’Neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J.; et al. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
  14. Naeimi, V.; Scipal, K.; Bartalis, Z.; Hasenauer, S.; Wagner, W. An Improved Soil Moisture Retrieval Algorithm for ERS and METOP Scatterometer Observations. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1999–2013. [Google Scholar] [CrossRef]
  15. Hegarat-Mascle, S.L.; Zribi, M.; Alem, F.; Weisse, A.; Loumagne, C. Soil moisture estimation from ERS/SAR data: Toward an operational methodology. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2647–2658. [Google Scholar] [CrossRef]
  16. Pathe, C.; Wagner, W.; Sabel, D.; Doubkova, M.; Basara, J.B. Using ENVISAT ASAR Global Mode Data for Surface Soil Moisture Retrieval Over Oklahoma, USA. IEEE Trans. Geosci. Remote Sens. 2009, 47, 468–480. [Google Scholar] [CrossRef]
  17. Srivastava, H.; Patel, P.; Sharma, Y.; Navalgund, R. Large-Area Soil Moisture Estimation Using Multi-Incidence-Angle RADARSAT-1 SAR Data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2528–2535. [Google Scholar] [CrossRef]
  18. Paloscia, S.; Pettinato, S.; Santi, E.; Notarnicola, C.; Pasolli, L.; Reppucci, A. Soil moisture mapping using Sentinel-1 images: Algorithm and preliminary validation. Remote Sens. Environ. 2013, 134, 234–248. [Google Scholar] [CrossRef]
  19. Gorrab, A.; Zribi, M.; Baghdadi, N.; Mougenot, B.; Fanise, P.; Chabaane, Z. Retrieval of Both Soil Moisture and Texture Using TerraSAR-X Images. Remote Sens. 2015, 7, 10098–10116. [Google Scholar] [CrossRef] [Green Version]
  20. Camps, A.; Vall·llossera, M.; Park, H.; Portal, G.; Rossato, L. Sensitivity of TDS-1 GNSS-R Reflectivity to Soil Moisture: Global and Regional Differences and Impact of Different Spatial Scales. Remote Sens. 2018, 10, 1856. [Google Scholar] [CrossRef] [Green Version]
  21. Chew, C.C.; Small, E.E. Soil Moisture Sensing Using Spaceborne GNSS Reflections: Comparison of CYGNSS Reflectivity to SMAP Soil Moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef] [Green Version]
  22. Chew, C.; Small, E. Description of the UCAR/CU Soil Moisture Product. Remote Sens. 2020, 12, 1558. [Google Scholar] [CrossRef]
  23. Chew, C.; Shah, R.; Zuffada, C.; Hajj, G.; Masters, D.; Mannucci, A.J. Demonstrating soil moisture remote sensing with observations from the UK TechDemoSat-1 satellite mission. Geophys. Res. Lett. 2016, 43, 3317–3324. [Google Scholar] [CrossRef] [Green Version]
  24. Camps, A.; Park, H.; Pablos, M.; Foti, G.; Gommenginger, C.P.; Liu, P.; Judge, J. Sensitivity of GNSS-R Spaceborne Observations to Soil Moisture and Vegetation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4730–4742. [Google Scholar] [CrossRef] [Green Version]
  25. Park, H.; Camps, A.; Castellvi, J.; Muro, J. Generic Performance Simulator of Spaceborne GNSS-Reflectometer for Land Applications. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3179–3191. [Google Scholar] [CrossRef]
  26. Camps, A.; Park, H.; Castellví, J.; Corbera, J.; Ascaso, E. Single-Pass Soil Moisture Retrievals Using GNSS-R: Lessons Learned. Remote Sens. 2020, 12, 2064. [Google Scholar] [CrossRef]
  27. Ruf, C.S.; Gleason, S.; Jelenak, Z.; Katzberg, S.; Ridley, A.; Rose, R.; Scherrer, J.; Zavorotny, V. The CYGNSS nanosatellite constellation hurricane mission. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 214–216. [Google Scholar] [CrossRef]
  28. Unwin, M.; Jales, P.; Blunt, P.; Duncan, S.; Brummitt, M.; Ruf, C. The SGR-ReSI and its application for GNSS reflectometry on the NASA EV-2 CYGNSS mission. In Proceedings of the 2013 IEEE Aerospace Conference, Big Sky, MT, USA, 2–9 March 2013; pp. 1–6. [Google Scholar] [CrossRef]
  29. Yan, Q.; Huang, W.; Jin, S.; Jia, Y. Pan-tropical soil moisture mapping based on a three-layer model from CYGNSS GNSS-R data. Remote Sens. Environ. 2020, 247, 111944. [Google Scholar] [CrossRef]
  30. Senyurek, V.; Lei, F.; Boyd, D.; Kurum, M.; Gurbuz, A.C.; Moorhead, R. Machine Learning-Based CYGNSS Soil Moisture Estimates over ISMN sites in CONUS. Remote Sens. 2020, 12, 1168. [Google Scholar] [CrossRef] [Green Version]
  31. Clarizia, M.P.; Pierdicca, N.; Costantini, F.; Floury, N. Analysis of CYGNSS Data for Soil Moisture Retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 2227–2235. [Google Scholar] [CrossRef]
  32. Al-Khaldi, M.M.; Johnson, J.T.; O’Brien, A.J.; Balenzano, A.; Mattia, F. Time-Series Retrieval of Soil Moisture Using CYGNSS. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4322–4331. [Google Scholar] [CrossRef]
  33. Jing, C.; Niu, X.; Duan, C.; Lu, F.; Di, G.; Yang, X. Sea Surface Wind Speed Retrieval from the First Chinese GNSS-R Mission: Technique and Preliminary Results. Remote Sens. 2019, 11, 3013. [Google Scholar] [CrossRef] [Green Version]
  34. Jales, P.; Esterhuizen, S.; Masters, D.; Nguyen, V.; Correig, O.N.; Yuasa, T.; Cartwright, J. The new Spire GNSS-R satellite missions and products. In Image and Signal Processing for Remote Sensing XXVI; Bruzzone, L., Bovolo, F., Santi, E., Eds.; International Society for Optics and Photonics, SPIE: Washington, DC, USA, 2020; Volume 11533. [Google Scholar] [CrossRef]
  35. Camps, A.; Golkar, A.; Gutierrez, A.; de Azua, J.A.R.; Munoz-Martin, J.F.; Fernandez, L.; Diez, C.; Aguilella, A.; Briatore, S.; Akhtyamov, R.; et al. FSSCat, the 2017 Copernicus Masters’ “Esa Sentinel Small Satellite Challenge” Winner: A Federated Polar and Soil Moisture Tandem Mission Based on 6U Cubesats. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 8285–8287. [Google Scholar] [CrossRef]
  36. European Space Agency. Introducing the Newest ESA Third Party Missions. Available online: https://earth.esa.int/eogateway/news/introducing-the-newest-esa-third-party-missions (accessed on 8 January 2020).
  37. Munoz-Martin, J.F.; Fernandez-Capon, L.; Ruiz-de-Azua, J.; Camps, A. The Flexible Microwave Payload-2: A SDR-Based GNSS-Reflectometer and L-Band Radiometer for CubeSats. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1298–1311. [Google Scholar] [CrossRef]
  38. Munoz-Martin, J.F.; Fernandez, L.; Perez, A.; de Azua, J.A.R.; Park, H.; Camps, A.; Domínguez, B.C.; Pastena, M. In-Orbit Validation of the FMPL-2 Instrument—The GNSS-R and L-Band Microwave Radiometer Payload of the FSSCat Mission. Remote Sens. 2020, 13, 121. [Google Scholar] [CrossRef]
  39. Kerr, Y.; Al-Yaari, A.; Rodriguez-Fernandez, N.; Parrens, M.; Molero, B.; Leroux, D.; Bircher, S.; Mahmoodi, A.; Mialon, A.; Richaume, P.; et al. Overview of SMOS performance in terms of global soil moisture monitoring after six years in operation. Remote Sens. Environ. 2016, 180, 40–63. [Google Scholar] [CrossRef]
  40. Center, B.E. Barcelona Expert Center Webpage. Available online: Http://bec.icm.csic.es/ (accessed on 22 December 2020).
  41. Portal, G.; Vall-llossera, M.; Piles, M.; Camps, A.; Chaparro, D.; Pablos, M.; Rossato, L. A Spatially Consistent Downscaling Approach for SMOS Using an Adaptive Moving Window. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1883–1894. [Google Scholar] [CrossRef]
  42. Pablos, M.; Vall-llossera, M.; Piles, M.; Camps, A.; González-Haro, C.; Turiel, A.; Herbert, C.J.; Chaparro, D.; Portal, G. Influence of Quality Filtering Approaches in BEC SMOS L3 Soil Moisture Products. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 6941–6944. [Google Scholar] [CrossRef]
  43. Pablos, M.; Piles, M.; Gonzalez-Haro, C. BEC SMOS Land Products Description. Available online: Http://bec.icm.csic.es/doc/BEC-SMOS-0003-PD-Land.pdf (accessed on 22 December 2020).
  44. Portal, G.; Jagdhuber, T.; Vall-llossera, M.; Camps, A.; Pablos, M.; Entekhabi, D.; Piles, M. Assessment of Multi-Scale SMOS and SMAP Soil Moisture Products across the Iberian Peninsula. Remote Sens. 2020, 12, 570. [Google Scholar] [CrossRef] [Green Version]
  45. Gherboudj, I.; Magagi, R.; Goita, K.; Berg, A.A.; Toth, B.; Walker, A. Validation of SMOS Data Over Agricultural and Boreal Forest Areas in Canada. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1623–1635. [Google Scholar] [CrossRef]
  46. Bitar, A.A.; Leroux, D.; Kerr, Y.H.; Merlin, O.; Richaume, P.; Sahoo, A.; Wood, E.F. Evaluation of SMOS Soil Moisture Products Over Continental U.S. Using the SCAN/SNOTEL Network. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1572–1586. [Google Scholar] [CrossRef] [Green Version]
  47. European Space Agency. Read-Me-First Note for the Release of the SMOS Level 2 Soil Moisture Data Products: Level 2 Soil Moisture V650; European Space Agency: Paris, France, 2017. [Google Scholar]
  48. Brodzik, M.J.; Billingsley, B.; Haran, T.; Raup, B.; Savoie, M.H. EASE-Grid 2.0: Incremental but Significant Improvements for Earth-Gridded Data Sets. ISPRS Int. J. Geo-Inf. 2012, 1, 32–45. [Google Scholar] [CrossRef] [Green Version]
  49. Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V006, 2015. Available online: https://doi.org/10.5067/MODIS/MOD13Q1.006 (accessed on 1 November 2020).
  50. Owens, R.; Hewson, T. ECMWF Forecast User Guide 2018. Available online: https://doi.org/10.21957/M1CS7H (accessed on 1 November 2020). [CrossRef]
  51. European Space Agency. Eight Years of SMOS Arctic Sea Ice Thickness Level Now Available from SMOS Data Dissemination Portal. Available online: https://earth.esa.int/web/guest/missions/esa-operational-eo-missions/smos/news/-/article/eight-years-data-of-smos-arctic-sea-ice-thickness-level-now-available-from-smos-data-dissemination-portal (accessed on 11 November 2019).
  52. Rodriguez-Fernandez, N.J.; Aires, F.; Richaume, P.; Kerr, Y.H.; Prigent, C.; Kolassa, J.; Cabot, F.; Jimenez, C.; Mahmoodi, A.; Drusch, M. Soil Moisture Retrieval Using Neural Networks: Application to SMOS. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5991–6007. [Google Scholar] [CrossRef]
  53. Eroglu, O.; Kurum, M.; Boyd, D.; Gurbuz, A.C. High Spatio-Temporal Resolution CYGNSS Soil Moisture Estimates Using Artificial Neural Networks. Remote Sens. 2019, 11, 2272. [Google Scholar] [CrossRef] [Green Version]
  54. Ying, X. An Overview of Overfitting and its Solutions. J. Phys. Conf. Ser. 2019, 1168, 022022. [Google Scholar] [CrossRef]
  55. Yan, Q.; Gong, S.; Jin, S.; Huang, W.; Zhang, C. Near Real-Time Soil Moisture in China Retrieved From CyGNSS Reflectivity. IEEE Geosci. Remote. Sens. Lett. 2020, 1–5. [Google Scholar] [CrossRef]
  56. Karnin, E.D. A simple procedure for pruning back-propagation trained neural networks. IEEE Trans. Neural Netw. 1990, 1, 239–242. [Google Scholar] [CrossRef] [PubMed]
  57. Piles, M.; Camps, A.; Vall-llossera, M.; Corbella, I.; Panciera, R.; Rüdiger, C.; Kerr, Y.H.; Walker, J. Downscaling SMOS-Derived Soil Moisture Using MODIS Visible/Infrared Data. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3156–3166. [Google Scholar] [CrossRef]
  58. Hajj, M.E.; Baghdadi, N.; Zribi, M.; Rodríguez-Fernández, N.; Wigneron, J.; Al-Yaari, A.; Bitar, A.A.; Albergel, C.; Calvet, J.C. Evaluation of SMOS, SMAP, ASCAT and Sentinel-1 Soil Moisture Products at Sites in Southwestern France. Remote Sens. 2018, 10, 569. [Google Scholar] [CrossRef] [Green Version]
  59. Edokossi, K.; Calabia, A.; Jin, S.; Molina, I. GNSS-Reflectometry and Remote Sensing of Soil Moisture: A Review of Measurement Techniques, Methods, and Applications. Remote Sens. 2020, 12, 614. [Google Scholar] [CrossRef] [Green Version]
  60. Unwin, M. The SGR-ReSI Experiment on the TechDemoSat-1 Mission; Technical report; Surrey Satellite Technology Ltd.: Guildford, UK, 2015. [Google Scholar]
  61. Park, H.; Pascual, D.; Camps, A.; Martin, F.; Alonso-Arroyo, A.; Carreno-Luengo, H. Analysis of Spaceborne GNSS-R Delay-Doppler Tracking. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1481–1492. [Google Scholar] [CrossRef]
  62. Munoz-Martin, J.F.; Onrubia, R.; Pascual, D.; Park, H.; Camps, A.; Rüdiger, C.; Walker, J.; Monerris, A. Single-Pass Soil Moisture Retrieval Using GNSS-R at L1 and L5 Bands: Results from Airborne Experiment. Remote Sens. 2021, 13, 797. [Google Scholar] [CrossRef]
  63. Valencia, E.; Camps, A.; Vall-llossera, M.; Monerris, A.; Bosch-Lluis, X.; Rodriguez-Alvarez, N.; Ramos-Perez, I.; Marchan-Hernandez, J.F.; Martinez-Fernandez, J.; Sanchez-Martin, N.; et al. GNSS-R Delay-Doppler Maps over land: Preliminary results of the GRAJO field experiment. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 3805–3808. [Google Scholar] [CrossRef]
  64. Emery, W.; Camps, A. Chapter 4-Microwave Radiometry. In Introduction to Satellite Remote Sensing; Elsevier: Amsterdam, The Netherlands, 2017; pp. 131–290. [Google Scholar] [CrossRef]
  65. Jiancheng, S.; Chen, K.S.; Qin, L.; Jackson, T.J.; O’Neill, P.E.; Leung, T. A parameterized surface reflectivity model and estimation of bare-surface soil moisture with L-band radiometer. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2674–2686. [Google Scholar] [CrossRef]
  66. Onrubia, R.; Pascual, D.; Querol, J.; Park, H.; Camps, A. The Global Navigation Satellite Systems Reflectometry (GNSS-R) Microwave Interferometric Reflectometer: Hardware, Calibration, and Validation Experiments. Sensors 2019, 19, 1019. [Google Scholar] [CrossRef] [Green Version]
Remotesensing 13 00994 g001 550
Figure 1. Soil Moisture and Ocean Salinity (SMOS)-derived Soil Moisture (SM) from [40] projected on a 36 km Equal-Area Scalable Earth (EASE) grid on (a) 15 October 2020 and (b) 5 November 2020, respectively, and and on a 9 km grid on (c) 15 October 2020 and (d) 5 November 2020, respectively.
Figure 1. Soil Moisture and Ocean Salinity (SMOS)-derived Soil Moisture (SM) from [40] projected on a 36 km Equal-Area Scalable Earth (EASE) grid on (a) 15 October 2020 and (b) 5 November 2020, respectively, and and on a 9 km grid on (c) 15 October 2020 and (d) 5 November 2020, respectively.
Remotesensing 13 00994 g001
Remotesensing 13 00994 g002 550
Figure 2. (a) Sixteen day averaged NDVI from MODIS [49] on 22 October 2020 and (b) skin temperature from ECMWF [50] on 15 October 2020.
Figure 2. (a) Sixteen day averaged NDVI from MODIS [49] on 22 October 2020 and (b) skin temperature from ECMWF [50] on 15 October 2020.
Remotesensing 13 00994 g002
Remotesensing 13 00994 g003 550
Figure 3. Flexible Microwave Payload-2 (FMPL-2) Microwave Radiometer (MWR) measurements geo-located using the Nearest Neighbor Interpolation (NNI) algorithm comprising five days of measurements with and centered on (a) 7 October 2020, (b) 21 October 2020, (c) 3 November 2020, and (d) 10 November 2020.
Figure 3. Flexible Microwave Payload-2 (FMPL-2) Microwave Radiometer (MWR) measurements geo-located using the Nearest Neighbor Interpolation (NNI) algorithm comprising five days of measurements with and centered on (a) 7 October 2020, (b) 21 October 2020, (c) 3 November 2020, and (d) 10 November 2020.
Remotesensing 13 00994 g003
Remotesensing 13 00994 g004 550
Figure 4. (a,d) GNSS-R reflectivity calibrated as shown in [37], (b,e) the SMOS SM (9 km) estimation interpolated over the GNSS-R specular reflection position, and (c,f) the incidence angle of the reflection. (a–c) from 1–31 October 2020 and (d,e) from 1 November to 4 December 2020.
Figure 4. (a,d) GNSS-R reflectivity calibrated as shown in [37], (b,e) the SMOS SM (9 km) estimation interpolated over the GNSS-R specular reflection position, and (c,f) the incidence angle of the reflection. (a–c) from 1–31 October 2020 and (d,e) from 1 November to 4 December 2020.
Remotesensing 13 00994 g004
Remotesensing 13 00994 g005 550
Figure 5. (a) Scatter-density plot between the ANN output using NDVI and skin temperature as input data and the SMOS SM product as the network reference value; and (b) the error histogram between the ANN output and the SMOS reference.
Figure 5. (a) Scatter-density plot between the ANN output using NDVI and skin temperature as input data and the SMOS SM product as the network reference value; and (b) the error histogram between the ANN output and the SMOS reference.
Remotesensing 13 00994 g005
Remotesensing 13 00994 g006 550
Figure 6. (a) Low resolution skin temperature (°C), and (b) sample FMPL-2 standard deviation (°K) in the along-track direction after applying the NNI algorithm. Note that land-water transitions in the northern part of Siberia are highlighted in red.
Figure 6. (a) Low resolution skin temperature (°C), and (b) sample FMPL-2 standard deviation (°K) in the along-track direction after applying the NNI algorithm. Note that land-water transitions in the northern part of Siberia are highlighted in red.
Remotesensing 13 00994 g006
Remotesensing 13 00994 g007a 550Remotesensing 13 00994 g007b 550
Figure 7. (a) Scatter-density plot between the ANN output using FMPL-2 data and the SMOS reference value; and (b) the error histogram between the ANN output and the SMOS reference.
Figure 7. (a) Scatter-density plot between the ANN output using FMPL-2 data and the SMOS reference value; and (b) the error histogram between the ANN output and the SMOS reference.
Remotesensing 13 00994 g007aRemotesensing 13 00994 g007b
Remotesensing 13 00994 g008 550
Figure 8. (a–d) FMPL-2/MWR down-scaled SM estimations corresponding to (a) 1–5 October 2020, (b) 10–15 October 2020, (c) 25–30 October 2020, and (d) 9–14 November 2020. (e–h) Errors with respect to the SMOS SM product, for the same date periods specified in (a–d). Note that, SMOS GT data are not available in regions that are blank (e.g., northern part of Russia).
Figure 8. (a–d) FMPL-2/MWR down-scaled SM estimations corresponding to (a) 1–5 October 2020, (b) 10–15 October 2020, (c) 25–30 October 2020, and (d) 9–14 November 2020. (e–h) Errors with respect to the SMOS SM product, for the same date periods specified in (a–d). Note that, SMOS GT data are not available in regions that are blank (e.g., northern part of Russia).
Remotesensing 13 00994 g008
Remotesensing 13 00994 g009 550
Figure 9. (left) Scatter-density plot and (right) error histogram of the GNSS-R based ANN output with respect to the collocated SMOS SM product from Barcelona Expert Center on Remote Sensing (BEC) [40], showing the four different values of N used to compute the movmean and movstd inputs for the network.
Figure 9. (left) Scatter-density plot and (right) error histogram of the GNSS-R based ANN output with respect to the collocated SMOS SM product from Barcelona Expert Center on Remote Sensing (BEC) [40], showing the four different values of N used to compute the movmean and movstd inputs for the network.
Remotesensing 13 00994 g009
Remotesensing 13 00994 g010 550
Figure 10. (a,c) GNSS-R-derived SM estimations corresponding to N = 20 . (b–d) Error with respect to the collocated SMOS SM product. The map presents the measurements collected by FMPL-2 from (a,b) 1–31 October 2020 and from 1 November to 4 December 2020. Only reflections collocated with SMOS SM data are presented.
Figure 10. (a,c) GNSS-R-derived SM estimations corresponding to N = 20 . (b–d) Error with respect to the collocated SMOS SM product. The map presents the measurements collected by FMPL-2 from (a,b) 1–31 October 2020 and from 1 November to 4 December 2020. Only reflections collocated with SMOS SM data are presented.
Remotesensing 13 00994 g010
Remotesensing 13 00994 g011 550
Figure 11. (left) Scatter-density plot and (right) the error histogram of the combined MWR and GNSS-R ANN output with respect to the collocated SMOS SM product from BEC [40], for the four different values of N used to compute movmean and movstd, used as inputs for the ANN.
Figure 11. (left) Scatter-density plot and (right) the error histogram of the combined MWR and GNSS-R ANN output with respect to the collocated SMOS SM product from BEC [40], for the four different values of N used to compute movmean and movstd, used as inputs for the ANN.
Remotesensing 13 00994 g011
Remotesensing 13 00994 g012 550
Figure 12. (a,c) Combined MWR and GNSS-R SM estimations corresponding to N = 20 . (b–d) Error with respect to the collocated SMOS SM product. The map presents the measurements collected by FMPL-2 from (a,b) 1–31 October 2020 and from 1 November to 4 December 2020. Only reflections collocated with SMOS SM data are presented.
Figure 12. (a,c) Combined MWR and GNSS-R SM estimations corresponding to N = 20 . (b–d) Error with respect to the collocated SMOS SM product. The map presents the measurements collected by FMPL-2 from (a,b) 1–31 October 2020 and from 1 November to 4 December 2020. Only reflections collocated with SMOS SM data are presented.
Remotesensing 13 00994 g012
Remotesensing 13 00994 g013 550
Figure 13. Std(Err) evolution as a function of the number of consecutive Fresnel zones used to derive the SM estimation. Comparison between the airborne case (Microwave Interferometric Reflectometer instrument [62]) and the spaceborne case (FMPL-2). Note that the X-axis is normalized by the number of Fresnel zones used to derive the SM estimation (i.e., the N parameter used in Section 3.3). A regression curve is fit to the Std(Err) of both error curves to ease the comparison.
Figure 13. Std(Err) evolution as a function of the number of consecutive Fresnel zones used to derive the SM estimation. Comparison between the airborne case (Microwave Interferometric Reflectometer instrument [62]) and the spaceborne case (FMPL-2). Note that the X-axis is normalized by the number of Fresnel zones used to derive the SM estimation (i.e., the N parameter used in Section 3.3). A regression curve is fit to the Std(Err) of both error curves to ease the comparison.
Remotesensing 13 00994 g013
Table
Table 1. Summary of the ANN based models implemented to estimate SM.
Table 1. Summary of the ANN based models implemented to estimate SM.
ModelInput DataGround Truth
Optical
  • NDVI from MODIS,
  • Skin temperature from ECMWF.
SMOS SM product at 36 km
Optical + MWR
  • NDVI from MODIS,
  • Skin temperature from ECMWF,
  • FMPL-2 L-band MWR T A .
SMOS SM product at 36 km
GNSS-R
  • FMPL-2 reflectivity data.
SMOS SM product at 9 km
GNSS-R + MWR
  • FMPL-2 reflectivity data,
  • FMPL-2 L-band MWR T A .
SMOS SM product at 9 km
Table
Table 2. Main performance parameters of the ANN based models implemented to infer SM from optical, MWR, and GNSS-R data.
Table 2. Main performance parameters of the ANN based models implemented to infer SM from optical, MWR, and GNSS-R data.
ModelRStd(Err) (m 3 / m 3 )Bias (m 3 / m 3 )
Optical0.560.084<10 − 4
Optical + MWR0.690.074~ 10 − 3
GNSS-R ( N = 20 )0.620.087~ 10 − 4
GNSS-R ( N = 20 ) + MWR0.820.063~ 10 − 3
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Munoz-Martin, J.F.; Llaveria, D.; Herbert, C.; Pablos, M.; Park, H.; Camps, A. Soil Moisture Estimation Synergy Using GNSS-R and L-Band Microwave Radiometry Data from FSSCat/FMPL-2. Remote Sens. 2021, 13, 994. https://doi.org/10.3390/rs13050994

AMA Style

Munoz-Martin JF, Llaveria D, Herbert C, Pablos M, Park H, Camps A. Soil Moisture Estimation Synergy Using GNSS-R and L-Band Microwave Radiometry Data from FSSCat/FMPL-2. Remote Sensing. 2021; 13(5):994. https://doi.org/10.3390/rs13050994

Chicago/Turabian Style

Munoz-Martin, Joan Francesc, David Llaveria, Christoph Herbert, Miriam Pablos, Hyuk Park, and Adriano Camps. 2021. "Soil Moisture Estimation Synergy Using GNSS-R and L-Band Microwave Radiometry Data from FSSCat/FMPL-2" Remote Sensing 13, no. 5: 994. https://doi.org/10.3390/rs13050994

APA Style

Munoz-Martin, J. F., Llaveria, D., Herbert, C., Pablos, M., Park, H., & Camps, A. (2021). Soil Moisture Estimation Synergy Using GNSS-R and L-Band Microwave Radiometry Data from FSSCat/FMPL-2. Remote Sensing, 13(5), 994. https://doi.org/10.3390/rs13050994

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop