Estimation of Extreme Significant Wave Height in the Northwest Pacific Using Satellite Altimeter Data Focused on Typhoons (1992–2016)
Abstract
:1. Introduction
2. Data and Methods
2.1. Satellite Data
2.2. In-Situ Data
2.3. Best Track Data of Typhoons
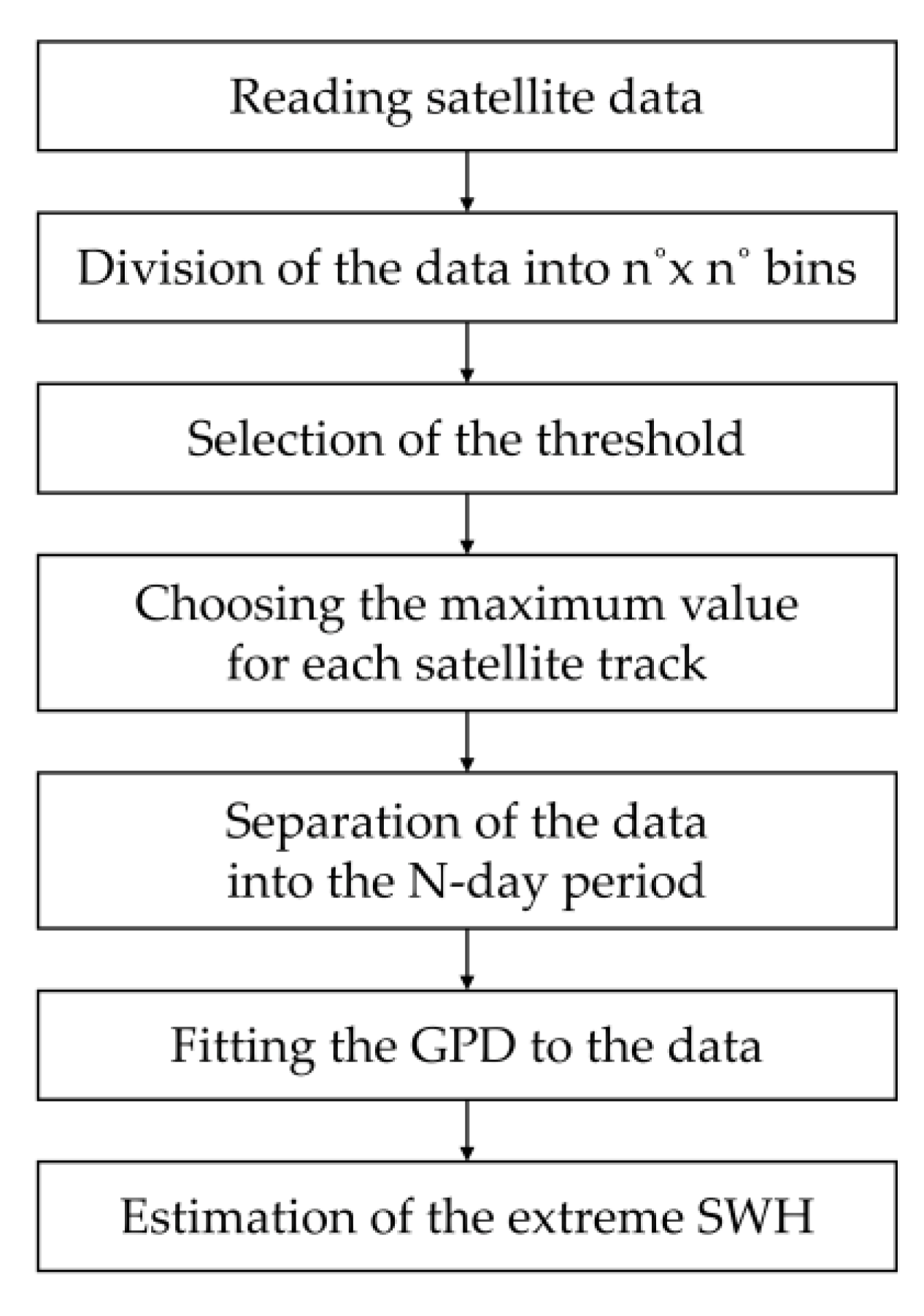
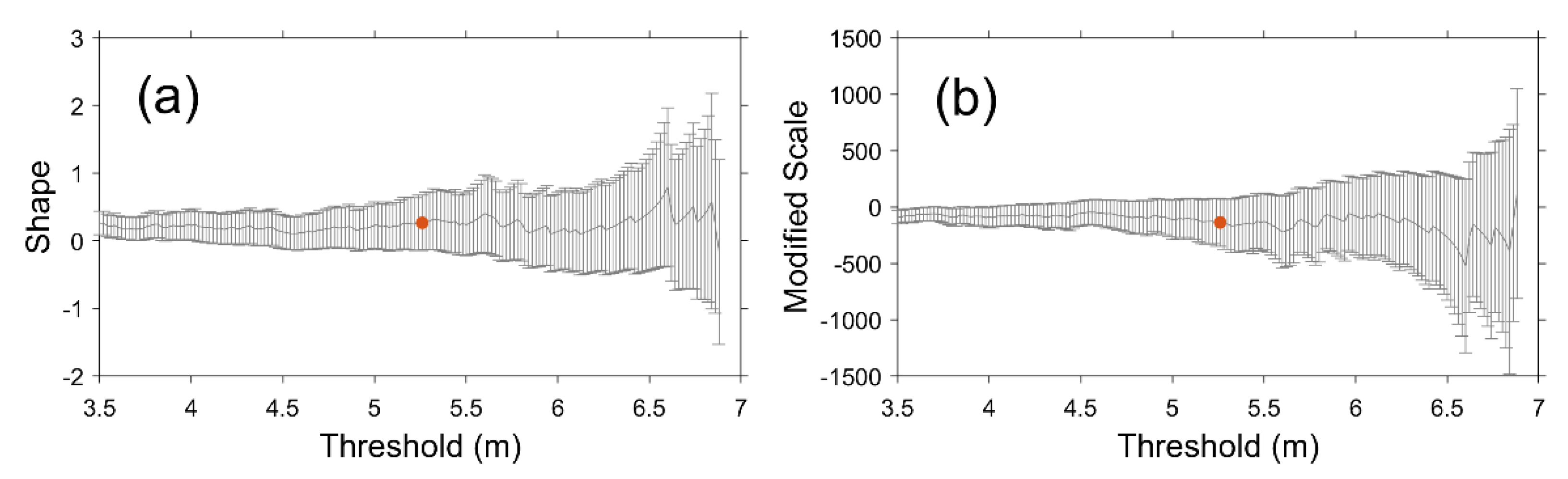
2.4. Estimation of Extreme Value
3. Results
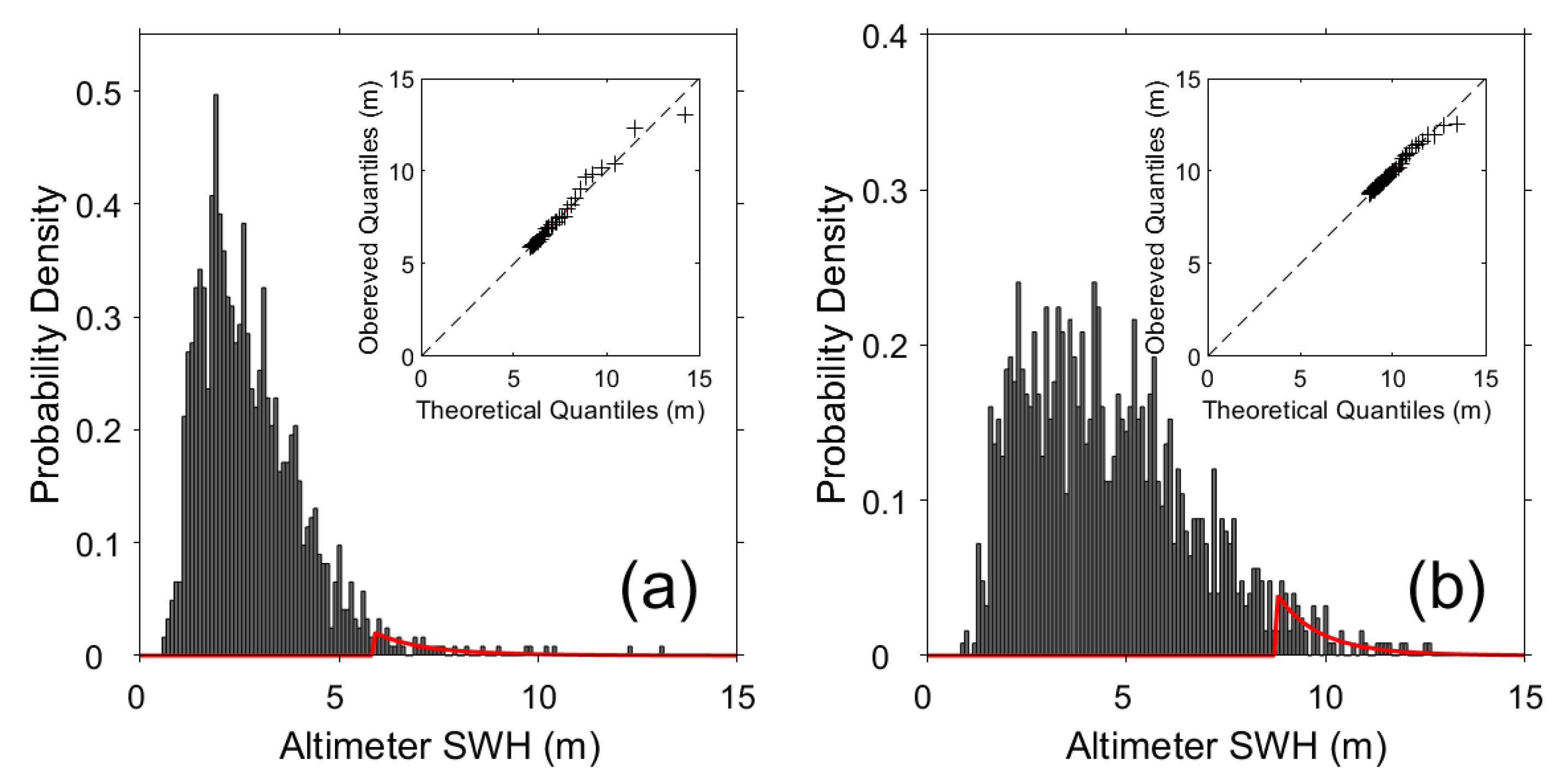
3.1. Validation of Satellite SWH Data
3.2. Estimation of Extreme SWH Using PoT Method
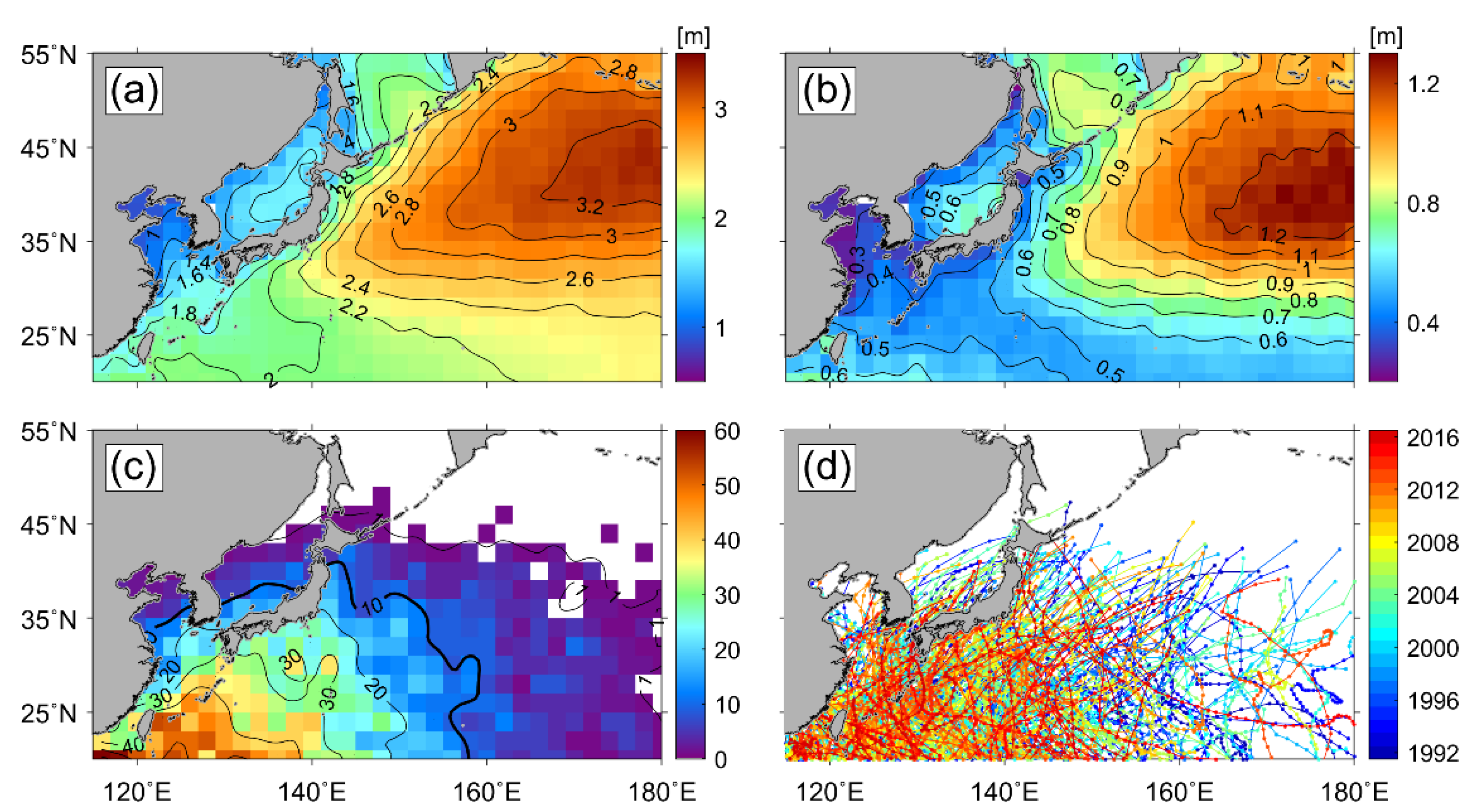
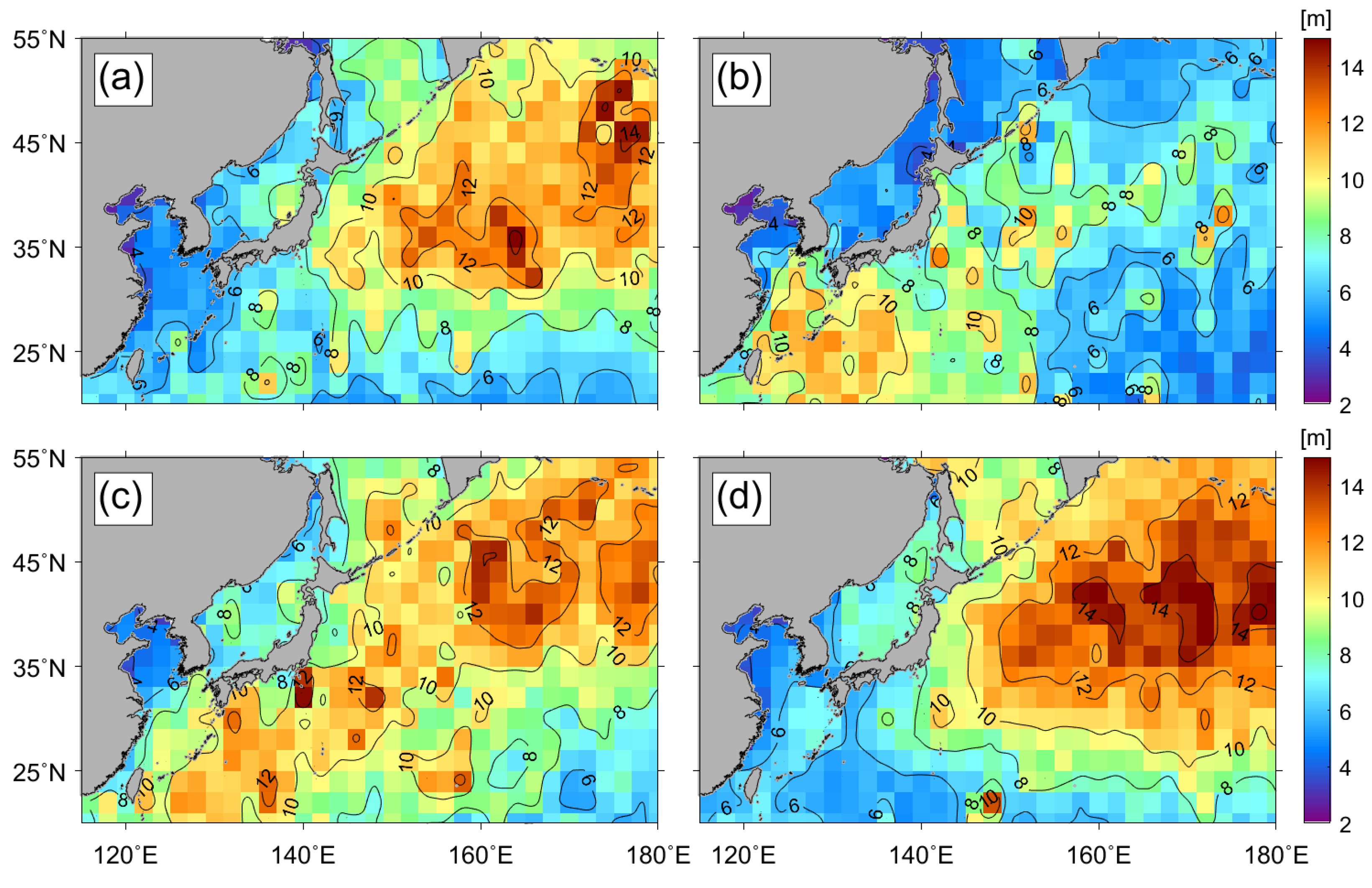
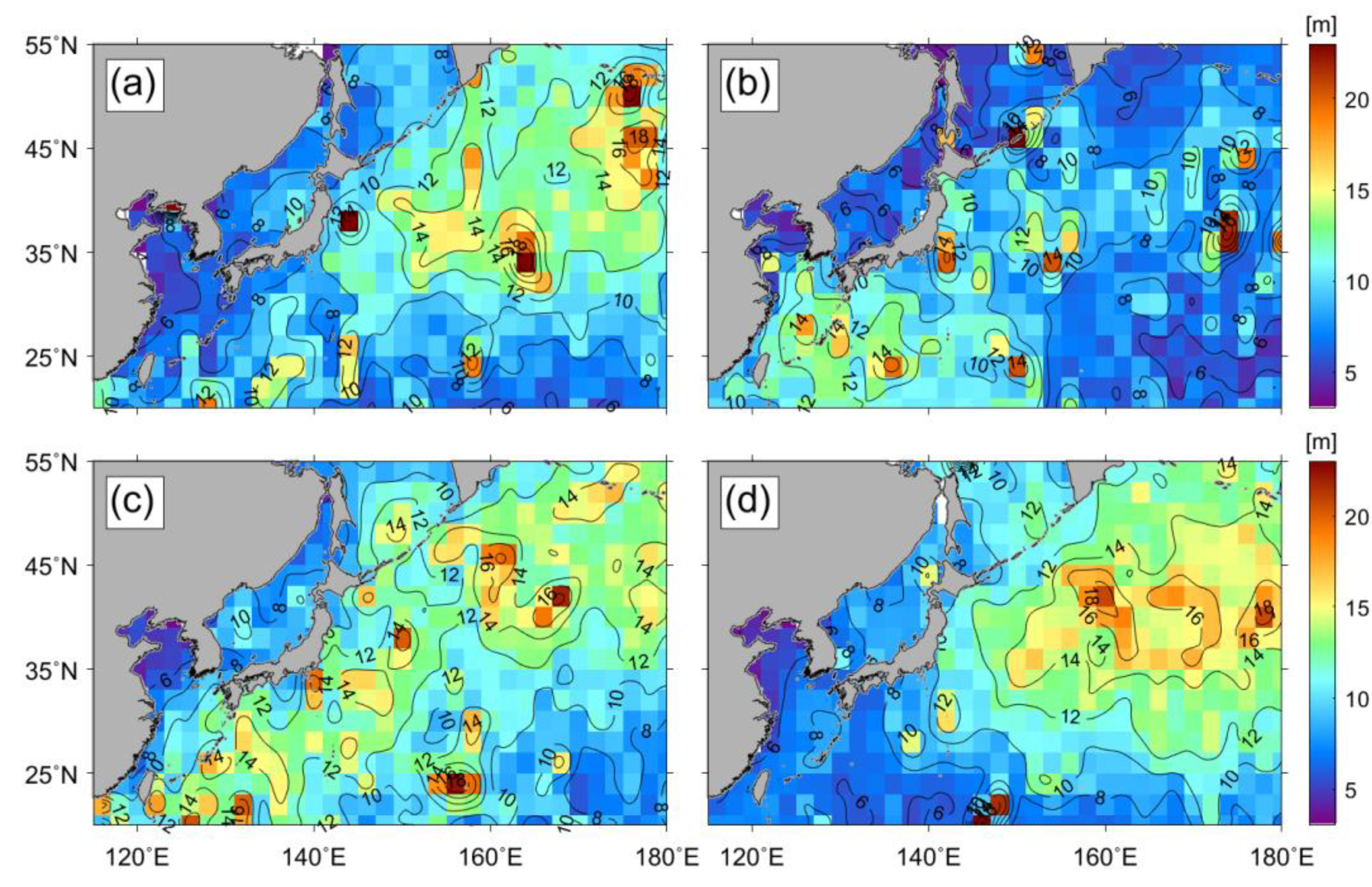
3.3. Spatial Distribution of Extreme Significant Wave Heights from Altimeter Data
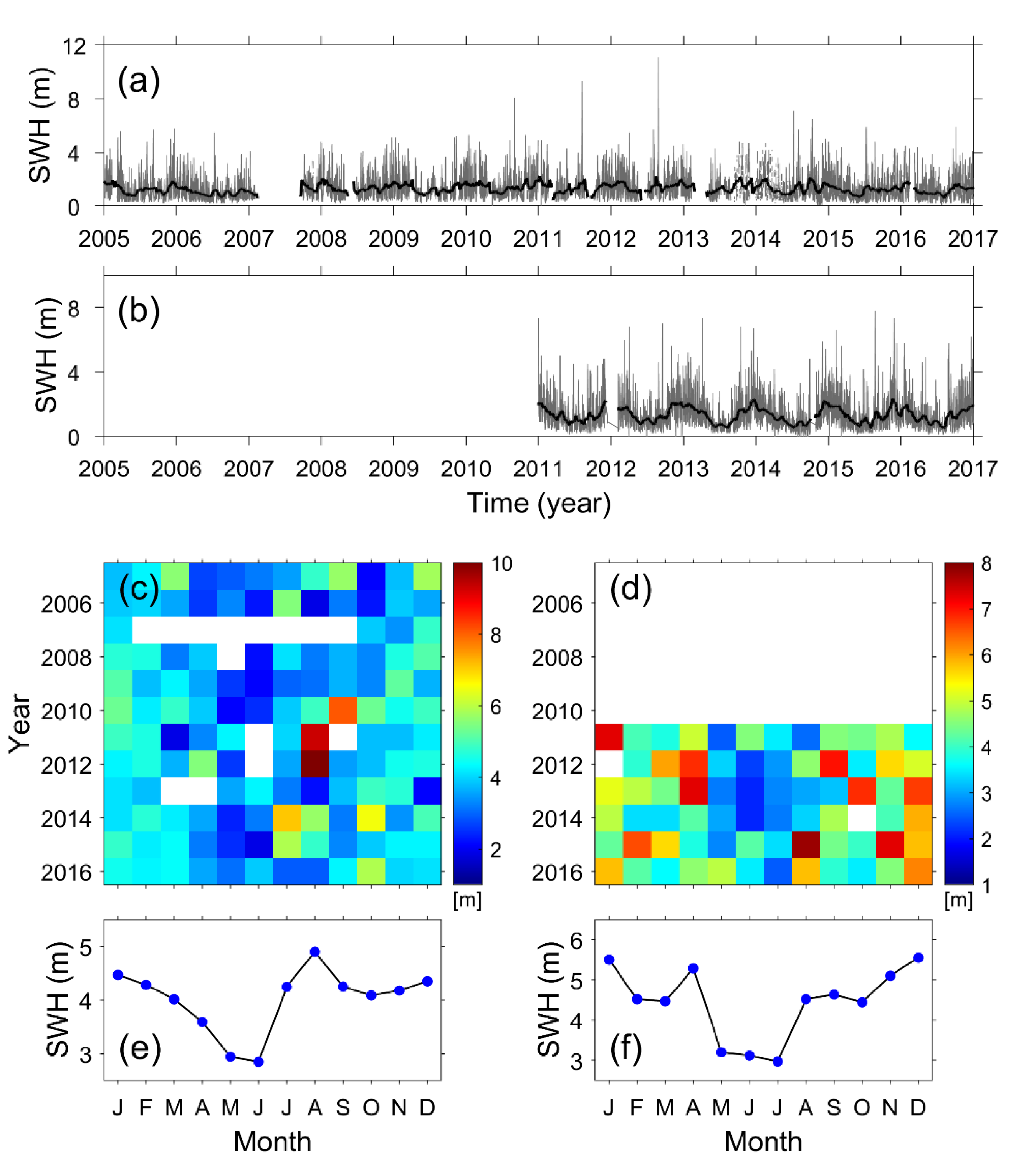
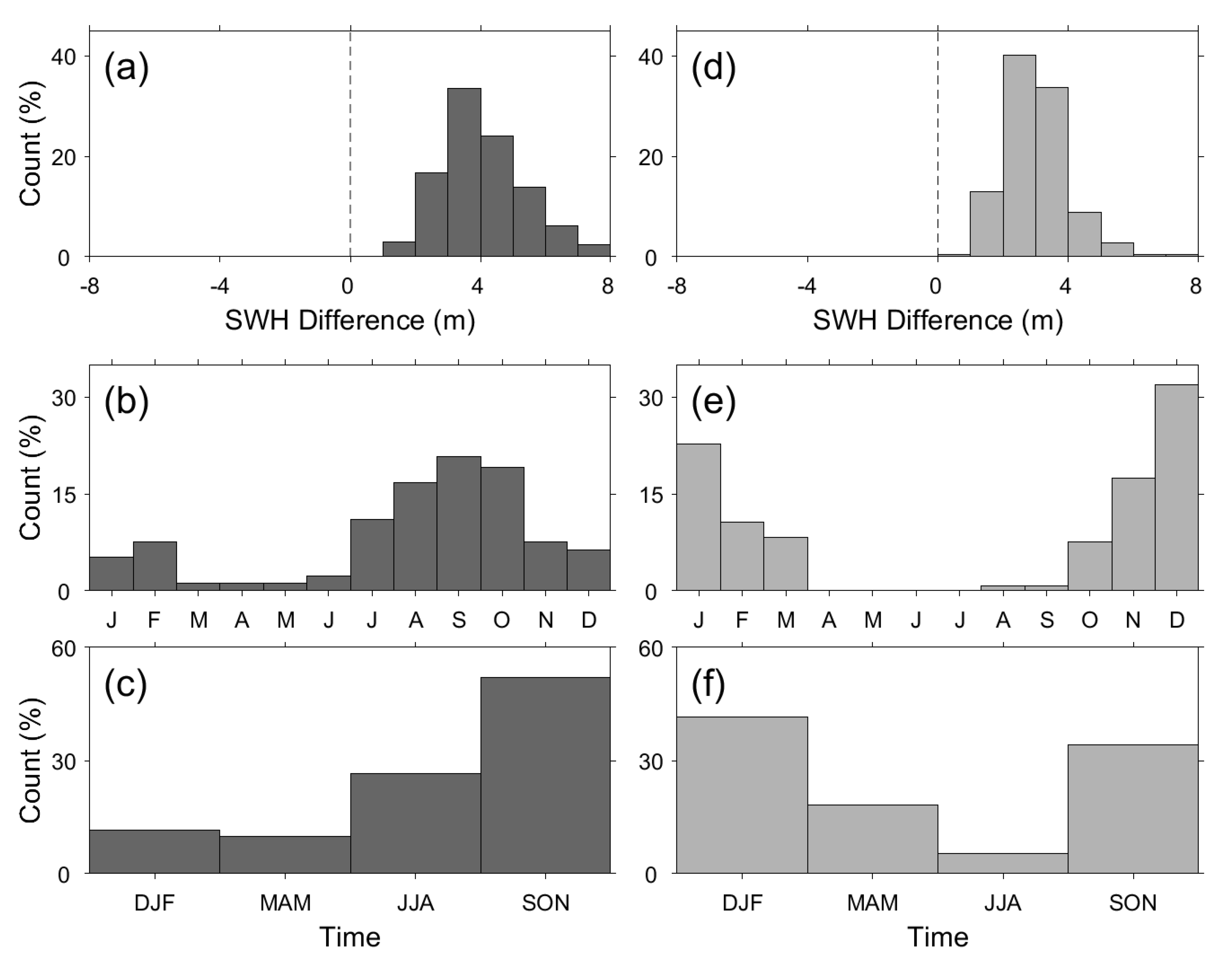
3.4. Seasonal Variability of Mean and Maximum Significant Wave Heights
3.5. Seasonal Variation of 100-Year Return Significant Wave Heights
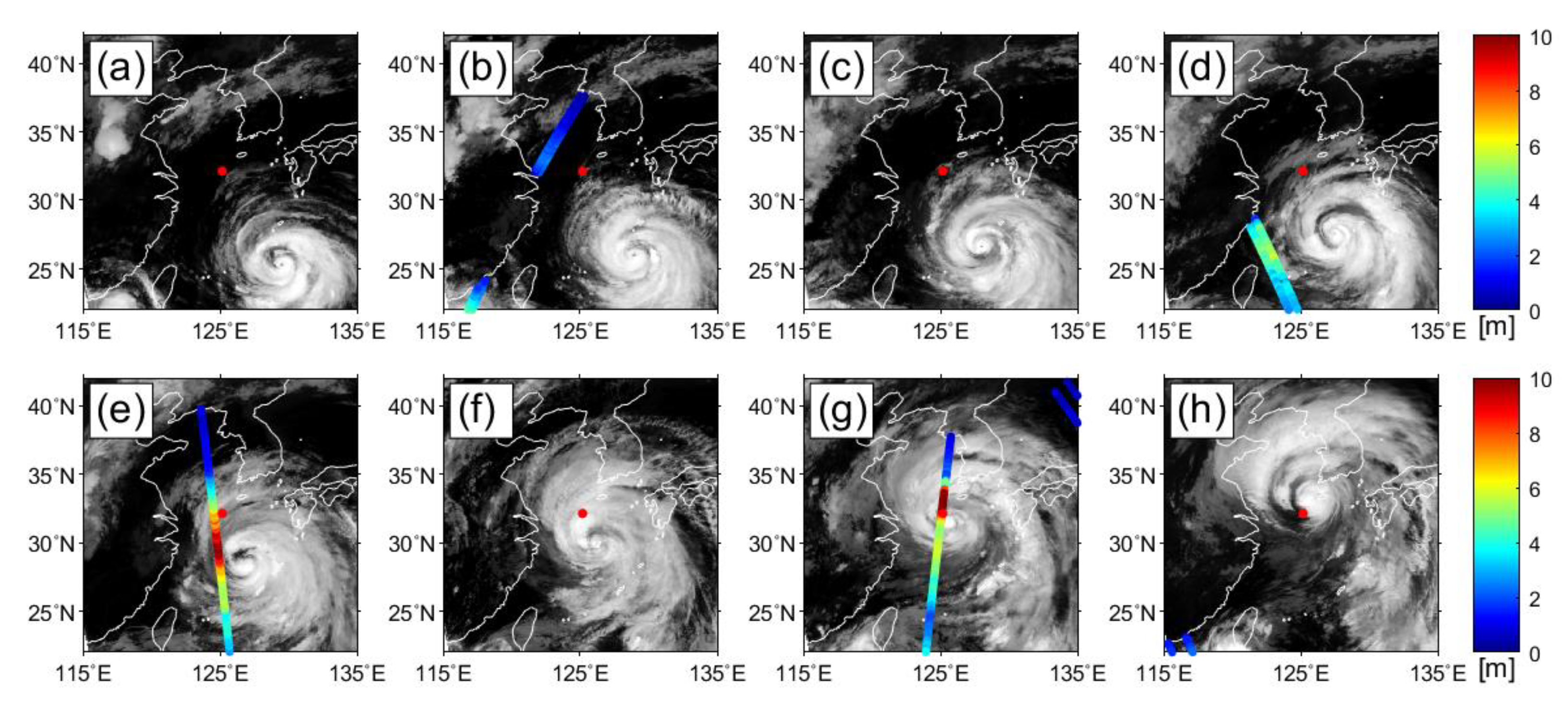
3.6. Effect of Tropical Cyclones on the Estimation of Extreme SWH
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AM | Annual Maximum |
| COMS/MI | Communication, Ocean, and Meteorological Satellite/Meteorological Imager |
| Envisat | Environmental Satellite |
| ERS-1 | European Remote Sensing-1 |
| ERS-2 | European Remote Sensing-2 |
| EVA | extreme value analysis |
| GPD | generalized Pareto distribution |
| GFO | Geosat Follow-On |
| IORS | Ieodo Ocean Research Station |
| IDM | Initial Distribution Method |
| IFREMER | Institut Français de Recherche pour l’Exploitation de la Mer |
| IBTrACS | International Best Track Archive for Climate Stewardship |
| Jason-1 | Joint Altimetry Satellite Oceanography Network-1 |
| Jason-2 | Joint Altimetry Satellite Oceanography Network-2 |
| KMA | Korea Meteorological Administration |
| PoT | Peak over Threshold |
| probability density function | |
| RMSE | root-mean-square error |
| SARAL | Satellite for Argos and Altika |
| SWH | significant wave height |
| TOPEX | Topography Experiment |
References
- Webster, P.J.; Holland, G.J.; Curry, J.A.; Chang, H.-R. Changes in tropical cyclone number, duration, and intensity in a warming environment. Science 2005, 309, 1844–1846. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Knutson, T.R.; McBride, J.L.; Chan, J.; Emanuel, K.; Holland, G.; Landsea, C.; Held, I.; Kossin, J.P.; Srivastava, A.; Sugi, M. Tropical cyclones and climate change. Nat. Geosci. 2010, 3, 157. [Google Scholar] [CrossRef] [Green Version]
- Kossin, J.P.; Emanuel, K.A.; Vecchi, G.A. The poleward migration of the location of tropical cyclone maximum intensity. Nature 2014, 509, 349–352. [Google Scholar] [CrossRef] [Green Version]
- Park, D.-S.R.; Ho, C.H.; Kim, J.H. Growing threat of intense tropical cyclone to East Asia over the period 1977–2010. Environ. Res. Lett. 2014, 9, 014008. [Google Scholar] [CrossRef] [Green Version]
- Lin, I.-I.; Chan, J.C.; Chan, J.C.L. Recent decrease in typhoon destructive potential and global warming implications. Nat. Commun. 2015, 6, 7182. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Allan, J.C.; Komar, P.D. Are ocean wave heights increasing in the eastern North Pacific? EOS 2000, 47, 561–567. [Google Scholar] [CrossRef]
- Ruggiero, P.; Komar, P.D.; Allan, J.C. Increasing wave heights and extreme value projections: The wave climate of the U.S. Pacific Northwest. Coast. Eng. 2010, 57, 539–552. [Google Scholar] [CrossRef]
- Semedo, A.; SušElj, K.; Rutgersson, A.; Sterl, A. A global view on the wind sea and swell climate and variability from ERA-40. J. Clim. 2011, 24, 1461–1479. [Google Scholar] [CrossRef]
- Young, I.R.; Zieger, S.; Babanin, A.V. Global trends in wind speed and wave height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Young, I.R.; Ribal, A. Multi-platform evaluation of global trends in wind speed and wave height. Science 2019, 364, 548–552. [Google Scholar] [CrossRef] [PubMed]
- Church, J.A.; White, N.J. A 20th century acceleration in global sea-level rise. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Rahmstorf, S. A Semi-Empirical Approach to Projecting Future Sea-Level Rise. Science 2007, 315, 368–370. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. Climate Change 2013: The Physical Science Basis: Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; p. 1535. [Google Scholar]
- Goda, Y. On the methodology of selecting design wave height. In Proceedings of the 21st International Conference on Coastal England, Malaga, Spain, 20–25 June 1988. [Google Scholar]
- Mathiesen, M.; Goda, Y.; Hawkes, P.J.; Mansard, E.; Martín, M.J.; Peltier, E.; Thompson, E.F.; Van Vledder, G. Recommended practice for extreme wave analysis. J. Hydraul. Res. 1994, 32, 803–814. [Google Scholar] [CrossRef]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2010; p. 708. [Google Scholar]
- Coles, S. An Introduction to Statistical Modelling of Extremes; Springer: Berlin, Germany, 2001. [Google Scholar]
- Carter, D.J.; Challenor, P.G. Estimating return values of environmental parameters. Q. J. R. Meteorol. Soc. 1981, 107, 259–266. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Soares, C.G. An Application of the Peaks over Threshold Method to Predict Extremes of Significant Wave Height. J. Offshore Mech. Arct. Eng. 1998, 120, 165. [Google Scholar] [CrossRef]
- Challenor, P.G.; Wimmer, W.; Ashton, I. Climate change and extreme wave heights in the North Atlantic. In Proceedings of the Envisat and ERS Symposuim, Salzburg, Austria, 6–10 September 2005. [Google Scholar]
- Mendez, F.J.; Mendez, M.; Luceno, A.; Losada, I.J. Estimation of the long-term variability of extreme significant wave height using a time-dependent Peak over Threshold (PoT) model. J. Geophys. Res. 2006, 111, 1–13. [Google Scholar] [CrossRef]
- Menéndez, M.; Méndez, F.J.; Losada, I.J.; Graham, N.E. Variability of extreme wave heights in the northeast Pacific Ocean based on buoy measurements. Geophys. Res. Lett. 2008, 35, L22607. [Google Scholar] [CrossRef]
- Sartini, L.; Cassola, F.; Besio, G. Extreme waves seasonality analysis: An application in the Mediterranean Sea. J. Geophys. Res. Oceans 2015, 120, 6266–6288. [Google Scholar] [CrossRef] [Green Version]
- Alves, J.H.G.M.; Young, I.R. On estimating extreme wave heights using combined Geosat, Topex/Poseidon and ERS-1 altimeter data. Appl. Ocean. Res. 2003, 25, 167–186. [Google Scholar] [CrossRef]
- Wimmer, W.; Challenor, P.; Retzler, C. Extreme wave heights in the North Atlantic from altimeter data. Renew. Energ. 2006, 31, 241–248. [Google Scholar] [CrossRef]
- Izaguirre, C.; Mendez, F.J.; Menéndez, M.; Luceño, A.; Losada, I.J. Extreme wave climate variability in southern Europe using satellite data. J. Geophys. Res. Space Phys. 2010, 115, 04009. [Google Scholar] [CrossRef]
- Izaguirre, C.; Mendez, F.J.; Menendez, M.; Losada, I.J. Global extreme wave height variability based on satellite data. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Vinoth, J.; Young, I.R. Global estimates of extreme wind speed and wave height. J. Clim. 2011, 24, 1647–1665. [Google Scholar] [CrossRef]
- Young, I.R.; Vinoth, J.; Zieger, S.; Babanin, A.V. Investigation of trends in extreme wave height and wind speed. J. Geophys. Res. 2012, 117, C00J06. [Google Scholar]
- Takbash, A.; Young, I.R.; Breivik, O. Global wind speed and wave height extremes derived from satellite records. J. Clim. 2019, 32, 109–126. [Google Scholar] [CrossRef]
- Wang, X.L.; Swail, V.R. Changes of extreme wave heights in Northern Hemisphere oceans and related atmospheric circulation regimes. J. Clim. 2001, 14, 2204–2221. [Google Scholar] [CrossRef]
- Cañellas, B.; Orfila, A.; Méndez, F.; Menéndez, M.; Tintoré, J. Application of a PoT model to estimate the extreme significant wave height levels around the Balearic Sea (Western Mediterranean). J. Coast. Res. Spec. Issue 2007, 50, 329–333. [Google Scholar]
- Meucci, A.; Young, I.R.; Breivik, O. Wind and wave extremes from atmosphere and wave model ensembles. J. Clim. 2018, 31, 8819–8893. [Google Scholar] [CrossRef]
- Gao, H.; Shao, Z.; Wu, G.; Li, P. Study of Directional Declustering for Estimating Extreme Wave Heights in the Yellow Sea. J. Mar. Sci. Eng. 2020, 8, 236. [Google Scholar] [CrossRef] [Green Version]
- Takbash, A.; Young, I.R. Long-Term and Seasonal Trends in Global Wave Height Extremes Derived from ERA-5 Reanalysis Data. J. Mar. Sci. Eng. 2020, 8, 1015. [Google Scholar] [CrossRef]
- Woo, H.J.; Park, K.A. Long-term trend of satellite-observed significant wave height and impact on ecosystem in the East/Japan Sea. Deep Sea Res. Part II Top. Stud. Oceanogr. 2016, 143, 1–14. [Google Scholar] [CrossRef]
- Neumann, C.J. Global Guide to Tropical Cyclone Forecasting; World Meteorological Organization: Geneva, Switzerland, 1993. [Google Scholar]
- Liu, K.S.; Chan, J.C. Inactive Period of Western North Pacific Tropical Cyclone Activity in 1998–2011. J. Clim. 2013, 26, 2614–2630. [Google Scholar] [CrossRef]
- Matsuura, T.; Yumoto, M.; Iizuka, S. A mechanism of interdecadal variability of tropical cyclone activity over the western North Pacific. Clim. Dyn. 2003, 21, 105–117. [Google Scholar] [CrossRef]
- Osinowo, A.; Lin, X.; Zhao, D.; Wang, Z. Long-term variability of extreme significant wave height in the South China sea. Adv. Meteorol. 2016, 2016, 2419353. [Google Scholar] [CrossRef] [Green Version]
- Kong, Y.; Zhang, X.; Sheng, L.; Chen, B. Validation and application of multi-source altimeter wave data in China’s offshore areas. Acta Oceanol. Sin. 2016, 35, 86–96. [Google Scholar] [CrossRef]
- Queffeulou, P.; Croizé-Fillon, D. Global Altimeter SWH Data Set; Laboratoire d’Océanographie Spatiale, IFREMER: Brest, France, 2017. [Google Scholar]
- Ha, K.-J.; Nam, S.H.; Jeong, J.-Y.; Moon, I.-J.; Lee, M.; Yun, J.; Jang, C.; Kim, Y.; Byun, D.-S.; Heo, K.-Y.; et al. Observations utilizing Korean Ocean Research Stations and their Applications for Process Studies. Bull. Am. Meteor. Soc. 2019, 100, 2061–2075. [Google Scholar] [CrossRef]
- Intergovernmental Oceanographic Commission. GTSPP Real-Time Quality Control Manual; Manuals and Guides 22; UNESCO: Paris, France, 1990. [Google Scholar]
- Intergovernmental Oceanographic Commission. Manual of Quality Control Procedures for Validation of Oceanographic Data; Manuals and Guides 26; UNESCO: Paris, France, 1993. [Google Scholar]
- Evans, D.; Conrad, C.; Paul, F. Handbook of Automated Data Quality Control Checks and Procedures of the National Data Buoy Center; NOAA/National Data Buoy Centre: Hancock, MS, USA, 2003; p. 44. [Google Scholar]
- Lee, H.S. Abnormal storm waves in the East Sea (Japan Sea) in April 2012. J. Coast. Res. 2013, 65, 748–753. [Google Scholar] [CrossRef]
- Heo, K.Y.; Choi, J.Y.; Jeong, S.H. Characteristics of High Swell-like Waves on East Coast of Korea Observed by Direct Measurements and Reanalysis Data Sets. J. Coast. Res. 2020, 95, 1433–1437. [Google Scholar] [CrossRef]
- Knapp, K.R.; Kruk, M.C.; Levinson, D.H.; Diamond, H.J.; Neumann, C.J. The international best track archive for climate stewardship (IBTrACS). Bull. Am. Met. Soc. 2010, 91, 363–376. [Google Scholar] [CrossRef]
- Cooper, C.K.; Forristall, G.Z. The use of satellite altimeter data to estimate the extreme wave climate. J. Atmos. Ocean Tech. 1997, 14, 254–266. [Google Scholar] [CrossRef]
- Caires, S.; Sterl, A. 100-year return value estimates for ocean wind speed and significant wave height from the ERA-40 data. J. Clim. 2005, 18, 1032–1048. [Google Scholar] [CrossRef]
- Woo, H.J.; Park, K.A.; Byun, D.S.; Lee, J.; Lee, E. Characteristics of the differences between significant wave height at Ieodo Ocean Research Station and satellite altimeter-measured data over a decade (2004~2016). Sea 2018, 23, 1–19, (In Korean with English abstract). [Google Scholar]




| Satellite | Operational Period | Data Period | Repeat Period (Days) |
|---|---|---|---|
| ERS-1 | 17 July 1991–10 March 2000 | 2 January 1992–2 June 1996 | 3, 35, 168 |
| TOPEX/Poseidon | 10 August 1992–9 October 2005 | 25 September 1992–8 October 2005 | 9.9156 |
| ERS-2 | 21 April 1995–5 September 2011 | 15 May 1995–2 July 2011 | 35 |
| GFO | 10 February 1998–22 October 2008 | 7 January 2000–7 September 2008 | 17 |
| Jason-1 | 7 December 2001–21 June 2013 | 15 January 2002–20 June 2013 | 9.9156 |
| Envisat | 1 March 2002–8 April 2012 | 14 May 2002–8 April 2012 | 35 |
| Jason-2 | 20 June 2008–9 October 2019 | 4 July 2008–31 December 2016 | 9.9156 |
| Cryosat-2 | 8 April 2010–Present | 16 July 2010–31 December 2016 | 30 |
| SARAL | 25 Feb 2013–Present | 14 Mar 2013–31 December 2016 | 35 |
| Station | |||||
|---|---|---|---|---|---|
| IORS | 12.83 | 11.83 | 13.95 | 16.49 | 3.66 |
| Donghae Buoy | 7.23 | 7.03 | 7.25 | 7.43 | 0.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Woo, H.-J.; Park, K.-A. Estimation of Extreme Significant Wave Height in the Northwest Pacific Using Satellite Altimeter Data Focused on Typhoons (1992–2016). Remote Sens. 2021, 13, 1063. https://doi.org/10.3390/rs13061063
Woo H-J, Park K-A. Estimation of Extreme Significant Wave Height in the Northwest Pacific Using Satellite Altimeter Data Focused on Typhoons (1992–2016). Remote Sensing. 2021; 13(6):1063. https://doi.org/10.3390/rs13061063
Chicago/Turabian StyleWoo, Hye-Jin, and Kyung-Ae Park. 2021. "Estimation of Extreme Significant Wave Height in the Northwest Pacific Using Satellite Altimeter Data Focused on Typhoons (1992–2016)" Remote Sensing 13, no. 6: 1063. https://doi.org/10.3390/rs13061063
APA StyleWoo, H.-J., & Park, K.-A. (2021). Estimation of Extreme Significant Wave Height in the Northwest Pacific Using Satellite Altimeter Data Focused on Typhoons (1992–2016). Remote Sensing, 13(6), 1063. https://doi.org/10.3390/rs13061063








