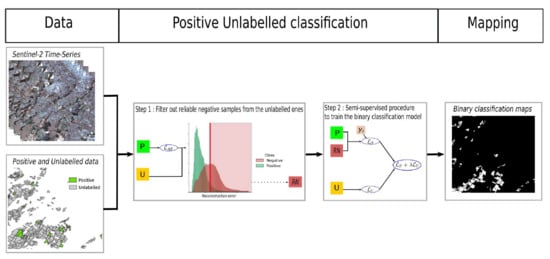
Figure 1.
The VAERNN is trained on the set of positively labelled samples P. Then, the model is applied on the set of unlabelled samples U. Successively, the reconstruction error for each is derived, and the set of reliable negative samples is identified based on the reconstruction error. The vertical red line indicates the average reconstruction error () on the set of unlabelled samples U. Samples with a reconstruction error bigger than are possible candidates for the reliable negative set .
Figure 1.
The VAERNN is trained on the set of positively labelled samples P. Then, the model is applied on the set of unlabelled samples U. Successively, the reconstruction error for each is derived, and the set of reliable negative samples is identified based on the reconstruction error. The vertical red line indicates the average reconstruction error () on the set of unlabelled samples U. Samples with a reconstruction error bigger than are possible candidates for the reliable negative set .
Figure 2.
Visual representation of the GRU and FCGRU cells [
17].
Figure 2.
Visual representation of the GRU and FCGRU cells [
17].
Figure 3.
The training strategy involves two models trained simultaneously. The first model is trained on the set of perturbed positive labelled P and reliable negative samples by the autoencoder with the supervised BCE loss on true labels . The second is the final classification model trained on P and samples, with a semi-supervised process involving two losses: the binary cross entropy loss on the true labels () and the KL divergence between the generated soft labels and to enforce consistency (). The hyper-parameter weights the importance of the unsupervised term.
Figure 3.
The training strategy involves two models trained simultaneously. The first model is trained on the set of perturbed positive labelled P and reliable negative samples by the autoencoder with the supervised BCE loss on true labels . The second is the final classification model trained on P and samples, with a semi-supervised process involving two losses: the binary cross entropy loss on the true labels () and the KL divergence between the generated soft labels and to enforce consistency (). The hyper-parameter weights the importance of the unsupervised term.
Figure 4.
Haute-Garonne is located in the southwest of France (a). The spatial distribution of the land covers (Cereals/Oilseeds and Forest) considered as positive classes (b). The Sentinel-2 RGB composite obtained over the year 2019 (c).
Figure 4.
Haute-Garonne is located in the southwest of France (a). The spatial distribution of the land covers (Cereals/Oilseeds and Forest) considered as positive classes (b). The Sentinel-2 RGB composite obtained over the year 2019 (c).
Figure 5.
Overview of the acquisition dates of Sentinel-2 (S2) images over Haute-Garonne. S2 acquisitions are sparsely distributed due to the ubiquitous cloudiness.
Figure 5.
Overview of the acquisition dates of Sentinel-2 (S2) images over Haute-Garonne. S2 acquisitions are sparsely distributed due to the ubiquitous cloudiness.
Figure 6.
Confusion matrices of (a) RFPUL, (b) ENSEMBLEPUL, (c) OCSVM, and (d) PUL-SITS considering the case in which the land cover class of interest (the positive class) is Cereals/Oilseeds with the number of positive training data objects (n) equal to 80.
Figure 6.
Confusion matrices of (a) RFPUL, (b) ENSEMBLEPUL, (c) OCSVM, and (d) PUL-SITS considering the case in which the land cover class of interest (the positive class) is Cereals/Oilseeds with the number of positive training data objects (n) equal to 80.
Figure 7.
Confusion matrices of (a) RFPUL, (b) ENSEMBLEPUL, (c) OCSVM, and (d) PUL-SITS considering the case in which the land cover class of interest (the positive class) is Forest with the number of positive training objects (n) equal to 80.
Figure 7.
Confusion matrices of (a) RFPUL, (b) ENSEMBLEPUL, (c) OCSVM, and (d) PUL-SITS considering the case in which the land cover class of interest (the positive class) is Forest with the number of positive training objects (n) equal to 80.
Figure 8.
A first visual evaluation zone with (a) its RGB composite and the corresponding binary classification maps for (b) RFPUL, (c) ENSEMBLEPUL, (d) OCSVM, and (e) PUL-SITS for the positive class Cereals/Oilseeds with the number of positive training data objects (n) equal to 80.
Figure 8.
A first visual evaluation zone with (a) its RGB composite and the corresponding binary classification maps for (b) RFPUL, (c) ENSEMBLEPUL, (d) OCSVM, and (e) PUL-SITS for the positive class Cereals/Oilseeds with the number of positive training data objects (n) equal to 80.
Figure 9.
A second visual evaluation zone with (a) its RGB composite and the corresponding binary classification maps for (b) RFPUL, (c) ENSEMBLEPUL, (d) OCSVM, and (e) PUL-SITS for the positive class Cereals/Oilseeds with the number of positive training data objects (n) equal to 80.
Figure 9.
A second visual evaluation zone with (a) its RGB composite and the corresponding binary classification maps for (b) RFPUL, (c) ENSEMBLEPUL, (d) OCSVM, and (e) PUL-SITS for the positive class Cereals/Oilseeds with the number of positive training data objects (n) equal to 80.
Figure 10.
A first visual evaluation zone with (a) its RGB composite and the corresponding binary classification maps for (b) RFPUL, (c) ENSEMBLEPUL, (d) OCSVM, and (e) PUL-SITS for the positive class Forest with the number of positive training data objects (n) equal to 80.
Figure 10.
A first visual evaluation zone with (a) its RGB composite and the corresponding binary classification maps for (b) RFPUL, (c) ENSEMBLEPUL, (d) OCSVM, and (e) PUL-SITS for the positive class Forest with the number of positive training data objects (n) equal to 80.
Figure 11.
A second visual evaluation zone with (a) its RGB composite and the corresponding binary classification maps for (b) RFPUL, (c) ENSEMBLEPUL, (d) OCSVM, and (e) PUL-SITS for the positive class Forest with the number of positive training data objects (n) equal to 80.
Figure 11.
A second visual evaluation zone with (a) its RGB composite and the corresponding binary classification maps for (b) RFPUL, (c) ENSEMBLEPUL, (d) OCSVM, and (e) PUL-SITS for the positive class Forest with the number of positive training data objects (n) equal to 80.
Table 1.
Haute-Garonne ground truth characteristics.
Table 1.
Haute-Garonne ground truth characteristics.
| Class | # of Objects | # of Pixels |
|---|
| Cereals/Oilseeds | 898 | 336,044 |
| Forest | 846 | 186,870 |
| Other land cover classes | 6460 | 323,925 |
| Total | 7358 | 846,838 |
Table 2.
Number of positive, unlabelled, and negative objects/pixels in the training and test set when the positive samples belong to the Cereals/Oilseeds land cover class.
Table 2.
Number of positive, unlabelled, and negative objects/pixels in the training and test set when the positive samples belong to the Cereals/Oilseeds land cover class.
| # of Objects Training (P/U) | # of Pixels Training (P/U) | # of Objects Test (P/N) | # of Pixels Test (P/N) |
|---|
| 20/3659 | 7010/410,712 | 451/3228 | 168,404/260,711 |
| 40/3639 | 14,618/403,104 |
| 60/3619 | 21,001/403,822 |
| 80/3599 | 28,955/388,767 |
| 100/3579 | 36,442/381,280 |
Table 3.
Number of positive, unlabelled, and negative objects/pixels in the training and test set when the positive samples belong to the Forest land cover class.
Table 3.
Number of positive, unlabelled, and negative objects/pixels in the training and test set when the positive samples belong to the Forest land cover class.
| # of Objects Train (P/U) | # of Pixels Train (P/U) | # of Objects Test (P/N) | # of Pixels Test (P/N) |
|---|
| 20/3658 | 4206/413,517 | 428/3250 | 95,725/333,390 |
| 40/3638 | 9565/408,157 |
| 60/3618 | 13,900/403,822 |
| 80/3598 | 17,865/399,857 |
| 100/3578 | 22,143/395,579 |
Table 4.
Performances in terms of the F-Measure of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
Table 4.
Performances in terms of the F-Measure of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 46.2 ± 1.7 | 47.3 ± 1.5 | 61.6 ± 4.0 | 80.3± 2.3 | 75.5 ± 3.5 | 78.9 ± 4.0 |
| 40 | 46.7 ± 1.7 | 49.3 ± 1.7 | 63.8 ± 2.7 | 84.9 ± 1.9 | 82.0 ± 2.3 | 85.3± 2.8 |
| 60 | 47.2 ± 1.8 | 52.4 ± 1.6 | 64.7 ± 2.0 | 86.6 ± 2.8 | 84.2 ± 2.0 | 87.3± 2.2 |
| 80 | 48.3 ± 2.0 | 55.7 ± 2.1 | 64.7 ± 2.3 | 86.5 ± 2.3 | 85.0 ± 2.5 | 88.0± 2.6 |
| 100 | 50.2 ± 1.6 | 60.1 ± 1.8 | 64.3 ± 2.0 | 86.2 ± 3.0 | 85.5 ± 1.8 | 88.6± 1.3 |
Table 5.
Performances in terms of the Accuracy of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
Table 5.
Performances in terms of the Accuracy of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 60.9 ± 1.4 | 61.3 ± 1.3 | 63.9 ± 2.1 | 80.9± 2.0 | 76.3 ± 3.1 | 79.5 ± 3.6 |
| 40 | 61.1 ± 1.4 | 62.1 ± 1.2 | 65.1 ± 2.2 | 85.0 ± 1.9 | 82.3 ± 2.2 | 85.4± 2.8 |
| 60 | 61.3 ± 1.4 | 63.5 ± 1.2 | 66.0 ± 1.6 | 86.6 ± 2.8 | 84.2 ± 2.0 | 87.3± 2.1 |
| 80 | 61.8 ± 1.5 | 65.1 ± 1.3 | 65.4 ± 1.9 | 86.5 ± 2.3 | 85.1 ± 2.4 | 87.9± 2.5 |
| 100 | 62.6 ± 1.3 | 67.5 ± 1.2 | 65.2 ± 1.7 | 86.1 ± 2.9 | 85.5 ± 1.8 | 88.6± 1.3 |
Table 6.
Performances in terms of the Sensitivity of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
Table 6.
Performances in terms of the Sensitivity of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 100± 0.0 | 99.8 ± 0.1 | 81.5 ± 5.0 | 91.7 ± 4.1 | 88.1 ± 3.5 | 88.6 ± 8.9 |
| 40 | 100± 0.0 | 99.6 ± 0.2 | 79.6 ± 3.9 | 88.4 ± 2.8 | 89.0 ± 1.8 | 90.3 ± 2.0 |
| 60 | 100± 0.0 | 99.3 ± 0.3 | 77.3 ± 3.8 | 86.7 ± 5.8 | 87.3 ± 3.6 | 88.3 ± 2.5 |
| 80 | 100± 0.0 | 99.1 ± 0.2 | 77.0 ± 3.6 | 86.6 ± 5.3 | 88.9 ± 2.5 | 88.7 ± 2.0 |
| 100 | 99.9± 0.1 | 98.9 ± 0.2 | 77.7 ± 3.2 | 85.1 ± 5.9 | 87.4 ± 2.8 | 89.4 ± 2.0 |
Table 7.
Performances in term of the Specificity of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
Table 7.
Performances in term of the Specificity of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 0.3 ± 0.3 | 1.6 ± 0.8 | 36.9 ± 11.2 | 65.3 ± 9.8 | 59.3 ± 10.0 | 66.6± 13.6 |
| 40 | 0.9 ± 0.6 | 4.0 ± 2.2 | 42.7 ± 7.7 | 80.0± 4.7 | 72.4 ± 5.2 | 78.2 ± 5.3 |
| 60 | 1.4 ± 0.7 | 8.1 ± 2.1 | 47.4 ± 6.8 | 85.9 ± 2.9 | 79.6 ± 5.0 | 85.9± 5.0 |
| 80 | 2.7 ± 0.9 | 12.4 ± 3.0 | 47.7 ± 6.9 | 86.1 ± 4.2 | 79.4 ± 5.5 | 86.8± 4.5 |
| 100 | 5.0 ± 1.2 | 18.8 ± 2.8 | 45.9 ± 6.0 | 87.6± 3.1 | 82.7 ± 3.7 | 87.3 ± 4.3 |
Table 8.
Performances in term of the Kappa measure of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
Table 8.
Performances in term of the Kappa measure of the different competing strategies when the land cover class of interest (the positive class) is Cereals/Oilseeds.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 0.00 ± 0.00 | 0.02 ± 0.01 | 0.19 ± 0.07 | 0.59± 0.05 | 0.49 ± 0.07 | 0.56 ± 0.07 |
| 40 | 0.01 ± 0.01 | 0.04 ± 0.02 | 0.23 ± 0.05 | 0.68 ± 0.04 | 0.62 ± 0.05 | 0.69± 0.06 |
| 60 | 0.02 ± 0.01 | 0.09 ± 0.02 | 0.25 ± 0.04 | 0.72 ± 0.05 | 0.67 ± 0.04 | 0.74± 0.04 |
| 80 | 0.03 ± 0.01 | 0.14 ± 0.03 | 0.25 ± 0.04 | 0.72 ± 0.04 | 0.69 ± 0.05 | 0.75± 0.05 |
| 100 | 0.06 ± 0.01 | 0.21 ± 0.03 | 0.24 ± 0.04 | 0.72 ± 0.05 | 0.70 ± 0.03 | 0.76± 0.03 |
Table 9.
Performances in terms of the F-Measure of the different competing strategies when the land cover class of interest (the positive class) is Forest.
Table 9.
Performances in terms of the F-Measure of the different competing strategies when the land cover class of interest (the positive class) is Forest.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 68.4 ± 2.7 | 69.8 ± 2.4 | 82.7 ± 3.0 | 86.1 ± 1.8 | 89.7 ± 2.0 | 91.4± 1.9 |
| 40 | 69.7 ± 2.7 | 72.8 ± 3.1 | 83.1 ± 2.6 | 85.1 ± 3.4 | 89.8 ± 3.7 | 92.9± 2.3 |
| 60 | 71.6 ± 2.9 | 76.4 ± 3.1 | 84.4 ± 2.5 | 86.5 ± 2.5 | 90.1 ± 2.2 | 92.6± 2.5 |
| 80 | 73.9 ± 3 | 79.5 ± 3.1 | 84.7 ± 2.4 | 86.6 ± 2.9 | 88.8 ± 2.9 | 91.4± 3.5 |
| 100 | 76.8 ± 2.7 | 83.1 ± 2.8 | 85.2 ± 2.4 | 85.0 ± 1.7 | 88.7 ± 2.8 | 91.9± 1.8 |
Table 10.
Performances in terms of the Accuracy of the different competing strategies when the land cover class of interest (the positive class) is Forest.
Table 10.
Performances in terms of the Accuracy of the different competing strategies when the land cover class of interest (the positive class) is Forest.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 77.9 ± 1.9 | 78.4 ± 1.8 | 85.0 ± 2.1 | 83.2 ± 2.3 | 87.9 ± 2.6 | 90.1± 2.7 |
| 40 | 78.4 ± 1.9 | 79.8 ± 2.1 | 85.8 ± 1.9 | 81.9 ± 4.6 | 88.0 ± 4.8 | 92.1± 2.8 |
| 60 | 79.3 ± 2.0 | 81.7 ± 2.1 | 86.7 ± 1.8 | 83.8 ± 3.8 | 88.4 ± 2.9 | 91.5± 3.1 |
| 80 | 80.4 ± 2.0 | 83.5 ± 2.2 | 86.9 ± 1.8 | 83.7 ± 3.9 | 86.7 ± 3.7 | 90.1± 4.3 |
| 100 | 81.9 ± 1.9 | 85.8 ± 2.1 | 87.2 ± 1.8 | 81.8 ± 2.3 | 86.7 ± 3.7 | 90.8± 2.2 |
Table 11.
Performances in terms of the Sensitivity of the different competing strategies when the land cover class of interest (the positive class) is Forest.
Table 11.
Performances in terms of the Sensitivity of the different competing strategies when the land cover class of interest (the positive class) is Forest.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 100± 0.0 | 99.9 ± 0.1 | 99.7 ± 0.2 | 81.6 ± 2.5 | 87.2 ± 3.0 | 89.7 ± 2.9 |
| 40 | 100± 0.0 | 99.8 ± 0.1 | 99.7 ± 0.3 | 80.1 ± 5.1 | 87.1 ± 5.5 | 91.9 ± 3.3 |
| 60 | 99.9± 0.0 | 99.8 ± 0.2 | 99.7 ± 0.2 | 82.0 ± 3.7 | 87.6 ± 3.4 | 91.2 ± 3.6 |
| 80 | 99.9± 0.1 | 99.8 ± 0.1 | 99.7 ± 0.2 | 82.2 ± 4.3 | 85.7 ± 4.3 | 89.5 ± 5.0 |
| 100 | 99.8± 0.1 | 99.7 ± 0.1 | 99.7 ± 0.1 | 79.9 ± 2.6 | 85.6 ± 4.3 | 90.2 ± 2.6 |
Table 12.
Performances in terms of the Specificity of the different competing strategies when the land cover class of interest (the positive class) is Forest.
Table 12.
Performances in terms of the Specificity of the different competing strategies when the land cover class of interest (the positive class) is Forest.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 0.8 ± 0.4 | 3.7 ± 1.3 | 36.0 ± 7.8 | 97.3± 1.01 | 94.1 ± 1.5 | 94.0 ± 1.6 |
| 40 | 3.4 ± 2.4 | 10.1 ± 3.7 | 37.2 ± 7.2 | 97.6± 1.26 | 95.2 ± 1.8 | 93.6 ± 2.5 |
| 60 | 7.5 ± 3.2 | 18.7 ± 5.2 | 41.1 ± 6.9 | 97.9± 1.0 | 95.5 ± 1.7 | 94.3 ± 2.9 |
| 80 | 12.5 ± 4.2 | 26.8 ± 6.3 | 42.0 ± 6.5 | 97.9± 1.0 | 96.2 ± 1.5 | 95.2 ± 2.2 |
| 100 | 19.6 ± 4.7 | 37.3 ± 6.8 | 43.6 ± 6.5 | 98.3± 0.7 | 96.3 ± 1.4 | 94.9 ± 2.0 |
Table 13.
Performances in terms of the Kappa measure of the different competing strategies when the land cover class of interest (the positive class) is Forest.
Table 13.
Performances in terms of the Kappa measure of the different competing strategies when the land cover class of interest (the positive class) is Forest.
| # of Obj Samples | RFPUL | ENSEMBLEPUL | OCSVM | PUL-SITSnoReg | PUL-SITSreco | PUL-SITS |
|---|
| 20 | 0.01 ± 0.01 | 0.05 ± 0.02 | 0.46 ± 0.09 | 0.46 ± 0.05 | 0.55 ± 0.07 | 0.61± 0.08 |
| 40 | 0.05 ± 0.04 | 0.14 ± 0.05 | 0.47 ± 0.07 | 0.44 ± 0.08 | 0.57 ± 0.13 | 0.67± 0.09 |
| 60 | 0.11 ± 0.05 | 0.26 ± 0.07 | 0.51 ± 0.07 | 0.47 ± 0.08 | 0.57 ± 0.08 | 0.66± 0.1 |
| 80 | 0.18 ± 0.06 | 0.36 ± 0.08 | 0.52 ± 0.07 | 0.48 ± 0.08 | 0.54 ± 0.08 | 0.62± 0.1 |
| 100 | 0.27 ± 0.06 | 0.47 ± 0.08 | 0.54 ± 0.07 | 0.44 ± 0.05 | 0.53 ± 0.07 | 0.63± 0.05 |