Absolute Frequency Readout of Cavity against Atomic Reference
Abstract
:1. Introduction
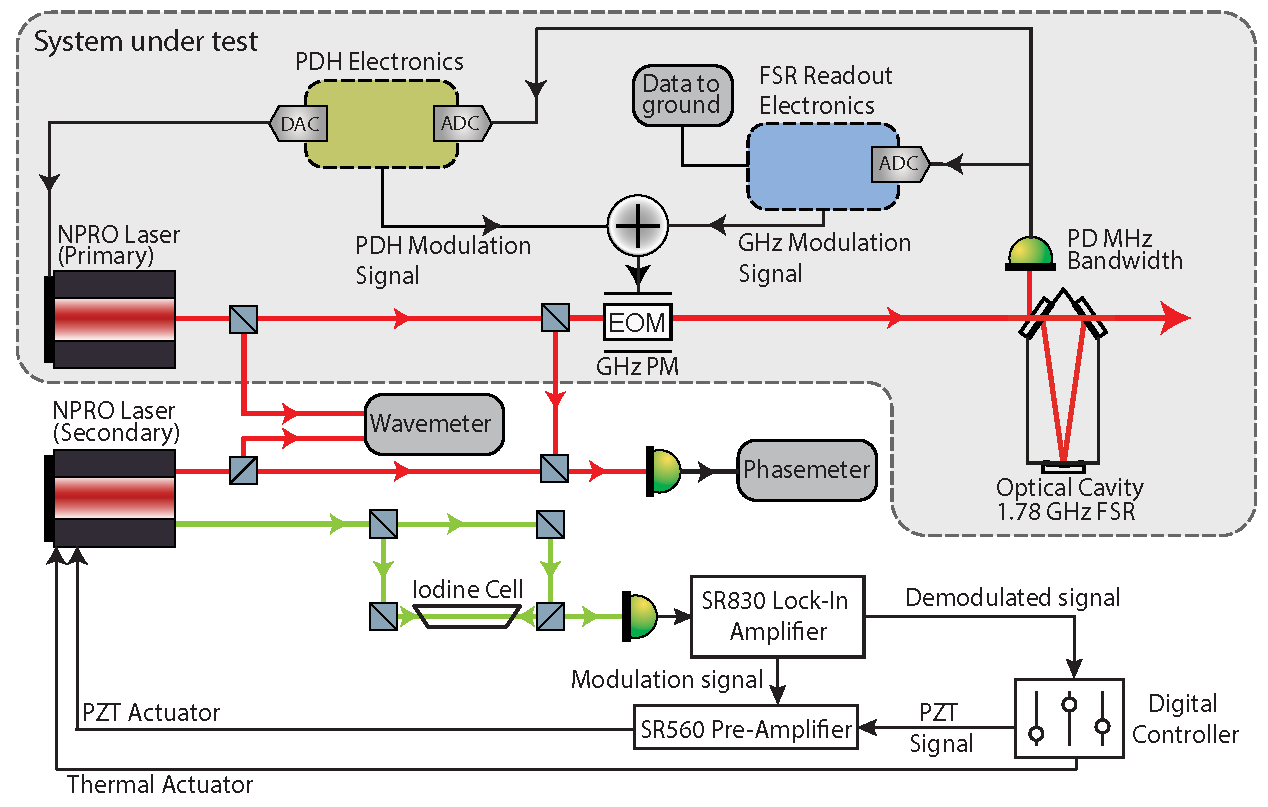
2. Materials and Methods
3. Results
3.1. Identification of Iodine R56(32)-0 A10 Transition
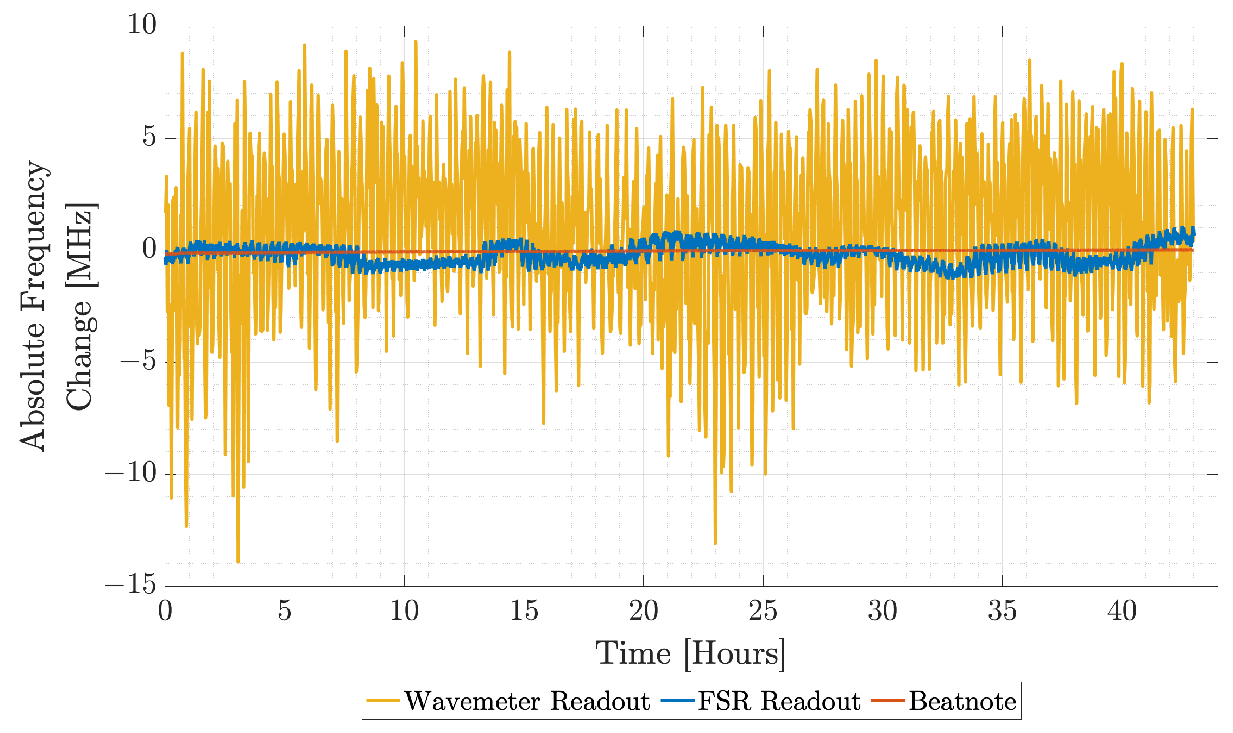
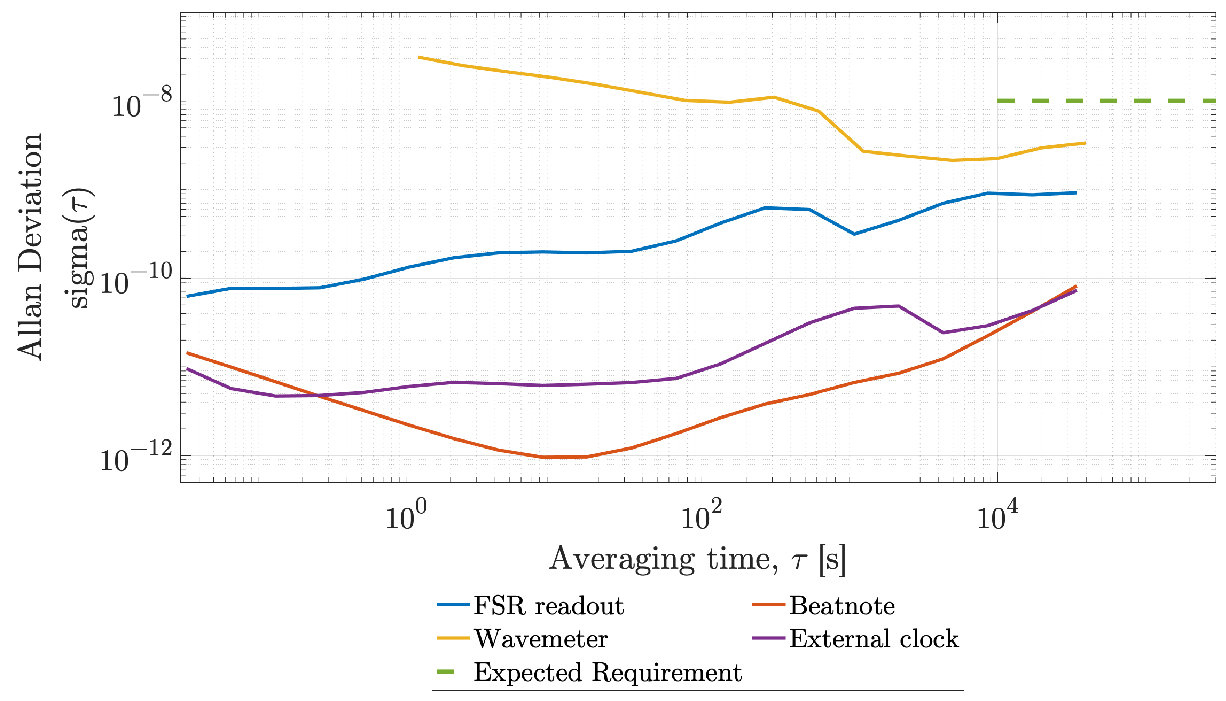
3.2. FSR Readout Results—Static
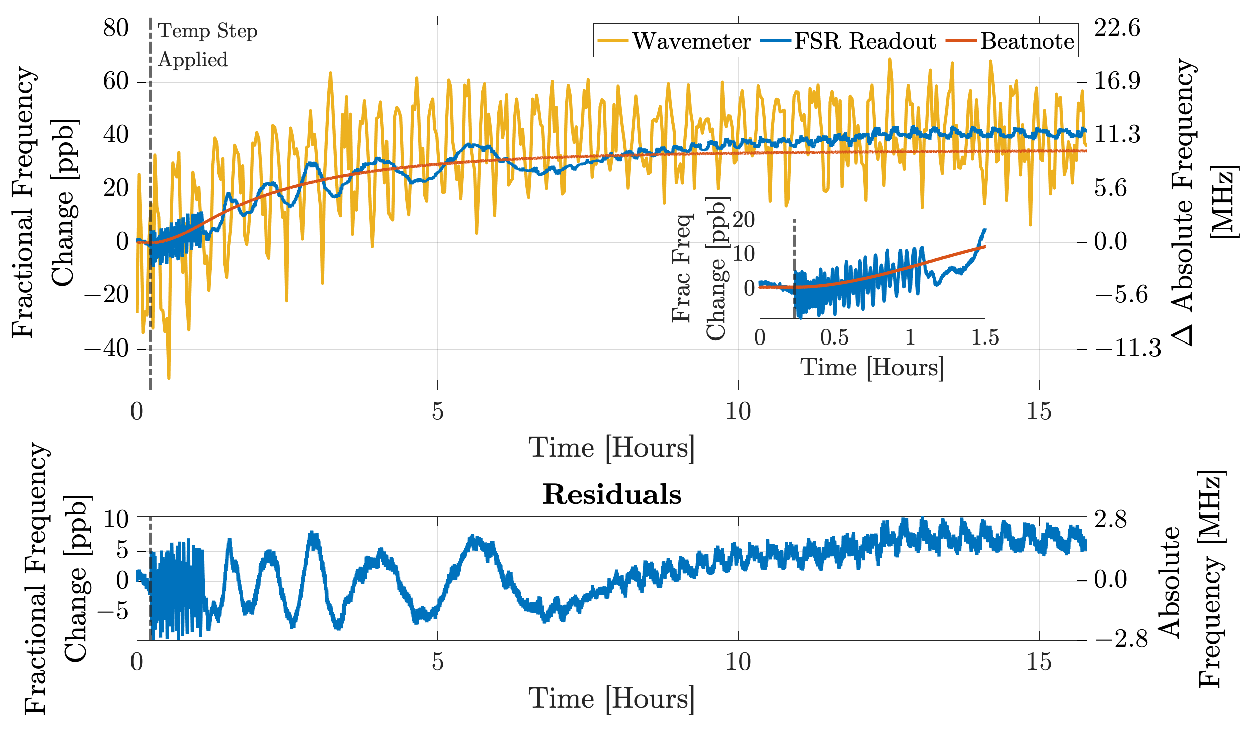
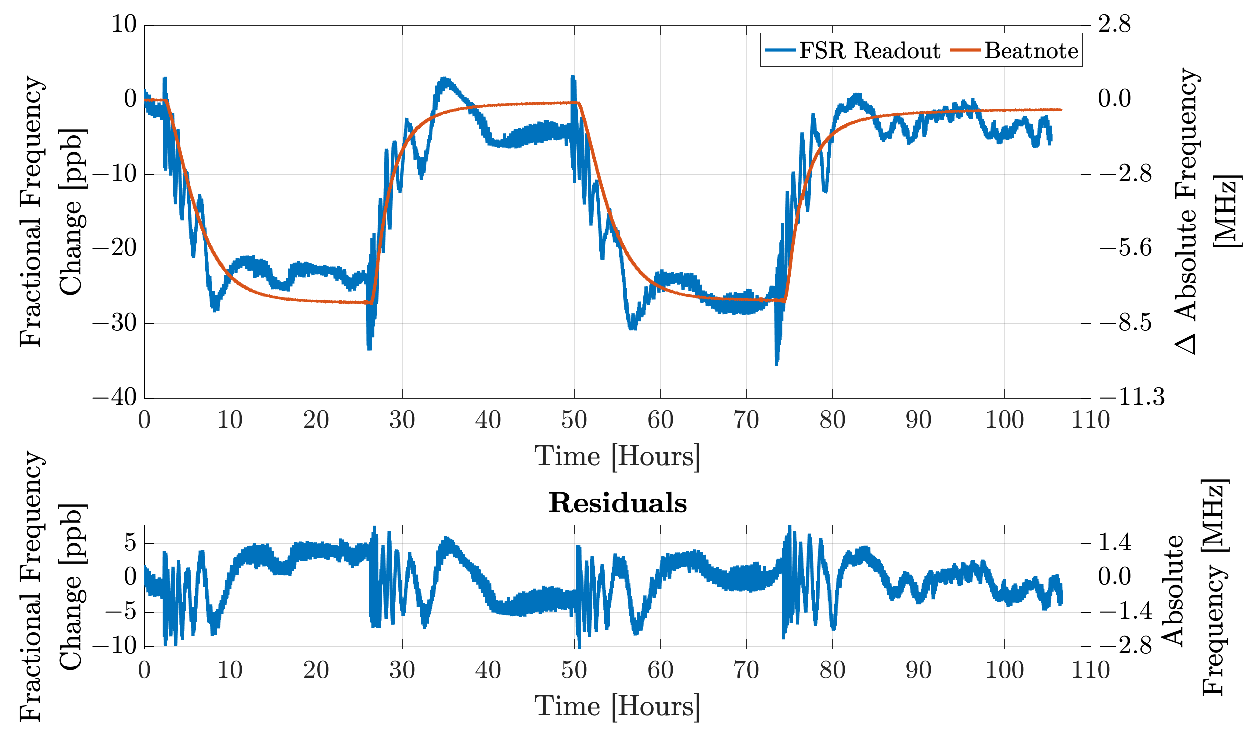
3.3. FSR Readout Results—With Temperature Step
3.4. Mode Number Determination
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tapley, B.D.; Bettadpur, S.; Ries, J.C.; Thompson, P.F.; Watkins, M.M. GRACE Measurements of Mass Variability in the Earth System. Science 2004, 305, 503–505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ghobadi-Far, K.; Han, S.C.; McCullough, C.M.; Wiese, D.N.; Yuan, D.N.; Landerer, F.W.; Sauber, J.; Watkins, M.M. GRACE Follow-On Laser Ranging Interferometer Measurements Uniquely Distinguish Short-Wavelength Gravitational Perturbations. Geophys. Res. Lett. 2020, 47, e2020GL089445. [Google Scholar] [CrossRef]
- Conklin, J.; Yu, T.; Guzman, F.; Klipstein, B.; Lee, J.; Leitch, J.; Numata, K.; Petroy, S.; Spero, R.E.; Ware, B.; et al. LRI Technology Summary and Roadmap for Mass Change Mission; Technical Report; NASA Jet Propulsion Laboratory: Pasadena, CA, USA, May 2020. [Google Scholar]
- Nicklaus, K.; Cesare, S.; Massotti, L.; Bonino, L.; Mottini, S.; Pisani, M.; Silvestrin, P. Laser Metrology Concept Consolidation for NGGM. CEAS Space J. 2020, 12, 313–330. [Google Scholar] [CrossRef]
- Wen, H.Y.; Kruizinga, G.; Paik, M.; Landerer, F.; Bertiger, W.; Sakumura, C.; Bandikova, T.; Mccullough, C. Gravity Recovery and Climate Experiment Follow-on (GRACE-FO) Level-1 Data Product User Handbook; Technical Report JPL D-56935 (URS270772); NASA Jet Propulsion Laboratory California Institute of Technology: Pasadena, CA, USA, 2019. [Google Scholar]
- NASA. ORCLS—Optical-Radio Coherence for Laser Stability; NASA: Pasadena, CA, USA. Available online: https://techport.nasa.gov/view/94040 (accessed on 8 June 2021).
- Rees, E.R.; Wade, A.R.; Sutton, A.J.; Spero, R.E.; Shaddock, D.A.; Mckenzie, K. Absolute Frequency Readout Derived from ULE Cavity for next Generation Geodesy Missions. Opt. Express 2021, 29, 26014–26027. [Google Scholar] [CrossRef] [PubMed]
- DeVoe, R.G.; Brewer, R.G. Laser-frequency division and stabilization. Phys. Rev. A 1984, 30, 2827–2829. [Google Scholar] [CrossRef]
- Thompson, R.; Folkner, W.M.; de Vine, G.; Klipstein, W.; McKenzie, K.; Spero, R.E.; Yu, N.; Stephens, M.; Leitch, J.; Pierce, R.; et al. A Flight-like Optical Reference Cavity for GRACE Follow-on Laser Frequency Stabilization. In Proceedings of the 2011 Joint Conference of the IEEE International Frequency Control and the European Frequency and Time Forum (FCS) Proceedings, San Francisco, CA, USA, 2–5 May 2011; pp. 1–3. [Google Scholar] [CrossRef]
- Drever, R.W.P.; Hall, J.L.; Kowalski, F.V.; Hough, J.; Ford, G.M.; Munley, A.J.; Ward, H. Laser Phase and Frequency Stabilization Using an Optical Resonator. Appl. Phys. B 1983, 31, 97–105. [Google Scholar] [CrossRef]
- Döringshoff, K.; Gutsch, F.B.; Schkolnik, V.; Kürbis, C.; Oswald, M.; Pröbster, B.; Kovalchuk, E.V.; Bawamia, A.; Smol, R.; Schuldt, T.; et al. Iodine Frequency Reference on a Sounding Rocket. Phys. Rev. Appl. 2019, 11, 054068. [Google Scholar] [CrossRef]
- Weise, D.; Schuldt, T.; Döringshoff, K.; Reggentin, M.; Kovalchuk, E.V.; Gohlke, M.; Johann, U.; Peters, A.; Braxmaier, C. A High-Performance Iodine-Based Frequency Reference for Space Applications. In Proceedings of the International Conference on Space Optics—ICSO 2012, SPIE, Ajaccio, Corse, France, 9–12 October 2017; Volume 10564, p. 71. [Google Scholar] [CrossRef] [Green Version]
- Schawlow, A.L. Spectroscopy in a New Light. Rev. Mod. Phys. 1982, 54, 697–707. [Google Scholar] [CrossRef]
- Wallard, A.J. Frequency Stabilization of the Helium-Neon Laser by Saturated Absorption in Iodine Vapour. J. Phys. E Sci. Instrum. 1972, 5, 926–930. [Google Scholar] [CrossRef]
- Hanes, G.R.; Baird, K.M.; DeRemigis, J. Stability, Reproducibility, and Absolute Wavelength of a 633-Nm He–Ne Laser Stabilized to an Iodine Hyperfine Component. Appl. Opt. 1973, 12, 1600. [Google Scholar] [CrossRef] [PubMed]
- Bristol Instruments. 671 Series-Laser Wavelength Meter Specifications. Available online: https://www.bristol-inst.com//wp-content/uploads/2020/01/Bristol-671-Series-Laser-Wavelength-Meter-Specifications.pdf (accessed on 31 January 2022).
- Liquid Instruments. MokuLab-Specifications. Available online: https://download.liquidinstruments.com/documentation/specs/hardware/mokulab/MokuLab-Specifications.pdf (accessed on 31 January 2022).
- Rohde & Schwarz. R&S®SMA100B RF and Microwave Signal Generator Specification; Rohde & Schwarz: Munich, Germany, 2021; Available online: https://scdn.rohde-schwarz.com/ur/pws/dl_downloads/dl_common_library/dl_brochures_and_datasheets/pdf_1/SMA100B_dat-sw_en_5215-1018-22_v0600.pdf (accessed on 31 January 2022).
- Gerstenkorn, S.; Luc, P. Atlas Du Spectre d’absorption de La Molecule d’iode 14800-20000 Cm-1; Editions du Centre National de la Recherche Scientifique (CNRS): Paris, France, 1978. [Google Scholar]
- Arie, A.; Byer, R.L. Laser Heterodyne Spectroscopy of 127I2 Hyperfine Structure near 532 Nm. J. Opt. Soc. Am. B 1993, 10, 1990. [Google Scholar] [CrossRef]
- Fang, H.M.; Wang, S.C.; Liu, L.C.; Cheng, W.Y.; Wu, K.Y.; Shy, J.T. Measurement of Hyperfine Splitting of Molecular Iodine at 532 Nm by Double-Passed Acousto Optic Modulator Frequency Shifter. Jpn. J. Appl. Phys. 2006, 45, 2776. [Google Scholar] [CrossRef] [Green Version]
- Nevsky, A.Y.; Holzwarth, R.; Reichert, J.; Udem, T.; Hänsch, T.W.; von Zanthier, J.; Walther, H.; Schnatz, H.; Riehle, F.; Pokasov, P.V.; et al. Frequency Comparison and Absolute Frequency Measurement of I2-stabilized Lasers at 532 Nm. Opt. Commun. 2001, 192, 263–272. [Google Scholar] [CrossRef]
- Zhang, Y.; Ishikawa, J.; Hong, F.L. Accurate Frequency Atlas of Molecular Iodine near 532 Nm Measured by an Optical Frequency Comb Generator. Opt. Commun. 2001, 200, 209–215. [Google Scholar] [CrossRef]
- Diddams, S.A.; Jones, D.J.; Ye, J.; Cundiff, S.T.; Hall, J.L.; Ranka, J.K.; Windeler, R.S.; Holzwarth, R.; Udem, T.; Hänsch, T.W. Direct Link between Microwave and Optical Frequencies with a 300 THz Femtosecond Laser Comb. Phys. Rev. Lett. 2000, 84, 5102–5105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Abich, K.; Abramovici, A.; Amparan, B.; Baatzsch, A.; Okihiro, B.B.; Barr, D.C.; Bize, M.P.; Bogan, C.; Braxmaier, C.; Burke, M.J.; et al. In-Orbit Performance of the GRACE Follow-on Laser Ranging Interferometer. Phys. Rev. Lett. 2019, 123, 031101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Durand, M.; Wang, Y.; Lawall, J. Accurate Gouy Phase Measurement in an Astigmatic Optical Cavity. Appl. Phys. B 2012, 108, 749–753. [Google Scholar] [CrossRef]
- Kogelnik, H.; Li, T. Laser Beams and Resonators. Appl. Opt. 1966, 5, 1550–1567. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Experimental Value |
|---|---|
| Cavity FSR () | 1.781813197 GHz 1 |
| Cavity Finesse | 9400 |
| PDH sidebands | 4.5131 MHz |
| PDH sideband modulation depth | 0.04 rad |
| FSR carrier tone | 1.781813197 GHz 1 |
| FSR carrier modulation depth | 0.75 rad |
| Scale factor modulation tone | 2.1 MHz |
| Scale factor modulation depth | 0.3 rad |
| Component | Uncertainty | Equivalent Uncertainty (Optical Frequency— 281,630 GHz) (Hz) |
|---|---|---|
| Wavemeter—absolute accuracy [16] | ||
| Wavemeter—repeatability [16] | ||
| Phasemeter—frequency set point precision () [17] | - | negligible |
| FSR Readout Signal Generator— clock frequency offset [18] | < | |
| FSR Readout Signal Generator—clock frequency ageing (specified) [18] | < per day | < per day |
| FSR Readout Signal Generator—clock frequency ageing (measured) | < per day | < per day |
| FSR Readout Signal Generator— frequency synthesis resolution [18] | ||
| Stabilized Iodine system (measured) |
| Hyperfine Transition | Measured (MHz) | Literature 1 (MHz) [20] | Difference (kHz) | Literature 2 (MHz) [21] | Difference (kHz) |
|---|---|---|---|---|---|
| a1 | 0 | 0 | 0 | 0 | 0 |
| a2 | 259.70 | 259.698 | −2.33 | 259.701 | 0.67 |
| a3/a4 1 | 285.87 | 285.862 | −6.02 | 285.881 | 12.98 |
| a5 | 311.37 | 311.360 | −13.24 | 311.364 | −9.24 |
| a6 | 401.49 | 401.480 | −14.85 | 401.490 | −4.85 |
| a7 | 417.14 | 416.998 | −137.03 | 417.009 | −126.03 |
| a8 | 439.58 | 439.626 | 45.97 | 439.626 | 45.97 |
| a9 | 455.36 | 455.341 | −18.25 | 455.354 | −5.25 |
| a10 | 571.59 | 571.548 | −45.67 | 571.556 | −37.67 |
| a11 | 698.28 | 698.045 | −233.12 | 698.066 | −212.12 |
| a12 | 702.82 | 702.774 | −44.75 | 702.779 | −39.75 |
| a13 | 725.90 | 726.031 | 126.31 | 726.059 | 154.31 |
| a14 | 732.18 | 732.211 | 30.27 | 732.238 | 57.27 |
| a15 | 857.97 | 857.960 | −11.81 | 857.985 | 13.19 |
| st. dev. | 86.12 | 87.47 |
| Hyperfine Transition | Measured (GHz) | Literature 1 (GHz) [20] | Difference (MHz) | Literature 2 (GHz) [21] | Difference (MHz) |
|---|---|---|---|---|---|
| a1 | 281,629.7965 | 281,629.8260 | 29.5 | 281,629.8260 | 29.5 |
| a2 | 281,629.9313 | 281,629.9558 | 24.6 | 281,629.9558 | 24.6 |
| a3/a4 1 | 281,629.9436 | 281,629.9689 | 25.4 | 281,629.9689 | 25.4 |
| a5 | 281,629.9533 | 281,629.9817 | 28.4 | 281,629.9817 | 28.4 |
| a6 | 281,630.0015 | 281,630.0267 | 25.2 | 281,630.0267 | 25.2 |
| a7 | 281,630.0060 | 281,630.0345 | 28.5 | 281,630.0345 | 28.5 |
| a8 | 281,630.0201 | 281,630.0458 | 25.7 | 281,630.0458 | 25.7 |
| a9 | 281,630.0279 | 281,630.0537 | 25.7 | 281,630.0537 | 25.7 |
| a10 | 281,630.0848 | 281,630.1118 | 26.9 | 281,630.1118 | 26.9 |
| a11 | 281,630.1487 | 281,630.1750 | 26.3 | 281,630.1750 | 26.3 |
| a12 | 281,630.1454 | 281,630.1774 | 31.9 | 281,630.1774 | 31.9 |
| a13 | 281,630.1610 | 281,630.1890 | 28.0 | 281,630.1890 | 28.0 |
| a14 | 281,630.1675 | 281,630.1921 | 24.6 | 281,630.1921 | 24.6 |
| a15 | 281,630.2279 | 281,630.2550 | 27.0 | 281,630.2550 | 27.0 |
| st. dev. | 2.1 | 2.1 |
| Measured Laser Frequency () (Wavemeter) (GHz) | Measured FSR (FSR Readout Signal Generator) (GHz) | / |
|---|---|---|
| 281,602.378 | 1.781813193 | 158,042.593 |
| 281,604.162 | 1.781813192 | 158,043.595 |
| 281,605.939 | 1.781813204 | 158,044.591 |
| 281,607.730 | 1.781813198 | 158,045.597 |
| 281,609.510 | 1.781813188 | 158,046.597 |
| 281,611.289 | 1.781813188 | 158,047.595 |
| 281,613.072 | 1.781813200 | 158,048.595 |
| 281,614.853 | 1.781813204 | 158,049.594 |
| 281,616.632 | 1.781813201 | 158,050.592 |
| 281,618.417 | 1.781813197 | 158,051.595 |
| 281,620.197 | 1.781813200 | 158,052.593 |
| 281,621.982 | 1.781813205 | 158,053.595 |
| 281,623.763 | 1.781813209 | 158,054.594 |
| 281,625.544 | 1.781813208 | 158,055.594 |
| 281,627.263 | 1.781813196 | 158,056.559 |
| 281,629.108 | 1.781813188 | 158,057.595 |
| 281,630.890 | 1.781813199 | 158,058.595 |
| 281,632.671 | 1.781813203 | 158,059.593 |
| 281,634.456 | 1.781813190 | 158,060.597 |
| 281,636.239 | 1.781813185 | 158,061.598 |
| 281,638.021 | 1.781813193 | 158,062.597 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rees, E.R.; Wade, A.R.; Sutton, A.J.; McKenzie, K. Absolute Frequency Readout of Cavity against Atomic Reference. Remote Sens. 2022, 14, 2689. https://doi.org/10.3390/rs14112689
Rees ER, Wade AR, Sutton AJ, McKenzie K. Absolute Frequency Readout of Cavity against Atomic Reference. Remote Sensing. 2022; 14(11):2689. https://doi.org/10.3390/rs14112689
Chicago/Turabian StyleRees, Emily Rose, Andrew R. Wade, Andrew J. Sutton, and Kirk McKenzie. 2022. "Absolute Frequency Readout of Cavity against Atomic Reference" Remote Sensing 14, no. 11: 2689. https://doi.org/10.3390/rs14112689
APA StyleRees, E. R., Wade, A. R., Sutton, A. J., & McKenzie, K. (2022). Absolute Frequency Readout of Cavity against Atomic Reference. Remote Sensing, 14(11), 2689. https://doi.org/10.3390/rs14112689






