The Influence of the Signal-to-Noise Ratio upon Radio Occultation Retrievals
Abstract
1. Introduction
2. Data and Methods
- 1.
- Evaluation of the excess phase model. Our model employs MSISE-90 (Mass-Spectrometer-Incoherent-Scatter Model Extended) [37], which describes the dry atmosphere. We complement MSISE-90 refractivity profiles with a constant relative humidity of 90% below 15 km. This model has been used for a long period of time, and it is proven to predict the Doppler frequency within 25 Hz [38]. From the model refractivity profile, we evaluate the bending angle profile , where is the bending angle and is the ray impact parameter. This profile is exponentially extrapolated below the Earth’s surface. Given orbit data, this profile can be transformed into the parametric form using geometric–optical equations [6]. Because the model refractivity profile is a smooth function, this guarantees that both functions of time are single-valued. The extrapolation is used in order to cover the whole occultation including the shadow zone. From the extended bending angle profile, we evaluate the model excess phase by inverting the standard geometric optical (GO) procedure of the evaluation of the bending angle from the excess phase [39]. The resulting excess phase model satisfies the requirements formulated by Sokolovskiy [38]: it is capable of describing the Doppler frequency with the accuracy of 10–15 Hz, which falls within the −25–25 Hz range corresponding to a 50 Hz sampling rate.
- 2.
- Based on the above model of the signal, we evaluate two characteristics of the amplitude record: the mean SNR in the 60–80 km height range, and the Noise Floor (NF). The NF is evaluated by averaging the SNR for the samples with a model impact parameter below km. The 60–80 km height range encompasses the ionospheric D-layer and is optimal to estimate the signal strength that would be observed in the absence of an atmosphere. It is high enough for the attenuation due to the regular atmospheric refraction to be negligible. On the other hand, the influence of the ionosphere at these heights manifests itself in small-scale fluctuations that do not influence the average value. This height range does not reach the E-layer, where the amplitude perturbation can be stronger [40,41]. The average SNR in this height range as a measure of the signal strength was introduced in [31].
- 3.
- The removal of navigation bits (demodulation) [30]. This step is necessary for COSMIC and Spire data. Navigation bits are supplied by CDAAC in the gpsBit data product. COSMIC-2 data are supplied in conPhs format, which contains the demodulated excess phase. METOP data, although provided in atmPhs format, are also already demodulated.
- 4.
- The evaluation of the Badness Score (BS) [36] employs the radio holographic analysis of the complex wave field , where is the wavenumber, are the channel frequencies, c is the light speed in a vacuum, and is the satellite-to-satellite distance. The model excess phase is used to down-convert the frequency. The BS is estimated from the spectral width of the signal, and it provides the basis for the Quality Control (QC). We specify a fixed BS threshold, which is found empirically and equals 35. The events with a BS below the threshold pass our QC.
- 5.
- The evaluation of the GO bending angle (BA) profile [39]. This procedure is based on the assumption of single-ray propagation. Both the bending angle and impact parameter p are evaluated from the derivative of the excess phase.
- 6.
- The evaluation of the wave optical (WO) BA profile [34]. We apply the Canonical Transform of Type 2 (CT2) in order to evaluate the tropospheric part of the BA profile below 20 km. The lower point of the BA profile, or the shadow border, is determined from the amplitude of the wave field transformed to the representation of the impact parameter, referred to as the CT amplitude. Because in this representation, the multipath effects are mostly eliminated and the variations of amplitude are only caused by the horizontal gradients, we evaluate the cutoff height of the BA profile from the maximum of the correlation of the CT amplitude with the Heaviside step function [36,42].
- 7.
- GO and WO BA profiles are combined and undergo the ionospheric correction combined with the statistical optimization [8]. The resulting neutral atmospheric BA profile , where p is the impact parameter, is inverted to produce the refractivity profile , where z is the altitude above the geoid. The retrieved refractivities are used to evaluate the penetration.
3. Results
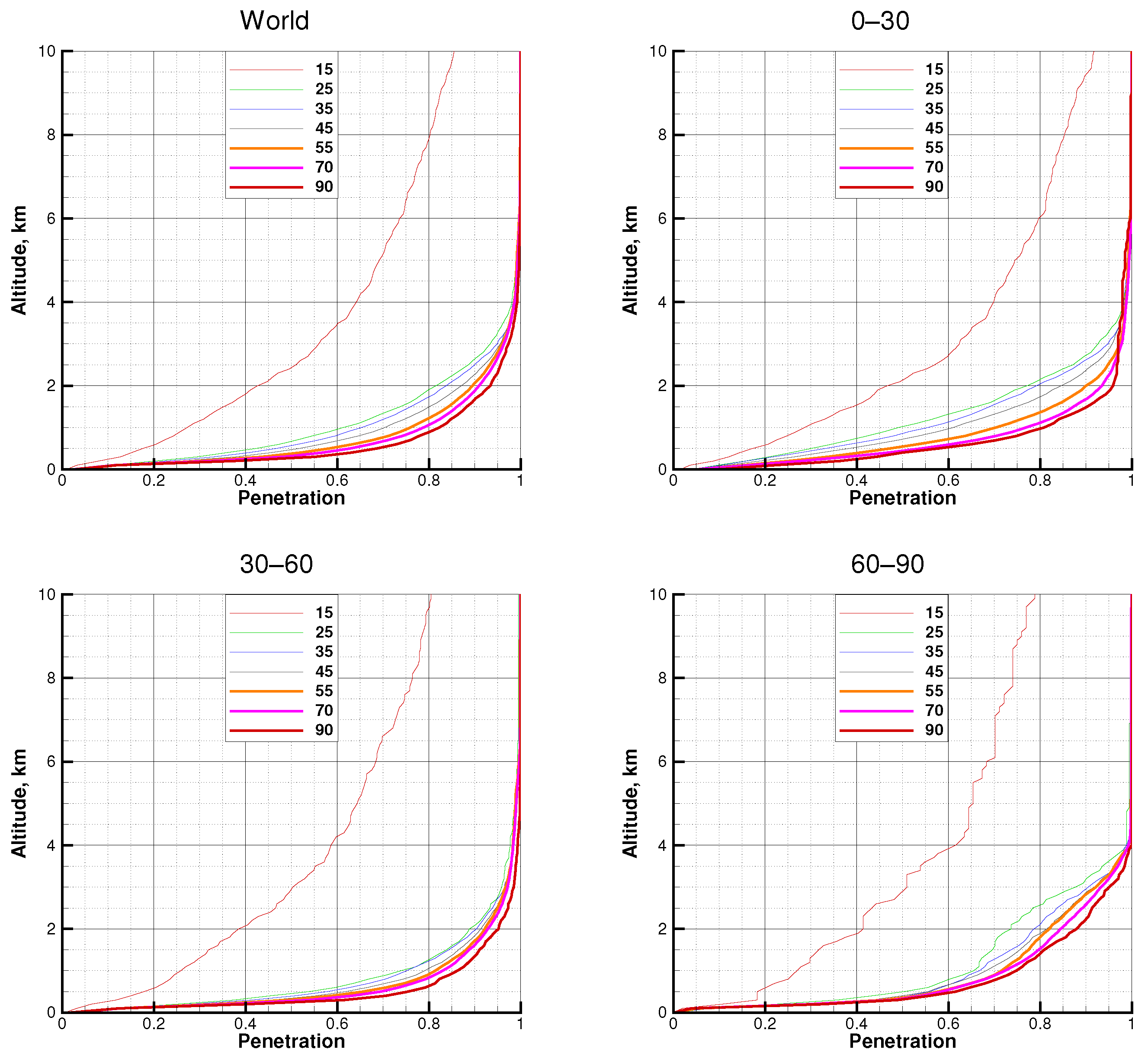
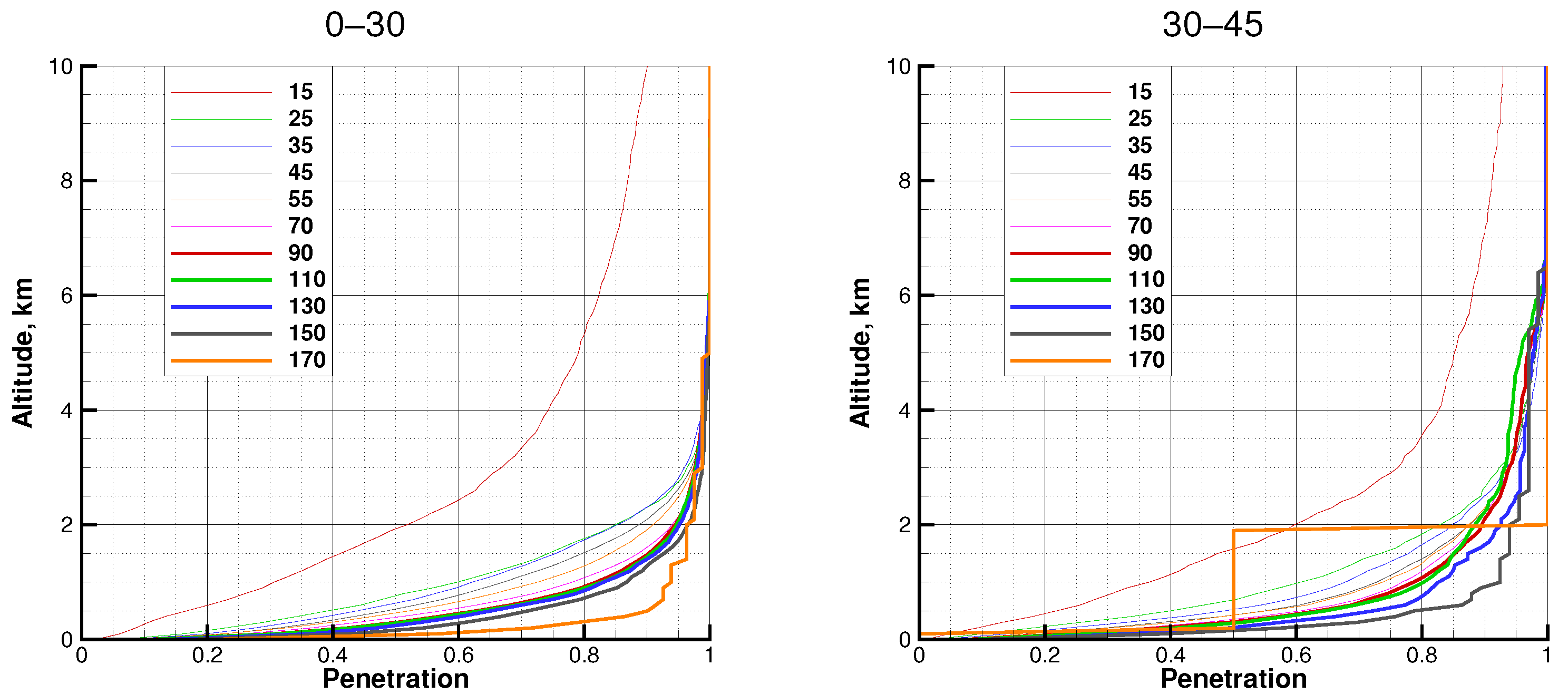
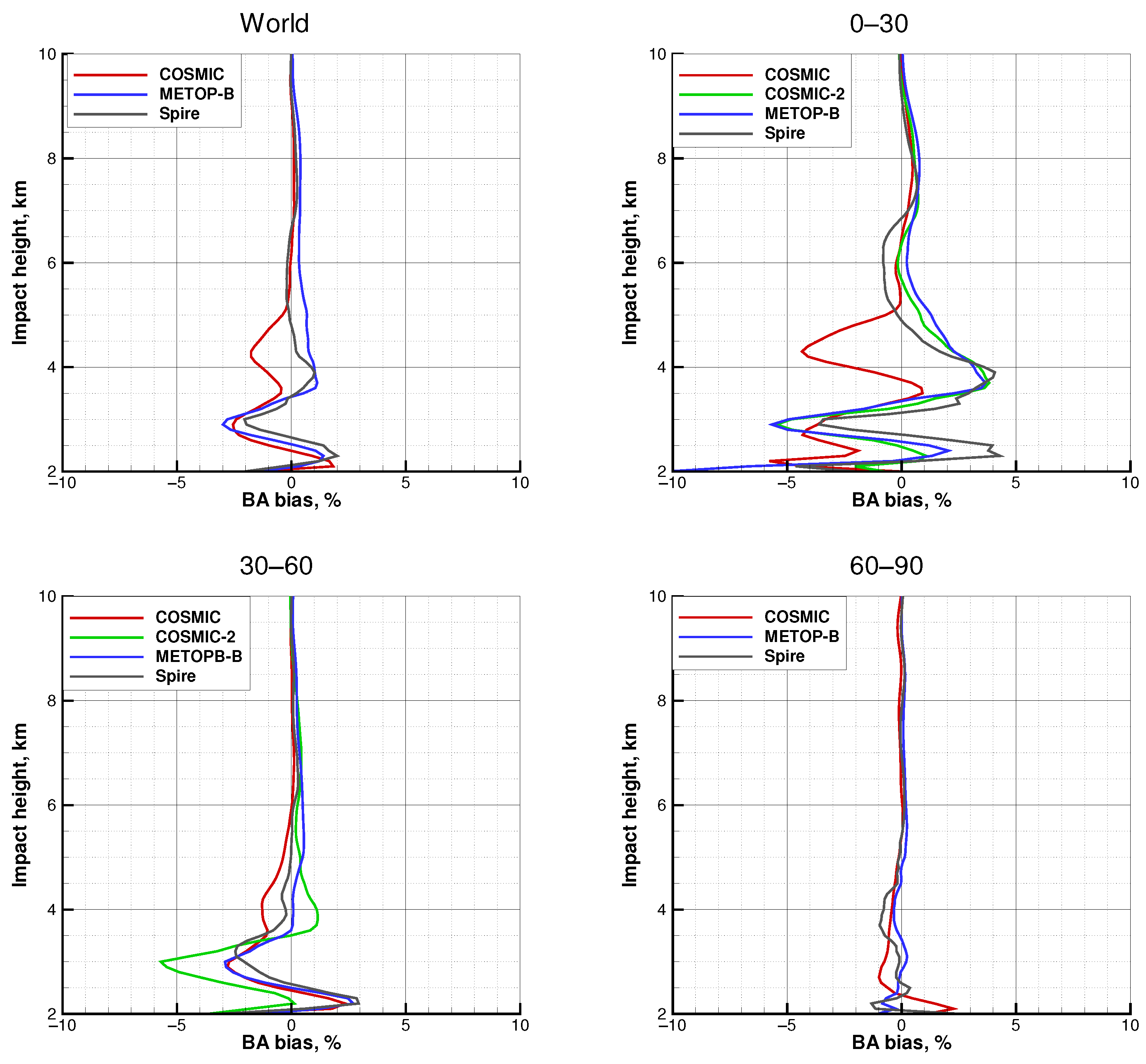
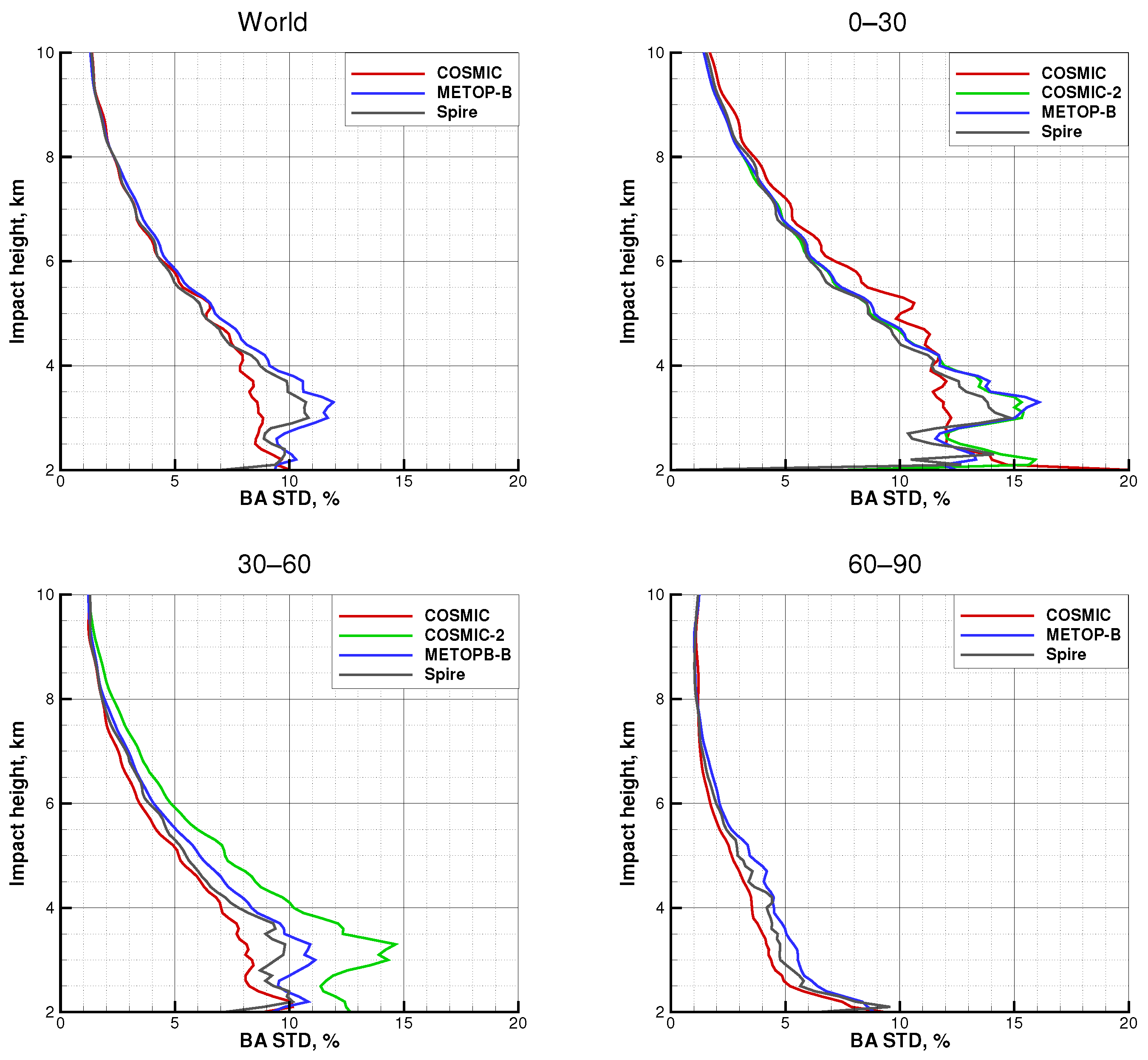
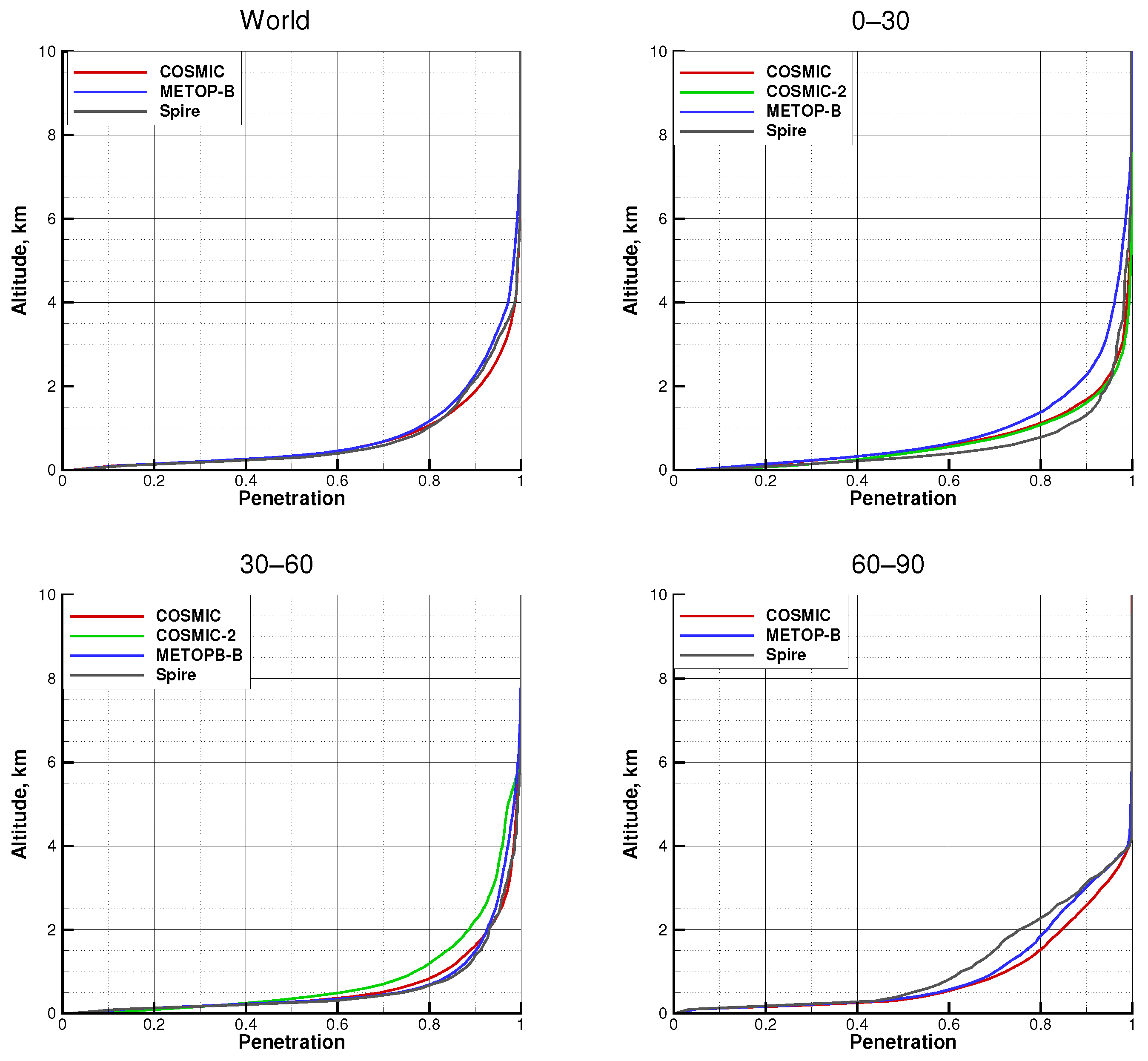
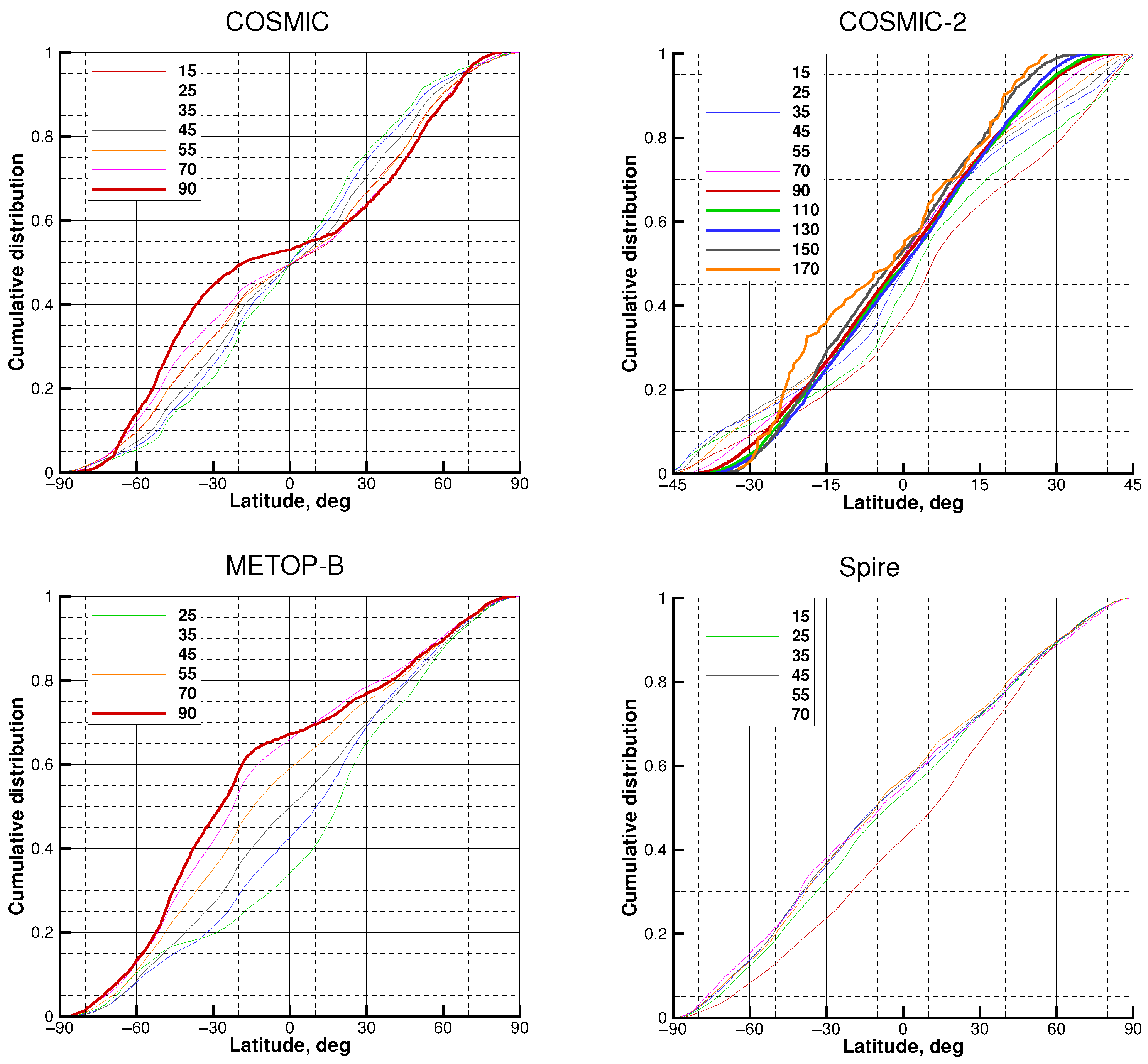
3.1. The Statistical Ensemble
3.2. COSMIC
3.3. COSMIC-2
3.4. Spire
3.5. METOP-B
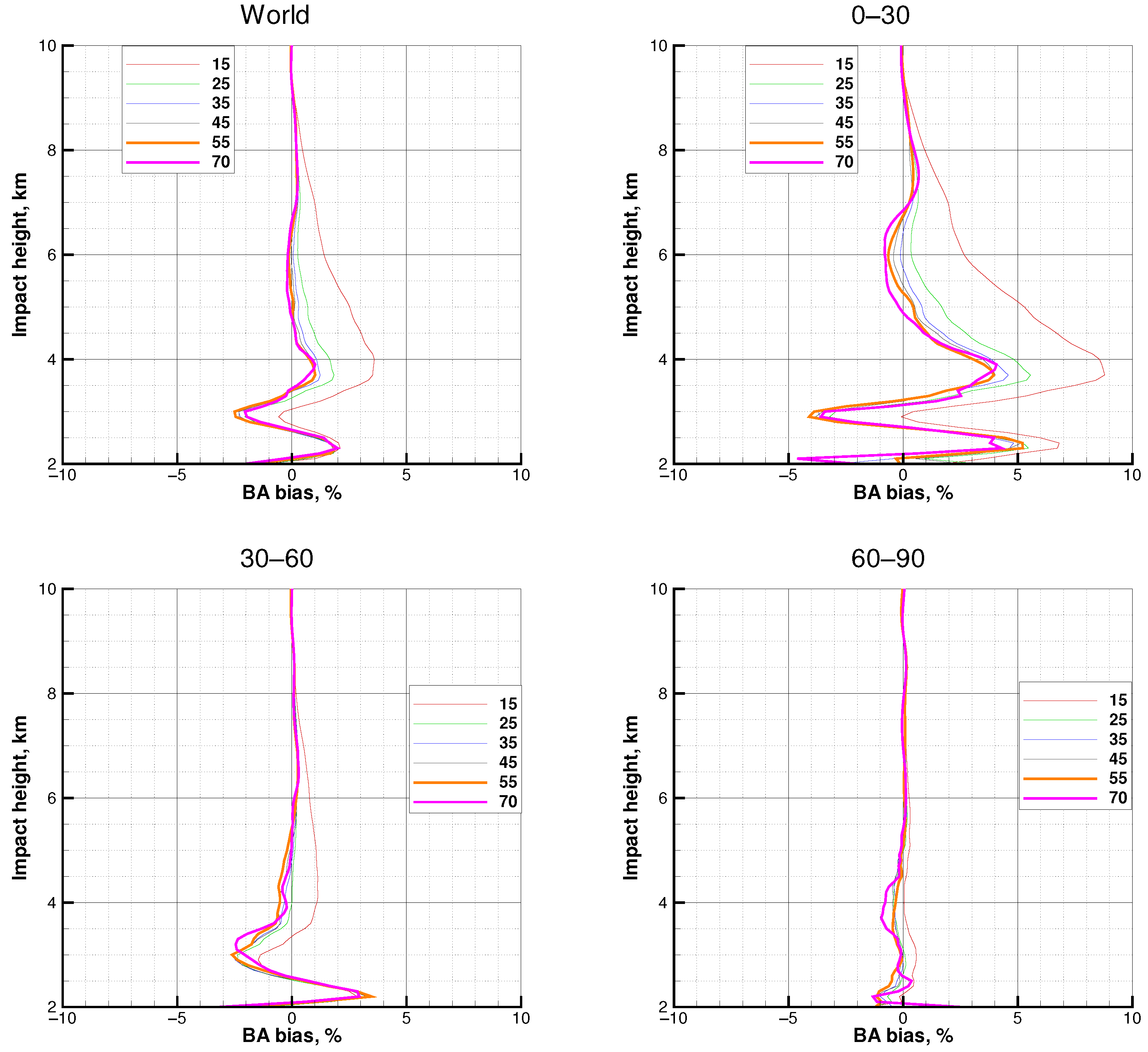
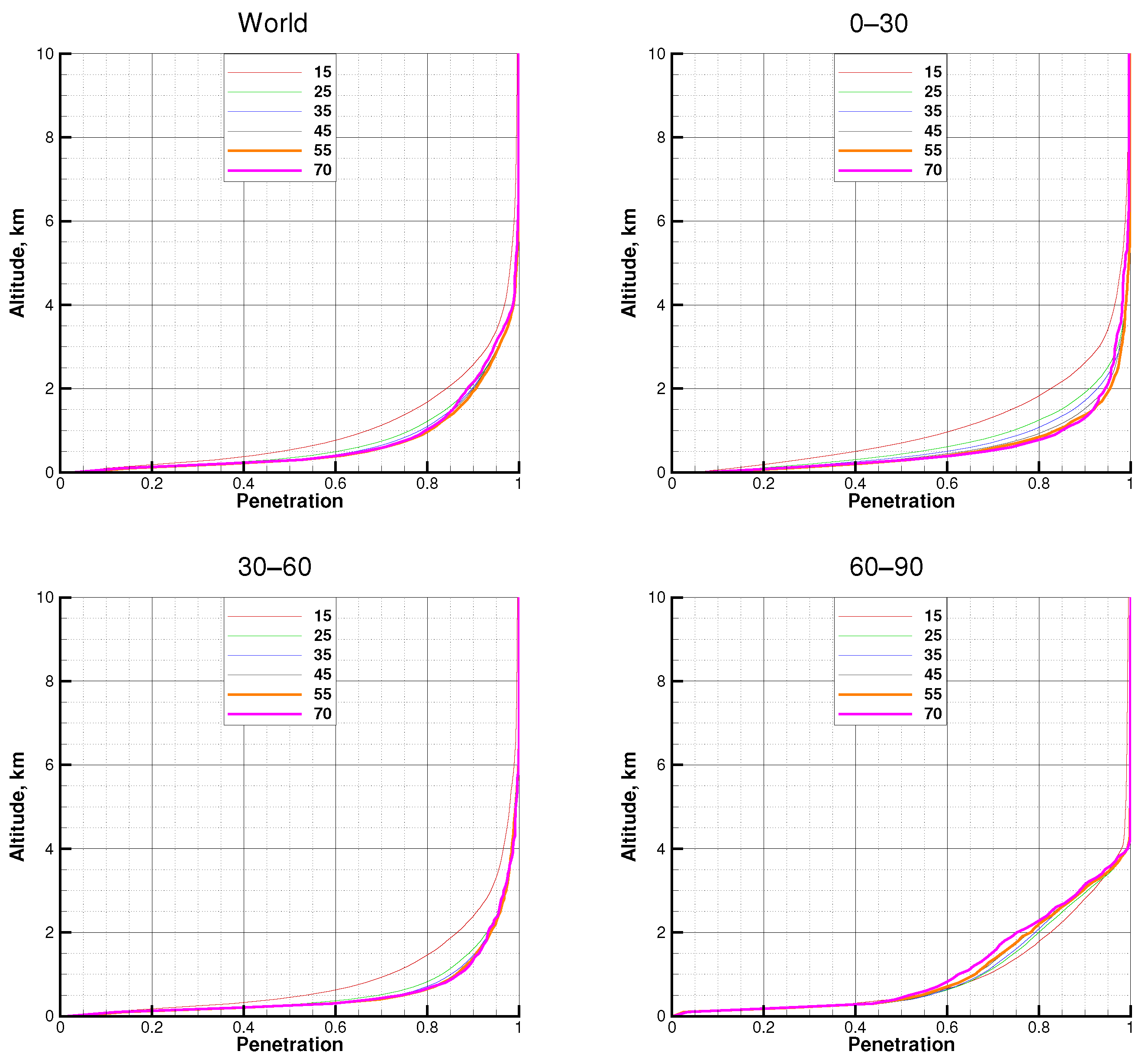
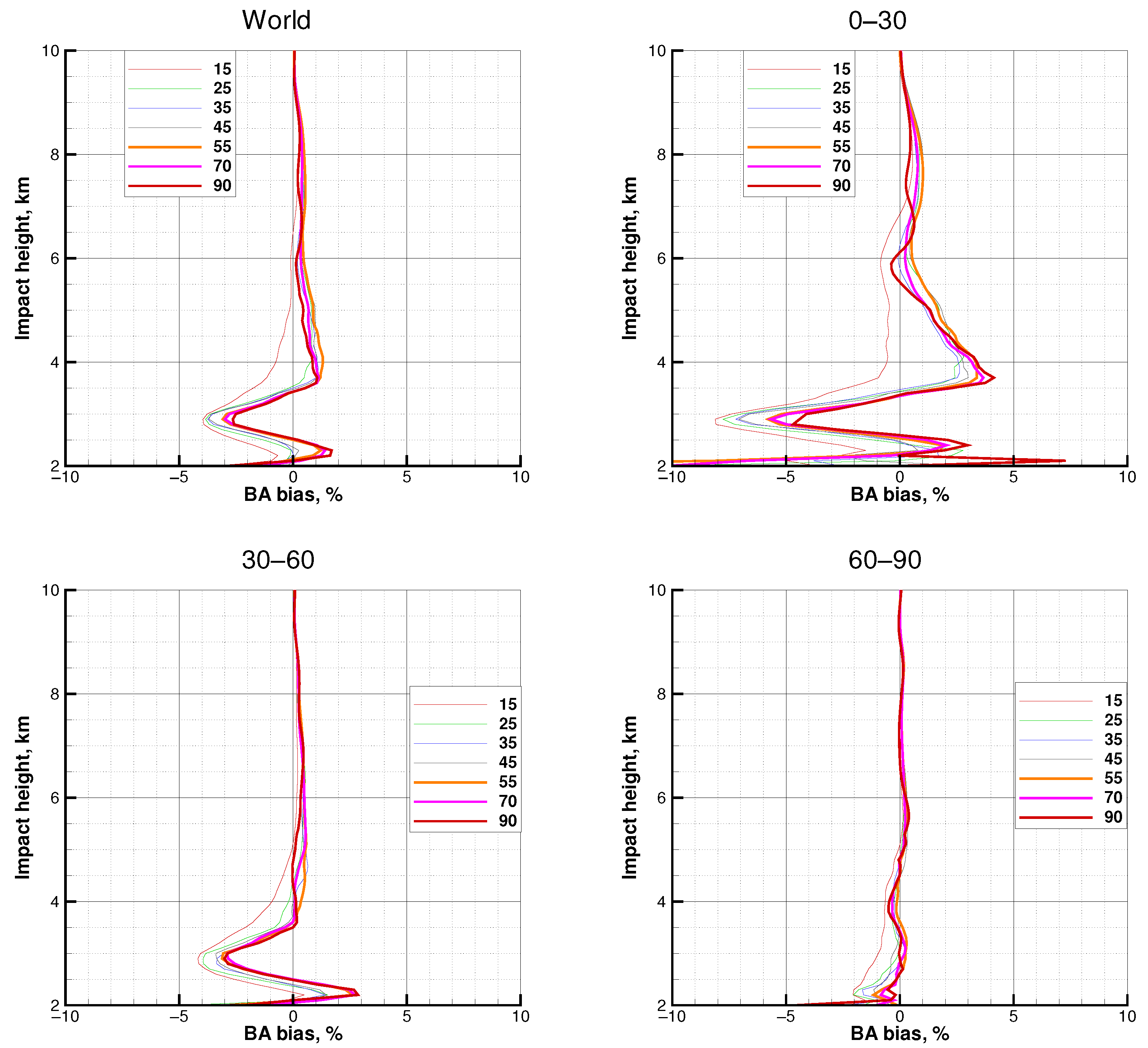
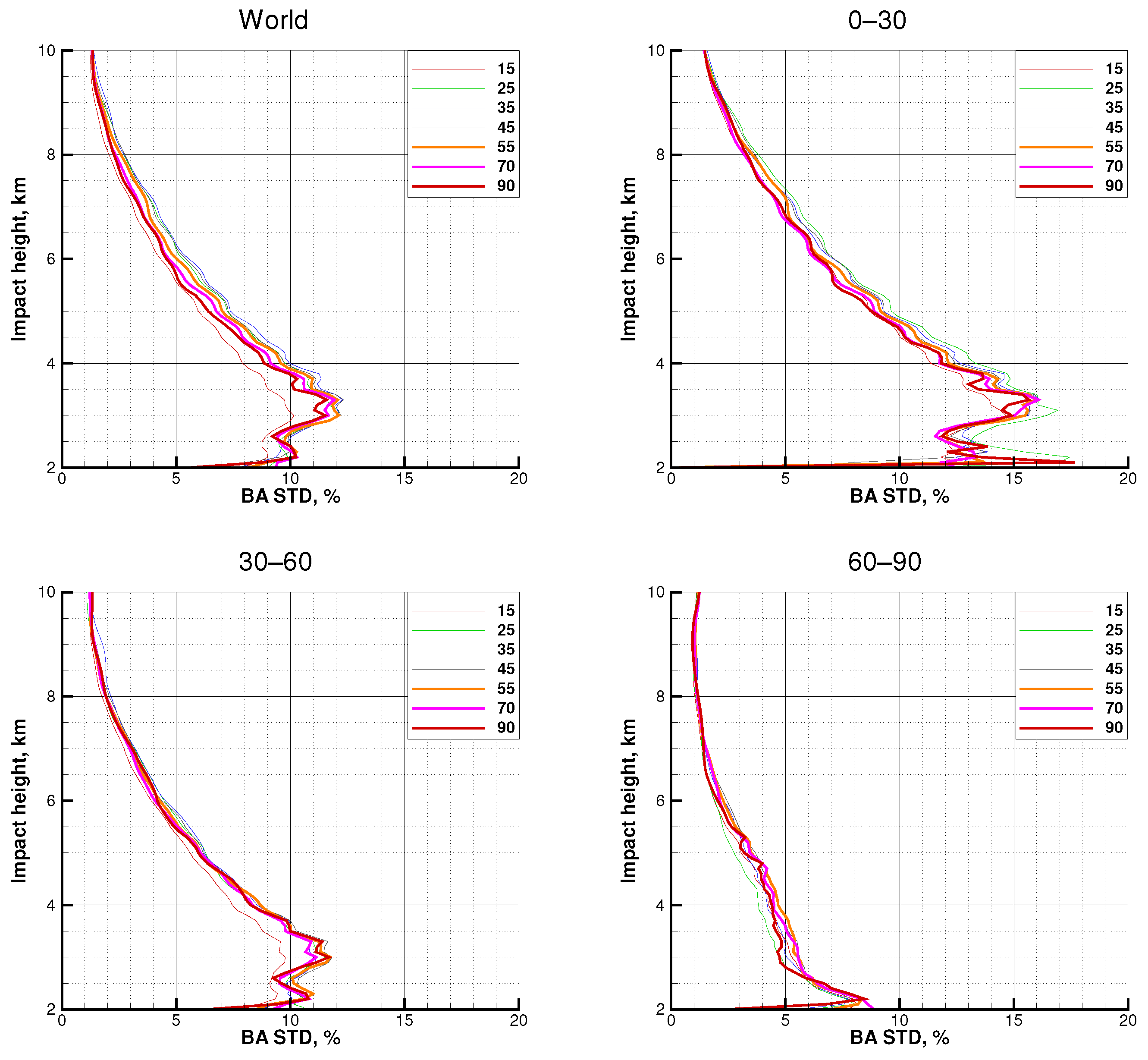
3.6. All the Missions, SNR = 70
3.7. All the Missions, Median SNR
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BA | Bending Angle |
| BS | Badness Score |
| CDAAC | COSMIC Data Analysis and Archive Center |
| COSMIC | Constellation Observing System for Meteorology, Ionosphere, and Climate |
| CT2 | Canonical Transform |
| GFS | Global Forecast System |
| GNSS | Global Navigation Satellite Signal System |
| GO | Geometric Optics |
| LEO | Low Earth Orbiter |
| MSISE | Mass-Spectrometer-Incoherent-Scatter model Extended |
| MSL | Mean Sea Level |
| NCEP | of National Centers for Environmental Prediction |
| NF | Noise Floor |
| NWP | Numerical Weather Prediction |
| PBL | Planetary Boundary Layer |
| QC | Quality Control |
| RO | Radio Occultation |
| SNR | Signal-to-Noise Ratio |
References
- Von Engeln, A.; Nedoluha, G.; Kirchengast, G.; Bühler, S. One-dimensional variational (1-D Var) retrieval of temperature, water vapor, and a reference pressure from radio occultation measurements: A sensitivity analysis. J. Geophys. Res. 2003, 108, 4337. [Google Scholar] [CrossRef]
- Healy, S.B.; Thépaut, J.N. Assimilation experiments with CHAMP GPS radio occultation measurements. Quart. J. Roy. Meteor. Soc. 2006, 132, 605–623. [Google Scholar] [CrossRef]
- Healy, S.B.; Eyre, J.R.; Hamrud, M.; Thépaut, J.N. Assimilating GPS radio occultation measurements with two-dimensional bending angle observation operators. Quart. J. Roy. Meteor. Soc. 2007, 133, 1213–1227. [Google Scholar] [CrossRef]
- Cucurull, L.; Derber, J.C.; Purser, R.J. A bending angle forward operator for global positioning system radio occultation measurements. J. Geophys. Res. 2013, 118, 14–28. [Google Scholar] [CrossRef]
- Burrows, C.P.; Healy, S.B.; Culverwell, I.D. Improving the bias characteristics of the ROPP refractivity and bending angle operators. Atmos. Meas. Tech. 2014, 7, 3445–3458. [Google Scholar] [CrossRef][Green Version]
- Gorbunov, M.; Stefanescu, R.; Irisov, V.; Zupanski, D. Variational Assimilation of Radio Occultation Observations into Numerical Weather Prediction Models: Equations, Strategies, and Algorithms. Remote Sens. 2019, 11, 2886. [Google Scholar] [CrossRef]
- Syndergaard, S. On the ionosphere calibration in GPS radio occultation measurements. Radio Sci. 2000, 35, 865–883. [Google Scholar] [CrossRef]
- Gorbunov, M.E. Ionospheric correction and statistical optimization of radio occultation data. Radio Sci. 2002, 37, 17-1–17-9. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Schreiner, W.; Rocken, C.; Hunt, D. Optimal Noise Filtering for the Ionospheric Correction of GPS Radio Occultation Signals. J. Atmos. Ocean. Technol. 2009, 26, 1398–1403. [Google Scholar] [CrossRef]
- Angling, M.J.; Elvidge, S.; Healy, S.B. Improved model for correcting the ionospheric impact on bending angle in radio occultation measurements. Atmos. Meas. Tech. 2018, 11, 2213–2224. [Google Scholar] [CrossRef]
- Danzer, J.; Haas, S.J.; Schwaerz, M.; Kirchengast, G. Performance of the Ionospheric Kappa-Correction of Radio Occultation Profiles Under Diverse Ionization and Solar Activity Conditions. Earth Space Sci. 2021, 8, e2020EA001581. [Google Scholar] [CrossRef] [PubMed]
- Aragon-Angel, A.; Rovira-Garcia, A.; Arcediano-Garrido, E.; Ibáñez-Segura, D. Galileo Ionospheric Correction Algorithm Integration into the Open-Source GNSS Laboratory Tool Suite (gLAB). Remote Sens. 2021, 13, 191. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Schreiner, W.; Zeng, Z.; Hunt, D.; Lin, Y.C.; Kuo, Y.H. Observation, analysis, and modeling of deep radio occultation signals: Effects of tropospheric ducts and interfering signals. Radio Sci. 2014, 49, 954–970. [Google Scholar] [CrossRef]
- Bonnedal, M.; Christensen, J.; Carlström, A.; Berg, A. Metop-GRAS in-orbit instrument performance. GPS Solut. 2010, 14, 109–120. [Google Scholar] [CrossRef]
- Schreiner, W.; Sokolovskiy, S.; Hunt, D.; Rocken, C.; Kuo, Y.H. Analysis of GPS radio occultation data from the FORMOSAT-3/COSMIC and Metop/GRAS missions at CDAAC. Atmos. Meas. Tech. 2011, 4, 2255–2272. [Google Scholar] [CrossRef]
- Xu, X.; Zou, X. Comparison of MetOp-A/-B GRAS radio occultation data processed by CDAAC and ROM. GPS Solut. 2020, 24. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Schreiner, W.; Weiss, J.; Zeng, Z.; Hunt, D.; Braun, J. Initial Assessment of COSMIC-2 Data in the Lower Troposphere. In Proceedings of the Joint 6th ROM SAF Data User Workshop and 7th IROWG Workshop, Konventum, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Schreiner, W.S.; Weiss, J.; Anthes, R.A.; Braun, J.J.; Chu, V.; Fong, J.; Hunt, D.; Kuo, Y.H.; Meehan, T.K.; Xia-Serafino, W.; et al. COSMIC-2 Radio Occultation Constellation: First Results. Geophys. Res. Lett. 2020, 47, e2019GL086841. [Google Scholar] [CrossRef]
- Ho, S.P.; Zhou, X.; Shao, X.; Zhang, B.; Adhikari, L.; Kireev, S.; He, Y.; Yoe, J.G.; Xia-Serafino, W.; Lynch, E. Initial Assessment of the COSMIC-2/FORMOSAT-7 Neutral Atmosphere Data Quality in NESDIS/STAR Using In Situ and Satellite Data. Remote Sens. 2020, 12, 4099. [Google Scholar] [CrossRef]
- Lin, C.Y.; Lin, C.C.H.; Liu, J.Y.; Rajesh, P.K.; Matsuo, T.; Chou, M.Y.; Tsai, H.F.; Yeh, W.H. The Early Results and Validation of FORMOSAT-7/COSMIC-2 Space Weather Products: Global Ionospheric Specification and Ne-Aided Abel Electron Density Profile. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028028. [Google Scholar] [CrossRef]
- Rieckh, T.; Sjoberg, J.P.; Anthes, R.A. The Three-Cornered Hat Method for Estimating Error Variances of Three or More Atmospheric Datasets. Part II: Evaluating Radio Occultation and Radiosonde Observations, Global Model Forecasts, and Reanalyses. J. Atmos. Ocean. Technol. 2021, 38, 1777–1796. [Google Scholar] [CrossRef]
- Kursinski, E.R. Weather & Space Weather RO Data from PlanetiQ Commercial GNSS RO. In Proceedings of the Joint 6th ROM SAF Data User Workshop and 7th IROWG Workshop, Konventum, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Chang, H.; Lee, J.; Wang, Y.; Breitsch, B.; Morton, Y.J. Preliminary Assessment of CICERO Radio Occultation Performance by Comparing with COSMIC I Data. In Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation. Institute of Navigation, Manassas, VA, USA, 21–25 September 2020. [Google Scholar] [CrossRef]
- Irisov, V.; Duly, T.; Nguyen, V.; Masters, D.; Nogues-Correig, O.; Tan, L.; Yuasa, T.; Ector, D. Recent radio occultation profile results obtained from Spire CubeSat GNSS-RO constellation. In Proceedings of the AGU Fall Meeting, Washington, DC, USA, 10–14 December 2018. [Google Scholar]
- Irisov, V.; Ector, D.; Duly, T.; Nguyen, V.; Nogues-Correig, O.; Tan, L.; Yuasa, T. Atmospheric Radio Occultation Observation from Spire CubeSat Nanosatellites. In Proceedings of the AMS Annual Meeting, Austin, TX, USA, 7–11 January 2018. [Google Scholar]
- Gorbunov, M.; Koval, O.; Kirchengast, G. Kirkwood Distribution Function and its Applicationfor the Analysis of Radio Occultation Observations. In Proceedings of the Joint 6th ROM SAF User Workshop and 7th IROWG Workshop, EUMETSAT ROM SAF, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Irisov, V.; Nguyen, V.; Duly, T.; Nogues-Correig, O.; Tan, L.; Yuasa, T.; Masters, D.; Sikarin, R.; Gorbunov, M.; Rocken, C. Radio Occultation Observations and Processing from Spire’s CubeSat Constellation. In Proceedings of the Joint 6th ROM SAF User Workshop and 7th IROWG Workshop, EUMETSAT ROM SAF, Elsinore, Denmark, 19–25 September 2019. [Google Scholar]
- Bowler, N.E. An assessment of GNSS radio occultation data produced by Spire. Q. J. R. Meteorol. Soc. 2020, 146, 3772–3788. [Google Scholar] [CrossRef]
- Lonitz, K.; Marquardt, C.; Bowler, N.; Healy, S. Final Technical Note of Impact Assessment of Commercial GNSS-RO Data; ESA Contract Report 4000131086/20/NL/FF/a; European Centre for Medium Range Weather Forecasts: Reading, UK, 2021. [Google Scholar]
- Sokolovskiy, S.; Rocken, C.; Hunt, D.; Schreiner, W.; Johnson, J.; Masters, D.; Esterhuizen, S. GPS profiling of the lower troposphere from space: Inversion and demodulation of the open-loop radio occultation signals. Geophys. Res. Lett. 2006, 33, L14816. [Google Scholar] [CrossRef]
- Kuo, Y.H.; Wee, T.K.; Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D.; Anthes, R.A. Inversion and Error Estimation of GPS Radio Occultation Data. J. Meteorolog. Soc. Jpn. 2004, 82, 507–531. [Google Scholar] [CrossRef]
- Gorbunov, M.; Irisov, V.; Rocken, C. Noise Floor and Signal-to-Noise Ratio of Radio Occultation Observations: A Cross-Mission Statistical Comparison. Remote Sens. 2022, 14, 691. [Google Scholar] [CrossRef]
- Anthes, R.; Sjoberg, J.; Feng, X.; Syndergaard, S. Comparison of COSMIC and COSMIC-2 Radio Occultation Refractivity and Bending Angle Uncertainties in August 2006 and 2021. Atmosphere 2022, 13, 790. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B. Analysis of wave fields by Fourier integral operators and its application for radio occultations. Radio Sci. 2004, 39, RS4010. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Lauritsen, K.B.; Rodin, A.; Tomassini, M.; Kornblueh, L. Analysis of the CHAMP experimental data on radio-occultation sounding of the Earth’s atmosphere. Izv. Atmos. Ocean. Phys. 2005, 41, 726–740. [Google Scholar]
- Gorbunov, M.E.; Lauritsen, K.B.; Rhodin, A.; Tomassini, M.; Kornblueh, L. Radio holographic filtering, error estimation, and quality control of radio occultation data. J. Geophys. Res. 2006, 111, D10105. [Google Scholar] [CrossRef]
- Hedin, A.E. Extension of MSIS thermosphere model into the middle and lower atmosphere. J. Geophys. Res. 1991, 96, 1159–1172. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V. Modeling and inverting radio occultation signals in the moist troposphere. Radio Sci. 2001, 36, 441–458. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Sokolovskiy, S.V. Remote Sensing of Refractivity from Space for Global Observations of Atmospheric Parameters; Report 119; Max-Planck Institute for Meteorology: Hamburg, Germany, 1993; 58p. [Google Scholar]
- Gorbunov, M.E.; Gurvich, A.S.; Shmakov, A.V. Back-propagation and radio-holographic methods for investigation of sporadic ionospheric E-layers from Microlab-1 data. Int. J. Remote Sens. 2002, 23, 675–685. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V.; Schreiner, W.; Rocken, C.; Hunt, D. Detection of high-altitude ionospheric irregularities with GPS/MET. Geophys. Res. Let. 2002, 29, 3-1–3-4. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Shmakov, A.V.; Leroy, S.S.; Lauritsen, K.B. COSMIC Radio Occultation Processing: Cross-center Comparison and Validation. J. Atmos. Ocean. Technol. 2011, 28, 737–751. [Google Scholar] [CrossRef]
- Kan, V.; Gorbunov, M.E.; Shmakov, A.V.; Sofieva, V.F. The Reconstruction of the Parameters of Internal Gravity Waves in the Atmosphere from Amplitude Fluctuations in the Radio Occultation Experiment. Izv. Atm. Ocean. Phys. 2020, 56, 435–447. [Google Scholar] [CrossRef]
- Kan, V.; Gorbunov, M.E.; Fedorova, O.V.; Sofieva, V.F. Latitudinal Distribution of the Parameters of Internal Gravity Waves in the Atmosphere Derived from Amplitude Fluctuations of Radio Occultation Signals. Izv. Atm. Ocean. Phys. 2020, 56, 564–575. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Kirchengast, G. Uncertainty propagation through wave optics retrieval of bending angles from GPS radio occultation: Theory and simulation results. Radio Sci. 2015, 50, 1086–1096. [Google Scholar] [CrossRef]
- Sokolovskiy, S.V. Effect of super refraction on inversions of radio occultation signals in the lower troposphere. Radio Sci. 2003, 38, 1058. [Google Scholar] [CrossRef]
- Sokolovskiy, S.; Rocken, C.; Schreiner, W.; Hunt, D. On the uncertainty of radio occultation inversions in the lower troposphere. J. Geophys. Res. 2010, 115, D22111. [Google Scholar] [CrossRef]
- Gorbunov, M.E.; Vorob’ev, V.V.; Lauritsen, K.B. Fluctuations of refractivity as a systematic error source in radio occultations. Radio Sci. 2015, 50, 656–669. [Google Scholar] [CrossRef]
- Ho, S.p.; Anthes, R.A.; Ao, C.O.; Healy, S.; Horanyi, A.; Hunt, D.; Mannucci, A.J.; Pedatella, N.; Randel, W.J.; Simmons, A.; et al. The COSMIC/FORMOSAT-3 Radio Occultation Mission after 12 Years: Accomplishments, Remaining Challenges, and Potential Impacts of COSMIC-2. Bull. Am. Meteorol. Soc. 2020, 101, E1107–E1136. [Google Scholar] [CrossRef]










| Median Dynamic SNR | |
|---|---|
| COSMIC | 55 |
| COSMIC-2 | 66 |
| METOP-B | 41 |
| Spire | 26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gorbunov, M.; Irisov, V.; Rocken, C. The Influence of the Signal-to-Noise Ratio upon Radio Occultation Retrievals. Remote Sens. 2022, 14, 2742. https://doi.org/10.3390/rs14122742
Gorbunov M, Irisov V, Rocken C. The Influence of the Signal-to-Noise Ratio upon Radio Occultation Retrievals. Remote Sensing. 2022; 14(12):2742. https://doi.org/10.3390/rs14122742
Chicago/Turabian StyleGorbunov, Michael, Vladimir Irisov, and Christian Rocken. 2022. "The Influence of the Signal-to-Noise Ratio upon Radio Occultation Retrievals" Remote Sensing 14, no. 12: 2742. https://doi.org/10.3390/rs14122742
APA StyleGorbunov, M., Irisov, V., & Rocken, C. (2022). The Influence of the Signal-to-Noise Ratio upon Radio Occultation Retrievals. Remote Sensing, 14(12), 2742. https://doi.org/10.3390/rs14122742






