Measurements and Modelling of Total Ozone Columns near St. Petersburg, Russia
Abstract
:1. Introduction
2. Materials and Methods
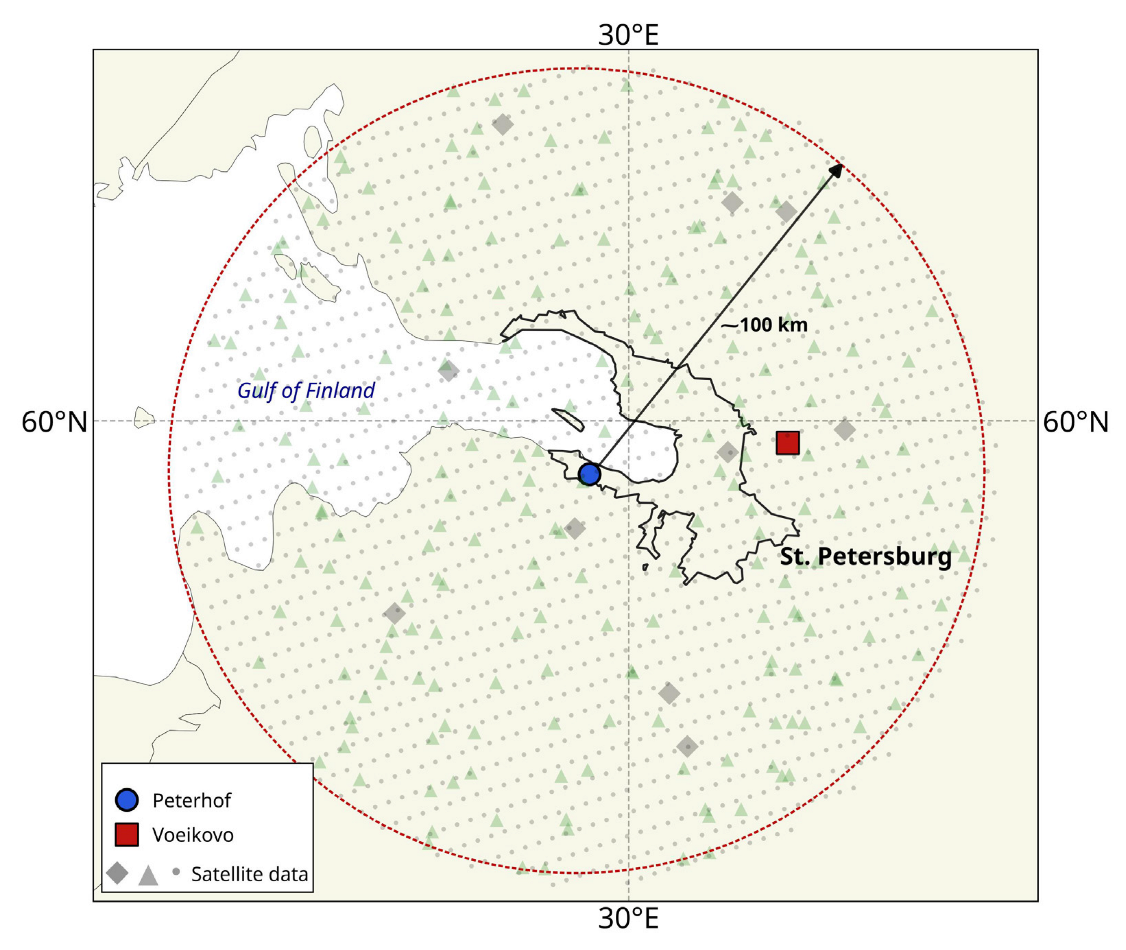
2.1. Ground-Based Observations
2.2. Satellite Observations
2.3. Model Data
3. Results and Discussion
3.1. Comparison of TOC Observations near St. Petersburg
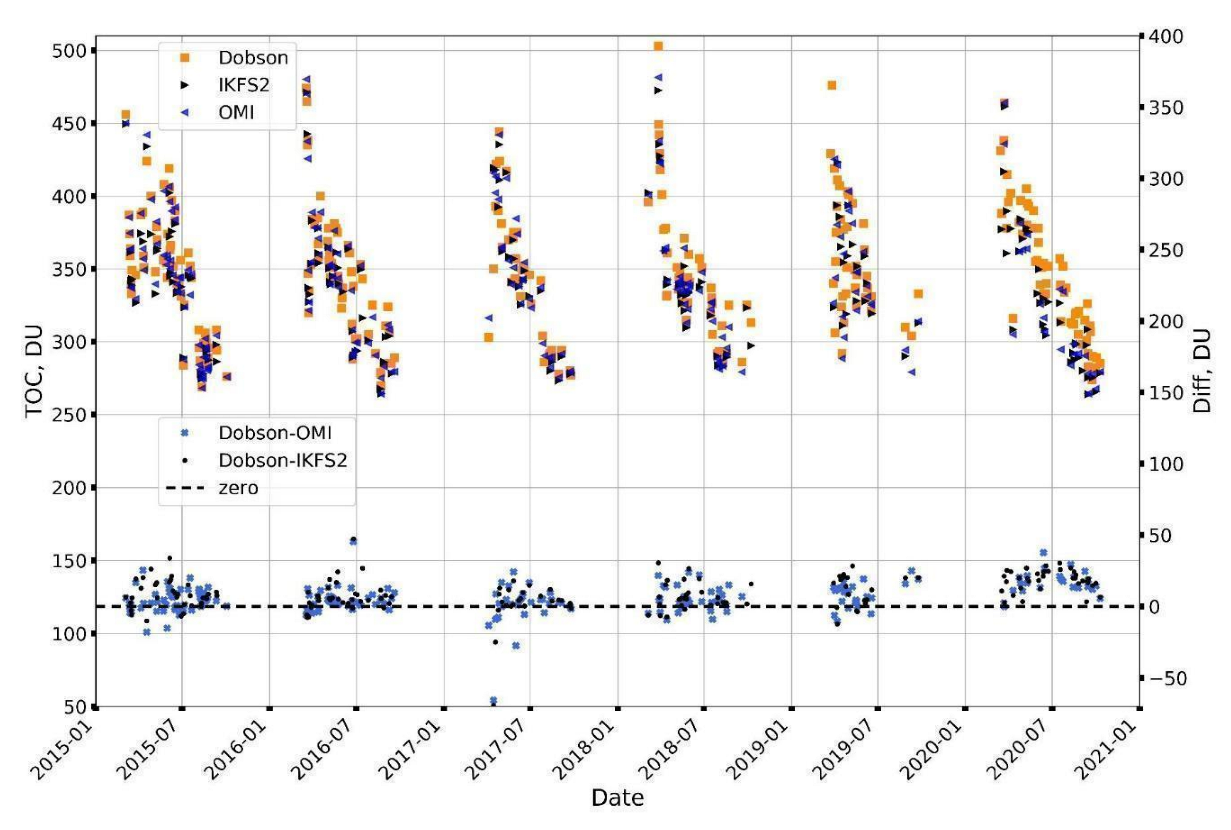
3.1.1. Ground-Based Observations
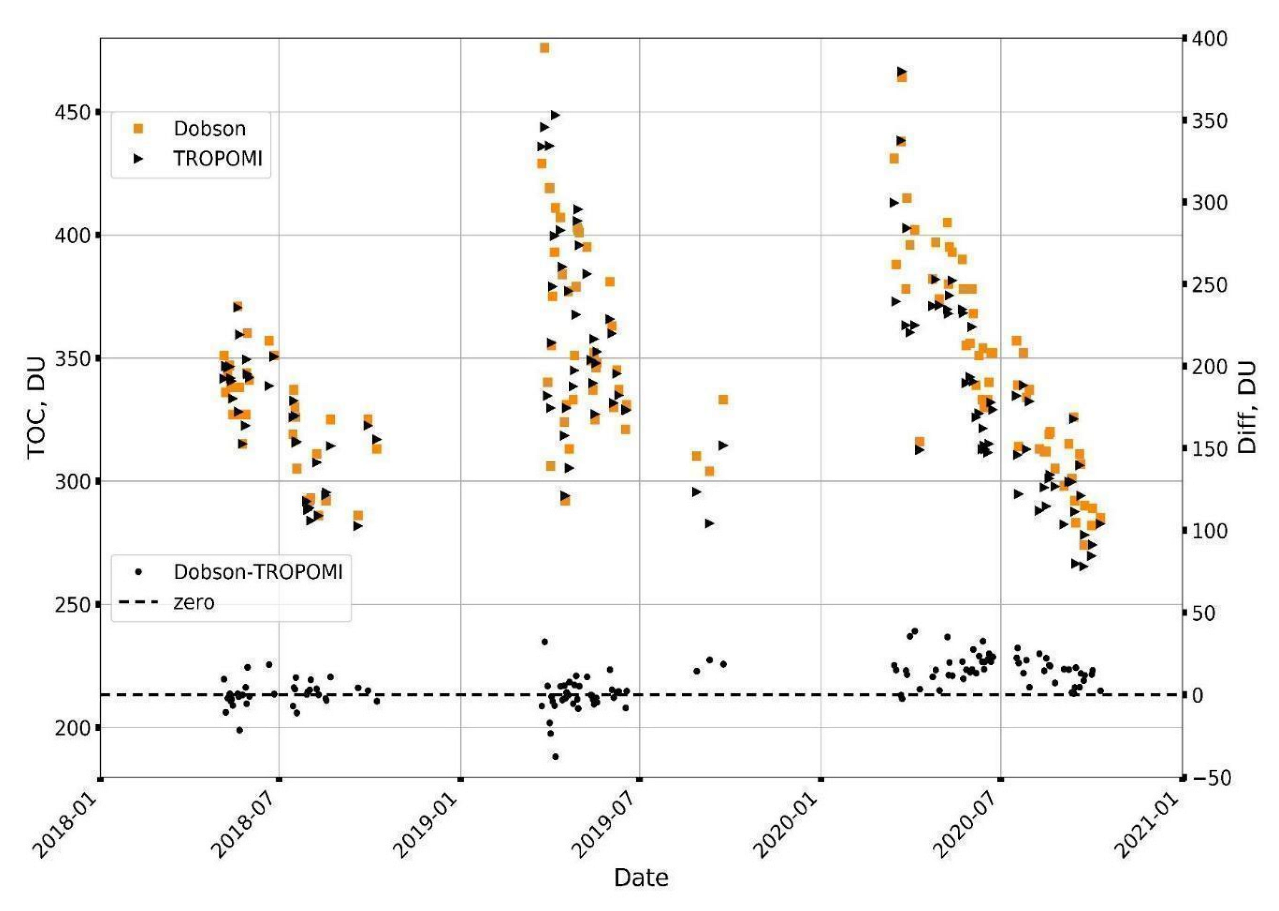
3.1.2. Satellite and Dobson Observations
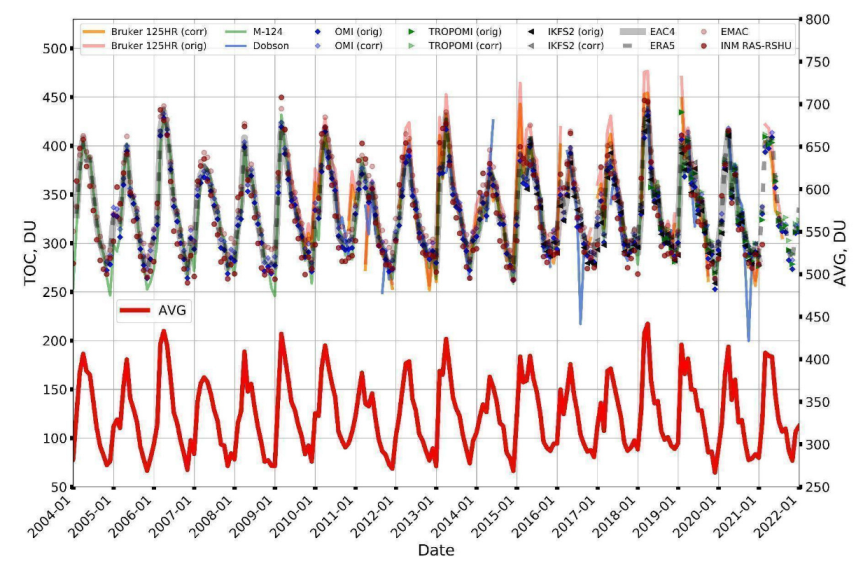
3.1.3. Satellite Observations
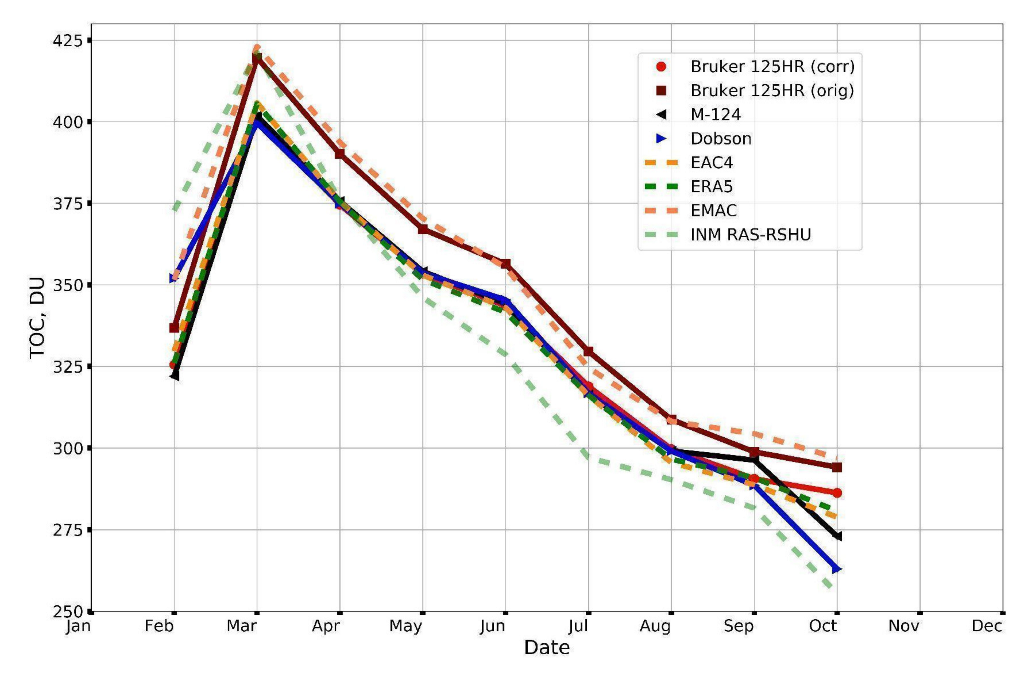
3.1.4. Satellite and Ground-Based (Bruker 125 HR and M-124) Observations
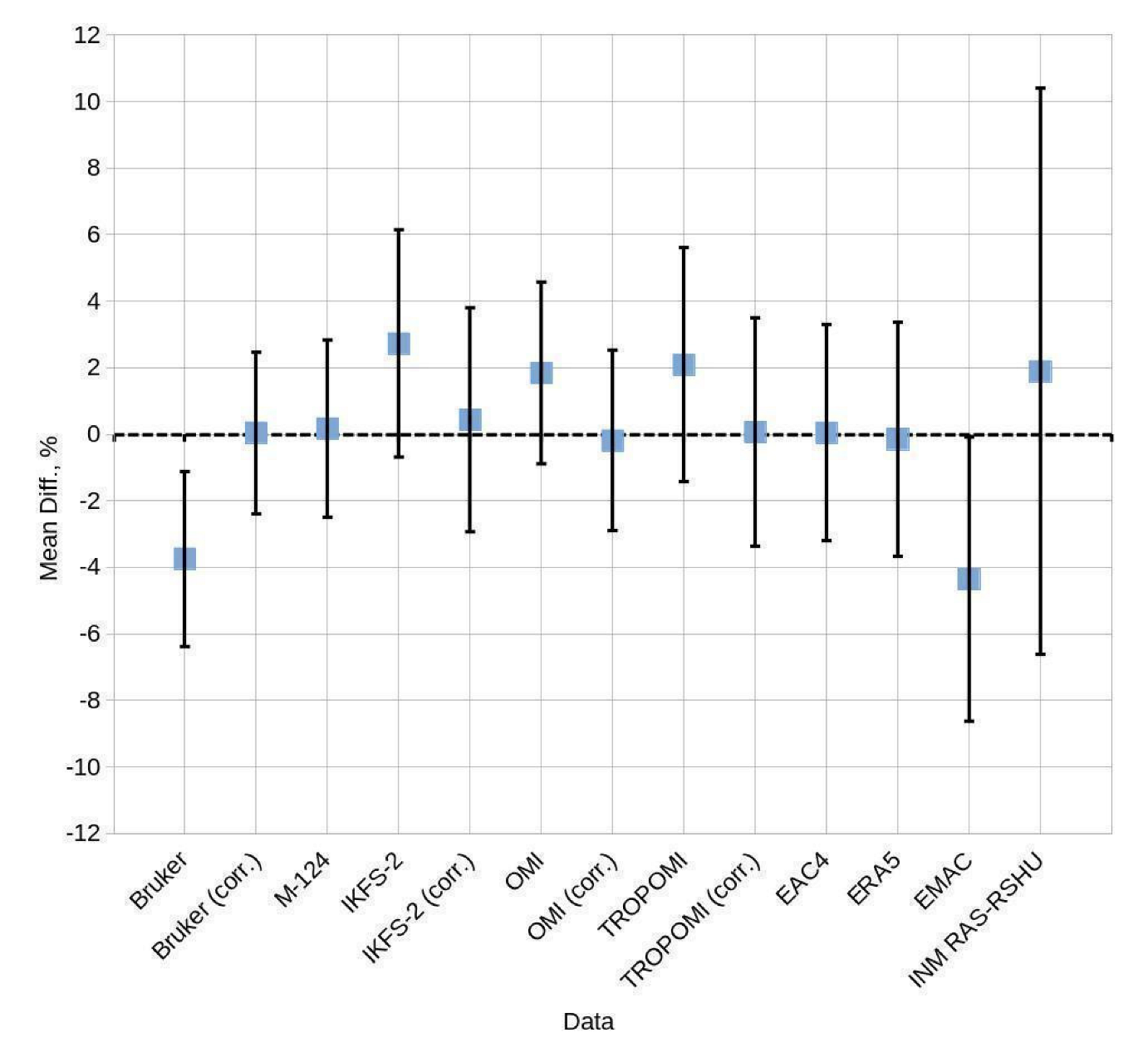
3.2. Correction of TOC Measurements
3.3. Comparison of TOC Observations and Modelled Data
3.3.1. Ground-Based Observations and Modelling
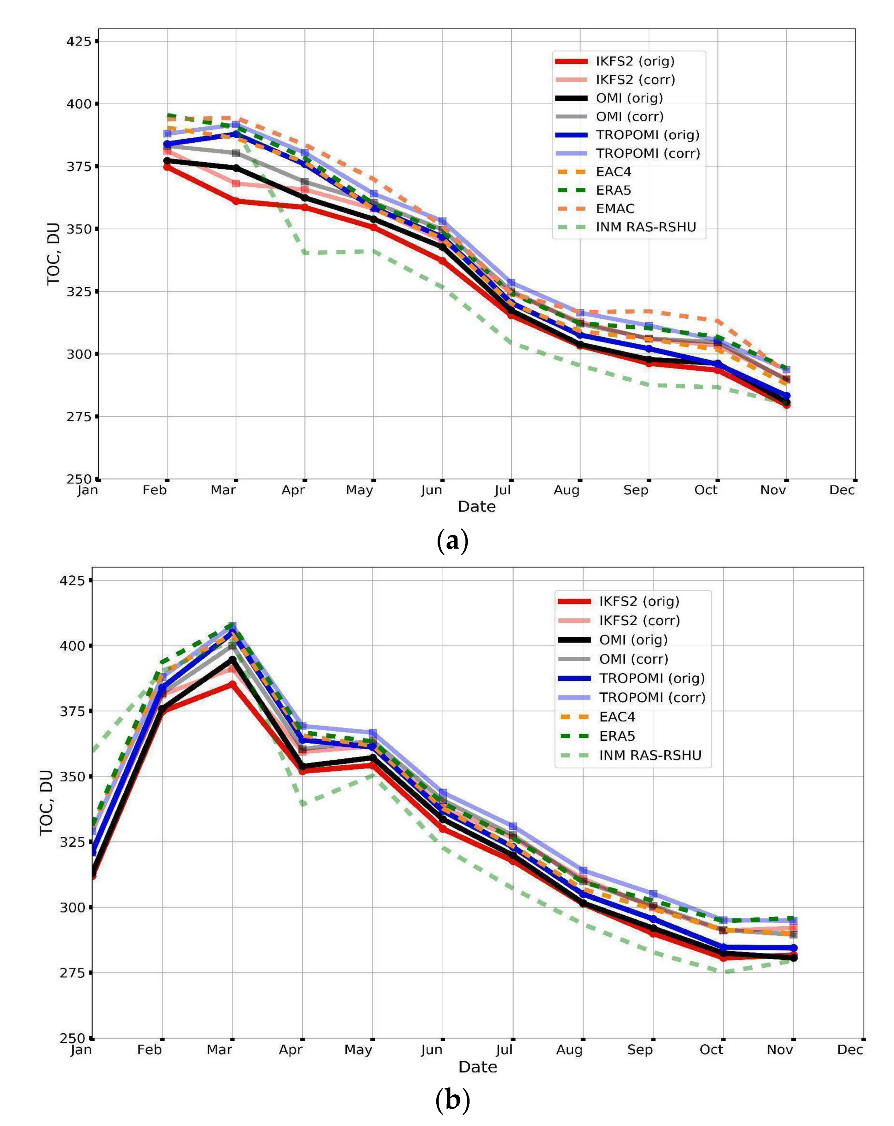
3.3.2. Satellite Observations and Modelling
3.4. Analysis of TOC Trend near St. Petersburg
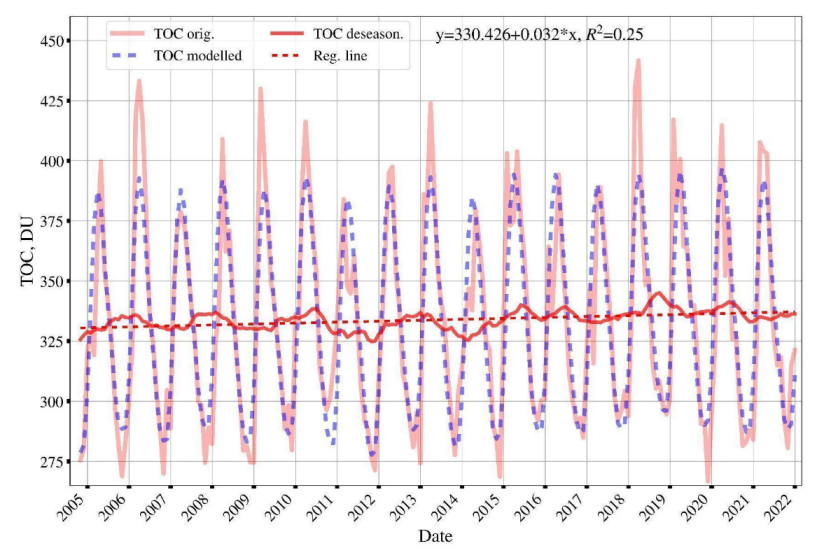
3.4.1. Variations in Monthly Averaged TOC
3.4.2. Estimation and Analysis of TOC Trend
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Meteorological Organization. Assessment of Ozone Depletion: 2018—Global Ozone Research and Monitoring Project Report No. 58; WHO: Geneva, Switzerland, 2018; p. 588. [Google Scholar]
- Seinfeld, J.H.; Pandis, S.N. Atmospheric Chemistry and Physics: From Air Pollution to Climate Change, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006; p. 1225. [Google Scholar]
- Müller, R. A brief history of stratospheric ozone research. Meteorol. Z. 2009, 18, 3–24. [Google Scholar] [CrossRef]
- Logan, J.A. An analysis of ozonesonde data for the troposphere: Recommendations for testing 3-D models and development of a gridded climatology for tropospheric ozone. J. Geophys. Res. Atmos. 1999, 104, 16115–16149. [Google Scholar] [CrossRef]
- Couach, O.; Balin, I.; Jiménez, R.; Ristori, P.; Perego, S.; Kirchner, F.; Simeonov, V.; Calpini, B.; van den Bergh, H. An investigation of ozone and planetary boundary layer dynamics over the complex topography of Grenoble combining measurements and modeling. Atmos. Chem. Phys. 2003, 3, 549–562. [Google Scholar] [CrossRef]
- Molina, M.J.; Rowland, F.S. Stratospheric sink for chlorofluoromethanes: Chlorine atom-catalysed destruction of ozone. Nature 1974, 249, 810–812. [Google Scholar] [CrossRef]
- Solomon, S. Stratospheric ozone depletion: A review of concepts and history. Rev. Geophys. 1999, 37, 275–316. [Google Scholar] [CrossRef]
- Solomon, S.; Ivy, D.J.; Kinnison, D.; Mills, M.J.; Neely, R.R.; Schmidt, A. Emergence of healing in the Antarctic ozone layer. Science 2016, 353, 269–274. [Google Scholar] [CrossRef] [PubMed]
- Bowman, H.; Turnock, S.; Bauer, S.E.; Tsigaridis, K.; Deushi, M.; Oshima, N.; O’Connor, F.M.; Horowitz, L.; Wu, T.; Zhang, J.; et al. Changes in anthropogenic precursor emissions drive shifts in the ozone seasonal cycle throughout the northern midlatitude troposphere. Atmos. Chem. Phys. 2022, 22, 3507–3524. [Google Scholar] [CrossRef]
- Ball, W.T.; Alsing, J.; Mortlock, D.J.; Staehelin, J.; Haigh, J.D.; Peter, T.; Tummon, F.; Stübi, R.; Stenke, A.; Anderson, J.; et al. Evidence for a continuous decline in lower stratospheric ozone offsetting ozone layer recovery. Atmos. Chem. Phys. 2018, 18, 1379–1394. [Google Scholar] [CrossRef]
- Balis, D.; Kroon, M.; Koukouli, M.E.; Brinksma, E.J.; Labow, G.; Veefkind, J.P.; McPeters, R.D. Validation of Ozone Monitoring Instrument total ozone column measurements using Brewer and Dobson spectrophotometer ground-based observations. J. Geophys. Res. 2007, 112, D24S46. [Google Scholar] [CrossRef]
- Labow, G.J.; McPeters, R.D.; Bhartia, P.K.; Kramarova, N. A comparison of 40 years of SBUV measurements of column ozone with data from the Dobson/Brewer network. J. Geophys. Res. Atmos. 2013, 118, 7370–7378. [Google Scholar] [CrossRef]
- Boynard, A.; Clerbaux, C.; Coheur, P.-F.; Hurtmans, D.; Turquety, S.; George, M.; Hadji-Lazaro, J.; Keim, C.; Meyer-Arnek, J. Measurements of total and tropospheric ozone from IASI: Comparison with correlative satellite, ground-based and ozonesonde observations. Atmos. Chem. Phys. 2009, 9, 6255–6271. [Google Scholar] [CrossRef]
- Balis, D.; Lambert, J.-C.; Van Roozendael, M.; Spurr, R.; Loyola, D.; Livschitz, Y.; Valks, P.; Amiridis, V.; Gerard, P.; Granville, J.; et al. Ten years of GOME/ERS2 total ozone data—The new GOME data processor (GDP) version 4: 2. Ground-based validation and comparisons with TOMS V7/V8. J. Geophys. Res. 2007, 112, D07307. [Google Scholar] [CrossRef]
- Antón, M.; Loyola, D.; López, M.; Vilaplana, J.M.; Bañón, M.; Zimmer, W.; Serrano, A. Comparison of GOME-2/MetOp total ozone data with Brewer spectroradiometer data over the Iberian Peninsula. Ann. Geophys. 2009, 27, 1377–1386. [Google Scholar] [CrossRef]
- Loyola, D.G.; Koukouli, M.; Valks, P.; Balis, D.; Hao, N.; Van Roozendael, M.; Spurr, R.; Zimmer, W.; Kiemle, S.; Lerot, C.; et al. The GOME-2 Total Column Ozone Product: Retrieval Algorithm and Ground-Based Validation. J. Geophys. Res. 2011, 116, D07302. [Google Scholar] [CrossRef]
- Koukouli, M.E.; Balis, D.S.; Loyola, D.; Valks, P.; Zimmer, W.; Hao, N.; Lambert, J.-C.; Van Roozendael, M.; Lerot, C.; Spurr, R.J.D. Geophysical validation and long-term consistency between GOME-2/MetOp-A total ozone column and measurements from the sensors GOME/ERS-2, SCIAMACHY/ENVISAT and OMI/Aura. Atmos. Meas. Tech. 2012, 5, 2169–2181. [Google Scholar] [CrossRef]
- Virolainen, Y.A.; Timofeyev, Y.M.; Poberovsky, A.V. Intercomparison of satellite and ground-based ozone total column measurements. Izv. Atmos. Ocean. Phys. 2013, 49, 993–1001. [Google Scholar] [CrossRef]
- Virolainen, Y.; Timofeyev, Y.; Polyakov, A.; Ionov, D.; Poberovsky, A. Intercomparison of satellite and ground-based measurements of ozone, NO2, HF, and HCl near Saint Petersburg, Russia. Int. J. Remote. Sens. 2014, 35, 5677–5697. [Google Scholar] [CrossRef]
- Dufour, G.; Eremenko, M.; Griesfeller, A.; Barret, B.; LeFlochmoen, E. Validation of three different scientific ozone products retrieved from IASI spectra using ozonesondes. Atmos. Meas. Tech. 2012, 5, 611–630. [Google Scholar] [CrossRef]
- Vaz Peres, L.; Bencherif, H.; Mbatha, N.; Passaglia Schuch, A.; Toihir, A.M.; Bègue, N.; Portafaix, T.; Anabor, V.; Kirsch Pinheiro, D.; Paes Leme, N.M.; et al. Measurements of the total ozone column using a Brewer spectrophotometer and TOMS and OMI satellite instruments over the Southern Space Observatory in Brazil. Ann. Geophys. 2017, 35, 25–37. [Google Scholar] [CrossRef]
- Ionov, D.V.; Timofeyev, Y.M.; Shalamyanskii, A.M. Comparison of Satellite- and Ground-Based Measurements of Total Ozone Content. Mapp. Sci. Remote Sens. 2003, 40, 1–16. [Google Scholar] [CrossRef]
- Virolainen, Y.A.; Timofeyev, Y.M.; Poberovskii, A.V.; Polyakov, A.V.; Shalamyanskii, A.M. Empirical Assessment of Errors in Total Ozone Measurements with Different Instruments and Methods. Atmos. Ocean. Opt. 2017, 30, 382–388. [Google Scholar] [CrossRef]
- Hassler, B.; Petropavlovskikh, I.; Staehelin, J.; August, T.; Bhartia, P.K.; Clerbaux, C.; Degenstein, D.; Mazière, M.D.; Dinelli, B.M.; Dudhia, A.; et al. Past changes in the vertical distribution of ozone—Part 1: Measurement techniques, uncertainties and availability. Atmos. Meas. Tech. 2014, 7, 1395–1427. [Google Scholar] [CrossRef]
- Timofeev, Y.M. Study of Atmosphere by a Transparency Method; Nauka: St. Peterburg, Russia, 2016; p. 367. (In Russian) [Google Scholar]
- Dobson, G.M.B. Observers handbook for the ozone spectrophotometer. Ann. Int. Geophys. Year 1957, 5, 46–89. [Google Scholar]
- Kerr, J.B.; McElroy, C.T.; Olafson, R.A. Measurements of ozone with the Brewer spectrophotometer. In Quadrennial International Ozone Symposium; London, J., Ed.; WMO: Boulder, CO, USA, 1981; pp. 74–79. [Google Scholar]
- Kerr, J.B.; Asbridge, I.A.; Evans, W.F.J. Intercomparison of total ozone measured by the Brewer and Dobson spectrophotometers at Toronto. J. Geophys. Res. 1988, 93, 11129–11140. [Google Scholar] [CrossRef]
- Shalamyanskii, A.M.; Romashkina, K.I.; Privalov, V.I. Comparison of methods and instruments for ground-based measurements of total ozone column. Prikl. Meteorol. 2004, 5, 187–206. (In Russian) [Google Scholar]
- Hase, F.; Hannigan, J.W.; Coffey, M.T.; Goldman, A.; Hopfner, M.; Jones, N.B.; Rinsland, C.P.; Wood, S.W. Intercomparison of retrieval codes used for the analysis of high resolution, ground based FTIR measurements. J. Quant. Spectrosc. Rad. Transf. 2004, 87, 25–52. [Google Scholar] [CrossRef]
- Timofeyev, Y.M. Global Monitoring System of Atmospheric and Surface Parameters; St. Petersburg University: St. Petersburg, Russia, 2010; p. 129. [Google Scholar]
- Garkusha, A.S.; Polyakov, A.V.; Timofeev, Y.M.; Virolainen, Y.A. Determination of the total ozone content from data of satellite IR Fourier-spectrometer. Izv. Atmos. Ocean. Phys. 2017, 53, 433–440. [Google Scholar] [CrossRef]
- Bhartia, P.K.; Levelt, P.F.; Tamminen, J.; Torres, O. Recent results from the Ozone Monitoring Instrument (OMI) on EOS Aura. Remote Sens. Atmos. Clouds 2006, 6408, 192–202. [Google Scholar] [CrossRef]
- Bernath, P.F.; McElroy, C.T.; Abrams, M.C.; Boone, C.D.; Butler, M.; Camy-Peyret, C.; Carleer, M.; Clerbaux, C.; Coheur, P.-F.; Colin, R.; et al. Atmospheric Chemistry Experiment (ACE): Mission overview. Geophys. Res. Lett. 2005, 32, L15S01. [Google Scholar] [CrossRef]
- Smyshlyaev, S.P.; Vargin, P.N.; Motsakov, M.A. Numerical Modeling of Ozone Loss in the Exceptional Arctic Stratosphere Winter-Spring of 2020. Atmosphere 2021, 12, 1470. [Google Scholar] [CrossRef]
- Timofeyev, Y.M.; Smyshlyaev, S.P.; Virolainen, Y.A.; Garkusha, A.S.; Polyakov, A.V.; Motsakov, M.A.; Kirner, O. Case study of ozone anomalies over northern Russia in the 2015/2016 winter: Measurements and numerical modelling. Ann. Geophys. 2018, 36, 1495–1505. [Google Scholar] [CrossRef]
- Timofeyev, Y.M.; Virolainen, Y.A.; Smyshlyaev, S.P.; Motsakov, M.A. Ozone over St. Petersburg: Comparison of experimental data and numerical simulation. Atmos. Ocean. Opt. 2017, 30, 263–268. [Google Scholar] [CrossRef]
- Rozanov, E.; Egorova, T.; Egli, L.; Karagodin-Doyennel, A.; Sukhodolov, T.; Schill, H.; Stübi, R.; Gröbner, J. Representativeness of the Arosa/Davos Measurements for the Analysis of the Global Total Column Ozone Behavior. Front. Earth Sci. 2021, 9, 675084. [Google Scholar] [CrossRef]
- Egorova, T.; Rozanov, E.; Arsenovic, P.; Sukhodolov, T. Ozone Layer Evolution in the Early 20th Century. Atmosphere 2020, 11, 169. [Google Scholar] [CrossRef]
- Kirner, O.; Ruhnke, R.; Buchholz-Dietsch, J.; Jöckel, P.; Brühl, C.; Steil, B. Simulation of polar stratospheric clouds in the chemistry-climate-model EMAC via the submodel PSC. Geosci. Model Dev. 2011, 4, 169–182. [Google Scholar] [CrossRef]
- Fioletov, V.E.; Labow, G.; Evans, R.; Hare, E.W.; Köhler, U.; McElroy, C.T.; Miyagawa, K.; Redondas, A.; Savastiouk, V.; Shalamyanskii, A.M.; et al. Performance of the ground-based total ozone network assessed using satellite data. J. Geophys. Res. 2008, 113, D14313. [Google Scholar] [CrossRef]
- Koukouli, M.E.; Lerot, C.; Granville, J.; Goutail, F.; Lambert, J.-C.; Pommereau, J.-P.; Balis, D.; Zyrichidou, I.; Van Roozendael, M.; Coldewey-Egbers, M.; et al. Evaluating a new homogeneous total ozone climate data record from GOME/ERS-2, SCIAMACHY/Envisat, and GOME-2/MetOp-A. J. Geophys. Res. 2015, 120, 12296–12312. [Google Scholar] [CrossRef]
- Bak, J.; Liu, X.; Kim, J.H.; Chance, K.; Haffner, D.P. Validation of OMI total ozone retrievals from the SAO ozone profile algorithm and three operational algorithms with Brewer measurements. Atmos. Chem. Phys. 2015, 15, 667–683. [Google Scholar] [CrossRef]
- Garane, K.; Lerot, C.; Coldewey-Egbers, M.; Verhoelst, T.; Koukouli, M.E.; Zyrichidou, I.; Balis, D.S.; Danckaert, T.; Goutail, F.; Granville, J.; et al. Quality assessment of the Ozone_cci Climate Research Data Package (release 2017)—Part 1: Ground-based validation of total ozone column data products. Atmos. Meas. Tech. 2018, 11, 1385–1402. [Google Scholar] [CrossRef]
- Timofeyev, Y.; Virolainen, Y.; Makarova, M.; Poberovsky, A.; Polyakov, A.; Ionov, D.; Osipov, S.; Imhasin, H. Ground-based spectroscopic measurements of atmospheric gas composition near Saint Petersburg (Russia). J. Mol. Spectrosc. 2016, 323, 2–14. [Google Scholar] [CrossRef]
- Virolainen, Y.; Timofeyev, Y.; Polyakov, A.; Ionov, D.; Kirner, O.; Poberovskii, A.; Imhasin, H. Comparison of ground-based measurements of total ozone, HNO3, HCL and NO2 content with numerical model data. Izv. RAN. FAO 2015, 51, 1–10. (In Russian) [Google Scholar]
- Bhartia, P.K. OMI/Aura Ozone (O3) Total Column 1-Orbit L2 Swath 13 × 24 km V003; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2005; Available online: https://10.5067/Aura/OMI/DATA2024 (accessed on 22 December 2021).
- Copernicus Sentinel Data Processed by ESA, German Aerospace Center (DLR). Sentinel-5P TROPOMI Total Ozone Column 1-Orbit L2 5.5 km × 3.5 km; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2019; Available online: https://10.5270/S5P-fqouvyz (accessed on 21 December 2021).
- Polyakov, A.; Virolainen, Y.; Nerobelov, G.; Timofeyev, Y.; Solomatnikova, A. Total ozone measurements using IKFS-2 spectrometer aboard Meteor-M N2 satellite in 2019–2020. Int. J. Remote Sens. 2021, 42, 8709–8733. [Google Scholar] [CrossRef]
- Timofeyev, Y.; Uspensky, A.; Zavelevich, F.; Polyakov, A.; Virolainen, Y.; Rublev, A.; Kukharsky, A.; Kiseleva, J.; Kozlov, D.; Kozlov, I.; et al. Hyperspectral infrared atmospheric sounder IKFS-2 on “Meteor-M” No. 2—Four years in orbit. J. Quant. Spectrosc. Radiat. Transf. 2019, 238, 106579. [Google Scholar] [CrossRef]
- Polyakov, A.V. The Method of Artificial Neural Networks in Retrieving Vertical Profiles of Atmospheric Parameters. Atmos. Ocean. Opt. 2014, 27, 247–252. [Google Scholar] [CrossRef]
- Levelt, P.F.; van den Oord, G.H.J.; Dobber, M.R.; Malkki, A.; Visser, H.; de Vries, J.; Stammes, P.; Lundell, J.O.V.; Saari, H. The Ozone Monitoring Instrument. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1093–1101. [Google Scholar] [CrossRef]
- Veefkind, J.; Aben, I.; McMullan, K.; Förster, H.; de Vries, J.; Otter, G.; Claas, J.; Eskes, H.; de Haan, J.; Kleipool, Q.; et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES mission for global observations of the atmospheric composition for climate, air quality and ozone layer applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Biavati, G.; Horányi, A.; Muñoz Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Rozum, I.; et al. ERA5 hourly data on single levels from 1979 to present. Copernic. Clim. Change Serv. Clim. Data Store 2018, 10. [Google Scholar] [CrossRef]
- Cariolle, D.; Déqué, M. Southern hemisphere medium-scale waves and total ozone disturbances in a spectral general circulation model. J. Geophys. Res. 1986, 91, 10825–10846. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Inness, A.; Ades, M.; Agustí-Panareda, A.; Barré, J.; Benedictow, A.; Blechschmidt, A.-M.; Dominguez, J.J.; Engelen, R.; Eskes, H.; Flemming, J.; et al. The CAMS reanalysis of atmospheric composition. Atmos. Chem. Phys. 2019, 19, 3515–3556. [Google Scholar] [CrossRef]
- Flemming, J.; Huijnen, V.; Arteta, J.; Bechtold, P.; Beljaars, A.; Blechschmidt, A.-M.; Diamantakis, M.; Engelen, R.J.; Gaudel, A.; Inness, A.; et al. Tropospheric chemistry in the Integrated Forecasting System of ECMWF. Geosci. Model Dev. 2015, 8, 975–1003. [Google Scholar] [CrossRef]
- Galin, V.Y.; Smyshlyaev, S.P.; Volodin, E.M. Combined Chemistry-Climate Model of the Atmosphere. Izv. Atmos. Ocean. Phys. 2007, 43, 399–412. [Google Scholar] [CrossRef]
- Jöckel, P.; Kerkweg, A.; Pozzer, A.; Sander, R.; Tost, H.; Riede, H.; Baumgaertner, A.; Gromov, S.; Kern, B. Development cycle 2 of the Modular Earth Submodel System (MESSy2). Geosci. Model Dev. 2010, 3, 717–752. [Google Scholar] [CrossRef]
- Virolainen, Y.; Timofeyev, Y.; Ionov, D.; Poberovskii, A.; Shalamyanskii, A. Ground-based measurements of total ozone column by IR method. Izv. RAN FAO 2011, 47, 521–532. (In Russian) [Google Scholar]
- Virolainen, Y.; Polyakov, A.; Timofeyev, Y. Analysis of the variation of stratospheric gases according to ground-based spectroscopic measurements near St. Petersburg. Izv. RAN FAO 2021, 57, 163–174. (In Russian) [Google Scholar]
- Wallace, J.; Hobbs, P. Atmospheric Science—An Introductory Survey, 2nd ed.; Elsevier Academic Press: Amsterdam, The Netherlands, 2006; p. 484. [Google Scholar]
- Schneider, M.; Redondas, A.; Hase, F.; Guirado, C.; Blumenstock, T.; Cuevas, E. Comparison of ground-based Brewer and FTIR total column O3 monitoring techniques. Atmos. Chem. Phys. 2008, 8, 5535–5550. [Google Scholar] [CrossRef]
- Viatte, C.; Schneider, M.; Redondas, A.; Hase, F.; Eremenko, M.; Chelin, P.; Flaud, J.-M.; Blumenstock, T.; Orphal, J. Comparison of ground-based FTIR and Brewer O3 total column with data from two different IASI algorithms and from OMI and GOME-2 satellite instruments. Atmos. Meas. Tech. 2011, 4, 535–546. [Google Scholar] [CrossRef]
- Kim, S.; Park, S.-J.; Lee, H.; Ahn, D.H.; Jung, Y.; Choi, T.; Lee, B.Y.; Kim, S.-J.; Koo, J.-H. Evaluation of Total Ozone Column from Multiple Satellite Measurements in the Antarctic Using the Brewer Spectrophotometer. Remote Sens. 2021, 13, 1594. [Google Scholar] [CrossRef]
- Zhang, L.N.; Solomon, S.; Stone, K.A.; Shanklin, J.D.; Eveson, J.D.; Colwell, S.; Burrows, J.P.; Weber, M.; Levelt, P.F.; Kramarova, N.A.; et al. On the use of satellite observations to fill gaps in the Halley station total ozone record. Atmos. Chem. Phys. 2021, 21, 9829–9838. [Google Scholar] [CrossRef]
- Skalski, J.; Ryding, K.; Millspaugh, J. Wildlife Demography, 8-Analysis of Population Indices; Academic Press: Cambridge, MA, USA, 2005; pp. 359–433. [Google Scholar] [CrossRef]
- Coldewey-Egbers, M.; Loyola, D.G.; Labow, G.; Frith, S.M. Comparison of GTO-ECV and adjusted MERRA-2 total ozone columns from the last 2 decades and assessment of interannual variability. Atmos. Meas. Tech. 2020, 13, 1633–1654. [Google Scholar] [CrossRef]
- Ozone-cci User Requirement Document. Available online: https://climate.esa.int/sites/default/files/filedepot/incoming/Ozone_cci_urd_v3.0_final.pdf (accessed on 1 June 2022).
- Bernet, L.; von Clarmann, T.; Godin-Beekmann, S.; Ancellet, G.; Maillard Barras, E.; Stübi, R.; Steinbrecht, W.; Kämpfer, N.; Hocke, K. Ground-based ozone profiles over central Europe: Incorporating anomalous observations into the analysis of stratospheric ozone trends. Atmos. Chem. Phys. 2019, 19, 4289–4309. [Google Scholar] [CrossRef]
- Weatherhead, E.C.; Reinsel, G.C.; Tiao, G.C.; Meng, X.; Choi, D.; Cheang, W.; Keller, T.; DeLuisi, J.; Wuebbles, D.J.; Kerr, J.B.; et al. Factors affecting the detection of trends: Statistical considerations and applications to environmental data. J. Geophys. Res. 1998, 103, 17149–17161. [Google Scholar] [CrossRef]
- Vigouroux, C.; Blumenstock, T.; De Mazière, M.; Errera, Q.; García, O.E.; Grutter, M.; Hannigan, J.; Hase, F.; Jones, N.; Mahieu, E.; et al. Trends and Variability of Ozone Total, Stratospheric, and Tropospheric Columns from Long-Term FTIR Measurements of the NDACC Network. In Proceedings of the Quadrennial Ozone Symposium, Seoul, Korea, 3–9 October 2021. [Google Scholar]


| Instrument | Method | Horizontal Resolution, km | TOC Retrieval Error, % | Period of Observations Used |
|---|---|---|---|---|
| Bruker 125 HR | direct IR solar radiation | 10–30, depending on solar zenith angle | 2–3 | 2009–2020 |
| Dobson | direct and scattered UV solar radiation | 10–100, depending on solar zenith angle | 1–2 | 2009–2020 |
| M-124 | 3–5 | 1985–2020 | ||
| IKFS-2 | TR * | 35 × 35 | 3–4 | 2015–2020 |
| OMI | RS * | 24 × 13 | 1–2 | 2004–2021 |
| TROPOMI | 7 × 3 | <2–3 | 2018–2021 |
| Data | Horizontal Resolution | Vertical Resolution | Time Coverage and Frequency | Assimilation of Meteorological Measurements | Assimilation of Ozone Measurements |
|---|---|---|---|---|---|
| ERA5 | Hor. 0.25° (~31 km) | up to ~0.01 hPa (~80 km) | 1979–2021, 3 h | Yes (in situ, satellite, radiosonde, radar data, etc.) | Yes (TOC, partial column, and profiles) |
| EAC4 | Hor. 0.75° (~80 km) | up to ~0.1 hPa (~70 km) | 2003–2021, 3 h | Yes (in situ, satellite, radiosonde, radar data, etc.) | Yes (TOC, partial column, and profiles) |
| INM RAS—RSHU | Hor. 4 × 5° (~300 × 400 km2) | up to ~90 km | 2004–2021, 6 h | Yes (nudging of meteorological parameters) | No |
| EMAC | Hor. 2.8° (~155 km) | up to ~0.01 hPa (~80 km) | 2002–2019, 1 h | Yes (nudging of meteorological parameters) | No |
| Instrument | Bruker 125 HR | M-124 | Dobson | IKFS-2 | OMI | TROPOMI |
|---|---|---|---|---|---|---|
| Bruker 125 HR | - | 3.9/3.2 a | 3.9/2.8 a | 6.4/3.3 b | 5.3/2.2 b | 3.5/1.5 c |
| M-124 | −3.9/3.2 a | - | 0.0/2.3 a | 2.6/4.3 b | 1.6/3.3 b | 0.9/3.6 c |
| Dobson | −3.9/2.8 a | 0.0/2.3 a | - | 2.4/3.6 d | 1.8/3.3 d | 2.2/3.7 e |
| IKFS-2 | −6.4/3.3 b | −2.6/4.3 b | −2.4/3.6 d | - | −0.7/3.1 f | −2.1/3.2 f |
| OMI | −5.3/2.2 b | −1.6/3.3 b | −1.8/3.3 d | 0.7/3.1 f | - | −1.4/2.1 f |
| TROPOMI | −3.5/1.5 c | −0.9/3.6 c | −2.2/3.7 e | 2.1/3.2 f | 1.4/2.1 f | - |
| Instrument | Bruker 125 HR | M-124 | Dobson | IKFS-2 | OMI | TROPOMI |
|---|---|---|---|---|---|---|
| Bruker 125 HR | - | 48.5/45.3 a | 48.5/46.2 a | 58.9/54.5 b | 58.9/55.9 b | 46.3/45.8 c |
| M-124 | 45.3/48.5 a | - | 45.3/46.2 a | 54.4/54.5 b | 54.3/55.9 b | 44.6/45.8 c |
| Dobson | 46.2/48.5 a | 46.2/45.3 a | - | 46.5/47.2 d | 46.5/48.0 d | 40.2/41.0 e |
| IKFS-2 | 54.5/58.9 b | 54.5/54.4 b | 47.2/46.5 d | - | 44.8/47.4 f | 44.8/47.6 f |
| OMI | 55.9/58.9 b | 55.9/54.3 b | 48.0/46.5 d | 47.4/44.8 f | - | 47.4/47.6 f |
| TROPOMI | 45.8/46.3 c | 45.8/44.6 c | 41.0/40.2 e | 47.6/44.8 f | 47.6/47.4 f | - |
| Instrument | Bruker 125 HRcorr | M-124 | Dobson | IKFS-2corr | OMIcorr | TROPOMIcorr |
|---|---|---|---|---|---|---|
| Bruker 125 HRcorr | - | −0.1/2.9 a | 0.1/2.6 a | 0.0/2.8 b | −0.7/1.8 b | −2.3/1.4 c |
| M-124 | 0.1/2.9 a | - | 0.0/2.3 a | 0.3/4.3 b | −0.5/3.2 b | −1.3/3.5 c |
| Dobson | −0.1/2.6 a | 0.0/2.3 a | - | 0.1/3.6 d | −0.3/3.2 d | 0.1/3.6 e |
| IKFS-2corr | 0.0/2.8 b | −0.3/4.3 b | −0.1/3.6 d | - | −0.4/3.0 f | −1.7/2.9 f |
| OMIcorr | 0.7/1.8 b | 0.5/3.2 b | 0.3/3.2 d | 0.4/3.0 f | - | −1.3/2.0 f |
| TROPOMIcorr | 2.3/1.4 c | 1.3/3.5 c | −0.1/3.6 e | 1.7/2.9 f | 1.3/2.0 f | - |
| Instrument | Bruker 125 HR | М-124 | Dobson | IKFS-2 | OMI | TROPOMI | ERA5 | EAC4 | EMAC |
|---|---|---|---|---|---|---|---|---|---|
| ERA5 | −4.2/2.4 a | −0.4/3.7 a | −0.2/3.9 a | 3.9/3.3 b | 2.9/2.7 b | 1.5/2.0 b | - | 0.8/1.7 c | −2.9/3.6 c |
| EAC4 | −4.1/2.2 a | −0.3/3.4 a | −0.1/3.7 a | 2.8/3.3 b | 1.8/2.7 b | 0.4/2.0 b | −0.8/1.7 c | - | −3.6/3.2 c |
| EMAC | 0.5/3.7 a | 4.3/4.3 a | 4.5/4.5 a | 5.0/4.1 b | 3.9/4.2 b | 2.6/3.8 b | 2.9/3.6 c | 3.6/3.2 c | - |
| INM RAS—RSHU | −5.4/8.5 a | −1.6/8.6 a | −1.4/8.6 a | −1.2/8.3 b | −2.3/8.6 b | −3.6/8.4 b | −2.3/8.7 c | −1.5/8.7 c | −5.1/7.8 c |
| Instrument | Bruker 125 HR | М-124 | Dobson | IKFS-2 | OMI | TROPOMI | ERA5 | EAC4 | EMAC |
|---|---|---|---|---|---|---|---|---|---|
| ERA5 | −0.2/2.3 a | −0.4/3.7 a | −0.2/3.9 a | 1.4/3.4 b | 0.7/2.6 b | −0.6/1.9 b | - | 0.8/1.7 c | −2.9/3.6 c |
| EAC4 | −0.1/2.1 a | −0.3/3.4 a | −0.1/3.7 a | 0.3/3.3 b | −0.4/2.7 b | −1.7/2.0 b | −0.8/1.7 c | - | −3.6/3.2 c |
| EMAC | 4.5/3.5 a | 4.3/4.3 a | 4.5/4.5 a | 2.4/4.0 b | 1.7/4.1 b | 0.4/3.5 b | 2.9/3.6 c | 3.6/3.2 c | - |
| INM RAS—RSHU | −1.4/8.4 a | −1.6/8.6 a | −1.4/8.6 a | −3.8/8.2 b | −4.5/8.4 b | −5.8/8.1 b | −2.3/8.7 c | −1.5/8.7 c | −5.1/7.8 c |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nerobelov, G.; Timofeyev, Y.; Virolainen, Y.; Polyakov, A.; Solomatnikova, A.; Poberovskii, A.; Kirner, O.; Al-Subari, O.; Smyshlyaev, S.; Rozanov, E. Measurements and Modelling of Total Ozone Columns near St. Petersburg, Russia. Remote Sens. 2022, 14, 3944. https://doi.org/10.3390/rs14163944
Nerobelov G, Timofeyev Y, Virolainen Y, Polyakov A, Solomatnikova A, Poberovskii A, Kirner O, Al-Subari O, Smyshlyaev S, Rozanov E. Measurements and Modelling of Total Ozone Columns near St. Petersburg, Russia. Remote Sensing. 2022; 14(16):3944. https://doi.org/10.3390/rs14163944
Chicago/Turabian StyleNerobelov, Georgy, Yuri Timofeyev, Yana Virolainen, Alexander Polyakov, Anna Solomatnikova, Anatoly Poberovskii, Oliver Kirner, Omar Al-Subari, Sergei Smyshlyaev, and Eugene Rozanov. 2022. "Measurements and Modelling of Total Ozone Columns near St. Petersburg, Russia" Remote Sensing 14, no. 16: 3944. https://doi.org/10.3390/rs14163944
APA StyleNerobelov, G., Timofeyev, Y., Virolainen, Y., Polyakov, A., Solomatnikova, A., Poberovskii, A., Kirner, O., Al-Subari, O., Smyshlyaev, S., & Rozanov, E. (2022). Measurements and Modelling of Total Ozone Columns near St. Petersburg, Russia. Remote Sensing, 14(16), 3944. https://doi.org/10.3390/rs14163944







