Algorithm of Additional Correction of Level 2 Remote Sensing Reflectance Data Using Modelling of the Optical Properties of the Black Sea Waters
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Field Measurements
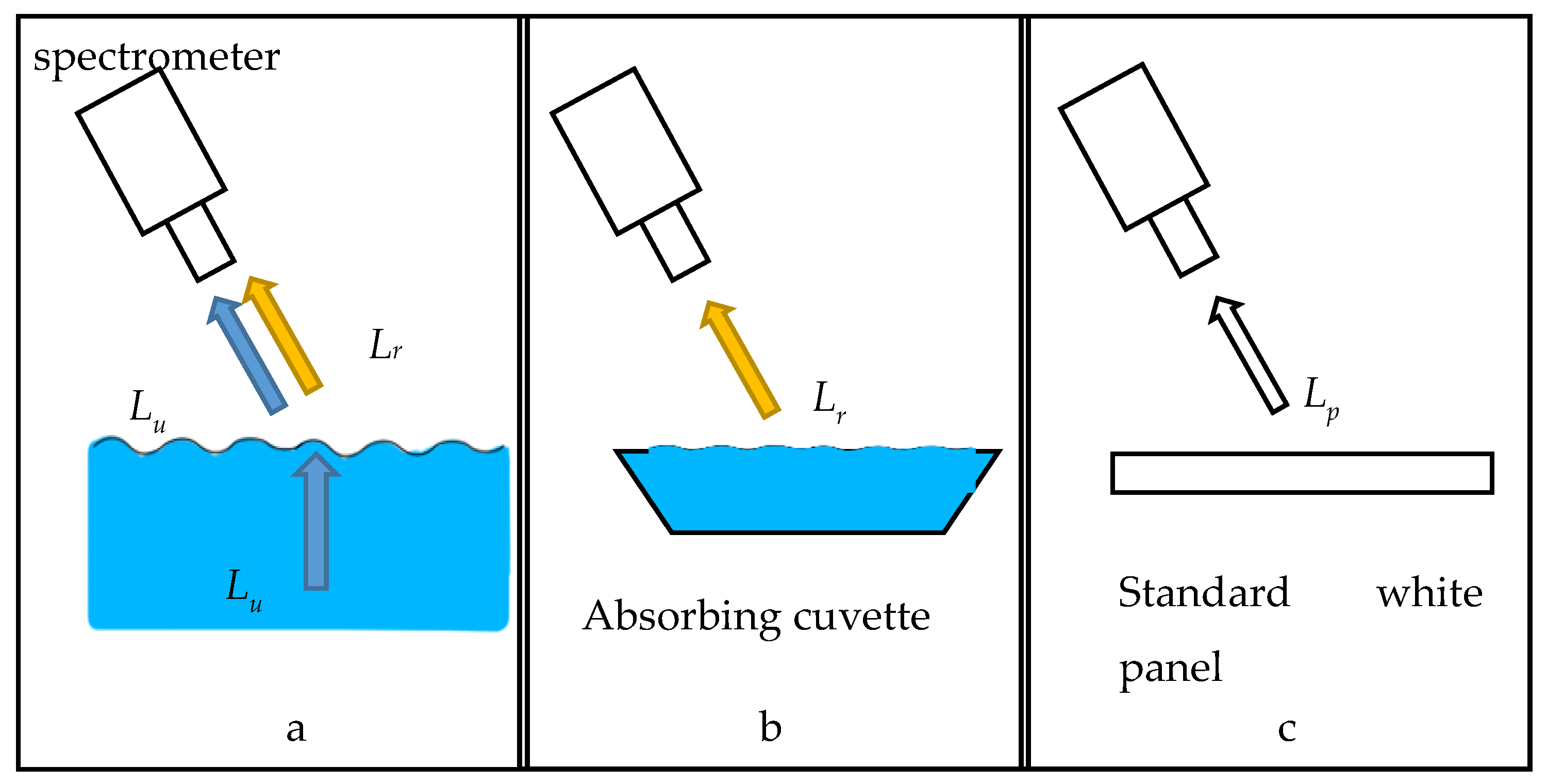
2.2.1. Upwelling Radiation Hyperspectral Measurements
2.2.2. Atmospheric Measurements
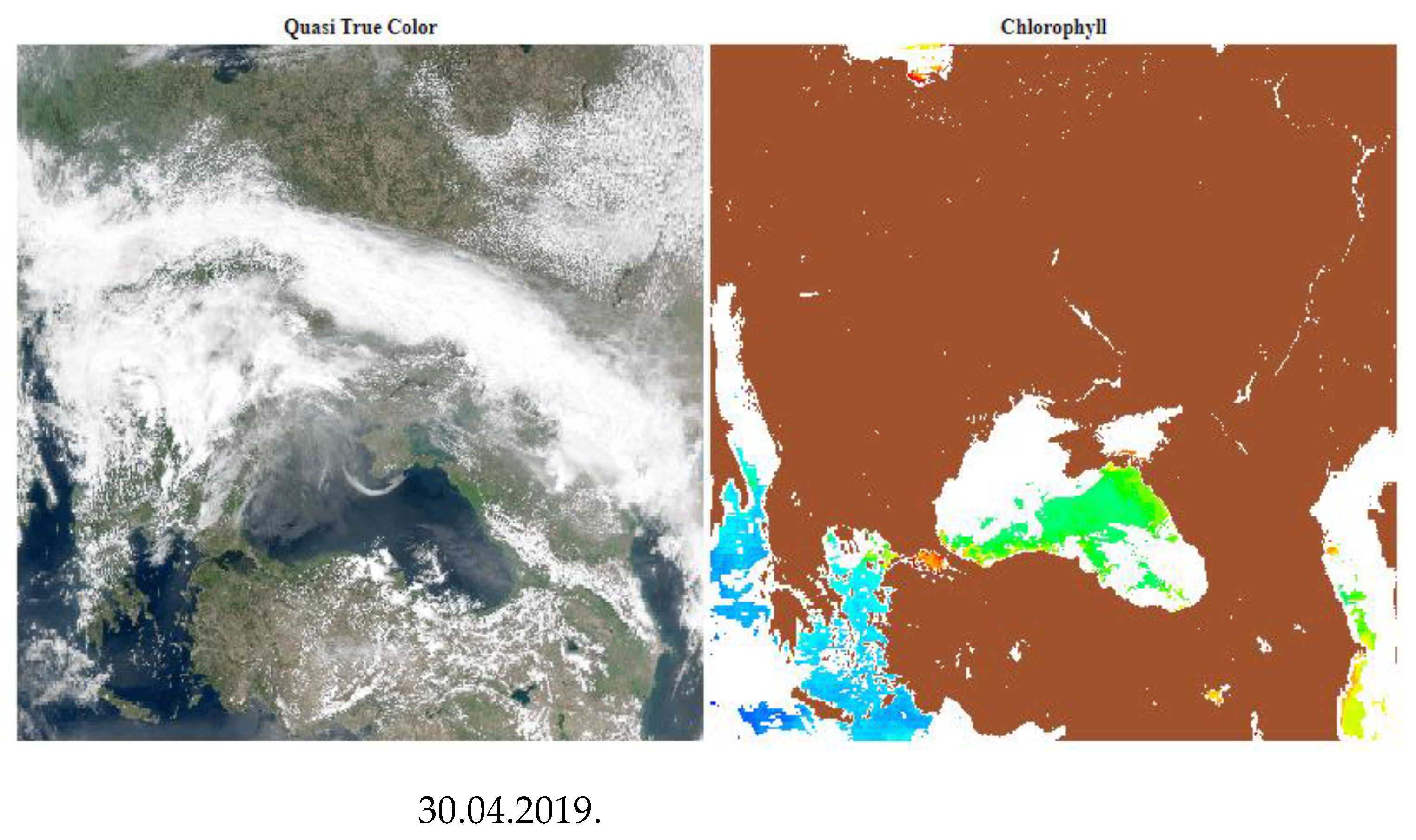
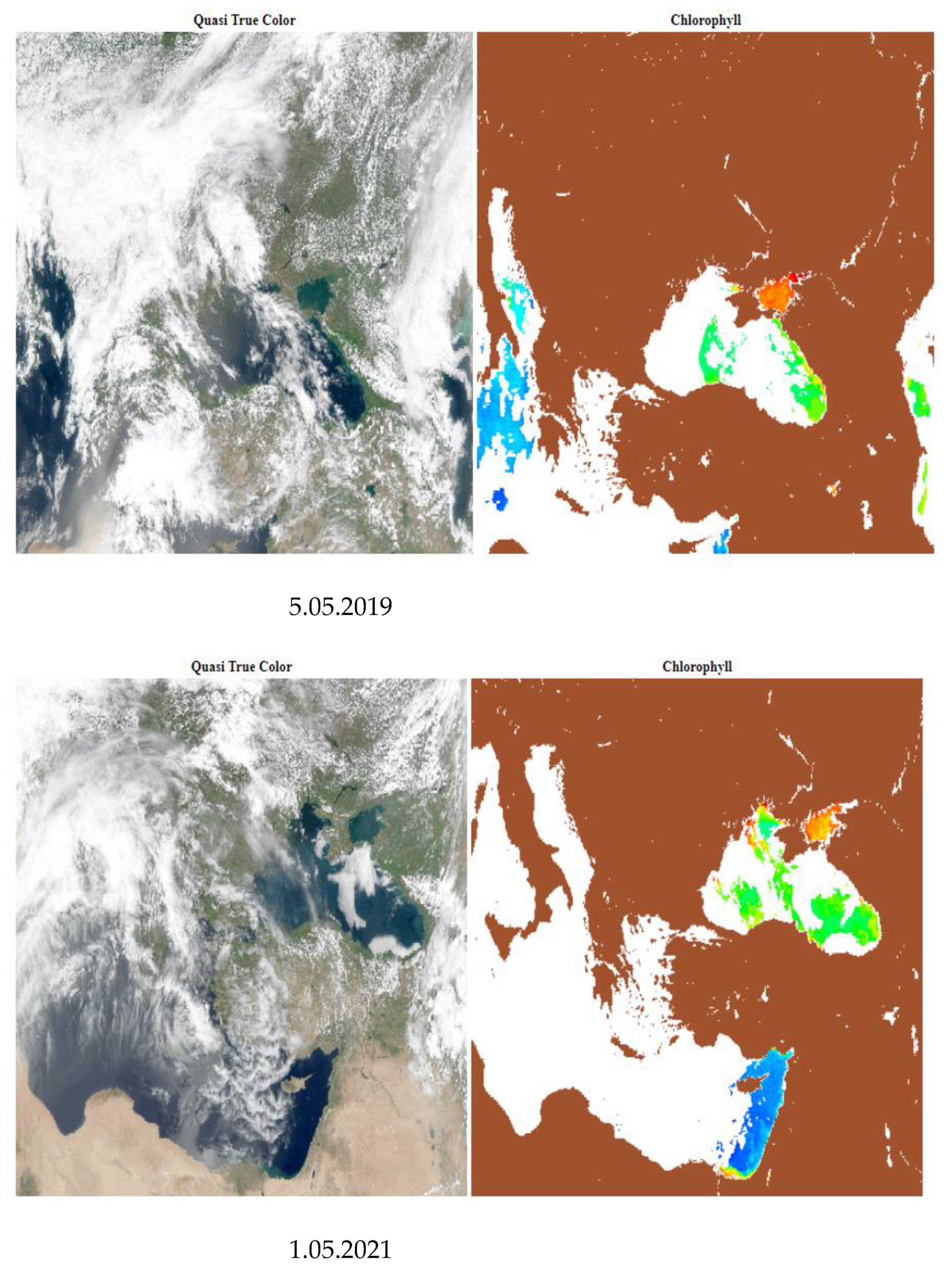
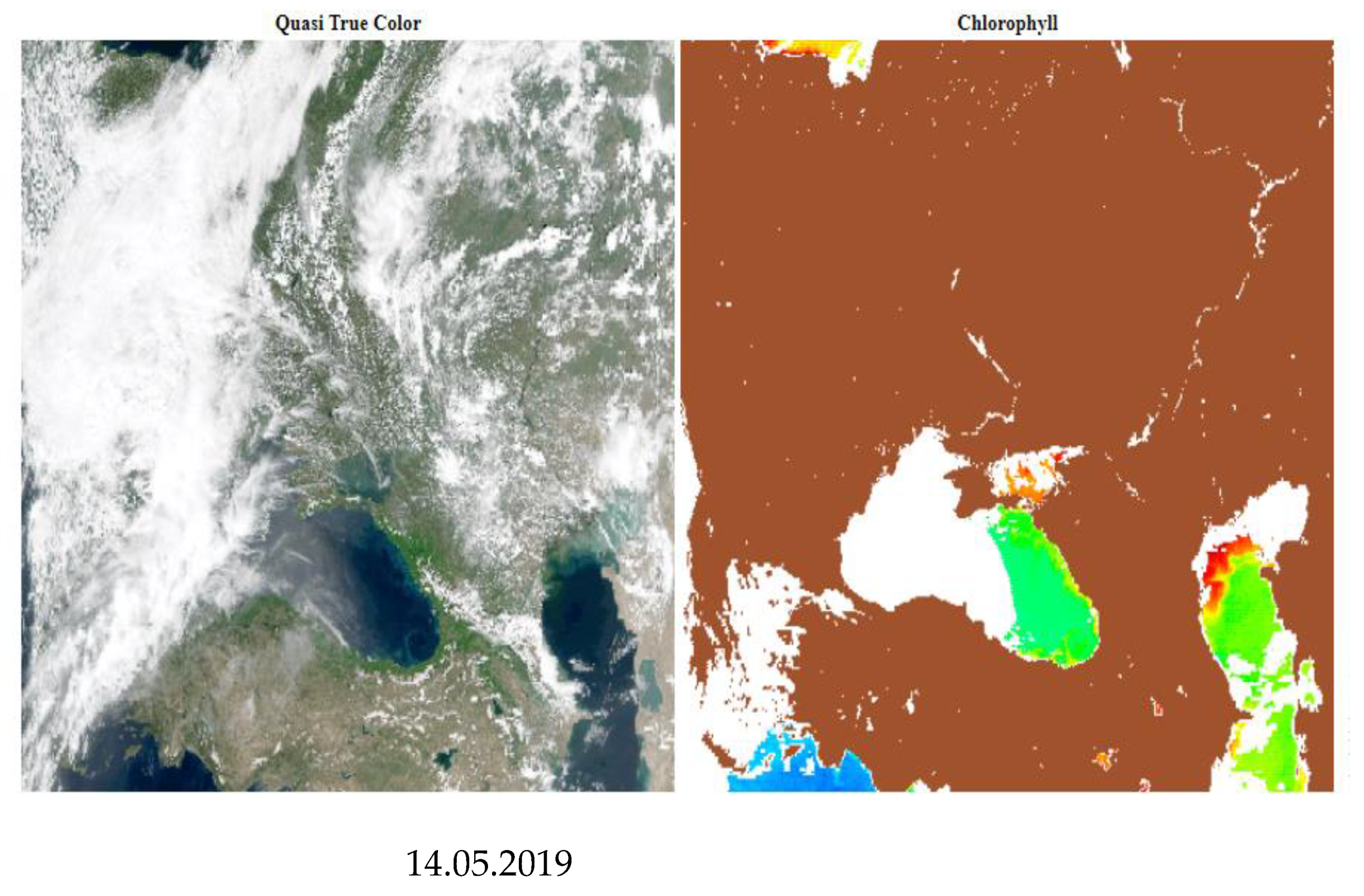
2.3. Satellite Data
2.4. Standard Atmospheric Correction Performance
2.5. Additional Correction
- Starting from two measurements e.g., for MODIS, at 488 and 547 nm, find A and B, using Equations (12) and (13)—arrow 1 in Figure 4;
- Using Equation (11), find and —arrow 2;
- Find and from Equation (8)—arrow 3;
- Find X and Y using Equations (9) and (10);
- Find spectral values —Equation (7) and after that, —Equation (6).
3. Results
3.1. Reflectance In Situ Spectra
3.2. Atmospheric Data
3.3. Comparison of Satellite and In Situ Reflectances
3.4. Comparison of Atmospheric Parameters
3.5. Results of Additional Correction
4. Discussion
4.1. Effect of Additional Correction
4.2. Possible Source of Errors in Additional Correction Algorithm
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Lee, Z.; Marra, J.; Perry, M.J.; Kahru, M. Estimating oceanic primary productivity from ocean color remote sensing: A strategic assessment. J. Mar. Syst. 2015, 149, 50–59. [Google Scholar] [CrossRef]
- Karalli, P.G.; Glukhovets, D.I. Retrieving optical characteristics of the Russian Arctic seas water surface layer from shipboard and satellite data. Mod. Probl. Remote Sens. Earth Space 2020, 17, 191–202. [Google Scholar] [CrossRef]
- Gordon, H.R.; Wang, M. Retrieval of water-leaving radiance and aerosol optical thickness over the oceans with SeaWiFS: A preliminary algorithm. Appl. Opt. 1994, 33, 443–452. [Google Scholar] [CrossRef]
- Ahmad, Z.; Franz, B.; McClain, C.; Kwiatkowska, E.; Werdell, J.; Shettle, E.; Holben, B. New aerosol models for the retrieval of aerosol optical thickness and normalized water-leaving radiances from the SeaWiFS and MODIS sensors over coastal regions and Open Oceans. Appl. Opt. 2010, 49, 5545–5560. [Google Scholar] [CrossRef]
- Wang, M.; Gordon, H.R. A Simple, Moderately Accurate, Atmospheric Correction Algorithm for Seawifs. Remote Sens. Environ. 1994, 50, 231–239. [Google Scholar] [CrossRef]
- Mobley, C.; Werdell, J.; Franz, B.; Ahmad, Z.; Bailey, S. Atmospheric Correction for Satellite Ocean Color Radiometry. Available online: https://oceancolor.gsfc.nasa.gov/docs/technical/NASA-TM-2016-217551.pdf (accessed on 25 December 2021).
- Lee, S.J.; Ahn, M.-H.; Chung, S.-R. Atmospheric Profile Retrieval Algorithm for Next Generation Geostationary Satellite of Korea and Its Application to the Advanced Himawari Imager. Remote Sens. 2017, 9, 1294. [Google Scholar] [CrossRef] [Green Version]
- Moses, W.J.; Sterckx, S.; Montes, M.J.; De Keukelaere, L.; Knaeps, E. Atmospheric correction for inland waters. In Bio-Optical Modeling and Remote Sensing of Inland Waters; Elsevier: Amsterdam, The Netherlands, 2017; pp. 69–100. [Google Scholar] [CrossRef]
- Giardino, C.; Brando, V.E.; Gege, P.C.; Pinnel, N.; Hochberg, E.; Knaeps, E.; Reusen, I.; Doerffer, R.; Bresciani, M.; Braga, F.; et al. Imaging Spectrometry of Inland and Coastal Waters: State of the Art, Achievements and Perspectives. Surv. Geophys. 2019, 40, 401–429. [Google Scholar] [CrossRef] [Green Version]
- Karabashev, G.S.; Evdoshenko, M.A. The wavelength of satellite reflectance maximum as a remote indicator of water exchange between ecologically different aquatic areas. Oceanology 2015, 55, 327–338. [Google Scholar] [CrossRef]
- Afonin, S.V.; Solomatov, D.V. Solution of problems of atmospheric correction of satellite IR measurements accounting for optical-meteorological state of the atmosphere. Atmos. Ocean. Opt. 2008, 21, 125–131. [Google Scholar]
- Santer, R.; Schmechtig, C. Adjacency effects of water surfaces: Primary scattering approximation and sensitivity study. Appl. Opt. 2000, 39, 361–375. [Google Scholar] [CrossRef]
- Wang, T.; Du, L.; Yi, W.; Hong, J.; Zhang, L.; Zheng, J.; Li, C.; Ma, X.; Zhang, D.; Fang, W.; et al. An adaptive atmospheric correction algorithm for the effective adjacency effect correction of submeter-scale spatial resolution optical satellite images: Application to a WorldView-3 panchromatic image. Remote Sens. Environ. 2021, 259, 112412. [Google Scholar] [CrossRef]
- Ueda, S.; Miura, K.; Kawata, R.; Furutani, H.; Uematsu, M.; Omori, Y.; Tanimoto, H. Number–size distribution of aerosol particles and new particle formation events in tropical and subtropical Pacific Oceans. Atmos. Environ. 2016, 142, 324–339. [Google Scholar] [CrossRef] [Green Version]
- Mordas, G.; Plauškaitė, K.; Prokopčiuk, N.; Dudoitis, V.; Bozzetti, C.; Ulevicius, V. Observation of new particle formation on Curonian Spit located between continental Europe and Scandinavia. J. Aerosol Sci. 2016, 97, 38–55. [Google Scholar] [CrossRef]
- Kalinskaya, D.V.; Papkova, A.S. Optical characteristics of atmospheric aerosol from satellite and photometric measurements at the dust transfers dates. In Proceedings of the SPIE 26th International Symposium on Atmospheric and Ocean Optics, Atmospheric Physics, Moskow, Russia, 12 November 2020; p. 115603S. [Google Scholar] [CrossRef]
- Varenik, A.V.; Kalinskaya, D.V. The Effect of Dust Transport on the Concentration of Chlorophyll-A in the Surface Layer of the Black Sea. Appl. Sci. 2021, 11, 4692. [Google Scholar] [CrossRef]
- Zhang, M.; Hu, C.; Barnes, B.B. Performance of POLYMER Atmospheric Correction of Ocean Color Imagery in the Presence of Absorbing Aerosols. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6666–6674. [Google Scholar] [CrossRef]
- Song, Z.; He, X.; Bai, Y.; Wang, D.; Hao, Z.; Gong, F.; Zhu, Q. Changes and Predictions of Vertical Distributions of Global Light-Absorbing Aerosols Based on CALIPSO Observation. Remote Sens. 2020, 12, 3014. [Google Scholar] [CrossRef]
- Kokhanovsky, A.A.; Breon, F.-M.; Cacciari, A.; Carboni, E.; Diner, D.; Di Nicolantio, W.; Grainger, R.G.; Grey, W.M.F.; Höller, R.; Lee, K.-H.; et al. Aerosol remote sensing over land: A comparison of satellite retrievals using different algorithms and instruments. Atmos. Res. 2007, 85, 372394. [Google Scholar] [CrossRef]
- Pokazeev, K.; Sovga, E.; Chaplina, T. General Oceanographic Characteristics of the Black Sea. In Pollution in the Black Sea; Springer Oceanography; Springer: Cham, Switzerland, 2021; pp. 55–63. [Google Scholar] [CrossRef]
- Kopelevich, O.V.; Sahling, I.V.; Vazyulya, S.V.; Glukhovets, D.I.; Sheberstov, S.V.; Burenkov, V.I.; Karalli, P.G.; Yushmanova, A.V. Electronic Atlas. Bio-Optical Characteristics of the Seas, Surrounding the Western Part of Russia, from Data of the Satellite Ocean Color Scanners of 1998–2018. Available online: http://optics.ocean.ru/ (accessed on 25 December 2021).
- Solonenko, M.G.; Mobley, C.D. Inherent optical properties of Jerlov water types. Appl. Opt. 2015, 54, 5392. [Google Scholar] [CrossRef]
- Morel, A.; Prieur, L. Analysis of variations in ocean color. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Yunev, O.; Carstensen, J.; Stelmakh, L.; Belokopytov, V.; Suslin, V. Reconsideration of the phytoplankton seasonality in the open Black Sea. L&O Lett. 2020, 6, 51–59. [Google Scholar] [CrossRef]
- Mobley, C.D. Estimation of the remote sensing reflectance from above–water methods. Appl. Opt. 1999, 38, 7442–7455. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.E.; Shybanov, E.B.; Korchemkina, E.N.; Martynov, O.V. Retrieval of concentrations of seawater natural components from reflectance spectrum. In Proceedings of the SPIE 22nd International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Tomsk, Russia, 29 November 2016; p. 100352Y. [Google Scholar] [CrossRef]
- Coloured Optical Glass. Specifications. Available online: https://docs.cntd.ru/document/1200023782 (accessed on 28 January 2022).
- Mueller, J.L.; Pietras, C.; Hooker, S.B.; Austin, R.W.; Miller, M.; Knobelspiesse, K.D.; Frouin, R.; Holben, B.; Voss, K. Ocean Optics Protocols for Satellite Ocean Color Sensor Validation, Revision 4, Volume II: Instrument Specifications, Characterization and Calibration; NASA’s Goddard Space Flight Center: Greenbelt, MD, USA, 2003; pp. 1–63. [CrossRef]
- Karalli, P.G.; Kopelevich, O.V.; Sahling, I.V.; Sheberstov, S.V.; Pautova, L.V.; Silkin, V.A. Validation of remote sensing estimates of coccolitophore bloom parameters in the Barents Sea from field measurements. Fundam. Apll. Hydrophys. 2018, 11, 55–63. [Google Scholar] [CrossRef]
- Korchemkina, E.N.; Mankovskaya, E.V. Bio-optical properties of Black Sea waters during coccolithophore bloom in July 2017. In Proceedings of the SPIE 25th International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Novosibirsk, Russia, 18 December 2019; p. 1120851. [Google Scholar] [CrossRef]
- Sakerin, S.M.; Kabanov, D.M.; Rostov, A.P.; Turchinovich, S.A.; Knyazev, V.V. Sun photometers for measuring spectral air transparency in stationary and mobile conditions. Atmos. Ocean. Opt. 2013, 26, 352–356. [Google Scholar] [CrossRef]
- Kabanov, D.M.; Veretennikov, V.V.; Voronina, Y.V.; Sakerin, S.M.; Turchinovich, Y.S. Information system for network solar photometers. Atmos. Ocean. Opt. 2009, 22, 121–127. [Google Scholar] [CrossRef]
- Firsov, K.M.; Bobrov, E.V. Restoring the aerosol optical depth by ground measurements of SPM photometer. Math. Phys. Comput. Modeling 2014, 2, 57–65. [Google Scholar] [CrossRef]
- Kalinskaya, D.V.; Kabanov, D.M.; Latushkin, A.A.; Sakerin, S.M. Atmospheric aerosol optical depth measurements in the Black sea region (2015–2016). Opt. Atmos. Okeana 2017, 30, 489–496, In Russian. [Google Scholar] [CrossRef]
- O’Neill, N.T.; Dubovik, O.; Eck, T.F. A modified Angstrom coefficient for the characterization of sub-micron aerosols. Appl. Opt. 2001, 40, 2368–2375. [Google Scholar] [CrossRef] [PubMed]
- O’Neill, N.T.; Eck, T.F.; Smirnov, A.; Holben, B.N.; Thulasiraman, S. Spectral discrimination of coarse and fine mode optical depth. J. Geophys. Res. 2003, 108, 4559–4573. [Google Scholar] [CrossRef]
- Oceancolor Web. Available online: https://oceancolor.gsfc.nasa.gov/ (accessed on 23 December 2021).
- Copernicus Online Data Access. Available online: https://coda.eumetsat.int (accessed on 23 December 2021).
- Korchemkina, E.N.; Shybanov, E.B.; Lee, M.E. Improved method of remote sensing retrieval of sea water admixtures concentrations. In Proceedings of the IV International Conference «Current Problems in Optics of Natural Waters», Nizhny Novgorod, Russia, 11–15 September 2007; pp. 171–174. [Google Scholar]
- Maritorena, S.; Siegel, D.A.; Peterson, A.R. Optimization of a semianalytical ocean color model for global-scale applications. Appl. Opt. 2002, 41, 2705. [Google Scholar] [CrossRef]
- Smith, R.C.; Baker, K.S. Optical properties of the clearest natural waters (200–800 nm). Appl. Opt. 1981, 20, 177–184. [Google Scholar] [CrossRef]
- Churilova, T.; Moiseeva, N.; Efimova, T.; Suslin, V.; Krivenko, O.; Zemlianskaia, E. Annual variability in light absorption by particles and colored dissolved organic matter in coastal waters of Crimea (the Black Sea). In Proceedings of the SPIE 23rd International Symposium on Atmospheric and Ocean Optics: Atmospheric Physics, Irkutsk, Russia, 30 November 2017; p. 104664B. [Google Scholar] [CrossRef]
- Churilova, T.; Suslin, V.; Krivenko, O.; Efimova, T.; Moiseeva, N.; Mukhanov, V.; Smirnova, L. Light Absorption by Phytoplankton in the Upper Mixed Layer of the Black Sea: Seasonality and Parametrization. Front. Mar. Sci. 2017, 4, 90. [Google Scholar] [CrossRef] [Green Version]
- Kalinskaya, D.V.; Papkova, A.S.; Kabanov, D.M. Research of the Aerosol Optical and Microphysical Characteristics of the Atmosphere over the Black Sea Region by the FIRMS System during the Forest Fires in 2018–2019. Phys. Oceanogr. 2020, 27, 514–524. [Google Scholar] [CrossRef]
- Pacпиcaниe пoгoды [Weather Schedule]. Available online: https://rp5.ru (accessed on 23 December 2021).
- Mishra, S.; Mishra, D.R. Normalized difference chlorophyll index: A novel model for remote estimation of chlorophyll-a concentration in turbid productive waters. Remote Sens. Environ. 2012, 117, 394–406. [Google Scholar] [CrossRef]





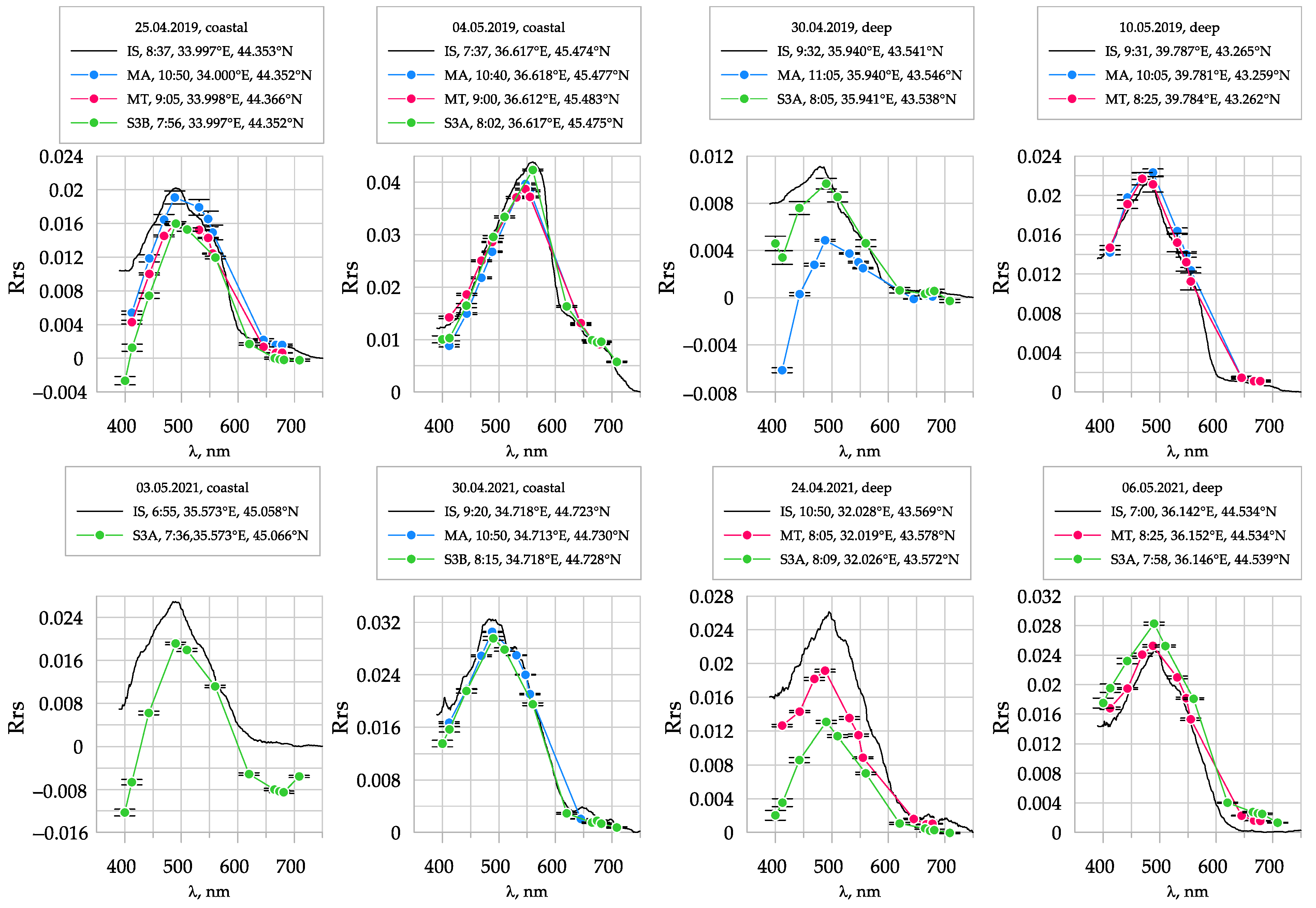
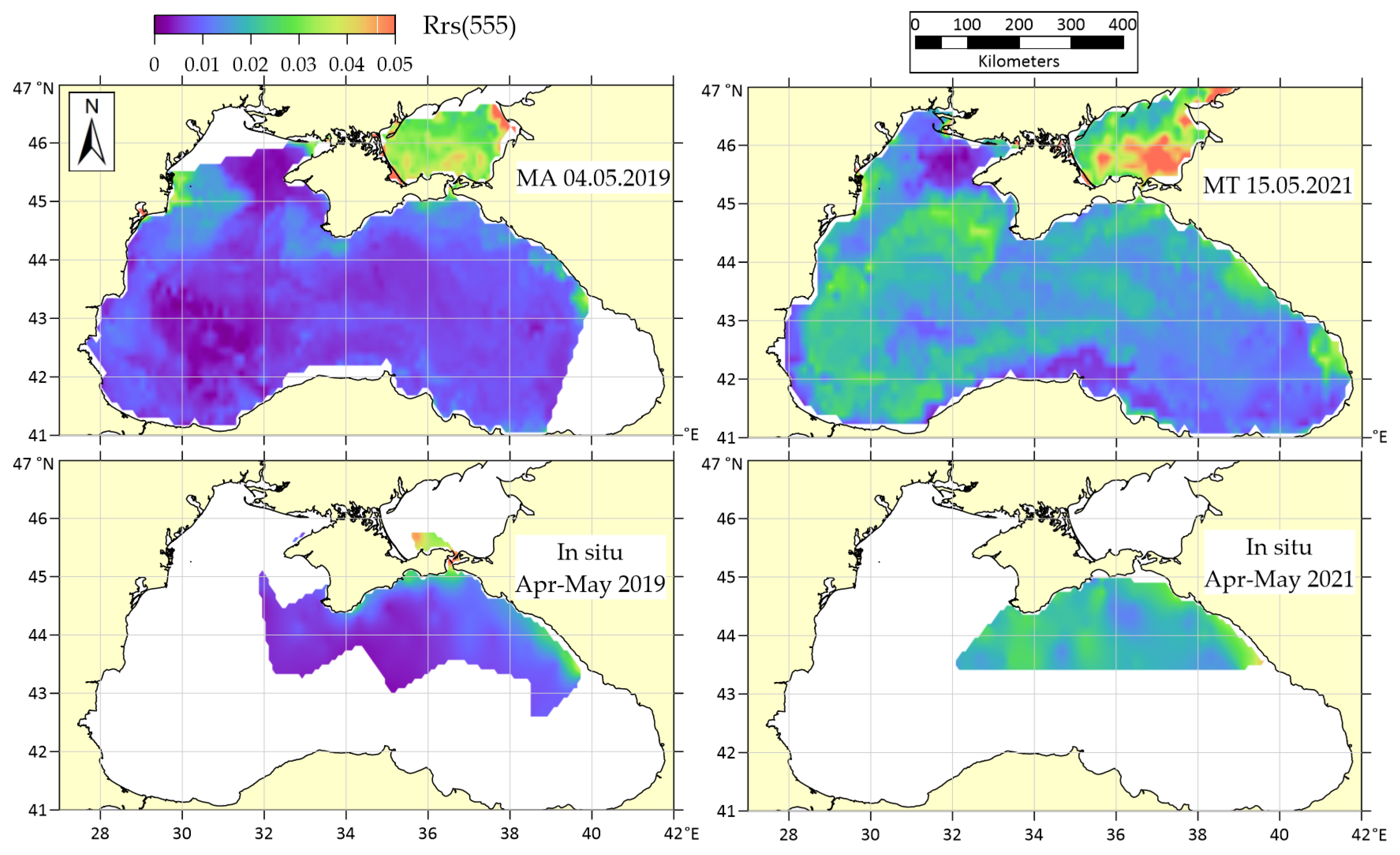

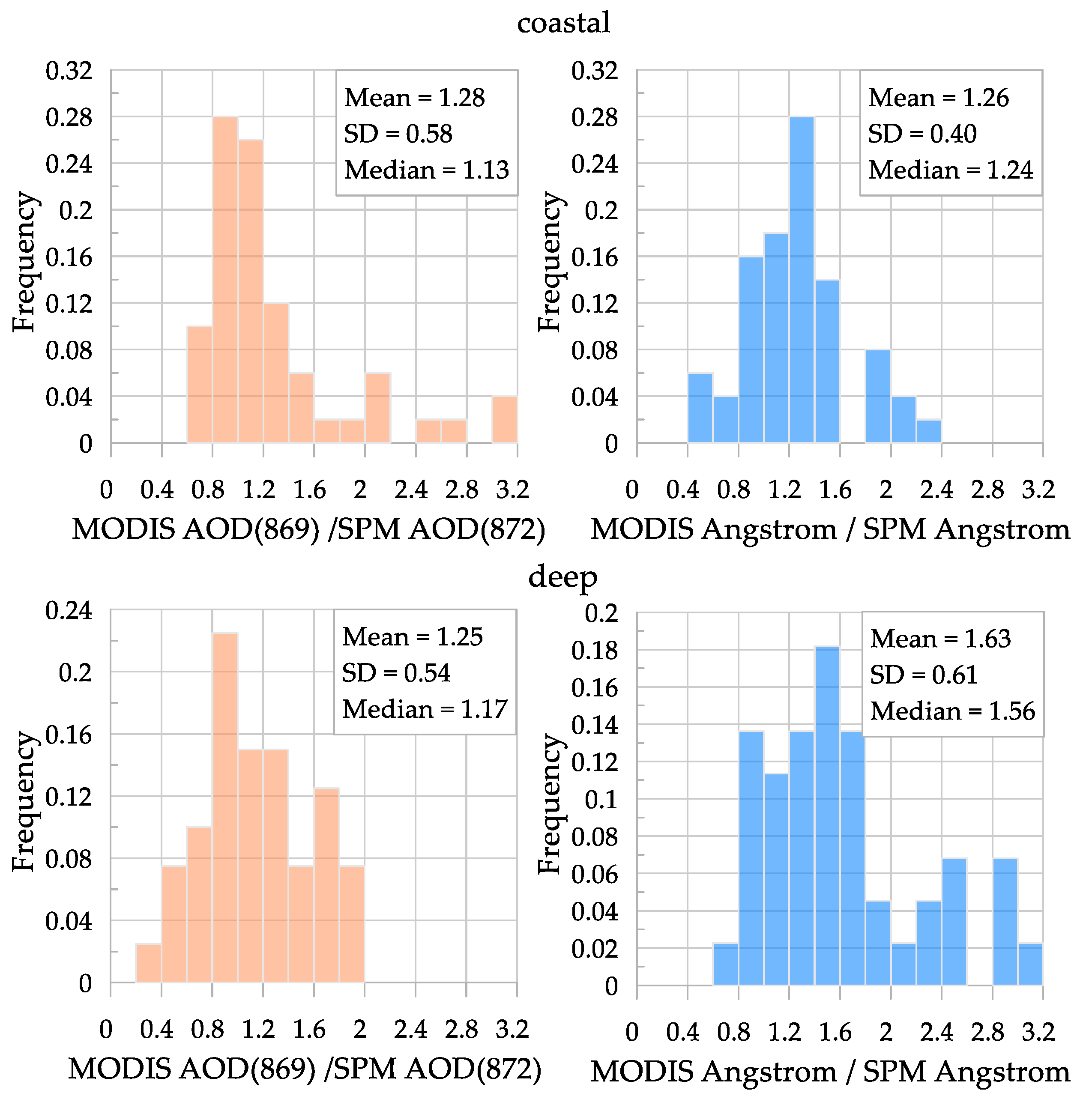
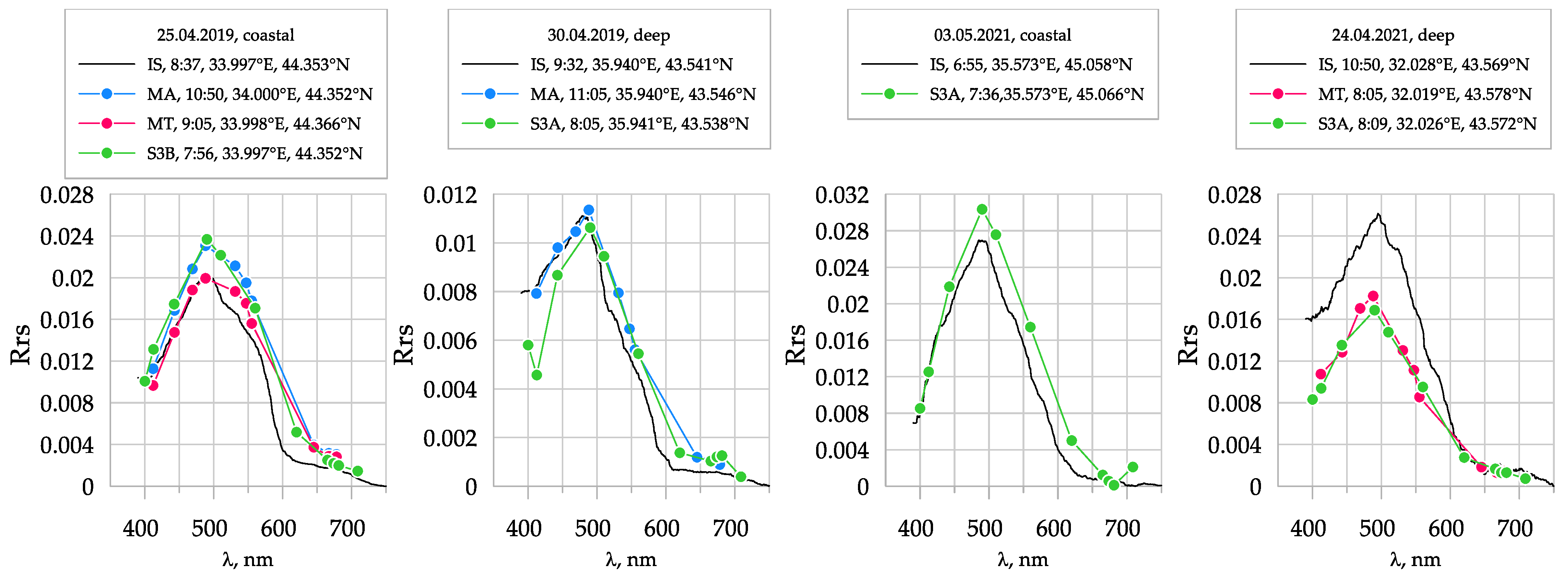


| 106th Cruise, 2019 | 116th Cruise, 2021 | |||||
|---|---|---|---|---|---|---|
| Region | N | Rrsmax | λmax, nm | N | ρmax | λmax, nm |
| Deep central part | 56 | 0.012 ± 0.004 | 483 ± 7 | 53 | 0.032 ± 0.005 | 491 ± 6 |
| North-western shelf | 8 | 0.011 ± 0.004 | 489 ± 2 | - | - | - |
| Crimean shore | 20 | 0.021 ± 0.009 | 491 ± 6 | 25 | 0.033 ± 0.008 | 492 ± 5 |
| Caucasian shore | 7 | 0.039 ± 0.009 | 486 ± 6 | 7 | 0.040 ± 0.005 | 496 ± 12 |
| The Kerch Strait + the Azov Sea. | 13 | 0.037±0.006 | 557 ± 4 | - | - | - |
| MODIS Aqua | MODIS Terra | SPM | |||||
|---|---|---|---|---|---|---|---|
| α | α | α | |||||
| 2019 | Mean | 0.096 | 1.47 | 0.088 | 1.36 | 0.075 | 1.15 |
| SD | 0.051 | 0.34 | 0.051 | 0.40 | 0.030 | 0.33 | |
| Median | 0.091 | 1.56 | 0.068 | 1.43 | 0.071 | 1.20 | |
| 2021 | Mean | 0.106 | 1.49 | 0.093 | 1.50 | 0.094 | 1.07 |
| SD | 0.053 | 0.41 | 0.047 | 0.34 | 0.057 | 0.28 | |
| Median | 0.102 | 1.61 | 0.076 | 1.52 | 0.071 | 1.11 | |
| Cruise | 106th Cruise, 2019 | 116th Cruise, 2021 | ||
|---|---|---|---|---|
| Stations | Coastal | Deep-Sea | Coastal | Deep-Sea |
| MODIS A/T | 20 | 29 | 9 | 18 |
| OLCI S3A/B | 16 | 17 | 20 | 26 |
| Model | 3-Parametric | 2-Parametric | ||
|---|---|---|---|---|
| S = 0.017 nm–1 | S = 0.009 nm–1 | S = 0.012 nm–1 | S = 0.018 nm–1 | |
| Band, nm | ||||
| 400 | 6.1 | 14.1 | 16.1 | 21.1 |
| 412 | 4.7 | 15.8 | 20.3 | 32.7 |
| 678 | 84.1 | 85.0 | 87.3 | 88.7 |
| 709 | 119.8 | 118.6 | 119.5 | 119.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Korchemkina, E.N.; Kalinskaya, D.V. Algorithm of Additional Correction of Level 2 Remote Sensing Reflectance Data Using Modelling of the Optical Properties of the Black Sea Waters. Remote Sens. 2022, 14, 831. https://doi.org/10.3390/rs14040831
Korchemkina EN, Kalinskaya DV. Algorithm of Additional Correction of Level 2 Remote Sensing Reflectance Data Using Modelling of the Optical Properties of the Black Sea Waters. Remote Sensing. 2022; 14(4):831. https://doi.org/10.3390/rs14040831
Chicago/Turabian StyleKorchemkina, Elena N., and Daria V. Kalinskaya. 2022. "Algorithm of Additional Correction of Level 2 Remote Sensing Reflectance Data Using Modelling of the Optical Properties of the Black Sea Waters" Remote Sensing 14, no. 4: 831. https://doi.org/10.3390/rs14040831
APA StyleKorchemkina, E. N., & Kalinskaya, D. V. (2022). Algorithm of Additional Correction of Level 2 Remote Sensing Reflectance Data Using Modelling of the Optical Properties of the Black Sea Waters. Remote Sensing, 14(4), 831. https://doi.org/10.3390/rs14040831






