Asymmetric Interseismic Strain across the Western Altyn Tagh Fault from InSAR
Abstract
:1. Introduction
2. Data and Methods
2.1. GPS Data
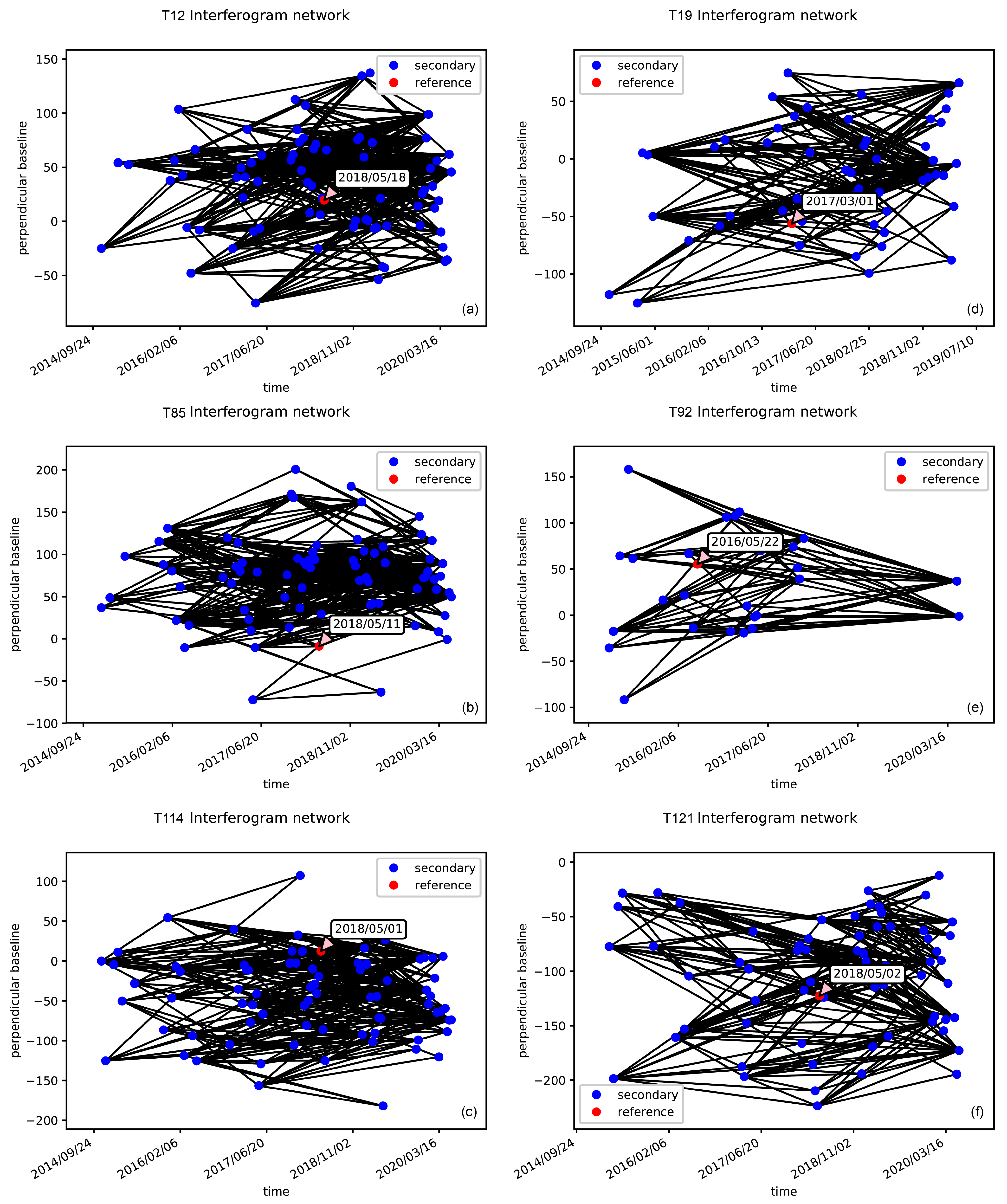
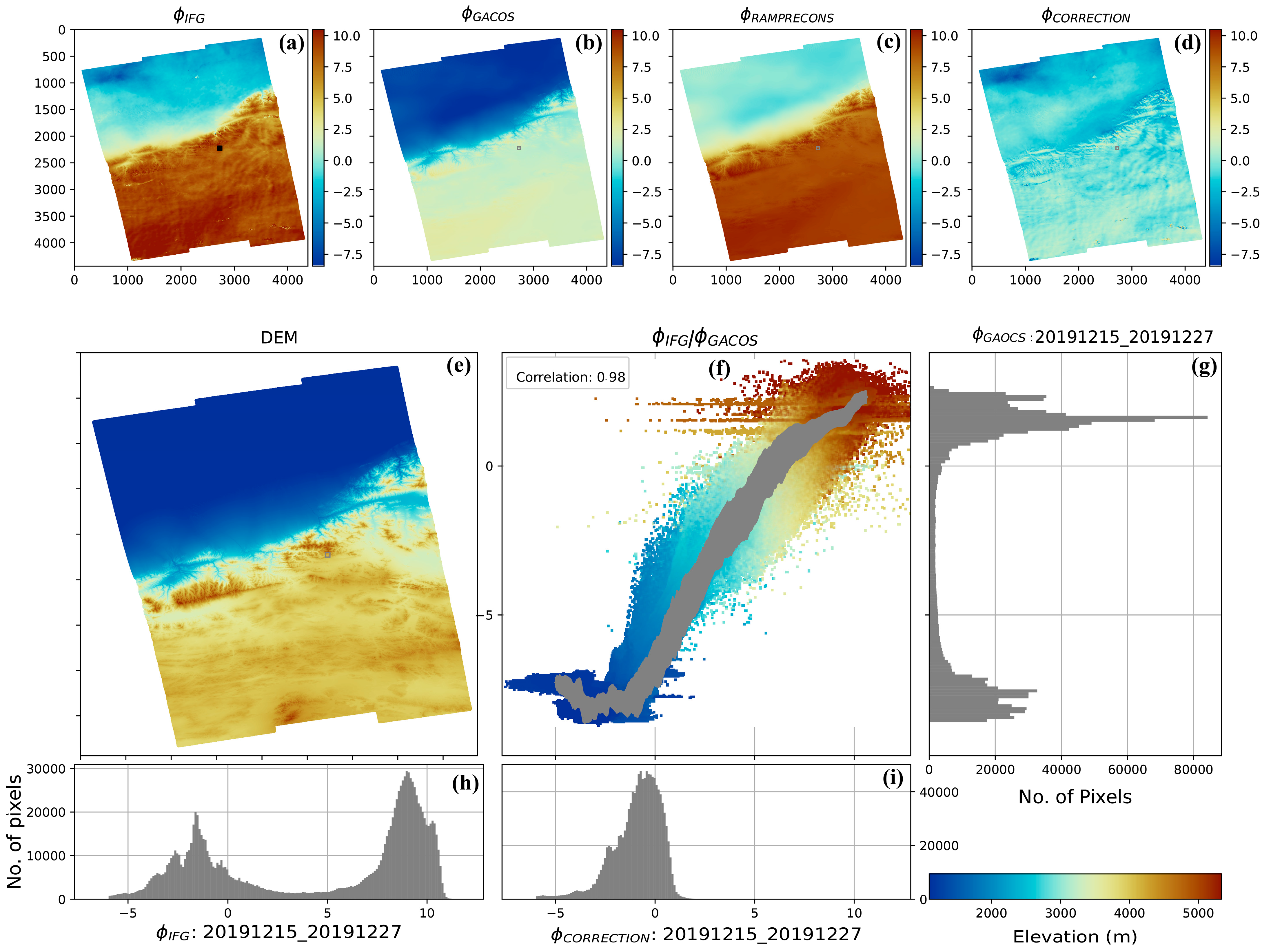
2.2. InSAR Data and Processing
3. Results
3.1. InSAR LOS Velocity Field
3.2. ATF-Parallel and Vertical Surface Velocities
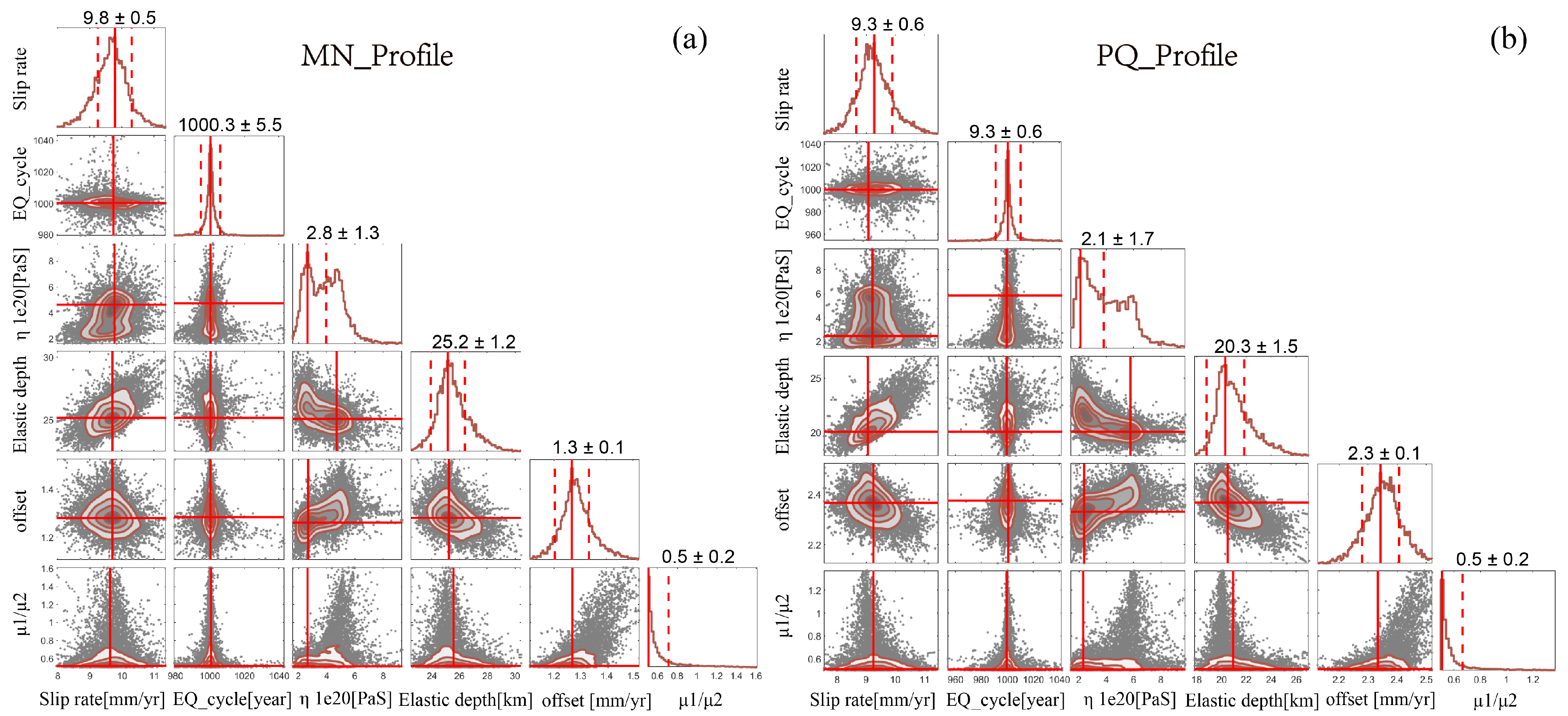
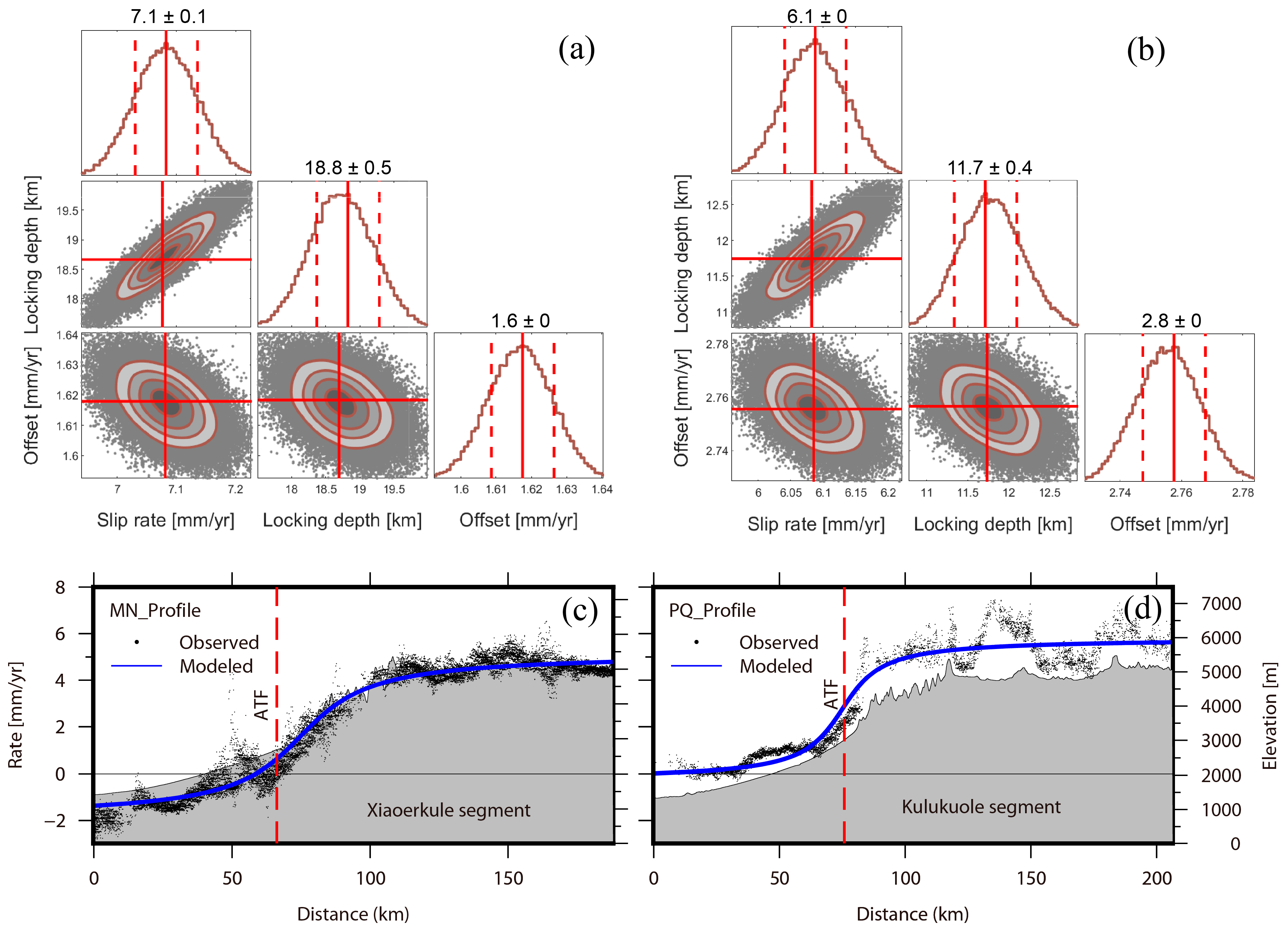
3.3. Locking Depth and Slip Rate
4. Discussion
4.1. Strain Asymmetry
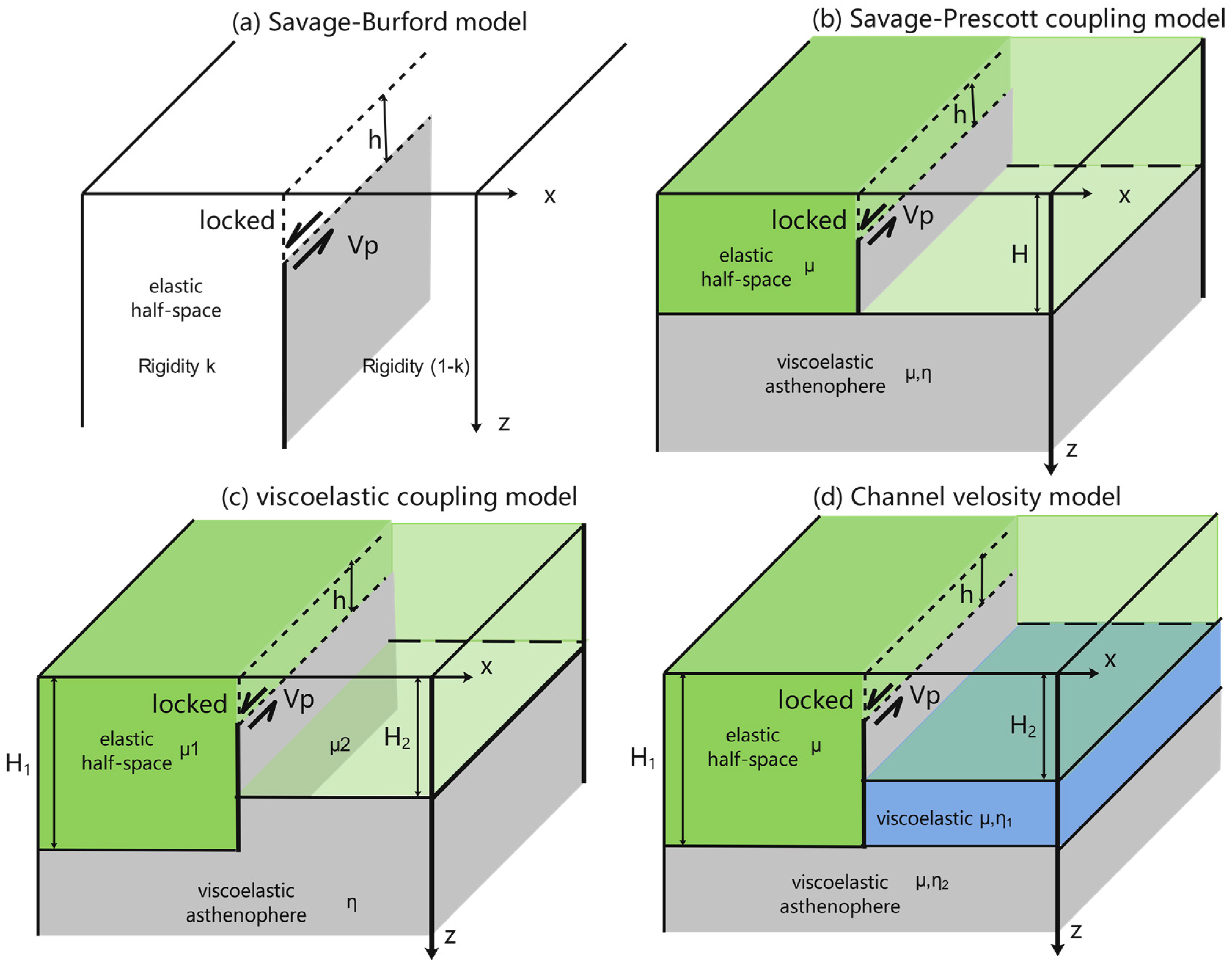
4.1.1. Modified Half-Space Model
4.1.2. Viscoelastic-Coupling Models
4.1.3. Three-Layer Model
4.1.4. Summary
4.2. Interseismic Slip Rate
5. Conclusions
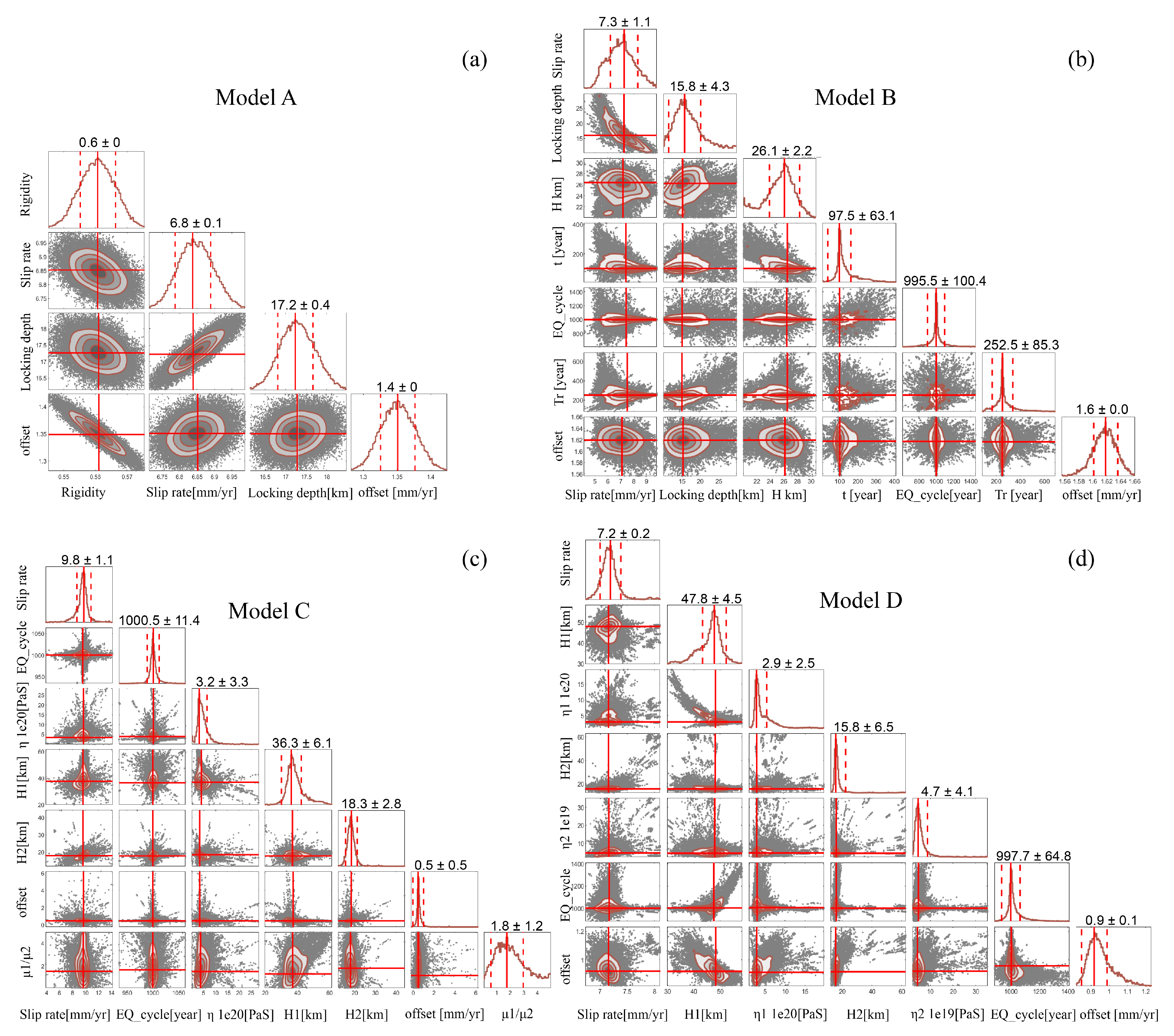
- Different models are used to invert the fault slip rate and locking depth of the western segment of ATF. In the viscoelastic model, the media on both sides of the fault are divided into the elastic upper crust, viscoelastic lower crust, and upper mantle, and stratified lateral inhomogeneity parameters are considered. From the west to east section, the inferred sinistral strike-slip rate of the ATF is 9.8 ± 1.1 mm/yr and 8.6 ± 1.1 mm/yr, respectively, and the locking depth is 15.8 ± 4.3 km and 14.8 ± 4.9 km respectively. Based on the elastic model fitting, the left-lateral strike-slip rates of the ATF are 7.1 ± 0.1 mm/yr and 6.1 ± 0 mm/yr, respectively, and the locking depths are 18.1 ± 0.6 km and 11.7 ± 0.4 km, respectively. The results show that ignoring the viscoelastic effect will significantly affect the estimation of fault slip rate and locking degree;
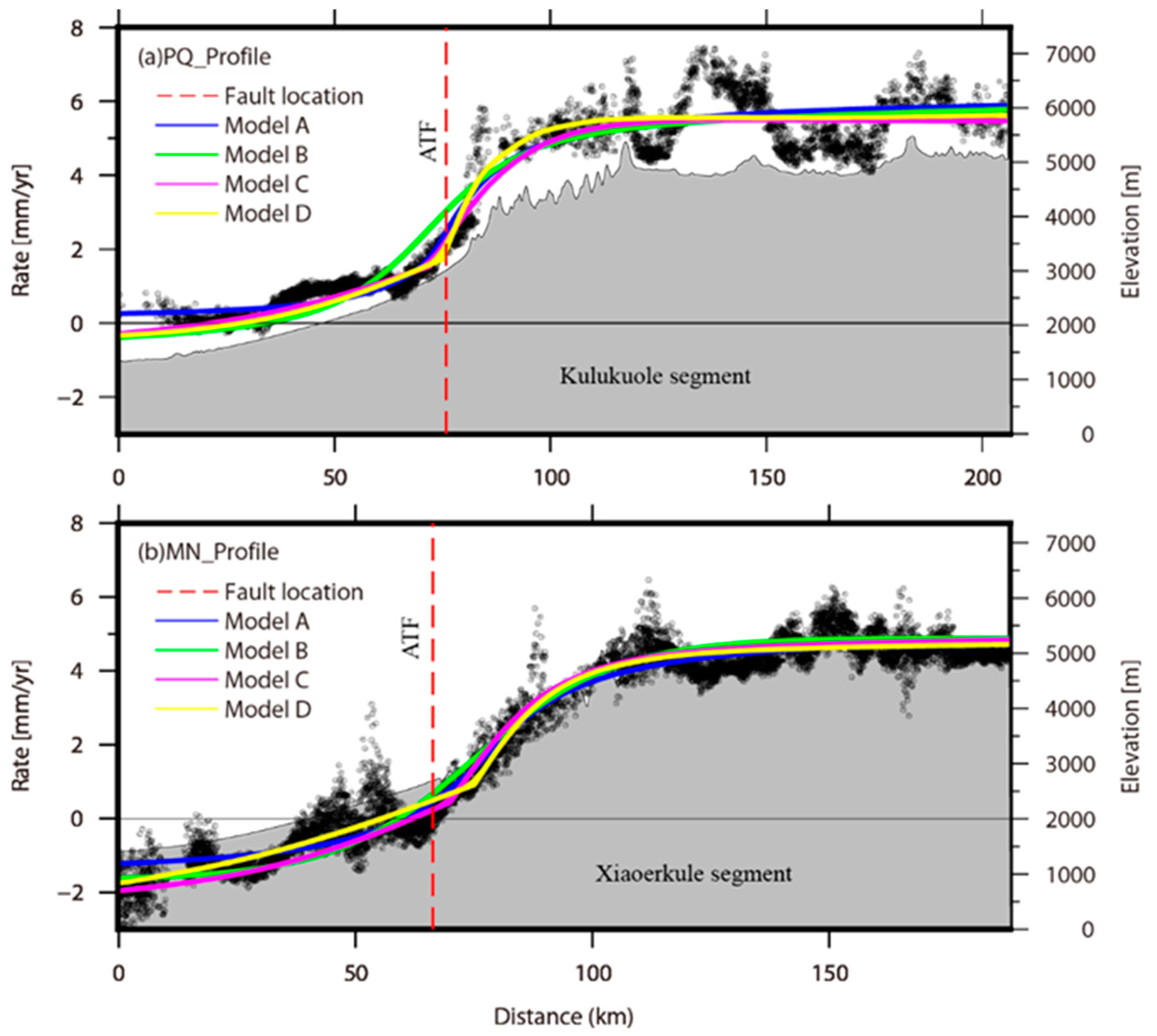
- The decomposition of the ascending and descending LOS velocities into fault parallel and vertical components in this paper shows that although the ATF is mainly strike-slip, it is accompanied by a small amount of thrust, and the thrust component gradually increases from west to east, reaching 1 mm/yr in the Altyn Mountains. If the vertical deformation of InSAR data is ignored, it may bias the interpretation of crustal deformation. Constrained by the fault parallel velocity field from west to east, the sinistral strike-slip rates of the ATF obtained in this paper are 9.8 ± 1.1 mm/yr and 8.6 ± 1.1 mm/yr, respectively, in line with the characteristics that the ATF is in low slip rates and decreases gradually from west to east which is obtained by GPS inversion;
- The velocity profile across the ATF shows that there is asymmetry across the fault. The results integrate the combined test results of different parameters of Models B and C and the previous research results on the thickness of the elastic layer around the TP; we believe that the difference between elastic layer thickness and shear modulus on both sides of the fault jointly causes the asymmetry of interseismic velocity.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| Parameter | Minimum | Maximum | Priori Value |
|---|---|---|---|
| Fault slip rate (mm/yr) | −20 | 20 | 10 |
| Locking depth (km) | 0 | 35 | 18 |
| Velocity offset (mm/yr) | 0 | 15 | 3 |
| Recurrence interval (years) | 800 | 1500 | 1000 |
| Time since last earthquake (years) | 100 | 100 | 100 |
| Elastic thickness of FNE, H1 (km) | 10 | 65 | 35 |
| Elastic thickness of FSW, H2 (km) | 10 | 65 | 20 |
| Viscosity η | 1016 | 1022 | 1019 |
| Viscoelastic lower crust η2 | 1016 | 1022 | 1019 |
| Rigidity ratio, μ1/μ2 | 0 | 5 | 2 |
References
- Molnar, P.; Burchfiel, B.C.; K’uangyi, L.; Ziyun, Z. Geomorphic Evidence for Active Faulting in the Altyn Tagh and Northern Tibet and Qualitative Estimates of Its Contribution to the Convergence of India and Eurasia. Geology 1987, 15, 249–253. [Google Scholar] [CrossRef]
- Tapponnier, P.; Xu, Z.Q.; Roger, F.; Meyer, B.; Arnaud, N.; Wittlinger, G.; Yang, J.S. Oblique Stepwise Rise and Growth of the Tibet Plateau. Science 2001, 294, 1671–1677. [Google Scholar] [CrossRef] [PubMed]
- Cowgill, E.; Arrowsmith, J.R.; Yin, A.; Wang, X.; Chen, Z. The Akato Tagh Bend along the Altyn Tagh Fault, Northwest Tibet 2: Active Deformation and the Importance of Transpression and Strain Hardening within the Altyn Tagh System. Bull. Geol. Soc. Am. 2004, 116, 1443–1464. [Google Scholar] [CrossRef] [Green Version]
- Yin, A.; Rumelhart, P.E.; Butler, R.; Cowgill, E.; Harrison, T.M.; Foster, D.A.; Ingersoll, R.V.; Zhang, Q.; Zhou, X.Q.; Wang, X.F.; et al. Tectonic History of the Altyn Tagh Fault System in Northern Tibet Inferred from Cenozoic Sedimentation. Geol. Soc. Am. Bull. 2002, 114, 1257–1295. [Google Scholar] [CrossRef]
- Cowgill, E.S. Tectonic Evolution of the Altyn Tagh Western Kunlun Fault System, Northwestern China. Ph.D. Dissertation, University of California, Los Angeles, CA, USA, 2001. [Google Scholar]
- Mériaux, A.S.; Ryerson, F.J.; Tapponnier, P.; Van der Woerd, J.; Finkel, R.C.; Xu, X.; Xu, Z.; Caffee, M.W. Rapid Slip along the Central Altyn Tagh Fault: Morphochronologic Evidence from Cherchen He and Sulamu Tagh. J. Geophys. Res. Solid Earth 2004, 109, 1–23. [Google Scholar] [CrossRef]
- Gold, R.D.; Cowgill, E.; Arrowsmith, J.R.; Chen, X.; Sharp, W.D.; Cooper, K.M.; Wang, X.F. Faulted Terrace Risers Place New Constraints on the Late Quaternary Slip Rate for the Central Altyn Tagh Fault, Northwest Tibet. Bull. Geol. Soc. Am. 2011, 123, 958–978. [Google Scholar] [CrossRef]
- Zheng, W.J.; Zhang, P.Z.; Ge, W.P.; Molnar, P.; Zhang, H.; Yuan, D.Y.; Liu, J. Late Quaternary Slip Rate of the South Heli Shan Fault (Northern Hexi Corridor, NW China) and Its Implications for Northeastward Growth of the Tibetan Plateau. Tectonics 2013, 32, 271–293. [Google Scholar] [CrossRef]
- Avouac, J.-P.; Tapponnier, P. Kinematic Model of Active Deformation in Central Asia. Geophys. Res. Lett. 1993, 20, 895–898. [Google Scholar] [CrossRef] [Green Version]
- Peltzer, G.; Tapponnier, P. Formation and Evolution of Strike-Slip Faults, Rifts, and Basins during the India-Asia Collision: An Experimental Approach. J. Geophys. Res. Solid Earth 1988, 93, 15085–15117. [Google Scholar] [CrossRef]
- Royden, L.H.; Burchfiel, B.C.; King, R.W.; Wang, E.; Chen, Z.; Shen, F.; Liu, Y. Surface Deformation and Lower Crustal Flow in Eastern Tibet. Science 1997, 276, 788–790. [Google Scholar] [CrossRef]
- England, P.; Molnar, P. The Field of Crustal Velocity in Asia Calculated from Quaternary Rates of Slip on Faults. Geophys. J. Int. 1997, 130, 551–582. [Google Scholar] [CrossRef]
- Molnar, P.; Stock, J.M. Slowing of India’s Convergence with Eurasia since 20 Ma and Its Implications for Tibetan Mantle Dynamics. Tectonics 2009, 28, TC3001. [Google Scholar] [CrossRef]
- Cowgill, E.; Yin, A.; Harrison, T.M.; Wang, X.-F. Reconstruction of the Altyn Tagh Fault Based on U-Pb Geochronology: Role of Back Thrusts, Mantle Sutures, and Heterogeneous Crustal Strength in Forming the Tibetan Plateau. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A New Algorithm for Surface Deformation Monitoring Based on Small Baseline Differential SAR Interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef] [Green Version]
- Doin, M.-P.; Lodge, F.; Guillaso, S.; Jolivet, R.; Lasserre, C.; Ducret, G.; Grandin, R.; Pathier, E.; Pinel, V. Presentation of the Small Baseline NSBAS Processing Chain on a Case Example: The Etna Deformation Monitoring from 2003 to 2010 Using Envisat Data. In Proceedings of the ESA’Fringe 2011 Work, Frascati, Italy, 19–23 September 2011; pp. 19–23. [Google Scholar]
- Wang, C.; Wang, X.S.; Xu, Y.; Zhang, B.; Jiang, M.; Xiong, S.; Zhang, Q.; Li, W.; Li, Q. A new likelihood function for consistent phase series estimation in distributed scatterer interferometry. IEEE Trans. Geosci. Remote Sens. 2022. [Google Scholar] [CrossRef]
- López-Quiroz, P.; Doin, M.P.; Tupin, F.; Briole, P.; Nicolas, J.M. Time Series Analysis of Mexico City Subsidence Constrained by Radar Interferometry. J. Appl. Geophys. 2009, 69, 1–15. [Google Scholar] [CrossRef]
- Wright, T.J.; Parsons, B.; England, P.C.; Fielding, E.J. InSAR Observations of Low Slip Rates on the Major Faults of Western Tibet. Science 2004, 305, 236–239. [Google Scholar] [CrossRef] [Green Version]
- Elliott, J.R.; Biggs, J.; Parsons, B.; Wright, T.J. InSAR Slip Rate Determination on the Altyn Tagh Fault, Northern Tibet, in the Presence of Topographically Correlated Atmospheric Delays. Geophys. Res. Lett. 2008, 35, L12309. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Xu, C.J.; Wen, Y.M.; Liu, Y. Interseismic Deformation of the Altyn Tagh Fault Determined by Interferometric Synthetic Aperture Radar (InSAR) Measurements. Remote Sens. 2016, 8, 233. [Google Scholar] [CrossRef] [Green Version]
- Jolivet, R.; Cattin, R.; Chamot-Rooke, N.; Lasserre, C.; Peltzer, G. Thin-Plate Modeling of Interseismic Deformation and Asymmetry across the Altyn Tagh Fault Zone. Geophys. Res. Lett. 2008, 35, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.C.; Nocquet, J.-M.; Shan, X.J. Crustal Deformation across the Western Altyn Tagh Fault (86°E) from GPS and InSAR. Geophys. J. Int. 2021, 228, 1361–1372. [Google Scholar] [CrossRef]
- De Zan, F.; Guarnieri, A.M. TOPSAR: Terrain Observation by Progressive Scans. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2352–2360. [Google Scholar] [CrossRef]
- Grandin, R. Interferometric Processing of SLC Sentinel-1 TOPS Data. In Proceedings of the 2015 ESA Fringe Workshop, Frascati, Italy, 23–27 March 2015; Volume SP-731, pp. 1–14. [Google Scholar] [CrossRef] [Green Version]
- Prats-Iraola, P.; Scheiber, R.; Marotti, L.; Wollstadt, S.; Reigber, A. TOPS Interferometry with TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3179–3188. [Google Scholar] [CrossRef] [Green Version]
- Geudtner, D.; Torres, R.; Snoeij, P.; Davidson, M.; Rommen, B. Sentinel-1 System Capabilities and Applications. In Proceedings of the 2014 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Quebec City, QC, Canada, 13–18 July 2014; pp. 1457–1460. [Google Scholar] [CrossRef]
- Yague-Martinez, N.; Prats-Iraola, P.; Gonzalez, F.R.; Brcic, R.; Shau, R.; Geudtner, D.; Eineder, M.; Bamler, R. Interferometric Processing of Sentinel-1 TOPS Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2220–2234. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.S.; Jiang, W.L.; Zhang, J.; Li, B.; Yan, R.; Wang, X. Sentinel-1 SAR-Based Coseismic Deformation Monitoring Service for Rapid Geodetic Imaging of Global Earthquakes. Nat. Hazards Res. 2021, 1, 11–19. [Google Scholar] [CrossRef]
- He, J.K.; Vernant, P.; Chéry, J.; Wang, W.; Lu, S.; Ku, W.; Xia, W.; Bilham, R. Nailing down the Slip Rate of the Altyn Tagh Fault. Geophys. Res. Lett. 2013, 40, 5382–5386. [Google Scholar] [CrossRef]
- Li, Y.C.; Shan, X.J.; Qu, C.Y.; Liu, Y.H.; Han, N.N. Crustal Deformation of the Altyn Tagh Fault Based on GPS. J. Geophys. Res. Solid Earth 2018, 123, 10309–10322. [Google Scholar] [CrossRef]
- Wang, M.; Shen, Z.K. Present-Day Crustal Deformation of Continental China Derived from GPS and Its Tectonic Implications. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018774. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Qiao, X.; Yang, S.; Wang, D. Present-Day Velocity Field and Block Kinematics of Tibetan Plateau from GPS Measurements. Geophys. J. Int. 2017, 208, 1088–1102. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Chou, T.A.; Woodhouse, J.H. Determination of Earthquake Source Parameters from Waveform Data for Studies of Global and Regional Seismicity. J. Geophys. Res. 1981, 86, 2825–2852. [Google Scholar] [CrossRef]
- Werner, C.; Wegmller, U.; Strozzi, T.; Wiesmann, A. GAMMA SAR and Interferometric Processing Software. In Proceedings of the ERS-Envisat Symposium, Gothenburg, Sweden, 16–20 October 2000; pp. 211–219. [Google Scholar]
- Qin, Y.; Perissin, D.; Bai, J. Investigations on the Coregistration of Sentinel-1 TOPS with the Conventional Cross-Correlation Technique. Remote Sens. 2018, 10, 1405. [Google Scholar] [CrossRef] [Green Version]
- Yague-Martinez, N.; De Zan, F.; Prats-Iraola, P. Coregistration of Interferometric Stacks of Sentinel-1 TOPS Data. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1002–1006. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.Y.; Li, Y.S.; Zhang, J.F.; Luo, Y. InSAR Technique Applied to the Monitoring of the Qinghai-Tibet Railway. Nat. Hazards Earth Syst. Sci. 2019, 19, 2229–2240. [Google Scholar] [CrossRef] [Green Version]
- Garthwaite, M.C.; Wang, H.; Wright, T.J. Broadscale Interseismic Deformation and Fault Slip Rates in the Central Tibetan Plateau Observed Using InSAR. J. Geophys. Res. Solid Earth 2013, 118, 5071–5083. [Google Scholar] [CrossRef]
- Daout, S.; Doin, M.P.; Peltzer, G.; Socquet, A.; Lasserre, C. Large-Scale InSAR Monitoring of Permafrost Freeze-Thaw Cycles on the Tibetan Plateau. Geophys. Res. Lett. 2017, 44, 901–909. [Google Scholar] [CrossRef]
- Strozzi, T.; Antonova, S.; Günther, F.; Mätzler, E.; Vieira, G.; Wegmüller, U.; Westermann, S.; Bartsch, A. Sentinel-1 SAR Interferometry for Surface Deformation Monitoring in Low-Land Permafrost Areas. Remote Sens. 2018, 10, 1360. [Google Scholar] [CrossRef] [Green Version]
- Zou, D.F.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.J.; Wu, T.H.; Wu, J.C.; Xie, C.W.; Wu, X.D.; Pang, Q.Q.; et al. A New Map of Permafrost Distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef] [Green Version]
- Liu, L.; Schaefer, K.; Zhang, T.; Wahr, J. Estimating 1992–2000 Average Active Layer Thickness on the Alaskan North Slope from Remotely Sensed Surface Subsidence. J. Geophys. Res. Earth Surf. 2012, 117, 1–14. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, T.; Wahr, J. InSAR Measurements of Surface Deformation over Permafrost on the North Slope of Alaska. J. Geophys. Res. Earth Surf. 2010, 115, 1–14. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T.; Doutsu, M.; Ohgushi, F.; Kai, H. Updates of Aw3d30’ Alos Global Digital Surface Model with Other Open Access Datasets. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2020, XLIII-B4-2, 183–190. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T.; Tsutsui, K.; Ichikawa, M. Validation of “Aw3D” Global DSM Generated from Alos Prism. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, III-4, 25–31. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.M.; Werner, C.L. Radar Interferogram Filtering for Geophysical Applications. Geophys. Res. Lett. 1998, 25, 4035–4038. [Google Scholar] [CrossRef] [Green Version]
- Costantini, M. A novel phase unwrapping method based on Network Programming. IEEE Trans. Geosci. Remote Sens. 1998, 36, 813–821. [Google Scholar] [CrossRef]
- Daout, S.; Doin, M.P.; Peltzer, G.; Lasserre, C.; Socquet, A.; Volat, M.; Sudhaus, H. Strain Partitioning and Present-Day Fault Kinematics in NW Tibet From Envisat SAR Interferometry. J. Geophys. Res. Solid Earth 2018, 123, 2462–2483. [Google Scholar] [CrossRef]
- Daout, S.; Parsons, B.; Walker, R. Post-Earthquake Fold Growth Imaged in the Qaidam Basin, China, with InSAR. J. Geophys. Res. Solid Earth 2020, 126, 1–27. [Google Scholar] [CrossRef]
- Shen, L.; Hooper, A.; Elliott, J. A Spatially Varying Scaling Method for InSAR Tropospheric Corrections Using a High-Resolution Weather Model. J. Geophys. Res. Solid Earth 2019, 124, 4051–4068. [Google Scholar] [CrossRef] [Green Version]
- Shirzaei, M.; Bürgmann, R. Topography Correlated Atmospheric Delay Correction in Radar Interferometry Using Wavelet Transforms. Geophys. Res. Lett. 2012, 39, 1–6. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Walters, R.J.; Wright, T.J.; Hooper, A.J.; Parker, D.J. Statistical Comparison of InSAR Tropospheric Correction Techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef] [Green Version]
- Fattahi, H.; Amelung, F. InSAR Bias and Uncertainty Due to the Systematic and Stochastic Tropospheric Delay. J. Geophys. Res. Solid Earth 2015, 120, 8758–8773. [Google Scholar] [CrossRef] [Green Version]
- Tymofyeyeva, E.; Fialko, Y. Mitigation of Atmospheric Phase Delays in InSAR Data, with Application to the Eastern California Shear Zone. J. Geophys. Res. Solid Earth 2015, 120, 5952–5963. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.H.; Penna, N.T.; Crippa, P. Generic Atmospheric Correction Model for Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2018, 123, 9202–9222. [Google Scholar] [CrossRef]
- Yu, C.; Penna, N.T.; Li, Z. Generation of Real-time Mode High-resolution Water Vapor Fields from GPS Observations. J. Geophys. Res. Atmos. 2017, 122, 2008–2025. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.; Penna, N.T. Interferometric Synthetic Aperture Radar Atmospheric Correction Using a GPS-Based Iterative Tropospheric Decomposition Model. Remote Sens. Environ. 2018, 204, 109–121. [Google Scholar] [CrossRef]
- Murray, K.D.; Bekaert, D.P.S.; Lohman, R.B. Tropospheric Corrections for InSAR: Statistical Assessments and Applications to the Central United States and Mexico. Remote Sens. Environ. 2019, 232, 111326. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, W.; Xu, B.; Wei, G. Assessing the Use of GACOS Products for SBAS-InSAR Deformation Monitoring: A Case in Southern California. Sensors 2019, 19, 3894. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Chang, L.; Feng, W.P.; Samsonov, S.; Zheng, W. Topography-Correlated Atmospheric Signal Mitigation for InSAR Applications in the Tibetan Plateau Based on Global Atmospheric Models. Int. J. Remote Sens. 2021, 42, 4364–4382. [Google Scholar] [CrossRef]
- Jiang, G.Y.; Wang, Y.B.; Wen, Y.M.; Liu, Y.J.; Xu, C.; Xu, C.J. Afterslip Evolution on the Crustal Ramp of the Main Himalayan Thrust Fault Following the 2015 Mw 7.8 Gorkha (Nepal) Earthquake. Tectonophysics 2019, 758, 29–43. [Google Scholar] [CrossRef]
- Feng, W.P.; Samsonov, S.; Liang, C.R.; Li, J.H.; Charbonneau, F.; Yu, C.; Li, Z.H. Source Parameters of the 2017 Mw 6.2 Yukon Earthquake Doublet Inferred from Coseismic GPS and ALOS-2 Deformation Measurements. Geophys. J. Int. 2019, 216, 1517–1528. [Google Scholar] [CrossRef] [Green Version]
- Dogru, F. The Importance of Atmospheric Corrections on InSAR Surveys Over Turkey: Case Study of Tectonic Deformation of Bodrum-Kos Earthquake. Pure Appl. Geophys. 2020, 177, 5761–5780. [Google Scholar] [CrossRef]
- Yu, C.; Li, Z.H.; Penna, N.T. Triggered Afterslip on the Southern Hikurangi Subduction Interface Following the 2016 Kaikōura Earthquake from InSAR Time Series with Atmospheric Corrections. Remote Sens. Environ. 2020, 251, 112097. [Google Scholar] [CrossRef]
- Cavalié, O.; Doin, M.P.; Lasserre, C.; Briole, P. Ground Motion Measurement in the Lake Mead Area, Nevada, by Differential Synthetic Aperture Radar Interferometry Time Series Analysis: Probing the Lithosphere Rheological Structure. J. Geophys. Res. Solid Earth 2007, 112, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Biggs, J.; Wright, T.; Lu, Z.; Parsons, B. Multi-Interferogram Method for Measuring Interseismic Deformation: Denali Fault, Alaska. Geophys. J. Int. 2007, 170, 1165–1179. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Wright, T.J. Satellite Geodetic Imaging Reveals Internal Deformation of Western Tibet. Geophys. Res. Lett. 2012, 39, L07303. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Wright, T.J.; Liu-Zeng, J.; Peng, L. Strain Rate Distribution in South-Central Tibet From Two Decades of InSAR and GPS. Geophys. Res. Lett. 2019, 46, 5170–5179. [Google Scholar] [CrossRef] [Green Version]
- Hussain, E.; Hooper, A.; Wright, T.J.; Walters, R.J.; Bekaert, D.P.S. Interseismic Strain Accumulation across the Central North Anatolian Fault from Iteratively Unwrapped InSAR Measurements. J. Geophys. Res. Solid Earth 2016, 121, 9000–9019. [Google Scholar] [CrossRef] [Green Version]
- Walters, R.J.; Parsons, B.; Wright, T.J. Constraining Crustal Velocity Fields with InSAR for Eastern Turkey: Limits to the Block-like Behavior of Eastern Anatolia. J. Geophys. Res. Solid Earth 2014, 119, 5215–5234. [Google Scholar] [CrossRef]
- Weiss, J.R.; Walters, R.J.; Morishita, Y.; Wright, T.J.; Lazecky, M.; Wang, H.; Hussain, E.; Hooper, A.J.; Elliott, J.R.; Rollins, C.; et al. High-Resolution Surface Velocities and Strain for Anatolia From Sentinel-1 InSAR and GNSS Data. Geophys. Res. Lett. 2020, 47. [Google Scholar] [CrossRef]
- “Altyn Active Fault Zone” Team. The Altyn Tagh Active Fault System; Seismology Publishing House: Beijing, China, 1992. (In Chinese) [Google Scholar]
- Fialko, Y.; Sandwell, D.; Agnew, D.; Simons, M.; Shearer, P.; Minster, B. Deformation on Nearby Faults Induced by the 1999 Hector Mine Earthquake. Science 2002, 297, 1858–1862. [Google Scholar] [CrossRef] [Green Version]
- Lindsey, E.O.; Fialko, Y.; Bock, Y.; Sandwell, D.T.; Bilham, R. Localized and Distributed Creep along the Southern San Andreas Fault. J. Geophys. Res. Solid Earth 2014, 119, 7909–7922. [Google Scholar] [CrossRef]
- Peltzer, G.; Crampé, F.; King, G. Evidence of Nonlinear Elasticity of the Crust from the Mw7.6 Manyi (Tibet) Earthquake. Science 1999, 286, 272–276. [Google Scholar] [CrossRef] [Green Version]
- Ryder, I.; Parsons, B.; Wright, T.J.; Funning, G.J. Post-Seismic Motion Following the 1997 Manyi (Tibet) Earthquake: InSAR Observations and Modelling. Geophys. J. Int. 2007, 169, 1009–1027. [Google Scholar] [CrossRef] [Green Version]
- Feng, M.X.; Bie, L.D.; Rietbrock, A. Probing the Rheology of Continental Faults: Decade of Post-Seismic InSAR Time-Series Following the 1997 Manyi (Tibet) Earthquake. Geophys. J. Int. 2018, 215, 600–613. [Google Scholar] [CrossRef]
- Zhao, D.Z.; Qu, C.Y.; Bürgmann, R.; Gong, W.Y.; Shan, X.J. Relaxation of Tibetan Lower Crust and Afterslip Driven by the 2001 Mw7.8 Kokoxili, China, Earthquake Constrained by a Decade of Geodetic Measurements. J. Geophys. Res. Solid Earth 2021, 126, 1–33. [Google Scholar] [CrossRef]
- Ran, Y.H.; Li, X.; Cheng, G.D.; Zhang, T.J.; Wu, Q.B.; Jin, H.J.; Jin, R. Distribution of Permafrost in China: An Overview of Existing Permafrost Maps. Permafr. Periglac. Process. 2012, 23, 322–333. [Google Scholar] [CrossRef]
- Guo, D.L.; Wang, H.J.; Li, D. A Projection of Permafrost Degradation on the Tibetan Plateau during the 21st Century. J. Geophys. Res. Atmos. 2012, 117, 1–15. [Google Scholar] [CrossRef]
- Fort, M.; Vliet-lanoe, B. Van Permafrost and Periglacial Environment of Western Tibet. Landf. Anal. 2014, 5, 25–29. [Google Scholar]
- Yang, M.; Nelson, F.E.; Shiklomanov, N.I.; Guo, D.; Wan, G. Permafrost Degradation and Its Environmental Effects on the Tibetan Plateau: A Review of Recent Research. Earth-Sci. Rev. 2010, 103, 31–44. [Google Scholar] [CrossRef]
- Cheng, G.D.; Wu, T.H. Responses of Permafrost to Climate Change and Their Environmental Significance, Qinghai-Tibet Plateau. J. Geophys. Res. Earth Surf. 2007, 112, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Rouyet, L.; Lauknes, T.R.; Christiansen, H.H.; Strand, S.M.; Larsen, Y. Seasonal Dynamics of a Permafrost Landscape, Adventdalen, Svalbard, Investigated by InSAR. Remote Sens. Environ. 2019, 231, 111236. [Google Scholar] [CrossRef]
- Li, Z.W.; Zhao, R.; Hu, J.; Wen, L.X.; Feng, G.C.; Zhang, Z.Y.; Wang, Q.J. InSAR Analysis of Surface Deformation over Permafrost to Estimate Active Layer Thickness Based on One-Dimensional Heat Transfer Model of Soils. Sci. Rep. 2015, 5, 15542. [Google Scholar] [CrossRef]
- Zhao, R.; Li, Z.W.; Feng, G.C.; Wang, Q.J.; Hu, J. Monitoring Surface Deformation over Permafrost with an Improved SBAS-InSAR Algorithm: With Emphasis on Climatic Factors Modeling. Remote Sens. Environ. 2016, 184, 276–287. [Google Scholar] [CrossRef]
- Savage, J.C.; Burford, R.O. Geodetic Determination of Relative Plate Motion in Central California. J. Geophys. Res. 1973, 78, 832–845. [Google Scholar] [CrossRef] [Green Version]
- Lindsey, E.O.; Fialko, Y. Geodetic Constraints on Frictional Properties and Earthquake Hazard in the Imperial Valley, Southern California. J. Geophys. Res. Solid Earth 2016, 121, 1097–1113. [Google Scholar] [CrossRef]
- Johnson, K.M.; Fukuda, J. New Methods for Estimating the Spatial Distribution of Locked Asperities and Stress-Driven Interseismic Creep on Faults with Application to the San Francisco Bay Area, California. J. Geophys. Res. Solid Earth 2010, 115, 1–28. [Google Scholar] [CrossRef]
- Fukuda, J.; Johnson, K.M. Mixed Linear-Non-Linear Inversion of Crustal Deformation Data: Bayesian Inference of Model, Weighting and Regularization Parameters. Geophys. J. Int. 2010, 181, 1441–1458. [Google Scholar] [CrossRef] [Green Version]
- Fukuda, J.; Johnson, K.M. A Fully Bayesian Inversion for Spatial Distribution of Fault Slip with Objective Smoothing. Bull. Seismol. Soc. Am. 2008, 98, 1128–1146. [Google Scholar] [CrossRef]
- Foreman-Mackey, D.; Hogg, D.W.; Lang, D.; Goodman, J. Emcee: The MCMC Hammer. Publ. Astron. Soc. Pac. 2013, 125, 306–312. [Google Scholar] [CrossRef] [Green Version]
- Goodman, J.; Weare, J. Ensemble Samplers with Affine invariance. Commun. Appl. Math. Comput. Sci. 2010, 5, 65–80. [Google Scholar] [CrossRef]
- Le Pichon, X.; Kreemer, C.; Chamot-Rooke, N. Asymmetry in Elastic Properties and the Evolution of Large Continental Strike-Slip Faults. J. Geophys. Res. Solid Earth 2005, 110, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Vaghri, A.; Hearn, E.H. Can Lateral Viscosity Contrasts Explain Asymmetric Interseismic Deformation around Strike-Slip Faults? Bull. Seismol. Soc. Am. 2012, 102, 490–503. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.J.; Johnson, K.M. Strain Accumulation across Strike-Slip Faults: Investigation of the Influence of Laterally Varying Lithospheric Properties. J. Geophys. Res. Solid Earth 2012, 117, 1–16. [Google Scholar] [CrossRef]
- Fialko, Y. Interseismic Strain Accumulation and the Earthquake Potential on the Southern San Andreas Fault System. Nature 2006, 441, 968–971. [Google Scholar] [CrossRef] [PubMed]
- Lindsey, E.O.; Fialko, Y. Geodetic Slip Rates in the Southern San Andreas Fault System: Effects of Elastic Heterogeneity and Fault Geometry. J. Geophys. Res. Solid Earth 2013, 118, 689–697. [Google Scholar] [CrossRef] [Green Version]
- Jolivet, R.; Bürgmann, R.; Houlié, N. Geodetic Exploration of the Elastic Properties across and within the Northern San Andreas Fault Zone. Earth Planet. Sci. Lett. 2009, 288, 126–131. [Google Scholar] [CrossRef]
- Meade, B.J. Estimates of Seismic Potential in the Marmara Sea Region from Block Models of Secular Deformation Constrained by Global Positioning System Measurements. Bull. Seismol. Soc. Am. 2002, 92, 208–215. [Google Scholar] [CrossRef] [Green Version]
- Aktuğ, B.; Doğru, A.; Özener, H.; Peyret, M. Slip Rates and Locking Depth Variation along Central and Easternmost Segments of North Anatolian Fault. Geophys. J. Int. 2015, 202, 2133–2149. [Google Scholar] [CrossRef] [Green Version]
- Fay, N.P.; Humphreys, E.D. Fault Slip Rates, Effects of Elastic Heterogeneity on Geodetic Data, and the Strength of the Lower Crust in the Salton Trough Region, Southern California. J. Geophys. Res. B Solid Earth 2005, 110, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Chéry, J. Geodetic Strain across the San Andreas Fault Reflects Elastic Plate Thickness Variations (Rather than Fault Slip Rate). Earth Planet. Sci. Lett. 2008, 269, 352–365. [Google Scholar] [CrossRef]
- Lundgren, P.; Hetland, E.A.; Liu, Z.; Fielding, E.J. Southern San Andreas-San Jacinto Fault System Slip Rates Estimated from Earthquake Cycle Models Constrained by GPS and Interferometric Synthetic Aperture Radar Observations. J. Geophys. Res. Solid Earth 2009, 114, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Le Pichon, X.; Chamot-Rooke, N.; Rangin, C.; Sengör, A.M.C. The North Anatolian Fault in the Sea of Marmara. J. Geophys. Res. Solid Earth 2003, 108, 1–20. [Google Scholar] [CrossRef]
- Johnson, K.M.; Segall, P. Viscoelastic Earthquake Cycle Models with Deep Stress-Driven Creep along the San Andreas Fault System. J. Geophys. Res. Solid Earth 2004, 109, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Savage, J.C.; Prescott, W.H. Asthenosphere Readjustment and the Earthquake Cycle. J. Geophys. Res. 1978, 83, 3369–3376. [Google Scholar] [CrossRef]
- Meade, B.J.; Hager, B.H. Block Models of Crustal Motion in Southern California Constrained by GPS Measurements. J. Geophys. Res. B Solid Earth 2005, 110, 1–19. [Google Scholar] [CrossRef]
- Ravikumar, M.; Singh, B.; Pavan Kumar, V.; Satyakumar, A.V.; Ramesh, D.S.; Tiwari, V.M. Lithospheric Density Structure and Effective Elastic Thickness Beneath Himalaya and Tibetan Plateau: Inference from the Integrated Analysis of Gravity, Geoid, and Topographic Data Incorporating Seismic Constraints. Tectonics 2020, 39, 1–26. [Google Scholar] [CrossRef]
- Chen, B.; Liu, J.X.; Chen, C.; Du, J.S.; Sun, Y. Elastic Thickness of the Himalayan-Tibetan Orogen Estimated from the Fan Wavelet Coherence Method, and Its Implications for Lithospheric Structure. Earth Planet. Sci. Lett. 2015, 409, 1–14. [Google Scholar] [CrossRef]
- Chen, B.; Chen, C.; Kaban, M.K.; Du, J.S.; Liang, Q.; Thomas, M. Variations of the Effective Elastic Thickness over China and Surroundings and Their Relation to the Lithosphere Dynamics. Earth Planet. Sci. Lett. 2013, 363, 61–72. [Google Scholar] [CrossRef]
- Devries, P.M.R.; Meade, B.J. Earthquake Cycle Deformation in the Tibetan Plateau with a Weak Mid-Crustal Layer. J. Geophys. Res. Solid Earth 2013, 118, 3101–3111. [Google Scholar] [CrossRef] [Green Version]
- Bai, D.H.; Unsworth, M.J.; Meju, M.A.; Ma, X.B.; Teng, J.W.; Kong, X.R.; Sun, Y.; Sun, J.; Wang, L.F.; Jiang, C.S.; et al. Crustal Deformation of the Eastern Tibetan Plateau Revealed by Magnetotelluric Imaging. Nat. Geosci. 2010, 3, 358–362. [Google Scholar] [CrossRef]
- Sun, Y.J.; Dong, S.W.; Zhang, H.; Li, H.; Shi, Y.L. 3D Thermal Structure of the Continental Lithosphere beneath China and Adjacent Regions. J. Asian Earth Sci. 2013, 62, 697–704. [Google Scholar] [CrossRef]
- Zhang, P.Z.; Deng, Q.D.; Zhang, G.M.; Ma, J.; Gan, W.J.; Min, W.; Mao, F.Y.; Wang, Q. Active Tectonic Blocks and Strong Earthquakes in the Continent of China. Sci. China Ser. D Earth Sci. 2003, 46, 13–24. [Google Scholar] [CrossRef]
- Xu, X.; Wang, F.; Zheng, R.; Chen, W.; Ma, W.; Yu, G.; Chen, G.; Tapponnier, P.; Van Der Woerd, J.; Meriaux, A.-S.; et al. Late Quaternary Sinistral Slip Rate along the Altyn Tagh Fault and Its Structural Transformation Model. Sci. China Ser. D Earth Sci. 2005, 48, 384–397. [Google Scholar] [CrossRef]
- Mériaux, A.S.; Tapponnier, P.; Ryerson, F.J.; Xu, X.W.; King, G.; Van der Woerd, J.; Finkel, R.C.; Li, H.B.; Caffee, M.W.; Xu, Z.Q.; et al. The Aksay Segment of the Northern Altyn Tagh Fault: Tectonic Geomorphology, Landscape Evolution, and Holocene Slip Rate. J. Geophys. Res. Solid Earth 2005, 110, 1–32. [Google Scholar] [CrossRef]
- Zhang, P.Z.; Molnar, P.; Xu, X.W. Late Quaternary and Present-Day Rates of Slip along the Altyn Tagh Fault, Northern Margin of the Tibetan Plateau. Tectonics 2007, 26, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Cowgill, E. Impact of Riser Reconstructions on Estimation of Secular Variation in Rates of Strike-Slip Faulting: Revisiting the Cherchen River Site along the Altyn Tagh Fault, NW China. Earth Planet. Sci. Lett. 2007, 254, 239–255. [Google Scholar] [CrossRef]
- Gold, R.D.; Cowgill, E.; Arrowsmith, J.R.; Gosse, J.; Chen, X.; Wang, X.F. Riser Diachroneity, Lateral Erosion, and Uncertainty in Rates of Strikeslip Faulting: A Case Study from Tuzidun along the Altyn Tagh Fault, NW China. J. Geophys. Res. Solid Earth 2009, 114, 1–24. [Google Scholar] [CrossRef] [Green Version]
- Cowgill, E.; Gold, R.D.; Chen, X.; Wang, X.-F.; Arrowsmith, J.R.; Southon, J. Low Quaternary Slip Rate Reconciles Geodetic and Geologic Rates along the Altyn Tagh Fault Northwestern Tibet. Geology 2009, 37, 647–650. [Google Scholar] [CrossRef]
- Bendick, R.; Bilham, R.; Freymueller, J.; Larson, K.; Yin, G. Geodetic Evidence for a Low Slip Rate in the Altyn Tagh Fault System. Nature 2000, 404, 69–72. [Google Scholar] [CrossRef]
- Zhang, P.Z.; Shen, Z.K.; Wang, M.; Gan, W.J.; Bürgmann, R.; Molnar, P.; Wang, Q.; Niu, Z.J.; Sun, J.Z.; Wu, J.C.; et al. Continuous Deformation of the Tibetan Plateau from Global Positioning System Data. Geology 2004, 32, 809–812. [Google Scholar] [CrossRef]
- Wallace, K.; Yin, G.; Bilham, R. Inescapable Slow Slip on the Altyn Tagh Fault. Geophys. Res. Lett. 2004, 31, 6–9. [Google Scholar] [CrossRef] [Green Version]
- Mériaux, A.S.; Van Der Woerd, J.; Tapponnier, P.; Ryerson, F.J.; Finkel, R.C.; Lasserre, C.; Xu, X. The Pingding Segment of the Altyn Tagh Fault (91°E): Holocene Slip-Rate Determination from Cosmogenic Radionuclide Dating of Offset Fluvial Terraces. J. Geophys. Res. Solid Earth 2012, 117, 1–26. [Google Scholar] [CrossRef] [Green Version]
- Wessel, P.; Smith, W.H.F.; Scharroo, R.; Luis, J.; Wobbe, F. Generic Mapping Tools: Improved Version Released. EOS Trans. Am. Geophys. Union 2013, 94, 409–410. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Zhao, D.; Shan, X. Asymmetric Interseismic Strain across the Western Altyn Tagh Fault from InSAR. Remote Sens. 2022, 14, 2112. https://doi.org/10.3390/rs14092112
Liu Y, Zhao D, Shan X. Asymmetric Interseismic Strain across the Western Altyn Tagh Fault from InSAR. Remote Sensing. 2022; 14(9):2112. https://doi.org/10.3390/rs14092112
Chicago/Turabian StyleLiu, Yunhua, Dezheng Zhao, and Xinjian Shan. 2022. "Asymmetric Interseismic Strain across the Western Altyn Tagh Fault from InSAR" Remote Sensing 14, no. 9: 2112. https://doi.org/10.3390/rs14092112
APA StyleLiu, Y., Zhao, D., & Shan, X. (2022). Asymmetric Interseismic Strain across the Western Altyn Tagh Fault from InSAR. Remote Sensing, 14(9), 2112. https://doi.org/10.3390/rs14092112






