Strain and Moment Rates from GPS and Seismological Data in Northern Iran: Implications for an Evaluation of Stress Trajectories and Probabilistic Fault Rupture Hazard

Abstract

This study provides a multi-disciplinary overview of the seismology and geodetic data with tectonics analysis in order to provide an evaluation of stress trajectories, and probabilistic fault rupture hazard assessment. Based on the different scenarios obtained from the comparison of several overviews and their interpretation, we investigated the kinematics and active tectonics of different structural zones. In this study, the magnitudes and directions of seismic and geodetic strain rates (SSR and GSR) were evaluated using reliable earthquake focal mechanisms and all available GPS data (1999–2015) in the structural subzones of northern Iran, where have experienced more than 14 strong instrumental earthquakes (Mw ≥ 6). In addition, a tectonic stress model was inferred from the Focal Mechanism Stress Inversion (FMSI). The new crustal stress map was proposed by the weighted average analysis of the SSR, GSR, and FMSI. N35.5° E and N104° E were estimated for the Alborz and Talesh mountains, respectively. The numerical analysis of stress regimes confirms the slip partitioning mechanism of oblique shortening on the sub-parallel thrusts and strike-slip faults in the area. Four main stress regime categories were defined, including thrust (49.37%), strike-slip (39.24%), thrust with a strike-slip component (2.53%), normal (1.27%), and unknown faulting (7.59%). Seismic and geodetic moment rates (SMR and GMR) and their comparison were also calculated in order to evaluate the function of these parameters in determining the seismicity arrangement. The ratio of the seismic/geodetic moment rates for the area is ~70.7%. This ratio for the Alborz, western Koppeh-Dagh, north part of Central Iran, South Caspian Basin, and Talesh is ~0.9, 0.3, 11.9, 0.3, and 57.3, respectively, which indicates the most elastic energy has been released in the Talesh and the north part of Central Iran. The comparison of geodetic moment rates in the subzones of the area indicates that geodetic deformation is high in the Central Alborz (networks 8, 9, 17) and western Koppeh-Dagh (networks 5, 13).

1. Introduction

Geomorphological evidence indicates that some continental areas have experienced intense tectonic activity. From a seismic, geodetic, and tectonics viewpoint, it is necessary to consider the possibility of fault rupture hazard assessment in some of these areas with a high human population. Northern Iran is one of these areas which is home to Iran’s capital (Tehran) and more than 23 million people. In this article, we will compare our interpretation of the multidisciplinary data from northern Iran to that from other parts of the world, including the United States [1], Basin and Range [2], the west and south of the Lut block [3], and the NE of the Lut block [4,5].

The destructive earthquakes in northern Iran from 1953 to 2021 have caused about ~168.5 km surface ruptures and ~54,810 human casualties. The fault rupture hazard assessment in this region is not accurate because of no detailed deformation style estimations (distinguishing seismic from aseismic deformation). It is important that the seismicity of a region and its spatial and temporal variations are considered snapshots of ongoing tectonic activities. Therefore, the identification of deformation patterns may provide complementary deductions for more realistic analysis and interpretation of observations.

Destructive earthquakes in the Talesh-Alborz range, the South Caspian Basin, and the northern part of Central Iran indicate strong tectonic activity in the northern Iran region [6,7,8,9,10,11,12,13]. The region with a V-shaped geometry includes the main faults with NW-SE and NE-SW directions in its western and eastern parts, respectively. In these parts, the overall deformation style has been specified by a system of double-verging folds, left-lateral strike-slip, and reverse faults sub-parallel to the range trend [14,15].

Several studies in Iran have presented a distribution of the geodetic deformation [16,17,18] and seismic deformations by the earthquake focal mechanism stress inversion [19,20,21]. Comparing the geodetic and seismic strain rates with tectonics interpretations has provided some information in order to assess aseismic and seismic deformation using uniform grids and non-uniform triangular mesh [16,22,23]. A few studies associated the deformation style of northern Iran [22]. This study addresses magnitudes and azimuths of the principal geodetic and seismic strain rates and discusses their results in terms of the crustal deformation processes and present-day stress map of northern Iran which is a good example of compression-shear ranges word-wide. In this study, all published GPS data (2006–2015), and earthquake slip vectors (1978–2020) are analyzed using more grids. The comparison and combination of these data sets give insights into the present active tectonic pattern [23]. In tectonically active regions where there are mismatches between the earthquake slip vectors and the GPS imply some form of strain partitioning and/or vertical axis rotations have taken place [23,24] and permit understanding of the processes involved. In this study, based on numerical analysis of stress regimes, the deformation style of northern Iran which can be expressed as “Homogenous” and “Partitioned” [25] are determined.

In addition to the ratio of the seismic/geodetic strain rates, this article calculated the ratio of the seismic/geodetic moment rates in order to contribute to the seismicity analysis of the region. Geodetic moment rates can be used to estimate the degree of locking on the fault surface, and its comparison with seismic moment rates provides inferences on the seismogenic potential of active faults in a region [26,27,28,29]. Moreover, this comparison can provide valuable information about earthquake moment production and deformation mechanisms [30].

2. Tectonic Setting and Seismicity

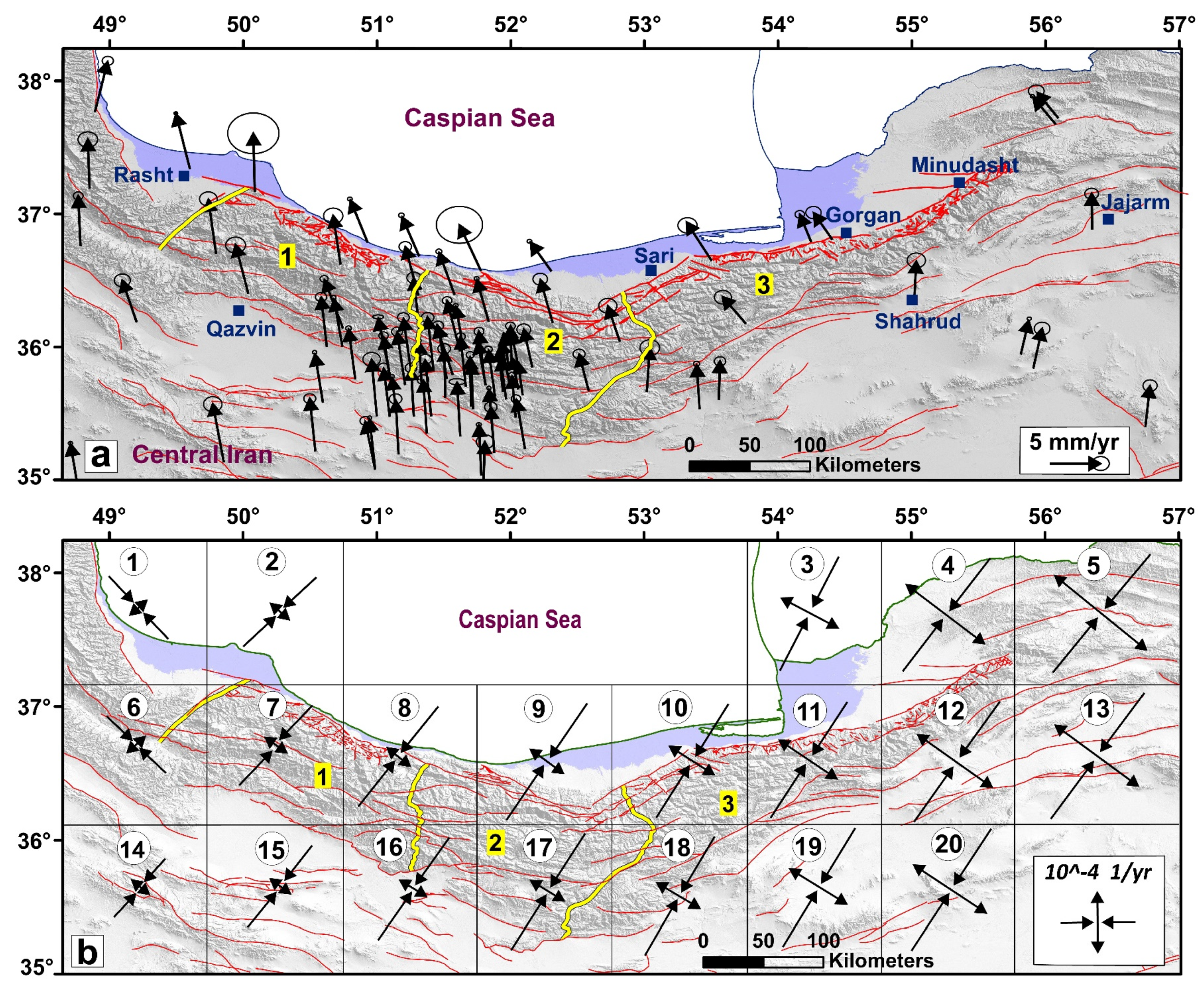
The Alborz-Talesh range of northern Iran (Figure 1a) was formed in a series of tectonic events related to the collision of Eurasia with Central Iran in the Triassic (Cimmerian Orogeny) and the Paleocene collision of Eurasia with Arabia (Laramide orogeny) [31,32,33]. Intra-continental deformation resulting from the convergence of the Eurasian-Arabian plates continues until the present time in an NNE-oriented with a slip rate of ~22 mm/yr [34]. The global positioning system (GPS) (Figure 1b) indicates 5 ± 2 mm/yr of NNE-oriented shortening in the Alborz and 4 ± 2 mm/yr of left-lateral movements [35]. The Kopeh Dagh range, as the eastern continuation of the Alborz-Talesh range, includes Tertiary and Mesozoic sediments, which have been folded during the Oligo-Miocene orogeny [36,37]. The Kopeh Dagh Fault system, with a slip rate of 9.1± 1.3 mm/yr, is characterized as the NW-boundary of the range [38].

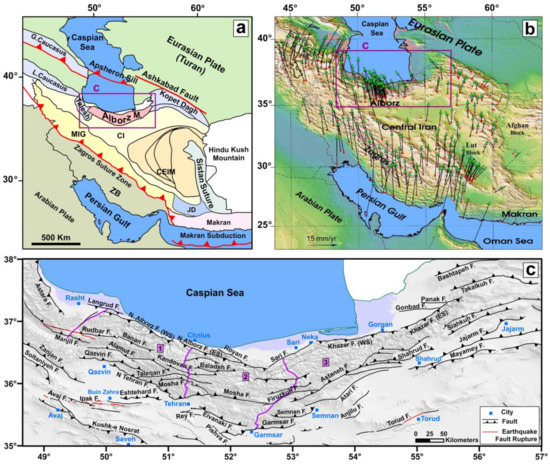
Figure 1. (a) The regional structure of Arabia-Eurasia collision, and the location of the understudy subzones (Alborz, Talesh, north of Central Iran; purple box) (ZB = Zagros Belt, MIG = Zone of Intruded Granitoides and Metamorphic Rocks, CEIM = Microcontinent of Central-East Iran, CI = Central Iran, and JD = Jazmurian Depression). (b) The GPS velocity field relative to the Eurasian reference frame [18,53]. (c) Active faults in the study area (the faults after [50,54,55]). Numbers 1, 2, and 3 are location of the West Alborz, Central Alborz, and East Alborz, respectively which are separated by purple lines.

The south Caspian basin (SCB) in the west of Kopeh Dagh and the north/northeast of Alborz-Talesh range is noticeable for its thick sedimentary deposits [39]. This basin, as one of the deepest sedimentary basins in the world, contains ~20 km of sedimentary deposits [39]. The thick sediments of the SCB overlie a high-velocity basement that is thinner inside the basin, and thicker around its edges [40]. The basement beneath the basin unusually could be thinned continental crust or thick oceanic crust [41,42]. Earthquakes with depths down to 40 km occur beneath the Caucasus and Talesh mountains of the western margin of the SCB and down to 80 km in the north of the Apsheron Sill at its northern margin [42,43]. The deep earthquakes of the Apsheron sill are the results of subduction and underthrusting of the SCB basement, with the onset of subduction often assumed to correlate with the increase in sediment accumulation at 5.5 Ma [44].

The main active structures of the Alborz-Talesh range with a dominant component of thrust motion surrounded from the south (e.g., North Tehran, Garmsar, Pishva, and Jajarm N-dipping faults) to the north (e.g., Khazar, North Alborz, and Astara SSW-dipping faults), while the left-lateral strike-slip motion with the minor normal and thrust components concentrate within the range, (e.g., Firuzkuh, Mosha, Taleghan, and Rudbar) (Figure 1c). Some researchers have reported that right-lateral strike-slip motion must be available along the northern Talesh mountains [42,45,46] to adopt a part of the Arabia-Eurasia convergence. However, the focal mechanisms of earthquakes have not confirmed the right-lateral strike-slip mechanism.

In the Alborz range, after the Pliocene (3–5 Ma), oblique shortening is partitioned into pure thrust and pure strike-slip [42,47]. The motion of the SCB relative to both Eurasia (10.4 +/− 1.1 mm/yr in direction 333° +/− 5) and central Iran (4.8 +/− 0.8 mm/yr in direction 236° +/− 14) enhances westward underthrusting of the basin beneath the Talesh mountains of Iran and Azerbaijan [38,42,48]. The general wrenching of the belt was dependent on these motions, which in some parts have led to the normal component of some faults (e.g., Sari, Firouzkuh, and Astaneh faults) [49,50].

In the Alborz-Talesh range, in addition to the instrumental earthquakes which have been associated with financial and human losses (e.g., the 1935 Mw 6.8 Kusut, 1953 Mw 6.5 Troud, 1957 Mw 7 Sangchal, 1962 Mw 7.2 Buin-Zahra, 1980 Mw 6.6 Shirabad, 1990 Mw 7.3 Rudbar, 2002 Mw 6.5 Avaj, and 2004 Mw 6.4 Baladeh), a large number of strong historical earthquakes have also reported [7,10,51,52]. The historical sites in Tehran (the capital of Iran), which were situated in the immediate southern foothills of the Central Alborz, have been destroyed by historical earthquakes several times [7,52]. The North Tehran, Rey, and Eivanaki faults (Figure 1c) have been recognized as the sources of historical earthquakes in 1384 AD, 1177 (Ms∼7.2), 855 (Ms∼7.1), 743 (Ms∼7.2), and 312–280 BC (Ms∼7.6) [7,52]. So, Tehran with a population of more than 13 million people can again face a critical seismic hazard.

3. Data and Methodology

The lack of enough seismic or geodetic data in an active area has always been a problem for tectonic interpretation. Using both data sets can usually solve this problem. The patterns obtained as the results of focal mechanism stress inversion (FMSI) revealed many interesting “complications” of the stress field which were not applied along with geodetic and tectonic interpretations in the previous studies in northern Iran.

A scattered seismicity pattern influences northern Iran, mostly earthquakes with different magnitudes concentrated within the Alborz-Talesh range (Figure 2 and Table 1). In this study, 79 reliable focal mechanisms (4 ≤ Mw ≤ 7.4) from different catalogs, including GCMT (Global Centroid Moment Tensor); IIEES (International Institute of Earthquake Engineering and Seismology); IRSC (Iranian Seismological Center); ISC (Instrumental Earthquake Catalogue); ZUR_RMT (Zurich Moment Tensors); UPIES (moment tensors, University of Potsdam, Germany), were selected to perform the stress inversions (Figure 2 and Table 1). To do a more complete evaluation of the seismic deformation in the area, using all events, with and without focal mechanism, is also crucial, which can be reflected in local variations of strain and/or originated from the structures already present and reactivated such as weakness areas. For this purpose in this study, all earthquakes were used for calculating the seismic moment rates.

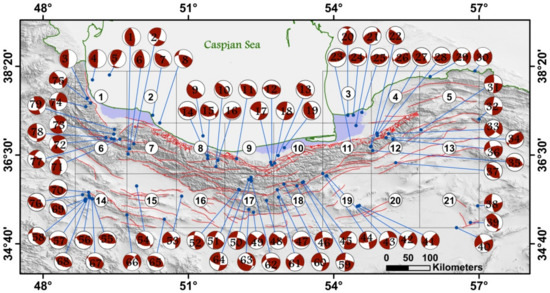
Figure 2. The earthquake focal mechanisms in northern Iran during 1978–2020 from various catalogues. Labels on the focal mechanism refer to the first column of Table 1. Labels within grids show grid number.

Table 1. Parameters of the earthquake source are applied to calculate the seismic strain rate (φ, δ, and λ symbols represent strike, dip, and rake angles of the preferred nodal planes, respectively). The first column label refers to the focal mechanisms in Figure 2. Lat. and Long. refer to EHB (Engdahl bulletin), IIEES (International Institute of Earthquake Engineering and Seismology), and IRSC (Iranian Seismological Center). Abbreviations of References label: GCMT (Global Centroid Moment Tensor); ISC (Instrumental Earthquake Catalogue); ZUR_RMT (Zurich Moment Tensors); UPIES (moment tensors, University of Potsdam, Germany).

Label	Date (y/m/d)	Time	Lat.	Long.	Mw	Dep.	φ1	δ1	λ1	Reference
1	2002/04/19	13:46:51	36.519	49.753	5.2	29	183	26	103	GCMT
2	2015/05/10	22:08:58	36.73	49.87	4.3	5	25	68	165	IRSC
3	1978/11/04	15:22:20	37.674	48.912	6.4	26	177	9	87	GCMT
4	1980/05/04	18:35:19	38.053	49.018	6.6	20	179	5	88	GCMT
5	1981/08/04	18:35:43	38.154	49.369	5.6	26	159	26	40	GCMT
6	1990/06/21	9:02:16	36.63	49.785	5.8	14	204	26	121	GCMT
7	1980/07/22	5:17:08	37.322	50.262	5.6	25	135	20	95	GCMT
8	1980/12/03	4:26:13	37.126	50.43	5.3	16	160	52	136	GCMT
9	2004/05/29	9:23:49	36.488	51.396	4.7	14	185	3	145	ZUR_RMT
10	2004/05/28	19:47:05	36.426	51.398	6.4	27	119	24	72	GCMT
11	2002/04/08	18:30:55	36.422	51.992	4.8	9	134	42	104	ZUR_RMT
12	1992/09/22	14:05:56	36.294	52.722	5.1	35	268	44	75	GCMT
13	2012/01/11	17:08:02	36.489	52.853	5	17.5	114	31	71	GCMT
14	2012/07/27	21:39:03	36.896	51.3	4.3	8.5	276	56	81	IIEES
15	2004/05/28	12:38:45	36.259	51.566	4.5	25	76	40	35	ZUR_RMT
16	2004/05/28	13:35:56	36.39	51.61	4.4	28	75	13	98	UPIES
17	2008/03/26	18:49:54	36.349	52.697	4.6	38.5	9	74	159	IIEES
18	2012/03/18	2:38:15	36.33	52.78	4.3	10	13	84	166	IRSC
19	2018/09/22	22:34:44	36.65	52.98	4.4	15.6	144	20	76	IRSC
20	2015/09/15	17:35:50	37.32	54.29	4.3	20	206	66	125	IRSC
21	2004/10/07	21:46:15	37.109	54.461	6.2	22	27	46	53	GCMT
22	2014/09/06	21:34:19	36.67	54.76	4.4	10	164	27	119	IRSC
23	2000/08/16	12:53:02	36.706	54.366	4.9	25	240	34	78	GCMT
24	1999/11/19	4:40:25	37.324	54.405	5.4	31	57	34	51	GCMT
25	2005/01/10	18:47:25	37.38	54.58	5.6	15	62	30	60	GCMT
26	1985/10/29	13:13:41	36.68	54.772	6.1	15	97	31	122	GCMT
27	1999/11/26	4:27:23	36.953	54.896	5.3	10	106	22	58	GCMT
28	1985/10/29	14:23:05	36.901	54.899	6.2	13	113	21	124	ISC
29	2020/09/26	5:46:51	38.12	55.99	5.2	6	144	89	−174	IRSC
30	2015/10/12	21:37:26	38.36	56.92	5.1	7	146	86	175	IRSC
31	2016/12/27	20:56:19	37.02	55.8	4.6	7	271	80	−7	GCMT
32	2018/07/17	3:58:30	37.24	57.02	4.8	7.4	187	84	−179	GCMT
33	2020/09/06	21:34:23	36.94	55.13	5	7	36	61	−7	IRSC
34	2014/06/13	9:12:27	36.857	55.081	4.3	8	80	43	122	IRSC
35	2011/08/11	22:32:16	36.592	54.802	5.2	15.5	97	43	77	GCMT
36	2018/08/16	6:41:49	36.82	55.22	4.4	6.5	253	64	16	IRSC
37	2015/08/17	17:36:01	36.34	55.28	4.1	8	140	39	92	IRSC
38	2016/10/25	11:58:14	35.45	56.97	4.1	9	174	77	−172	IRSC
39	1979/12/09	9:12:03	35.105	56.82	5.6	9	129	53	63	GCMT
40	2019/08/13	23:31:08	34.93	56.54	4	14.6	153	87	171	IRSC
41	2010/08/28	0:29:02	35.456	54.529	4.9	12.5	127	71	172	IIEES
42	2010/08/27	19:23:52	35.441	54.488	5.9	12.5	212	78	−2	GCMT
43	2006/12/20	5:00:36	36.072	53.855	4.3	20.5	257	71	165	IIEES
44	2013/03/21	19:37:03	36.142	53.694	4.6	5	78	73	3	GCMT
45	2012/04/22	6:38:56	35.947	53.374	4.2	13.5	206	73	−169	IIEES
46	2008/07/16	16:33:42	35.862	53.239	4.1	3.5	262	67	5	IIEES
47	2010/01/20	5:20:06	35.783	52.835	4.5	3.5	109	32	120	IIEES
48	2015/08/25	17:36:33	35.56	52.61	4.5	9	320	67	164	IRSC
49	1988/08/22	21:23:38	35.317	52.342	5.3	23	317	75	−175	GCMT
50	1983/03/25	11:57:49	36.039	52.292	5.5	20	280	68	5	GCMT
51	2020/05/07	20:18:21	35.78	52.05	4.9	7	292	68	15	GCMT
52	2020/05/27	9:11:37	35.79	52.04	4	12	179	70	132	IRSC
53	2017/12/20	19:57:40	35.65	50.86	4.9	30.3	336	66	169	GCMT
54	2012/09/01	20:27:41	35.86	49.93	4	40	108	39	59	IRSC
55	2002/06/22	6:45:38	35.585	48.869	6.5	11	295	29	99	GCMT
56	2004/10/17	21:31:02	35.62	48.96	5.4	29	119	57	103	ZUR_RMT
57	2002/06/26	18:18:16	35.546	48.869	4.5	8	113	41	111	ZUR_RMT
58	2002/06/22	14:27:18	35.594	48.876	4.4	57	160	52	136	GCMT
59	2012/08/06	7:04:17	35.932	53.353	4.3	3.5	184	87	162	IIEES
60	1990/01/20	1:27:12	35.9	52.97	6	30	357	66	172	GCMT
61	2003/06/21	15:00:05	35.628	52.859	4.5	24	116	80	155	ZUR_RMT
62	2014/08/16	23:55:57	35.97	52.3	4.1	12	147	64	139	IRSC
63	1988/08/23	5:30:51	35.377	52.246	5.2	25	348	32	−41	GCMT
64	1983/03/26	4:07:19	35.991	52.244	5.4	20	104	61	17	GCMT
65	2003/12/24	3:50:00	35.174	50.503	4.7	15	114	45	83	ZUR_RMT
66	2013/10/16	8:49:32	35.28	49.69	4.6	8	314	44	−168	IRSC
67	2002/06/22	21:33:26	35.663	48.946	4.9	25	136	49	112	ZUR_RMT
68	2002/06/22	3:32:01	35.594	49.009	4.1	33	117	48	94	ZUR_RMT
69	2002/06/22	2:58:23	35.597	49.02	4.4	10	125	45	91	ZUR_RMT
70	2015/03/02	6:08:41	35.73	48.94	4.2	8	284	63	97	IRSC
71	1991/11/28	17:19:56	36.827	49.584	5.6	15	219	36	130	GCMT
72	1990/06/24	9:45:59	36.839	49.408	5.3	15	234	69	−163	GCMT
73	2002/02/14	20:06:22	36.933	49.46	4.2	15	61	81	−178	ZUR_RMT
74	2006/11/05	20:06:40	37.5	48.88	5	14	188	67	−2	GCMT
75	2002/01/05	14:43:45	37.576	48.98	4.4	23	69	66	17	ZUR_RMT
76	2002/09/02	1:00:06	35.679	48.814	5.2	22	105	34	71	GCMT
77	1990/06/20	21:00:31	36.828	49.468	7.3	15	200	59	160	GCMT
78	1990/07/06	19:34:52	36.864	49.298	5.3	20	94	37	6	GCMT
79	1995/10/15	6:56:35	37.03	49.473	5.2	25	66	49	178	GCMT

Comparing the geodetic and seismic moment rates can provide important insights for identifying fault behavior in the tectonically active zone. The analysis of Ward [1] and Pancha et al. [2] for the seismic hazard has been obtained by using the moment rates. According to the hazard analysis objectives, the new information about the moment rates (GMR, SMR) is regarded in comparison with the seismic and geodetic strain rates (GSR, SSR).

More useful information can be obtained on the fault activities and their seismic risks when the moment rates are dependent on the amount of released and accumulated energy. ArcGIS software was used for mapping the seismic and geodetic moment rates. Several interpolation tools were suggested by ArcGIS Spatial Analyst to create surface grids from point data [56], some of which are the Kriging, Spline, and IDW interpolation methods. The Kriging interpolation, as a powerful statistical method [56], was used in this study, which within a specified radius fits a function to a specified number of all points or some points to evaluate the output amount for each location.

3.1. Seismic Strain Rate (SSR)

The seismic strain-rate tensor for each grid of networking performed for the study area is calculated by applying Kostrov’s formulation [57] and the Win-Tensor program [58]. The grids include at least 3 seismic events of the focal mechanism. Although some common earthquakes were used in two grids due to their boundary location, there were no considerable earthquake mechanisms in networks 2, 4, 13, 16, and 20 (Figure 2).

The stress inversion is conducted for deriving principal stress directions. Stress analysis is generally according to the maximum shear stress direction inside the dislocation plane [59]. Fault plane and slip parameters are used for establishing the stress ratio, R, and the stress tensor including the direction of three orthogonal principal stress axes (σ₁, σ₂, and σ₃) (Equation (1)).

$$R=\frac{{\sigma }_2-{\sigma }_3}{{\sigma }_1-{\sigma }_3}$$

(1)

In this study, Rotational optimization [58] and Right Dihedron [60] stress inversion methods were used to determine stress tensor. The Right Dihedron method is used for defining the principal stress axes (P, B, and T) [60]. This method follows an iterative inversion procedure [58] by minimizing a misfit function of many different stress tensors through a grid search. In this method, both focal mechanism nodal planes are compared with a stress tensor, and the plane with the smaller value of the misfit is evaluated as the main fault plane. Thus, before the inversion, it is not necessary to determine which nodal plane is the fault plane. Eventually, the final inversion is included only in focal planes with the best fitting using a uniform stress field. The chosen fault planes are then inverted to determine the stress ratio and the principal stress axes [61]. The results are plotted on the projection of an equal-area to let us assess the overall quality of the outcome.

The Right Dihedron method allows for the first estimation of stress ratio R, directions of principal stress, and the first filtering of compatible with fault-slip data [62]. The chosen fault-slip data and initial tensor are applied as a beginning point in the repetitive grid search inversion procedures of the Rotational Optimization method. In addition, it is allowed to restrict the search area during the inversion. Therefore, the whole grid should not be searched [62], which minimizes α as the misfit angle by using the tested stress tensor and favors magnitudes of lower normal stress and higher shear stress on the plane to develop slip [62].

In the following, we have calculated the parameters resulting from focal mechanism stress inversion (FMSI) methods.

3.1.1. Stress Regimes Using FMSI

The parameter of the stress regime (R’) was used according to the determined stress ratio (Equation (1)) in order to demonstrate numerical values of the tectonic stress regime for the study area. The types of regimes considered in different studies [58,63] are as follows:

Normal faulting regimes     R′ = R

(2)

$$\mathrm{Strike}-\mathrm{slip}\mathrm{faulting}\mathrm{regimes}{R}^{\prime }=\left(2-R\right)$$

(3)

$$\mathrm{Thrust}\mathrm{faulting}\mathrm{regimes}{R}^{\prime }=\left(2+R\right)$$

(4)

Regarding a normal tectonic regime, the obtained R′ is in the range of 0–1, while the values in the ranges of 1–2, and 2–3 are for strike-slip and thrust faulting tectonic regimes, respectively. Word Stress Map (WSM) standard was used for calculating stress regimes. TS, SS, NF, TF, NS, and UF symbols are thrust faulting with a strike-slip component, strike-slip faulting, normal faulting, thrust faulting, and normal faulting with a strike-slip component, as well as the unknown regimes, respectively. For each earthquake, these tectonic regimes are obtained based on the Zoback method [64] (Table 2).

Table 2. The calculated parameters from the stress tensor of the earthquake focal mechanisms.

No.	Date (d/m/y)	Fault Plane		Slip Line		Slip	Moment Stress Axes						SH		R′	Reg.
		Dip	Dip Dir.	Azim.	Plunge	Sense	P		B		T		Max	Min
							Azim.	Incl.	Azim.	Incl.	Azim.	Incl.	Azim.	Azim.
1	2002/04/19	26	273	25	259	ID	20	84	6	352	70	247	86	176	2/5	TF
2	2015/05/10	68	115	14	31	ID	5	252	63	151	26	344	73	163	1/5	SS
3	1978/11/04	9	267	9	270	IS	36	90	0	180	54	271	89	179	2/5	UF
4	1980/05/04	5	269	5	271	IS	40	91	0	181	50	271	91	1	2/5	UF
5	1981/08/04	26	249	16	302	IS	26	106	20	206	56	329	95	5	2/5	TF
6	1990/06/21	26	294	22	260	ID	22	91	13	355	64	236	98	8	2/5	TF
7	1980/07/22	20	225	20	220	ID	25	41	2	311	65	217	42	132	2/5	TF
8	1980/12/03	52	250	33	191	ID	3	39	35	308	55	134	40	130	2/5	TF
9	2004/05/29	3	275	2	220	ID	43	42	2	310	47	217	66	156	2/5	UF
10	2004/05/28	24	209	23	229	IS	22	43	7	136	67	243	39	129	2/5	TF
11	2002/04/08	42	224	40	205	ID	4	34	10	303	80	146	35	125	2/5	TF
12	1992/09/22	44	358	42	18	IS	2	188	10	279	80	87	8	98	2/5	TF
13	2012/01/11	31	204	29	226	IS	15	38	10	131	72	252	35	125	2/5	TF
14	2012/07/27	56	6	55	22	IS	11	13	8	281	77	156	14	104	2/5	TF
15	2004/05/28	40	166	22	228	IS	16	23	32	124	53	270	17	107	2/5	TF
16	2004/05/28	13	165	13	157	ID	32	338	2	247	58	155	160	70	2/5	TF
17	2008/03/26	74	99	20	15	ID	3	58	64	153	26	326	57	147	1/5	SS
18	2012/03/18	84	103	14	14	ID	6	59	75	170	14	328	58	148	1/5	SS
19	2018/09/22	20	234	19	249	IS	26	65	5	157	64	257	61	151	2/5	TF
20	2015/09/15	66	296	48	236	ID	14	271	32	10	55	161	86	176	2/5	TF
21	2004/10/07	46	117	35	164	IS	5	322	26	54	64	222	140	50	2/5	TF
22	2014/09/06	27	254	23	222	ID	21	52	13	318	65	198	58	148	2/5	TF
23	2000/08/16	34	330	33	344	IS	12	158	7	250	77	9	156	66	2/5	TF
24	1999/11/19	34	147	26	191	IS	16	354	20	91	64	229	169	79	2/5	TF
25	2005/01/10	30	152	26	186	IS	18	354	15	89	67	216	169	79	2/5	TF
26	1985/10/29	31	187	26	151	ID	17	344	16	249	66	119	169	79	2/5	TF
27	1999/11/26	22	196	19	230	IS	25	41	11	136	62	248	34	124	2/5	TF
28	1985/10/29	21	203	17	167	ID	27	357	12	261	60	149	6	96	2/5	TF
29	2020/09/26	89	234	6	324	ND	5	9	84	153	4	279	9	99	1/5	SS
30	2015/10/12	86	236	5	146	ID	1	191	84	287	6	101	11	101	1/5	SS
31	2016/12/27	80	1	7	272	NS	12	227	78	37	2	136	47	137	1/5	SS
32	2018/07/17	84	277	1	7	ND	5	52	84	268	4	142	52	142	1/5	SS
33	2020/09/06	61	126	6	39	NS	25	356	60	140	16	259	172	82	1/5	SS
34	2014/06/13	43	170	35	129	ID	6	328	22	235	67	73	150	60	2/5	TF
35	2011/08/11	43	187	42	205	IS	3	16	9	107	81	271	16	106	2/5	TF
36	2018/08/16	64	343	14	66	IS	8	206	60	310	29	112	24	114	1/5	SS
37	2015/08/17	39	230	39	227	ID	6	48	1	318	84	214	48	138	2/5	TF
38	2016/10/25	77	264	8	352	ND	15	38	75	231	3	128	38	128	1/5	SS
39	1979/12/09	53	219	45	259	IS	4	238	21	146	68	339	59	149	2/5	TF
40	2019/08/13	87	243	9	153	ID	4	198	81	315	8	108	18	108	1/5	SS
41	2010/08/28	71	217	8	130	ID	8	352	69	242	19	85	173	83	1/5	SS
42	2010/08/27	78	302	2	212	NS	10	168	78	311	7	76	167	77	1/5	SS
43	2006/12/20	71	347	14	262	ID	3	124	66	26	24	215	125	35	1/5	SS
44	2013/03/21	73	168	3	257	IS	10	34	73	157	14	301	33	123	1/5	SS
45	2012/04/22	73	296	11	23	ND	20	69	70	261	4	160	70	160	1/5	SS
46	2008/07/16	67	352	5	80	IS	12	218	66	338	20	124	36	126	1/5	SS
47	2010/01/20	32	199	27	165	ID	16	358	15	263	67	132	2	92	2/5	TF
48	2015/08/25	67	50	15	326	ID	5	187	62	86	27	280	8	98	1/5	SS
49	1988/08/22	75	47	5	136	ND	14	181	74	28	7	272	2	92	1/5	SS
50	1983/03/25	68	10	5	98	IS	12	236	67	356	19	142	54	144	1/5	SS
51	2020/05/07	68	22	14	106	IS	5	245	63	346	26	153	64	154	1/5	SS
52	2020/05/27	70	269	44	200	ID	14	240	39	342	47	134	55	145	2/5	TS
53	2017/12/20	66	66	10	341	ID	9	202	64	92	24	296	24	114	1/5	SS
54	2012/09/01	39	198	33	236	IS	9	40	19	133	69	285	37	127	2/5	TF
55	2002/06/22	29	25	29	15	ID	16	199	4	107	73	3	20	110	2/5	TF
56	2004/10/17	57	209	55	186	ID	11	200	11	292	74	65	18	108	2/5	TF
57	2002/06/26	41	203	38	176	ID	6	8	14	277	75	120	9	99	2/5	TF
58	2002/06/22	52	250	33	191	ID	3	39	35	308	55	134	40	130	2/5	TF
59	2012/08/06	87	274	18	185	ID	10	231	72	355	15	138	50	140	1/5	SS
60	1990/01/20	66	87	7	0	ID	12	221	65	105	22	316	43	133	1/5	SS
61	2003/06/21	80	206	25	121	ID	10	166	63	276	25	71	164	74	1/5	SS
62	2014/08/16	64	237	36	168	ID	6	205	43	300	47	108	23	113	2/5	TS
63	1988/08/23	32	78	20	24	NS	57	350	24	123	21	223	142	52	0/5	NF
64	1983/03/26	61	194	15	276	IS	9	57	57	162	32	322	55	145	1/5	SS
65	2003/12/24	45	204	45	214	IS	0	209	5	119	85	299	29	119	2/5	TF
66	2013/10/16	44	44	8	125	ND	37	163	43	28	24	273	174	84	1/5	UF
67	2002/06/22	49	226	44	194	ID	2	210	17	301	73	115	30	120	2/5	TF
68	2002/06/22	48	207	48	201	ID	3	204	3	294	86	69	24	114	2/5	TF
69	2002/06/22	45	215	45	214	ID	0	214	0	304	89	124	34	124	2/5	TF
70	2015/03/02	63	14	62	359	ID	18	9	6	101	71	210	6	96	2/5	TF
71	1991/11/28	36	309	27	263	ID	15	101	22	5	63	222	106	16	2/5	TF
72	1990/06/24	69	324	16	48	ND	27	95	63	283	3	187	96	6	1/5	SS
73	2002/02/14	81	151	2	241	ND	8	286	81	139	5	16	106	16	1/5	SS
74	2006/11/05	67	278	2	189	NS	18	146	67	284	15	51	144	54	1/5	SS
75	2002/01/05	66	159	15	242	IS	6	22	61	123	28	289	21	111	1/5	SS
76	2002/09/02	34	195	32	218	IS	12	29	11	121	74	251	27	117	2/5	TF
77	1990/06/20	59	290	17	211	ID	9	68	54	325	35	164	71	161	1/5	SS
78	1990/07/06	37	184	4	269	IS	31	59	37	176	38	301	46	136	2/5	UF
79	1995/10/15	49	156	2	67	ID	26	284	49	159	29	30	112	22	1/5	UF

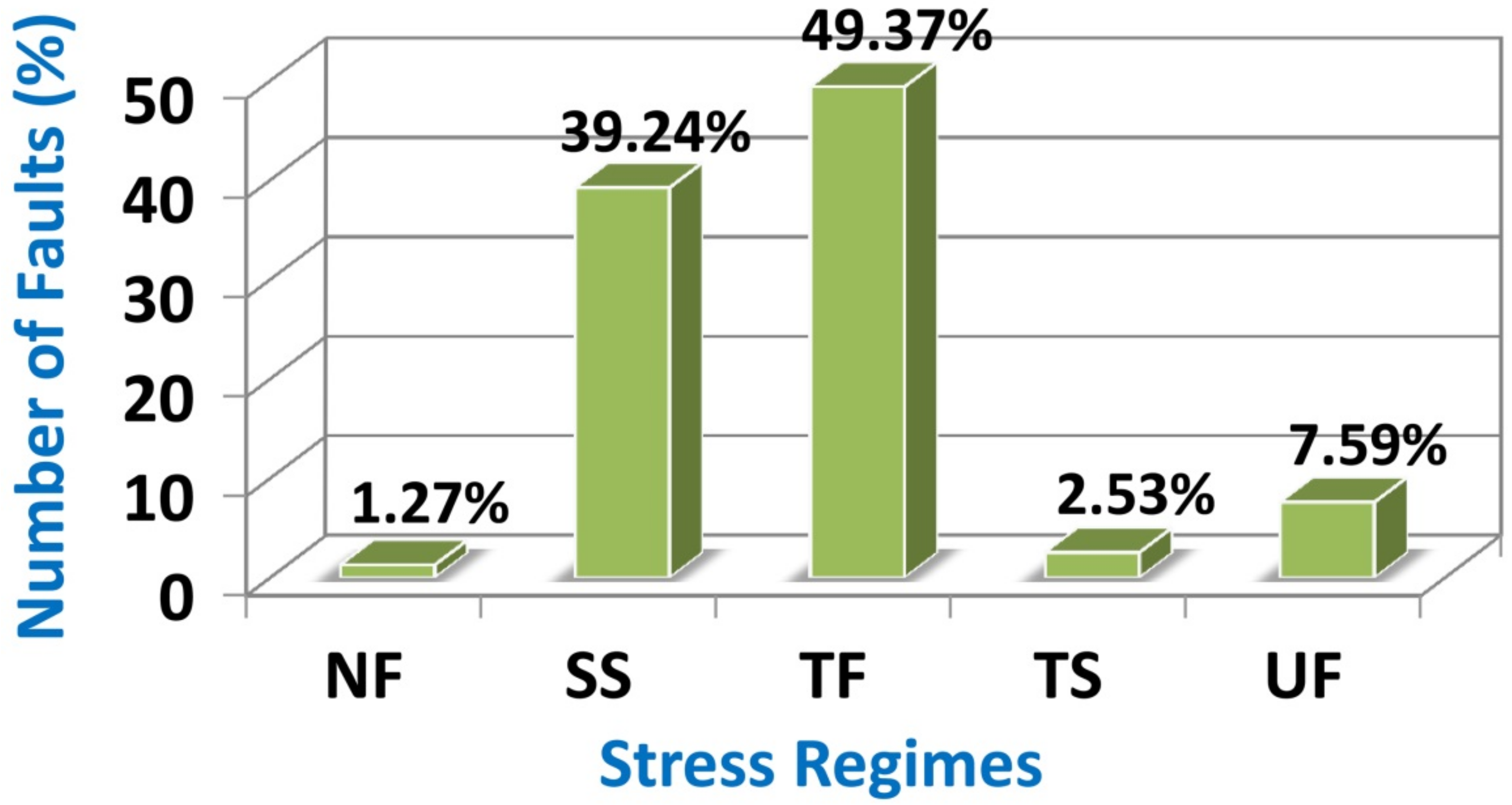
In this study, the statistical calculation related to the stress regimes indicates 49.37% thrust faulting, 39.24% strike-slip faulting, 2.53% thrust faulting with a strike-slip component, 1.27% normal faulting, and 7.59% unknown faulting (Figure 3). This calculation confirms the slip partitioning mechanism of oblique shortening, which is consistent with previous studies on the active tectonics in the area [42,49,50,65,66,67].

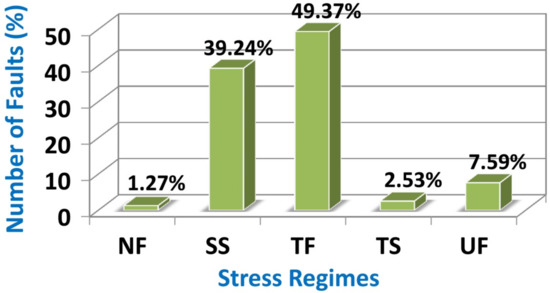
Figure 3. The statistical evaluation of tectonic stress regimes estimated from the focal mechanisms for the study area (NF, SS, TF, TS, and UF symbols are normal, strike-slip, thrust, thrust with a strike-slip, and unknown faulting, respectively).

3.1.2. Stress Directions Using FMSI

The moment stress axes T, P, and B indicate the maximum extension, maximum shortening, and unbiased axis, respectively (Table 2). In this study, to determine these axes, focal mechanism solutions are applied in the Right Dihedron method [58].

The horizontal stress directions are usually exhibited in accordance with two perpendicular horizontal axes, including Sh_min and Sh_max, as the minimum and maximum horizontal stress. Lund–Townend and Zoback methods are used for calculating the horizontal axes [68,69]. In this study, the Lund–Townend method, which is utilized in the Win-Tensor program, was applied (Table 2).

Based on the results of stress inversion in this study, no significant difference was obtained between the Right Dihedron and the Rotational Optimization methods. Anyway, the results may be more accurate in the Rotational Optimization method due to adjusting errors (Table 3).

Table 3. The obtained parameters from the Rotational Optimization method for the networks (nt: the number of used data for the networks, σ₁, σ₂, σ₃: the axes position of the main principal stress, R: the stress value, R′: the stress regime index, and Sh_min and Sh_max are the azimuths of minimum (compressional) and maximum (extensional) axes for the seismic strain rate, respectively).

Nework	n	nt	σ1 (pl/az)	σ2 (pl/az)	σ3 (pl/az)	R	R′	Shmax	Shmin	Stress Regime
1	6	5	39/094	03/187	51/281	0.04	2.04 ± 0.33	094 ± 31	184 ± 31	UF
2	4	2	09/042	47/302	42/140	0	2 ± 0.23	041 ± 12	131 ± 12	TS
3	6	3	30/004	11/101	57/208	0.93	2.93 ± 0.31	123 ± 39	213 ± 39	TF
5	6	3	02/023	80/281	10/113	0.04	1.96 ± 0.58	022 ± 13	112 ± 13	SS
6	8	6	16/093	69/316	14/187	0.27	1.73 ± 0.24	094 ± 11	184 ± 11	SS
7	8	4	05/258	17/349	72/153	0.5	2.5 ± 0.26	076 ± 16	166 ± 16	TF
8	10	5	17/026	01/116	73/208	0.66	2.66 ± 0.27	024 ± 38	114 ± 38	TF
9	8	4	11/032	11/300	74/166	0.33	2.33 ± 0.33	034 ± 15	122 ± 15	TF
10	8	4	08/050	00/140	82/233	0.25	2.25 ± 0.32	050 ± 14	140 ± 14	TF
11	12	6	16/354	04/263	73/158	0.73	2.73 ± 0.22	179 ± 34	089 ± 34	TF
12	16	10	02/025	10/294	79/127	0.67	2.67 ± 0.21	025 ± 27	115 ± 27	TF
14	20	10	06/201	22/109	67/306	0.18	2.18 ± 0.27	022 ± 12	112 ± 12	TF
15	6	3	03/018	35/110	55/283	0.55	2.55 ± 0.2	017 ± 19	107 ± 19	TF
17	10	8	03/233	52/326	38/141	0.3	1.7 ± 0.29	052 ± 13	142 ± 13	SS
18	8	7	07/223	83/059	02/313	0.17	1.83 ± 0.34	043 ± 16	133 ± 16	SS
19	4	4	01/173	77/266	13/083	0.66	1.34 ± 0.49	173 ± 21	083 ± 21	SS
21	6	3	04/049	82/292	07/140	0.2	1.8 ± 0.29	049 ± 9	139 ± 9	SS
Total	48	79	09/030	04/299	80/186	0.41	2.41 ± 0.34	030 ± 24	120 ± 24	TF

The calculation of seismic strain rate is here based on the Kostrov formula [57], already intensively used for example in the Ibero-Maghrebian region [70], Greece [71], Umbria-Marche Apennines [72], central and east Asia [73], and Mediterranean domain [74]. In the Kostrov formula, μ indicates the modulus of shear, V shows the volume of deforming seismic, N is considered as the total number of events in the time period of t, Mⁿ_ij refers to the element of seismic moment tensor for the events, and M_ij is known as the total seismic tensors.

$$\acute{\epsilon }=\frac{1}{2\mu Vt}{\displaystyle \sum }_{n=1}^N{M}_{ij}^n=\frac{1}{2\mu Vt}{M}_{ij}$$

(5)

It is noteworthy that μ and V have no effect on directions related to the principal strain axes and only are effective on the strain values [75]. The Aid and Richard’s approach [76] was used for calculating the elements of seismic strain tensor according to focal mechanism inversions (Equation (6)):

$$F_{XX}=-\left(sin\delta cos\theta sin2\phi +sin2\delta sin\theta sin2\phi \right)$$

(6)

$$F_{XY}=sin\delta cos\theta cos2\phi +0.5sin2\delta sin\theta sin2\phi$$

$$F_{XZ}=-\left(cos\delta cos\theta cos\phi +cos2\delta sin\theta sin\phi \right)$$

$$F_{YY}=sin\delta cos\theta sin2\phi -sin2\delta sin\theta cos2\phi$$

$$F_{YZ}=-\left(cos\delta cos\theta sin\phi -cos2\delta sin\theta cos\phi \right)$$

$$F_{ZZ}=sin2\delta sin\theta$$

$$F_{XY}=F_{YX}$$

$$F_{XZ}=F_{ZX}$$

$$F_{YZ}=F_{ZY}$$

ϕ refers to the fault azimuth, and δ and θ are considered as the dip and rake parameters, respectively.

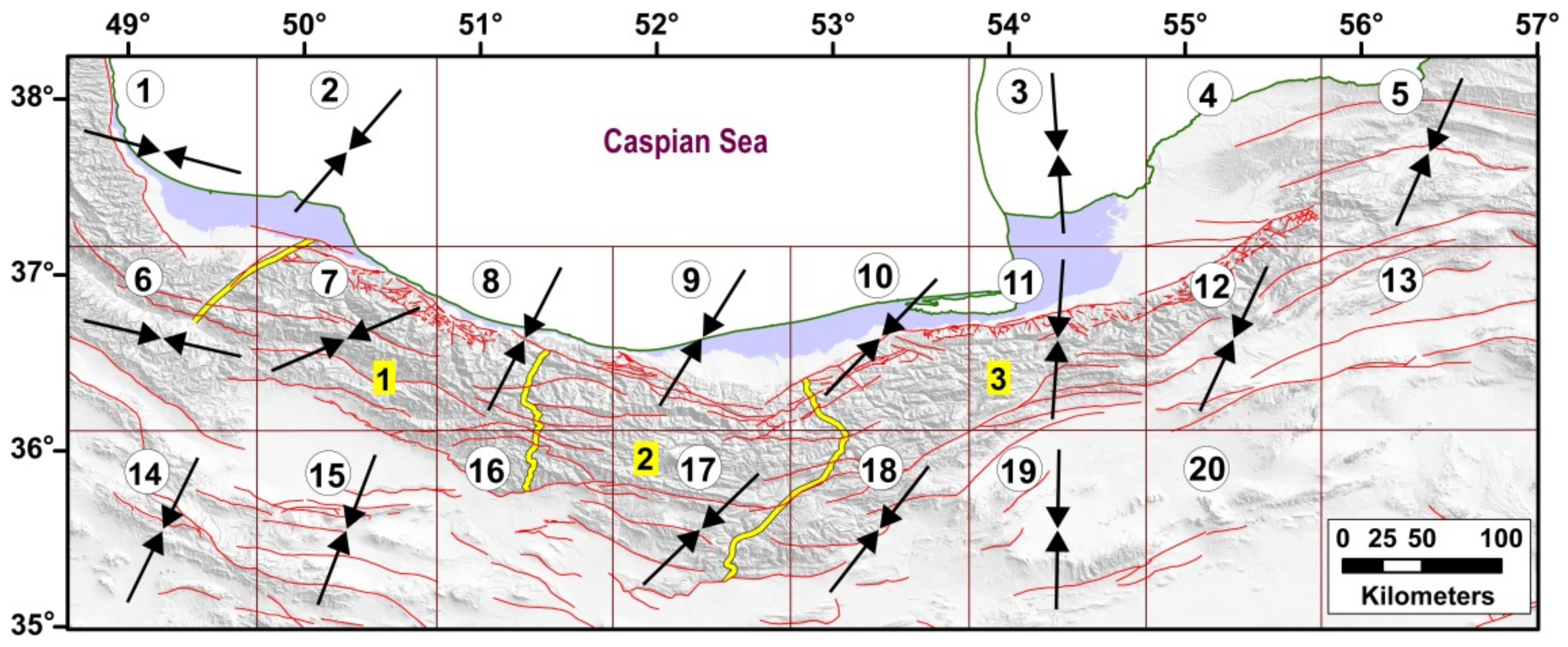
Table 4 and Figure 4 represent the magnitude and direction of the principal axes of seismic strain rates in the study area. The magnitude of seismic strain rates indicates the variable rate of deformation in different grids as well as the dominant state of the deformational regime in terms of the extension or compression.

Table 4. The azimuths and values of the compressional and extensional axes of SSR in the area.

Network	Shmax	SSR (Nanostrain/yr) for Shmax—Compressional	Shmin	SSR (Nanostrain/yr) for Shmin—Extensional
1	094 ± 31	−7.13298 × 10−9	184 ± 31	7.15106 × 10−9
3	123 ± 39	−5.87253 × 10−9	213 ± 39	6.97607 × 10−9
5	022 ± 13	−1.54027 × 10−8	112 ± 13	2.89142 × 10−8
6	094 ± 11	−1.52843 × 10−8	184 ± 11	2.4853 × 10−8
7	076 ± 16	−4.85688 × 10−9	166 ± 16	2.73138 × 10−9
8	024 ± 38	−2.7139 × 10−8	114 ± 38	1.24535 × 10−8
9	031 ± 15	−6.2759 × 10-9	121 ± 15	1.34858 × 10−8
10	050 ± 14	−1.91608 × 10−8	140 ± 14	3.26372 × 10−8
11	179 ± 34	−1.05345 × 10−8	089 ± 34	6.49058 × 10−9
12	025 ± 27	−9.32152 × 10−9	115 ± 27	1.34223 × 10−8
14	022 ± 12	−3.09085 × 10−8	112 ± 12	2.34738 × 10−8
15	017 ± 19	−9.83905 × 10−9	107 ± 19	1.23236 × 10−8
17	052 ± 13	−1.05814 × 10−8	142 ± 13	6.5344 × 10−9
18	043 ± 16	−1.34738 × 10−8	133 ± 16	1.03733 × 10−8
19	173 ± 21	−2.94161 × 10−8	083 ± 21	1.6126 × 10−8
21	049 ± 9	−3.5357 × 10−9	139 ± 9	2.10022 × 10−9
Total	030 ± 24	−3.39714 × 10−9	120 ± 24	3.29056 × 10−9

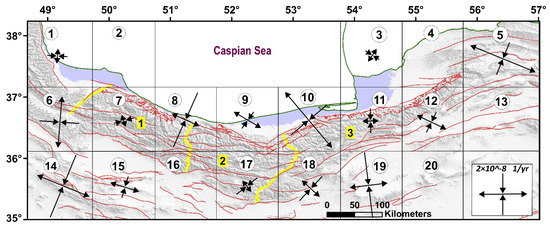
Figure 4. The direction and the magnitude of principal axes of SSR in the area. Labels within grids show grid number. Numbers 1, 2, and 3 are location of the West Alborz, Central Alborz, and East Alborz, respectively which are separated by yellow lines.

3.2. Geodetic Strain Rate (GSR)

To evaluate the GSR, we combined the reported GPS velocities [18,53] in order to provide the densest velocity field for the area. The GPS velocities [16,29] were collected during 1999–2015 and those are relative to the Eurasian reference frame (Figure 1b and Figure 5a; Table 5).

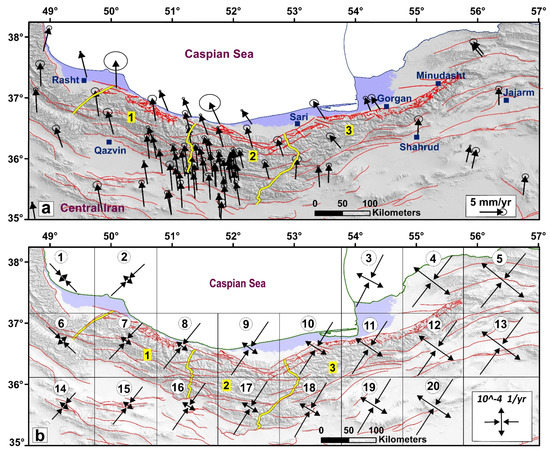
Figure 5. (a) The GPS velocity field with their error ellipses in the area which are relative to the Eurasian reference frame. (b) The principal axes of the geodetic strain rate obtained from the GPS velocities. Labels within grids show grid number. Numbers 1, 2, and 3 are location of the West Alborz, Central Alborz, and East Alborz, respectively which are separated by yellow lines.

Table 5. The GPS velocities used in this paper which are relative to Eurasian reference frame [18,53].

Site	Lat.	Long.	VE (mm/yr)	VN (mm/yr)	σVE (mm/yr)	σVN (mm/yr)	Solution
ABSD	35.6612	52.0912	−1.32	9.21	0.11	0.14	IPGN
AKHT	35.5883	50.6006	−1.52	11.71	0.13	0.1	IPGN
ARDH	37.8288	47.6501	1.02	12.9	0.15	0.16	IPGN
ARNG	35.9284	51.0749	−1.64	9.45	0.11	0.43	IPGN
BIAJ	36.0861	55.8052	1.1	8.42	0.11	0.12	IPGN
BLDH	36.2083	51.8287	−2.3	10.03	0.21	0.11	IPGN
BOJD	37.4803	57.2716	−2.36	4.56	0.1	0.11	IPGN
CHIT	35.7287	51.2132	−1.55	12.31	0.44	0.47	IPGN
CHSM	35.0876	50.9894	−1.2	12.13	0.1	0.09	IPGN
ESFN	37.0495	57.4946	0.87	6.07	0.16	0.18	IPGN
FOIM	35.4093	51.166	−1.29	12.25	0.11	0.11	IPGN
FOPM	35.7648	50.84	−1.26	11.93	0.2	0.17	IPGN
GARM	35.985	51.6457	−1.57	10.43	0.1	0.14	IPGN
HAMD	34.8691	48.5343	−1.39	13.01	0.15	0.11	IPGN
HSGD	36.0067	50.747	−1.68	11.5	0.1	0.11	IPGN
MABD	36.5884	52.2852	−4.17	7.06	0.11	0.12	IPGN
MAVT	37.801	55.9439	−4.56	6.19	0.12	0.13	IPGN
MOBK	35.0529	51.7947	−0.63	12.29	0.12	0.13	IPGN
NKAD	36.685	51.3098	−3.43	9.59	0.13	0.16	IPGN
PLOR	35.8496	52.064	−1.72	8.93	0.11	0.27	IPGN
PLZI	35.6303	51.971	−1.31	10.25	0.15	0.18	IPGN
POOL	36.4031	51.5742	−2.97	9.91	0.13	0.16	IPGN
ROKM	35.4872	51.0983	−1.21	11.49	0.4	0.36	IPGN
RSHT	37.323	49.6244	−2.29	12.89	0.1	0.1	IPGN
RTCL	35.5744	51.711	−0.37	11.24	0.65	0.3	IPGN
RTKM	35.4864	51.0989	−1.17	11.46	0.22	0.26	IPGN
SHOR	35.2772	51.8842	−1.05	13.62	0.17	0.12	IPGN
SMNN	35.5882	53.4207	−0.85	10.33	0.33	0.15	IPGN
TEHN	35.6973	51.3341	−0.43	11.28	0.16	0.1	IPGN
TKBN	36.7859	50.9301	−3.22	9.94	0.1	0.11	IPGN
TLGN	36.1436	50.745	−3.43	11.42	0.34	0.18	IPGN
TPTG	34.9019	57.2485	0.59	8.64	0.37	0.54	IPGN
ZMAN	35.5896	56.7719	0.27	9.67	0.53	0.56	IPGN
ABAL	35.793	51.986	−1.09	10.34	0.52	0.51	RA
AGKA	37.169	48.005	−0.56	13.04	0.53	0.54	RA
AMIN	35.701	52.586	−1.95	8.55	0.47	0.46	RA
ARBI	38.477	48.231	4.6	12.48	0.47	0.46	RA
ATTA	37.156	50.1	−0.14	13.5	2.1	2.09	RA
BADA	36.764	48.814	−0.17	11.61	0.36	0.35	RA
BASH	35.705	53.025	0.32	10.28	0.76	0.78	RA
BIAR	35.988	55.906	1.14	9.36	0.59	0.61	RA
BIJA	36.232	47.93	−1.98	13.59	0.36	0.35	RA
BOND	36.623	50.732	−1.37	11.28	0.74	0.76	RA
BOOM	35.73	51.812	−1.62	10.61	0.36	0.34	RA
CHSH	35.088	50.988	−1.76	11.19	0.43	0.43	RA
DAMA	35.701	52.059	−1.63	9.63	0.38	0.38	RA
DAND	36.607	48.183	0.51	12.11	0.66	0.69	RA
ESFA	37.159	57.427	0.87	4.71	0.64	0.65	RA
GHAB	36.43	54.989	−0.09	10	0.71	0.72	RA
GHAR	35.14	49.851	−1.92	13.59	0.74	0.72	RA
GHO1	36.699	49.812	−1.37	12.77	0.68	0.71	RA
GOSM	38.706	48.419	5.18	13.09	0.95	0.83	RA
GRME	37.042	56.264	−0.56	8.25	0.52	0.53	RA
HASH	37.764	48.922	2.49	11.8	0.44	0.46	RA
HEFZ	38	48.458	4.13	12.21	0.81	0.85	RA
HELI	36.206	52.305	−2.47	10.03	0.58	0.56	RA
KORD	36.86	54.199	−2.3	6.24	0.36	0.34	RA
LARZ	36.078	52.811	−2.49	8.2	0.68	0.69	RA
MARTZ	37.845	55.956	−4.27	6.03	0.58	0.61	RA
MARG	37.187	48.891	−0.13	11.51	0.7	0.72	RA
MEHR	35.868	52.157	−1.71	8.88	0.52	0.52	RA
MF01	35.683	51.955	−1.31	9.97	0.42	0.42	RA
MF02	35.801	51.797	−0.96	10.39	0.33	0.33	RA
MF03	35.649	51.885	−1.41	10.89	0.32	0.32	RA
MF04	35.258	52.117	−1.94	11.65	0.36	0.36	RA
MF05	35.493	51.277	−0.68	12.2	0.44	0.43	RA
MF06	35.227	50.543	−1.07	12.17	0.43	0.43	RA
MF07	35.897	52.008	−0.4	8.74	0.33	0.34	RA
MF10	36.394	51.304	−2.5	11.48	0.46	0.47	RA
MF12	36.15	51.315	−1.12	12.04	0.54	0.54	RA
MF13	36.009	50.632	−1.1	11.57	0.44	0.44	RA
MF15	35.988	51.613	−2.37	11.65	0.33	0.33	RA
MF16	35.724	51.665	−1.17	11.92	0.33	0.33	RA
MF17	35.753	51.108	−1.43	10.9	0.32	0.33	RA
MOBA	34.977	51.808	0.09	10.71	0.77	0.76	RA
NEYA	36.401	50.045	−2.21	11.43	0.76	0.8	RA
NOSH	36.586	51.768	−4.08	10.47	1.93	1.75	RA
ORTA	37.929	47.869	3.5	13.87	0.61	0.61	RA
PISH	35.224	51.885	−0.76	10.97	0.52	0.51	RA
SEMN	35.662	53.564	−0.02	8.87	0.42	0.4	RA
SHA1	36.679	53.492	−4.6	8.21	0.74	0.76	RA
SHIR	37.814	57.308	−2.79	3.55	0.45	0.41	RA
TANG	35.492	52.043	−0.85	9.97	0.36	0.36	RA
TF01	35.812	51.257	−1.6	12.9	0.42	0.42	RA
TF09	35.833	51.425	−1.25	12.56	0.5	0.5	RA
TF16	35.774	51.522	−1.7	12.36	0.41	0.41	RA
TF20	35.808	51.568	−3.19	11.43	0.51	0.52	RA
TN01	35.493	51	−1.03	13.22	0.7	0.7	RA
TN02	35.203	51.17	−0.68	12.99	0.45	0.46	RA
TN03	35.366	51.379	−0.78	12.85	0.48	0.49	RA
TN04	35.495	51.409	−1.28	13.3	0.46	0.47	RA
TN05	35.633	51.515	−0.31	11.41	0.49	0.5	RA
TN06	35.55	51.724	−0.46	11.3	0.4	0.4	RA
TN07	35.763	51.994	−1.75	9.72	0.47	0.48	RA
VRMN	35.344	51.632	−0.77	12.72	0.25	0.63	RA
KAHO	36.236	53.739	−4.46	5.93	0.71	0.72	RA
GRGN	36.876	54.353	−3.72	6.21	0.61	0.61	RA
KRMD	36.196	49.211	−2.4	9.75	0.61	0.61	RA

The geodetic strain rate tensor (GSRT) is estimated using three methods are used to [77]: inversion of baseline variations [78], networked (gridded) using either a spherical wavelet-based multiscale approach [79], or interpolation of bi-cubic spline [80], and the triangle [81]. In the gridded method, a functional relation is defined between displacement and position with basic functions to measure an interpolated velocity grid in order to calculate GSRT. Thus, the quality of the outputs is strongly dependent on the quality of the velocity field, which is particularly true for the triangle method. Therefore, an error in the velocity at only one station creates a large error in the GSRT calculated for the triangles adjacent to this station [16]. So, in this study, in order to perform calculations with the least error, the Grid_strain MATLAB^TM toolbox [82] was used to measure the horizontal geodetic strain rates with the grid pattern from GPS horizontal velocities. The obtained deformation field pattern is a set of the principal components of the strain calculated on a regular grid whose limits and steps can be selected by the user (see [82,83] for both a general description of the implemented method and examples of its application to GPS-based regional-scale analysis of a strain field). The computations in the Grid_strain toolbox are performed using a modified least square method (MLS) [84]. Since our stations are not uniformly distributed, the MLS method works well and produces a more meaningful solution [82].

The strain rates at the center of each cell of a ~100×~100 km square grid (network) were estimated by including 98 Eurasia-fixed GPS velocities (Figure 5a,b). In the MLS approach, the velocity of the close stations contributes more to the solutions, and a more reasonable strain rate field is evaluated for such a heterogeneous tectonic area where different deformation mechanisms and kinematics can be observed. Table 6 and Figure 5 indicate the geodetic strain rate within each grid of the study area.

Table 6. The min and max horizontal extension values with their azimuths (geodetic strain rates).

Network	Grid Cells		Max Horizontal Extension (e1H) (Nano-Strain/yr)	Azimuth of e1H (Degrees)	Min Horizontal Extension (e2H) (Nano-Strain/yr)	Azimuth of e2H (Degrees)
	X	Y
1	49.2483	37.6682	0.000162898	46.9	−0.001204939	136.9
2	50.2483	37.6682	0.000329513	130.4	−0.001475233	40.4
3	54.2483	37.6682	0.000994944	117.3	−0.001967151	27.3
4	55.2483	37.6682	0.001358583	118.8	−0.002143497	28.8
5	56.2483	37.6682	0.001639143	119.7	−0.002278049	29.7
6	49.2483	36.6682	0.00020837	43.7	−0.001150128	133.7
7	50.2483	36.6682	0.000359024	127.7	−0.001536166	37.7
8	51.2483	36.6682	0.000495266	122.3	−0.001916237	32.3
9	52.2483	36.6682	0.000608155	118.2	−0.002146157	28.2
10	53.2483	36.6682	0.000755598	115.5	−0.002035001	25.5
11	54.2483	36.6682	0.000999034	115.6	−0.002087938	25.6
12	55.2483	36.6682	0.001315729	117	−0.002234682	27
13	56.2483	36.6682	0.00147653	117.4	−0.002351095	27.4
14	49.2483	35.6682	0.000203814	128	−0.001055016	38
15	50.2483	35.6682	0.000338303	123.3	−0.00147974	33.3
16	51.2483	35.6682	0.000463716	119	−0.001882042	29
17	52.2483	35.6682	0.000590397	116.1	−0.002105185	26.1
18	53.2483	35.6682	0.000740699	114.1	−0.002089573	24.1
19	54.2483	35.6682	0.000961116	114.3	−0.002106891	24.3
20	55.2483	35.6682	0.001211232	115.3	−0.002230437	25.3
21	56.2483	35.6682	0.001274437	115.6	−0.002304888	25.6

3.3. Present Crustal Stress Map of Northern Iran

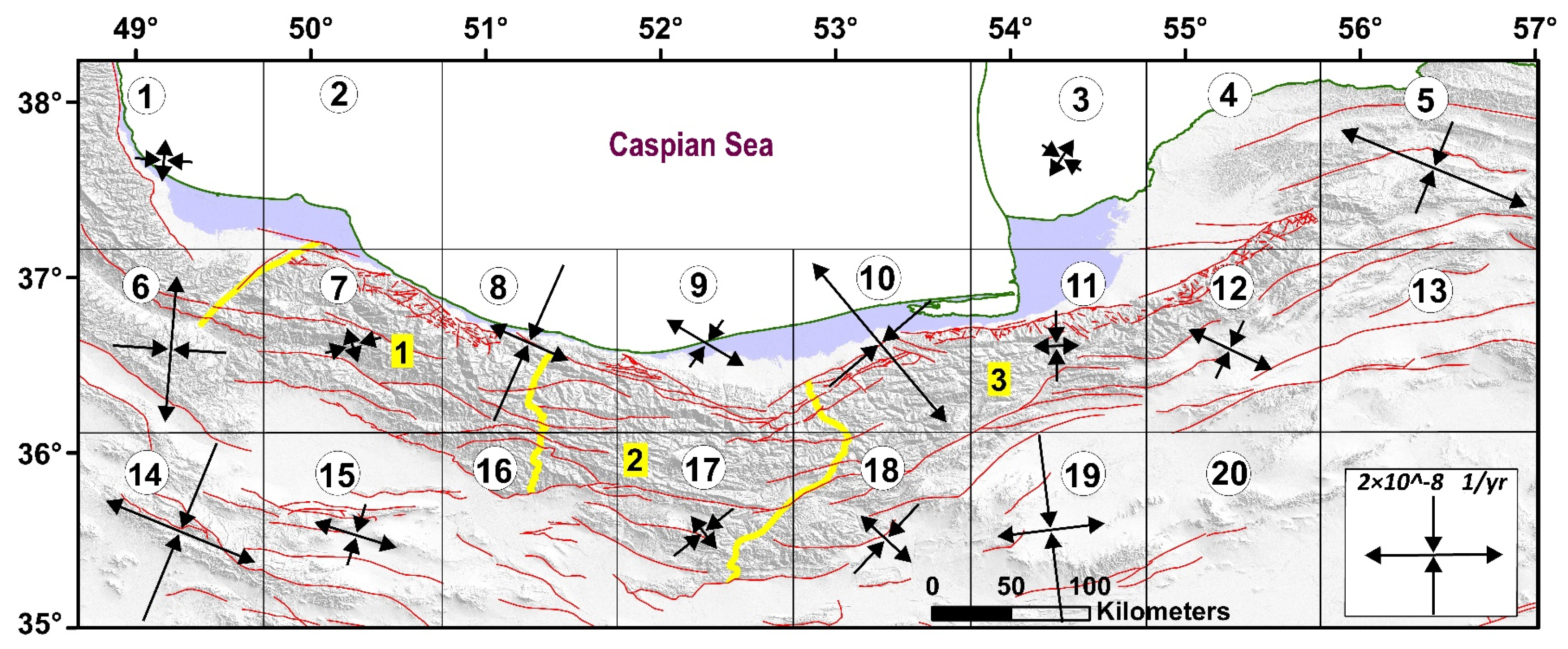
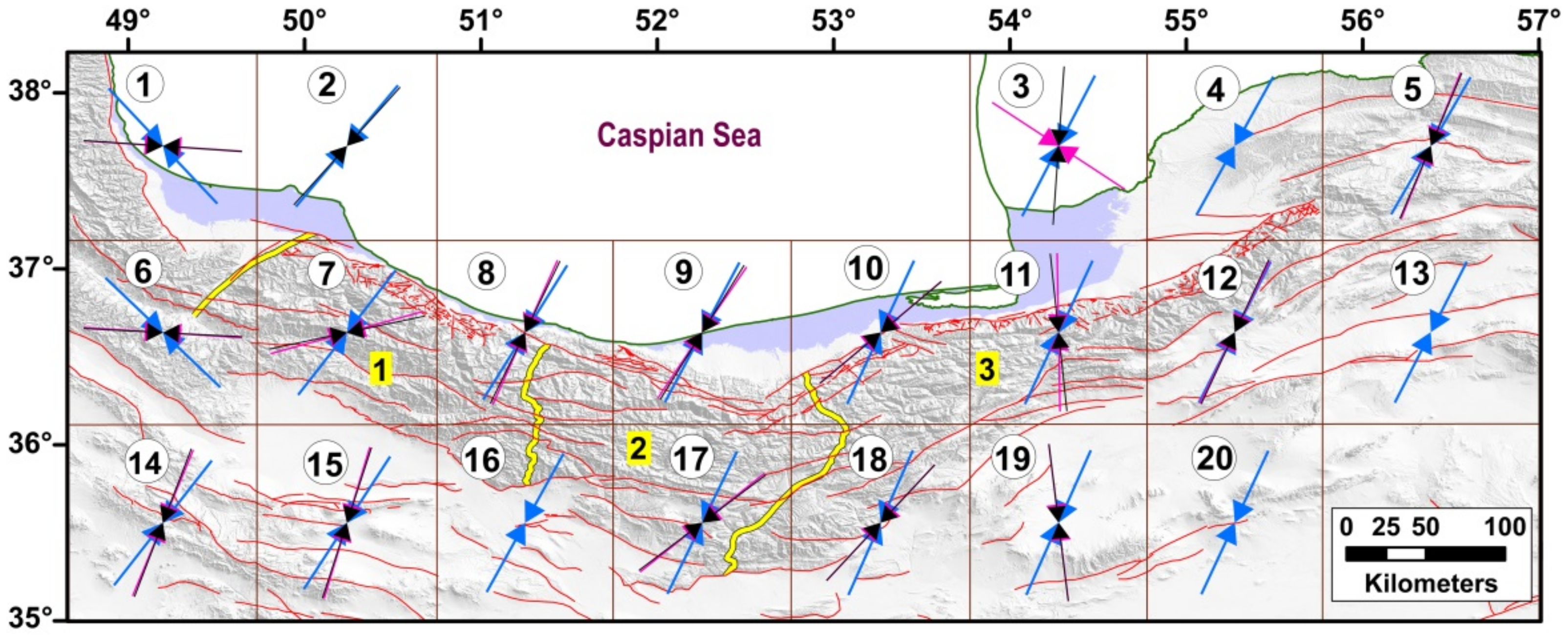
In this section, the output of SSR, FMSI, and GSR were compared to evaluate the relationship between the stress and strain directions. Figure 6 shows the direction of the compressional axes of the three methods for each network.

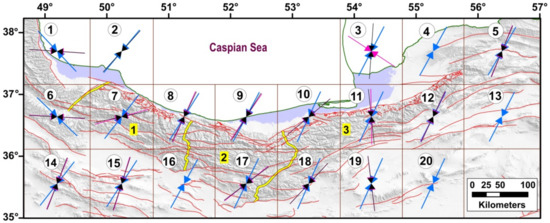
Figure 6. The compression directions of the principal axes resulted from the geodetic strain rates (blue), stress inversion (black), and seismic strain rates (purple). Labels within grids show grid number. Numbers 1, 2, and 3 are location of the West Alborz, Central Alborz, and East Alborz, respectively which are separated by yellow lines.

Like in the study of Zarifi et al. [22], the Pearson’s correlation coefficient of SSR, FMSI, and GSR were estimated, and accordingly, a new crustal stress field was suggested. The coefficient is determined as the covariance of two variables divided by the product of their standard deviations [85], as shown in Equation (7).

$$p_{xy}=\frac{Cov\left(x,y\right)}{{\sigma }_x{\sigma }_y}$$

(7)

Furthermore, it indicates a measurement for the linear correlation among the two data collections in which the range (p) varies from −1 to +1.

In general, an acceptable correlation was observed between the strain and stress tensors. The results indicated a correlation between FMSI and GSR (p = +0.9), SSR and GSR (p = +0.8), and FMSI and SSR (p = +0.9). In addition, along with the absolute deviation value of each method of analyzing strain/stress tensor, the mean direction of the compression stress (and strain rate) was calculated in each network. Equations (8)–(10) are used for measuring a new stress field in the area.

$$Weighte{d}_{AVE}=\frac{Coe{f}_{FMSI}\times FMSI+Coe{f}_{SSR}\times SSR+Coe{f}_{GSR}\times GSR}{Coe{f}_{FMSI}+Coe{f}_{SSR}+Coe{f}_{GSR}}$$

(8)

$${\mathrm{Coef}}_{\mathrm{Method}}=\frac{\sum \mathrm{Dev}.\mathrm{Methods}-\left|\mathrm{Dev}.\mathrm{from}\mathrm{mean}\mathrm{method}\right|}{\sum \mathrm{Dev}\mathrm{methods}}$$

(9)

$$\begin{gathered} \sum \mathrm{Dev}.\mathrm{methods}=|\mathrm{Dev}.\mathrm{from}\mathrm{mean}\mathrm{FMSI}|+\left|\mathrm{Dev}.\mathrm{from}\mathrm{mean}\mathrm{SSR}\right| \\ +\left|\mathrm{Dev}.\mathrm{from}\mathrm{mean}\mathrm{GSR}\right| \end{gathered}$$

(10)

where | | is the absolute value and “Dev. from mean FMSI” indicates the deviation of the FMSI result in each network from the mean value of the three methods by representing the direction of stress in that network. The maximum weight belongs to the method with the minimum deviation from the mean value and vice versa. Table 7 shows the outputs related to the statistical method, and Figure 7 displays the direction of the weighted average compression stress in the study area.

Table 7. The weighted average of the maximum horizontal compression axes obtained from the FMSI, SSR, and GSR for the study area.

Network	Mean Value of Azimuth	Dev. from Mean (FMSI)	Dev. from Mean (SSR)	Dev. from Mean (GSR)	Weighted Average of Azimuths
1	108.3	14.3	14.3	28.6	105
2	41.13	0.87	0.13	0.73	41
3	171.43	12.57	48.43	35.87	176
5	24.9	1.9	2.9	4.8	24
6	106.9	13.9	12.9	26.8	103
7	63.9	14.1	12.1	26.2	67
8	27.43	1.43	3.43	4.87	27
9	31.4	0.6	2.6	3.2	32
10	41.83	8.17	8.17	16.33	44
11	186.2	12.2	7.2	19.4	184
12	25.66	0.66	0.66	1.34	25
14	27	6	5	11	26
15	22.76	4.76	5.76	10.54	21
17	43.7	9.3	8.3	17.6	46
18	36.7	6.3	6.3	12.6	38
19	183.43	10.43	10.43	20.87	181

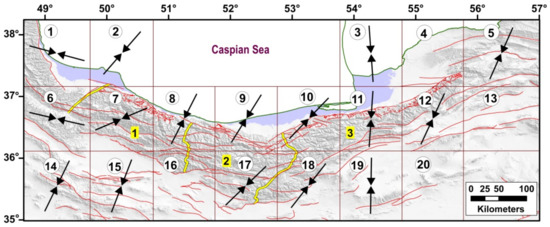
Figure 7. The extracted direction of the weighted average of the maximum horizontal compression stress from GSR, SSR, and FMSI. Labels within grids show grid number. Numbers 1, 2, and 3 are location of the West Alborz, Central Alborz, and East Alborz, respectively which are separated by yellow lines.

3.4. Geodetic Moment Rate (GMR)

The geodetic moment, which can be measured using the GPS velocity vector, indicates the cumulative and released energy which occurs in the study area. In this study, the GMR was measured in each grid based on the procedure suggested by Kostrov [57], as shown in Equation (11) where, μ, A, and Hs indicate rigidity, grid area, and seismogenic thickness, respectively. The geodetic monitoring can be quantified into potential seismic activities within the grids by the known values of A, T, μ (3 × 10¹⁰ Pa), and Hs (~25 km) even if the activity is dependent on the hidden faults or the faults with a too slow slip that usually these are not applied for evaluating using seismological techniques.

$$Ṁ=2\mu A{H}_S\acute{Ԑ}=\left(1/T\right){\displaystyle \sum }_{n=1}^m{M}_n$$

(11)

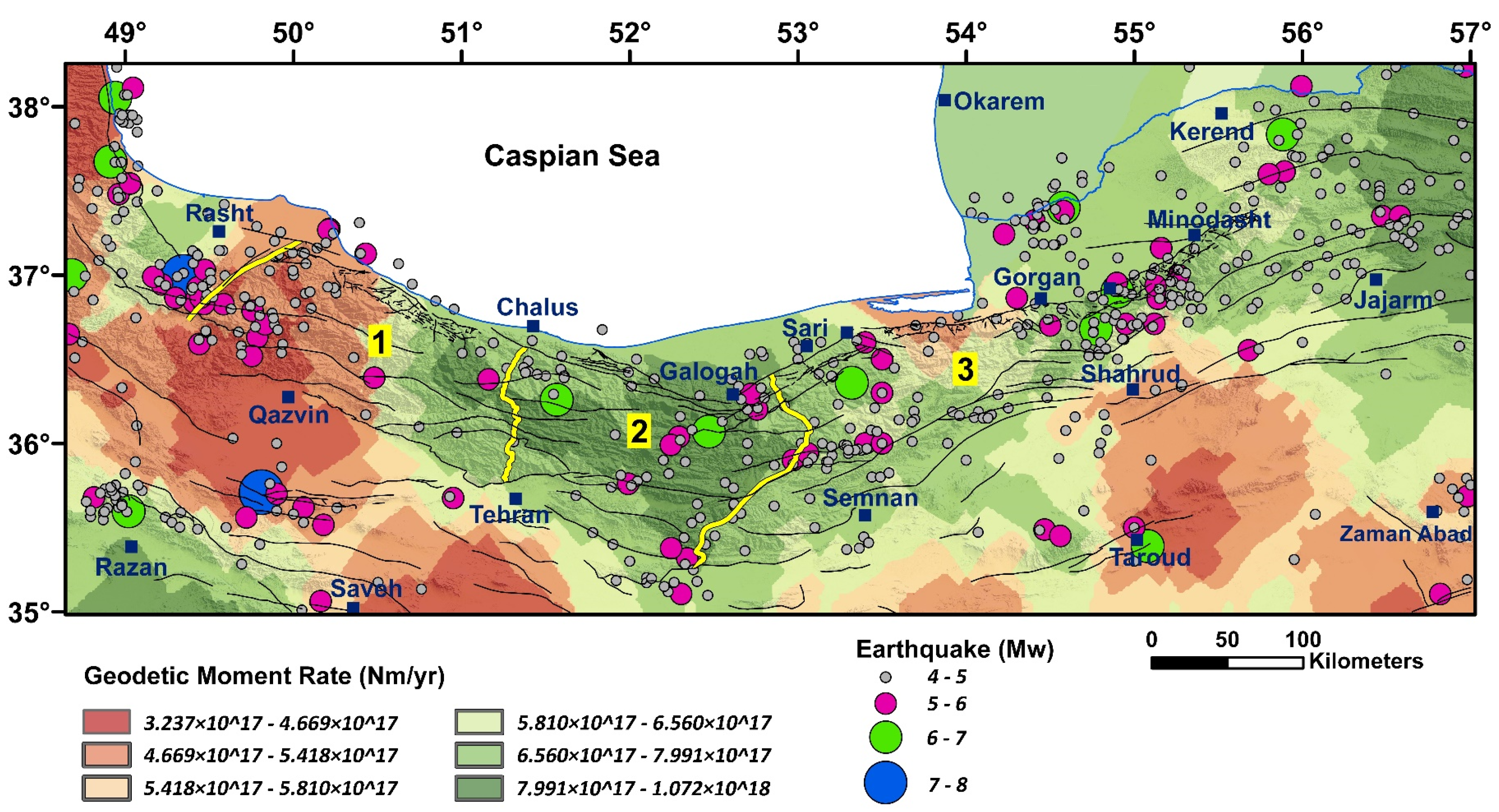
The outputs (Table 8 and Figure 8) indicate that in some networks, such as 5, 8, 9, and 17, the geodetic moment rates are higher than in others. There are some faults with a history of high seismic activity, such as the eastern segment of the North Alborz, Royan (within the networks 8, 9), Mosha, Garmsar, Eivanaki (within the network 17), and Bashtapeh, Takalkuh (within the network 5) faults.

Table 8. The maximum principal amount (eigenvalues) of the strain rate tensor, and geodetic moment rates in the area.

Network	Area (km2)	Maximum Principal Amount of Strain Rate Tensor	Ṁ = Geodetic Moment Rate (Nm/yr)
1	11,194.47599	27.70711674	4.65 × 1017
2	10,712.5321	34.41816646	5.53 × 1017
3	10,568.26425	36.81068353	5.84 × 1017
4	10,508.36422	43.57258493	6.87 × 1017
5	12,985.56011	54.67529617	1.06 × 1018
6	11,088.32668	24.66397772	4.10 × 1017
7	10,601.42425	20.36183083	3.24 × 1017
8	10,371.90613	66.79501698	1.04 × 1018
9	10,464.66935	68.25293202	1.07 × 1018
10	10,522.52897	40.89540687	6.45 × 1017
11	10,410.4953	33.52953634	5.24 × 1017
12	10,333.08338	43.43789994	6.73 × 1017
13	12,771.5384	43.32692631	8.30 × 1017
14	11,953.12154	40.31620524	7.23 × 1017
15	11,446.90983	33.40766078	5.74 × 1017
16	11,211.42643	35.19185973	5.92 × 1017
17	11,330.47318	61.91950157	1.05 × 1018
18	11,408.08301	44.63381377	7.64 × 1017
19	11,307.8592	43.37250864	7.36 × 1017
20	11,234.47032	27.45658691	4.63 × 1017
21	13,906.84458	26.20196298	5.47 × 1017

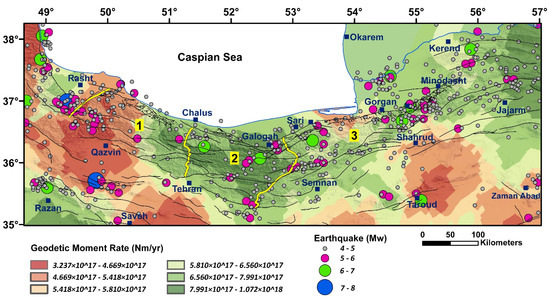
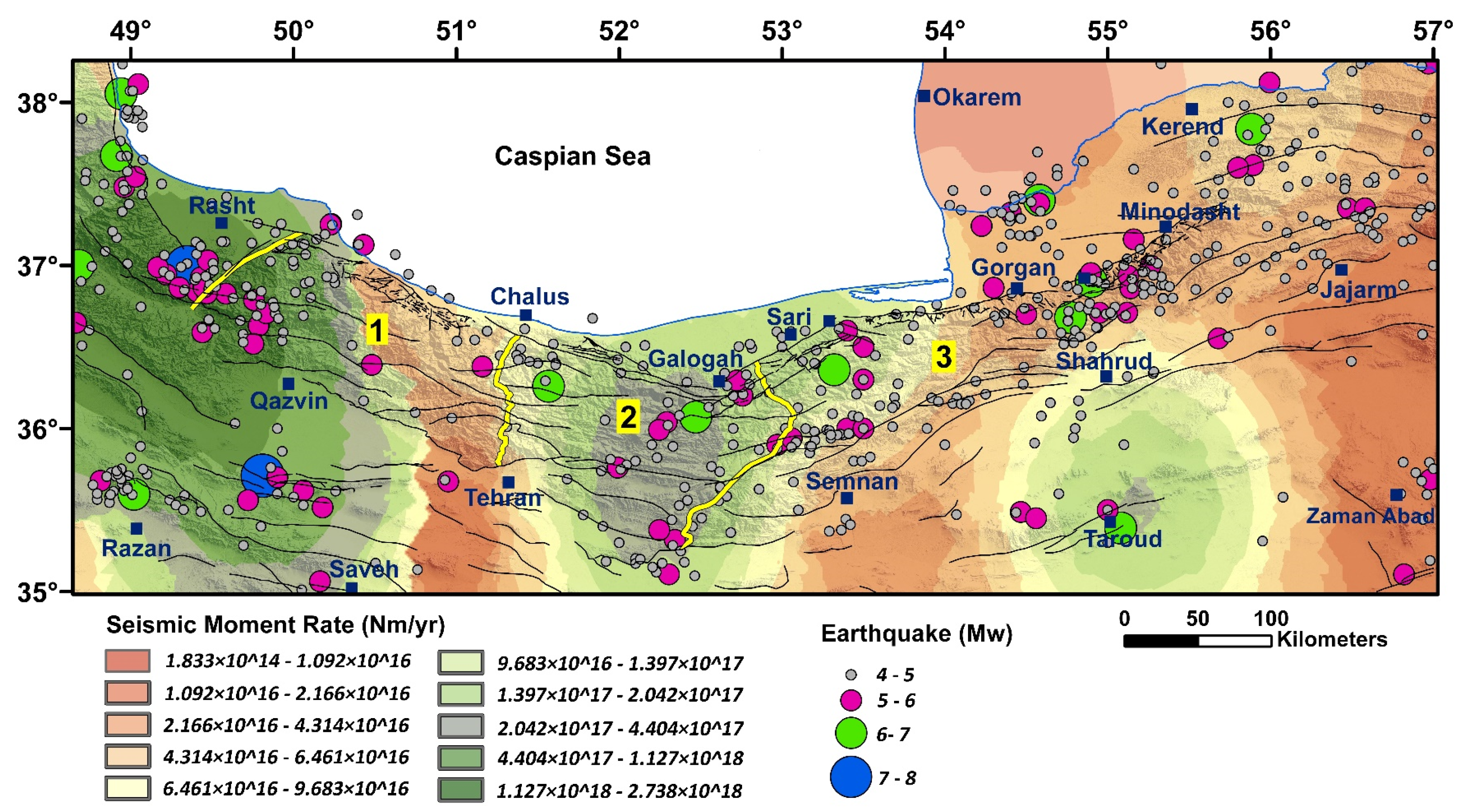
Figure 8. Zoning map of GMR with the distribution of the earthquakes (1900–2020). Numbers 1, 2, and 3 are location of the West Alborz, Central Alborz, and East Alborz, respectively which are separated by yellow lines.

3.5. Seismic Moment Rate (SMR)

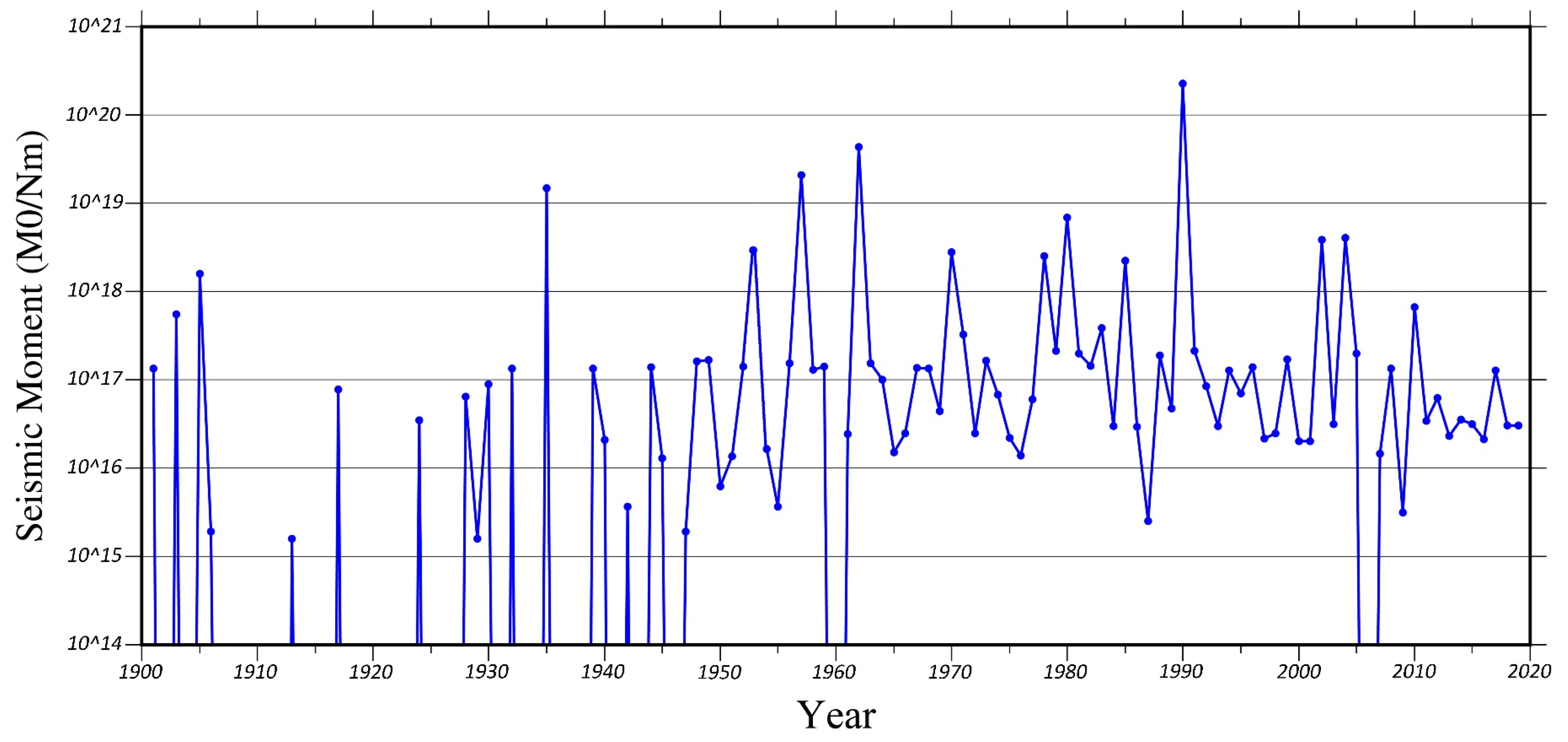
SMR only measures the deformation accommodated by faulting [1]. To estimate it in different parts of the area, all of the earthquakes that occurred from 1900 to 2020 are displayed in Figure 9. Based on the magnitude of earthquakes, the amount of seismic moment for each earthquake is calculated (Equation (12)).

LogM0 = Cm + d

(12)

where m indicates magnitude, M0 shows the seismic moment, and C and d are considered constant parameters related to the law suggested by Hanks and Kanamori [86].

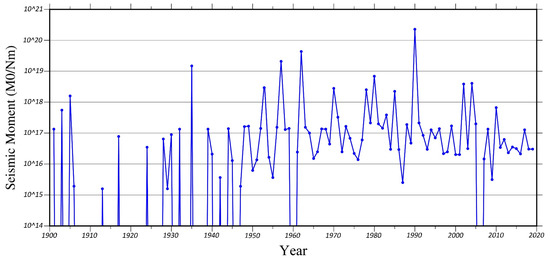
Figure 9. The seismic moment variation for the area during 1900–2020.

According to the seismic moment calculations (during the catalog years), the maximum amount of released energy occurred in 1990, 1962, 1957, 1935, 1980, 2004, 2002, and 1953 when the main earthquakes happened (Figure 9 and Table 9).

Table 9. The destructive earthquakes in the study area with high seismic moment (1900–2020).

ID	Date		Earthquake Name	Mw	Seismic Moment (Nm)
1	1990	20.06.1990	Rudbar	7.3	3.57635 × 1020
		20.01.1990	Firuzkouh (Gaduk)	6.0
		21.06.1990	Rudbar	5.8
2	1962	1.09.1962	Buin-Zahra	7.2	6.36565 × 1019
		4.09.1962		5.6
		13.10.1962		5.5
3	1957	2.07.1957	Band-e pay	7.0	3.17278 × 1019
4	1935	11.04.1935	Kusut	6.8	1.68755 × 1019
		5.03.1935	S. Dauab	5.8
		12.04.1935	Kusut	5.6
		12.04.1935		5.5
5	1980	4.05.1980	Shirabad	6.6	8.35681 × 1018
		22.07.1980	Lahijan	5.6
6	2004	28.05.2004	Baladeh (Firuzabad-e Kojur)	6.4	6.08709 × 1018
		7.10.2004	AqQala, Gorgan	6.2
7	2002	22.06.2002	Changureh(Abdareh, Avaj)	6.5	5.88132 × 1018
8	1953	12.02.1953	Torud	6.5	5.77132 × 1018
9	1970	30.07.1970	Karnaveh	6.4	4.45476 × 1018
10	1978	4.11.1978	Siahbil	6.4	4.02346 × 1018
11	1985	29.10.1985	Nomal	6.2	3.49503 × 1018
		29.10.1985	Nomal	6.1
12	1905	9.01.1905	Darram	6.2	1.99526 × 1018
13	2010	27.08.2010	Kuh Zar, Torud	5.9	8.18611 × 1017
14	1903	24.06.1903	Anzali	5.9	7.39569 × 1017
15	1983	22.07.1983	Charazeh	5.6	5.88678 × 1017
		25.03.1983	Baijan	5.5
16	1971	14.02.1971	Serokhi	5.7	5.08224 × 1017

Using the average seismic moment of earthquakes [1] and the cumulative seismic moment diagram [2] methods, the seismic moment was converted to the seismic moment rate (Table 10).

Table 10. The seismic moment rate for each networks in the area.

Network	Seismic Moment Rate Using Average Seismic Moment of Earthquakes (Nm/yr)	Seismic Moment Rate Using Chart of Cumulative Seismic-Moment (Nm/yr)
1	1.15301 × 1017	1.93 × 1017
2	7.90178 × 1015	7.78 × 1015
3	3.13053 × 1016	4.64 × 1016
4	2.62172 × 1015	1.82 × 1015
5	7.40225 × 1016	5.76 × 1016
6	3.11717 × 1018	4.90 × 1018
7	1.11562 × 1016	1.51 × 1016
8	7.64361 × 1016	4.76 × 1016
9	3.48831 × 1015	3.22 × 1015
10	1.75802 × 1017	9.83 × 1016
11	1.84283 × 1016	2.63 × 1016
12	3.93429 × 1016	6.84 × 1016
13	2.51943 × 1015	2.23 × 1015
14	1.0757 × 1017	1.34 × 1017
15	1.48034 × 1018	3.92 × 1018
16	1.83342 × 1015	1.20 × 1015
17	3.61648 × 1017	3.06 × 1017
18	2.52176 × 1016	2.04 × 1016
19	1.24076 × 1016	5.81 × 1015
20	2.39596 × 1017	2.76 × 1017
21	6.54321 × 1015	6.73 × 1015

The maximum seismic moment rates are obtained in the networks 6, 15, 17, 20, 10, 1, and 14 (Table 10 and Figure 10), where the main faults are Manjil, Rudbar, Ipak, Eshtehard, Kushk-e-Nosrat, Garmsar, Eivanaki, Mosha, Torud, Khazar, Sari, and Astara faults. Some faults, such as Rudbar, Ipak, Torud, and Sari faults, had a significant contribution to the resulting seismic moment rate.

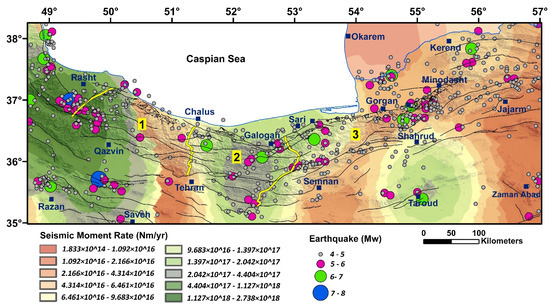
Figure 10. Zoning map of the SMR with the earthquake distribution (1900–2020). Numbers 1, 2, and 3 are location of the West Alborz, Central Alborz, and East Alborz, respectively which are separated by yellow lines.

4. Results and Discussion

The crustal faults (Figure 1c) with different slip rates in Alborz and its surrounding area have a crucial role in evaluating different seismicity patterns. In the eastern part of the Alborz range, the left lateral strike-slip movement varies from ~2 in the south to ~5 mm/yr in the north of the range, while in the western part, mainly a left-lateral component changes by ~2 mm/yr in the north to ∼1 in the south of the range [87]. Therefore, determining the stress and strain fields resulting from the movement of the earth’s crust in an area can help to better understand the active tectonics [19,88,89]. In this study, a stress map is suggested for northern Iran using a combination of the obtained results from GSR, SSR, and FMSI according to a multi-disciplinary method (Figure 7). The compressional stress directions are approximately WNW-SSE in the Talesh Mountains, and NNE-SSW in the Alborz and its surrounding area (Figure 7), which is in line with the results of previous studies [22]. Directions are the result of the progressive collision of the South Caspian Basin with Central Iran (in the late Miocene; ~6–2 Ma) and the clockwise rotation of the South Caspian Basin [49,90].

The stress directions in most networks are oblique to the faults strike except for NW-SE trending faults in the central Alborz (e.g., the faults within networks 8 and 9) with the reverse dominant components, and E-W trending faults in the east Alborz (e.g., the faults within networks 11 and 19) where are associated with folding [50,91] (Figure 7). Therefore, the current stress in the area usually leads to the shearing and reversing of the rock units along the active faults.

Strike-slip faults with an acute angle related to the stress direction include segments with en-echelon arrays which show the sense of shearing and lateral motion on the fault planes [92,93,94,95,96,97]. In the area, most fault systems (even those with present reverse mechanisms) indicate clear en-echelon segmentation. Some of them, such as the southern margin fault of the eastern Alborz, or Shahrud fault system [98], include the Garmsar, Semnan, Atari, Shahrud, and Jajarm fault segments (Figure 1c), each of which is known as an isolated faults zone.

In northern Iran, a transition zone occurs between Talesh and the western Alborz at ~49°40′E. The differential motions of these subzones, which are accompanied by the strike-slip and reverse faults, are well-established based on the obtained stress directions (Figure 7). Regarding the seismic and geodetic strain rate, higher seismic deformation zones (e.g., the Talesh-Alborz transition zone) are correlated well with the distribution of large earthquakes (e.g., the 1990 Mw 7.3 Rudbar). For seismic hazard assessment, the study area was divided into 21 networks, and the geodetic, seismic strain, and moment rates were calculated to investigate the seismicity pattern.

4.1. Analysis of Geodetic and Seismic Strain Rates

The geodetic strain rate in networks 13, 5, 12, and 20 are larger than the others (Figure 5b). These networks are located in the western Koppeh-Dagh, and eastern Alborz mountains where the main faults are the Jajarm, Siahkuh, Takalkuh, Bashtapeh, Shahrud, and east segment of the Khazar fault (see the name of faults in Figure 1c). The geodetic strain rate is also large in network 9 where the main faults are Royan, the east segment of north Alborz faults [50], and where the 2004 Mw 6.4 Baladeh earthquake occurred [12].

About 168.5 km of surface ruptures have been formed by the four destructive earthquakes, including the 1953 Mw 6.5 Troud, the 1962 Mw 7.2 Buin-Zahra, the 1990 Mw 7.3 Rudbar (label 77 on Figure 2), and the 2002 Mw 6.5 Changureh (label 55 on Figure 2), with more than 53,391 deaths [13,99]. The earthquake of 12 December1953 (Mw 6.5) occurred along the Torud fault within network 20, where the geodetic strain rate is high (Figure 5b). Networks 6, 14, and 15 in the Talesh and NW of Central Iran, which indicate low geodetic strain rates (Figure 2) are included in the other three earthquakes (Buin-Zahra, Rudbar, and Changureh earthquakes). The Rudbar, Avaj (or Kushk-e Nosrat), and Ipak as destructive earthquake faults with Astara and Eshtehard faults are located in these subzones.

Other destructive earthquakes that have not reported their surface rupture are (Table 9): the 1903 Mw 5.9 Anzali (within network 1), the 1978 Mw 6.4 Siahbil (within network 1; label 3 on Figure 2), and the 1980 Mw 6.6 Shirabad (within network 1; label 4 on Figure 2) due to the activity of the Astara fault; the 2004 Mw 6.2 AqQala (within network 11; label 21 on Figure 2) due to the activity of the Gonbad or Khazar faults; the 1905 Mw 6.2 Darram (within network 6), the 1957 Mw 7 Band-e pay (within network 6), and the 2004 Mw 6.4 Baladeh (within network 8; label 10 on Figure 2) due to the activity of the north Alborz and Royan faults; the 1935 Mw 6.8 Kusut (within network 10), the 1985 Mw 6.1 Nomal (Between networks 11 and 12; label 26 on Figure 2), and the 1990 Mw 6 Firuzkouh (within network 18; label 60 on Figure 2) due to the activity of the Astaneh or Firouzkuh faults; the 2010 Mw 5.9 Kuh Zar (within network 19; label 42 on Figure 2) due to the activity of the Torud fault.

The seismic strain rate for each network was estimated using instrumental earthquakes in order to explain most of the seismic strain (Figure 4). In networks 14 and 19 (the northern parts of central Iran), the networks 8 and 10 (the northern parts of the Alborz), the network 5 (the western part of the Koppeh-Dagh), and network 6 (the southern part of the Talesh), where the distribution of the earthquakes indicates shearing and compression, patterns of deformations for small and large earthquakes are observed. Relatively large extensional components of seismic strain rate are evident in these networks (networks 10, 5, 6, 14, and 19), where there are the main left-lateral strike-slip faults such as Sari, Khazar, Rudbar, Avaj (or Kushk-e Nosrat), and Torud faults.

In the study area, the directions of the seismic strain rate are generally coaxial with the geodetic strain rate (Figure 6). This uniformity between the directions of seismic and geodetic strain rates highlights the use of discontinuous or continuous assumptions for calculating the style and direction of the strain rates. In fact, the seismic strain corresponds to discontinuous deformation within a network due to the displacements along faults, while the geodetic strain is computed from continuous deformation. In networks 14, 8, 19, 6, 10, and 5 despite the consistency in directions of the principal stress and strain axes, there is geodetically and seismically a significant relative inconsistency between the magnitudes of the compressional strain rates (Figure 4 and Figure 5b). This discrepancy can be related to the occurrence of large earthquakes, as well as the recurrence interval of earthquakes in this area.

4.2. Analysis of Geodetic and Seismic Moment Rates

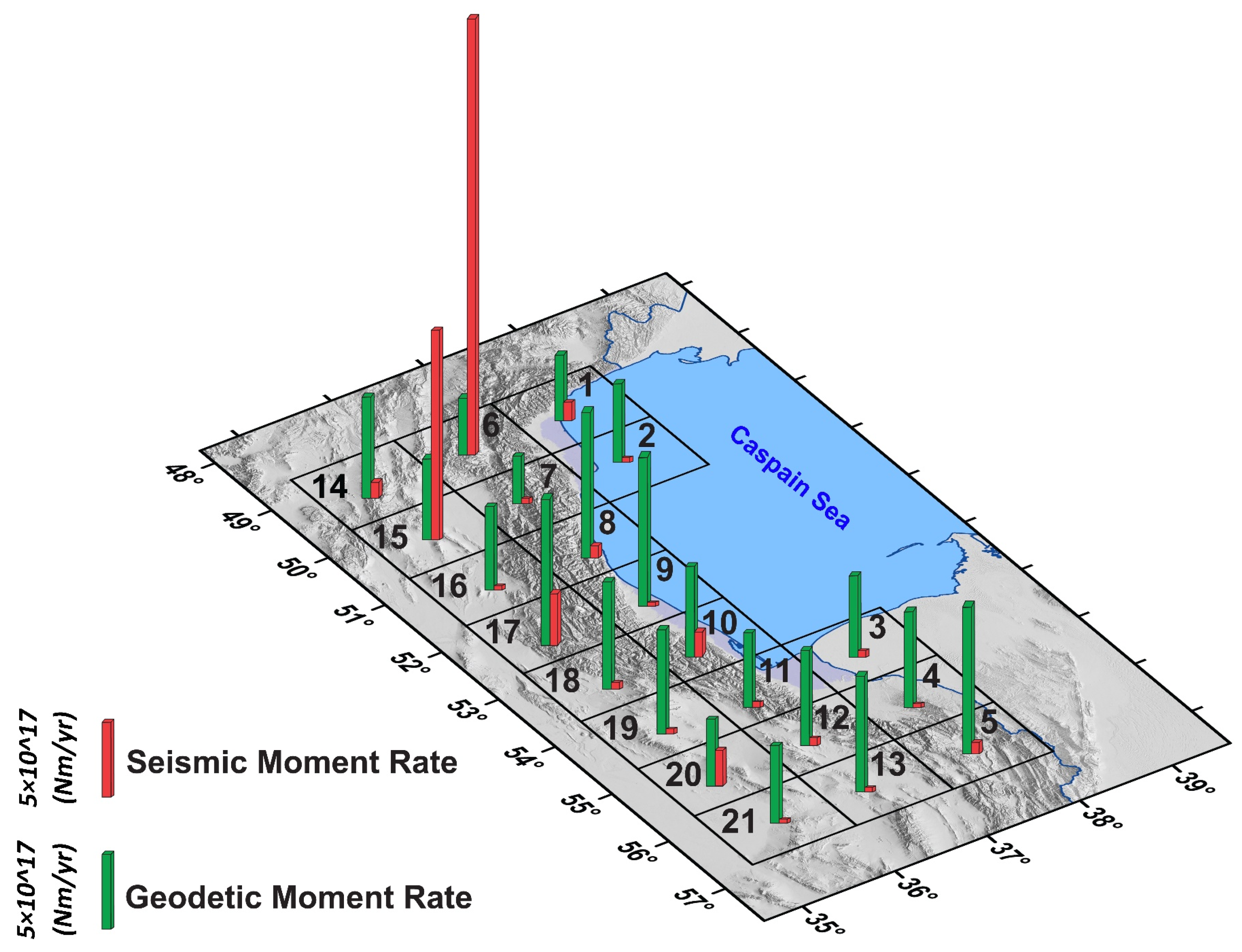
In the subzones of northern Iran, the values of the seismic moment rates in the networks 6, 15, 17, 20, and 10, and the geodetic moment rates in the networks 8, 9, 17, 5, and 13 are relatively significant (Figure 11).

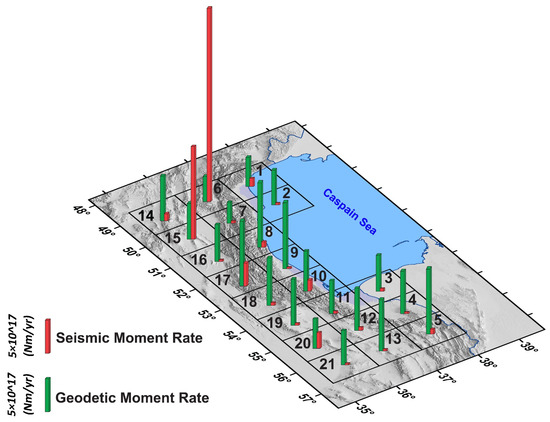
Figure 11. The seismic and geodetic moment rates in the area.

The ratio of seismic to geodetic moment rate denotes low values for networks 16, 4, 13, 9, and 19, and high values for networks 6, 15, 20, 1, and 17. Network 6 is characterized by higher released energy, which can be interpreted as due to the active faults interaction in the Talesh-Alborz transfer zone. The high released energy in networks 15 and 20 is related to the Ipak and Torud faults in the northern part of the Central Iran subzone. The Astara fault in the Talesh subzone is considered the reason for releasing energy in network 1. Mosha, Eivanaki, and Garmsar faults were significant faults in occurring of the earthquake in the network 17.

The west segment of the Mosha, North Tehran, Taleghan, Gonbad, Siahkuh, Jajarm, Royan, the east segment of the north Alborz, and Atari faults (in Figure 1c) shows a low seismic moment rate (Figure 10). It is noteworthy that geomorphological evidence indicates the high activity for those [65,98,100,101,102,103]. Therefore, they should be considered from a seismic point of view. The seismic/geodetic moment rate is a significant indicator in analyzing to release of more energy [2]. This ratio in the study area with ~0.23 × 10⁶ km² area is 70.7 which can be compared with the results of the previous studies in the United States [1], Basin and Range [2], the west and south Lut block [3]., and the east and north Lut block [4] (Table 11). The seismic/geodetic moment rate in the area is higher than that of the Basin and Range and the west-south Lut Block where morphotectonic studies emphasize its activity [104,105,106]. The obtained results indicate the Alborz (networks 7, 8, 9, 17, 10, 18, 11, and 12), western Koppeh-Dagh (networks 5, 13), northern part of Central Iran (networks 14, 15, 16, 19, 20, and 21), South Caspian Sea (networks 2, 3, and 4), and Talesh (networks 1 and 6) had, respectively, a portion of 0.9, 0.3, 11.9, 0.3, and 57.3 of the seismic/geodetic moment rates, which shows much of the elastic energy has been released in the Talesh and northern part of Central Iran.

Table 11. The ratio of the seismic/geodetic moment rates in the different areas [1,2,3].

Regional	Area km2	Ṁ Geodetic 1019 Nm/yr	Ṁ Seismic 1019 Nm/yr	$\left[\frac{{\mathbf{Ṁ}}_{\mathbf{s}\mathbf{e}\mathbf{i}\mathbf{s}\mathbf{m}\mathbf{i}\mathbf{c}}}{{\mathbf{Ṁ}}_{\mathbf{g}\mathbf{e}\mathbf{o}\mathbf{d}\mathbf{e}\mathbf{t}\mathbf{i}\mathbf{c}}}\right]$
Study area	0.23 × 106	1.431	1.013	70.7
West and South Lut Block	0.993 × 105	1.07	0.154	14.4
East and North Lut Block	1.005 × 105	0.153	0.141	92.1
USA	7.945 × 106	4.58	3.62	79
S.Calif	0.15 × 106	1.23	1.06	86
N.Calif	0.240 × 106	0.89	0.66	74
Basin and Range	0.775 × 106	1.08 0.39–0.69	0.55 0.58–1.12	51
Northwest	1.027 × 106	0.72	0.18	25
Central	2.730 × 106	0.52	0.013	2.5

5. Conclusions

Using the analysis of the GSR, SSR, and FMSI, the N35.5° E and N104° E are the proposed directions of the maximum compressive stress in the Alborz and Talesh, respectively.

The results of FMSI indicate the slip partitioning mechanism of oblique shortening on the subparallel thrusts and strike-slip faults in the area where stress regimes include thrust (49.37%), strike-slip (39.24%), thrust with a strike-slip component (2.53%), normal (1.27%), and unknown (7.59%) faulting.

High GSR belongs to the networks 13, 5, 12, and 20, where the main faults are the Jajarm, Siahkuh, Takalkuh, Bashtapeh, Shahrud, and the eastern segment of the Khazar fault. The GSR is also high in network 9, where the main faults are Royan and the east segment of the north Alborz faults.

Large extensional components of the SSR are rather evident in networks 10, 5, 6, 14, and 19, where there are the main left-lateral strike-slip faults such as Sari, Khazar, Rudbar, Kushk-e Nosrat, and Torud faults.

The significant relative inconsistency geodetically and seismically between the magnitudes of the compressional strain rates in networks 14, 8, 19, 6, 10, and 5 can be attributed to the occurrence of large earthquakes, as well as the recurrence interval of earthquakes in this area.

High SMR are belong to the faults in the Talesh-Alborz transfer zone (such as Rudbar faults), north of central Iran (such as Ipak and Torud faults), Talesh subzone (such as Astara fault), Alborz mountain (such as the eastern segment of the Mosha, Eivanaki, and Garmsar faults), while low SMR is related to the west segment of the Mosha, North Tehran, Taleghan, Gonbad, Siahkuh, Jajarm, Royan, east segment of the north Alborz, and Atari faults within Alborz mountains.

Regarding the seismic and geodetic strain and moment rates, seismic hazard is significant along the western and eastern segments of the north Alborz, Royan, Mosha, and Eivanaki faults.