The authors would like to make the following corrections to this paper [1]:
In the original article, the variables used in the derivation of the equations in Sections 2.1 and 2.2 are different. For scientific rigor and to ensure the consistency of the variables used in Section 2, the authors wish to rewrite Section 2.2 to:
“According to previous studies, the positioning error of triangulation is not only related to the observation error of EO sensors but also depends on the configuration between the LOS vectors and the baseline of two EO sensors. In order to analyze the RMS position error of the proposed triangulation algorithm, we rewrite Equation (15) as:
where is a weighting matrix and is an identity matrix, and then the space debris position error is given by:
where and are the position errors of points M and N, respectively, and the vectors and are their direction vectors. In order to obtain the expressions of RMS position error, we have to derive the expressions of and .
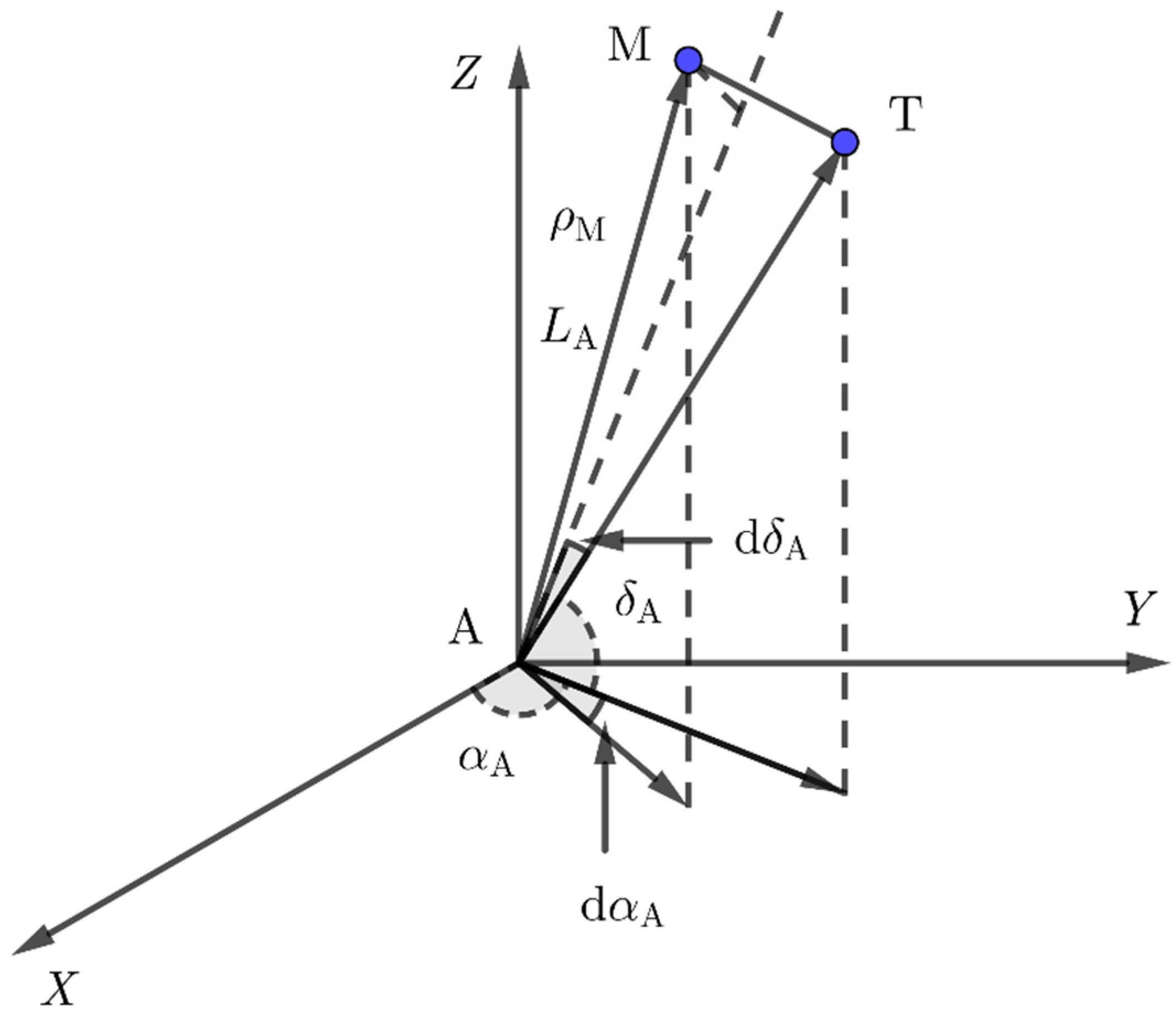
From Figure 3, the two EO sensors located at two arbitrary observation sites are denoted by A and B, respectively. The actual position of space debris is denoted by T. and are the LOS vector errors in the topocentric coordinate systems. Similarly, , are the LOS vector errors in the topocentric coordinate systems. Since , are small, by Equation (6), the RMS position error of point M in triangulation is given by:
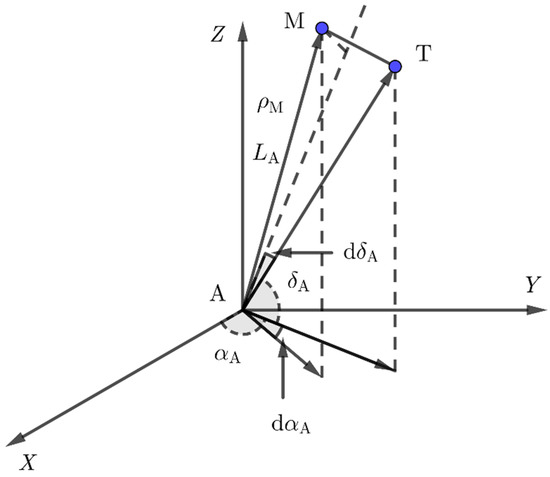
Figure 3.
Error analysis of triangulation.
Similarly, with Equation (7), the RMS position error of point N in triangulation is given by:
Substituting Equations (19) and (20) into Equation (18) yields:
Since it is impossible to know the actual space debris position, the vectors and cannot be solved. However, we can approximately think vector is equal to vector , which is the unit vector of , because the actual space debris position is near the line segment MN. Similarly, the vector is equal to vector , approximately. Therefore, Equation (30) can be rewritten as:
where because the line segment MN is the common perpendicular of and ”.
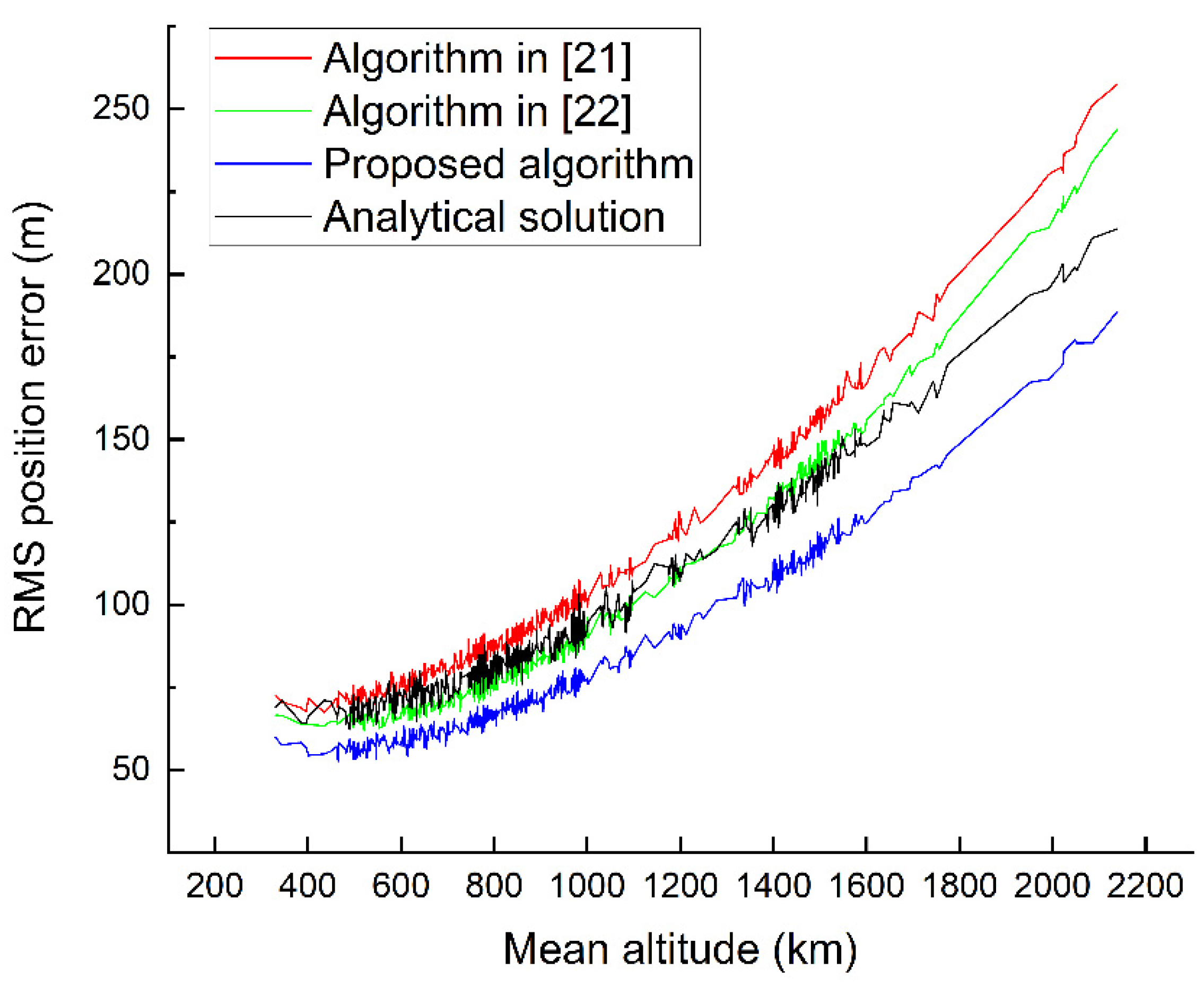
As a result of the above changes, Figure 5 in the original article should be replaced with:
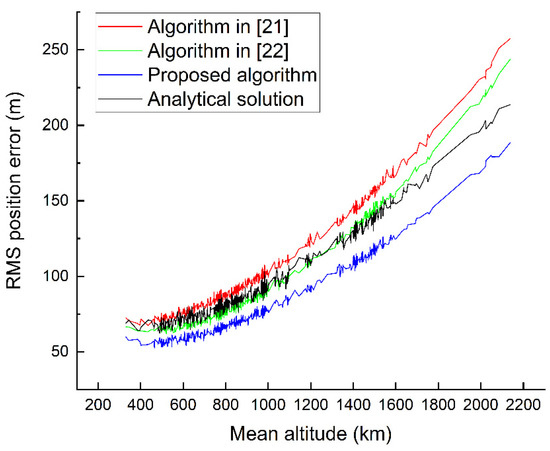
Figure 5.
The RMS position errors for LEO space debris.
In Section 5, the text “Equation (30)” should be “Equation (21)”; the text “Equation (32)” should be “Equation (22)”; the text “” should be “”.
The authors apologize for any inconvenience caused and state that the scientific conclusions are unaffected. The original publication has also been updated.
Reference
- Chen, L.; Liu, C.; Li, Z.; Kang, Z. A New Triangulation Algorithm for Positioning Space Debris. Remote Sens. 2021, 13, 4878. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).