DRL-Based Load-Balancing Routing Scheme for 6G Space–Air–Ground Integrated Networks
Abstract
:1. Introduction
2. Related Work
2.1. LEO Satellite Routing
2.2. Load Balancing of LEO Satellites
2.3. Machine-Learning-Based Satellite Routing
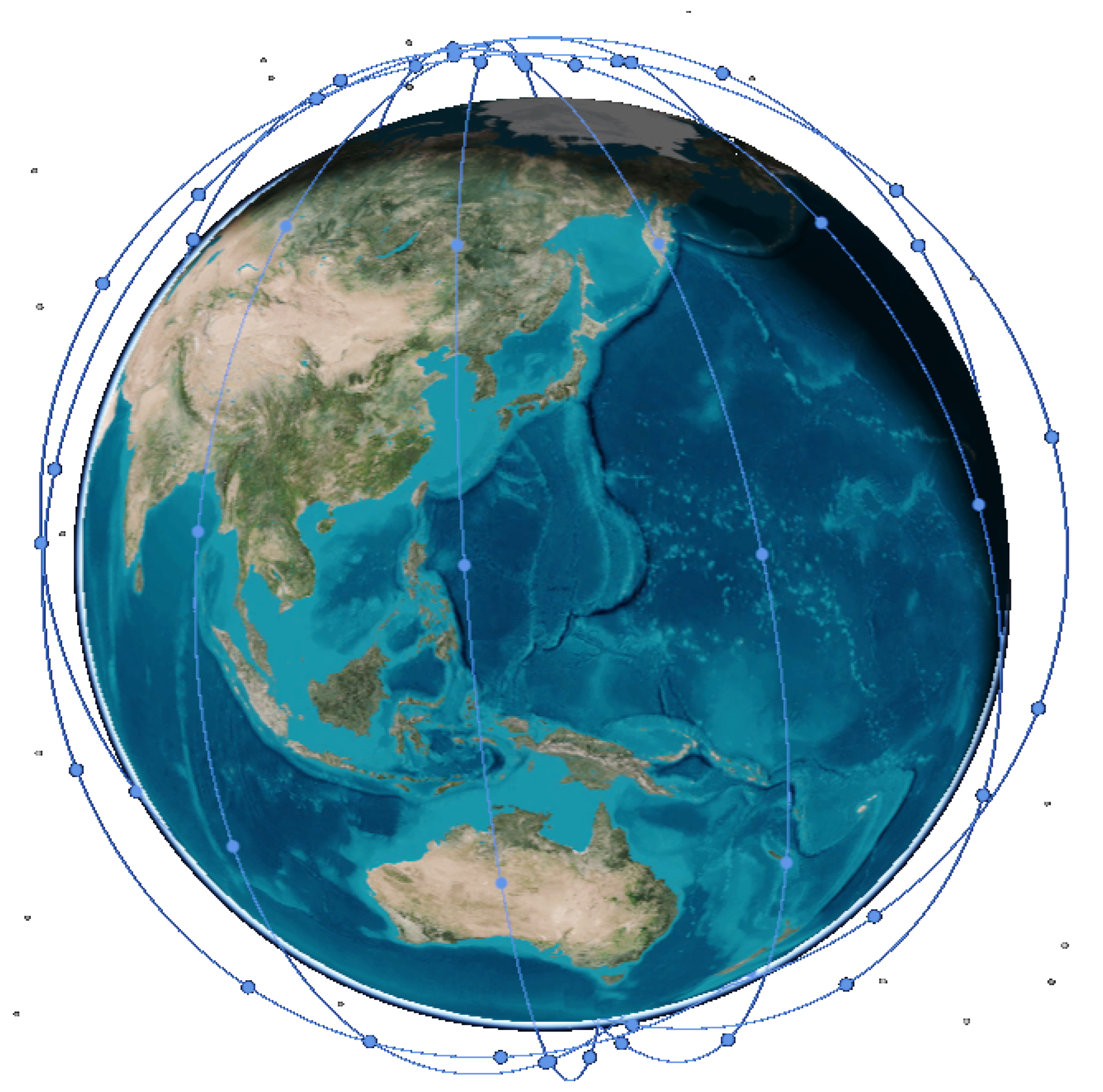
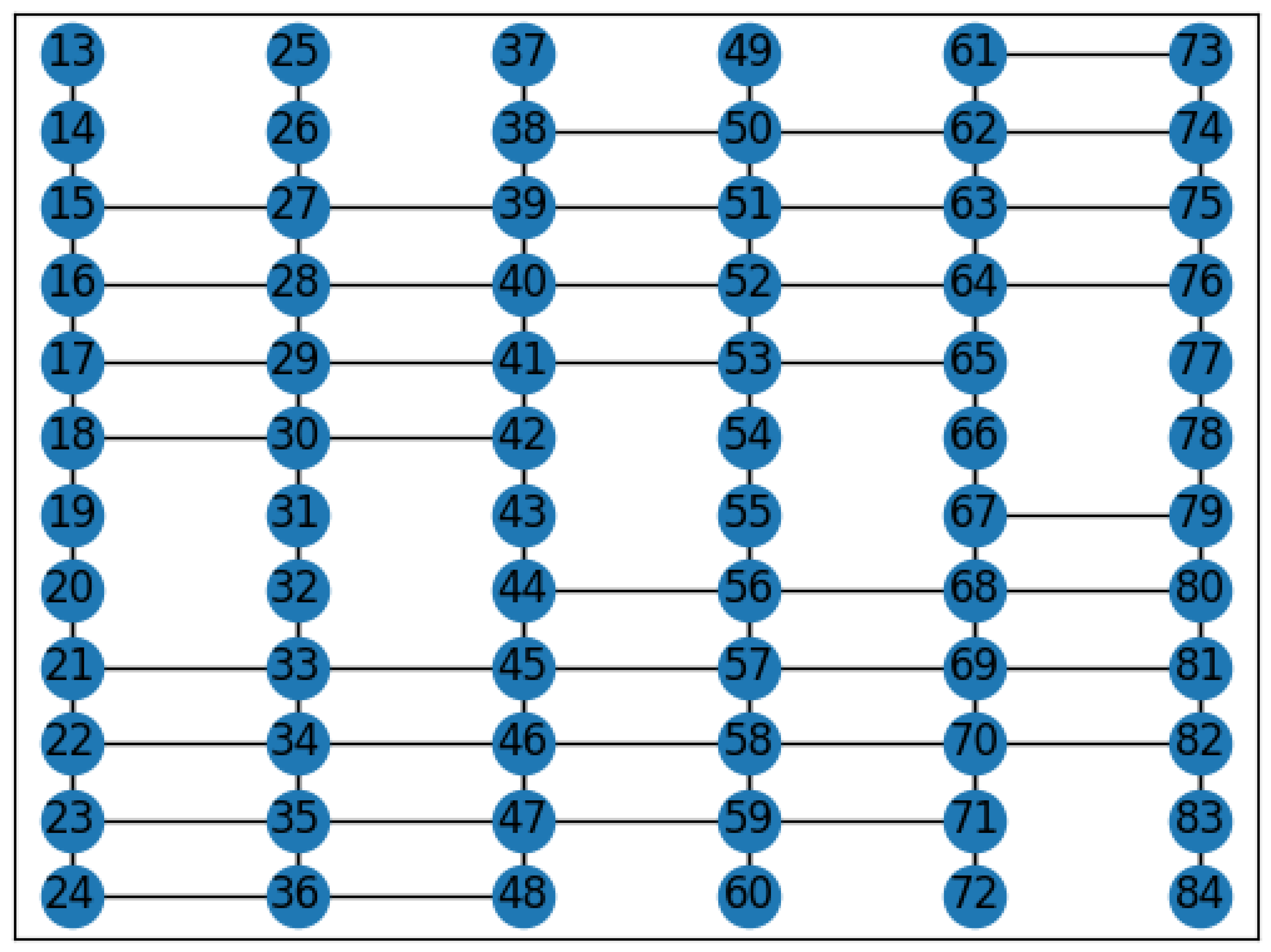
3. System Model
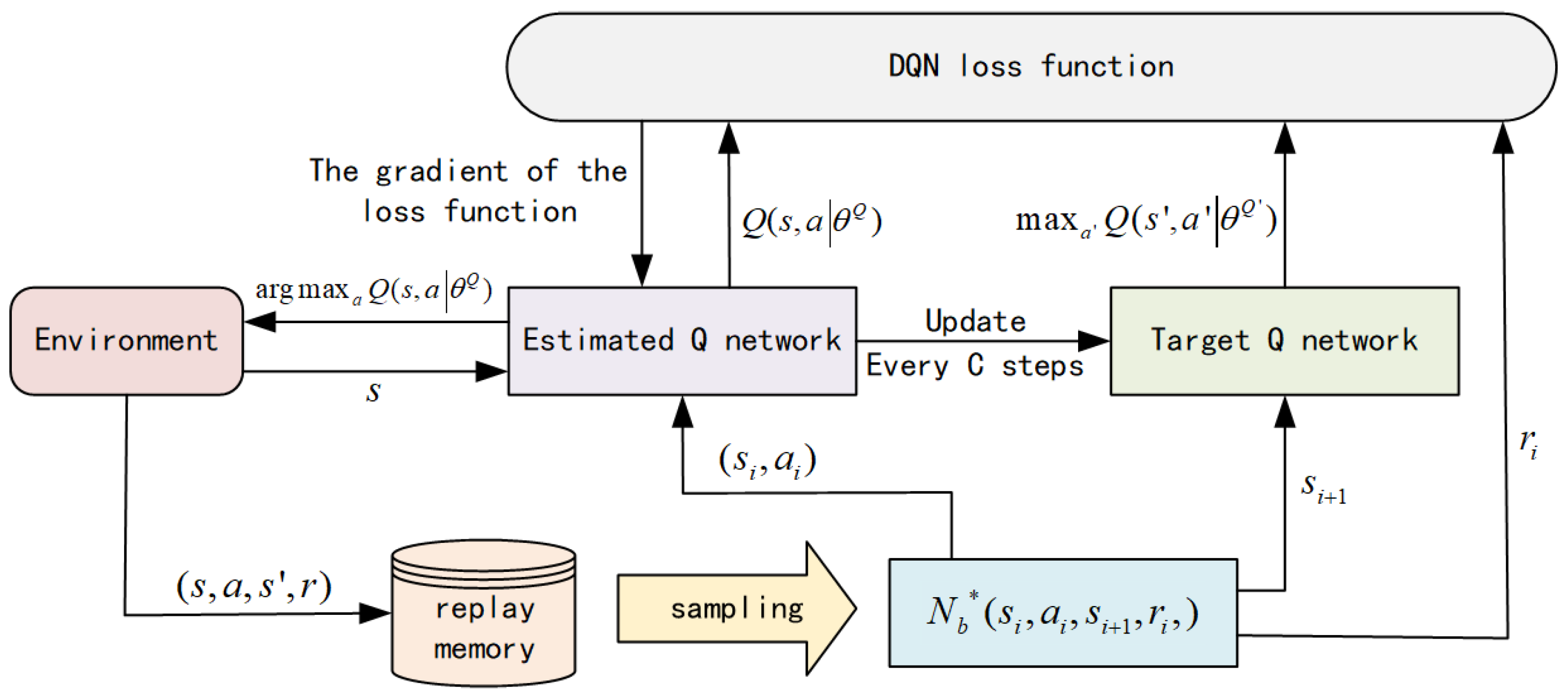
4. Dqn-Based Load-Balancing Routing Algorithm
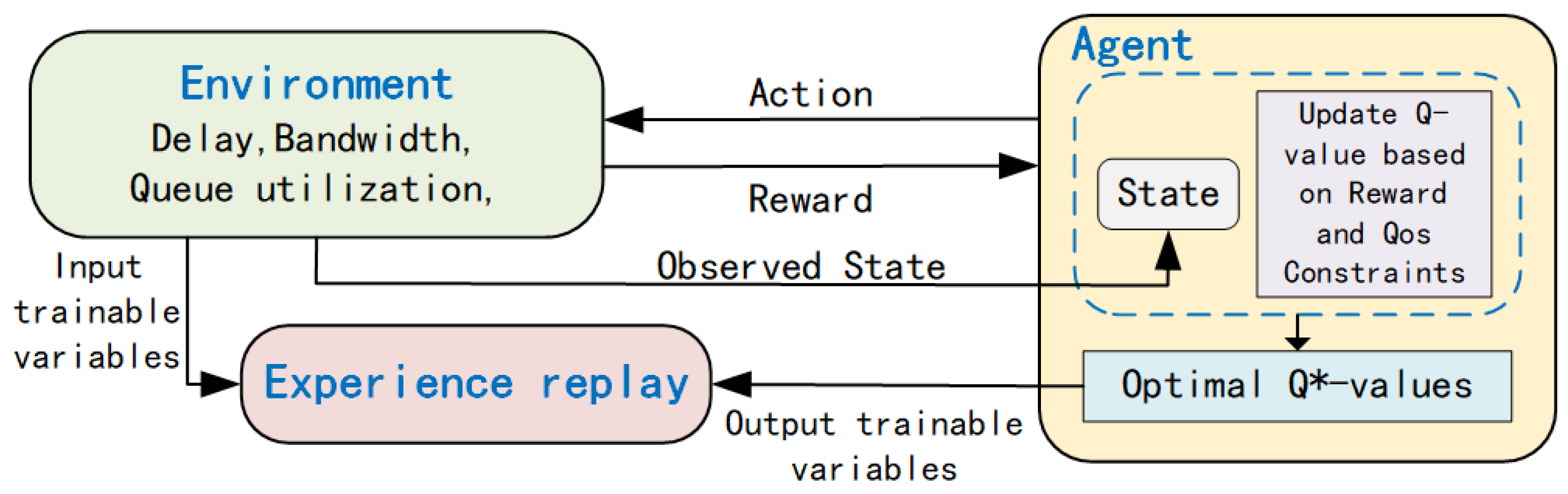
4.1. DQN-LLRA Framework and Mechanisms
|
|
|
|
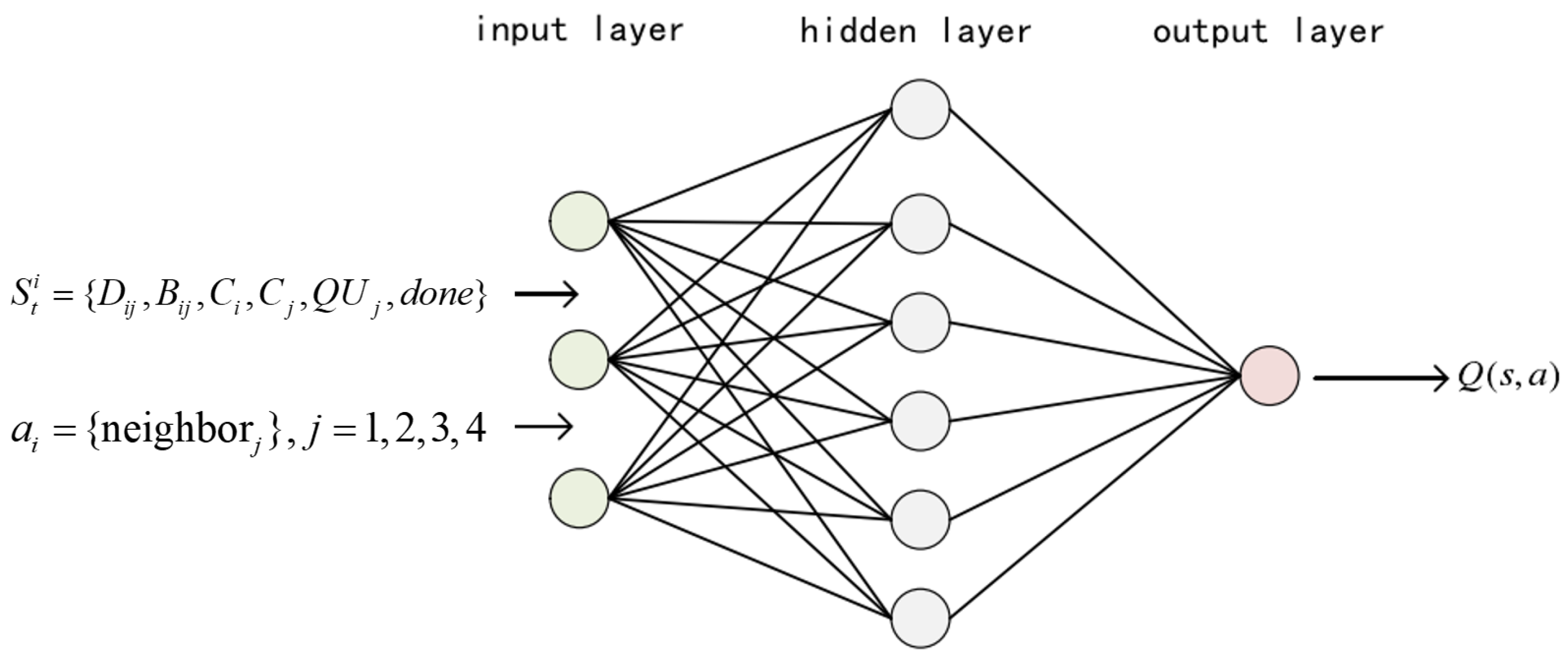
4.2. Basic Model of the DQN
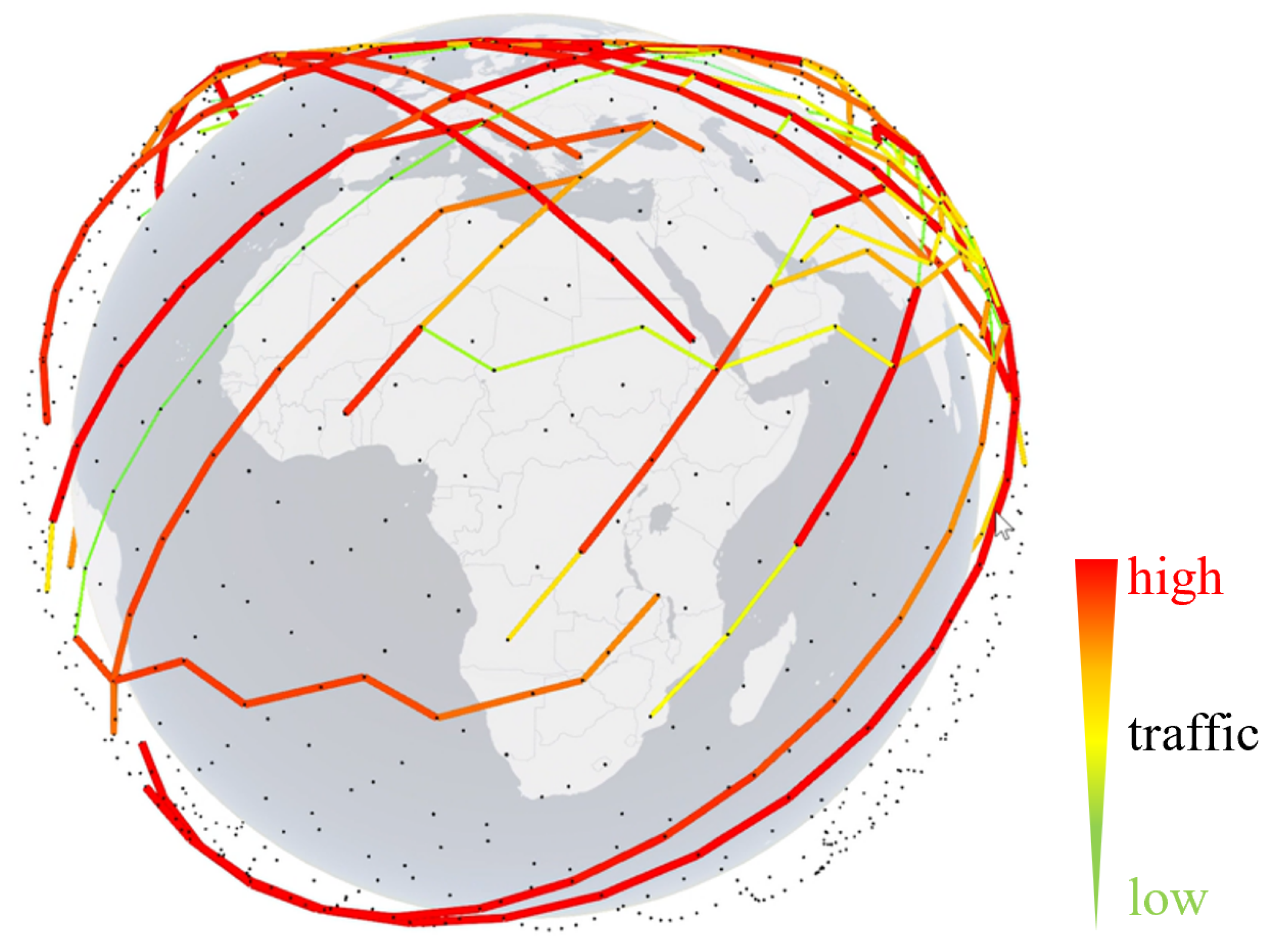
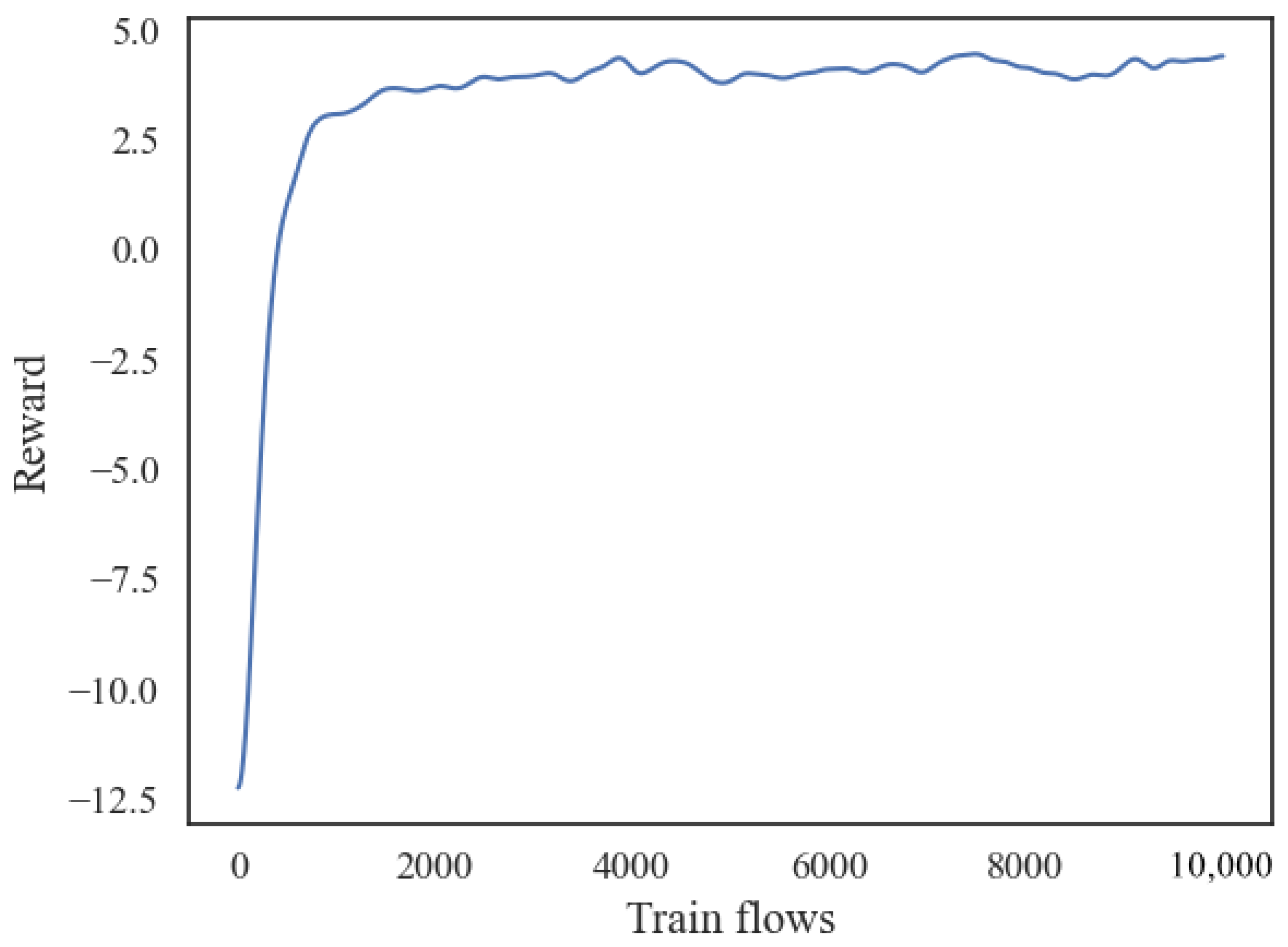
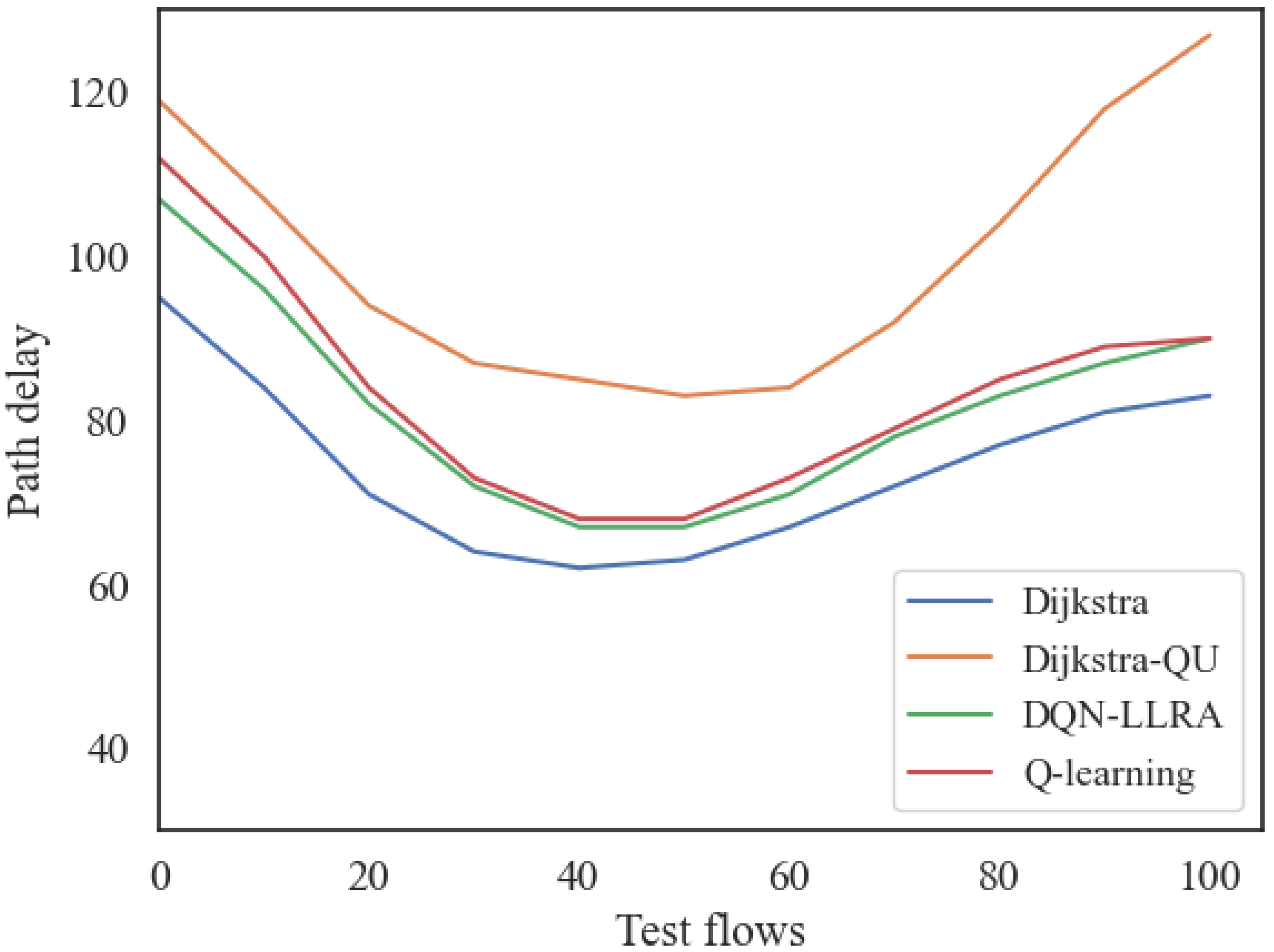
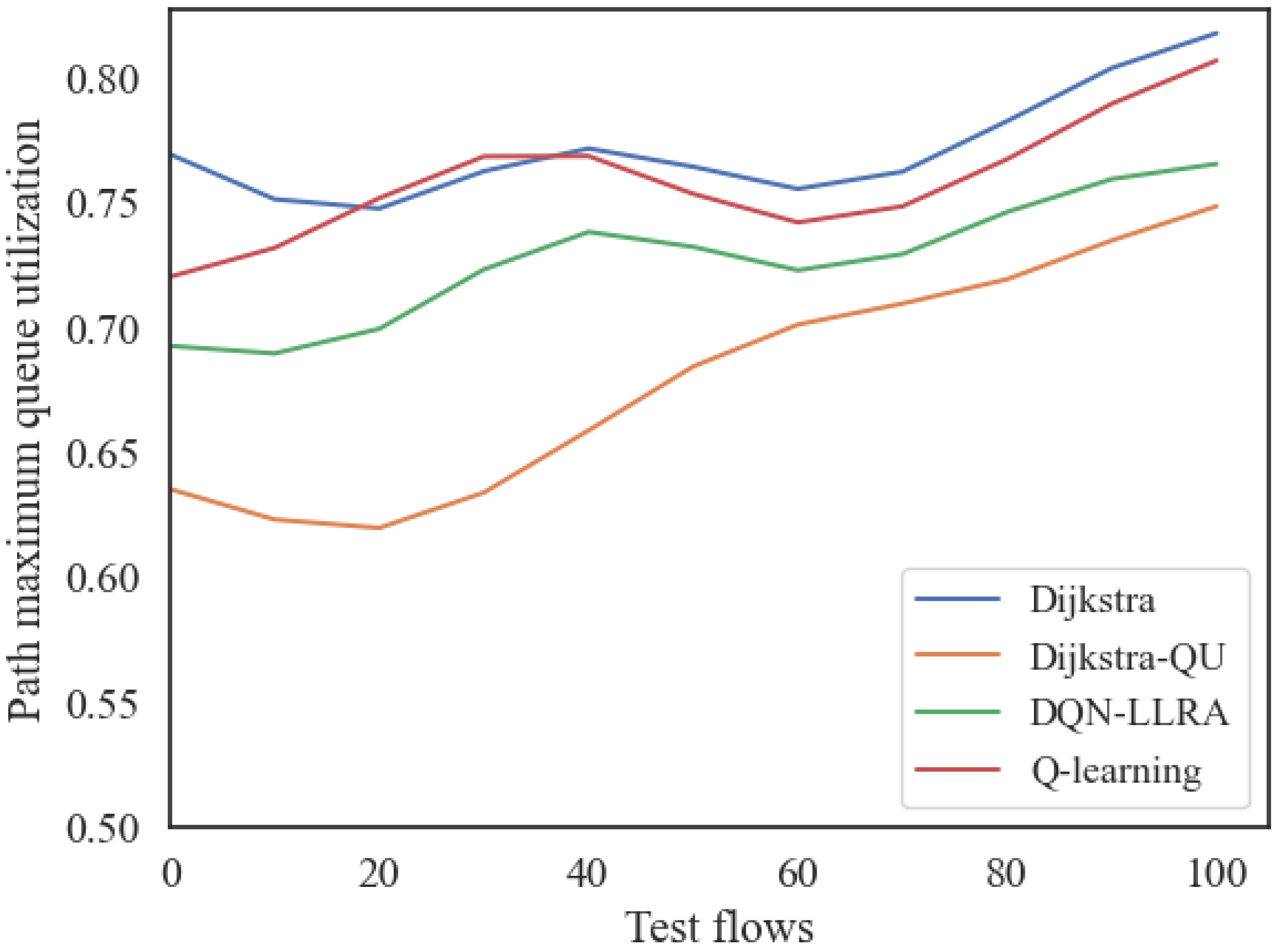
5. Simulation and Performance Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SAGIN | Space–Air–Ground Integrated Network |
| GEO | Geosynchronous Earth Orbit |
| MEO | Medium Earth Orbit |
| LEO | Low Earth Orbit |
| DQN | Deep Q-Network |
| ISLs | inter-satellite links |
| DQN-LLRA | DQN-based load-balancing routing algorithm for LEO satellites |
| DRA | Discrete Relaxation Algorithm |
| DHRP | Distributed Hierarchical Routing Protocol |
| HGL | Hybrid Global–Local Load Balancing Routing |
| PIR | Probability ISL Routing |
| ELB | Elastic Load Balancing |
| IoT | Internet of Things |
| WSNs | Wireless Sensor Networks |
| DDPG | Deep Deterministic Policy Gradient |
| MADDPG | Multiagent Deep Deterministic Policy Gradient |
| MDP | Markov Decision Process |
| TD | Temporal Difference |
| GNN | Graph Neural Networks |
References
- Mohori, M.; vigelj, A.; Kandus, G.; Werner, M. Performance evaluation of adaptive routing algorithms in packet-switched intersatellite link networks. Int. J. Satell. Commun. Netw. 2002, 20, 97–120. [Google Scholar] [CrossRef]
- Liu, L.; Feng, J.; Pei, Q.; Chen, C.; Ming, Y.; Shang, B.; Dong, M. Blockchain-Enabled Secure Data Sharing Scheme in Mobile-Edge Computing: An Asynchronous Advantage Actor–Critic Learning Approach. IEEE Internet Things J. 2021, 8, 2342–2353. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, C.; Liu, L.; Lan, D.; Jiang, H.; Wan, S. Aerial Edge Computing on Orbit: A Task Offloading and Allocation Scheme. IEEE Trans. Netw. Sci. Eng. 2023, 10, 275–285. [Google Scholar] [CrossRef]
- Chen, C.; Wang, C.; Liu, B.; He, C.; Cong, L.; Wan, S. Edge Intelligence Empowered Vehicle Detection and Image Segmentation for Autonomous Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 1–12. [Google Scholar] [CrossRef]
- Chen, C.; Yao, G.; Liu, L.; Pei, Q.; Song, H.; Dustdar, S. A Cooperative Vehicle-Infrastructure System for Road Hazards Detection With Edge Intelligence. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5186–5198. [Google Scholar] [CrossRef]
- Alagoz, O.; Hsu, H.E.; Schaefer, A.J.; Roberts, M.S. Markov Decision Processes: A Tool for Sequential Decision Making under Uncertainty. Med. Decis. Mak. 2010, 30, 474–483. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.A.; Fidjeland, A.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Saǧ, E.; Kavas, A. Modelling and Performance Analysis of 2.5 Gbps Inter-satellite Optical Wireless Communication (IsOWC) System in LEO Constellation. J. Commun. 2018, 13, 553–558. [Google Scholar] [CrossRef]
- Pizzicaroli, J.C. Launching and Building the IRIDIUM® Constellation. In Proceedings of the Mission Design & Implementation of Satellite Constellations; van der Ha, J.C., Ed.; Springer: Dordrecht, The Netherlands, 1998; pp. 113–121. [Google Scholar]
- Henderson, T.; Katz, R. On distributed, geographic-based packet routing for LEO satellite networks. In Proceedings of the Globecom’00-IEEE. Global Telecommunications Conference. Conference Record (Cat. No.00CH37137), San Francisco, CA, USA, 27 November–1 December 2000; Volume 2, pp. 1119–1123. [Google Scholar] [CrossRef]
- Svigelj, A.; Mohorcic, M.; Kandus, G.; Kos, A.; Pustisek, M.; Bester, J. Routing in ISL networks considering empirical IP traffic. IEEE J. Sel. Areas Commun. 2004, 22, 261–272. [Google Scholar] [CrossRef]
- Liu, L.; Zhao, M.; Yu, M.; Jan, M.A.; Lan, D.; Taherkordi, A. Mobility-Aware Multi-Hop Task Offloading for Autonomous Driving in Vehicular Edge Computing and Networks. IEEE Trans. Intell. Transp. Syst. 2022, 24, 2169–2182. [Google Scholar] [CrossRef]
- Gounder, V.; Prakash, R.; Abu-Amara, H. Routing in LEO-based satellite networks. In Proceedings of the 1999 IEEE Emerging Technologies Symposium. Wireless Communications and Systems (IEEE Cat. No.99EX297), Richardson, TX, USA, 12–13 April 1999; pp. 22.1–22.6. [Google Scholar] [CrossRef]
- Long, H.; Shen, Y.; Guo, M.; Tang, F. LABERIO: Dynamic load-balanced Routing in OpenFlow-enabled Networks. In Proceedings of the 2013 IEEE 27th International Conference on Advanced Information Networking and Applications (AINA), Barcelona, Spain, 25–28 March 2013; pp. 290–297. [Google Scholar] [CrossRef]
- Franck, L.; Maral, G. Routing in networks of intersatellite links. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 902–917. [Google Scholar] [CrossRef]
- Mohorcic, M.; Werner, M.; Svigelj, A.; Kandus, G. Adaptive routing for packet-oriented intersatellite link networks: Performance in various traffic scenarios. IEEE Trans. Wirel. Commun. 2002, 1, 808–818. [Google Scholar] [CrossRef]
- Kucukates, R.; Ersoy, C. Minimum flow maximum residual routing in LEO satellite networks using routing set. Wirel. Netw. 2008, 14, 501–517. [Google Scholar] [CrossRef]
- Cigliano, A.; Zampognaro, F. A Machine Learning approach for routing in satellite Mega-Constellations. In Proceedings of the 2020 International Symposium on Advanced Electrical and Communication Technologies (ISAECT), Virtual, 25–27 November 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, H.; Ran, Y.; Zhao, L.; Wang, J.; Luo, J.; Zhang, T. GRouting: Dynamic Routing for LEO Satellite Networks with Graph-based Deep Reinforcement Learning. In Proceedings of the 2021 4th International Conference on Hot Information-Centric Networking (HotICN), Nanjing, China, 25–27 November 2021; pp. 123–128. [Google Scholar] [CrossRef]
- Kucukates, R.; Ersoy, C. High performance routing in a LEO satellite network. In Proceedings of the Eighth IEEE Symposium on Computers and Communications, Kemer-Antalya, Turkey, 30 June–3 July 2003; Volume 2, pp. 1403–1408. [Google Scholar] [CrossRef]
- Liu, W.; Tao, Y.; Liu, L. Load-Balancing Routing Algorithm Based on Segment Routing for Traffic Return in LEO Satellite Networks. IEEE Access 2019, 7, 112044–112053. [Google Scholar] [CrossRef]
- Ju, Y.; Zou, G.; Bai, H.; Liu, L.; Pei, Q.; Wu, C.; Otaibi, S.A. Random Beam Switching: A Physical Layer Key Generation Approach to Safeguard mmWave Electronic Devices. IEEE Trans. Consum. Electron. 2023, 1. [Google Scholar] [CrossRef]
- Taleb, T.; Mashimo, D.; Jamalipour, A.; Hashimoto, K.; Nemoto, Y.; Kato, N. SAT04-3: ELB: An Explicit Load Balancing Routing Protocol for Multi-Hop NGEO Satellite Constellations. In Proceedings of the IEEE Globecom 2006, San Francisco, CA, USA, 27 November–1 December 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Taleb, T.; Mashimo, D.; Jamalipour, A.; Kato, N.; Nemoto, Y. Explicit Load Balancing Technique for NGEO Satellite IP Networks With On-Board Processing Capabilities. IEEE/ACM Trans. Netw. 2009, 17, 281–293. [Google Scholar] [CrossRef]
- Song, G.; Chao, M.; Yang, B.; Zheng, Y. TLR: A Traffic-Light-Based Intelligent Routing Strategy for NGEO Satellite IP Networks. IEEE Trans. Wirel. Commun. 2014, 13, 3380–3393. [Google Scholar] [CrossRef]
- Liu, J.; Luo, R.; Huang, T.; Meng, C. A Load Balancing Routing Strategy for LEO Satellite Network. IEEE Access 2020, 8, 155136–155144. [Google Scholar] [CrossRef]
- Geng, S.; Liu, S.; Fang, Z.; Gao, S. An optimal delay routing algorithm considering delay variation in the LEO satellite communication network. Comput. Netw. 2020, 173, 107166. [Google Scholar] [CrossRef]
- Wei, S.; Cheng, H.; Liu, M.; Ren, M. Optimal Strategy Routing in LEO Satellite Network Based on Cooperative Game Theory. In Proceedings of the Space Information Networks: Second International Conference, SINC 2017, Yinchuan, China, 10–11 August 2017. [Google Scholar]
- Jiang, Z.; Liu, C.; He, S.; Li, C.; Lu, Q. A QoS routing strategy using fuzzy logic for NGEO satellite IP networks. Wirel. Netw. 2018, 24, 295–307. [Google Scholar] [CrossRef]
- Pan, T.; Huang, T.; Li, X.; Chen, Y.; Xue, W.; Liu, Y. OPSPF: Orbit Prediction Shortest Path First Routing for Resilient LEO Satellite Networks. In Proceedings of the ICC 2019–2019 IEEE International Conference on Communications (ICC), Shanghai, China, 20–24 May 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Hao, L.; Ren, P.; Du, Q. Satellite QoS Routing Algorithm Based on Energy Aware and Load Balancing. In Proceedings of the 2020 International Conference on Wireless Communications and Signal Processing (WCSP), Nanjing, China, 21–23 October 2020; pp. 685–690. [Google Scholar] [CrossRef]
- Zuo, P.; Wang, C.; Wei, Z.; Li, Z.; Zhao, H.; Jiang, H. Deep Reinforcement Learning Based Load Balancing Routing for LEO Satellite Network. In Proceedings of the 2022 IEEE 95th Vehicular Technology Conference: (VTC2022-Spring), Helsinki, Finland, 19–22 June 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Xu, Q.; Zhang, Y.; Wu, K.; Wang, J.; Lu, K. Evaluating and Boosting Reinforcement Learning for Intra-Domain Routing. In Proceedings of the 2019 IEEE 16th International Conference on Mobile Ad Hoc and Sensor Systems (MASS), Monterey, CA, USA, 4–7 November 2019; pp. 265–273. [Google Scholar] [CrossRef]
- Ju, Y.; Chen, Y.; Cao, Z.; Liu, L.; Pei, Q.; Xiao, M.; Ota, K.; Dong, M.; Leung, V.C.M. Joint Secure Offloading and Resource Allocation for Vehicular Edge Computing Network: A Multi-Agent Deep Reinforcement Learning Approach. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5555–5569. [Google Scholar] [CrossRef]
- Liu, Y.; Lu, D.; Zhang, G.; Tian, J.; Xu, W. Q-Learning Based Content Placement Method for Dynamic Cloud Content Delivery Networks. IEEE Access 2019, 7, 66384–66394. [Google Scholar] [CrossRef]
- Pan, S.; Li, P.; Zeng, D.; Guo, S.; Hu, G. A Q-Learning Based Framework for Congested Link Identification. IEEE Internet Things J. 2019, 6, 9668–9678. [Google Scholar] [CrossRef]
- Wei, Z.; Liu, F.; Zhang, Y.; Xu, J.; Ji, J.; Lyu, Z. A Q-learning algorithm for task scheduling based on improved SVM in wireless sensor networks. Comput. Netw. 2019, 161, 138–149. [Google Scholar] [CrossRef]
- Qiao, G.; Leng, S.; Maharjan, S.; Zhang, Y.; Ansari, N. Deep Reinforcement Learning for Cooperative Content Caching in Vehicular Edge Computing and Networks. IEEE Internet Things J. 2020, 7, 247–257. [Google Scholar] [CrossRef]
- Tu, Z.; Zhou, H.; Li, K.; Li, G.; Shen, Q. A Routing Optimization Method for Software-Defined SGIN Based on Deep Reinforcement Learning. In Proceedings of the 2019 IEEE Globecom Workshops (GC Wkshps), Big Island, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.M.O.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Ju, Y.; Yang, M.; Chakraborty, C.; Liu, L.; Pei, Q.; Xiao, M.; Yu, K. Reliability-Security Tradeoff Analysis in mmWave Ad Hoc Based CPS. ACM Trans. Sens. Netw. 2023. [Google Scholar] [CrossRef]
- Ju, Y.; Wang, H.; Chen, Y.; Zheng, T.X.; Pei, Q.; Yuan, J.; Al-Dhahir, N. Deep Reinforcement Learning Based Joint Beam Allocation and Relay Selection in mmWave Vehicular Networks. IEEE Trans. Commun. 2023, 71, 1997–2012. [Google Scholar] [CrossRef]
- Lowe, R.; Wu, Y.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments. In Proceedings of the 31st International Conference on Neural Information Processing Systems NIPS’17, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 6382–6393. [Google Scholar]
- Qin, Z.; Yao, H.; Mai, T. Traffic Optimization in Satellites Communications: A Multi-agent Reinforcement Learning Approach. In Proceedings of the 2020 International Wireless Communications and Mobile Computing (IWCMC), Limassol, Cyprus, 15–19 June 2020; pp. 269–273. [Google Scholar] [CrossRef]
- Yin, Y.; Huang, C.; Wu, D.; Huang, S.C.; Ashraf, M.W.A.; Guo, Q. Reinforcement Learning-Based Routing Algorithm in Satellite-Terrestrial Integrated Networks. Wirel. Commun. Mob. Comput. 2021, 2021, 3759631. [Google Scholar] [CrossRef]





| Parameter | Symbol | Value |
|---|---|---|
| link delay | random value (10–20 ms) | |
| link bandwidth | 10 Mbps | |
| discount factor | 0.99 | |
| learning rate | 0.005 | |
| reward parameter weights |
| 0.45, 0.35, 0.1, 0.1 0.50, 0.30, 0.1, 0.1 0.40, 0.40, 0.1, 0.1 0.50, 0.30, 0.1, 0.1 |
| reward adjustment factors | 10, 20, 20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, F.; Song, J.; Zhang, Y.; Wang, Y.; Huang, T. DRL-Based Load-Balancing Routing Scheme for 6G Space–Air–Ground Integrated Networks. Remote Sens. 2023, 15, 2801. https://doi.org/10.3390/rs15112801
Dong F, Song J, Zhang Y, Wang Y, Huang T. DRL-Based Load-Balancing Routing Scheme for 6G Space–Air–Ground Integrated Networks. Remote Sensing. 2023; 15(11):2801. https://doi.org/10.3390/rs15112801
Chicago/Turabian StyleDong, Feihu, Jiaxin Song, Yasheng Zhang, Yuqi Wang, and Tao Huang. 2023. "DRL-Based Load-Balancing Routing Scheme for 6G Space–Air–Ground Integrated Networks" Remote Sensing 15, no. 11: 2801. https://doi.org/10.3390/rs15112801
APA StyleDong, F., Song, J., Zhang, Y., Wang, Y., & Huang, T. (2023). DRL-Based Load-Balancing Routing Scheme for 6G Space–Air–Ground Integrated Networks. Remote Sensing, 15(11), 2801. https://doi.org/10.3390/rs15112801






