A Data-Fusion Approach to Assessing the Contribution of Wildland Fire Smoke to Fine Particulate Matter in California
Abstract
:1. Introduction
2. Materials and Methods
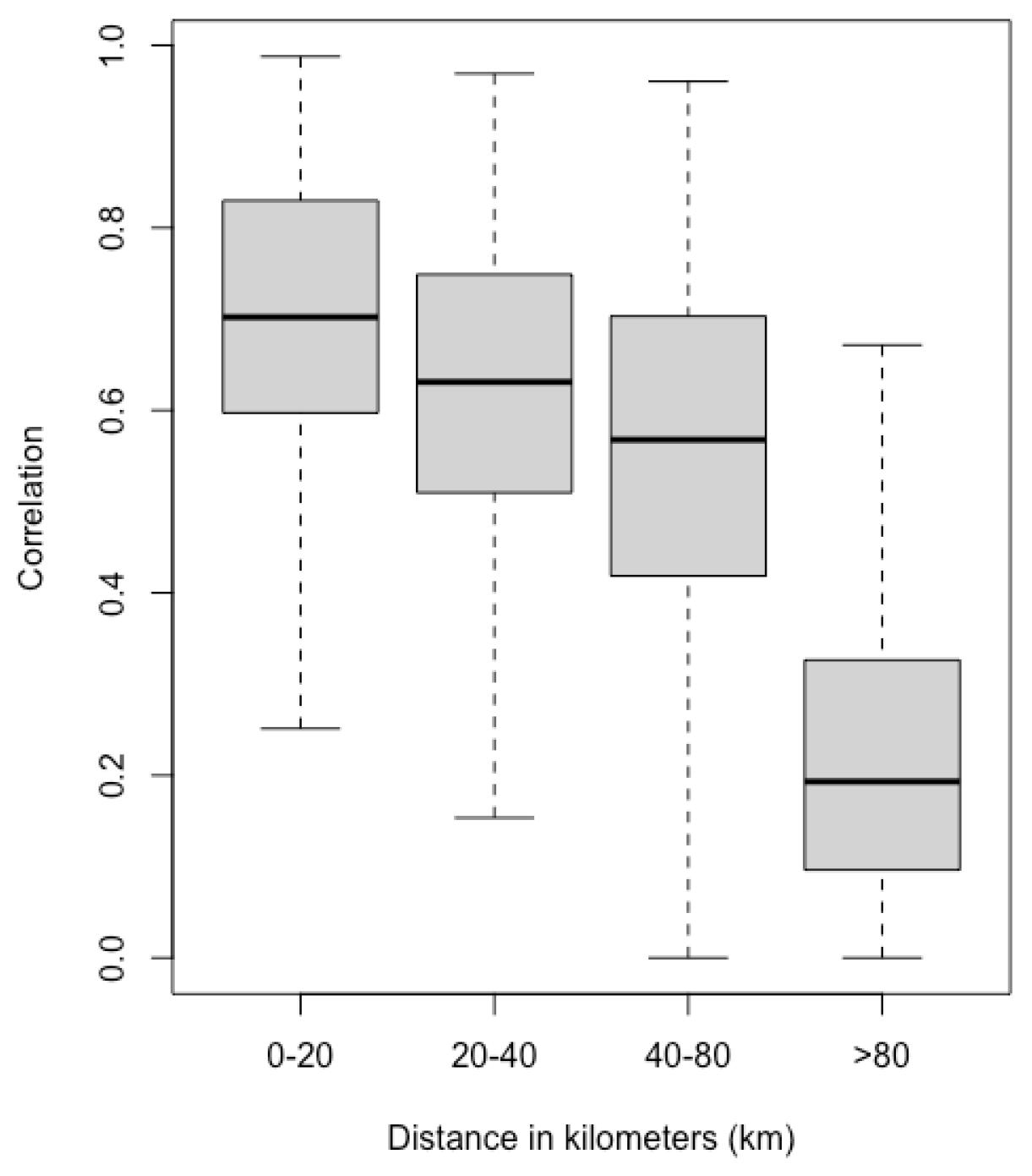
2.1. Data Sources and Exploratory Analysis
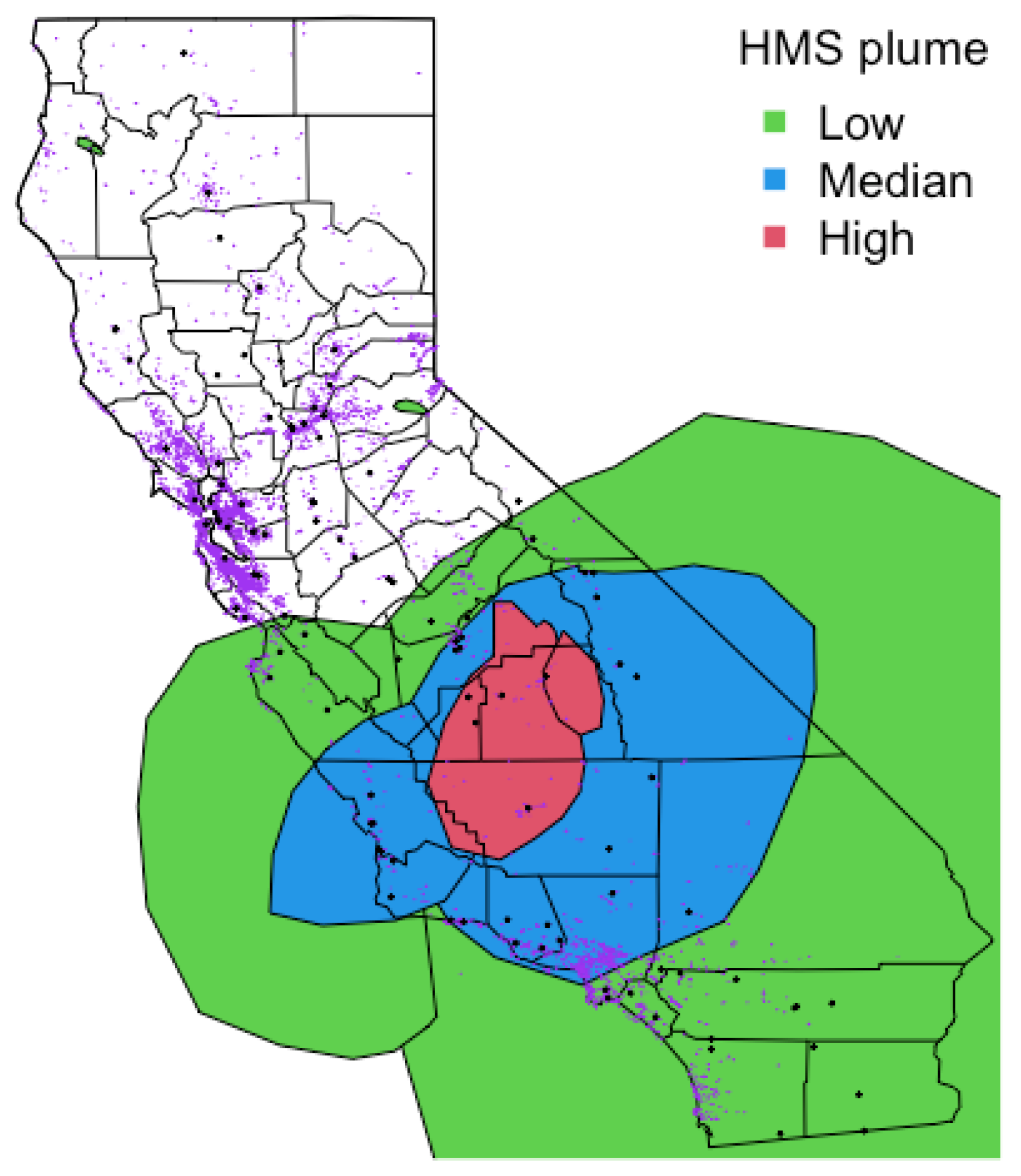
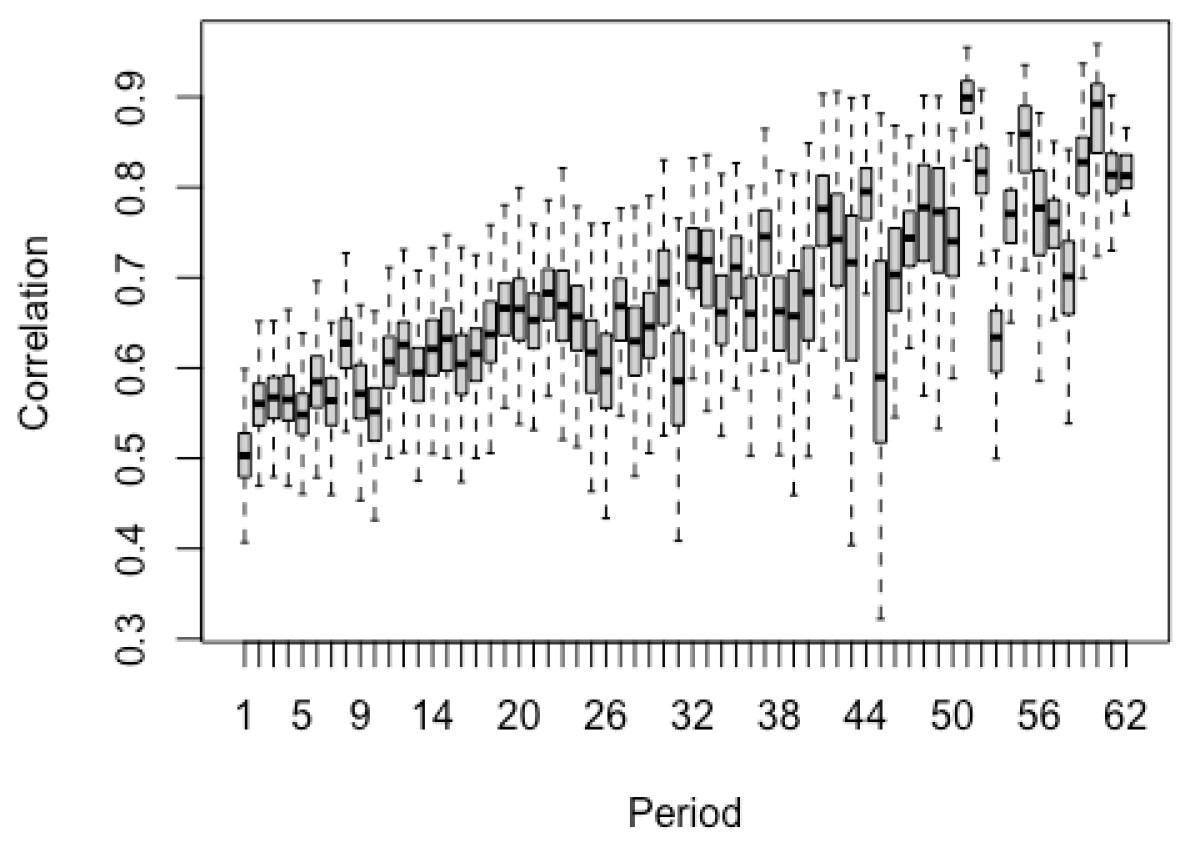
2.1.1. Satellite-Derived Smoke Plume Indicators
2.1.2. AQS Monitoring Stations
2.1.3. PA Sensors
2.2. Statistical Model
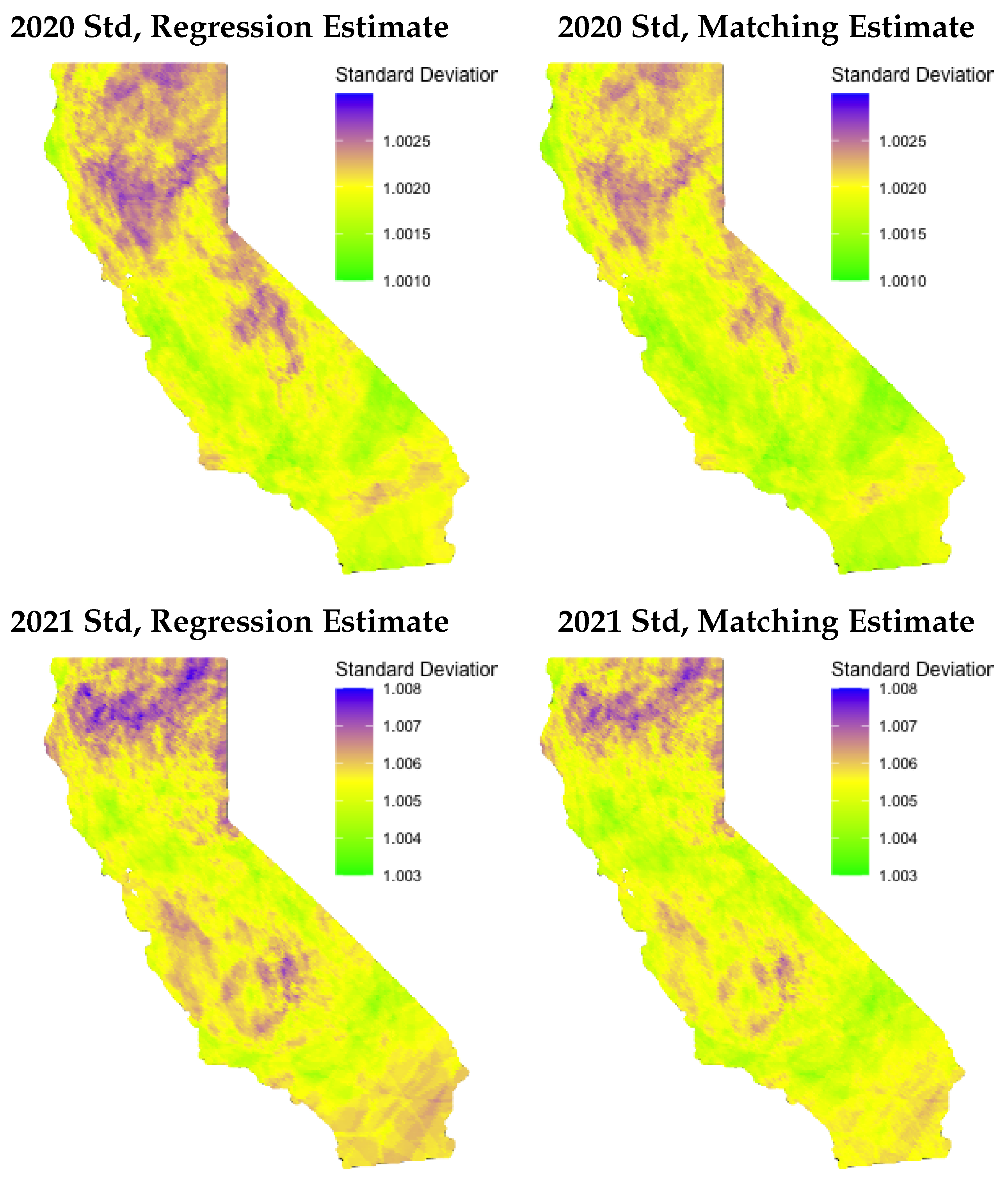
2.3. Quantifying the Wildland Fire Contribution
- Regression estimator:
- Matching estimator: for
2.4. Computational Algorithm
3. Results
3.1. Summary of the Fitted Model
3.2. Model Comparisons
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. MCMC Algorithm
Appendix B. Simulation Results
| Type | Covariate | True Value | Average Post Mean | Coverage | ESS |
|---|---|---|---|---|---|
| PM | Temperature | 0.118 | 0.117 (0.013) | 100% | 420.23 (0.14) |
| Humidity | 0.064 | 0.069 (0.022) | 96% | 307.27 (0.10) | |
| Plume-Low | 0.007 | 0.006 (0.132) | 100% | 875.99 (0.29) | |
| Plume-Medium | 0.022 | 0.020 (0.037) | 98% | 376.91 (0.13) | |
| Plume-High | 0.049 | 0.050 (0.176) | 100% | 480.22 (0.16) | |
| Bias | Temperature | −0.002 | 0.003 (0.019) | 92% | 168.75 (0.06) |
| Humidity | 0.012 | 0.009 (0.041) | 96% | 176.97 (0.06) |
Appendix C. MCMC Convergence
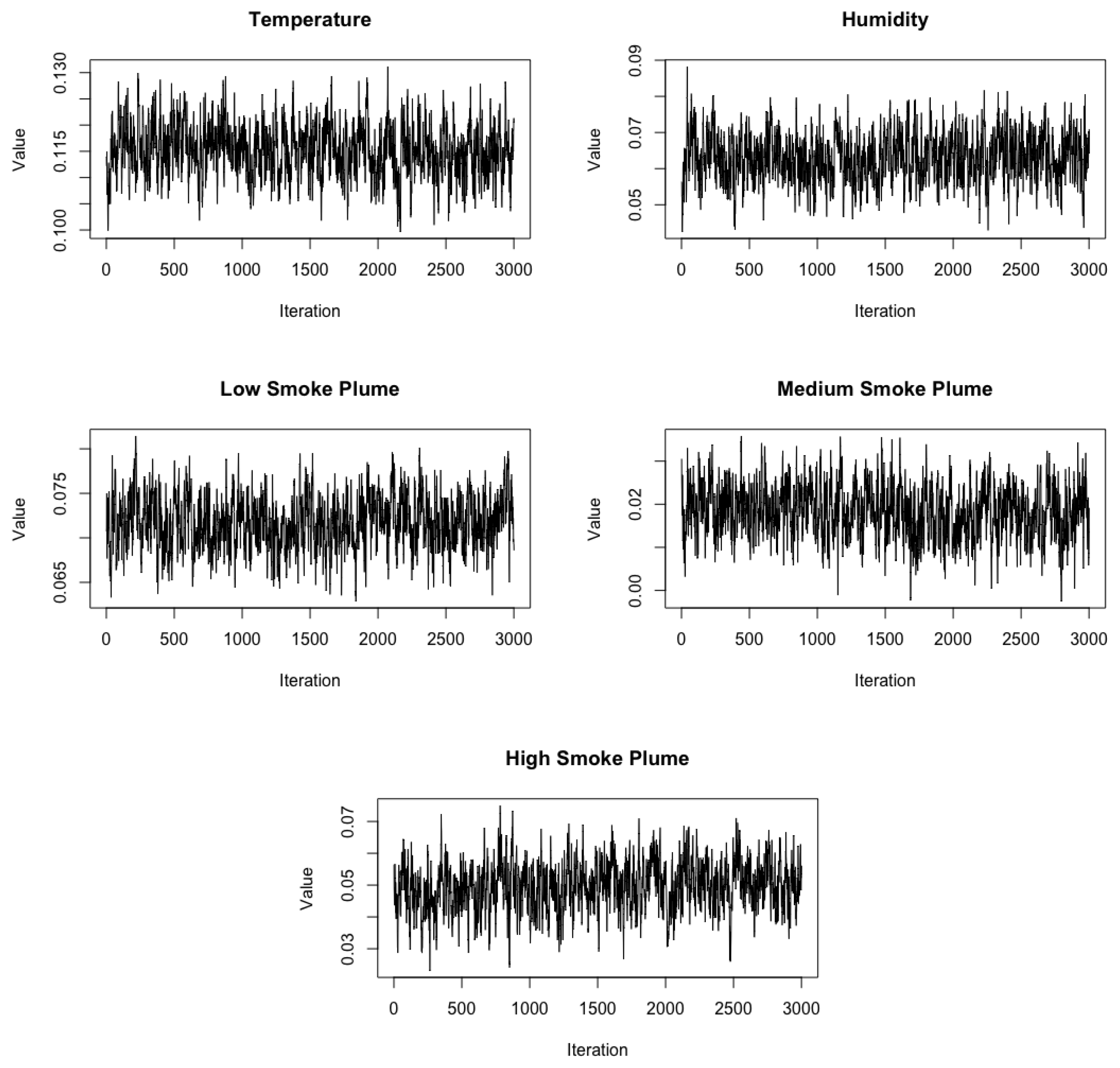
References
- Dennekamp, M.; Abramson, M.J. The effects of bushfire smoke on respiratory health. Respirology 2011, 16, 198–209. [Google Scholar] [CrossRef]
- Dennekamp, M.; Straney, L.D.; Erbas, B.; Abramson, M.J.; Keywood, M.; Smith, K.; Sim, M.R.; Glass, D.C.; Del Monaco, A.; Haikerwal, A.; et al. Forest fire smoke exposures and out-of-hospital cardiac arrests in Melbourne, Australia: A case-crossover study. Environ. Health Perspect. 2015, 123, 959–964. [Google Scholar] [CrossRef] [PubMed]
- Melnick, R.S. Regulation and the Courts: The Case of the Clean Air Act; Brookings Institution Press: Washington, DC, USA, 2010. [Google Scholar]
- Sager, L.; Singer, G. Clean Identification? The Effects of the Clean Air Act on Air Pollution, Exposure Disparities and House Prices. 2022. Available online: https://www.lse.ac.uk/granthaminstitute/wp-content/uploads/2022/05/working-paper-376-Sager-Singer_May-2023.pdf (accessed on 1 May 2023).
- McClure, C.D.; Jaffe, D.A. US particulate matter air quality improves except in wildfire-prone areas. Proc. Natl. Acad. Sci. USA 2018, 115, 7901–7906. [Google Scholar] [CrossRef] [PubMed]
- Johnston, F.H.; Henderson, S.B.; Chen, Y.; Randerson, J.T.; Marlier, M.; DeFries, R.S.; Kinney, P.; Bowman, D.M.; Brauer, M. Estimated global mortality attributable to smoke from landscape fires. Environ. Health Perspect. 2012, 120, 695–701. [Google Scholar] [CrossRef] [PubMed]
- Rappold, A.G.; Stone, S.L.; Cascio, W.E.; Neas, L.M.; Kilaru, V.J.; Carraway, M.S.; Szykman, J.J.; Ising, A.; Cleve, W.E.; Meredith, J.T.; et al. Peat bog wildfire smoke exposure in rural North Carolina is associated with cardiopulmonary emergency department visits assessed through syndromic surveillance. Environ. Health Perspect. 2011, 119, 1415–1420. [Google Scholar] [CrossRef] [PubMed]
- Haikerwal, A.; Akram, M.; Sim, M.R.; Meyer, M.; Abramson, M.J.; Dennekamp, M. Fine particulate matter (PM2.5) exposure during a prolonged wildfire period and emergency department visits for asthma. Respirology 2016, 21, 88–94. [Google Scholar] [CrossRef]
- Thilakaratne, R.; Hoshiko, S.; Rosenberg, A.; Hayashi, T.; Buckman, J.R.; Rappold, A.G. Wildfires and the changing landscape of air pollution–related gealth burden in California. Am. J. Respir. Crit. Care Med. 2023, 207, 887–898. [Google Scholar] [CrossRef]
- Li, L.; Girguis, M.; Lurmann, F.; Pavlovic, N.; McClure, C.; Franklin, M.; Wu, J.; Oman, L.; Breton, C.; Gilliland, F. Ensemble-based deep learning for estimating PM2.5 over California with multisource big data including wildfire smoke. Environ. Int. 2020, 145, 106143. [Google Scholar] [CrossRef]
- Romanov, A.A.; Tamarovskaya A., N.; Gusev B., A.; Leonenko, E.V.; Vasiliev, A.S.; Krikunov, E.E. Catastrophic PM2.5 emissions from Siberian forest fires: Impacting factors analysis. Environ. Pollut. 2022, 306, 119324. [Google Scholar] [CrossRef]
- Ikeda, K.; Tanimoto, H. Exceedances of air quality standard level of PM2.5 in Japan caused by Siberian wildfires. Environ. Res. Lett. 2015, 10, 105001. [Google Scholar]
- Larsen, A.E.; Reich, B.J.; Ruminski, M.; Rappold, A.G. Impacts of fire smoke plumes on regional air quality, 2006–2013. J. Expo. Sci. Environ. Epidemiol. 2018, 28, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Matz, C.J.; Egyed, M.; Xi, G.; Racine, J.; Pavlovic, R.; Rittmaster, R.; Henderson, S.B.; Stieb, D.M. Health impact analysis of PM2.5 from wildfire smoke in Canada (2013–2015, 2017–2018). Sci. Total Environ. 2020, 725, 138506. [Google Scholar] [PubMed]
- Barkjohn, K.; Gantt, B.; Clements, A. Development and Application of a United States wide correction for PM2.5 data collected with the PurpleAir sensor. Atmos. Meas. Tech. Discuss. 2020, 2020, 7304881. [Google Scholar] [CrossRef]
- Tryner, J.; L’Orange, C.; Mehaffy, J.; Miller-Lionberg, D.; Hofstetter, J.C.; Wilson, A.; Volckens, J. Laboratory evaluation of low-cost PurpleAir PM monitors and in-field correction using co-located portable filter samplers. Atmos. Environ. 2020, 220, 117067. [Google Scholar] [CrossRef]
- Wallace, L.; Bi, J.; Ott, W.R.; Sarnat, J.; Liu, Y. Calibration of low-cost PurpleAir outdoor monitors using an improved method of calculating PM2.5. Atmos. Environ. 2021, 256, 118432. [Google Scholar] [CrossRef]
- Holder, A.L.; Mebust, A.K.; Maghran, L.A.; McGown, M.R.; Stewart, K.E.; Vallano, D.M.; Elleman, R.A.; Baker, K.R. Field evaluation of low-cost particulate matter sensors for measuring wildfire smoke. Sensors 2020, 20, 4796. [Google Scholar] [CrossRef]
- Kosmopoulos, G.; Salamalikis, V.; Pandis, S.; Yannopoulos, P.; Bloutsos, A.; Kazantzidis, A. Low-cost sensors for measuring airborne particulate matter: Field evaluation and calibration at a South-Eastern European site. Sci. Total Environ. 2020, 748, 141396. [Google Scholar] [CrossRef]
- Durrant-Whyte, H.; Henderson, T.C. Multisensor data fusion. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 867–896. [Google Scholar]
- Luo, R.C.; Kay, M.G. A tutorial on multisensor integration and fusion. In Proceedings of the IECON’90: 16th Annual Conference of IEEE Industrial Electronics Society, Pacific Grove, CA, USA, 27–30 November 1990; pp. 707–722. [Google Scholar]
- Reich, B.J.; Chang, H.H.; Foley, K.M. A spectral method for spatial downscaling. Biometrics 2014, 70, 932–942. [Google Scholar] [CrossRef]
- Warren, J.L.; Miranda, M.L.; Tootoo, J.L.; Osgood, C.E.; Bell, M.L. Spatial distributed lag data fusion for estimating ambient air pollution. Ann. Appl. Stat. 2021, 15, 323. [Google Scholar] [CrossRef]
- Friberg, M.D.; Zhai, X.; Holmes, H.A.; Chang, H.H.; Strickland, M.J.; Sarnat, S.E.; Tolbert, P.E.; Russell, A.G.; Mulholland, J.A. Method for fusing observational data and chemical transport model simulations to estimate spatiotemporally resolved ambient air pollution. Environ. Sci. Technol. 2016, 50, 3695–3705. [Google Scholar] [CrossRef]
- Friberg, M.D.; Kahn, R.A.; Holmes, H.A.; Chang, H.H.; Sarnat, S.E.; Tolbert, P.E.; Russell, A.G.; Mulholland, J.A. Daily ambient air pollution metrics for five cities: Evaluation of data-fusion-based estimates and uncertainties. Atmos. Environ. 2017, 158, 36–50. [Google Scholar] [CrossRef]
- Nguyen, H.; Cressie, N.; Braverman, A. Spatial statistical data fusion for remote sensing applications. J. Am. Stat. Assoc. 2012, 107, 1004–1018. [Google Scholar] [CrossRef]
- Gressent, A.; Malherbe, L.; Colette, A.; Rollin, H.; Scimia, R. Data fusion for air quality mapping using low-cost sensor observations: Feasibility and added-value. Environ. Int. 2020, 143, 105965. [Google Scholar] [CrossRef] [PubMed]
- Datta, A.; Saha, A.; Zamora, M.L.; Buehler, C.; Hao, L.; Xiong, F.; Gentner, D.R.; Koehler, K. Statistical field calibration of a low-cost PM2.5 monitoring network in Baltimore. Atmos. Environ. 2020, 242, 117761. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.C.; Chi, W.J.; Lin, Y.Q. The improvement of spatial-temporal resolution of PM2. 5 estimation based on micro-air quality sensors by using data fusion technique. Environ. Int. 2020, 134, 105305. [Google Scholar] [CrossRef]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote. Sens. 2006, 44, 2207–2218. [Google Scholar]
- Hu, D.g.; Shu, H. Spatiotemporal interpolation of precipitation across Xinjiang, China using space-time CoKriging. J. Cent. South Univ. 2019, 26, 684–694. [Google Scholar] [CrossRef]
- Stein, M.L. Statistical methods for regular monitoring data. J. R. Stat. Soc. Ser. Stat. Methodol. 2005, 67, 667–687. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration. Hazard Mapping System Fire and Smoke Product. Available online: https://www.ospo.noaa.gov/Products/land/hms.html (accessed on 15 October 2022).
- O’Dell, K.; Ford, B.; Fischer, E.V.; Pierce, J.R. Contribution of wildland-fire smoke to US PM2.5 and its influence on recent trends. Environ. Sci. Technol. 2019, 53, 1797–1804. [Google Scholar] [CrossRef]
- Buysse, C.E.; Kaulfus, A.; Nair, U.; Jaffe, N.A. Relationships between particulate matter, ozone, and nitrogen oxides during urban smoke events in the western US. Environ. Sci. Technol. 2019, 53, 12519–12528. [Google Scholar] [CrossRef]
- Barkjohn, K.K.; Holder, A.L.; Frederick, S.G.; Clements, A.L. Relationships between particulate matter, ozone, and nitrogen oxides during urban smoke events in the western US. Sensors 2022, 22, 9669. [Google Scholar] [PubMed]
- California Department of Forestry and Fire Protection. Top 20 Largest California Wildfires. Available online: https://www.fire.ca.gov/our-impact/statistics (accessed on 1 February 2023).
- Draxler, R.; Rolph, G. HYSPLIT (HYbrid Single-Particle Lagrangian Integrated Trajectory) Model Access via NOAA ARL READY; NOAA Air Resources Laboratory: Silver Spring, MD, USA, 2010; Volume 25. Available online: https://www.ready.noaa.gov/HYSPLIT.php (accessed on 1 May 2023).
- Su, L.; Yuan, Z.; Fung, J.C.; Lau, A.K. A comparison of HYSPLIT backward trajectories generated from two GDAS datasets. Sci. Total Environ. 2015, 506, 527–537. [Google Scholar] [CrossRef] [PubMed]
- Geyer, C.J. Introduction to Markov Chain Monte Carlo. In Handbook of Markov Chain Monte Carlo; Chapman and Hall/CRC: Boca Raton, FL, USA, 2011; Volume 20116022, p. 45. [Google Scholar]



| 2020 Fire Season | ||
|---|---|---|
| Parameter | True PM | Bias Correction |
| Temperature | 0.115 (0.106,0.125) *** | −0.002 (−0.009,0.005) |
| Humidity | 0.064 (0.048,0.080) *** | 0.012 (−0.002,0.035) |
| Plume—Low | 0.007 (0.003,0.011) *** | / |
| Plume—Medium | 0.022 (0.012,0.032) *** | / |
| Plume—High | 0.049 (0.033,0.065) *** | / |
| 2021 Fire Season | ||
| Parameter | True PM | Bias Correction |
| Temperature | 0.006 (0.004,0.008) *** | 0.006 (−0.003,0.015) |
| Humidity | 0.000 (−0.001,0.001) | −0.011 (−0.026,0.003) |
| Plume—Low | 0.011 (0.001,0.021) *** | / |
| Plume—Medium | 0.018 (0.007,0.029) *** | / |
| Plume—High | 0.041 (0.031,0.051) *** | / |
| 2020 Fire Season | |||
|---|---|---|---|
| Parameter | Data Fusion | AQS Only | Naive |
| Temperature | 0.115 (0.005) *** | 0.105 (0.024) *** | −0.418 (0.066) *** |
| Humidity | 0.064 (0.008) *** | 0.086 (0.022) *** | −1.125 (0.052) *** |
| Plume—Low | 0.007 (0.002) *** | 0.005 (0.012) | 0.107 (0.078) |
| Plume—Medium | 0.022 (0.005) *** | 0.020 (0.014) | 0.271 (0.052) *** |
| Plume—High | 0.049 (0.008) *** | 0.042 (0.016) *** | 0.637 (0.079) *** |
| 2021 Fire Season | |||
| Parameter | Data Fusion | AQS Only | Naive |
| Temperature | 0.006 (0.001) *** | 0.015 (0.003) *** | −0.014 (0.006) *** |
| Humidity | 0.000 (0.000) | 0.008 (0.002) *** | −0.039 (0.003) *** |
| Plume—Low | 0.011 (0.004) *** | −0.001 (0.014) | −0.330 (0.032) *** |
| Plume—Medium | 0.018 (0.004) *** | 0.023 (0.016) | 0.230 (0.074) *** |
| Plume—High | 0.041 (0.005) *** | 0.054 (0.017) *** | 0.980 (0.071) *** |
| Model | RMSE | Coverage | Ave Var |
|---|---|---|---|
| Data Fusion | 0.42 | 0.89 | 0.13 |
| AQS only | 0.40 | 0.91 | 0.16 |
| Naive | 0.66 | 0.73 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Ruiz-Suarez, S.; Reich, B.J.; Guan, Y.; Rappold, A.G. A Data-Fusion Approach to Assessing the Contribution of Wildland Fire Smoke to Fine Particulate Matter in California. Remote Sens. 2023, 15, 4246. https://doi.org/10.3390/rs15174246
Yang H, Ruiz-Suarez S, Reich BJ, Guan Y, Rappold AG. A Data-Fusion Approach to Assessing the Contribution of Wildland Fire Smoke to Fine Particulate Matter in California. Remote Sensing. 2023; 15(17):4246. https://doi.org/10.3390/rs15174246
Chicago/Turabian StyleYang, Hongjian, Sofia Ruiz-Suarez, Brian J. Reich, Yawen Guan, and Ana G. Rappold. 2023. "A Data-Fusion Approach to Assessing the Contribution of Wildland Fire Smoke to Fine Particulate Matter in California" Remote Sensing 15, no. 17: 4246. https://doi.org/10.3390/rs15174246
APA StyleYang, H., Ruiz-Suarez, S., Reich, B. J., Guan, Y., & Rappold, A. G. (2023). A Data-Fusion Approach to Assessing the Contribution of Wildland Fire Smoke to Fine Particulate Matter in California. Remote Sensing, 15(17), 4246. https://doi.org/10.3390/rs15174246






