Application of Filtering Techniques to Smooth a Surface of Hybrid Digital Bathymetric Model
Abstract
:1. Introduction
2. Materials and Methods
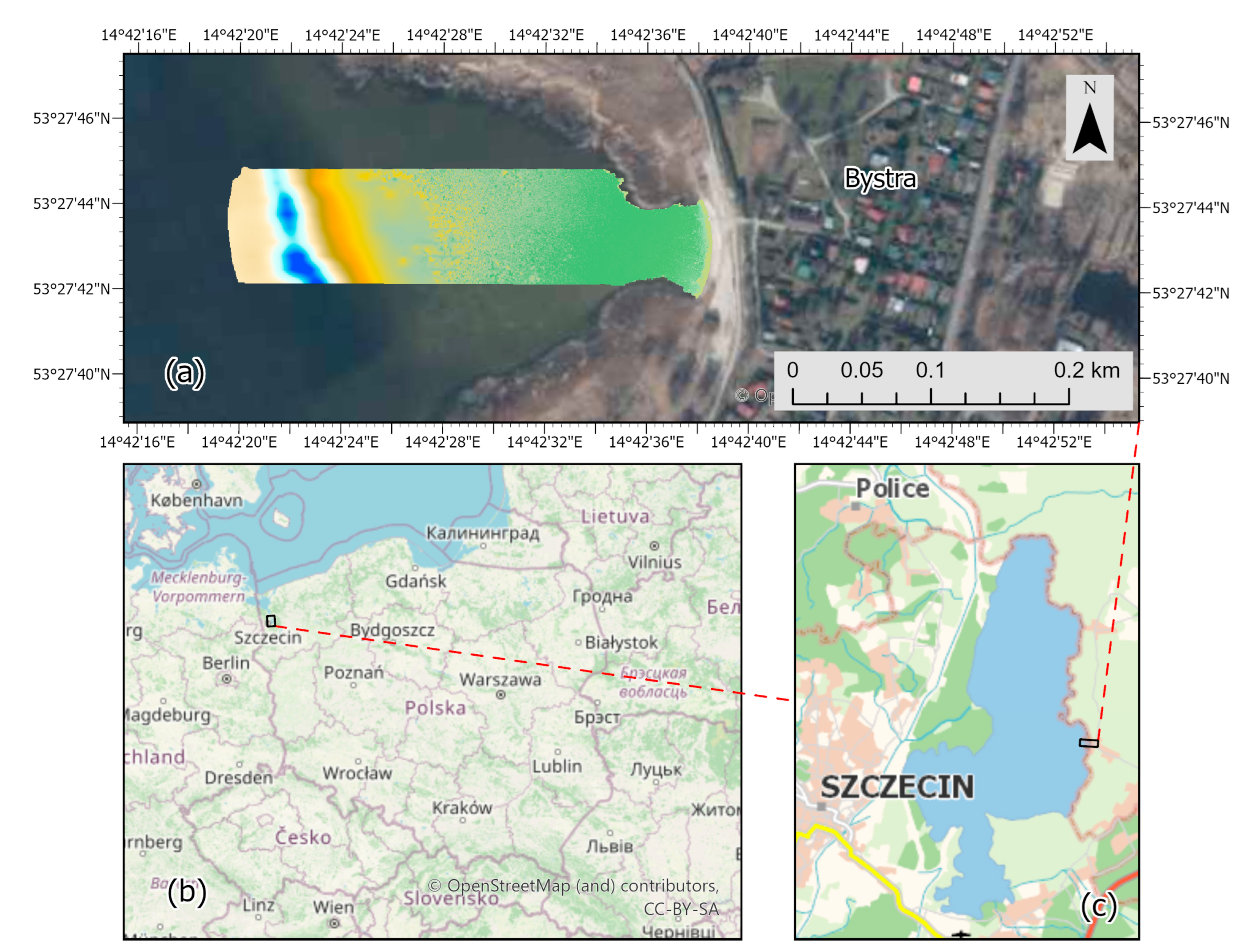
2.1. Study Area
2.2. Input Data
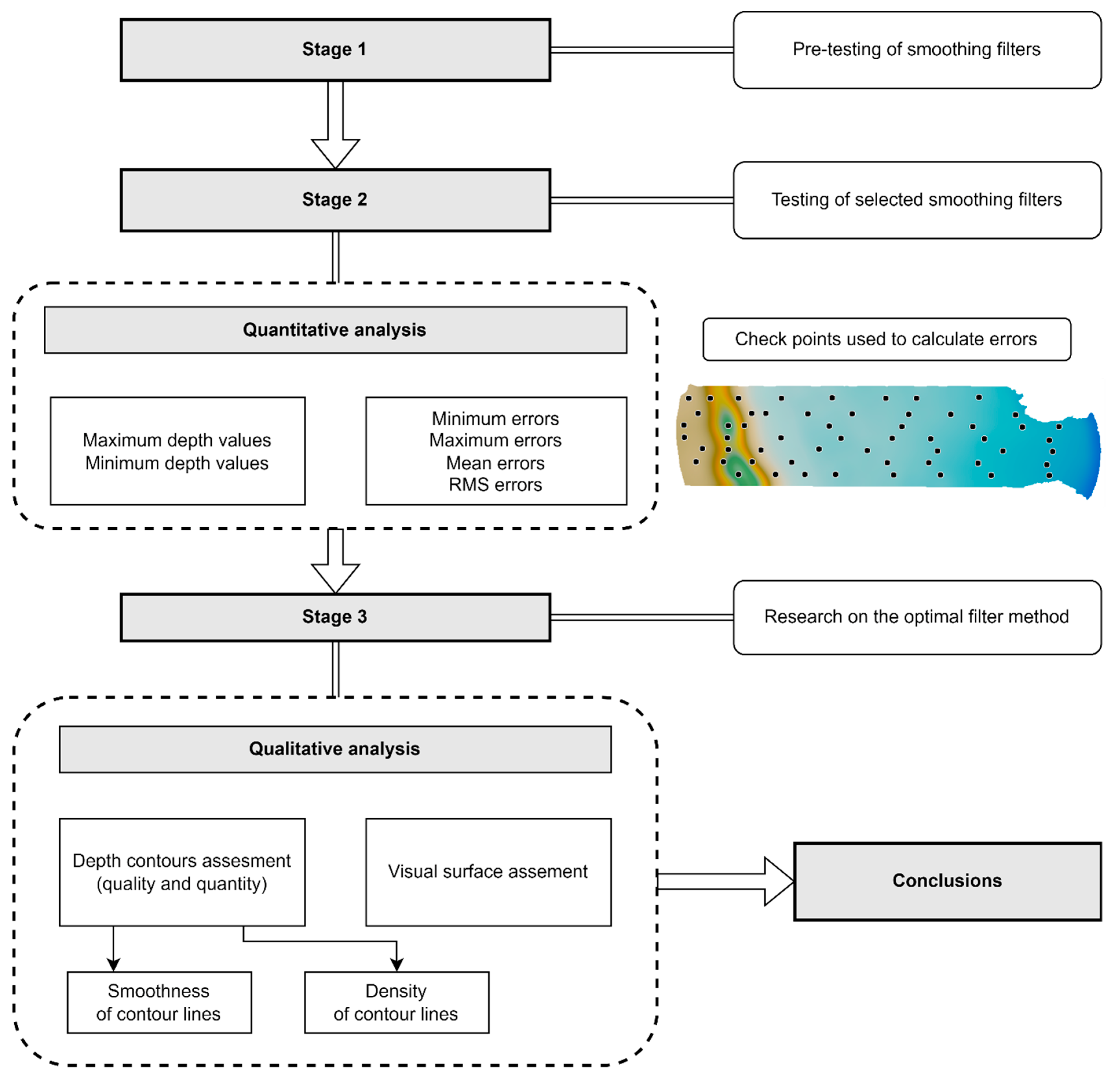
2.3. Research Methodology
2.4. Convolution Filters
3. Results
3.1. Stage 1: Pre-Testing of Smoothing Filters
Visual Analysis
3.2. Stage 2: Testing of Selected Smoothing Filters
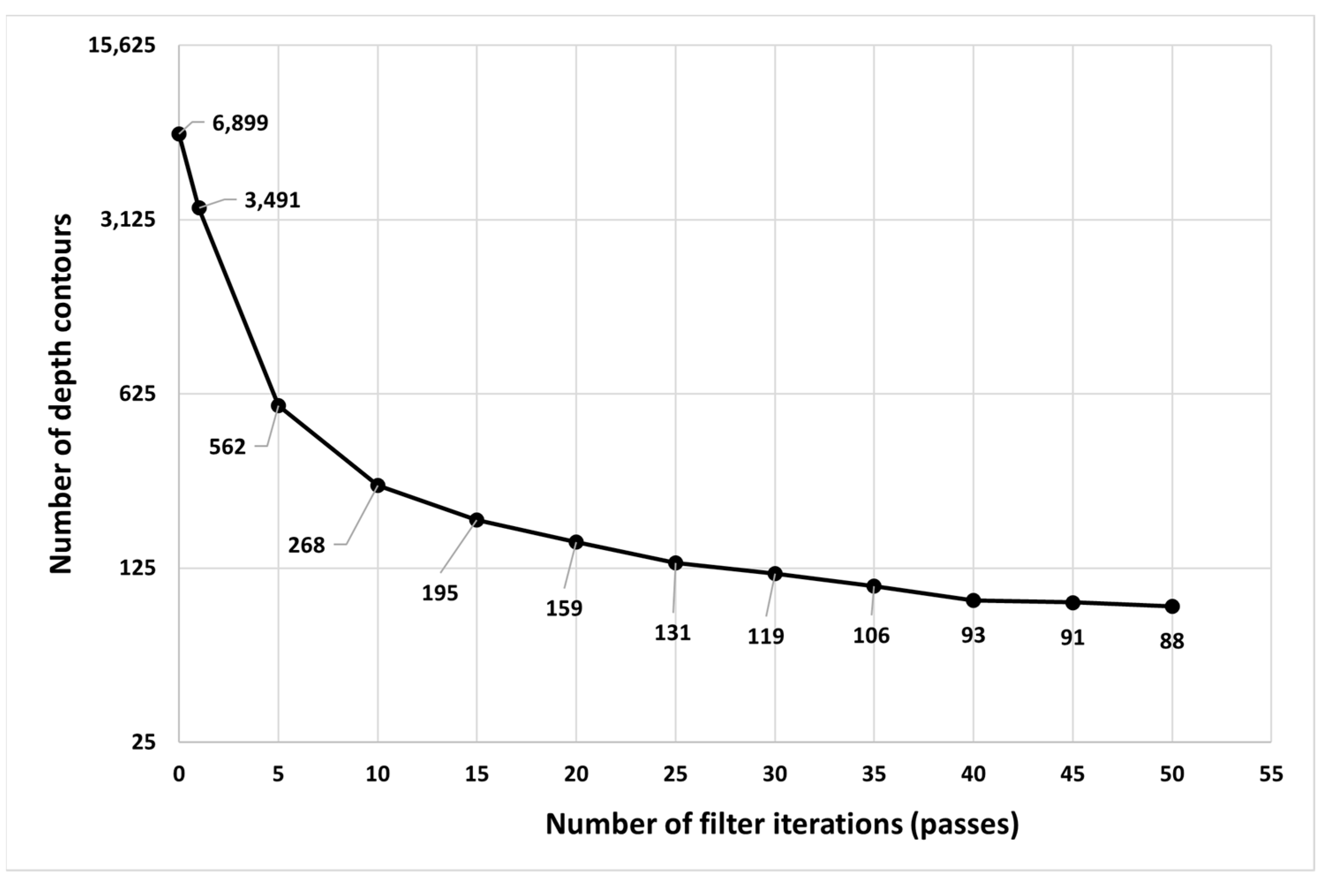
Error Analysis
3.3. Stage 3: Research on the Optimal Filter Method
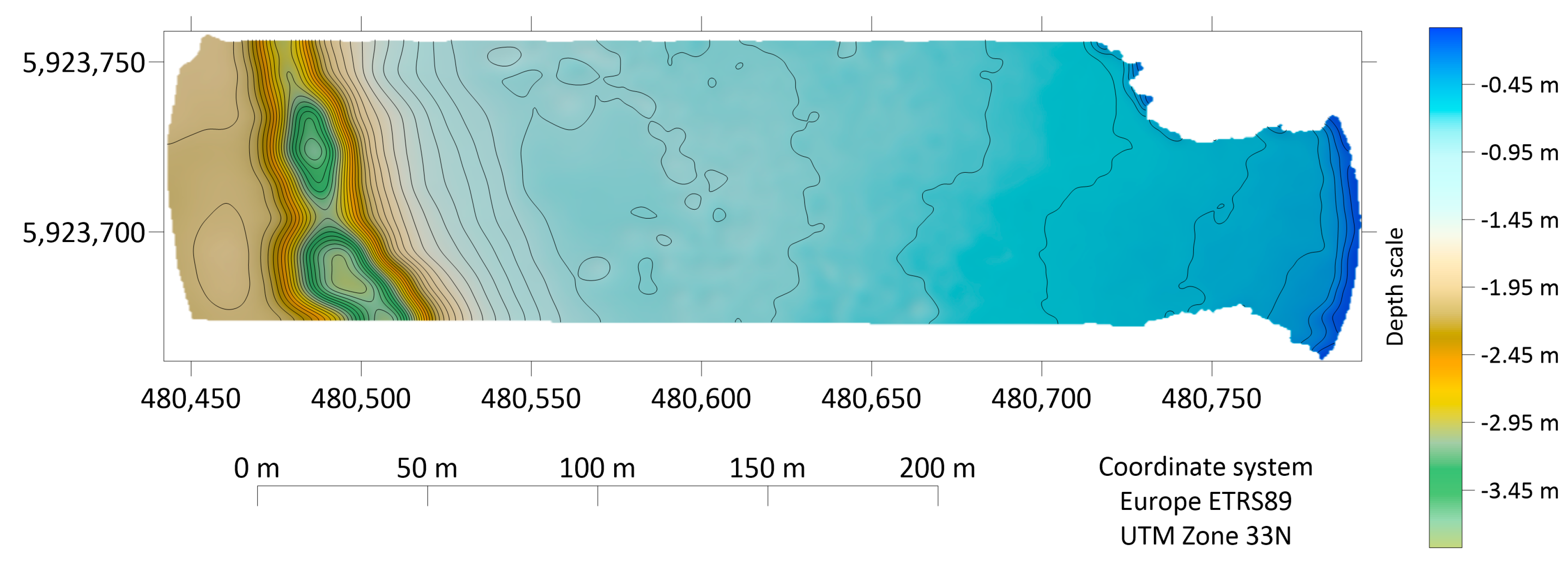
3.4. Exemplary Implementation of the Developed Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiménez-Jiménez, S.I.; Ojeda-Bustamante, W.; Marcial-Pablo, M.D.J.; Enciso, J. Digital Terrain Models Generated with Low-Cost UAV Photogrammetry: Methodology and Accuracy. ISPRS Int. J. Geo-Inf. 2021, 10, 285. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-Art: DTM Generation Using Airborne LIDAR Data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef] [PubMed]
- Brzank, A.; Heipke, C.; Goepfert, J.; Soergel, U. Aspects of Generating Precise Digital Terrain Models in the Wadden Sea from Lidar-Water Classification and Structure Line Extraction. ISPRS J. Photogramm. Remote Sens. 2008, 63, 510–528. [Google Scholar] [CrossRef]
- Alho, P.; Hyyppä, H.; Hyyppä, J. Consequence of DTM Precision for Flood Hazard Mapping: A Case Study in SW Finland. Nord. J. Surv. Real Estate Res. 2009, 6, 21–39. [Google Scholar]
- Yamazaki, D.; Ikeshima, D.; Tawatari, R.; Yamaguchi, T.; O’Loughlin, F.; Neal, J.C.; Sampson, C.C.; Kanae, S.; Bates, P.D. A High-Accuracy Map of Global Terrain Elevations. Geophys. Res. Lett. 2017, 44, 5844–5853. [Google Scholar] [CrossRef]
- Sampson, C.C.; Smith, A.M.; Bates, P.D.; Neal, J.C.; Trigg, M.A. Perspectives on Open Access High Resolution Digital Elevation Models to Produce Global Flood Hazard Layers. Front. Earth Sci. 2016, 3, 85. [Google Scholar] [CrossRef]
- International Hydrographic Organization (IHO). IHO Standards For Hydrographic Surveys, 6th ed.; International Hydrographic Bureau: Monaco, 2020. [Google Scholar]
- Lubczonek, J.; Wlodarczyk-Sielicka, M.; Lacka, M.; Zaniewicz, G. Methodology for Developing a Combined Bathymetric and Topographic Surface Model Using Interpolation and Geodata Reduction Techniques. Remote Sens. 2021, 13, 4427. [Google Scholar] [CrossRef]
- Stereńczak, K.; Ciesielski, M.; Bałazy, R.; Zawiła-Niedźwiecki, T. Comparison of Various Algorithms for DTM Interpolation from LIDAR Data in Dense Mountain Forests. Eur. J. Remote Sens. 2016, 49, 599–621. [Google Scholar] [CrossRef]
- Garnero, G.; Godone, D. Comparisons between Different Interpolation Techniques. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2013, 40, 139–144. [Google Scholar] [CrossRef]
- Arun, P.V. A Comparative Analysis of Different DEM Interpolation Methods. Egypt. J. Remote Sens. Sp. Sci. 2013, 16, 133–139. [Google Scholar] [CrossRef]
- Xie, J. Implementation and Performance Optimization of a Parallel Contour Line Generation Algorithm. Comput. Geosci. 2012, 49, 21–28. [Google Scholar] [CrossRef]
- Tan, L.; Wan, G.; Li, F.; Chen, X.; Du, W. GPU Based Contouring Method on Grid DEM Data. Comput. Geosci. 2017, 105, 129–138. [Google Scholar] [CrossRef]
- Ruiz, A.; Castillo, M.; Arbiol, R.; Colomer, J.L. ISAR DEM Data Processing for Contours Generation. In Proceedings of the OEEPE Workshop on Airborne Laserscanning and Interferometric SAR for Detailed Digital Elevation Models, Stockholm, Sweden, 1–3 March 2001. [Google Scholar]
- Sofia, G.; Eltner, A.; Nikolopoulos; Crosby, C. Leading Progress in Digital Terrain Analysis and Modeling. ISPRS Int. J. Geo-Inf. 2019, 8, 372. [Google Scholar] [CrossRef]
- Ruzickova, K.; Ruzicka, J.; Bitta, J. A New GIS-Compatible Methodology for Visibility Analysis in Digital Surface Models of Earth Sites. Geosci. Front. 2021, 12, 101109. [Google Scholar] [CrossRef]
- Achilleos, G.; Tsouchlaraki, A. Visibility and Viewshed Algorithms in an Information System for Environmental Management. In Management Information Systems 2004: Incorporating GIS and Remote Sensing; WIT Press: Southampton, UK, 2004; Volume 32, pp. 109–121. [Google Scholar]
- Wechsler, S.P. Uncertainties Associated with Digital Elevation Models for Hydrologic Applications: A Review. Hydrol. Earth Syst. Sci. 2007, 11, 1481–1500. [Google Scholar] [CrossRef]
- Chymyrov, A. Comparison of Different DEMs for Hydrological Studies in the Mountainous Areas. Egypt. J. Remote Sens. Sp. Sci. 2021, 24, 587–594. [Google Scholar] [CrossRef]
- Mandlburger, G.; Hauer, C.; Höfle, B.; Habersack, H.; Pfeifer, N. Optimisation of LiDAR Derived Terrain Models for River Flow Modelling. Hydrol. Earth Syst. Sci. 2009, 13, 1453–1466. [Google Scholar] [CrossRef]
- Lacroix, M.P.; Martz, L.W.; Kite, G.W.; Garbrecht, J. Using Digital Terrain Analysis Modeling Techniques for the Parameterization of a Hydrologic Model. Environ. Model. Softw. 2002, 17, 125–134. [Google Scholar] [CrossRef]
- Degetto, M.; Gregoretti, C.; Bernard, M. Comparative Analysis of the Differences between Using LiDAR and Contour-Based DEMs for Hydrological Modeling of Runoff Generating Debris Flows in the Dolomites. Front. Earth Sci. 2015, 3, 21. [Google Scholar] [CrossRef]
- Hatta Antah, F.; Khoiry, M.A.; Abdul Maulud, K.N.; Abdullah, A. Perceived Usefulness of Airborne Lidar Technology in Road Design and Management: A Review. Sustainability 2021, 13, 1773. [Google Scholar] [CrossRef]
- Bhakar, P.; Singh, A.P.; Mittal, R.K. Assessment of Groundwater Suitability Using Remote Sensing and GIS: A Case Study of Western Rajasthan, India. Arab. J. Geosci. 2022, 15, 41. [Google Scholar] [CrossRef]
- He, Q.; Chen, E.; An, R.; Li, Y. Above-Ground Biomass and Biomass Components Estimation Using LiDAR Data in a Coniferous Forest. Forests 2013, 4, 984–1002. [Google Scholar] [CrossRef]
- Romshoo, S.A.; Yousuf, A.; Altaf, S.; Amin, M. Evaluation of Various DEMs for Quantifying Soil Erosion Under Changing Land Use and Land Cover in the Himalaya. Front. Earth Sci. 2021, 9, 782128. [Google Scholar] [CrossRef]
- Badura, J.; Przybylski, B. Application of Digital Elevation Models to Geological and Geomorphological Studies-Some Examples. Prz. Geol. 2005, 53, 977–983. [Google Scholar]
- Grohmann, C.; Miliaresis, G. Geological Applications of Digital Terrain Analysis. Int. J. Geogr. Inf. Sci. 2013, 27, 1403–1404. [Google Scholar] [CrossRef]
- Xiong, L.; Li, S.; Tang, G.; Strobl, J. Geomorphometry and Terrain Analysis: Data, Methods, Platforms and Applications. Earth-Sci. Rev. 2022, 233, 104191. [Google Scholar] [CrossRef]
- Ahmad, M.J.; Ahmad, A.; Kanniah, K.D. Large Scale Topographic Mapping Based on Unmanned Aerial Vehicle and Aerial Photogrammetric Technique. IOP Conf. Ser. Earth Environ. Sci. 2018, 169, 2–9. [Google Scholar] [CrossRef]
- Mendes Junior, C.W.; Dani, N.; Arigony-Neto, J.; Simões, J.C.; Velho, L.F.; Ribeiro, R.R.; Parnow, I.; Bremer, U.F.; Fonseca Júnior, E.S.; Erwes, H.J.B. A New Topographic Map for Keller Peninsula, King George Island, Antarctica. Braz. Antarct. Res. 2012, 5, 105–113. [Google Scholar]
- Rizaldy, A.; Mayasari, R. Acceleration of Topographic Map Production Using Semi-Automatic DTM from DSM Radar Data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2016, 41, 47–54. [Google Scholar] [CrossRef]
- Li, Z.; Peng, Z.; Zhang, Z.; Chu, Y.; Xu, C.; Yao, S.; García-Fernández, Á.F.; Zhu, X.; Yue, Y.; Levers, A.; et al. Exploring Modern Bathymetry: A Comprehensive Review of Data Acquisition Devices, Model Accuracy, and Interpolation Techniques for Enhanced Underwater Mapping. Front. Mar. Sci. 2023, 10, 1178845. [Google Scholar] [CrossRef]
- Ryu, P.; Brown, D.; Arsenault, K.; Cho, B.; March, A.; Ali, W.H.; Charous, A.; Lermusiaux, P.F.J. A Wide-Area Deep Ocean Floor Mapping System: Design and Sea Tests. Geomatics 2023, 3, 290–311. [Google Scholar] [CrossRef]
- Mayer, L.; Jakobsson, M.; Allen, G.; Dorschel, B.; Falconer, R.; Ferrini, V.; Lamarche, G.; Snaith, H.; Weatherall, P. The Nippon Foundation-GEBCO Seabed 2030 Project: The Quest to See the World’s Oceans Completely Mapped by 2030. Geosciences 2018, 8, 63. [Google Scholar] [CrossRef]
- Shintani, C.; Fonstad, M.A. Comparing Remote-Sensing Techniques Collecting Bathymetric Data from a Gravel-Bed River. Int. J. Remote Sens. 2017, 38, 2883–2902. [Google Scholar] [CrossRef]
- Legleiter, C.J.; Harrison, L.R. Remote Sensing of River Bathymetry: Evaluating a Range of Sensors, Platforms, and Algorithms on the Upper Sacramento River, California, USA. Water Resour. Res. 2019, 55, 2142–2169. [Google Scholar] [CrossRef]
- Salavitabar, S.; Li, S.S.; Lak, B. Mapping Underwater Bathymetry of a Shallow River from Satellite Multispectral Imagery. Geosciences 2022, 12, 142. [Google Scholar] [CrossRef]
- Yang, H.; Guo, H.; Dai, W.; Nie, B.; Qiao, B.; Zhu, L. Bathymetric Mapping and Estimation of Water Storage in a Shallow Lake Using a Remote Sensing Inversion Method Based on Machine Learning. Int. J. Digit. Earth 2022, 15, 789–812. [Google Scholar] [CrossRef]
- Dost, R.J.J.; Mannaerts, C.M.M. Generation of Lake Bathymetry Using Sonar, Satellite Imagery and Gis. In Proceedings of the 28th Annual Esri International User Conference, San Diego, CA, USA, 4–8 August 2008. [Google Scholar]
- Elshazly, R.E.; Armanuos, A.M.; Zeidan, B.A.; Elshemy, M. Evaluating Remote Sensing Approaches for Mapping the Bathymetry of Lake Manzala, Egypt. Euro-Mediterr. J. Environ. Integr. 2021, 6, 77. [Google Scholar] [CrossRef]
- Yunus, A.P.; Dou, J.; Song, X.; Avtar, R. Improved Bathymetric Mapping of Coastal and Lake Environments Using Sentinel-2 and Landsat-8 Images. Sensors 2019, 19, 2788. [Google Scholar] [CrossRef]
- Ho, M.; El-Borgi, S.; Patil, D.; Song, G. Inspection and Monitoring Systems Subsea Pipelines: A Review Paper. Struct. Health Monit. 2020, 19, 606–645. [Google Scholar] [CrossRef]
- Clubley, S.; Manes, C.; Richards, D. 1400033: High-Resolution Sonars Set to Revolutionise Bridge Scour Inspections. Proc. Inst. Civ. Eng. Civ. Eng. 2015, 168, 58. [Google Scholar]
- Bouziani, M.; Boucht, F.; Nouri, F. Contribution of Bathymetric Multi-beam Sonar and Laser Scanners in 3D Modeling and Estimation of Siltation of Dam Basin in Morocco. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2021, 46, 5–9. [Google Scholar] [CrossRef]
- Zhang, W.; Zhou, T.; Li, J.; Xu, C. An Efficient Method for Detection and Quantitation of Underwater Gas Leakage Based on a 300-KHz Multibeam Sonar. Remote Sens. 2022, 14, 4301. [Google Scholar] [CrossRef]
- Adnan, N.A.; Atkinson, P.M. Remote Sensing of River Bathymetry for Use in Hydraulic Model Prediction of Flood Inundation. In Proceedings of the 2012 IEEE 8th International Colloquium on Signal Processing and its Applications, Malacca, Malaysia, 23–25 March 2012; pp. 159–163. [Google Scholar] [CrossRef]
- Dey, S.; Saksena, S.; Winter, D.; Merwade, V.; McMillan, S. Incorporating Network Scale River Bathymetry to Improve Characterization of Fluvial Processes in Flood Modeling. Water Resour. Res. 2022, 58, e2020WR029521. [Google Scholar] [CrossRef]
- Joo, J.; Kim, S.S.; Choi, J.W.; Pak, S.J.; Ko, Y.; Son, S.K.; Moon, J.W.; Kim, J. Seabed Mapping Using Shipboard Multibeam Acoustic Data for Assessing the Spatial Distribution of Ferromanganese Crusts on Seamounts in the Western Pacific. Minerals 2020, 10, 155. [Google Scholar] [CrossRef]
- International Hydrographic Organization (IHO). High Density (HD) ENC Production and Maintenance Guidance, 1st ed.; International Hydrographic Organization: Monaco, 2020. [Google Scholar]
- International Hydrographic Organization (IHO). Electronic Navigational Charts (ENCs) Production, Maintenance And Distribution Guidance, 2.1.0 ed.; International Hydrographic Organization: Monaco, 2017. [Google Scholar]
- Soeksmantono, B.; Utama, Y.P.; Syaifudin, F. Utilization of Airborne Topo-Bathymetric LiDAR Technology for Coastline Determination in Western Part of Java Island. IOP Conf. Ser. Earth Environ. Sci. 2021, 925, 012065. [Google Scholar] [CrossRef]
- Mandlburger, G.; Hauer, C.; Wieser, M.; Pfeifer, N. Topo-Bathymetric LiDAR for Monitoring River Morphodynamics and Instream Habitats-A Case Study at the Pielach River. Remote Sens. 2015, 7, 6160–6195. [Google Scholar] [CrossRef]
- Janowski, A.; Tȩgowski, J.; Nowak, J. Seafloor Mapping Based on Multibeam Echosounder Bathymetry and Backscatter Data Using Object-Based Image Analysis: A Case Study from the Rewal Site, the Southern Baltic. Oceanol. Hydrobiol. Stud. 2018, 47, 248–259. [Google Scholar] [CrossRef]
- Janowski, L.; Trzcinska, K.; Tegowski, J.; Kruss, A.; Rucinska-Zjadacz, M.; Pocwiardowski, P. Nearshore Benthic Habitat Mapping Based on Multi-Frequency, Multibeam Echosounder Data Using a Combined Object-Based Approach: A Case Study from the Rowy Site in the Southern Baltic Sea. Remote Sens. 2018, 10, 1983. [Google Scholar] [CrossRef]
- Lekkerkerk, H.-J. The Evolution Of a Bathymetric, State of the Art in Multibeam Echosounders. Hydro International, 30 October 2020. [Google Scholar]
- Al Najar, M.; Thoumyre, G.; Bergsma, E.W.J.; Almar, R.; Benshila, R.; Wilson, D.G. Satellite Derived Bathymetry Using Deep Learning. Mach. Learn. 2023, 112, 1107–1130. [Google Scholar] [CrossRef]
- Cesbron, G.; Melet, A.; Almar, R.; Lifermann, A.; Tullot, D.; Crosnier, L. Pan-European Satellite-Derived Coastal Bathymetry—Review, User Needs and Future Services. Front. Mar. Sci. 2021, 8, 740830. [Google Scholar] [CrossRef]
- Duplančić Leder, T.; Baučić, M.; Leder, N.; Gilić, F. Optical Satellite-Derived Bathymetry: An Overview and WoS and Scopus Bibliometric Analysis. Remote Sens. 2023, 15, 1294. [Google Scholar] [CrossRef]
- Jagalingam, P.; Akshaya, B.J.; Hegde, A.V. Bathymetry Mapping Using Landsat 8 Satellite Imagery. Procedia Eng. 2015, 116, 560–566. [Google Scholar] [CrossRef]
- Makar, A. Coastal Bathymetric Sounding in Very Shallow Water Using USV: Study of Public Beach in Gdynia, Poland. Sensors 2023, 23, 4215. [Google Scholar] [CrossRef] [PubMed]
- Specht, M.; Specht, C.; Szafran, M.; Makar, A.; Dabrowski, P.; Lasota, H.; Cywiński, P. The Use of USV to Develop Navigational and Bathymetric Charts of Yacht Ports on the Example of National Sailing Centre in Gdańsk. Remote Sens. 2020, 12, 2585. [Google Scholar] [CrossRef]
- Wang, D.; Xing, S.; He, Y.; Yu, J.; Xu, Q.; Li, P. Evaluation of a New Lightweight UAV-Borne Topo-Bathymetric LiDAR for Shallow Water Bathymetry and Object Detection. Sensors 2022, 22, 1379. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Zhou, X.; Li, W.; Zhao, D.; Song, B.; Xu, C.; Zhang, H.; Liu, Z.; Xu, J.; Lin, G.; et al. Development of a Lightweight Single-Band Bathymetric LiDAR. Remote Sens. 2022, 14, 5880. [Google Scholar] [CrossRef]
- Sotelo-Torres, F.; Alvarez, L.V.; Roberts, R.C. An Unmanned Surface Vehicle (USV): Development of an Autonomous Boat with a Sensor Integration System for Bathymetric Surveys. Sensors 2023, 23, 4420. [Google Scholar] [CrossRef]
- Noman, J.; Cassol, W.N.; Daniel, S.; Pham Van Bang, D. Bathymetric Data Integration Approach to Study Bedforms in the Estuary of the Saint-Lawrence River. Front. Remote Sens. 2023, 4, 1125898. [Google Scholar] [CrossRef]
- Makiello, L. Multi-Sensor Fusion for a UAV / USV Tandem System for Spatial Data Collection of Waterways. In Proceedings of the 33. Forum Bauinformatik, München, Germany, 7–9 September 2022. [Google Scholar]
- Joe, H.; Cho, H.; Sung, M.; Kim, J.; Yu, S. Cheol Sensor Fusion of Two Sonar Devices for Underwater 3D Mapping with an AUV. Auton. Robots 2021, 45, 543–560. [Google Scholar] [CrossRef]
- Ferreira, F.; Machado, D.; Ferri, G.; Dugelay, S.; Potter, J. Underwater Optical and Acoustic Imaging: A Time for Fusion? A Brief Overview of the State-of-the-Art. In Proceedings of the OCEANS 2016 MTS/IEEE Conference, Monterey, CA, USA, 19–23 September 2016. [Google Scholar] [CrossRef]
- Hao, Y.; Han, Q. Data Fusion of Multi-Beam Sonar and Side-Scan Sonar Base on Feature Contour Registration. In Proceedings of the 2011 International Conference on Consumer Electronics, Communications and Networks (CECNet), Xianning, China, 16–18 April 2011; pp. 174–177. [Google Scholar] [CrossRef]
- Cooper, I.; Hotchkiss, R.H.; Williams, G.P. Extending Multi-Beam Sonar with Structure from Motion Data of Shorelines for Complete Pool Bathymetry of Reservoirs. Remote Sens. 2021, 13, 35. [Google Scholar] [CrossRef]
- Alevizos, E.; Oikonomou, D.; Argyriou, A.V.; Alexakis, D.D. Fusion of Drone-Based RGB and Multi-Spectral Imagery for Shallow Water Bathymetry Inversion. Remote Sens. 2022, 14, 1127. [Google Scholar] [CrossRef]
- Alevizos, E.; Nicodemou, V.C.; Makris, A.; Oikonomidis, I.; Roussos, A.; Alexakis, D.D. Integration of Photogrammetric and Spectral Techniques for Advanced Drone-Based Bathymetry Retrieval Using a Deep Learning Approach. Remote Sens. 2022, 14, 4160. [Google Scholar] [CrossRef]
- Lubczonek, J.; Kazimierski, W.; Zaniewicz, G.; Lacka, M. Methodology for Combining Data Acquired by Unmanned Surface and Aerial Vehicles to Create Digital Bathymetric Models in Shallow and Ultra-Shallow Waters. Remote Sens. 2022, 14, 105. [Google Scholar] [CrossRef]
- Imhof, E. Cartographic Relief Presentation; ESRI Press: Redlands, CA, USA, 2012. [Google Scholar]
- Ardiansyah, P.O.D.; Yokoyama, R. DEM Generation Method from Contour Lines Based on the Steepest Slope Segment Chain and a Monotone Interpolation Function. ISPRS J. Photogramm. Remote Sens. 2002, 57, 86–101. [Google Scholar] [CrossRef]
- Li, X.; Shen, H.; Feng, R.; Li, J.; Zhang, L. DEM Generation from Contours and a Low-Resolution DEM. ISPRS J. Photogramm. Remote Sens. 2017, 134, 135–147. [Google Scholar] [CrossRef]
- Taud, H.; Parrot, J.-F.; Alvarez, R. DEM Generation by Contour Line Dilation. Comput. Geosci. 1999, 25, 775–783. [Google Scholar] [CrossRef]
- Kettunen, P.; Koski, C.; Oksanen, J. A Design of Contour Generation for Topographic Maps with Adaptive DEM Smoothing. Int. J. Cartogr. 2017, 3, 19–30. [Google Scholar] [CrossRef]
- Younan, N.H.; Lee, H.S.; King, R.L. DTM Error Minimization via Adaptive Smoothing. LIDAR Forest Measurements. IEEE Int. Geosci. Remote Sens. Symp. 2003, 6, 3611–3613. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Francioni, A.; Cockburn, J.M.H. LiDAR DEM Smoothing and the Preservation of Drainage Features. Remote Sens. 2019, 11, 17–19. [Google Scholar] [CrossRef]
- Chen, C.; Yue, T.; Dai, H.; Tian, M. The Smoothness of HASM. Int. J. Geogr. Inf. Sci. 2013, 27, 1651–1667. [Google Scholar] [CrossRef]
- Wojciech, M. The Use of Linear Smoothing Methods to Remove Artefacts Resulting from the Seabed’s DTM Lossy Compression. Appl. Geomat. 2022, 14, 199–212. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Yan, C.; Dai, H.; Liu, G. A Robust Algorithm of Multiquadric Method Based on an Improved Huber Loss Function for Interpolating Remote-Sensing-Derived Elevation Data Sets. Remote Sens. 2015, 7, 3347–3371. [Google Scholar] [CrossRef]
- Peters, R.Y.; Ledoux, H.; Meijers, B.M. Generation and Generalization of Safe Depth-Contours for Hydrographic Charts Using a Surface-Based Approach. In Proceedings of the 16th Workshop of the ICA Commission on Generalisation and Multiple Representation, Dresden, Germany, 23–24 August 2013. [Google Scholar]
- Skopeliti, A.; Tsoulos, L.; Pe’eri, S. Depth Contours and Coastline Generalization for Harbour and Approach Nautical Charts. ISPRS Int. J. Geo-Inf. 2021, 10, 197. [Google Scholar] [CrossRef]
- Zhang, X.; Guilbert, E. A Multi-Agent System Approach for Feature-Driven Generalization of Isobathymetric Line. Adv. Cartogr. GISci. 2011, 1, 477–495. [Google Scholar] [CrossRef]
- Hennau, M.; De Wulf, A. Smoothing Contour Lines of Hydrographical Maps. In Proceedings of the 15th International Congress of the International Federation of Hydrographic Societies, Antwerpen, Belgium, 6–9 November 2006; pp. 199–201. [Google Scholar]
- Rustomji, P. Semi-Automated Generation of Depth Contours for Electronic Navigation Charts (ENCs). Int. Hydrogr. Rev. 2018, 20, 33–40. [Google Scholar]
- Sanchez, A.; Bosselmann-Borsos, V.; Lieto, A. Di A Practical Approach to the Production of ENC with High Density Bathymetric Content. Int. Hydrogr. Rev. 2019, 22, 7–18. [Google Scholar]
- Monahan, D.; Casey, M.J. Contours and Contouring in Hydrography. Part I-the Fundamental Issues. Int. Hydrogr. Rev. 1985, 62, 105–120. [Google Scholar]
- Mather, P.M.; Koch, M. Filtering Techniques. In Computer Processing of Remotely-Sensed Images; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Field, D.A. Laplacian Smoothing and Delaunay Triangulations. Commun. Appl. Numer. Methods 1988, 4, 709–712. [Google Scholar] [CrossRef]
- Sorkine, O.; Cohen-Or, D.; Lipman, Y.; Alexa, M.; Rössl, C.; Seidel, H.P. Laplacian Surface Editing. ACM Int. Conf. Proceeding Ser. 2004, 71, 175–184. [Google Scholar] [CrossRef]
- Vartziotis, D.; Himpel, B. Laplacian Smoothing Revisited. arXiv 2014, arXiv:1406.4333. [Google Scholar] [CrossRef]
- Mujta, W.; Wlodarczyk-Sielicka, M.; Stateczny, A. Testing the Effect of Bathymetric Data Reduction on the Shape of the Digital Bottom Model. Sensors 2023, 23, 5445. [Google Scholar] [CrossRef]






















| UAV Type: DJI Phantom 4 Pro | GNSS Type: Sokkia GRX1 |
|---|---|
| Satellite positioning systems: GPS/GLONASS | Number of channels: 72 |
| Sensor: 1″ CMOS, effective pixels: 20 M | Tracked signals: GPS, GLONASS, SBAS |
| Photo: JPEG, DNG (RAW), JPEG + DNG | Frequency of measurement up to 20 Hz |
| Max flight time: approx. 30 min | Accuracy RTK: H 10 mm + 1 ppm, V 20 mm + 1 mm |
| Range: 3500 m | Data format: RTCM SC104 2.1/2.2/2.3/3.0/3.1, CMR, CMR+, NMEA, TPS |
| USV Type: Gerris | GNSS Type: RTK Emlid Reach M2 |
|---|---|
| Length, height, width: 1.2 m, 1 m, 0.36 m | Number of channels: 184 |
| Survey speed: 1.2 m/s | Tracked signals: GPS/QZSS, GLONASS, BeiDou, Galileo |
| Propulsion: 2 motors T200 Blue Robotics | Frequency of measurement is 20 Hz |
| Single beam echosounder: Echologger EU400 | Accuracy RTK: H: 7 mm + 1 ppm, V: 14 mm + 1 ppm |
| Echosounder range: 0.15 m~100 m | Data format: NTRIP, RTCM3ERB, text, NMEA (RMC, GGA, GSA, GSV), RINEX2.X, RINEX3.X |
| Moving Average (AVG) | Distance Weighting (DIST) | Inverse Distance (IDIST) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0.3333 | 0.3333 | 0.3333 | 0.3333 | 0.3333 | 0.3536 | 0.4472 | 0.5000 | 0.4472 | 0.3536 |
| 1 | 1 | 1 | 1 | 1 | 0.3333 | 0.6667 | 0.6667 | 0.6667 | 0.3333 | 0.4472 | 0.7071 | 1.0000 | 0.7071 | 0.4472 |
| 1 | 1 | 1 | 1 | 1 | 0.3333 | 0.6667 | 1.0000 | 0.6667 | 0.3333 | 0.5000 | 1.0000 | 2.000 | 1.0000 | 0.5000 |
| 1 | 1 | 1 | 1 | 1 | 0.3333 | 0.6667 | 0.6667 | 0.6667 | 0.3333 | 0.4472 | 0.7071 | 1.0000 | 0.7071 | 0.4472 |
| 1 | 1 | 1 | 1 | 1 | 0.3333 | 0.3333 | 0.3333 | 0.3333 | 0.3333 | 0.3536 | 0.4472 | 0.5000 | 0.4472 | 0.3536 |
| Gaussian Low-Pass (GAULP) | 5-Node + Averaging (5PAVG) | 5-Node X Averaging (5PXAVG) | ||||||||||||
| 0.0003 | 0.0067 | 0.0183 | 0.0067 | 0.0003 | ||||||||||
| 0.0067 | 0.1353 | 0.3679 | 0.1353 | 0.0067 | 0 | 1 | 0 | 1 | 0 | 1 | ||||
| 0.0183 | 0.3679 | 1.0000 | 0.3679 | 0.0183 | 1 | 1 | 1 | 0 | 1 | 0 | ||||
| 0.0067 | 0.1353 | 0.3679 | 0.1353 | 0.0067 | 0 | 1 | 0 | 1 | 0 | 1 | ||||
| 0.0003 | 0.0067 | 0.0183 | 0.0067 | 0.0003 | ||||||||||
| 9-Node Averaging (9PAVG) | Gaussian (GAUS) | Low-Pass 1 (LP1) | ||||||||||||
| 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | ||||||
| 1 | 1 | 1 | 2 | 4 | 2 | 1 | 2 | 1 | ||||||
| 1 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 1 | ||||||
| Low-Pass 2 (LP2) | Low-Pass 3 (LP3) | Laplacian 1 (LAP1) | ||||||||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | −1 | 0 | ||||||
| 1 | 4 | 1 | 1 | 12 | 1 | −1 | 4 | −1 | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | −1 | 0 | ||||||
| Laplacian 2 (LAP2) | Laplacian 3 (LAP3) | Laplacian 4 (LAP4) | ||||||||||||
| −1 | −1 | −1 | 1 | −2 | 1 | −1 | 0 | −1 | ||||||
| −1 | 8 | −1 | −2 | 4 | −2 | 0 | 4 | 0 | ||||||
| −1 | −1 | −1 | 1 | −2 | 1 | −1 | 0 | −1 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lubczonek, J.; Zaniewicz, G. Application of Filtering Techniques to Smooth a Surface of Hybrid Digital Bathymetric Model. Remote Sens. 2023, 15, 4737. https://doi.org/10.3390/rs15194737
Lubczonek J, Zaniewicz G. Application of Filtering Techniques to Smooth a Surface of Hybrid Digital Bathymetric Model. Remote Sensing. 2023; 15(19):4737. https://doi.org/10.3390/rs15194737
Chicago/Turabian StyleLubczonek, Jacek, and Grzegorz Zaniewicz. 2023. "Application of Filtering Techniques to Smooth a Surface of Hybrid Digital Bathymetric Model" Remote Sensing 15, no. 19: 4737. https://doi.org/10.3390/rs15194737
APA StyleLubczonek, J., & Zaniewicz, G. (2023). Application of Filtering Techniques to Smooth a Surface of Hybrid Digital Bathymetric Model. Remote Sensing, 15(19), 4737. https://doi.org/10.3390/rs15194737






