Spoofing Traction Strategy Based on the Generation of Traction Code

Abstract

Traction spoofing is an important component of Global Navigation Satellite System (GNSS) intermediate attacks, and the traction scheme directly determines the concealment of spoofing. However, spoofing via conventional traction strategies can be easily detected using Time of Arrival (TOA) and power detection. Based on a BPSK-modulated signal, a novel traction strategy using traction code is proposed to suppress part of the authentication signal and form an ideal correlation peak. This strategy was modeled and simulated to verify its theoretical feasibility. Effective spoofing data were generated based on the signal generation software to verify the spoofing effect with the reception of the software receiver. It can be inferred that no significant distortion occurred throughout the traction process, and the value range of the traction speed was expanded. The received results in different scenarios demonstrated that the observations’ Root-Mean-Square Error (RMSE) percentage change in the proposed strategy is significantly better than those of conventional strategies. A Ratio Test was also performed, verifying that the strategy can bypass Signal Quality Monitoring (SQM) detection. Meanwhile, the proposed strategy remained effective when the $\mathrm{C}/{\mathrm{N}}_0$ increased to 60 dBHz. In summary, the proposed strategy exhibits destructiveness, concealment, and adaptability on the battlefield.

1. Introduction

Recently, information and navigation warfare have become important trends in modern warfare. Several military weapons, equipment, and carriers that use GNSS to provide Positioning, Navigation and Timing services pose a threat to national security, such as unauthorized Unmanned Aerial Vehicles and military-guided weapons. In the face of such threats, conventional jamming methods, such as seizing radio control and suppression jamming, may cause the target to fall, resulting in secondary damage. Therefore, spoof jamming has gradually become a popular topic in GNSS jamming.

The spoofing signal has the same structure as the authentication signal. It can invade an enemy receiver that has no corresponding defensive measures without destroying the tracking loop or even being detected. Subsequently, it can change or control the positioning and timing results. Hence, it is an ideal means of controlling various military weapons, equipment, and carriers [1]. GNSS deception is predicted to play a significant role in modern warfare [2].

Traction spoofing is an important part of intermediate and sophisticated navigation spoofing. Among the five detection means of the receiver [3], TOA detection [4], power detection [5,6], and Angle Of Arrival (AOA) detection are all important methods for detecting traction spoofing. However, as there is no space for AOA detection to be overcome in the software, this is not the objective of this study. Power detection identifies spoofing by the monitoring signal power changes. As shown in Figure 1, TOA detection includes change detection of observations [7] and distortion detection of correlation values [8,9]. The observation objects can include the code frequency, carrier frequency, and other information.

Therefore, to address possible security threats, designing a traction strategy to bypass the spoofing detection means of the receiver and stably invading the target tracking loop is an important issue in traction spoofing.

2. Materials and Methods

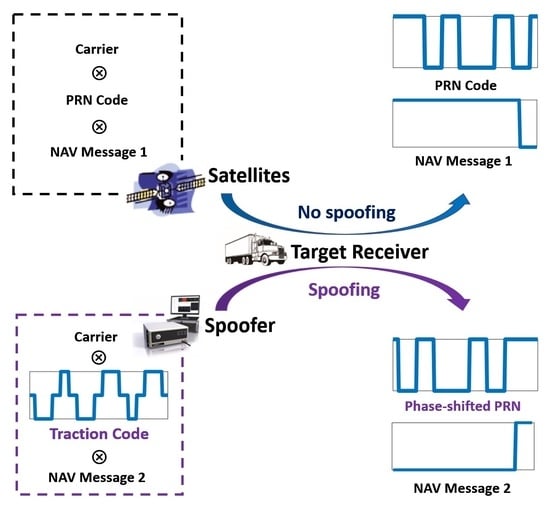
2.1. Conventional GNSS Traction Spoofing

The conventional traction process of spoofing can be divided into three steps:

Step 1: Signal reception. The receiving module of the spoofer receives a genuine signal, detects the location and speed of the target, and estimates the genuine signal’s key parameters.

Step 2: Determine the traction scheme. The parameters of the spoofing signal are set such that the correlation peak of the spoofing signal arriving at the target receiver aligns gradually with the actual peak. In a conventional traction strategy, the correlation peak envelope of the composite signal is distorted, as shown in Figure 2.

Step 3: Traction spoofing. The spoofing signal is generated to dominate the tracking loop and gradually enlarge the code phase difference to generate a pseudo-distance error, which eventually controls the target.

The correlation result between the local and authentication signals is defined as ${\mathrm{R}}_{\mathrm{al}}\left(\mathsf{\tau }\right)$, and thatbetween the local and superimposed signals is defined as ${\mathrm{R}}_{\mathrm{all}}\left(\mathsf{\tau }\right)$. If the correlation function between the spoofing signal and local replica is ${\mathrm{R}}_{\mathrm{sl}}\left(\mathsf{\tau }\right)$, then the distortion correlation peak envelope of the composite signal is as illustrated in Figure 2.

In the first step, the detection of the antenna position and speed of the spoofing target, power level, channel conditions, and other information is not within the scope of this study, assuming that the spoofer has obtained specific information. The content discussed in this study is the setting and generation module of the spoofing signal.

The discussion in this paper is based on a Binary Phase Shift Keying (BPSK) signal system. First, we can model the genuine signal as:

$${\mathrm{s}}_{\mathrm{a}}\left(\mathrm{t}\right)=\sqrt{{\mathrm{P}}_{\mathrm{a}}\left(\mathrm{t}\right)}·{\mathrm{D}}_{\mathrm{a}}\left(\mathrm{t}\right)·{\mathrm{C}}_{\mathrm{a}}\left(\mathrm{t}\right)·\cos (2\mathsf{\pi }({\mathrm{f}}_0+{\mathrm{f}}_{\mathrm{d}\_\mathrm{a}})\mathrm{t}+{\mathsf{\theta }}_{\mathrm{a}}),$$

(1)

Similarly, the spoofing signal can be expressed as

$${\mathrm{s}}_{\mathrm{s}}\left(\mathrm{t}\right)=\sqrt{{\mathrm{P}}_{\mathrm{s}}\left(\mathrm{t}\right)}·{\mathrm{D}}_{\mathrm{s}}\left(\mathrm{t}\right)·{\mathrm{C}}_{\mathrm{s}}\left(\mathrm{t}\right)·\cos \left(2\mathsf{\pi }\left({\mathrm{f}}_0+{\mathrm{f}}_{\mathrm{d}\_\mathrm{a}}+{\mathrm{f}}_{\mathrm{as}}\right)\mathrm{t}+{\mathsf{\theta }}_{\mathrm{a}}+{\mathsf{\theta }}_{\mathrm{as}}\right),$$

(2)

where the subscripts a and s represent the genuine and spoofing signals, respectively. In addition, $\mathrm{P}$, $\mathrm{D}$, $\mathrm{C}$, ${\mathrm{f}}_{\mathrm{d}}$ and $\mathsf{\theta }$ denote the satellite signal power, navigation message, pseudo code, Doppler shift, and initial carrier phase, respectively.

The traction modes in the latter two steps can be divided into synchronous and asynchronous traction according to the accuracy of the parameter estimation [10].

(1)

Synchronous traction

The diagram of synchronous traction is shown in Figure 3.

T1: At the beginning of traction, the spoofing code phase (Doppler) is aligned with the genuine code phase (Doppler).

T2: Increase the power of spoofing signals.

T3: Drag the correlation peak away from the original tracking point.

T4: Keep the power consistent with the genuine signal.

This method requires high measurement accuracy in the first step and is difficult to achieve in an actual scenario.

(2)

Asynchronous traction

A diagram of asynchronous traction is shown in Figure 4. Unlike synchronous traction, asynchronous traction does not require a spoofer to determine the exact parameters of an authentication signal. This traction mode directly generates a higher power correlation peak to control the loop, which is more suitable for application in actual scenarios.

Control of the distance velocity of the correlated peaks is defined as the traction code rate ${\mathrm{v}}_{\mathrm{drag}}$. In the third step of the spoofing traction process, according to whether the spoofing signal maintains the code and carrier phase consistency, conventional traction strategies can be divided into two types [11]:

Strategy 1 Adjust the code phase only

The code and carrier phase consistencies are broken, and only the code rate is altered.

$${\mathrm{f}}_{\mathrm{drag}}=0,$$

(3)

Strategy 2 Maintain code-carrier coherence

If the spoofing signal maintains code-carrier coherence, we obtain

$${\mathrm{f}}_{\mathrm{drag}}={\mathrm{v}}_{\mathrm{drag}}·\frac{{\mathrm{f}}_0}{{\mathrm{R}}_0}$$

(4)

where ${\mathrm{f}}_0$ and ${\mathrm{R}}_0$ represent the nominal carrier frequency and code rate, respectively.

The deception process of the spoofer is illustratedin Figure 5. The first light-grey area is the setting module of the spoofing signal, and the lower light-grey area is the generation module of the spoofing signal.

In conventional traction strategies, although the Pseudo-Random Noise (PRN) code ${\mathrm{C}}_{\mathrm{s}}\left(\mathrm{t}\right)$ used forspoofing is the same as the genuine signal, there is a designed phase difference ${\mathsf{\tau }}_{\mathrm{as}}$:

$${\mathrm{C}}_{\mathrm{s}}\left(\mathrm{t}\right)={\mathrm{C}}_{\mathrm{a}}\left(\mathrm{t}+{\mathsf{\tau }}_{\mathrm{as}}\right),$$

(5)

where

$${\mathsf{\tau }}_{\mathrm{as}}\left(\mathrm{t}\right)={\mathsf{\tau }}_{\mathrm{s}}\left(\mathrm{t}\right)-{\mathsf{\tau }}_{\mathrm{a}}\left(\mathrm{t}\right)={\mathrm{v}}_{\mathrm{drag}}·\mathrm{t}$$

(6)

After determining the traction speed ${\mathrm{v}}_{\mathrm{drag}}$, the phase difference ${\mathsf{\tau }}_{\mathrm{as}}$ can be obtained from Equation (6). Then ${\mathrm{C}}_{\mathrm{s}}\left(\mathrm{t}\right)$ can be obtained from Equation (5).

The distortion in Figure 2 is often the root cause of TOA and power detection; hence, traction strategies that can avoid correlation peak superposition are considered. In this case, replacing the code of the original system may be a novel idea, as discussed in the next section.

2.2. Proposed Spoofing Traction Strategy

In this section, the theory and implementation of an improved spoofing traction strategy are introduced.

2.2.1. Signal Model

To ignore the noise, there is

$${\mathrm{R}}_{\mathrm{all}}\left(\mathsf{\tau }\right)={\mathrm{R}}_{\mathrm{al}}\left(\mathsf{\tau }\right)+{\mathrm{R}}_{\mathrm{sl}}\left(\mathsf{\tau }\right)$$

(7)

A correlation function diagram for the proposed strategy is shown in Figure 6. The objective of the proposed traction strategy is to make ${\mathrm{R}}_{\mathrm{all}}$ replace ${\mathrm{R}}_{\mathrm{al}}$ to affect the decision making of the receiver. The code-phase relationship between ${\mathrm{R}}_{\mathrm{all}}$ and ${\mathrm{R}}_{\mathrm{al}}$ is determined using the traction speed ${\mathrm{v}}_{\mathrm{drag}}$. The ideal correlation peaks can be modeled as:

$$\mathrm{R}\left(\mathsf{\tau }\right)={\mathrm{A}}_{\mathrm{R}}\left(1-\left|\mathsf{\tau }\right|\right),\left|\mathsf{\tau }\right|\le 1$$

(8)

In addition, we intend to obtain

$${\mathsf{\tau }}_{\mathrm{al}}={\mathrm{v}}_{\mathrm{drag}}\mathrm{t},$$

(9)

which gives

$${\mathrm{R}}_{\mathrm{all}}\left(\mathsf{\tau }\right)=\mathrm{R}\left(\mathsf{\tau }+{\mathrm{v}}_{\mathrm{drag}}\mathrm{t}-{\mathsf{\tau }}_{\mathrm{al}}\right)=\mathrm{R}\left(\mathsf{\tau }\right)$$

(10)

The code used to replace the pseudo code of the original system may be called the traction code. From the expected ${\mathrm{R}}_{\mathrm{sl}}$ and the correlation theorem of the Fourier transform, the formula for the traction code sequence can be derived as

$${\mathrm{C}}_{\mathrm{s}}\left(\mathrm{t}\right)={\mathcal{F}}^{-1}\left\{\frac{\mathcal{F}\left[R_{sl}\right(\tau \left)\right]}{{\mathcal{F}}^{*}\left[C_l\right(t\left)\right]}\right\}={\mathrm{C}}_{\mathrm{l}}\left(\mathrm{t}\right)-{\mathrm{C}}_{\mathrm{a}}\left(\mathrm{t}\right)={\mathrm{C}}_{\mathrm{a}}\left(\mathrm{t}+{\mathsf{\tau }}_{\mathrm{al}}\right)-{\mathrm{C}}_{\mathrm{a}}\left(\mathrm{t}\right)$$

(11)

where ${\mathrm{C}}_{\mathrm{l}}\left(\mathrm{t}\right)$ denotes the desired local replica of the PRN code. The calculation method for the pseudocode sequence can be found in the Interface Control Document. It can be seen from Equation (11) that the traction code sequence ${\mathrm{C}}_{\mathrm{s}}\left(\mathrm{t}\right)$ is actually equal to the difference between ${\mathrm{C}}_{\mathrm{l}}\left(\mathrm{t}\right)$ and the PRN code sequence ${\mathrm{C}}_{\mathrm{a}}\left(\mathrm{t}\right)$ of the genuine signal. In other words, the desired phase-shifted PRN code is formed by superimposing a traction code on top of the genuine PRN code.

In an actual scenario, the power level of the genuine signal must be accurately estimated to determine the amplitude of the traction code. Additionally, the estimation belongs to the first step of the traction process, which is not within the scope of this study.

${\mathrm{C}}_{\mathrm{l}}\left(\mathrm{t}\right)$ and ${\mathrm{C}}_{\mathrm{a}}\left(\mathrm{t}\right)$ are the same set of conventional PRN codes with a code phase difference ${\mathsf{\tau }}_{\mathrm{al}}$, whereas ${\mathrm{C}}_{\mathrm{s}}\left(\mathrm{t}\right)$ is not. This is discussed in Section 2.2.2.

2.2.2. Generation of Traction Code

The generation of traction codes is the core innovation in the proposed traction strategy. The code embedded in the signal-generation software completes the generation of the spoofing code described above. Figure 7 presents the generation steps of the traction code, where ${\mathrm{T}}_{\mathrm{coh}}$ is the coherent integration time, which is equals to $1\mathrm{ms}$.

In S1, the selection of the traction speed ${\mathrm{v}}_{\mathrm{drag}}$ follows certain principles, which is discussed later. In S2, ${\mathsf{\tau }}_{\mathrm{al}}$ can be calculated using Equation (9). In S4, ${\mathrm{C}}_{\mathrm{s}}\left(\mathrm{t}\right)$ can be calculated using Equation (11).

Consider the BeiDou Navigation Satellite System No. 33 satellite as an example to generate a spoofed traction code. We generate data for 20 s, and traction was selected to start at 1 s and end at 16 s. Three time points are randomly selected to observe the changes in the pseudo-code layer in the initial, intermediate, and final stages of traction. Figure 8 shows the transition process of the traction code sequence. It can be observed that the traction code changes with the advancement of the traction process and has no fixed form; conventional PRN codes have values of $\pm 1$, whereas traction codes have values of $0$ and $\pm 2$; hence, it is not a PRN code in the conventional sense.

Figure 9 shows the transition process of the PRN code sequence received by the spoofing target. Under the assumption of the proposed strategy, the received code sequence is always in the form of an authentication PRN code, and there is a significant phase shift caused by the code Doppler change ${\mathrm{v}}_{\mathrm{r}}$ based on the real value.

Figure 10 shows a diagram of the deception process of the proposed traction strategy. In the dark-blue area, there is a procedure for generating the spoofing traction code, which is also a key step that differs from the other traction processes.

2.3. Methods of Simulation and Experiment

2.3.1. Theoretical Model of Received Signal

According to the signal model in Section 2.1, the composite signal r(t) is demodulated by the local receiver as follows:

$${\mathrm{i}}_{\mathrm{P}}\left(\mathrm{t}\right)=\mathrm{r}\left(\mathrm{t}\right){\mathrm{C}}_{\mathrm{a}}\left(\mathrm{t}+{\mathsf{\tau }}_{\mathrm{al}}\right)·\cos \left(2\mathsf{\pi }\left({\mathrm{f}}_0+{\mathrm{f}}_{\mathrm{d}\_\mathrm{a}}+{\mathrm{f}}_{\mathrm{al}}\right)\mathrm{t}+{\mathsf{\theta }}_{\mathrm{a}}+{\mathsf{\theta }}_{\mathrm{al}}\right)={\mathrm{i}}_{{\mathrm{P}}_{\mathrm{a}}}\left(\mathrm{t}\right)+{\mathrm{i}}_{{\mathrm{P}}_{\mathrm{s}}}\left(\mathrm{t}\right),$$

(12)

where ${\mathsf{\tau }}_{\mathrm{al}}$ is the code phase difference between the genuine and local signals, and the same is true for parameters ${\mathrm{f}}_{\mathrm{al}}$, ${\mathsf{\theta }}_{\mathrm{al}}$, ${\mathsf{\tau }}_{\mathrm{sl}}$, ${\mathrm{f}}_{\mathrm{sl}}$, ${\mathsf{\theta }}_{\mathrm{sl}}$ and other parameters.

Coherent integration of ${\mathrm{i}}_{{\mathrm{P}}_{\mathrm{a}}}\left(\mathrm{t}\right)$ is performed to obtain the prompt correlation values:

$${\mathrm{I}}_{{\mathrm{P}}_{\mathrm{a}}}=\frac{\sqrt{{\mathrm{P}}_{\mathrm{a}}}}{2}\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{al}}\right){\mathrm{T}}_{\mathrm{coh}}\sin \mathrm{c}\left({\mathrm{f}}_{\mathrm{al}}{\mathrm{T}}_{\mathrm{coh}}\right)\cos \left(2{\mathsf{\pi }\mathrm{f}}_{\mathrm{al}}\left({\mathrm{t}}_1+\frac{{\mathrm{T}}_{\mathrm{coh}}}{2}\right)+{\mathsf{\theta }}_{\mathrm{al}}\right)$$

(13)

${\mathrm{i}}_{{\mathrm{P}}_{\mathrm{s}}}\left(\mathrm{t}\right)$ are integrated and dumped to produce the prompt correlation results of spoofing signals:

$${\mathrm{I}}_{{\mathrm{P}}_{\mathrm{s}}}=\frac{\sqrt{{\mathrm{P}}_{\mathrm{sp}}}}{2}\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{sl}}\right){\mathrm{T}}_{\mathrm{coh}}\sin \mathrm{c}\left({\mathrm{f}}_{\mathrm{sl}}{\mathrm{T}}_{\mathrm{coh}}\right)\cos \left(2{\mathsf{\pi }\mathrm{f}}_{\mathrm{sl}}\left({\mathrm{t}}_1+\frac{{\mathrm{T}}_{\mathrm{coh}}}{2}\right)+{\mathsf{\theta }}_{\mathrm{sl}}\right)$$

(14)

Given ${\mathsf{\tau }}_{\mathrm{al}}$ and ${\mathsf{\tau }}_{\mathrm{sl}}$, we can obtain $\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{al}}\right)$ and $\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{sl}}\right)$ according to Equation (8).

Strategy 1

Assuming that the amplitude ratio between the spoofing and genuine signals is $\mathrm{h}=\sqrt{\frac{{\mathrm{P}}_{\mathrm{s}}}{{\mathrm{P}}_{\mathrm{a}}}}$, the correlation results can be simplified as

$${\mathrm{I}}_{\mathrm{P}}\left(\mathrm{t}\right)=\frac{\sqrt{{\mathrm{P}}_{\mathrm{a}}}}{2}{\mathrm{T}}_{\mathrm{coh}}\left(\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{al}}\right)+\mathrm{hR}\left({\mathsf{\tau }}_{\mathrm{sl}}\right)\right)$$

(15)

The same is true for ${\mathrm{I}}_{\mathrm{E}}$ and ${\mathrm{I}}_{\mathrm{L}}$.

Define ${\mathrm{v}}_{\mathrm{drag}}$ as the traction speed, then

$${\mathsf{\tau }}_{\mathrm{as}}\left(\mathrm{t}\right)={\mathsf{\tau }}_{\mathrm{s}}\left(\mathrm{t}\right)-{\mathsf{\tau }}_{\mathrm{a}}\left(\mathrm{t}\right)={\mathrm{v}}_{\mathrm{drag}}·\mathrm{t}$$

(16)

Then $\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{al}}\right)$, $\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{sl}}\right)$, the early and late correlation results can be derived.

When the carrier loop is in a steady state, the received signal power is not transferred from the in-phase components to quadrature components. The phase discriminator of the code tracking loop processes the early and late correlation results, and the output is

$${\mathsf{\delta }}_{\mathrm{cp}}=\frac{{\mathrm{I}}_{\mathrm{E}}-{\mathrm{I}}_{\mathrm{L}}}{{\mathrm{I}}_{\mathrm{E}}+{\mathrm{I}}_{\mathrm{L}}}=\frac{{\mathrm{R}}^{+}\left({\mathsf{\tau }}_{\mathrm{al}}\right)-{\mathrm{R}}^{-}\left({\mathsf{\tau }}_{\mathrm{al}}\right)+{\mathrm{hR}}^{+}\left({\mathsf{\tau }}_{\mathrm{sl}}\right)-{\mathrm{hR}}^{-}\left({\mathsf{\tau }}_{\mathrm{sl}}\right)}{{\mathrm{R}}^{+}\left({\mathsf{\tau }}_{\mathrm{al}}\right)+{\mathrm{R}}^{-}\left({\mathsf{\tau }}_{\mathrm{al}}\right)+{\mathrm{hR}}^{+}\left({\mathsf{\tau }}_{\mathrm{sl}}\right)+{\mathrm{hR}}^{-}\left({\mathsf{\tau }}_{\mathrm{sl}}\right)}$$

(17)

where ${\mathrm{R}}^{+}\left(\mathsf{\tau }\right)=\mathrm{R}\left(\mathsf{\tau }+\mathrm{d}\right)$, ${\mathrm{R}}^{-}\left(\mathsf{\tau }\right)=\mathrm{R}\left(\mathsf{\tau }-\mathrm{d}\right)$.

Local code Doppler ${\mathrm{cd}}_l$ is obtained after the filter of the code loop processing ${\mathsf{\delta }}_{\mathrm{cp}}$:

$${\mathrm{cd}}_l\left(\mathrm{n}\right)={\mathrm{k}}_{\mathrm{c}2}{\mathsf{\delta }}_{\mathrm{cp}}\left(\mathrm{n}\right)+{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{k}}_{\mathrm{c}1}{\mathsf{\delta }}_{\mathrm{cp}}\left(\mathrm{i}\right)$$

(18)

Strategy 2

If the spoofing signal maintains the code-carrier coherence, the frequency change in the spoofing signal directly influences the local carrier generation, and the received signal power is transferred to the quadrature components. The prompt correlation amplitude is expressed as follows:

$$\mathrm{P}=\left|{\mathrm{I}}_{\mathrm{P}}\left(\mathrm{n}\right)+{\mathrm{jQ}}_{\mathrm{P}}\left(\mathrm{n}\right)\right|=\left|\frac{\sqrt{{\mathrm{P}}_{\mathrm{a}}}}{2}\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{al}}\right){\mathrm{T}}_{\mathrm{coh}}\sin \mathrm{c}\left({\mathrm{f}}_{\mathrm{al}}{\mathrm{T}}_{\mathrm{coh}}\right){\mathrm{e}}^{\mathrm{j}{\mathsf{\varphi }}_{\mathrm{al}}}+\frac{\sqrt{{\mathrm{P}}_{\mathrm{sp}}}}{2}\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{sl}}\right){\mathrm{T}}_{\mathrm{coh}}\sin \mathrm{c}\left({\mathrm{f}}_{\mathrm{sl}}{\mathrm{T}}_{\mathrm{coh}}\right){\mathrm{e}}^{\mathrm{j}{\mathsf{\varphi }}_{\mathrm{sl}}}\right|$$

(19)

The output of the phase discriminator of the code tracking loop can be expressed as:

$${\mathsf{\delta }}_{\mathrm{cp}}=\frac{\mathrm{E}-\mathrm{L}}{\mathrm{E}+\mathrm{L}}$$

(20)

where the forms of the early and late correlation amplitudes are the same as those of the prompt correlation amplitude; only the function R(τ) is replaced by ${\mathrm{R}}^{+}\left(\mathsf{\tau }\right)$ or ${\mathrm{R}}^{-}\left(\mathsf{\tau }\right)$.

The output of the phase discriminator of the carrier loop is typically calculated using a two-quadrant arctangent function:

$${\mathsf{\varphi }}_{\mathrm{e}}\left(\mathrm{n}\right)=\arctan \left(\frac{{\mathrm{Q}}_{\mathrm{p}}\left(\mathrm{n}\right)}{{\mathrm{I}}_{\mathrm{p}}\left(\mathrm{n}\right)}\right)=\arctan \left(\frac{\sin {\mathsf{\varphi }}_{\mathrm{al}}+\mathrm{h}\frac{\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{sl}}\right)\sin \mathrm{c}\left({\mathrm{f}}_{\mathrm{sl}}{\mathrm{T}}_{\mathrm{coh}}\right)}{\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{al}}\right)\sin \mathrm{c}\left({\mathrm{f}}_{\mathrm{al}}{\mathrm{T}}_{\mathrm{coh}}\right)}\sin {\mathsf{\varphi }}_{\mathrm{sl}}}{\cos {\mathsf{\varphi }}_{\mathrm{al}}+\mathrm{h}\frac{\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{sl}}\right)\sin \mathrm{c}\left({\mathrm{f}}_{\mathrm{sl}}{\mathrm{T}}_{\mathrm{coh}}\right)}{\mathrm{R}\left({\mathsf{\tau }}_{\mathrm{al}}\right)\sin \mathrm{c}\left({\mathrm{f}}_{\mathrm{al}}{\mathrm{T}}_{\mathrm{coh}}\right)}\cos {\mathsf{\varphi }}_{\mathrm{sl}}}\right)$$

(21)

Local carrier Doppler ${\mathrm{fd}}_l$ is obtained after the filter of carrier loop processing ${\mathsf{\varphi }}_{\mathrm{e}}\left(\mathrm{n}\right)$:

$${\mathrm{fd}}_l\left(\mathrm{n}\right)={\mathrm{k}}_{\mathrm{f}2}{\mathsf{\varphi }}_{\mathrm{e}}\left(\mathrm{n}\right)+{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{k}}_{\mathrm{f}1}{\mathsf{\varphi }}_{\mathrm{e}}\left(\mathrm{i}\right)$$

(22)

Proposed Strategy Spoofing traction strategy based on the generation of traction code

The correlation results can be stable throughout the traction process, and the prompt correlation result $\mathrm{P}$ is always

$$\mathrm{P}\left(\mathrm{n}\right)=\frac{\sqrt{{\mathrm{P}}_{\mathrm{a}}}}{2}{\mathrm{T}}_{\mathrm{coh}}\mathrm{R}\left(v_{drag}t-{\tau }_{al}\right)$$

(23)

Similarly, the forms of the early and late correlation results are the same as those of the prompt correlation results. Only functions $\mathrm{R}\left(\mathsf{\tau }\right)$ are replaced by ${\mathrm{R}}^{-}\left(\mathsf{\tau }\right)$ and ${\mathrm{R}}^{+}\left(\mathsf{\tau }\right)$.

The ideal output of the phase discriminator of the code loop can be obtained:

$${\mathsf{\delta }}_{\mathrm{cp}}=\frac{{\mathrm{I}}_{\mathrm{E}}-{\mathrm{I}}_{\mathrm{L}}}{{\mathrm{I}}_{\mathrm{E}}+{\mathrm{I}}_{\mathrm{L}}}=\frac{{\mathrm{R}}^{-}\left({\mathrm{v}}_{\mathrm{drag}}\mathrm{t}-{\mathsf{\tau }}_{\mathrm{al}}\right)-{\mathrm{R}}^{+}\left({\mathrm{v}}_{\mathrm{drag}}\mathrm{t}-{\mathsf{\tau }}_{\mathrm{al}}\right)}{{\mathrm{R}}^{-}\left({\mathrm{v}}_{\mathrm{drag}}\mathrm{t}-{\mathsf{\tau }}_{\mathrm{al}}\right)+{\mathrm{R}}^{+}\left({\mathrm{v}}_{\mathrm{drag}}\mathrm{t}-{\mathsf{\tau }}_{\mathrm{al}}\right)}$$

(24)

2.3.2. Simulation and Conditions

Considering synchronous traction with a more hidden spoofing effect as an example, simulations were performed for three traction strategies according to the theoretical model of the received signal in Section 2.3.1. Because the simulation does not require mass data processing at a high sampling rate, it can quickly test traction success under a certain strategy. For the 20-s data, the simulation of Strategy 1 took less than 1 s, and the simulation of Strategy 2 took less than 2 s.

Spoofing was selected to enter at 1 s. Traction duration was determined by ${\mathrm{v}}_{\mathrm{drag}}$ and the tracking-loop structure. Because the carrier loop is only related to the prompt correlation value, when ${\mathsf{\tau }}_{\mathrm{al}}$ and ${\mathsf{\tau }}_{\mathrm{as}}$ are 1 chip, the two peaks have exited each other’s prompt tracking point, whereas the code loop needs to wait for the other correlation peak to exit the early or late tracking point. If the traction duration of the carrier loop is defined as ${\mathrm{t}}_{\mathrm{f}}$ and that of the code loop is defined as ${\mathrm{t}}_{\mathrm{c}}$, then

$${\mathrm{t}}_{\mathrm{f}}=\frac{1}{{\mathrm{v}}_{\mathrm{drag}}},$$

(25)

$${\mathrm{t}}_{\mathrm{c}}=\frac{1+\mathrm{d}}{{\mathrm{v}}_{\mathrm{drag}}},$$

(26)

In other words, according to the structural characteristics of the carrier and code loops, the traction duration should be at least ${\mathrm{t}}_{\mathrm{c}}$.

The maximum spoofing power of conventional spoofing signals is equal to the genuine signal power. The correlator spacing at the receiver was set as the typical value for satellite navigation receiver applications, i.e., D = 2d = 1. The spoofing signal has the same initial carrier and code phases as the genuine signal when added.

$${\mathsf{\theta }}_{\mathrm{sl}}={\mathsf{\theta }}_{\mathrm{al}}={\mathsf{\theta }}_{\mathrm{as}}=0$$

(27)

The first set of simulations (Nos. 1, 3, and 5) was used to directly compare the theoretical deception effects of the strategies.

The Simulation conditions are presented in

Table 1. Simulation conditions.

No.	Spoofer						Channel	Receiver
	Strategy	Traction Duration (s)		Data Length (s)	$v_{drag}$ (cps)	hmax	Nosie Padding	$D$ (Chips)
		Start Time	End Time
1	1	1	1 + $t_c$	20	0.1	1	Disabled	1
2					$\left|{\mathrm{v}}_{\mathrm{drag}}\right|\le 500\mathrm{cps}$
3	2				0.1
4					$\left|{\mathrm{v}}_{\mathrm{drag}}\right|\le 500\mathrm{cps}$
5	3				0.1
6					$\left|{\mathrm{v}}_{\mathrm{drag}}\right|\le 500\mathrm{cps}$

. When implementing a traction strategy to successfully implement spoofing traction, the selection of traction speed ${\mathrm{v}}_{\mathrm{drag}}$ follows certain principles. According to the code loop structure, the code phase offset within each coherence integration should not exceed 0.5 chips [12], that is the traction speed ${\mathrm{v}}_{\mathrm{drag}}$ should not be too fast. However, owing to the loose requirements, spoofing may fail even if the conditions are met.

When the traction strategy is determined, the range of traction speed that can make traction successful is determined. Therefore, the theoretical value range of the traction speeds of the three strategies can be determined via another set of traversal simulations (Nos. 2, 4, and 6).

2.3.3. Spoofing Experiment and Scenario

To verify the applicability of the proposed strategy in actual environments, effective intermediate-frequency spoofing data were generated based on the signal generation software, and noise was added to the composite signal. We then used a software receiver to examine the effects of the different spoofing traction strategies. No. 33 satellite signal was selected. The intermediate frequency was ${\mathrm{f}}_{\mathrm{IF}}=10\mathrm{MHz}$, sampling rate was ${\mathrm{f}}_{\mathrm{s}}=50\mathrm{MHz},$ and carrier-to-noise ratio was $\mathrm{C}/{\mathrm{N}}_0=50\mathrm{dBHz}$. Three traction strategies were simulated under these conditions.

However, to simulate the change in the signal strength caused by different noise environments and satellite altitude angle changes, $\mathrm{C}/{\mathrm{N}}_0$ was set to $30\mathrm{dBHz}$, $40\mathrm{dBHz}$ and $50\mathrm{dBHz}$, respectively. Owing to the particularity of spoofing, we expected the received results to be stably close to those of the genuine signal. Therefore, RMSE statistics were conducted on the results of the three traction strategies to observe the performance of the proposed strategy under different $\mathrm{C}/{\mathrm{N}}_0$. These statistics were compared with the genuine results.

A spoofing scenario of $60\mathrm{dBHz}$ $\mathrm{C}/{\mathrm{N}}_0$ was used to simulate the power enhancement in special scenarios, such as the battlefield. To simulate narrow correlators and pulse-aperture correlators, spoofing scenarios with narrow correlation intervals ($\mathrm{D}=0.2\mathrm{chips}$) were added.

The designed spoofing scenarios are presented in

Table 2. Overview of the spoofing scenarios.

No.	Spoofer						Channel	Receiver
	Strategy	Traction Duration (s)		Traction Duration (s)	$v_{drag}$ (cps)	hmax	$C/N_0$ (dBHz)	$D$ (Chips)
		Start Time	End Time
1	1	1	1 + $t_c$	1	0.1	1	30	1
2							40	1
3							50	1
4								0.2
5							60	1
6	2						30	1
7							40	1
8							50	1
9								0.2
10							60	1
11	3						30	1
12							40	1
13							50	1
14								0.2
15							60	1

.

2.3.4. Data Processing

Whether in the simulation or experiment, the local code phase is not directly known, and it must be obtained using the following formula:

$${\mathsf{\tau }}_{\mathrm{l}}\left(\mathrm{n}\right)={\mathsf{\tau }}_0+{\mathrm{T}}_{\mathrm{coh}}·{{\displaystyle \sum }}_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{cd}}_{\mathrm{l}}\left(\mathrm{i}\right),$$

(28)

where ${\mathsf{\tau }}_0$ is the initial code phase obtained from acquisition. The phase difference diagram can be obtained by subtracting ${\mathsf{\tau }}_{\mathrm{l}}$ from ${\mathsf{\tau }}_{\mathrm{a}}$ and ${\mathsf{\tau }}_{\mathrm{s}}$, respectively.

Once we obtain the tracking results, we must determine whether the spoofing traction was successful. For spoofing, whose frequency is locked to the genuine signal, we want ${\mathsf{\tau }}_{\mathrm{sl}}$ to be 0 to demonstrate that the code loop traction is successful, and for spoofing that maintains the code-carrier coherence, we also want ${\mathrm{f}}_{\mathrm{sl}}$ to be 0 to demonstrate that the carrier loop traction is successful. These results can be expressed using the following formulas:

$${\mathrm{T}}_1=\mathrm{sgn}\left\{\log \left|{\mathsf{\tau }}_{\mathrm{sl}}\right|\right\}$$

(29)

$${\mathrm{T}}_2=\mathrm{sgn}\left\{\log \left(\left|{\mathsf{\tau }}_{\mathrm{sl}}\right|+\left|{\mathrm{f}}_{\mathrm{sl}}\right|\right)\right\}$$

(30)

If ${\mathrm{T}}_1$ (or ${\mathrm{T}}_2$) is less than 0, traction succeeds; otherwise, traction fails.

Given the maximum traction speed ${\mathrm{v}}_{\mathrm{drag}\_\max }$ for a given strategy, the shortest time required for deceptive traction can be calculated using the following formula:

$${\mathrm{t}}_{\mathrm{c}\_\min }=\frac{1+\mathrm{d}}{{\mathrm{v}}_{\mathrm{drag}\_\max }}$$

(31)

Because there are several detection methods included in TOA and power detection, this study attempts to use a simple statistical analysis method and the SQM method as examples to verify the detection quantity. If we perform a statistical analysis on observation $\mathrm{X}$, the RMSE statistic is:

$$\mathrm{RMSE}=\sqrt{\frac{1}{\mathrm{N}}\sum _{\mathrm{i}=1}^{\mathrm{N}}{({\mathrm{X}}_i-{\mathrm{X}}_{0_i})}^2},$$

(32)

where ${\mathrm{X}}_{0_i}$ are the fitting values of the genuine signal observations. To reflect the influence of the spoofing signals of each strategy on the RMSE, the RMSE values are calculated as follows:

$${\mathrm{Percentage}}_{\Delta i}=\frac{{\mathrm{RMSE}}_i-{\mathrm{RMSE}}_0}{{\mathrm{RMSE}}_0}\times 100\%$$

(33)

where ${\mathrm{RMSE}}_0$ represents the RMSE statistic of the genuine signal observations.

In the SQM technique, we used a Ratio Test metric to identify correlation distortions. The Ratio Test metric is:

$${\mathrm{R}}_{\mathrm{SQM}+}=\frac{\mathrm{E}+\mathrm{L}}{2\mathrm{P}},$$

(34)

where $\mathrm{E}$, L, and P denote early, late, and prompt correlator outputs over the in-phase branch, respectively.

To observe fluctuations, we uniformly subtracted the ideal value of metric 1/2 from the metric when plotting.

3. Results

3.1. Simulation Results

The results of the spoofing simulation designed in Section 2.3.2 are listed in this section.

The simulation results for the three traction strategies are shown in Figure 11, Figure 12 and Figure 13. Figure 11a, Figure 12a and Figure 13a present the code phase difference diagrams, and we expect ${\mathsf{\tau }}_{\mathrm{sl}}$ (local spoofing) to always be on the x-axis. Figure 11b, Figure 12b and Figure 13b present the correlator output diagrams, and we expect these values to be stable. Figure 11c, Figure 12c and Figure 13c and Figure 11e, Figure 12e and Figure 13e are discriminator output diagrams, and we expect ${\mathsf{\delta }}_{\mathrm{cp}}$ and ${\mathsf{\varphi }}_{\mathrm{e}}$ to always be on the x-axis. Figure 11d,f, Figure 12d,f and Figure 13d,f are the filter output diagrams, and we expect the local code Doppler ${\mathrm{cd}}_{\mathrm{l}}$ and local carrier Doppler ${\mathrm{fd}}_{\mathrm{l}}$ to follow ${\mathrm{v}}_{\mathrm{drag}}$ and ${\mathrm{f}}_{\mathrm{drag}}$, respectively.

Via a traversal simulation, the theoretical value ranges of the traction speeds of the three strategies are presented in

Table 3. Value ranges of ${\mathrm{v}}_{\mathrm{drag}}$ for three strategies.

Traction Strategy	$\mathbf{Theoretical}\mathbf{Value}\mathbf{Ranges}\mathbf{of}{\mathbf{v}}_{\mathbf{drag}}$	${\mathbf{t}}_{\mathbf{c}\_\mathbf{min}}$
Strategy 1	$\left|{\mathrm{v}}_{\mathrm{drag}}\right|$ ≤ 2.79 cps	0.538 s
Strategy 2	$\left|{\mathrm{v}}_{\mathrm{drag}}\right|$≤ 0.104 cps	14.423 s
Proposed strategy	$\left|{\mathrm{v}}_{\mathrm{drag}}\right|$≤ 27.89 cps	0.054 s

.

3.2. Experimental Results

The results of the spoofing experiment designed in Section 2.3.3 are listed in this section.

Unlike the simulation results in Section 3.1, effective intermediate frequency spoofing data with noise were generated based on the signal generation software. The obtained results of the three spoofing traction strategies Under the $\mathrm{C}/{\mathrm{N}}_0$ $50\mathrm{dBHz}$ condition are shown in Figure 14, Figure 15 and Figure 16. Code-phase difference diagrams were plotted accordingly.

In Figure 17, Figure 18 and Figure 19, the results of the proposed traction strategy are given under $\mathrm{C}/{\mathrm{N}}_0$ of $60\mathrm{dBHz}$, $40\mathrm{dBHz}$, and $30\mathrm{dBHz}$, respectively.

Under a C/N₀ of 50 dBHz, the results obtained when the receiver is equipped with a narrow correlator are presented in Figure 20.

3.3. Stability Testes

The RMSE statistics were calculated for the observations of genuine signals and the three traction strategies. The statistical results are presented in

Table 4. Comparison of RMSE for different strategies and the genuine signal ($\mathrm{C}/{\mathrm{N}}_0$ = 30 dBHz, D = 1).

RMSE	Genuine Signal	Strategy 1		Strategy 2		Proposed Strategy
Code Doppler/cps	5.0126	4.8096	−4.05%	4.9474	−1.30%	5.0325	0.40%
Carrier Doppler/Hz	9.2118	8.1530	−11.49%	49.6585	439.07%	8.9270	−3.09%
Baseband signal power/dBHzm	11.7478	11.3715	−3.20%	11.7659	0.15%	11.4168	−2.82%

,

Table 5. Comparison of RMSE for different strategies and the genuine signal ($\mathrm{C}/{\mathrm{N}}_0$ = 40 dBHz, D = 1).

RMSE	Genuine Signal	Strategy 1		Strategy 2		Proposed Strategy
Code Doppler/cps	3.8620	3.0380	−21.34%	3.8313	−0.79%	3.8527	−0.24%
Carrier Doppler/Hz	3.1576	3.0254	−4.19%	51.8225	1541.20%	3.1742	0.53%
Baseband signal power/dBHzm	4.7131	5.8102	23.28%	7.4685	58.46%	4.7356	0.48%

,

Table 6. Comparison of RMSE of different strategies and the genuine signal ($\mathrm{C}/{\mathrm{N}}_0$ = 50 dBHz, D = 1).

RMSE	Genuine Signal	Strategy 1		Strategy 2		Proposed Strategy
Code Doppler/cps	1.3314	1.0161	−23.68%	2.3446	76.10%	1.3378	0.48%
Carrier Doppler/Hz	1.0219	0.9858	−3.53%	51.8179	4970.74%	1.0255	0.35%
Baseband signal power/dBHzm	1.4258	3.7214	161.00%	6.4803	354.50%	1.4225	−0.23%

,

Table 7. Comparison of RMSE for different strategies and the genuine signal ($\mathrm{C}/{\mathrm{N}}_0$ = 60 dBHz, D = 1).

RMSE	Genuine Signal	Strategy 1		Strategy 2		Proposed Strategy
Code Doppler/cps	0.4255	0.3392	−20.28%	2.0826	389.45%	0.4327	1.69%
Carrier Doppler/Hz	0.4713	0.4657	−1.19%	51.7133	10,872.48%	0.4739	0.55%
Baseband signal power/dBHzm	0.4440	3.4613	679.57%	6.4441	1351.37%	0.4493	1.19%

and

Table 8. Comparison of RMSE for different strategies and the genuine signal ($\mathrm{C}/{\mathrm{N}}_0$ = 50 dBHz, D = 0.2).

RMSE	Genuine Signal	Strategy 1		Strategy 2		Proposed Strategy
Code Doppler/cps	0.3338	0.2986	−10.55%	0.5735	71.81%	0.3453	3.45%
Carrier Doppler /Hz	1.0176	0.9403	−7.60%	1.7632	73.27%	1.0222	0.45%
Baseband signal power /dBm	1.4194	3.5533	150.34%	2.4744	74.33%	1.4155	−0.27%

.

Figure 21, Figure 22, Figure 23 and Figure 24 presents the SQM metric in the same four cases.

4. Discussion

4.1. Discussion on Simulation Results

This section discusses the results obtained in Section 3.1.

First, the advantages and theoretical feasibility of the proposed strategy compared to the conventional traction strategy are discussed.

The simulation results for the three strategies are presented in Figure 11, Figure 12 and Figure 13. All ${\mathsf{\tau }}_{\mathrm{sl}}$ in Figure 11a, Figure 12a and Figure 13a finally approach 0, indicating successful code-loop traction of the three strategies. According to Figure 12f, the local Doppler ${\mathrm{fd}}_{\mathrm{l}}$ is finally equal to the spoofing Doppler ${\mathrm{f}}_{\mathrm{drag}}$, and the carrier-loop traction of Strategy 2 is successful.

As can be observed in Figure 11a,c and Figure 12a,c, the code phase, code rate, and carrier frequency of the local loop cannot be followed up in real time, and there is a long loop adjustment process. Successful traction requires ${\mathrm{P}}_{\mathrm{s}}$ to be at least equal to ${\mathrm{P}}_{\mathrm{a}}$ within a certain period of time, which directly leads to considerable distortion when the correlation peaks are superimposed. The power will inevitably increase significantly, and distortion of the correlation peak and fluctuation of observations will be inevitable, as illustrated in Figure 11b and Figure 12b. Therefore, conventional traction strategies are at risk of being detected by power and TOA detection. Based on this limitation, a novel traction strategy for covert spoofing against TOA and power detection is proposed.

Therefore, because the conventional traction method risks being detected by power and TOA detection, we expect that the proposed strategy can circumvent these problems.

Figure 13 shows that the simulation results of the proposed method differ from those of the previous two methods. The conventional traction idea is a correlation peak superposition, and the spoofing signal slightly increases the spoofing signal power to take advantage. However, the proposed traction strategy essentially suppresses part of the genuine signals while realizing the generation of an ideal composite correlation peak.

The outputs of the correlators fluctuated slightly only when spoofing was added or when the traction speed returned to 0. This is because the adjustment process of the tracking loop causes ${\mathsf{\tau }}_{\mathrm{al}}$ to lag behind the changes in ${\mathrm{v}}_{\mathrm{drag}}$ for a short period at the beginning and end of the traction. Most of the time, we have

$${\mathrm{v}}_{\mathrm{drag}}\mathrm{t}\approx {\mathsf{\tau }}_{\mathrm{al}}$$

(35)

Then we have

$${\mathrm{I}}_{\mathrm{P}}\left(\mathrm{n}\right)\approx \frac{\sqrt{{\mathrm{P}}_{\mathrm{a}}}}{2}{\mathrm{T}}_{\mathrm{coh}}\mathrm{R}\left(0\right),$$

(36)

$${\mathsf{\delta }}_{\mathrm{cp}}=\frac{{\mathrm{I}}_{\mathrm{E}}-{\mathrm{I}}_{\mathrm{L}}}{{\mathrm{I}}_{\mathrm{E}}+{\mathrm{I}}_{\mathrm{L}}}\approx \frac{{\mathrm{R}}^{-}\left(0\right)-{\mathrm{R}}^{+}\left(0\right)}{{\mathrm{R}}^{-}\left(0\right)+{\mathrm{R}}^{+}\left(0\right)}=0$$

(37)

Therefore, the proposed strategy is theoretically feasible. Compared to conventional strategies, it has a more ideal spoofing effect.

The second part is the comparison of two conventional strategies.

Compared with Strategy 1, it can be determined that Strategy 2 leads to the deterioration of the stability of the carrier loop, and the change in the phase discriminator output is more complicated owing to the influence of the carrier.

The third part is the discussion on traction speed and traction duration.

From Table 3, it can be observed that the value range of the traction speed is extended under the proposed strategy. Because the selection of ${\mathrm{v}}_{\mathrm{drag}}$ directly affects the adjustment time of the loop traction, these two indicators must be weighed. In actual navigation wars, it is usually necessary to quickly seize the control of the tracking loop, and the traction time should not be too long, i.e., the traction speed should not be too slow. Compared to conventional traction strategies, the proposed strategy can more covertly and promptly control of the tracking loop.

4.2. Discussion on Experimental Results

This section discusses the experimental results obtained in Section 3.2 and Section 3.3.

First, the results of these strategies are discussed to clarify the feasibility of the proposed strategy.

All ${\mathsf{\tau }}_{\mathrm{sl}}$ values in Figure 14a, Figure 15a and Figure 16a finally approach 0, indicating successful code loop traction of the three strategies. According to Figure 15a, the output of filter ${\mathrm{fd}}_{\mathrm{l}}$ is finally equal to the spoofing Doppler ${\mathrm{f}}_{\mathrm{drag}}$, and the carrier loop traction of Strategy 2 is successful.

However, as shown in Figure 14a and Figure 15a, each received observation has a different degree of distortion under the two conventional strategies. By comparing Figure 14, Figure 15 and Figure 16 with Figure 11, Figure 12 and Figure 13, it can be observed that the experimental results are consistent with the simulation results, which confirms the correctness of the simulations.

From Figure 15, it can be seen that the received observations of the proposed strategy are stable without distortion, and the code phase of the tracking loop follows the preset code phase of spoofing, which verifies the feasibility of the proposed strategy under noise.

The second part presents the analysis of the proposed strategy under different spoofing scenarios.

In Table 4, Table 5, Table 6, Table 7 and Table 8, it can be observed that the observations’ RMSE percentage change in the proposed strategy is significantly better than those of Strategies 1 and 2, and the observations’ RMSE percentage change in Strategy 2 is the worst. Based on these data, we can infer that in all designed spoofing scenarios, the implementation of the proposed strategy has no significant effect on the statistical value of the signal.

As shown in Figure 20 and Table 8, the obtained results of the narrow correlator are similar to those of the wide correlator. The proposed strategy can also address narrow pulse-aperture correlators.

Because the 30 dBHz $\mathrm{C}/{\mathrm{N}}_0$ is already a very weak GNSS signal, there will be some difficulties in estimating the genuine signal in the first step. In Table 4, significant changes in the observations are easily lost in the noise;therefore, the meaning of the obtained results is relatively limited. As shown in Figure 19a, the received results are very poor, which also means that there will be some difficulties in the acquisition and extraction of navigation messages. However, as can be seen from Figure 19b, the phase is successfully pulled, so the proposed spoofing traction strategy also exhibits good performance under the condition of a poor $\mathrm{C}/{\mathrm{N}}_0$.

In conventional Strategy 1, the statistics of code Doppler and carrier Doppler are small because this strategy directly superimposes spoofing signals of the same format, and the effect of correlation peak superposition is equivalent to power enhancement, thus reducing the output of the phase discriminator to a certain extent.

In special scenarios, such as a battlefield, the GNSS of the defense side may be enhanced to improve the service accuracy and reduce the possibility of spoofing. Figure 17 and Table 7 demonstrate that the proposed strategy performs well in the case of a power-enhanced signal.

The third part presents the performance analysis of the proposed strategy in the context of the SQM technique.

From Figure 21, Figure 22, Figure 23 and Figure 24, it can be observed that the Ratio Test metric values of the genuine signal are in the range $\pm 0.15$, while the metric values of Strategies 1 and 2 are far beyond this range. As expected, the metric values of the proposed strategy are within a safe range. The threshold value can be easily derived according to the theory presented in [13], given a determinate false detection probability. A threshold is built around the shape of the metric function, and can be used to detect the presence of distortions in real time. These results demonstrate that this strategy can bypass the SQM detection.

4.3. Limitations and Prospects

The proposed strategy has certain limitations. First, the proposed traction strategy is only for BPSK modulation and is suitable for the BeiDou Navigation Satellite System B1I and Global Positioning System L1C/A. Second, the proposed traction strategy is actually a variant of conventional Strategy 1. If the code-carrier coherence is detected, the proposed strategy may be detected when the traction speed is high. Finally, the scope of this study is limited to the generation of spoofing signals and the spoofing effect for a single satellite; multi-satellite positioning and timing spoofing have not been analyzed.

However, the traction concept of the proposed strategy is worth investigating. According to this idea, the traction code can be derived provided the nominal correlation function is given. Therefore, the applicability of the proposed strategy to other modulated signals should be investigated further. In the case of a high traction rate, necessary improvements can be made to maintain the code-carrier coherence and avoid detection. After the traction is completed, the influence of the proposed strategy on the subsequent message demodulation and positioning also needs to be analyzed.

5. Conclusions

The correlation peak superposition of conventional strategies rendersthe observations of the receiver unstable. The receiver only needs to perform mathematical statistics on the observations of the receiver to detect spoofing, such as TOA and power detection. We assumed that we can design spoofing that can form an optimal correlation peak at the receiver to avoid the instability of the received results.

From the analysis of the desired ideal correlation peak, we determined that pseudo-code used in modulation could be replaced by a traction code, and this traction code was derived. The simulation and experimental results proved the feasibility of the traction code. Compared to conventional traction strategies, the proposed strategy has the following advantages:

• The change in the phase discriminator output is small, and the code loop, carrier frequency, and baseband signal power are ensured to be stable. The observations’ RMSE percentage change in the proposed strategy is significantly better than those of Strategies 1 and 2. The Ratio Test metric values prove that this strategy can bypass the SQM detection. Therefore, the proposed strategy can resist TOA and power detection.
• Under the condition of a high or low $\mathrm{C}/{\mathrm{N}}_0$, the proposed spoofing traction strategy also exhibits an optimal good performance; hence, it is still effective when the GNSS signal is enhanced in the battlefield or when the signal quality is poor owing to the low elevation.
• This strategy expands the range of traction speeds and has the potential to quickly and covertly accomplish traction.
• The proposed strategy can also be applied to narrow- and pulse-aperture correlators.