Evolution of Different Types of Eddies Originating from Different Baroclinic Instability Types
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
2.2.1. Eddy Detection and Tracking Algorithm
2.2.2. Composite Analysis of Eddies
2.2.3. Thermocline Identification
2.2.4. Baroclinic Instability Types and Their Potential Consequences
3. Results
3.1. Evolutionary Characteristics of the Vertical Structure of Global Eddies
3.2. Basic Properties of Different Types of Eddies and Their Evolutionary Characteristics
3.3. Evolutionary Characteristics of the Vertical Structure of Different Types of Eddies
4. Discussion
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samelson, R.M.; de Szoeke, R.A. Global observations of large oceanic eddies. Geophys. Res. Lett. 2007, 34, L15606. [Google Scholar] [CrossRef]
- Wunsch, C.; Ferrari, R. Vertical mixing, energy and the general circulation of the oceans. Annu. Rev. Fluid Mech. 2004, 36, 281–314. [Google Scholar] [CrossRef]
- Chen, G.; Wang, D.; Hou, Y. The features and interannual variability mechanism of mesoscale eddies in the Bay of Bengal. Cont. Shelf Res. 2012, 47, 178–185. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Liu, Y.; Chen, D. Global heat and salt transports by eddy movement. Nat. Commun. 2014, 5, 3294. [Google Scholar] [CrossRef] [PubMed]
- Ning, J.; Chen, K.; Gaube, P. Diverse variability of surface chlorophyll during the evolution of Gulf Stream rings. Geophys. Res. Lett. 2021, 48, e2020GL091461. [Google Scholar] [CrossRef]
- Gaube, P.; Chelton, D.B.; Samelson, R.M.; Schlax, M.G.; O’neill, L.W. Satellite observations of mesoscale eddy-induced Ekman pumping. J. Phys. Oceanogr. 2015, 45, 104–132. [Google Scholar] [CrossRef]
- Hausmann, U.; Czaja, A. The observed signature of mesoscale eddies in sea surface temperature and the associated heat transport. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2012, 70, 60–72. [Google Scholar] [CrossRef]
- Qiu, B.; Chen, S. Variability of the Kuroshio Extension jet, recirculation gyre, and mesoscale eddies on decadal time scales. J. Phys. Oceanogr. 2005, 35, 2090–2103. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, W.; Qiu, B. Oceanic mass transport by mesoscale eddies. Science 2014, 345, 322–324. [Google Scholar] [CrossRef]
- Sun, W.; Dong, C.; Tan, W.; Liu, Y.; He, Y.; Wang, J. Vertical structure anomalies of oceanic eddies and eddy-induced transports in the South China Sea. Remote Sens. 2018, 10, 795. [Google Scholar] [CrossRef]
- Xu, G.; Dong, C.; Liu, Y.; Gaube, P.; Yang, J. Chlorophyll Rings around Ocean Eddies in the North Pacific. Sci. Rep. 2019, 9, 2019. [Google Scholar] [CrossRef] [PubMed]
- Vallis, G.K. (Ed.) Atmospheric and Oceanic Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2006; pp. 247–287. [Google Scholar]
- Sun, W.; Yang, J.; Tan, W.; Liu, Y.; Zhao, B.; He, Y.; Dong, C. Eddy diffusivity and coherent mesoscale eddy analysis in the Southern Ocean. Acta Oceanol. Sin. 2021, 40, 1–16. [Google Scholar] [CrossRef]
- Sun, W.; Dong, C. Isopycnal and diapycnal mixing parameterization schemes for submesoscale processes induced by mesoscale eddies. Deep. Sea Res. Part II Top. Stud. Oceanogr. 2022, 202, 105139. [Google Scholar] [CrossRef]
- Gill, A.; Green, J.; Simmons, A. Energy partition in the large-scale ocean circulation and the production of mid-ocean eddies. Deep. Sea Res. Oceanogr. Abstr. 1974, 21, 499–528. [Google Scholar] [CrossRef]
- Pedlosky, J. Geophysical Fluid Dynamics, 2nd ed.; Springer: Berlin, Germany, 1987. [Google Scholar]
- Roullet, G.; McWilliams, J.C.; Capet, X.; Molemaker, M.J. Properties of steady geostrophic turbulence with isopycnal outcropping. J. Phys. Oceanogr. 2012, 42, 18–38. [Google Scholar] [CrossRef]
- Venaille, A.; Vallis, G.K.; Smith, K.S. Baroclinic turbulence in the ocean: Analysis with primitive equation and quasigeostrophic simulations. J. Phys. Oceanogr. 2015, 41, 1605–1623. [Google Scholar] [CrossRef]
- Smith, K.S. The geography of linear baroclinic instability in Earth’s oceans. J. Mar. Res. 2007, 65, 655–683. [Google Scholar] [CrossRef]
- Tulloch, R.; Marshall, J.; Hill, C.; Smith, K.S. Scales, growth rates, and spectral fluxes of baroclinic instability in the ocean. J. Phys. Oceanogr. 2011, 41, 1057–1076. [Google Scholar] [CrossRef]
- Beckmann, A. Vertical Structure of Midlatitude Mesoscale Instabilities. J. Phys. Oceanogr. 1988, 18, 1354–1371. [Google Scholar] [CrossRef]
- Feng, L.; Liu, C.; Köhl, A.; Stammer, D.; Wang, F. Four types of baroclinic instability waves in the global oceans and the implications for the vertical structure of mesoscale eddies. J. Geophys. Res. Ocean. 2021, 126, e2020JC016966. [Google Scholar] [CrossRef]
- Liu, Y.; Dong, C.; Guan, Y.; Chen, D.; McWilliams, J.; Nencioli, F. Eddy analysis in the subtropical zonal band of the North Pacific Ocean. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2012, 68, 54–67. [Google Scholar] [CrossRef]
- Yang, G.; Wang, F.; Li, Y.; Lin, P. Mesoscale eddies in the northwestern subtropical Pacific Ocean: Statistical characteristics and three-dimensional structures. J. Geophys. Res. Ocean. 2013, 118, 1906–1925. [Google Scholar] [CrossRef]
- Frenger, I.; Gruber, N.; Knutti, R.; Münnich, M. Southern Ocean eddy phenomenology. J. Geophys. Res.-Ocean. 2015, 120, 7413–7449. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Wang, W.; Huang, R.X. Universal structure of mesoscale eddies in the ocean. Geophys. Res. Lett. 2013, 40, 3677–3681. [Google Scholar] [CrossRef]
- Zhai, X.; Johnson, H.L.; Marshall, D.P. Significant sink of ocean-eddy energy near western boundaries. Nat. Geosci. 2010, 3, 608–612. [Google Scholar] [CrossRef]
- Evans, D.G.; Frajka-Williams, E.E.; Garabato, A.C.N.; Polzin, K.L.; Forryan, A. Mesoscale eddy dissipation by a “zoo” of submesoscale processes at a western boundary. J. Geophys. Res. Ocean. 2020, 125, e2020JC016246. [Google Scholar] [CrossRef]
- Dong, J.; Fox-Kemper, B.; Jing, Z.; Yang, Q.; Tian, J.; Dong, C. Turbulent Dissipation in the Surface Mixed Layer of an Anticyclonic Mesoscale Eddy in the South China Sea. Geophys. Res. Lett. 2022, 49, e2022GL100016. [Google Scholar] [CrossRef]
- Le Traon, P.Y.; Nadal, F.; Ducet, N. An Improved Mapping Method of Multisatellite Altimeter Data. J. Atmos. Ocean. Technol. 1998, 15, 522–534. [Google Scholar] [CrossRef]
- Nencioli, F.; Dong, C.; Dickey, T.; Washburn, L.; McWilliams, J.C. A vector geometry-based eddy detection algorithm and its application to a high-resolution numerical model product and high-frequency radar surface velocities in the Southern California Bight. J. Atmos. Ocean. Technol. 2010, 27, 564–579. [Google Scholar] [CrossRef]
- Dong, C.; Mavor, T.; Nencioli, F.; Jiang, S.; Uchiyama, Y.; McWilliams, J.C.; Dickey, T.; Ondrusek, M.; Zhang, H.; Clark, D.K. An oceanic cyclonic eddy on the lee side of Lanai Island, Hawai’i. J. Geophys. Res. Earth Surf. 2009, 114, C10008. [Google Scholar] [CrossRef]
- Dong, C.; Liu, Y.; Lumpkin, R.; Lankhorst, M.; Chen, D.; McWilliams, J.C.; Guan, Y. A Scheme to Identify Loops from Trajectories of Oceanic Surface Drifters: An Application in the Kuroshio Extension Region. J. Atmos. Ocean. Technol. 2011, 28, 1167–1176. [Google Scholar] [CrossRef]
- Dong, C.; Lin, X.; Liu, Y.; Nencioli, F.; Chao, Y.; Guan, Y.; Chen, D.; Dickey, T.; McWilliams, J.C. Three-dimensional oceanic eddy analysis in the Southern California Bight from a numerical product. J. Geophys. Res. Ocean. 2012, 117, C00H14. [Google Scholar] [CrossRef]
- Aguiar, A.C.B.; Peliz, Á.; Carton, X. A census of Meddies in a long-term high-resolution simulation. Prog. Oceanogr. 2013, 116, 80–94. [Google Scholar] [CrossRef]
- Lin, X.; Dong, C.; Chen, D.; Liu, Y.; Yang, J.; Zou, B.; Guan, Y. Three-dimensional properties of mesoscale eddies in the South China Sea based on eddy-resolving model output. Deep. Sea Res. Part I Oceanogr. Res. Pap. 2015, 99, 46–64. [Google Scholar] [CrossRef]
- Yang, X.; Xu, G.; Liu, Y.; Sun, W.; Xia, C.; Dong, C. Multi-source data analysis of mesoscale eddies and their effects on surface chlorophyll in the Bay of Bengal. Remote Sens. 2020, 12, 3485. [Google Scholar] [CrossRef]
- Sun, W.; An, M.; Liu, J.; Liu, J.; Yang, J.; Tan, W.; Dong, C.; Liu, Y. Comparative analysis of four types of mesoscale eddies in the Kuroshio-Oyashio extension region. Front. Mar. Sci. 2022, 9, 984244. [Google Scholar] [CrossRef]
- An, M.; Liu, J.; Liu, J.; Sun, W.; Yang, J.; Tan, W.; Liu, Y.; Sian, K.T.; Ji, J.; Dong, C. Comparative analysis of four types of mesoscale eddies in the north pacific subtropical countercurrent region—Part I spatial characteristics. Front. Mar. Sci. 2022, 9, 1004300. [Google Scholar] [CrossRef]
- Dong, C.; Liu, L.; Nencioli, F.; Bethel, B.J.; Liu, Y.; Xu, G.; Ma, J.; Ji, J.; Sun, W.; Shan, H.; et al. The near-global ocean mesoscale eddy atmospheric-oceanic-biological interaction observational dataset. Sci. Data 2022, 9, 436. [Google Scholar] [CrossRef]
- Chaigneau, A.; Le Texier, M.; Eldin, G.; Grados, C.; Pizarro, O. Vertical structure of mesoscale eddies in the eastern South Pacific Ocean: A composite analysis from altimetry and Argo profiling floats. J. Geophys. Res. Earth Surf. 2011, 116, C11025. [Google Scholar] [CrossRef]
- Yang, G.; Yu, W.; Yuan, Y.; Zhao, X.; Wang, F.; Chen, G.; Liu, L.; Duan, Y. Characteristics, vertical structures, and heat/salt transports of mesoscale eddies in the southeastern tropical Indian Ocean. J. Geophys. Res. Ocean. 2015, 120, 6733–6750. [Google Scholar] [CrossRef]
- Sun, W.; Dong, C.; Wang, R.; Liu, Y.; Yu, K. Vertical structure anomalies of oceanic eddies in the Kuroshio Extension region. J. Geophys. Res. 2017, 122, 1476–1496. [Google Scholar] [CrossRef]
- Lukas, R.; Lindstrom, E. The mixed layer of the western equatorial Pacific Ocean. J. Geophys. Res. Atmos. 1991, 96, 3343–3357. [Google Scholar] [CrossRef]
- Dong, S.; Sprintall, J.; Gille, S.T.; Talley, L. Southern Ocean mixed-layer depth from Argo float profiles. J. Geophys. Res. Earth Surf. 2008, 113, C06013. [Google Scholar] [CrossRef]
- Defant, A. Physical Oceanography; Pergamon: London, UK, 1961; Volume 1. [Google Scholar]
- Wyrtki, K. The thermal structure of the eastern Pacific Ocean. Dstch. Hydrogr. Zeit. Suppl. Ser. A 1964, 8, 6–84. [Google Scholar]
- Chu, P.C.; Liu, Q.Y.; Jia, Y.L.; Fan, C.W. Evidence of barrier layer in the Sulu and Celebes Seas. J. Phys. Oceanogr. 2002, 32, 3299–3309. [Google Scholar] [CrossRef]
- Holte, J.; Talley, L. A new algorithm for finding mixed layer depths with applications to Argo data and subantarctic mode water formation. J. Atmos. Ocean. Technol. 2009, 26, 1920–1939. [Google Scholar] [CrossRef]
- Samelson, R.M.; Schlax, M.G.; Chelton, D.B. Randomness, Symmetry, and Scaling of Mesoscale Eddy Life Cycles. J. Phys. Oceanogr. 2014, 44, 1012–1029. [Google Scholar] [CrossRef]
- Itoh, S.; Yasuda, I. Water Mass Structure of Warm and Cold Anticyclonic Eddies in the Western Boundary Region of the Subarctic North Pacific. J. Phys. Oceanogr. 2010, 40, 2624–2642. [Google Scholar] [CrossRef]
- Feng, L.; Liu, C.; Köhl, A.; Wang, F. Seasonality of four types of baroclinic instability in the global oceans. J. Geophys. Res. Ocean. 2022, 127, e2022JC018572. [Google Scholar] [CrossRef]
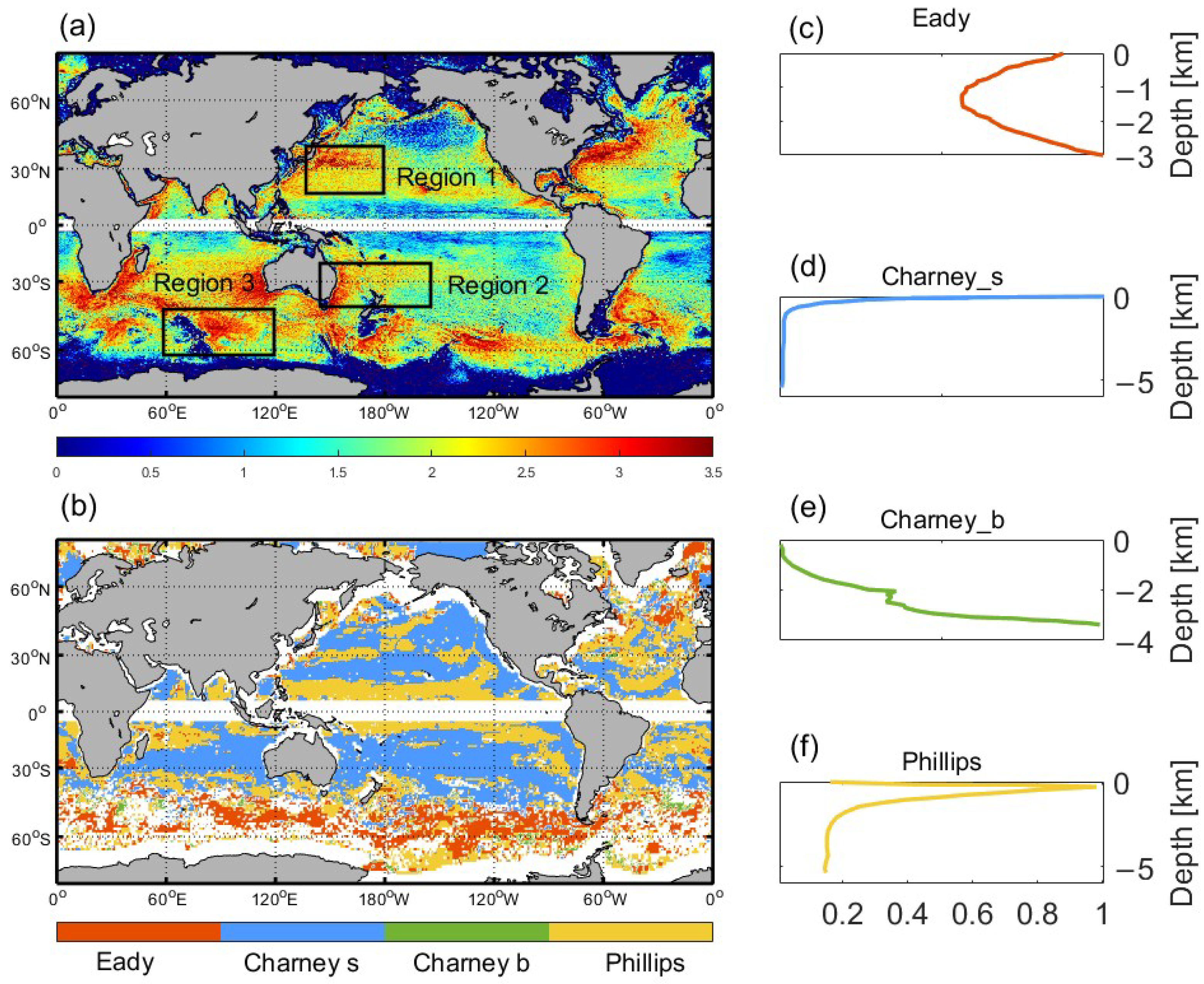
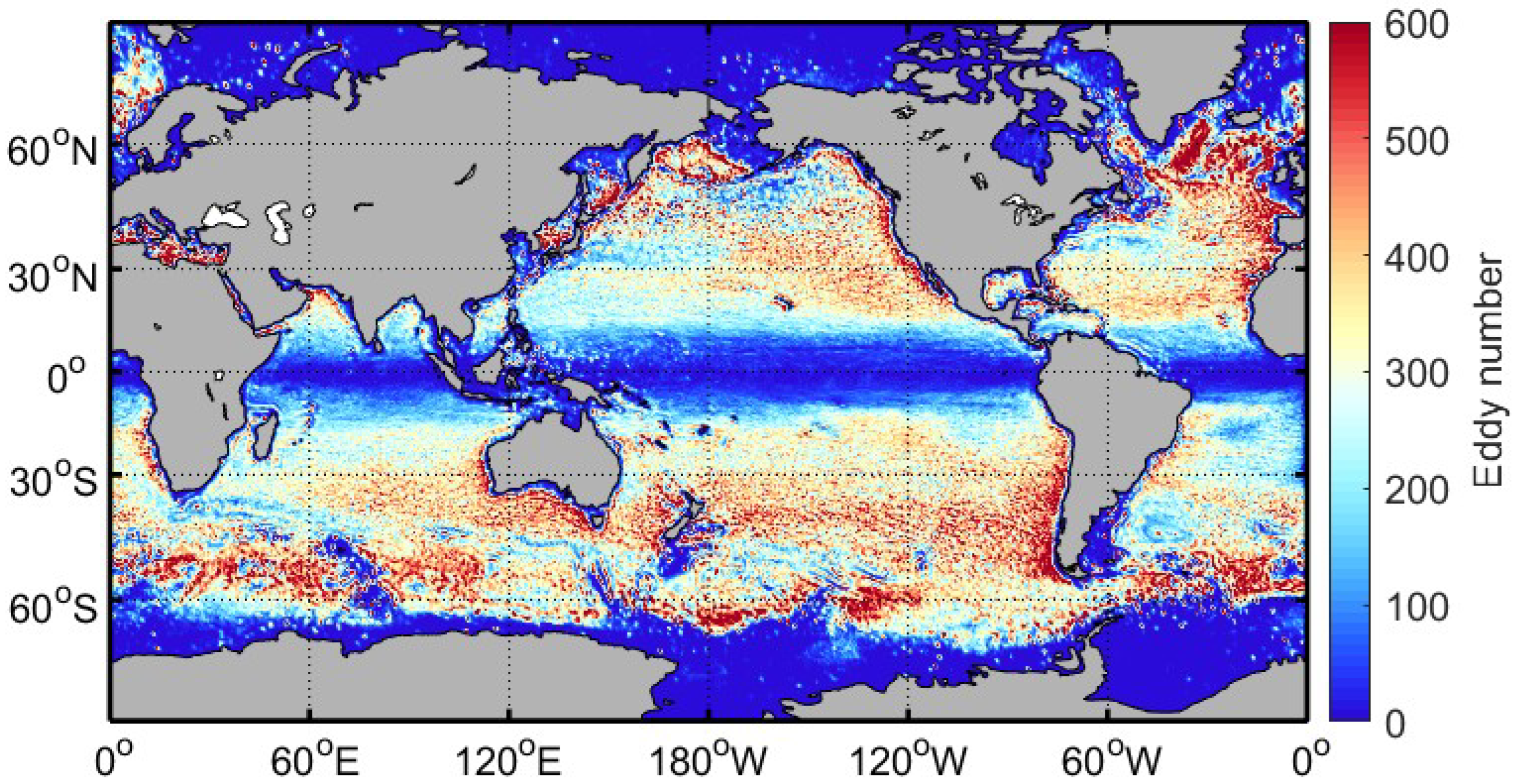
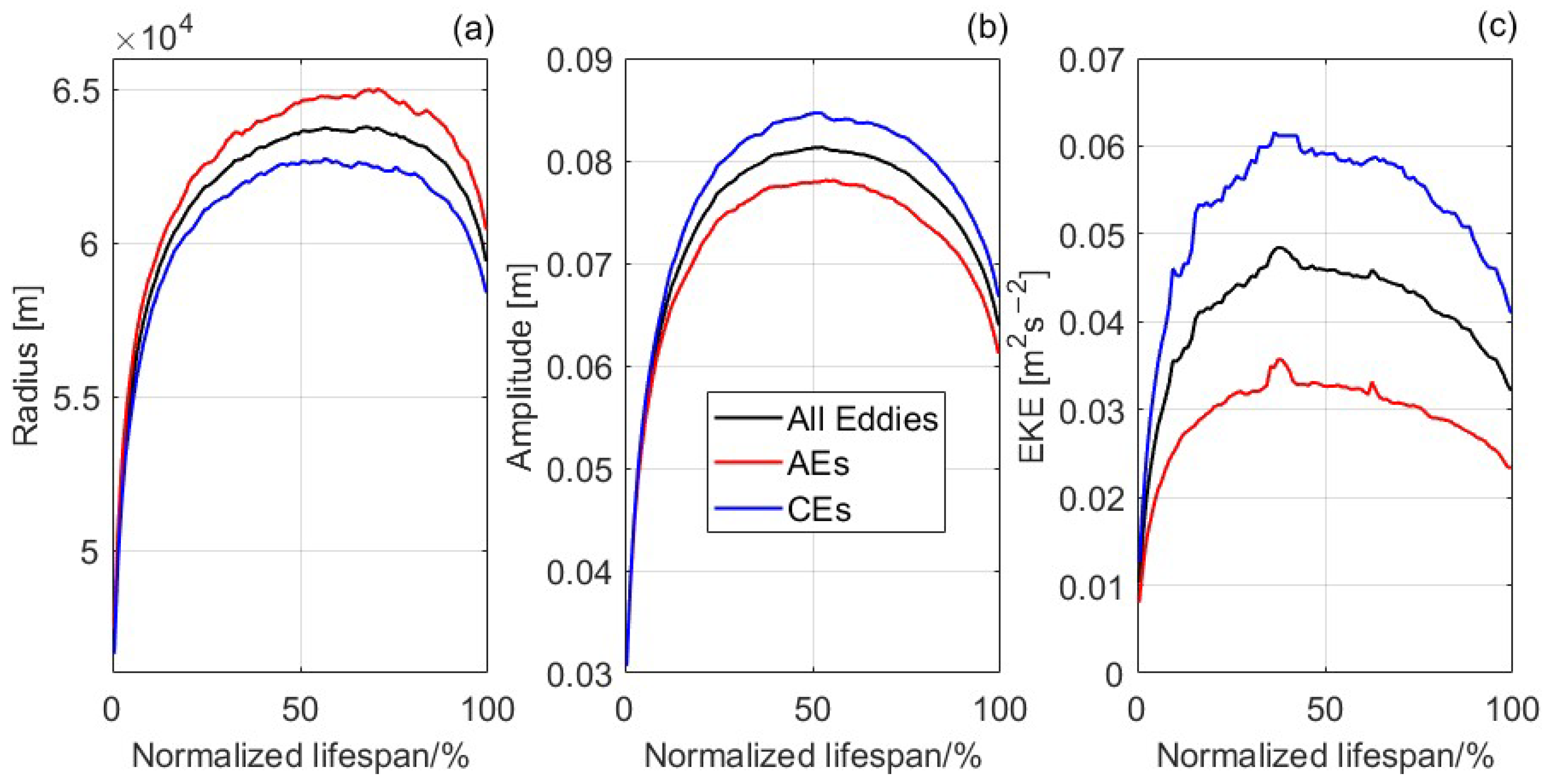
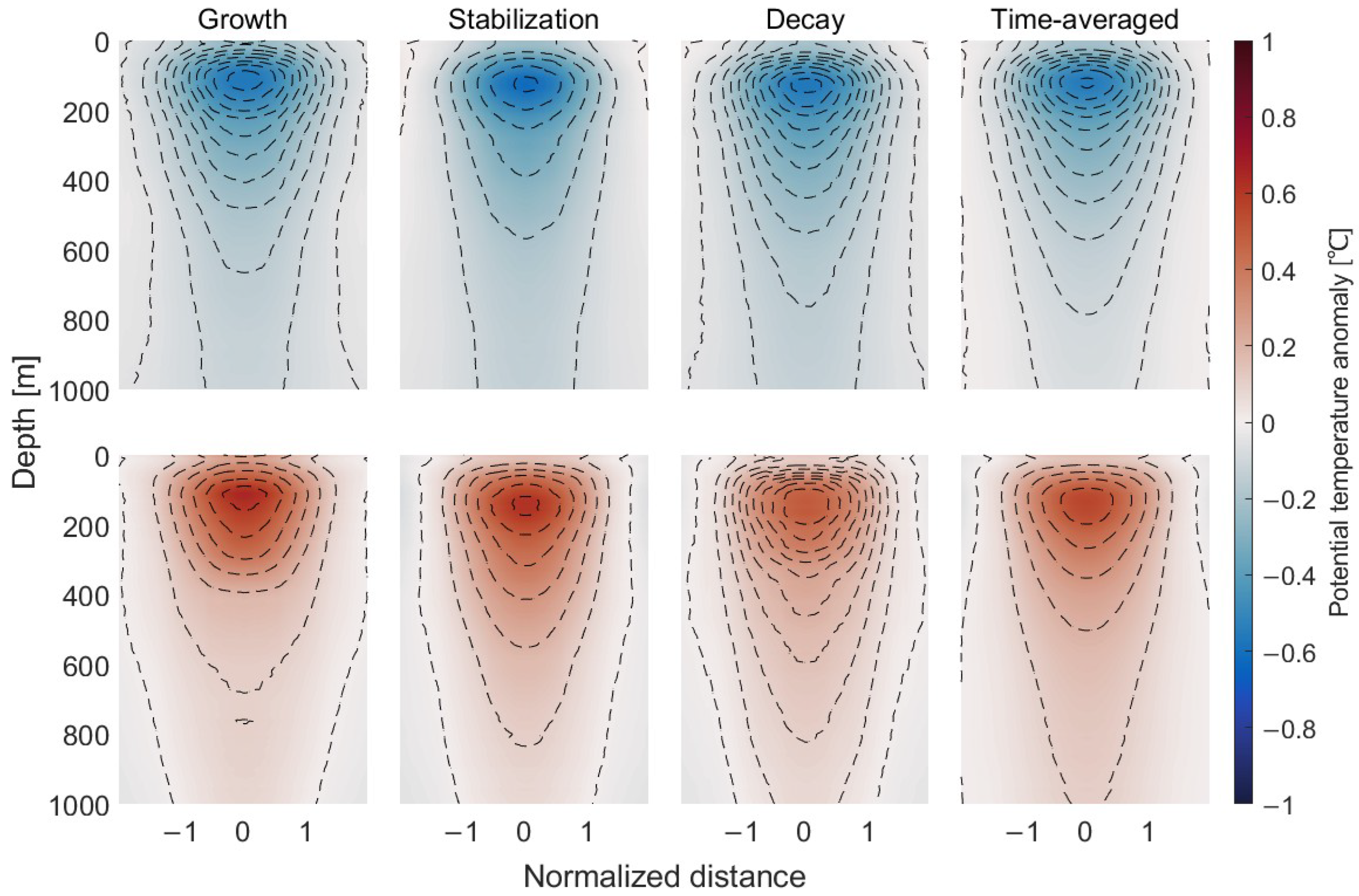
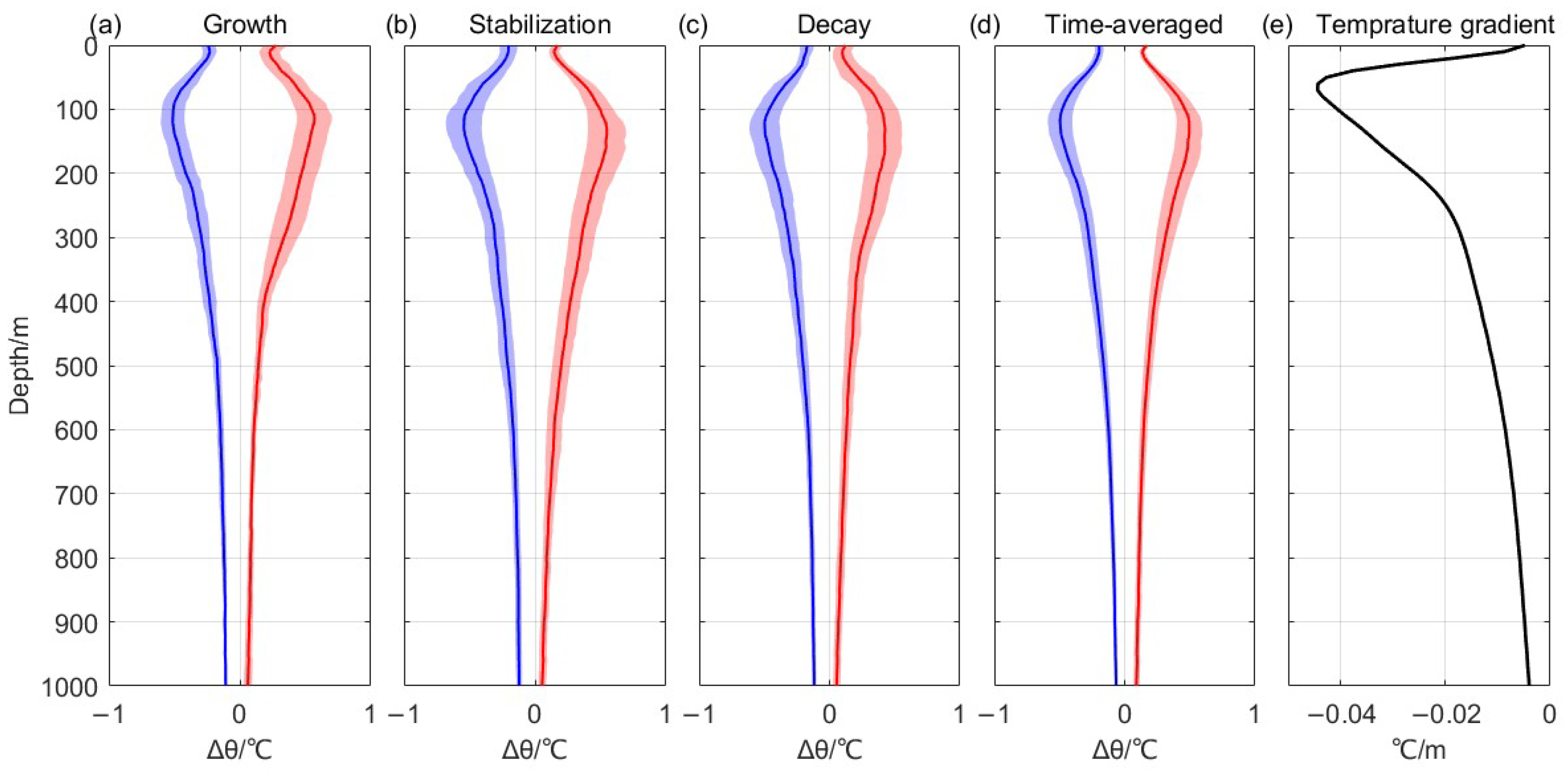
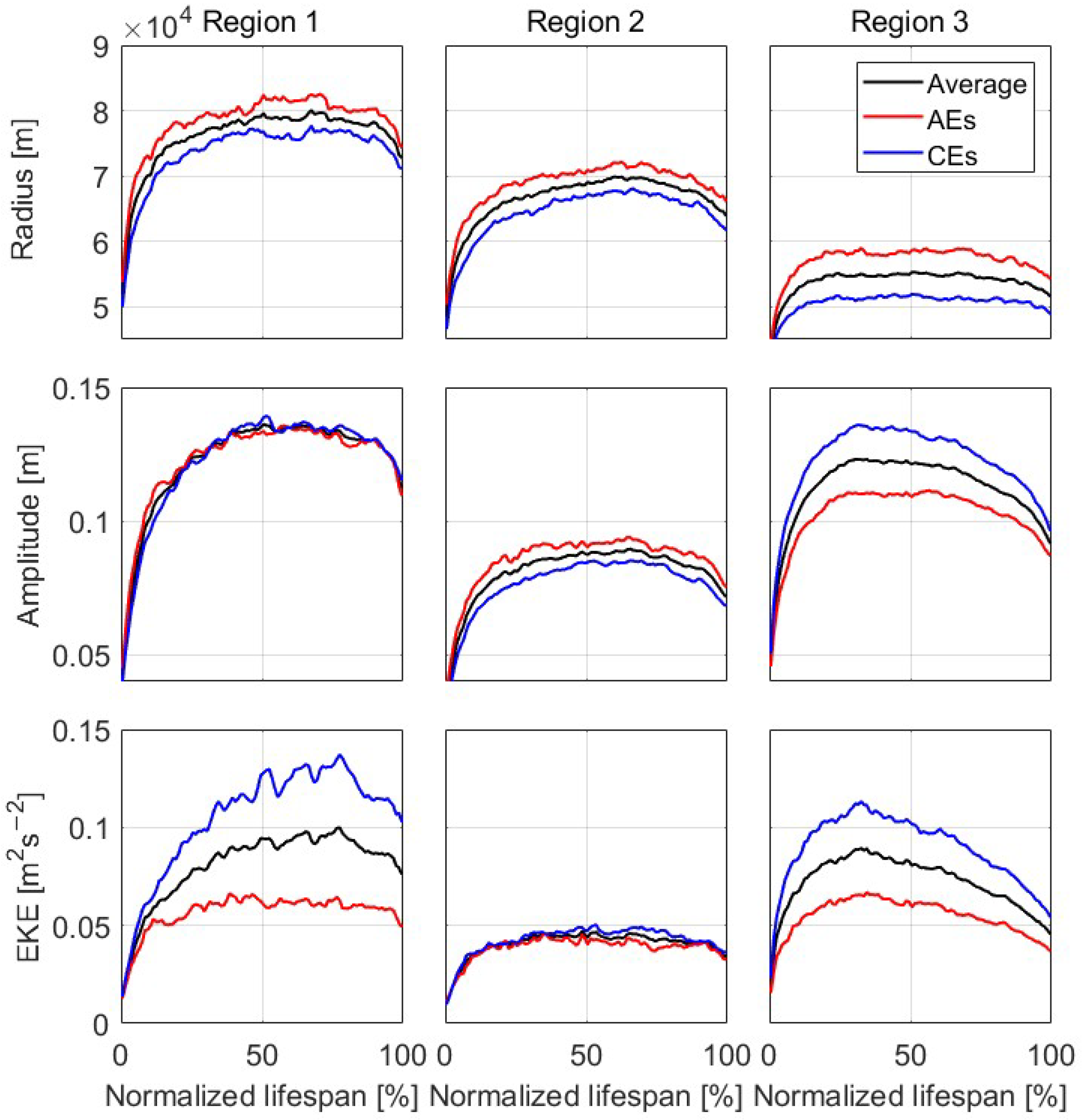
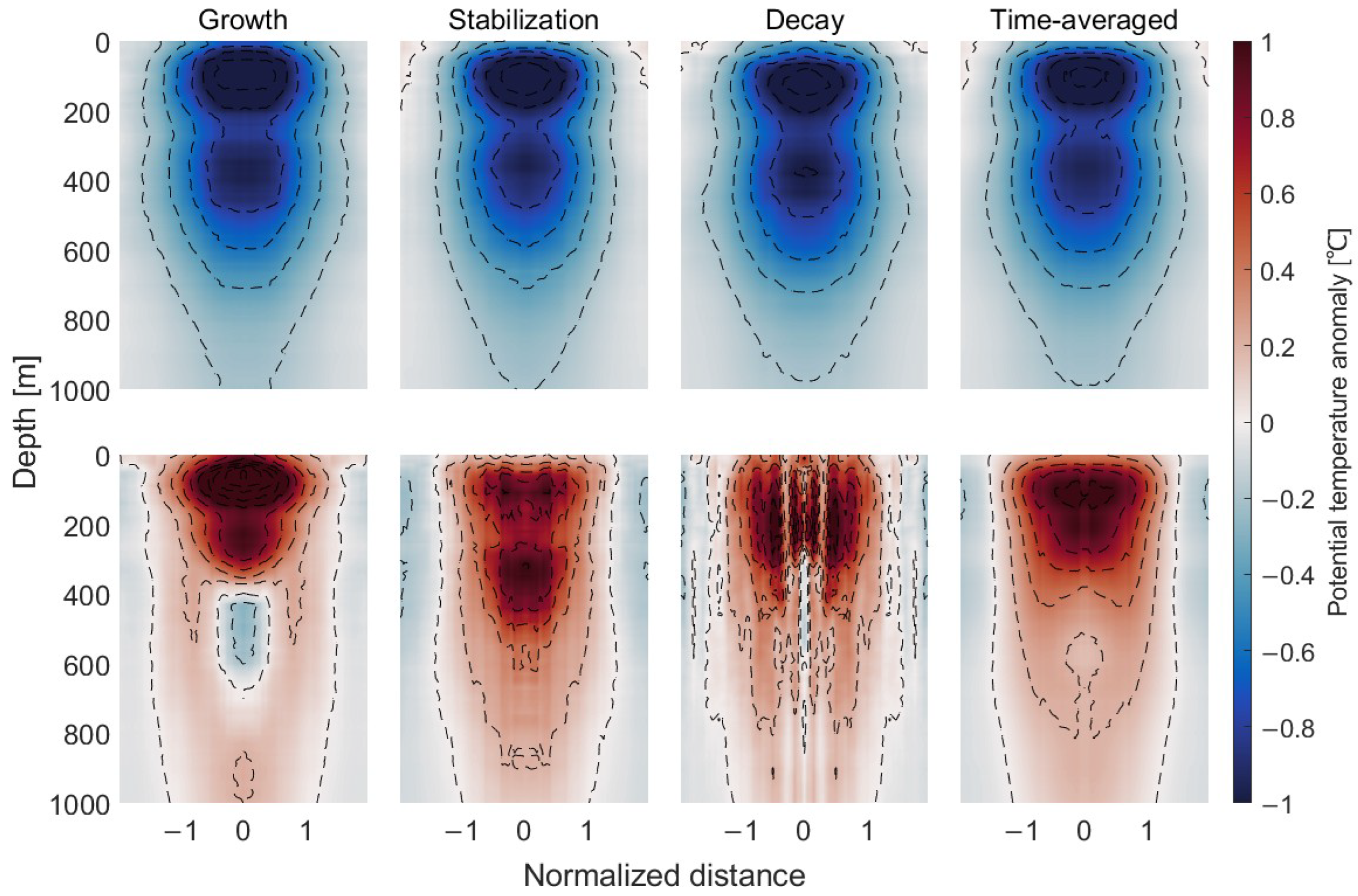
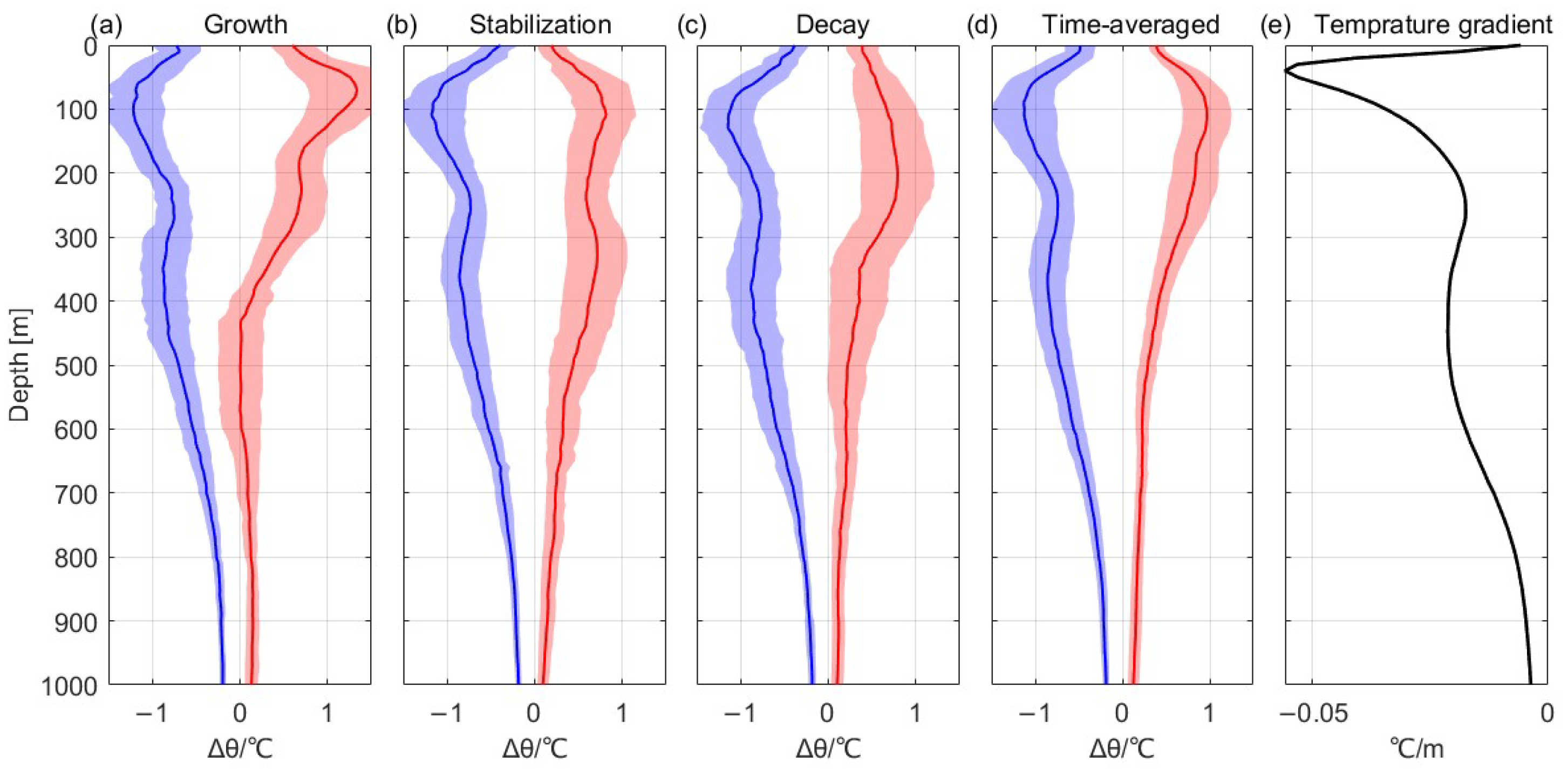

| Mean Properties | Region 1 | Region 2 | Region 3 | |||
|---|---|---|---|---|---|---|
| CEs | AEs | CEs | AEs | CEs | AEs | |
| Number of eddies | 5965 | 5852 | 9396 | 8960 | 6696 | 6007 |
| Lifetime (days) | 87 | 95 | 48 | 54 | 74 | 75 |
| Radius (km) | 67.55 | 72.65 | 56.97 | 60.63 | 49.31 | 54.66 |
| Amplitude (cm) | 9.63 | 9.76 | 5.55 | 6.01 | 9.99 | 9.52 |
| Translation speed (km/day) | 2.7 | 2.5 | 1.9 | 1.9 | 2.4 | 2.3 |
| Depth (m) | CEs | AEs | |||||
|---|---|---|---|---|---|---|---|
| Region 1 | 20 | −0.68 | −0.48 | −0.42 | 0.67 | 0.21 | 0.20 |
| 50 | −0.98 | −0.77 | −0.67 | 1.13 | 0.49 | 0.49 | |
| 250 | −0.78 | −0.73 | −0.79 | 0.68 | 0.58 | 0.76 | |
| 500 | −0.73 | −0.71 | −0.60 | 0.01 | 0.44 | 0.23 | |
| Region 2 | 20 | −0.37 | −0.36 | −0.32 | 0.23 | 0.15 | 0.11 |
| 60 | −0.46 | −0.38 | −0.37 | 0.38 | 0.39 | 0.34 | |
| 180 | −0.62 | −0.78 | −0.67 | 0.53 | 0.68 | 0.62 | |
| 400 | −0.58 | −0.67 | −0.57 | 0.58 | 0.65 | 0.56 | |
| Region 3 | 20 | −0.40 | −0.29 | −0.24 | 0.48 | 0.46 | 0.27 |
| 80 | −0.39 | −0.31 | −0.22 | 0.53 | 0.44 | 0.24 | |
| 180 | −0.35 | −0.21 | −0.28 | 0.54 | 0.34 | 0.48 | |
| 800 | −0.26 | −0.25 | −0.24 | 0.28 | 0.27 | 0.24 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Ning, J.; Chen, X. Evolution of Different Types of Eddies Originating from Different Baroclinic Instability Types. Remote Sens. 2023, 15, 5730. https://doi.org/10.3390/rs15245730
Liu J, Ning J, Chen X. Evolution of Different Types of Eddies Originating from Different Baroclinic Instability Types. Remote Sensing. 2023; 15(24):5730. https://doi.org/10.3390/rs15245730
Chicago/Turabian StyleLiu, Jiaxin, Jue Ning, and Xu Chen. 2023. "Evolution of Different Types of Eddies Originating from Different Baroclinic Instability Types" Remote Sensing 15, no. 24: 5730. https://doi.org/10.3390/rs15245730
APA StyleLiu, J., Ning, J., & Chen, X. (2023). Evolution of Different Types of Eddies Originating from Different Baroclinic Instability Types. Remote Sensing, 15(24), 5730. https://doi.org/10.3390/rs15245730




