Validation of Nadir SWH and Its Variance Characteristics from CFOSAT in China’s Offshore Waters
Abstract
:1. Introduction
2. Data and Methods
2.1. CFOSAT SWH Data
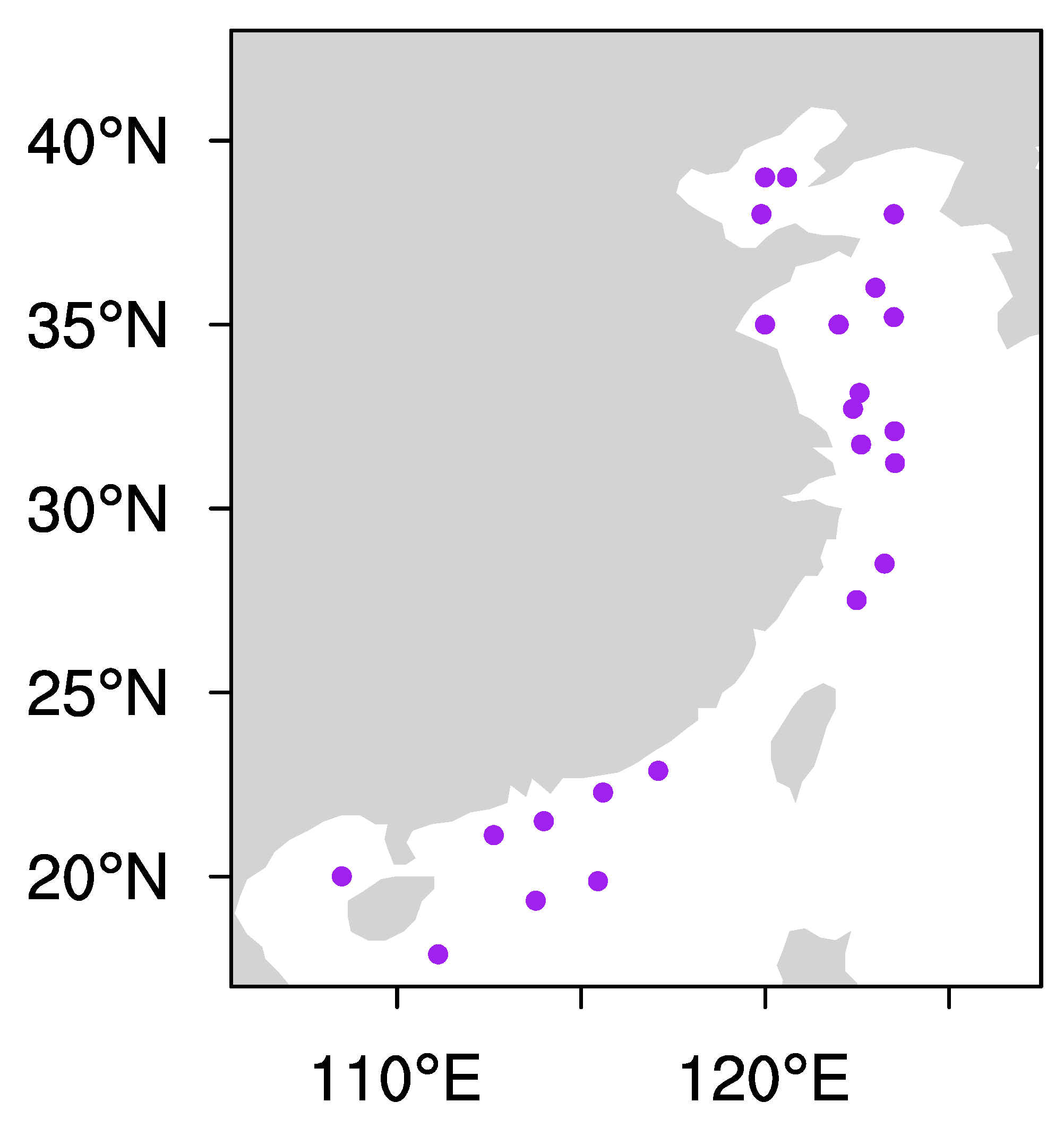
2.2. China’s Offshore Buoy SWH
2.3. HY−2B SWH Data
2.4. Methods
3. Results
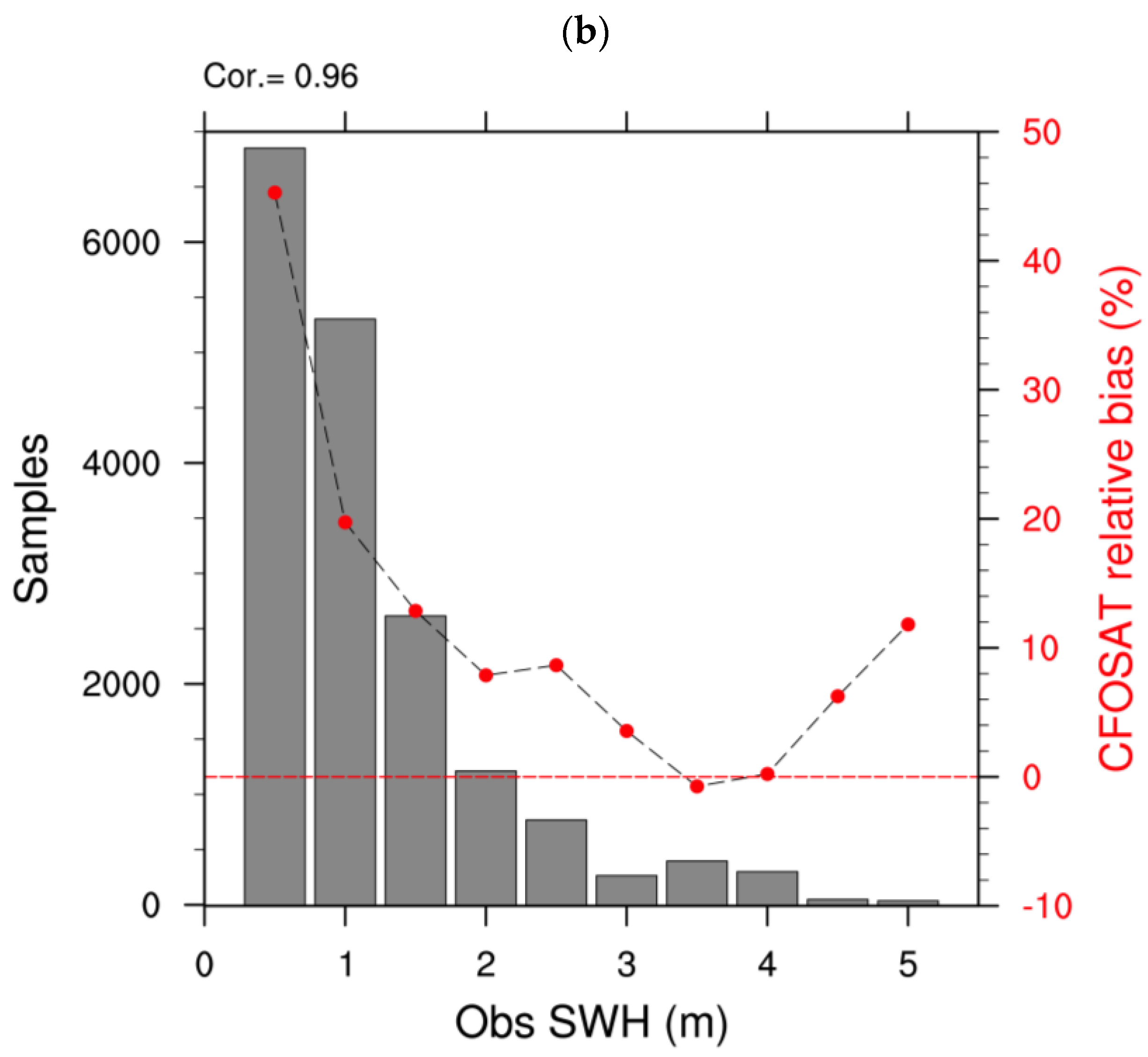
3.1. Validation of CFOSAT with In Situ SWH
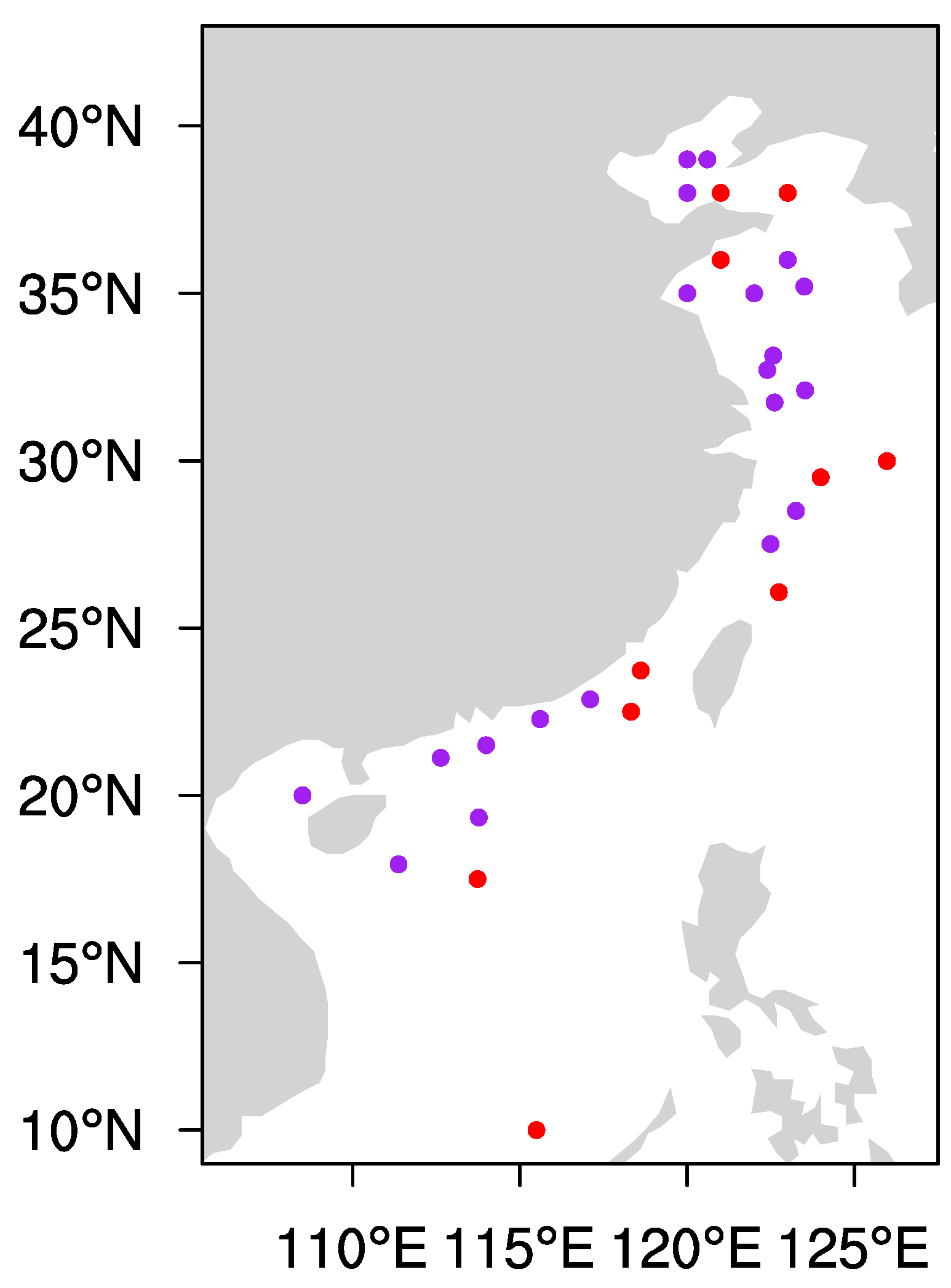
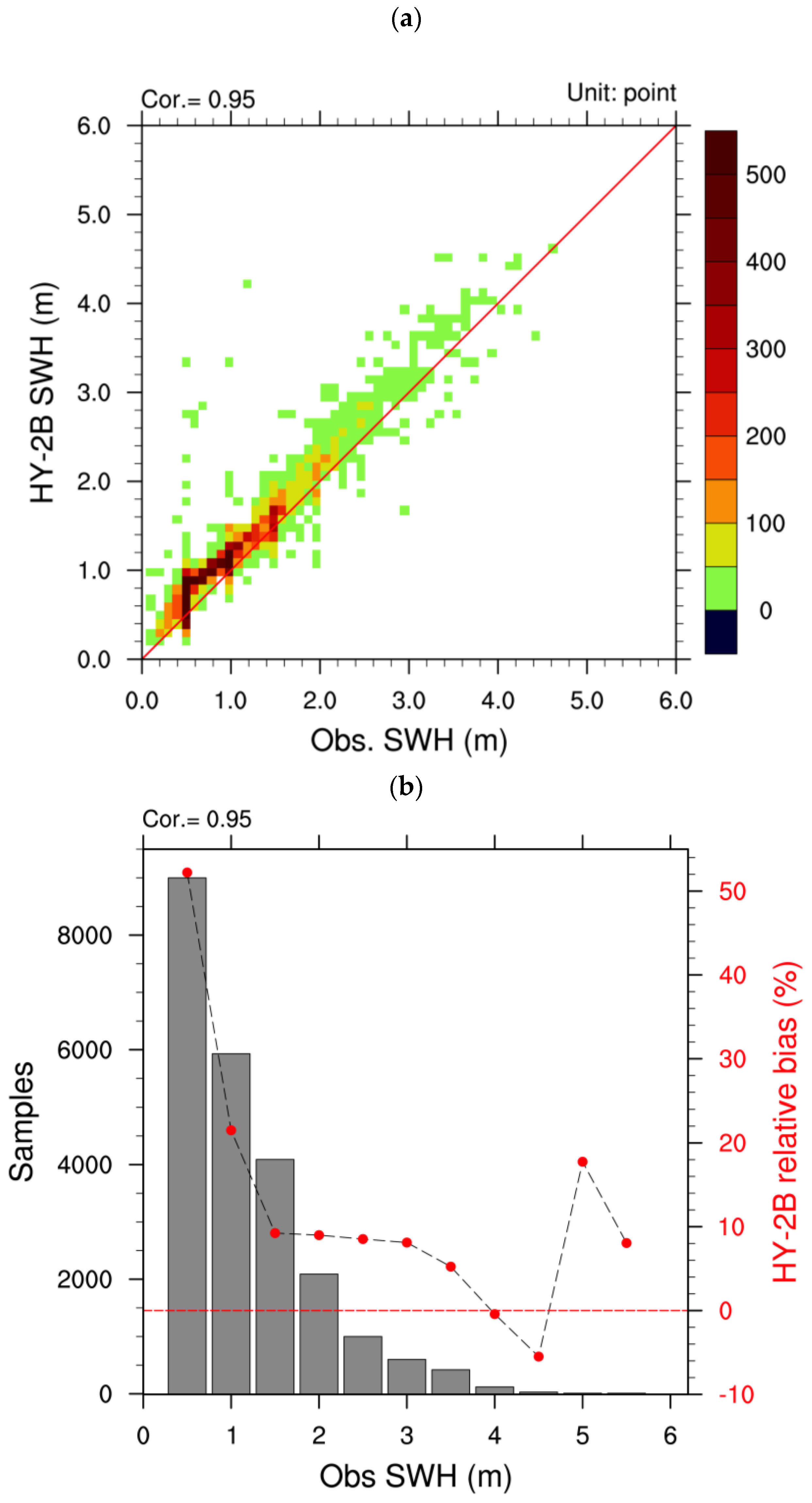
3.2. Evaluation of HY−2B Performance with In Situ SWH
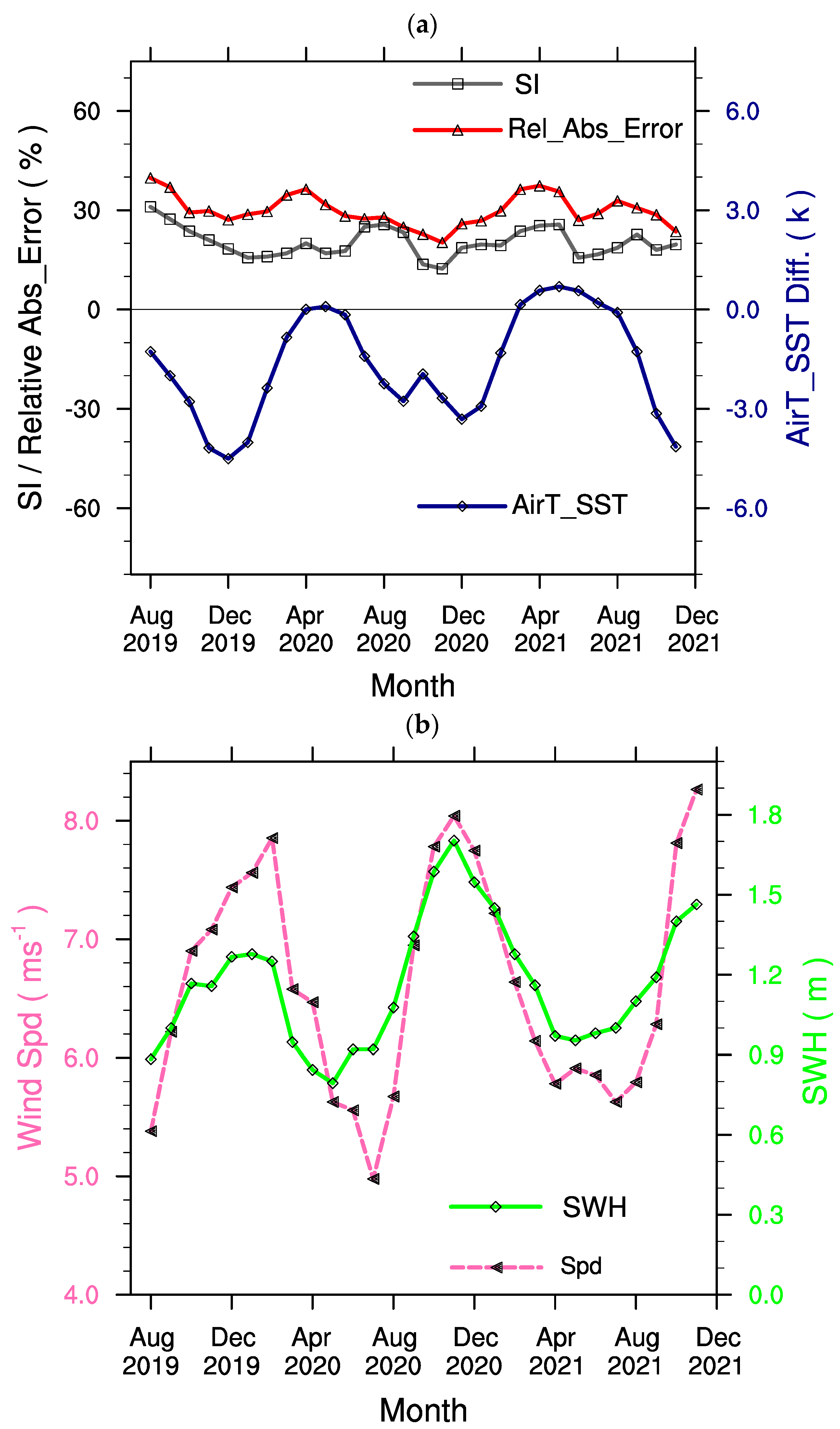
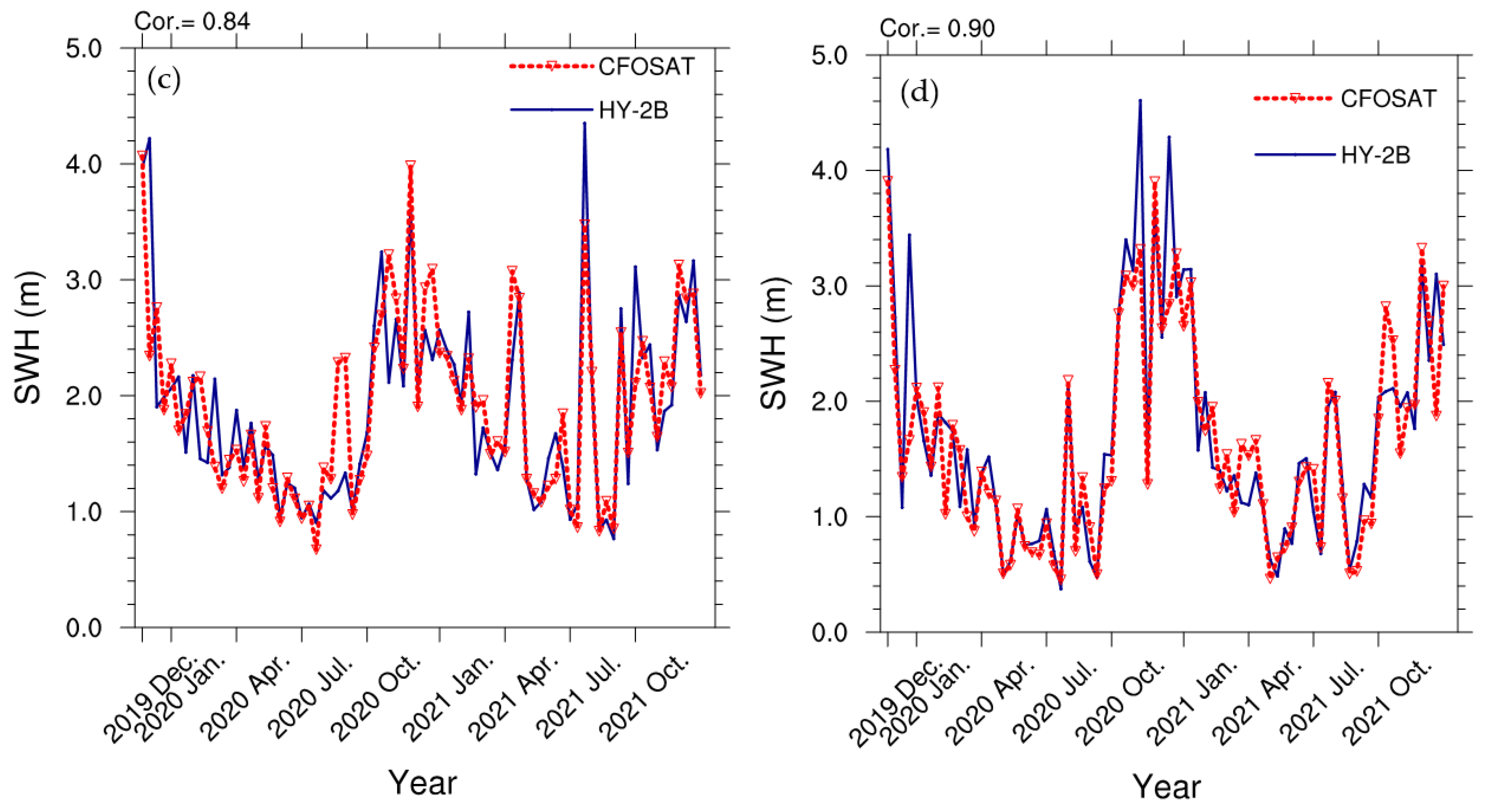
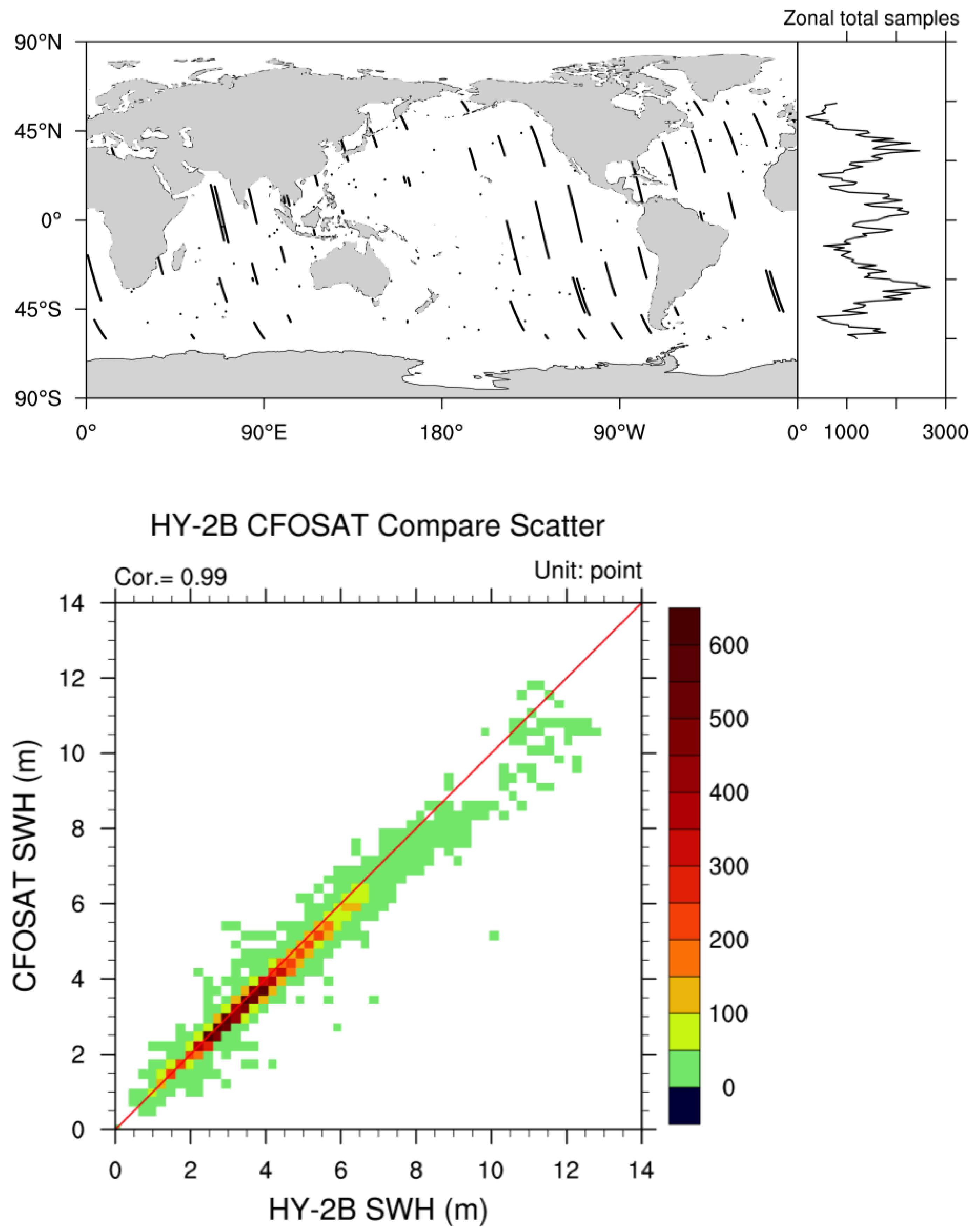
3.3. Comparison of CFOSAT and HY−2B SWHs Variation
4. Conclusions
- (1)
- On the basis of 23 in situ buoy observations in China’s offshore waters, CFOSAT tends to overestimate the SWH in the range of <2 m, especially in the range of <1.25 m, where the relative bias is about 20–40%. The highest point of accuracy is observed for the SWH in the range of around 4–4.5 m. The SI and RMSE of the CFOSAT nadir SWH are 20% and 0.29 m, respectively. The RAE shows an obvious seasonal cycle, varying in a narrow range near 35%. A linear−correction equation can be used to correct the CFOSAT SWHs in China’s offshore waters. The sea condition plays a crucial role in the RAE seasonal cycle, which is influenced by the sea−surface wind speed and air–sea temperature inversion. Both are controlled by seasonal mean flow.
- (2)
- Weighting the spatial coverage and time interval of the final gridded SWHs, a 10−day mean was used for interpolating CFOSAT and HY−2B swath SWHs into grid boxes. A comparison of the corrected CFOSAT grid−box SWH against that of HY−2B showed that the spatial distribution of SWH agreed well with that from HY−2B in the four seasons, with a field correlation coefficient exceeding 0.98 for two years of mean SWHs. In winter, when the SWH is greater, the field correlation coefficient is 0.97, as compared to spring, when the field correlation coefficient is 0.92.
- (3)
- Among four selected sea areas, the field mean SWH variance of CFOSAT and HY−2B showed a close relationship. Moreover, the correlation coefficient of the field mean SWH variance from CFOSAT and HY−2B increased with the mean SWH magnitude. Compared with HY−2B, more extremely high CFOSAT SWHs occurred in the Huanghai seawater area.
- (4)
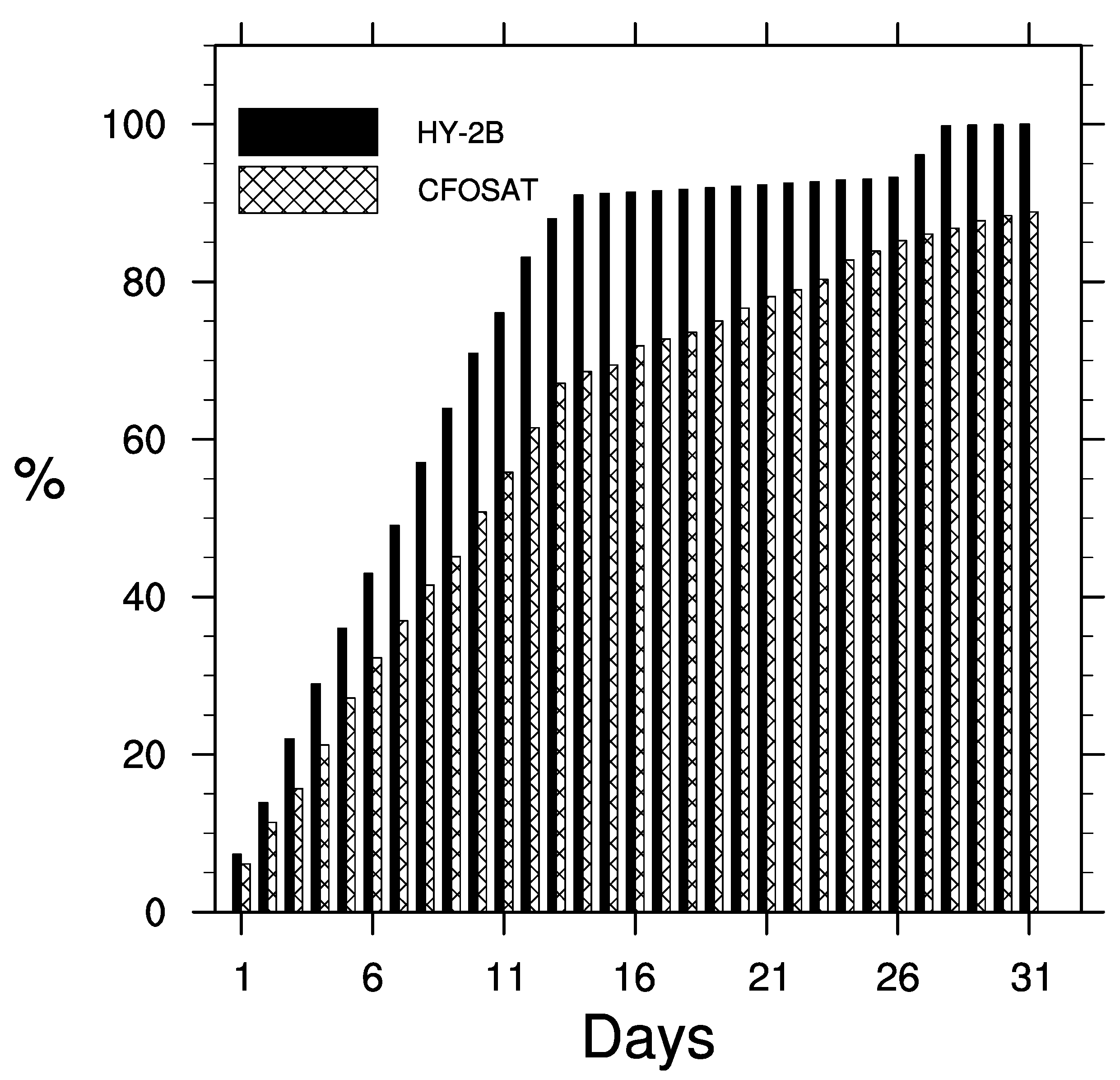
- For a broader coverage of HY−2B than CFOSAT, 24,896 matched SWHs from 30 buoys were found in almost the entire region of China’s offshore waters. The validation results indicated that, normally, the HY−2B SWH is higher than observed, with an RMSE of 0.34, which is greater than that of CFOSAT. The SWH of both CFOSAT and HY−2B shared a close relationship with the observed data, in which the HY−2B SWH showed a greater overestimation than CFOSAT in the SWH range of <1.25 m. Scatter−point density plots of CFOSAT and HY−2B SWHs versus buoy data suggest that linear correlation equations can be applied as a preliminary step to correct the SWHs of both satellites.
- (5)
- The matched points from the intercomparison of CFOSAT and HY−2B SWHs were distributed evenly over the latitudes. These SWHs from CFOSAT were consistent with those from HY−2B in all SWH ranges. In calm sea conditions (SWH < 1.25 m), both CFOSAT and HY−2B tend to overestimate the SWH.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xu, J.; Koldunov, N.; Remedio, A.R.C.; Sein, D.V.; Zhi, X.; Jiang, X.; Xu, M.; Zhu, X.; Fraedrich, K.; Jacob, D.J.C.d. On the role of horizontal resolution over the Tibetan Plateau in the REMO regional climate model. Clim. Dyn. 2019, 51, 4525–4542. [Google Scholar] [CrossRef]
- Xu, J.; Koldunov, N.V.; Remedio, A.R.C.; Sein, D.V.; Rechid, D.; Zhi, X.; Jiang, X.; Xu, M.; Zhu, X.; Fraedrich, K.; et al. Downstream effect of Hengduan Mountains on East China in the REMO regional climate model. Theor. Appl. Climatol. 2018, 135, 1641–1658. [Google Scholar] [CrossRef]
- Timmermans, B.W.; Gommenginger, C.P.; Dodet, G.; Bidlot, J.R. Global Wave Height Trends and Variability from New Multimission Satellite Altimeter Products, Reanalyses, and Wave Buoys. Geophys. Res. Lett. 2020, 47, 9. [Google Scholar] [CrossRef]
- Dobson, E.; Monaldo, F.; Goldhirsh, J.; Wilkerson, J. Validation of Geosat altimeter-derived wind speeds and significant wave heights using buoy data. J. Geophys. Res. Ocean. 1987, 92, 10719–10731. [Google Scholar] [CrossRef]
- Kettle, A.J. A diagram of wind speed versus air-sea temperature difference to understand the marine atmospheric boundary layer. Energy Procedia 2015, 76, 138–147. [Google Scholar] [CrossRef]
- Sun, M.; Du, J.; Yang, Y.; Yin, X. Evaluation of Assimilation in the MASNUM Wave Model Based on Jason-3 and CFOSAT. Remote Sens. 2021, 13, 3833. [Google Scholar] [CrossRef]
- Zhi, X.; Pan, M.; Song, B.; Wang, J. Investigating air-sea interactions in the North Pacific on interannual timescales during boreal winter. Atmos. Res. 2022, 269, 106043. [Google Scholar] [CrossRef]
- Durrant, T.H.; Greenslade, D.J.; Simmonds, I. Validation of Jason-1 and Envisat remotely sensed wave heights. J. Atmos. Ocean. Technol. 2009, 26, 123–134. [Google Scholar] [CrossRef]
- Koldunov, N.V.; Danilov, S.; Sidorenko, D.; Hutter, N.; Losch, M.; Goessling, H.; Rakowsky, N.; Scholz, P.; Sein, D.; Wang, Q. Fast EVP solutions in a high-resolution sea ice model. J. Adv. Model. Earth Syst. 2019, 11, 1269–1284. [Google Scholar] [CrossRef]
- Toledano, C.; Ghantous, M.; Lorente, P.; Dalphinet, A.; Aouf, L.; Sotillo, M.G. Impacts of an Altimetric Wave Data Assimilation Scheme and Currents-Wave Coupling in an Operational Wave System: The New Copernicus Marine IBI Wave Forecast Service. J. Mar. Sci. Eng. 2022, 10, 457. [Google Scholar] [CrossRef]
- Shao, W.; Jiang, T.; Zhang, Y.; Shi, J.; Wang, W. Cyclonic Wave Simulations Based on WAVEWATCH-III Using a Sea Surface Drag Coefficient Derived from CFOSAT SWIM Data. Atmosphere 2021, 12, 1610. [Google Scholar] [CrossRef]
- Donlon, C.; Berruti, B.; Buongiorno, A.; Ferreira, M.-H.; Féménias, P.; Frerick, J.; Goryl, P.; Klein, U.; Laur, H.; Mavrocordatos, C. The global monitoring for environment and security (GMES) sentinel-3 mission. Remote Sens. Environ. 2012, 120, 37–57. [Google Scholar] [CrossRef]
- Ribal, A.; Young, I.R. 33 years of globally calibrated wave height and wind speed data based on altimeter observations. Sci. Data 2019, 6, 77. [Google Scholar] [CrossRef]
- Jin, S.; Yang, S.; Yan, Q.; Jia, Y. Significant wave height estimation from CYGNSS delay-doppler map average observations. In Proceedings of the 2022 Photonics & Electromagnetics Research Symposium (PIERS), Hangzhou, China, 25–29 April 2022. [Google Scholar]
- Ren, L.; Yang, J.; Xiao, Q.; Zheng, G.; Wang, J. On CFOSAT swim wave spectrometer retrieval of ocean waves. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017. [Google Scholar]
- Xiang, K.; Yin, X.; Xing, S.; Kong, F.; Li, Y.; Lang, S.; Gao, Z. Preliminary Estimate of CFOSAT Satellite Products in Tropical Cyclones. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Aouf, L.; Dalphinet, A.; Hauser, D.; Delaye, L.; Tison, C.; Chapron, B.; Hermozo, L.; Tourain, C. On the Assimilation of CFOSAT Wave Data in the Wave Model MFWAM: Verification Phase. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Hauser, D.; Tourain, C.L.; Hermozo, L.; Alraddawi, D.; Aouf, L.; Chapron, B.; Dalphinet, A.; Delaye, L.; Dalila, M.; Dormy, E.; et al. New Observations from the SWIM Radar On-Board CFOSAT: Instrument Validation and Ocean Wave Measurement Assessment. IEEE Trans. Geosci. Remote Sens. 2020, 59, 5–26. [Google Scholar] [CrossRef]
- Liu, J.; Lin, W.; Dong, X.; Lang, S.; Yun, R.; Zhu, D.; Zhang, K.; Sun, C.; Mu, B.; Ma, J.; et al. First Results from the Rotating Fan Beam Scatterometer Onboard CFOSAT. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8793–8806. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.; Xie, L.; Sun, C.; Liu, J.; Li, J.; Xian, D. China-France Oceanography Satellite (CFOSAT) simultaneously observes the typhoon-induced wind and wave fields. Acta Oceanol. Sin. 2019, 38, 158–161. [Google Scholar] [CrossRef]
- Tang, S.; Chu, X.; Jia, Y.; Li, J.; Liu, Y.; Chen, Q.; Li, B.; Liu, J.; Chen, W. An Appraisal of CFOSAT Wave Spectrometer Products in the South China Sea. Earth Space Sci. 2022, 9. [Google Scholar] [CrossRef]
- Wang, J.K.; Aouf, L.; Dalphinet, A.; Zhang, Y.; Xu, Y.; Hauser, D.; Liu, J.Q. The Wide Swath Significant Wave Height: An Innovative Reconstruction of Significant Wave Heights from CFOSAT’s SWIM and Scatterometer Using Deep Learning. Geophys. Res. Lett. 2021, 6, 48. [Google Scholar] [CrossRef]
- Ren, L.; Yang, J.; Xu, Y.; Zhang, Y.; Zheng, G.; Wang, J.; Dai, J.; Jiang, C.L. Ocean Surface Wind Speed Dependence and Retrieval from Off-Nadir CFOSAT SWIM Data. Earth Space Sci. 2021, 8. [Google Scholar] [CrossRef]
- Freilich, M.H.; Dunbar, R.S. The accuracy of the NSCAT 1 vector winds: Comparisons with National Data Buoy Center buoys. J. Geophys. Res. 1999, 104, 11231–11246. [Google Scholar] [CrossRef]
- Meindl, E.A.; Hamilton, G.D. Programs of the National Data Buoy Center. Bull. Am. Meteorol. Soc. 1992, 73, 985–993. [Google Scholar] [CrossRef]
- Hamilton, G.D. National Data Buoy Center Programs. Bull. Am. Meteorol. Soc. 1986, 67, 411–415. [Google Scholar] [CrossRef]
- Teng, C.-c.; Cucullu, S.; McArthur, S.; Kohler, C.; Burnett, B.; Bernard, L. Buoy vandalism experienced by NOAA National Data Buoy Center. OCEANS 2009, 2009, 1–8. [Google Scholar]
- Hall, C.; Jensen, R.E. Utilizing Data from the NOAA National Data Buoy Center; Coastal and Hydraulics Laboratory: Vicksburg, MS, USA, 2021. [Google Scholar]
- Liang, G.; Yang, J.; Wang, J. Accuracy Evaluation of CFOSAT SWIM L2 Products Based on NDBC Buoy and Jason-3 Altimeter Data. Remote Sens. 2021, 13, 887. [Google Scholar] [CrossRef]
- Li, B.; Li, J.; Liu, J.; Tang, S.; Chen, W.; Shi, P.; Liu, Y. Calibration Experiments of CFOSAT Wavelength in the Southern South China Sea by Artificial Neural Networks. Remote Sens. 2022, 14, 773. [Google Scholar] [CrossRef]
- Li, X.; Xu, Y.; Liu, B.; Lin, W.; He, Y.; Liu, J. Validation and Calibration of Nadir SWH Products from CFOSAT and HY-2B With Satellites and In Situ Observations. J. Geophys. Res. Ocean. 2021, 126, e2020JC016689. [Google Scholar] [CrossRef]
- Quartly, G.D.; Chen, G.; Nencioli, F.; Morrow, R.; Picot, N. An Overview of Requirements, Procedures and Current Advances in the Calibration/Validation of Radar Altimeters. Remote Sens. 2021, 13, 125. [Google Scholar] [CrossRef]
- Zou, J.; Lin, M.; Zou, B.; Guo, M.; Cui, S. Fusion of sea surface wind vector data acquired by multi-source active and passive sensors in China sea. Int. J. Remote Sens. 2017, 38, 6477–6491. [Google Scholar] [CrossRef]
- Jia, Y.; Yang, J.; Lin, M.; Zhang, Y.; Ma, C.; Fan, C. Global assessments of the HY-2B measurements and cross-calibrations with Jason-3. Remote Sens. 2020, 12, 2470. [Google Scholar] [CrossRef]
- Dodet, G.; Piolle, J.-F.; Quilfen, Y.; Abdalla, S.; Accensi, M.; Ardhuin, F.; Ash, E.; Bidlot, J.-R.; Gommenginger, C.; Marechal, G. The Sea State CCI dataset v1: Towards a sea state climate data record based on satellite observations. Earth Syst. Sci. Data 2020, 12, 1929–1951. [Google Scholar] [CrossRef]
- Young, I.R.; Vinoth, J.; Zieger, S. Joint Calibration of Multiplatform Altimeter Measurements of Wind Speed and Wave Height over the Past 20 Years. J. Atmos. Ocean. Technol. 2009, 26, 2549–2564. [Google Scholar] [CrossRef]
- Xu, Y.; Hauser, D.; Liu, J.; Si, J.; Yan, C.; Chen, S.; Meng, J.; Fan, C.; Liu, M.; Chen, P. Statistical Comparison of Ocean Wave Directional Spectra Derived From SWIM/CFOSAT Satellite Observations and From Buoy Observations. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–20. [Google Scholar] [CrossRef]
- Jiang, H.; Mironov, A.; Ren, L.; Babanin, A.V.; Wang, J.; Mu, L. Validation of Wave Spectral Partitions from SWIM Instrument On-Board CFOSAT Against In Situ Data. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–13. [Google Scholar] [CrossRef]
- Hauser, D.; Tison, C.; Amiot, T.; Delaye, L.; Corcoral, N.; Castillan, P. SWIM: The First Spaceborne Wave Scatterometer. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3000–3014. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J.; Jia, Y.; Fan, C.; Cui, W. Validation of Sentinel-3A/3B and Jason-3 Altimeter Wind Speeds and Significant Wave Heights Using Buoy and ASCAT Data. Remote Sens. 2020, 12, 2079. [Google Scholar] [CrossRef]
- Tran, N.; Vandemark, D.; Zaron, E.D.; Thibaut, P.; Dibarboure, G.; Picot, N. Assessing the effects of sea-state related errors on the precision of high-rate Jason-3 altimeter sea level data. Adv. Space Res. 2021, 68, 963–977. [Google Scholar] [CrossRef]
- Han, L.; Ji, Q.; Jia, X.; Liu, Y.; Han, G.; Lin, X. Significant Wave Height Prediction in the South China Sea Based on the ConvLSTM Algorithm. J. Mar. Sci. Eng. 2022, 10, 1683. [Google Scholar] [CrossRef]
- Zhang, K.; Dong, X.; Zhu, D.; Yun, R. Estimation and Correction of Geolocation Errors of the CFOSAT Scatterometer Using Coastline Backscatter Coefficients. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 53–61. [Google Scholar] [CrossRef]
- Tourain, C.; Piras, F.; Ollivier, A.; Hauser, D.; Poisson, J.C.; Boy, F.; Thibaut, P.; Hermozo, L.; Tison, C. Benefits of the Adaptive Algorithm for Retracking Altimeter Nadir Echoes: Results from Simulations and CFOSAT/SWIM Observations. IEEE Trans. Geosci. Remote Sens. 2021, 59, 9927–9940. [Google Scholar] [CrossRef]
- Wang, J.; Aouf, L.; Jia, Y.; Zhang, Y. Validation and Calibration of Significant Wave Height and Wind Speed Retrievals from HY2B Altimeter Based on Deep Learning. Remote Sens. 2020, 12, 2858. [Google Scholar] [CrossRef]
- Xu, X.-Y.; Xu, K.; Shen, H.; Liu, Y.-L.; Liu, H.-G. Sea Surface Height and Significant Wave Height Calibration Methodology by a GNSS Buoy Campaign for HY-2A Altimeter. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 5252–5261. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, J. Validation of Sentinel-3A/3B satellite altimetry wave heights with buoy and Jason-3 data. Sensors 2019, 19, 2914. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Chen, Y.; Wang, F. Temperature inversion in China seas. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Shi, Q.; Bourassa, M.A. Coupling Ocean Currents and Waves with Wind Stress over the Gulf Stream. Remote Sens. 2019, 11, 1476. [Google Scholar] [CrossRef]
- Ye, X.; Lin, M.; Xu, Y. Validation of Chinese HY-2 satellite radar altimeter significant wave height. Acta Oceanol. Sin. 2015, 34, 60–67. [Google Scholar] [CrossRef]
- Yun, R.; Dong, X.; Liu, J.; Lin, W.; Zhu, D.; Ma, J.; Lang, S.; Wang, Z. CFOSAT Rotating Fan-Beam Scatterometer Backscatter Measurement Processing. Earth Space Sci. 2021, 8, 11. [Google Scholar] [CrossRef]
- Cressman, G.P. An Operational Objective Analysis System. Mon. Weather. Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Ram, K.R.; Narayan, S.; Ahmed, M.R.; Nakavulevu, P.; Lee, Y.-H. In situ near-shore wave resource assessment in the Fiji Islands. Energy Sustain. Dev. 2014, 23, 170–178. [Google Scholar] [CrossRef]
- Befus, K.M.; Cardenas, M.B.; Erler, D.V.; Santos, I.R.; Eyre, B.D. Heat transport dynamics at a sandy intertidal zone. Water Resour. Res. 2013, 49, 3770–3786. [Google Scholar] [CrossRef]
- Li, Y.; Chen, W.; Cai, H.; Sun, Z.; Xu, K. Spatio-temporal variation of benthic diatom diversity and community structure in a sandy intertidal zone of the Nanji Islands, China. Biodivers. Sci. 2017, 25, 981–989. [Google Scholar] [CrossRef] [Green Version]
- Choi, T.-J.; Choi, J.-Y.; Park, J.-Y.; Um, H.-Y.; Choi, J.-H. The Effects of Nourishments Using the Grain-Size Trend Analysis on the Intertidal Zone at a Sandy Macrotidal Beach. J. Coast. Res. 2016, 85, 426–430. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Makin, V. Impact of Swell on the Marine Atmospheric Boundary Layer. J. Phys. Oceanogr. 2004, 34, 934–949. [Google Scholar] [CrossRef]
- Mitsuyasu, H.; Maeda, Y. On the contribution of swell to sea surface phenomena. Int. J. Offshore Polar Eng. 1997, 12, 237–242. [Google Scholar]
- Wu, L.; Rutgersson, A.; Sahlée, E.; Larsén, X.G. Swell impact on wind stress and atmospheric mixing in a regional coupled atmosphere-wave model. J. Geophys. Res. 2016, 121, 4633–4648. [Google Scholar] [CrossRef]
- Mahmoodi, K.; Ghassemi, H.; Razminia, A. Temporal and spatial characteristics of wave energy in the Persian Gulf based on the ERA5 reanalysis dataset. Energy 2019, 15, 187. [Google Scholar] [CrossRef]


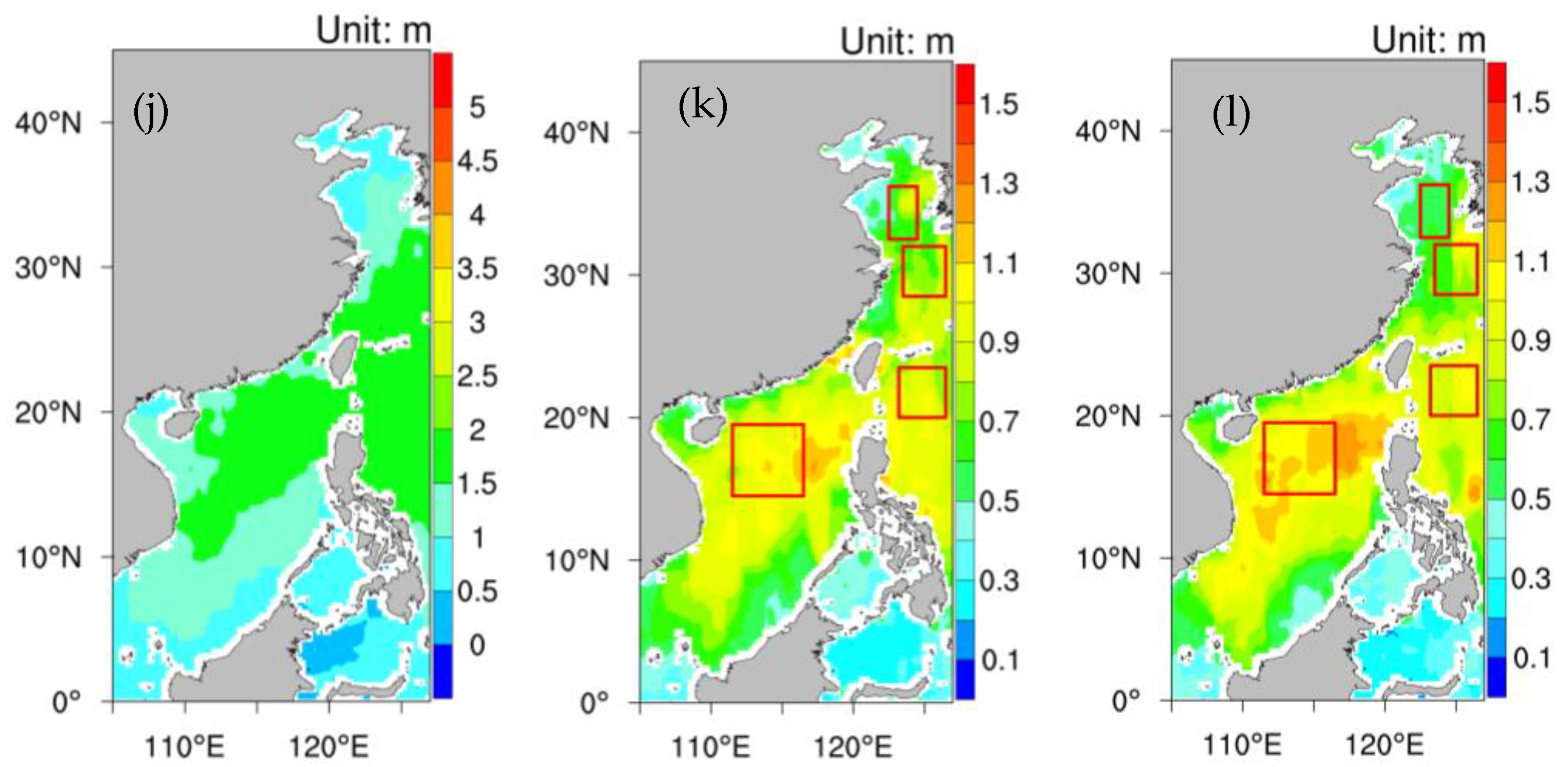

| Field Mean SWH (m) | DJF | MAM | JJA | SON | Annual | Correct Equation |
|---|---|---|---|---|---|---|
| HY−2B | 1.8 | 0.9 | 0.9 | 1.3 | 1.2 | y = 0.93x − 0.13 |
| CFOSAT | 1.8 | 1.0 | 0.9 | 1.3 | 1.2 | y = 0.97x − 0.17 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Wu, H.; Xu, Y.; Koldunov, N.V.; Zhang, X.; Kong, L.; Xu, M.; Fraedrich, K.; Zhi, X. Validation of Nadir SWH and Its Variance Characteristics from CFOSAT in China’s Offshore Waters. Remote Sens. 2023, 15, 1005. https://doi.org/10.3390/rs15041005
Xu J, Wu H, Xu Y, Koldunov NV, Zhang X, Kong L, Xu M, Fraedrich K, Zhi X. Validation of Nadir SWH and Its Variance Characteristics from CFOSAT in China’s Offshore Waters. Remote Sensing. 2023; 15(4):1005. https://doi.org/10.3390/rs15041005
Chicago/Turabian StyleXu, Jingwei, Huanping Wu, Ying Xu, Nikolay V. Koldunov, Xiuzhi Zhang, Lisha Kong, Min Xu, Klaus Fraedrich, and Xiefei Zhi. 2023. "Validation of Nadir SWH and Its Variance Characteristics from CFOSAT in China’s Offshore Waters" Remote Sensing 15, no. 4: 1005. https://doi.org/10.3390/rs15041005
APA StyleXu, J., Wu, H., Xu, Y., Koldunov, N. V., Zhang, X., Kong, L., Xu, M., Fraedrich, K., & Zhi, X. (2023). Validation of Nadir SWH and Its Variance Characteristics from CFOSAT in China’s Offshore Waters. Remote Sensing, 15(4), 1005. https://doi.org/10.3390/rs15041005






