An Ensemble Approach of Feature Selection and Machine Learning Models for Regional Landslide Susceptibility Mapping in the Arid Mountainous Terrain of Southern Peru
Abstract
:1. Introduction
2. Materials and Methods
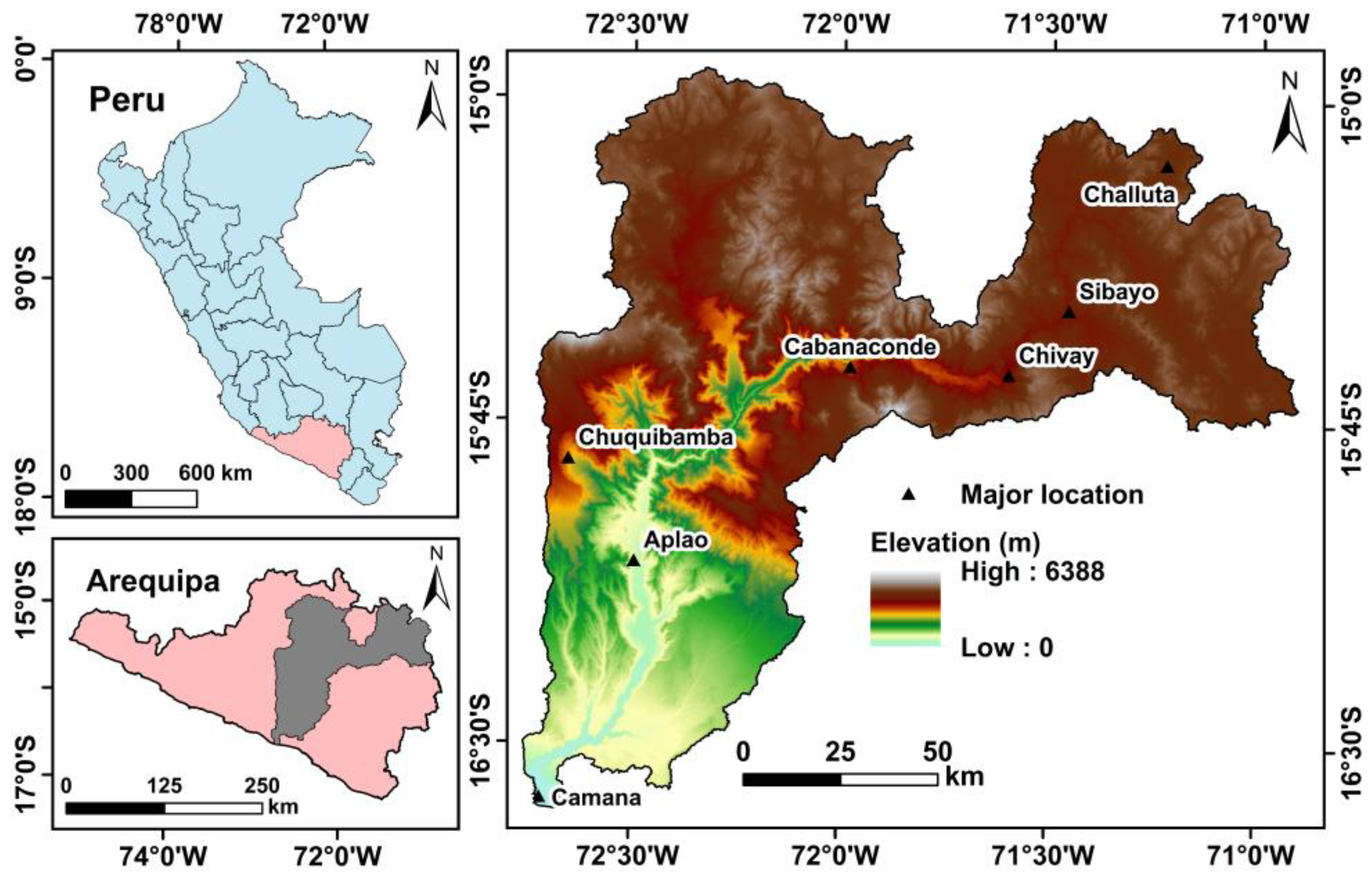
2.1. Study Area
2.2. Datasets
2.3. Methods
2.3.1. Landslide Inventory and Training Data Preparation
2.3.2. Preparation of Landslide Influencing Factors (LIFs)
- The slope is a measure of the steepness of topography, where the driving force of material increases with the slope angle. The slope angle also controls the subsurface flow, which impacts the moisture content and is therefore directly related to the occurrence of landslides [58]. Aspect can impact slope stability as it influences the wind direction, solar radiation, evapotranspiration, surface moisture, and vegetation cover [34,59].
- Curvature quantifies the terrain’s complexity and morphology. Plan curvature influences runoff acceleration and the erosion rate, whereas profile curvature affects the runoff velocity direction [60].
- The surface area ratio is a measure of the landscape’s topographic roughness: it is the ratio of surface area to its planimetric area [61]. A value close to 1 indicates a smoother surface, whereas values greater than 1 correspond to a rough surface [62]. The relief ratio is the ratio of basin relief and basin length, which represents the overall steepness of a basin [63]. The relief ratio plays a significant role in several geomorphic processes, such as drainage development, erosion on the slope, surface and subsurface water flow, moisture content, and landform development [64].
- Flow accumulation is derived from flow direction. It is computed by a cumulative count of other pixels that flow through that pixel. Regions of higher accumulation values are most likely to experience landslides, as they tend to concentrate a high volume of rainfall water [16,65]. Stream density refers to the total stream length per unit area. It indicates the closeness of the spacing of streams, which controls the landscape dissection and runoff [63]. High stream density usually occurs in impermeable areas, high relief, and barren surfaces, while low stream density is mostly associated with highly permeable surfaces, low relief, and densely vegetated surfaces [66]. Low drainage density develops a coarser drainage texture and implies low runoff and high infiltration, whereas high drainage density leads to the formation of fine drainage texture, higher runoff, and low infiltration [67].
- TWI represents the flow accumulation and slope of the area and typically corresponds to the water saturation zone [70]. Lower and higher values of TWI are typically associated with steep and flat or valley regions, respectively [71]. TRI describes surface heterogeneity as concave upward and convex slopes [72], whereas TPI computes the difference between the elevation of each pixel and its neighbors within a specified radius [73]. TPI can also be used to define geomorphic landforms as ridges (positive TPI), valleys (negative TPI), and flat areas (~0).
- Incoming solar radiation has been rarely used in LSM but it plays a significant role in a variety of physical processes that occur on the Earth’s surface, and therefore could be relevant to slope stability [74,75], particularly when considering a large spatial extent. Direct radiation represents the direct incoming solar radiation and direct duration radiation represents the duration of direct incoming solar radiation for each location. These were computed using the area solar radiation tool of the spatial analyst with default settings in ArcMap 10.8.
- The normalized difference vegetation index (NDVI) indicates vegetation coverage, which plays a significant role in decreasing the surface runoff and increasing the shear resistance of soil and rock types [76]. The roots of vegetation improve the stability of slope regions [77]. The NDVI was derived using near-infrared and red spectral bands of Landsat 8 reflectance data.
- Geology, hydrogeology, and geomorphology are commonly considered in most LSM as different rock types and landforms vary in their physical and mechanical properties, such as overlying soil strength, the intensity of weathering, porosity, and permeability, and therefore have a significant impact on slope stability [78,79].
- Geo-environmental LIFs such as geology, hydrogeology, geomorphology, LULC, 10 years annual average rainfall, soil type, distance from roads, distance from faults, distance from streams, distance from epicenters, and earthquake magnitude density were prepared in a GIS environment. The LIFs were resampled to 30 m using the nearest neighbor resampling method in a GIS environment to match the pixel size of remotely sensed data. Table 1 presents different data sources used in deriving the LIFs. Figure 5 displays six important LIFs derived in this study. The remaining LIFs are presented in the Supplementary Data (Figure S1).
2.3.3. Multicollinearity and Feature Selection (FS)
VIFs, Tolerance, and Pearson Correlation
Feature Selection Methods
2.3.4. Frequency Ratio (FR)
2.3.5. ML Methods
LDA
MDA
BC
BLR
KNN
ANN
SVM
RF
RTF
C5.0
Ensemble ML
2.3.6. Performance Measures
3. Results
3.1. Optimal Selection of LIFs
3.2. Spatial Relationship between Landslides and LIFs
3.3. Performance Evaluation of ML Models
3.4. Performance Evaluation of Ensemble ML Models
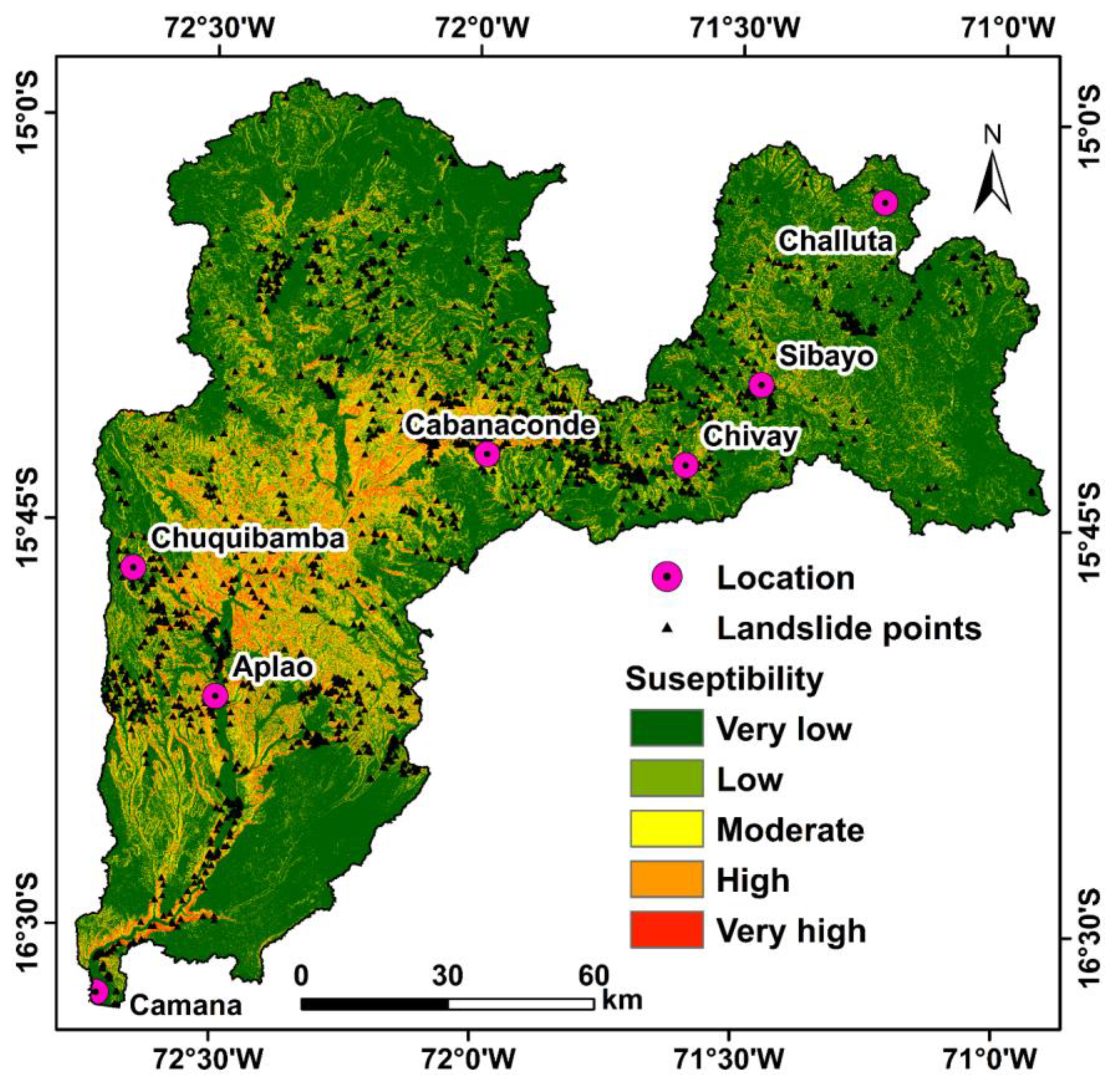
3.5. Landslide Susceptibility Mapping
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial neural networks |
| ASTER | Advanced Spaceborne Thermal Emission and Reflection Radiometer |
| AUC | Area under curve |
| BC | Bagged cart |
| BLR | Boosted logistic regression |
| DDR | Direct duration radiation |
| DEM | Digital elevation model |
| DTs | Decision trees |
| EFS | Ensemble feature selection |
| ESRI | Environmental Systems Research Institute |
| FN | False negative |
| FP | False positive |
| FR | Frequency ratio |
| FS | Feature selection |
| GIS | Geographic Information System |
| GPM | Global precipitation measurement |
| GR | Gain ratio |
| IDW | Inverse distance weighted |
| IG | Information gain |
| KNN | K-nearest neighbor |
| LDA | Linear discriminant analysis |
| LIFs | Landslide influencing factors |
| LSM | Landslide susceptibility mapping/modeling |
| LULC | Land use/landcover |
| MDA | Mixture discriminant analysis |
| NDVI | Normalized difference vegetation index |
| OA | Overall accuracy |
| PCA | Principal component analysis |
| RF | Random forest |
| RF | Relief-F |
| RI | Relative importance |
| ROC | Receiver operating characteristic |
| RTF | Rotation forest |
| SA | Simple averaging |
| SPI | Stream power index |
| STI | Sediment transportation index |
| SVM | Support vector machine |
| TN | True negative |
| TOL | Tolerance statistics |
| TP | True positive |
| TPI | Topographical position index |
| TRI | Topographical ruggedness index |
| TWI | Topographical wetness index |
| UNSA | Universidad Nacional de San Agustín |
| USGS | United States Geological Survey |
| VIF | Variance inflation factor |
References
- Cruden, D.M.; Novograd, S.; Pilot, G.A.; Krauter, E.; Bhandari, R.K.; Cotecchia, V.; Nakamura, H.; Okagbue, C.O.; Zhuoyuan, Z.; Hutchinson, J.N.; et al. Suggested nomenclature for landslides. Bull. Int. Assoc. Eng. Geol. 1990, 41, 13–16. [Google Scholar]
- Lin, L.; Lin, Q.; Wang, Y. Landslide susceptibility mapping on a global scale using the method of logistic regression. Nat. Hazards Earth Syst. Sci. 2017, 17, 1411–1424. [Google Scholar] [CrossRef] [Green Version]
- Highland, L.; Bobrowsky, P.T. The Landslide Handbook: A Guide to Understanding Landslides; US Geological Survey: Reston, VA, USA, 2008. [Google Scholar]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Guzzetti, F. Landslide Hazard and Risk Assessment; Rheinische Friedrich-Wilhelms-Universität Bonn: Perugia, Italy, 2006. [Google Scholar]
- Chae, B.-G.; Park, H.-J.; Catani, F.; Simoni, A.; Berti, M. Landslide prediction, monitoring and early warning: A concise review of state-of-the-art. Geosci. J. 2017, 21, 1033–1070. [Google Scholar] [CrossRef]
- Sarkar, S.; Kanungo, D. An integrated approach for landslide susceptibility mapping using remote sensing and GIS. Photo-Gramm. Eng. Remote Sens. 2004, 70, 617–625. [Google Scholar] [CrossRef]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- Pradhan, B. A comparative study on the predictive ability of the decision tree, support vector machine and neuro-fuzzy models in landslide susceptibility mapping using GIS. Comput. Geosci. 2013, 51, 350–365. [Google Scholar] [CrossRef]
- Korup, O.; Stolle, A. Landslide prediction from machine learning. Geol. Today 2014, 30, 26–33. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative study of landslide susceptibility mapping with different recurrent neural networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Ji, J.; Cui, H.; Zhang, T.; Song, J.; Gao, Y. A GIS-based tool for probabilistic physical modelling and prediction of landslides: GIS-FORM landslide susceptibility analysis in seismic areas. Landslides 2022, 19, 2213–2231. [Google Scholar] [CrossRef]
- Kundu, J.; Sarkar, K.; Ghaderpour, E.; Mugnozza, G.S.; Mazzanti, P. A GIS-Based Kinematic Analysis for Jointed Rock Slope Stability: An Application to Himalayan Slopes. Land 2023, 12, 402. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; E Gessler, P.; Foltz, R.B.; Elliot, W.J. Spatial Prediction of Landslide Hazard Using Logistic Regression and ROC Analysis. Trans. GIS 2006, 10, 395–415. [Google Scholar] [CrossRef]
- Hong, Y.; Adler, R.; Huffman, G. Use of satellite remote sensing data in the mapping of global landslide susceptibility. Nat. Hazards 2007, 43, 245–256. [Google Scholar] [CrossRef] [Green Version]
- Catani, F.; Lagomarsino, D.; Segoni, S.; Tofani, V. Landslide susceptibility estimation by random forests technique: Sensitivity and scaling issues. Nat. Hazards Earth Syst. Sci. 2013, 13, 2815–2831. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Fang, Z.; Hong, H. Comparison of convolutional neural networks for landslide susceptibility mapping in Yanshan County, China. Sci. Total Environ. 2019, 666, 975–993. [Google Scholar] [CrossRef]
- Adnan, M.; Rahman, S.; Ahmed, N.; Ahmed, B.; Rabbi, F.; Rahman, R. Improving Spatial Agreement in Machine Learning-Based Landslide Susceptibility Mapping. Remote Sens. 2020, 12, 3347. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M.V. Landslide susceptibility mapping using GIS-based statistical models and Remote sensing data in tropical environment. Sci. Rep. 2015, 5, 9899. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. Catena 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Kalantar, B.; Ueda, N.; Lay, U.S.; Al-Najjar, H.A.H.; Halin, A.A. Conditioning factors determination for landslide susceptibility mapping using support vector machine learning. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Yokohama, Japan, 28 July–2 August 2019. [Google Scholar]
- Lee, S. Current and future status of GIS-based landslide susceptibility mapping: A literature review. Korean J. Remote Sens. 2019, 35, 179–193. [Google Scholar]
- Di Napoli, M.; Carotenuto, F.; Cevasco, A.; Confuorto, P.; Di Martire, D.; Firpo, M.; Pepe, G.; Raso, E.; Calcaterra, D. Machine learning ensemble modelling as a tool to improve landslide susceptibility mapping reliability. Landslides 2020, 17, 1897–1914. [Google Scholar] [CrossRef]
- Sameen, M.I.; Pradhan, B.; Bui, D.T.; Alamri, A.M. Systematic sample subdividing strategy for training landslide susceptibility models. Catena 2019, 187, 104358. [Google Scholar] [CrossRef]
- Lee, S. Application of logistic regression model and its validation for landslide susceptibility mapping using GIS and remote sensing data. Int. J. Remote Sens. 2005, 26, 1477–1491. [Google Scholar] [CrossRef]
- Caniani, D.; Pascale, S.; Sdao, F.; Sole, A. Neural networks and landslide susceptibility: A case study of the urban area of Potenza. Nat. Hazards 2007, 45, 55–72. [Google Scholar] [CrossRef]
- Hong, H.; Liu, J.; Bui, D.T.; Pradhan, B.; Acharya, T.D.; Pham, B.T.; Zhu, A.-X.; Chen, W.; Ahmad, B.B. Landslide susceptibility mapping using J48 Decision Tree with AdaBoost, Bagging and Rotation Forest ensembles in the Guangchang area (China). Catena 2018, 163, 399–413. [Google Scholar] [CrossRef]
- Park, S.J.; Lee, C.-W.; Lee, S.; Lee, M.-J. Landslide Susceptibility Mapping and Comparison Using Decision Tree Models: A Case Study of Jumunjin Area, Korea. Remote Sens. 2018, 10, 1545. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Hamm, S.-Y.; Kim, J. Performance Evaluation of the GIS-Based Data-Mining Techniques Decision Tree, Random Forest, and Rotation Forest for Landslide Susceptibility Modeling. Sustainability 2019, 11, 5659. [Google Scholar] [CrossRef] [Green Version]
- Cervantes, J.; Garcia-Lamont, F.; Rodríguez-Mazahua, L.; Lopez, A. A comprehensive survey on support vector machine classification: Applications, challenges and trends. Neurocomputing 2020, 408, 189–215. [Google Scholar] [CrossRef]
- Guo, Z.; Shi, Y.; Huang, F.; Fan, X.; Huang, J. Landslide susceptibility zonation method based on C5.0 decision tree and K-means cluster algorithms to improve the efficiency of risk management. Geosci. Front. 2021, 12, 101249. [Google Scholar] [CrossRef]
- Tanyu, B.F.; Abbaspour, A.; Alimohammadlou, Y.; Tecuci, G. Landslide susceptibility analyses using Random Forest, C4.5 and C5.0 with balanced and unbalanced datasets. Catena 2021, 203, 105355. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R. Landslide susceptibility mapping using machine learning algorithms and comparison of their performance at Abha Basin, Asir Region, Saudi Arabia. Geosci. Front. 2021, 12, 639–655. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Sadhasivam, N.; Amiri, M.; Eskandari, S.; Santosh, M. Landslide susceptibility assessment and mapping using state-of-the art machine learning techniques. Nat. Hazards 2021, 108, 1291–1316. [Google Scholar] [CrossRef]
- Prakash, N.; Manconi, A.; Loew, S. Mapping Landslides on EO Data: Performance of Deep Learning Models vs. Traditional Machine Learning Models. Remote Sens. 2020, 12, 346. [Google Scholar] [CrossRef] [Green Version]
- Kumar, C.; Chatterjee, S.; Oommen, T.; Guha, A. Automated lithological mapping by integrating spectral enhancement techniques and machine learning algorithms using AVIRIS-NG hyperspectral data in Gold-bearing granite-greenstone rocks in Hutti, India. Int. J. Appl. Earth Obs. Geoinf. 2019, 86, 102006. [Google Scholar] [CrossRef]
- Kumar, C.; Chatterjee, S.; Oommen, T.; Guha, A.; Mukherjee, A. Multi-sensor datasets-based optimal integration of spectral, textural, and morphological characteristics of rocks for lithological classification using machine learning models. Geocarto Int. 2021, 37, 6004–6032. [Google Scholar] [CrossRef]
- Bhatt, P.; Maclean, A.; Dickinson, Y.; Kumar, C. Fine-Scale Mapping of Natural Ecological Communities Using Machine Learning Approaches. Remote Sens. 2022, 14, 563. [Google Scholar] [CrossRef]
- Liu, S.; Wang, L.; Zhang, W.; He, Y.; Pijush, S. A comprehensive review of machine learning-based methods in landslide susceptibility mapping. Geol. J. 2023. [Google Scholar] [CrossRef]
- Mohri, M.; Rostamizadeh, A.; Talwalkar, A. Foundations of Machine Learning; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Bommert, A.; Sun, X.; Bischl, B.; Rahnenführer, J.; Lang, M. Benchmark for filter methods for feature selection in high-dimensional classification data. Comput. Stat. Data Anal. 2019, 143, 106839. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Peng, L.; Hong, H. A comparative study of heterogeneous ensemble-learning techniques for landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2020, 35, 321–347. [Google Scholar] [CrossRef]
- Bolón-Canedo, V.; Alonso-Betanzos, A. Ensembles for feature selection: A review and future trends. Inf. Fusion 2018, 52, 1–12. [Google Scholar] [CrossRef]
- Fang, Z.; Wang, Y.; Duan, G.; Peng, L. Landslide Susceptibility Mapping Using Rotation Forest Ensemble Technique with Different Decision Trees in the Three Gorges Reservoir Area, China. Remote Sens. 2021, 13, 238. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, H.; Mei, H.; Xiao, D.; Li, Y.; Li, M. Landslide Susceptibility Mapping Using the Stacking Ensemble Machine Learning Method in Lushui, Southwest China. Appl. Sci. 2020, 10, 4016. [Google Scholar] [CrossRef]
- Roy, J.; Saha, S.; Arabameri, A.; Blaschke, T.; Bui, D.T. A Novel Ensemble Approach for Landslide Susceptibility Mapping (LSM) in Darjeeling and Kalimpong Districts, West Bengal, India. Remote Sens. 2019, 11, 2866. [Google Scholar] [CrossRef] [Green Version]
- Oza, N.C. Ensemble Data Mining Methods, in Encyclopedia of Data Warehousing and Mining, 2nd ed.; IGI Global: Hershey, PA, USA, 2009; pp. 770–776. [Google Scholar]
- Zhang, C.; Ma, Y. Ensemble Machine Learning: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Tan, A.C.; Gilbert, D. Ensemble Machine Learning on Gene Expression Data for Cancer Classification; The MIT Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Kadavi, P.R.; Lee, C.-W.; Lee, S. Application of ensemble-based machine learning models to landslide susceptibility map-ping. Remote Sens. 2018, 10, 1252. [Google Scholar] [CrossRef] [Green Version]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Sohrabi, M.; Kalantari, Z. GIS-based landslide susceptibility mapping using numerical risk factor bivariate model and its ensemble with linear multivariate regression and boosted regression tree algorithms. J. Mt. Sci. 2019, 16, 595–618. [Google Scholar] [CrossRef]
- Karra, K.; Kontgis, C.; Statman-Weil, Z.; Mazzariello, J.C.; Mathis, M.; Brumby, S.P. Global land use/land cover with Sentinel 2 and deep learning. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- Hengl, T.; De Jesus, J.M.; Heuvelink, G.B.M.; Gonzalez, M.R.; Kilibarda, M.; Blagotić, A.; Shangguan, W.; Wright, M.N.; Geng, X.; Bauer-Marschallinger, B.; et al. SoilGrids250m: Global gridded soil information based on machine learning. PLoS ONE 2017, 12, e0169748. [Google Scholar] [CrossRef] [Green Version]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomat. Nat. Hazards Risk 2017, 9, 49–69. [Google Scholar] [CrossRef]
- Goetz, J.N.; Brenning, A.; Petschko, H.; Leopold, P. Evaluating machine learning and statistical prediction techniques for landslide susceptibility modeling. Comput. Geosci. 2015, 81, 1–11. [Google Scholar] [CrossRef]
- Althuwaynee, O.F.; Pradhan, B.; Lee, S. A novel integrated model for assessing landslide susceptibility mapping using CHAID and AHP pair-wise comparison. Int. J. Remote Sens. 2016, 37, 1190–1209. [Google Scholar] [CrossRef]
- Zhu, A.X.; Miao, Y.; Wang, R.; Zhu, T.; Deng, Y.; Liu, J.; Yang, L.; Qin, C.Z.; Hong, H. A comparative study of an expert knowledge-based model and two data-driven models for landslide sus-ceptibility mapping. Catena 2018, 166, 317–327. [Google Scholar] [CrossRef]
- Magliulo, P.; Di Lisio, A.; Russo, F.; Zelano, A. Geomorphology and landslide susceptibility assessment using GIS and bivariate statistics: A case study in southern Italy. Nat. Hazards 2008, 47, 411–435. [Google Scholar] [CrossRef]
- Devkota, K.C.; Regmi, A.D.; Pourghasemi, H.R.; Yoshida, K.; Pradhan, B.; Ryu, I.C.; Dhital, M.R.; Althuwaynee, O.F. Landslide susceptibility mapping using certainty factor, index of entropy and logistic regression models in GIS and their comparison at Mugling–Narayanghat road section in Nepal Himalaya. Nat. Hazards 2013, 65, 135–165. [Google Scholar] [CrossRef]
- Oh, H.-J.; Pradhan, B. Application of a neuro-fuzzy model to landslide-susceptibility mapping for shallow landslides in a tropical hilly area. Comput. Geosci. 2011, 37, 1264–1276. [Google Scholar] [CrossRef]
- Jenness, J.S. Calculating landscape surface area from digital elevation models. Wildl. Soc. Bull. 2004, 32, 829–839. [Google Scholar] [CrossRef]
- A Aman, S.N.; Latif, Z.A.; Pradhan, B. Spatial probabilistic approach on landslide susceptibility assessment from high resolution sensors derived parameters. IOP Conf. Ser. Earth Environ. Sci. 2014, 18, 12057. [Google Scholar] [CrossRef] [Green Version]
- Schumm, S.A. Evolution of Drainage Systems and Slopes in Badlands at Perth Amboy, New Jersey. GSA Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Kamala, M.; Samynathan, M. Morphometric Analysis of Drainage Basin Using Gis Techniques a Case Study of Amaravathi River Basin, Tamilnadu. Int. J. Recent Sci. Res. 2018, 9, 28142–28147. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S.; Nonomura, A.; Yamanaka, M.; Masuda, T.; Nishino, K. GIS-based weights-of-evidence modelling of rainfall-induced landslides in small catchments for landslide susceptibility mapping. Environ. Geol. 2007, 54, 311–324. [Google Scholar] [CrossRef]
- Nag, S.; Chakraborty, S. Influence of rock types and structures in the development of drainage network in hard rock area. J. Indian Soc. Remote Sens. 2003, 31, 25–35. [Google Scholar] [CrossRef]
- Strahler, A.N. Part II. Quantitative geomorphology of drainage basins and channel networks. In Handbook of Applied Hydrology; McGraw-Hill: New York, NY, USA, 1964; pp. 4–39. [Google Scholar]
- Chen, C.-Y.; Yu, F.-C. Morphometric analysis of debris flows and their source areas using GIS. Geomorphology 2011, 129, 387–397. [Google Scholar] [CrossRef]
- Moore, I.D.; Wilson, J.P. Length-slope factors for the Revised Universal Soil Loss Equation: Simplified method of estimation. J. Soil Water Conserv. 1992, 47, 423–428. [Google Scholar]
- Regmi, N.R.; Giardino, J.R.; Vitek, J.D. Modeling susceptibility to landslides using the weight of evidence approach: Western Colorado, USA. Geomorphology 2010, 115, 172–187. [Google Scholar] [CrossRef]
- Vorpahl, P.; Elsenbeer, H.; Märker, M.; Schröder, B. How can statistical models help to determine driving factors of landslides? Ecol. Model. 2012, 239, 27–39. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. Index that quantifies topographic heterogeneity. Intermt. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Ali, S.A.; Parvin, F.; Vojteková, J.; Costache, R.; Linh, N.T.T.; Pham, Q.B.; Vojtek, M.; Gigović, L.; Ahmad, A.; Ghorbani, M.A. GIS-based landslide susceptibility modeling: A comparison between fuzzy multi-criteria and machine learning algorithms. Geosci. Front. 2020, 12, 857–876. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Jankowski, P. An optimized solution of multi-criteria evaluation analysis of landslide susceptibility using fuzzy sets and Kalman filter. Comput. Geosci. 2010, 36, 1005–1020. [Google Scholar] [CrossRef]
- Pradhan, B.; Sezer, E.A.; Gokceoglu, C.; Buchroithner, M.F. Landslide Susceptibility Mapping by Neuro-Fuzzy Approach in a Landslide-Prone Area (Cameron Highlands, Malaysia). IEEE Trans. Geosci. Remote Sens. 2010, 48, 4164–4177. [Google Scholar] [CrossRef]
- Nohani, E.; Moharrami, M.; Sharafi, S.; Khosravi, K.; Pradhan, B.; Pham, B.T.; Lee, S.; Melesse, A.M. Landslide Susceptibility Mapping Using Different GIS-Based Bivariate Models. Water 2019, 11, 1402. [Google Scholar] [CrossRef] [Green Version]
- Juliev, M.; Mergili, M.; Mondal, I.; Nurtaev, B.; Pulatov, A.; Hübl, J. Comparative analysis of statistical methods for landslide susceptibility mapping in the Bostanlik District, Uzbekistan. Sci. Total Environ. 2018, 653, 801–814. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, J.; Xu, C.; Xu, C.; Song, C. Local-scale landslide susceptibility mapping using the B-GeoSVC model. Landslides 2019, 16, 1301–1312. [Google Scholar] [CrossRef]
- Pal, M.; Foody, G.M. Feature selection for classification of hyperspectral data by SVM. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2297–2307. [Google Scholar] [CrossRef] [Green Version]
- Kalantar, B.; Ueda, N.; Saeidi, V.; Ahmadi, K.; Halin, A.A.; Shabani, F. Landslide Susceptibility Mapping: Machine and Ensemble Learning Based on Remote Sensing Big Data. Remote Sens. 2020, 12, 1737. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2013, 11, 425–439. [Google Scholar] [CrossRef]
- Alin, A. Multicollinearity. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 370–374. [Google Scholar] [CrossRef]
- Luo, X.; Lin, F.; Chen, Y.; Zhu, S.; Xu, Z.; Huo, Z.; Yu, M.; Peng, J. Coupling logistic model tree and random subspace to predict the landslide susceptibility areas with considering the uncertainty of environmental features. Sci. Rep. 2019, 9, 15369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, W.; Zhang, S.; Li, R.; Shahabi, H. Performance evaluation of the GIS-based data mining techniques of best-first decision tree, random forest, and naïve Bayes tree for landslide susceptibility modeling. Sci. Total Environ. 2018, 644, 1006–1018. [Google Scholar] [CrossRef]
- McHugh, M.L. The Chi-square test of independence. Biochem. Med. 2013, 23, 143–149. [Google Scholar] [CrossRef] [Green Version]
- Dağ, H.; Sayin, K.E.; Yenidoğan, I.; Albayrak, S.; Acar, C. Comparison of feature selection algorithms for medical data. In 2012 International Symposium on Innovations in Intelligent Systems and Applications; IEEE: Piscataway, NJ, USA, 2012. [Google Scholar]
- Yu, L.; Liu, H. Efficient feature selection via analysis of relevance and redundancy. J. Mach. Learn. Res. 2004, 5, 1205–1224. [Google Scholar]
- Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- Wu, B.; Chen, C.; Kechadi, T.M.; Sun, L. A comparative evaluation of filter-based feature selection methods for hyper-spectral band selection. Int. J. Remote Sens. 2013, 34, 7974–7990. [Google Scholar] [CrossRef]
- Kolde, R.; Laur, S.; Adler, P.; Vilo, J. Robust rank aggregation for gene list integration and meta-analysis. Bioinformatics 2012, 28, 573–580. [Google Scholar] [CrossRef] [Green Version]
- Lee, S.; Pradhan, B. Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Kuhn, M.; Wing, J.; Weston, S.; Williams, A.; Keefer, C.; Engelhardt, A.; Cooper, T.; Mayer, Z.; Kenkel, B.; Team, R.C. Package ‘caret’. R J. 2020, 223. Available online: https://CRAN.R-project.org/package=caret (accessed on 21 February 2023).
- Deane-Mayer, Z.A.; Knowles, J.E. caretEnsemble: Ensembles of Caret Models, R package version 2; 2019, p. 35. Available online: https://CRAN.R-project.org/package=caretEnsemble (accessed on 21 February 2023).
- Xanthopoulos, P.; Pardalos, P.M.; Trafalis, T.B. Linear Discriminant Analysis, in Robust Data Mining; Springer: Berlin/Heidelberg, Germany, 2013; pp. 27–33. [Google Scholar]
- Tharwat, A.; Gaber, T.; Ibrahim, A.; Hassanien, A.E. Linear discriminant analysis: A detailed tutorial. AI Commun. 2017, 30, 169–190. [Google Scholar] [CrossRef] [Green Version]
- Hosseinalizadeh, M.; Kariminejad, N.; Rahmati, O.; Keesstra, S.; Alinejad, M.; Behbahani, A.M. How can statistical and artificial intelligence approaches predict piping erosion susceptibility? Sci.Total Environ. 2019, 646, 1554–1566. [Google Scholar] [CrossRef]
- Oh, H.-J.; Syifa, M.; Lee, C.-W.; Lee, S. Land Subsidence Susceptibility Mapping Using Bayesian, Functional, and Meta-Ensemble Machine Learning Models. Appl. Sci. 2019, 9, 1248. [Google Scholar] [CrossRef] [Green Version]
- Everitt, B.S.; Landau, S.; Leese, M.; Stahl, D. Cluster Analysis, 5th ed.; John Wiley & Sons, Ltd.: New York, NY, USA, 2011; pp. 215–255. [Google Scholar] [CrossRef]
- Jain, A.; Mao, J.; Mohiuddin, K. Artificial neural networks: A tutorial. Computer 1996, 29, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of Different Machine Learning Methods and Deep-Learning Convolutional Neural Networks for Landslide Detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Application of Support Vector Machines in Landslide Susceptibility Assessment for the Hoa Binh Province (Vi-Etnam) with Kernel Functions Analysis; International Congress on Environmental Modelling and Software: Leipzig, Germany, 1 July 2012. [Google Scholar]
- Yao, X.; Tham, L.G.; Dai, F.C. Landslide susceptibility mapping based on Support Vector Machine: A case study on natural slopes of Hong Kong, China. Geomorphology 2008, 101, 572–582. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer: Berlin/Heidelberg, Germany, 2009; Volume 2. [Google Scholar]
- Kuhn, M.; Johnson, K. Classification Trees and Rule-Based Models, in Applied Predictive Modeling; Springer: Berlin/Heidelberg, Germany, 2013; pp. 369–413. [Google Scholar]
- Chen, W.; Shirzadi, A.; Shahabi, H.; Ahmad, B.B.; Zhang, S.; Hong, H.; Zhang, N. A novel hybrid artificial intelligence approach based on the rotation forest ensemble and naïve Bayes tree classifiers for a landslide susceptibility assessment in Langao County, China. Geomat. Nat. Hazards Risk 2017, 8, 1955–1977. [Google Scholar] [CrossRef] [Green Version]
- Hosmer, D.W.; Lemeshow, S.; Cook, E. Applied Logistic Regression, 2nd ed.; Jhon Wiley and Sons Inc.: New York, NY, USA, 2000. [Google Scholar]
- Saha, S.; Roy, J.; Pradhan, B.; Hembram, T.K. Hybrid ensemble machine learning approaches for landslide susceptibility mapping using different sampling ratios at East Sikkim Himalayan, India. Adv. Space Res. 2021, 68, 2819–2840. [Google Scholar] [CrossRef]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.B.; Panahi, M.; Hong, H.; et al. Landslide Detection and Susceptibility Mapping by AIRSAR Data Using Support Vector Machine and Index of Entropy Models in Cameron Highlands, Malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef] [Green Version]
- Sun, D.; Wen, H.; Wang, D.; Xu, J. A random forest model of landslide susceptibility mapping based on hyperparameter optimization using Bayes algorithm. Geomorphology 2020, 362, 107201. [Google Scholar] [CrossRef]
- Gilad-Bachrach, R.; Navot, A.; Tishby, N. An Information Theoretic Tradeoff between Complexity and Accuracy; Springer: Berlin/Heidelberg, Germany, 2003; pp. 595–609. [Google Scholar] [CrossRef]













| S. No. | LIFs | Data and Scale/Resolution |
|---|---|---|
| Topographical and hydrological LIFs | ||
| 1 | Elevation | ASTER DEM (30 × 30 m) |
| 2 | Aspect | |
| 3 | Slope | |
| 4 | Profile curvature | |
| 5 | Topographical position index | |
| 6 | Topographical roughness index | |
| 7 | Topographical wetness index | |
| 8 | Stream transportation index | |
| 9 | Stream power index | |
| 10 | Surface relief ratio | |
| 11 | Stream density | |
| 12 | Direct radiation | |
| 13 | Direct duration radiation | |
| Geo-environmental LIFs | ||
| 14 | NDVI | Landsat 8 OLI/TIRS (2020) (30 × 30 m) |
| 15 | Geology | Reference maps (Scale: 1:50,000) |
| 16 | Hydrogeology | |
| 17 | Geomorphology | |
| 18 | Land use/landcover | ESRI LULC map of 2020 (10 × 10 m) |
| 19 | Rainfall | 10 years of averaged GPM data (2010–2020) (10 × 10 km) |
| 20 | Soil type | A global soil type map (250 × 250 m) |
| 21 | Distance to faults | Reference map, scale: 1:50,000 |
| 22 | Earthquake magnitude | USGS historical earthquake data (1973–2021) |
| 23 | Distance to roads | Road networks (2021) |
| 24 | Distance to epicenter | USGS historical earthquake data (1973–2021) |
| Summary | Mathematical Framework | |
|---|---|---|
| (3) | |
| denotes the observed number of samples with the dependent variable , and a value of of the th category, . is the expected number of samples under the hypothesis of independence. | ||
| (4) | |
| and represent the dependent and independent variables, respectively. The higher the value of IG, the greater the importance of the corresponding variable. | ||
| (5) | ||
| is the entropy of an independent variable . In general, a variable that yields IG or GR values ≤ 0 should be excluded. | ||
| (6) | |
| is the number of samples of the training dataset and is the probability of a sample being from class of the dependent variable. denotes the value of on variable and the function calculates the difference between and . is a user-defined parameter that is used to define the number of nearest neighbors in computing the nearest hit (i.e., ) and the nearest miss (i.e., ). | ||
| (7) | |
| is the normalized rank variables vector, where is reordering of such that . is the binomial probability and denotes the order rank of variables to their scores. We further scaled the score of as for simplicity and obtained EFS scores. |
| Code | Symbol | LIFs | Tolerance | VIF |
|---|---|---|---|---|
| 1 | Elv | Elevation | 0.194 | 5.144 |
| 2 | Asp | Aspect | 0.953 | 1.050 |
| 3 | Slp | Slope | 0.203 | 4.928 |
| 4 | Prc | Profile curvature | 0.184 | 5.437 |
| 5 | Tpi | Topographical position index | 0.161 | 6.193 |
| 6 | Tri | Topographical roughness index | 0.666 | 1.501 |
| 7 | Twi | Topographical wetness index | 0.492 | 2.031 |
| 8 | Sti | Stream transportation index | 0.982 | 1.018 |
| 9 | Spi | Stream power index | 0.965 | 1.037 |
| 10 | Srr | Surface relief ratio | 0.724 | 1.381 |
| 11 | Rnf | Rainfall | 0.883 | 1.133 |
| 12 | Std | Stream density | 0.626 | 1.599 |
| 13 | Drr | Direct radiation | 0.187 | 5.358 |
| 14 | Ddr | Direct duration radiation | 0.327 | 3.057 |
| 15 | Ndv | Normalized difference vegetation index | 0.954 | 1.048 |
| 16 | Lit | Lithology | 0.827 | 1.209 |
| 17 | Hdg | Hydrogeology | 0.930 | 1.075 |
| 18 | Gmr | Geomorphology | 0.676 | 1.480 |
| 19 | Luc | Land use/landcover | 0.902 | 1.109 |
| 20 | Som | Soil type | 0.508 | 1.970 |
| 21 | Flb | Distance from faults | 0.940 | 1.064 |
| 22 | Eqd | Epicenter density | 0.895 | 1.118 |
| 23 | Rdb | Distance from roads | 0.767 | 1.304 |
| 24 | Ebf | Distance from epicenter | 0.969 | 1.032 |
| Chi-Square | Gain Ratio | Relief-F | EFS | ||||
|---|---|---|---|---|---|---|---|
| LIFs | RI | LIFs | RI | LIFs | RI | LIFs | RI |
| Slp | 0.542 | Slp | 0.109 | Asp | 0.078 | Slp | 0.994 |
| Drr | 0.418 | Drr | 0.079 | Gmr | 0.034 | Drr | 0.986 |
| Twi | 0.411 | Twi | 0.064 | Slp | 0.028 | Twi | 0.871 |
| Prc | 0.378 | Prc | 0.052 | Drr | 0.026 | Prc | 0.842 |
| Tpi | 0.346 | Tpi | 0.044 | Som | 0.025 | Ddr | 0.783 |
| Elv | 0.331 | Ddr | 0.043 | Ddr | 0.024 | Tpi | 0.664 |
| Srr | 0.322 | Srr | 0.043 | Eqd | 0.015 | Asp | 0.640 |
| Rnf | 0.320 | Tri | 0.036 | Rdb | 0.013 | Gmr | 0.625 |
| Gmr | 0.319 | Elv | 0.034 | Prc | 0.010 | Tri | 0.523 |
| Ddr | 0.295 | Rnf | 0.034 | Std | 0.004 | Srr | 0.383 |
| Tri | 0.261 | Spi | 0.033 | Ebf | 0.002 | Std | 0.268 |
| Spi | 0.259 | Gmr | 0.026 | Hdg | 0.001 | Spi | 0.111 |
| Asp | 0.219 | Asp | 0.023 | Srr | 0.000 | Elv | 0.051 |
| Ndv | 0.166 | Std | 0.020 | Tri | 0.000 | Sti | 0.000 |
| Std | 0.165 | Ndv | 0.019 | Sti | 0.000 | Rnf | 0.000 |
| Luc | 0.120 | Som | 0.012 | Spi | 0.000 | Ndv | 0.000 |
| Som | 0.116 | Luc | 0.012 | Ndv | 0.000 | Lit | 0.000 |
| Rdb | 0.089 | Hdg | 0.010 | Rnf | 0.000 | Hdg | 0.000 |
| Flb | 0.089 | Rdb | 0.007 | Luc | −0.001 | Luc | 0.000 |
| Hdg | 0.083 | Flb | 0.006 | Tpi | −0.003 | Som | 0.000 |
| Sti | 0.000 | Sti | 0.000 | Lit | −0.014 | Flb | 0.000 |
| Lit | 0.000 | Lit | 0.000 | Twi | −0.015 | Eqd | 0.000 |
| Eqd | 0.000 | Eqd | 0.000 | Flb | −0.016 | Rdb | 0.000 |
| Ebf | 0.000 | Ebf | 0.000 | Elv | −0.020 | Ebf | 0.000 |
| LDA | MDA | |||||||
|---|---|---|---|---|---|---|---|---|
| Number of LIFs | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA |
| 5 | 0.65 | 0.87 | 0.86 | 79 | 0.68 | 0.84 | 0.86 | 78 |
| 10 | 0.67 | 0.89 | 0.86 | 80 | 0.67 | 0.87 | 0.87 | 79 |
| 15 | 0.64 | 0.90 | 0.88 | 80 | 0.66 | 0.88 | 0.88 | 80 |
| 20 | 0.64 | 0.90 | 0.88 | 80 | 0.65 | 0.89 | 0.88 | 80 |
| 24 | 0.65 | 0.90 | 0.88 | 81 | 0.65 | 0.89 | 0.88 | 79 |
| Mean statistics | 0.65 | 0.89 | 0.87 | 80 | 0.66 | 0.87 | 0.87 | 79 |
| BC | BLR | |||||||
| Number of LIFs | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA |
| 5 | 0.68 | 0.82 | 0.84 | 77 | 0.47 | 0.90 | 0.81 | 74 |
| 10 | 0.67 | 0.84 | 0.86 | 78 | 0.66 | 0.82 | 0.81 | 79 |
| 15 | 0.70 | 0.85 | 0.88 | 79 | 0.76 | 0.81 | 0.85 | 79 |
| 20 | 0.71 | 0.86 | 0.89 | 80 | 0.70 | 0.83 | 0.85 | 78 |
| 24 | 0.73 | 0.87 | 0.89 | 82 | 0.68 | 0.82 | 0.82 | 76 |
| Mean statistics | 0.70 | 0.85 | 0.87 | 79 | 0.64 | 0.83 | 0.83 | 77 |
| KNN | ANN | |||||||
| Number of LIFs | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA |
| 5 | 0.72 | 0.82 | 0.86 | 78 | 0.71 | 0.85 | 0.87 | 79 |
| 10 | 0.71 | 0.85 | 0.87 | 80 | 0.69 | 0.86 | 0.88 | 80 |
| 15 | 0.68 | 0.86 | 0.88 | 79 | 0.70 | 0.85 | 0.88 | 79 |
| 20 | 0.67 | 0.86 | 0.88 | 79 | 0.72 | 0.86 | 0.87 | 81 |
| 24 | 0.69 | 0.87 | 0.88 | 80 | 0.72 | 0.86 | 0.88 | 81 |
| Mean statistics | 0.70 | 0.85 | 0.87 | 79 | 0.71 | 0.86 | 0.88 | 80 |
| SVM | RF | |||||||
| Number of LIFs | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA |
| 5 | 0.68 | 0.85 | 0.86 | 79 | 0.69 | 0.82 | 0.85 | 77 |
| 10 | 0.68 | 0.87 | 0.87 | 80 | 0.72 | 0.83 | 0.87 | 79 |
| 15 | 0.69 | 0.87 | 0.88 | 80 | 0.75 | 0.86 | 0.90 | 82 |
| 20 | 0.71 | 0.89 | 0.90 | 82 | 0.74 | 0.86 | 0.90 | 81 |
| 24 | 0.72 | 0.89 | 0.90 | 82 | 0.76 | 0.87 | 0.91 | 82 |
| Mean statistics | 0.69 | 0.87 | 0.88 | 81 | 0.73 | 0.85 | 0.89 | 80 |
| RTF | C5.0 | |||||||
| Number of LIFs | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA |
| 5 | 0.68 | 0.84 | 0.86 | 78 | 0.64 | 0.84 | 0.85 | 76 |
| 10 | 0.71 | 0.86 | 0.88 | 80 | 0.76 | 0.82 | 0.88 | 80 |
| 15 | 0.73 | 0.87 | 0.90 | 81 | 0.81 | 0.86 | 0.91 | 84 |
| 20 | 0.76 | 0.85 | 0.90 | 81 | 0.81 | 0.86 | 0.92 | 84 |
| 24 | 0.76 | 0.87 | 0.90 | 83 | 0.81 | 0.87 | 0.93 | 84 |
| Mean statistics | 0.73 | 0.86 | 0.89 | 81 | 0.76 | 0.85 | 0.90 | 82 |
| KNN | ANN | SVM | RF | RTF | C5.0 | |
|---|---|---|---|---|---|---|
| BC | 0.68 | 0.75 | 0.77 | 0.86 | 0.92 | 0.83 |
| KNN | 1 | 0.74 | 0.76 | 0.76 | 0.72 | 0.78 |
| ANN | 1 | 0.87 | 0.82 | 0.77 | 0.88 | |
| SVM | 1 | 0.83 | 0.84 | 0.89 | ||
| RF | 1 | 0.94 | 0.94 | |||
| RTF | 1 | 0.91 |
| KNN + BC | KNN + ANN | KNN + SVM | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LIFs | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA |
| 5 | 0.70 | 0.83 | 0.86 | 78 | 0.72 | 0.84 | 0.86 | 79 | 0.70 | 0.84 | 0.86 | 79 |
| 10 | 0.70 | 0.85 | 0.87 | 80 | 0.69 | 0.86 | 0.87 | 80 | 0.69 | 0.86 | 0.87 | 80 |
| 15 | 0.73 | 0.87 | 0.90 | 82 | 0.72 | 0.87 | 0.88 | 81 | 0.70 | 0.87 | 0.89 | 80 |
| 20 | 0.72 | 0.87 | 0.90 | 82 | 0.72 | 0.86 | 0.88 | 81 | 0.71 | 0.87 | 0.89 | 81 |
| 24 | 0.75 | 0.87 | 0.90 | 82 | 0.73 | 0.86 | 0.89 | 81 | 0.71 | 0.89 | 0.90 | 82 |
| MS | 0.72 | 0.86 | 0.89 | 81 | 0.72 | 0.86 | 0.88 | 80 | 0.70 | 0.87 | 0.88 | 80 |
| KNN + RF | KNN + RTF | KNN + C5.0 | ||||||||||
| LIFs | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA |
| 5 | 0.68 | 0.83 | 0.86 | 78 | 0.73 | 0.83 | 0.86 | 79 | 0.70 | 0.83 | 0.86 | 78 |
| 10 | 0.72 | 0.84 | 0.87 | 80 | 0.71 | 0.87 | 0.88 | 81 | 0.68 | 0.85 | 0.88 | 79 |
| 15 | 0.74 | 0.86 | 0.90 | 82 | 0.72 | 0.87 | 0.89 | 81 | 0.74 | 0.87 | 0.91 | 82 |
| 20 | 0.75 | 0.87 | 0.90 | 82 | 0.75 | 0.87 | 0.91 | 82 | 0.76 | 0.88 | 0.92 | 84 |
| 24 | 0.77 | 0.86 | 0.91 | 83 | 0.75 | 0.87 | 0.91 | 82 | 0.78 | 0.89 | 0.93 | 85 |
| MS | 0.73 | 0.85 | 0.89 | 81 | 0.73 | 0.86 | 0.89 | 81 | 0.73 | 0.86 | 0.90 | 82 |
| SVM + BC | ANN + BC | ANN + RTF | ||||||||||
| LIFs | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA | Sen | Spec | AUC | OA |
| 5 | 0.67 | 0.85 | 0.86 | 78 | 0.70 | 0.84 | 0.87 | 78 | 0.72 | 0.83 | 0.86 | 79 |
| 10 | 0.68 | 0.87 | 0.88 | 80 | 0.67 | 0.88 | 0.87 | 80 | 0.70 | 0.86 | 0.88 | 80 |
| 15 | 0.72 | 0.88 | 0.90 | 82 | 0.70 | 0.88 | 0.89 | 81 | 0.72 | 0.87 | 0.90 | 81 |
| 20 | 0.72 | 0.89 | 0.91 | 82 | 0.71 | 0.88 | 0.90 | 81 | 0.73 | 0.86 | 0.90 | 81 |
| 24 | 0.73 | 0.89 | 0.91 | 83 | 0.74 | 0.87 | 0.90 | 82 | 0.73 | 0.86 | 0.90 | 81 |
| MS | 0.70 | 0.88 | 0.89 | 81 | 0.70 | 0.87 | 0.89 | 81 | 0.72 | 0.86 | 0.89 | 80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kumar, C.; Walton, G.; Santi, P.; Luza, C. An Ensemble Approach of Feature Selection and Machine Learning Models for Regional Landslide Susceptibility Mapping in the Arid Mountainous Terrain of Southern Peru. Remote Sens. 2023, 15, 1376. https://doi.org/10.3390/rs15051376
Kumar C, Walton G, Santi P, Luza C. An Ensemble Approach of Feature Selection and Machine Learning Models for Regional Landslide Susceptibility Mapping in the Arid Mountainous Terrain of Southern Peru. Remote Sensing. 2023; 15(5):1376. https://doi.org/10.3390/rs15051376
Chicago/Turabian StyleKumar, Chandan, Gabriel Walton, Paul Santi, and Carlos Luza. 2023. "An Ensemble Approach of Feature Selection and Machine Learning Models for Regional Landslide Susceptibility Mapping in the Arid Mountainous Terrain of Southern Peru" Remote Sensing 15, no. 5: 1376. https://doi.org/10.3390/rs15051376
APA StyleKumar, C., Walton, G., Santi, P., & Luza, C. (2023). An Ensemble Approach of Feature Selection and Machine Learning Models for Regional Landslide Susceptibility Mapping in the Arid Mountainous Terrain of Southern Peru. Remote Sensing, 15(5), 1376. https://doi.org/10.3390/rs15051376






