Towards a Consistent Wind Data Record for the CFOSAT Scatterometer
Abstract
:1. Introduction
2. Data and Methods
2.1. Data
2.2. Methods
- (1)
- The quality control (QC)-accepted data and the observations in the latitudes between 60°S and 60°N were selected for further analysis;
- (2)
- The subsets were differentiated according to polarization and the incidence angle in bins of 1° for θ ∈ [28°, 51°];
- (3)
- In each incidence angle bin, the dataset was further separated into 64 categories according to the antenna azimuth in bins of 5.625°, in line with the onboard look-up table for the slice construction [1];
- (4)
- In each incidence–azimuth category, collocations were separated into certain groups following the ECMWF wind speed in bins of 1 m/s and the relative wind direction in bins of 10°, and the difference between the mean measured σ0s and the mean simulated σ0s (i.e., ) was calculated for each group.
3. Overview of the CSCAT Stabilities
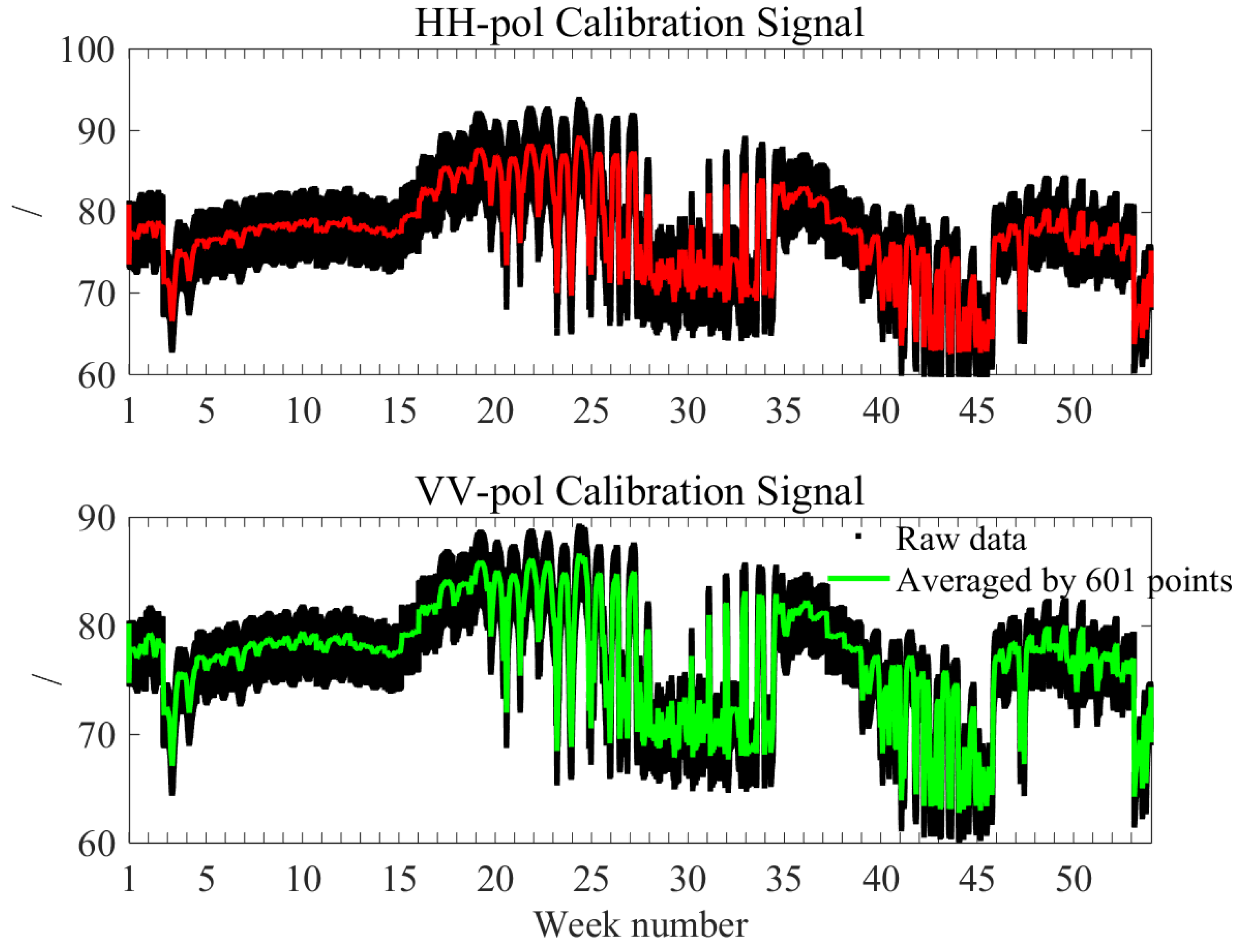
3.1. Ocean Calibration Coefficients Δσ0
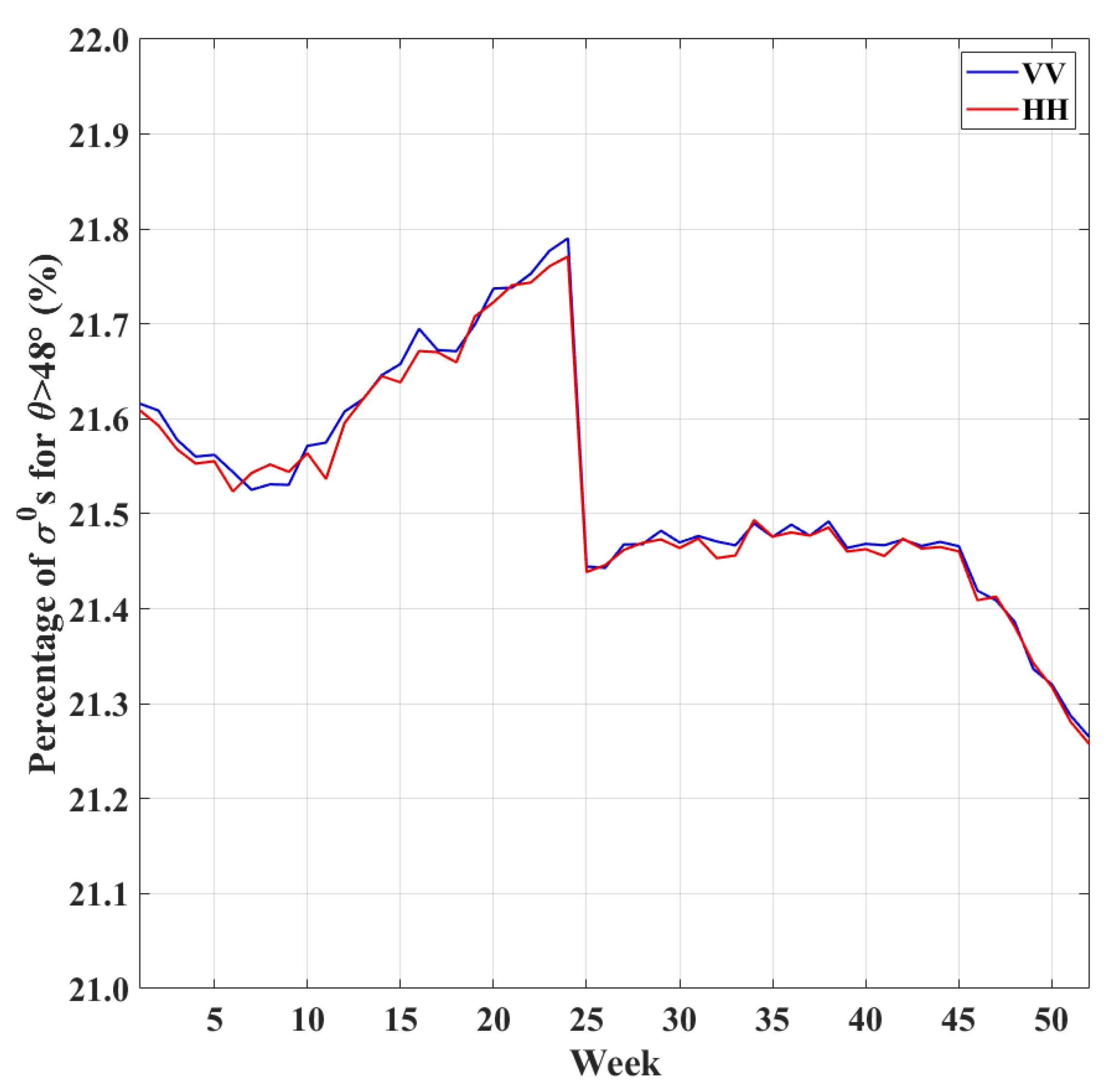
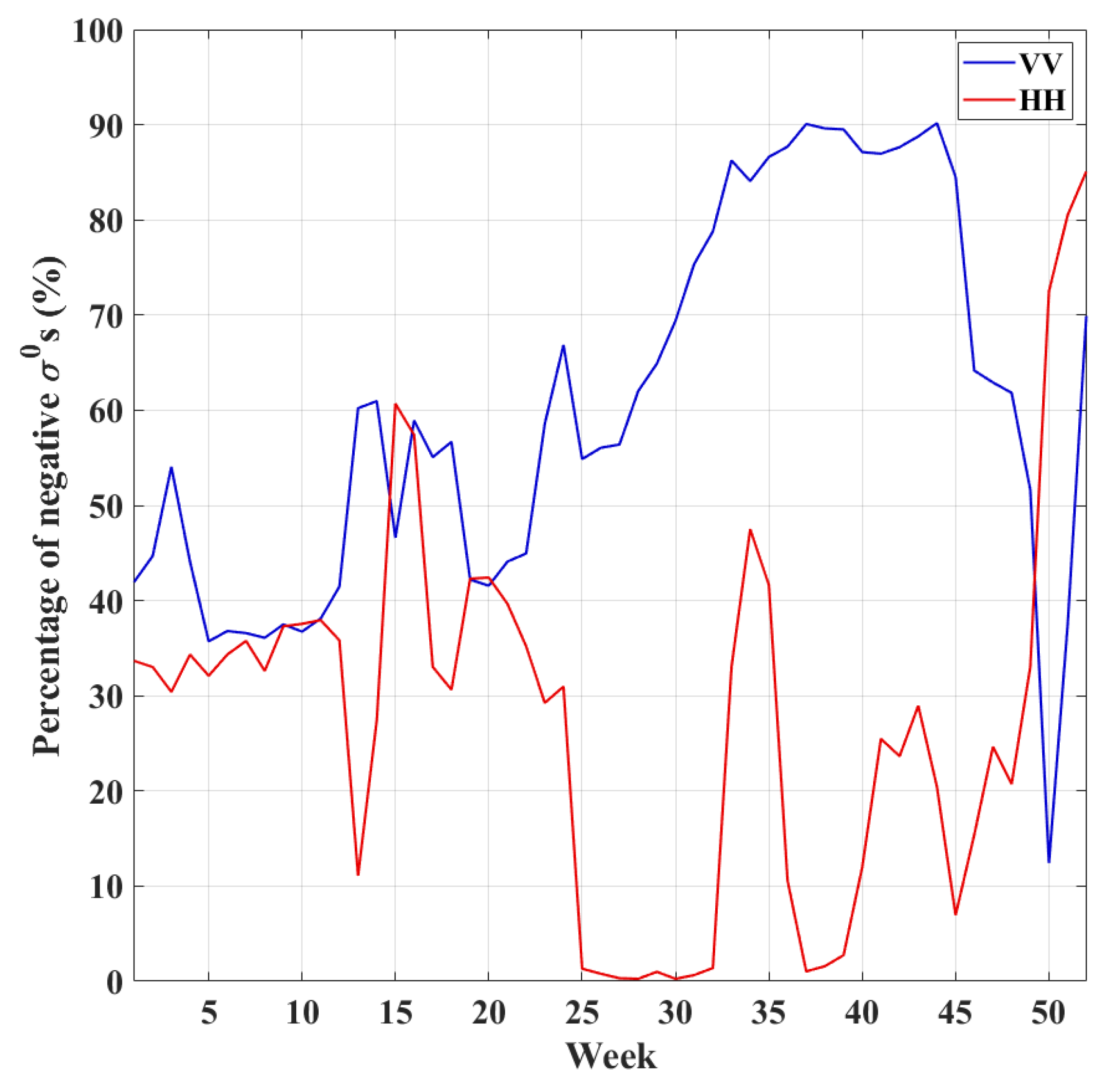
3.2. Low SNR Measurements
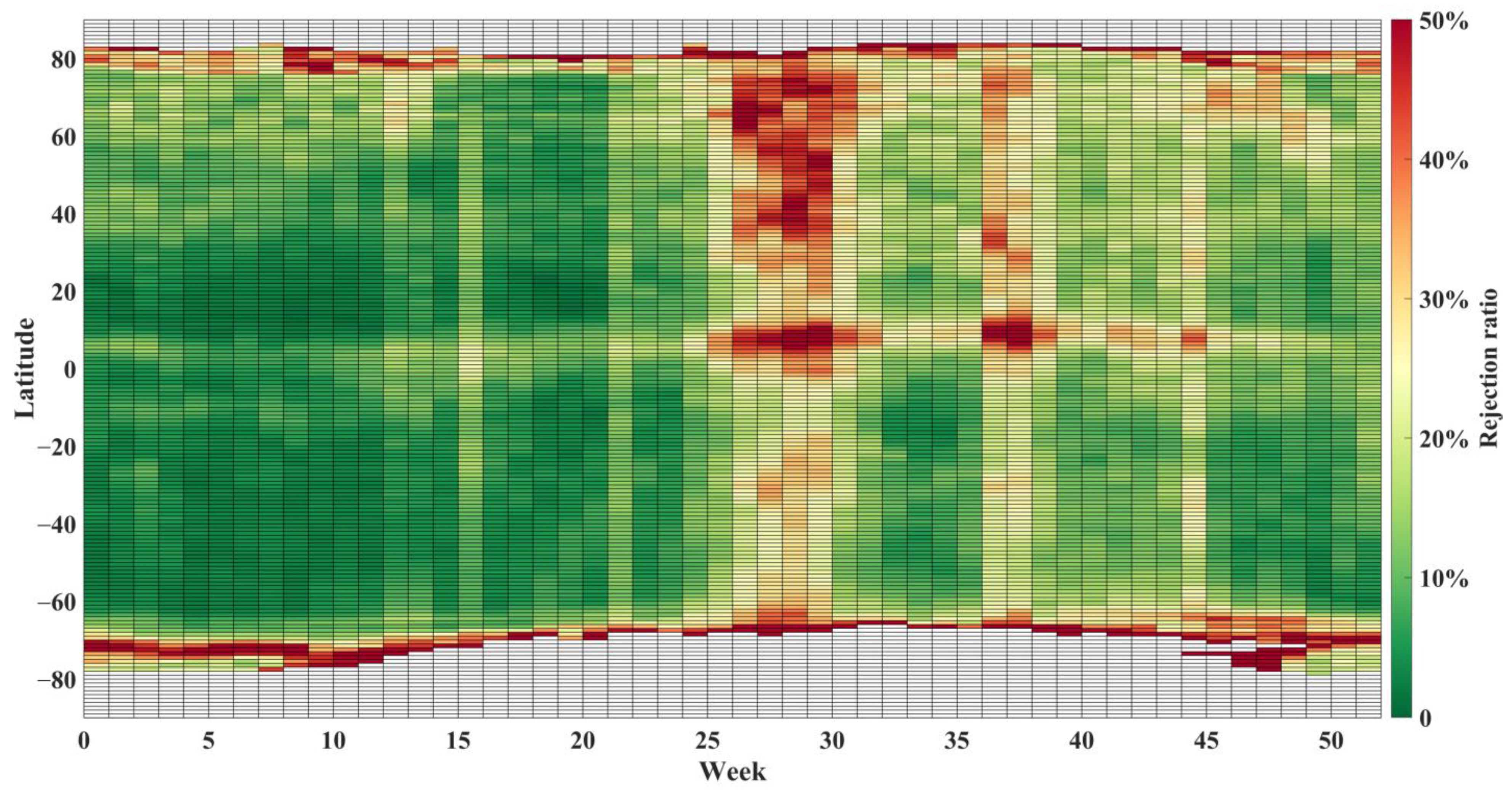
3.3. Inversion Residual
4. Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, J.; Lin, W.; Dong, X.; Lang, S.; Yun, R.; Zhu, D.; Zhang, K.; Sun, C.; Mu, B.; Ma, J.; et al. First results from the rotating fan beam scatterometer onboard CFOSAT. IEEE Trans. Geosci. Remote Sens. 2020, 58, 8793–8806. [Google Scholar] [CrossRef]
- Lin, W.; Dong, X. Design and optimization of a Ku-band rotating, range-gated fanbeam scatterometer. Int. J. Remote Sens. 2011, 32, 2151–2171. [Google Scholar] [CrossRef]
- Lin, W.; Dong, X.; Portabella, M.; Lang, S.; He, Y.; Yun, R.; Wang, Z.; Xu, X.; Zhu, D.; Liu, J. A perspective on the performance of the CFOSAT rotating fan-beam scatterometer. IEEE Trans. Geosci. Remote Sens. 2018, 57, 627–639. [Google Scholar] [CrossRef] [Green Version]
- Ye, H.; Li, J.; Li, B.; Liu, J.; Tang, D.; Chen, W.; Yang, H.; Zhou, F.; Zhang, R.; Wang, S. Evaluation of CFOSAT scatterometer wind data in global oceans. Remote Sens. 2021, 13, 1926. [Google Scholar] [CrossRef]
- Zhai, X.; Wang, Z.; Zheng, Z.; Xu, R.; Dou, F.; Xu, N.; Zhang, X. Sea Ice Monitoring with CFOSAT Scatterometer Measurements Using Random Forest Classifier. Remote Sens. 2021, 13, 4686. [Google Scholar] [CrossRef]
- Li, Z.; Verhoef, A.; Stoffelen, A. Bayesian sea ice detection algorithm for CFOSAT. Remote Sens. 2022, 14, 3569. [Google Scholar] [CrossRef]
- Chen, Y.; Cui, Y.; Lin, W.; Liu, J.; Sun, C.; Lang, S. The impacts of assimilating CFOSAT scatterometer winds for Typhoon cases based on real-time rain quality control. Atmos. Res. 2023, 285, 106621. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, J.; Xie, L.; Sun, C.; Liu, J.; Li, J.; Xian, D. China-France Oceanography Satellite (CFOSAT) simultaneously observes the typhoon-induced wind and wave fields. Acta Oceanol. Sin. 2019, 38, 158–161. [Google Scholar] [CrossRef]
- Wu, W.; Du, Y.; Qian, Y.K.; Chen, J.; Jiang, X. Large South Equatorial Current meander in the southeastern tropical Indian Ocean captured by surface drifters deployed in 2019. Geophys. Res. Lett. 2022, 49, e2021GL095124. [Google Scholar] [CrossRef]
- Verhoef, A.; Vogelzang, J.; Verspeek, J.; Stoffelen, A. Long-term scatterometer wind climate data records. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2186–2194. [Google Scholar] [CrossRef]
- Ricciardulli, L. ASCAT on MetOp-A Data Product Update Notes. Remote Sens. Syst. Tech. Rep. 2016, 5, 40416. [Google Scholar]
- Ricciardulli, L.; Wentz, F.J. A scatterometer geophysical model function for climate-quality winds: QuikSCAT Ku-2011. J. Atmos. Ocean. Technol. 2015, 32, 1829–1846. [Google Scholar] [CrossRef]
- Fore, A.G.; Stiles, B.W.; Chau, A.H.; Williams, B.A.; Dunbar, R.S.; Rodríguez, E. Point-wise wind retrieval and ambiguity removal improvements for the QuikSCAT climatological data set. IEEE Trans. Geosci. Remote Sens. 2013, 52, 51–59. [Google Scholar] [CrossRef]
- Zhao, X.; Lin, W.; Portabella, M.; Wang, Z.; He, Y. Effects of rain on CFOSAT scatterometer measurements. Remote Sens. Environ. 2022, 274, 113015. [Google Scholar] [CrossRef]
- Bidlot, J.-R.; Holmes, D.J.; Wittmann, P.A.; Lalbeharry, R.; Chen, H.S. Intercomparison of the performance of operational ocean wave forecasting systems with buoy data. Weather Forecast 2002, 17, 287–310. [Google Scholar] [CrossRef]
- Liu, W.T.; Katsaros, K.B.; Businger, J.A. Bulk parameterization of air-sea exchanges of heat and water vapor including the molecular constraints at the interface. J. Atmos. Sci. 1979, 36, 1722–1735. [Google Scholar] [CrossRef]
- Yun, R.; Dong, X.; Liu, J.; Lin, W.; Zhu, D.; Ma, J.; Lang, S.; Wang, Z. CFOSAT Rotating Fan-Beam Scatterometer Backscatter Measurement Processing. Earth Space Sci. 2021, 8, e2021EA001969. [Google Scholar] [CrossRef]
- Stoffelen, A. A simple method for calibration of a scatterometer over the ocean. J. Atmos. Ocean. Technol. 1999, 16, 275–282. [Google Scholar] [CrossRef]
- Li, Z.; Stoffelen, A.; Verhoef, A.; Verspeek, J. NWP Ocean Calibration for the CFOSAT wind scatterometer and wind retrieval evaluation. Earth Space Sci. 2021, 8, e2020EA001606. [Google Scholar] [CrossRef]
- Portabella, M.; Stoffelen, A. Characterization of residual information for SeaWinds quality control. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2747–2759. [Google Scholar] [CrossRef]
- Stoffelen, A.; Portabella, M. On Bayesian scatterometer wind inversion. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1523–1533. [Google Scholar] [CrossRef]
- Plant, W.J. Effects of wind variability on scatterometry at low wind speeds. J. Geophys. Res. 2000, 105, 16899–16910. [Google Scholar] [CrossRef]
- Wang, Z.; Stoffelen, A.; Fois, F.; Verhoef, A.; Zhao, C.; Lin, M.; Chen, G. SST dependence of Ku-and C-band backscatter measurements. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2135–2146. [Google Scholar] [CrossRef]
- Zhang, K.; Dong, X.; Zhu, D.; Yun, R.; Wang, B.; Yu, M. An improved method of noise subtraction for the CFOSAT scatterometer. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7506–7515. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mou, X.; Lin, W.; He, Y. Towards a Consistent Wind Data Record for the CFOSAT Scatterometer. Remote Sens. 2023, 15, 2081. https://doi.org/10.3390/rs15082081
Mou X, Lin W, He Y. Towards a Consistent Wind Data Record for the CFOSAT Scatterometer. Remote Sensing. 2023; 15(8):2081. https://doi.org/10.3390/rs15082081
Chicago/Turabian StyleMou, Xiaoheng, Wenming Lin, and Yijun He. 2023. "Towards a Consistent Wind Data Record for the CFOSAT Scatterometer" Remote Sensing 15, no. 8: 2081. https://doi.org/10.3390/rs15082081





