Evaluation of River Water Quality Index Using Remote Sensing and Artificial Intelligence Models
Abstract
:1. Introduction
1.1. Literature Review
1.2. Objectives and Research Organization
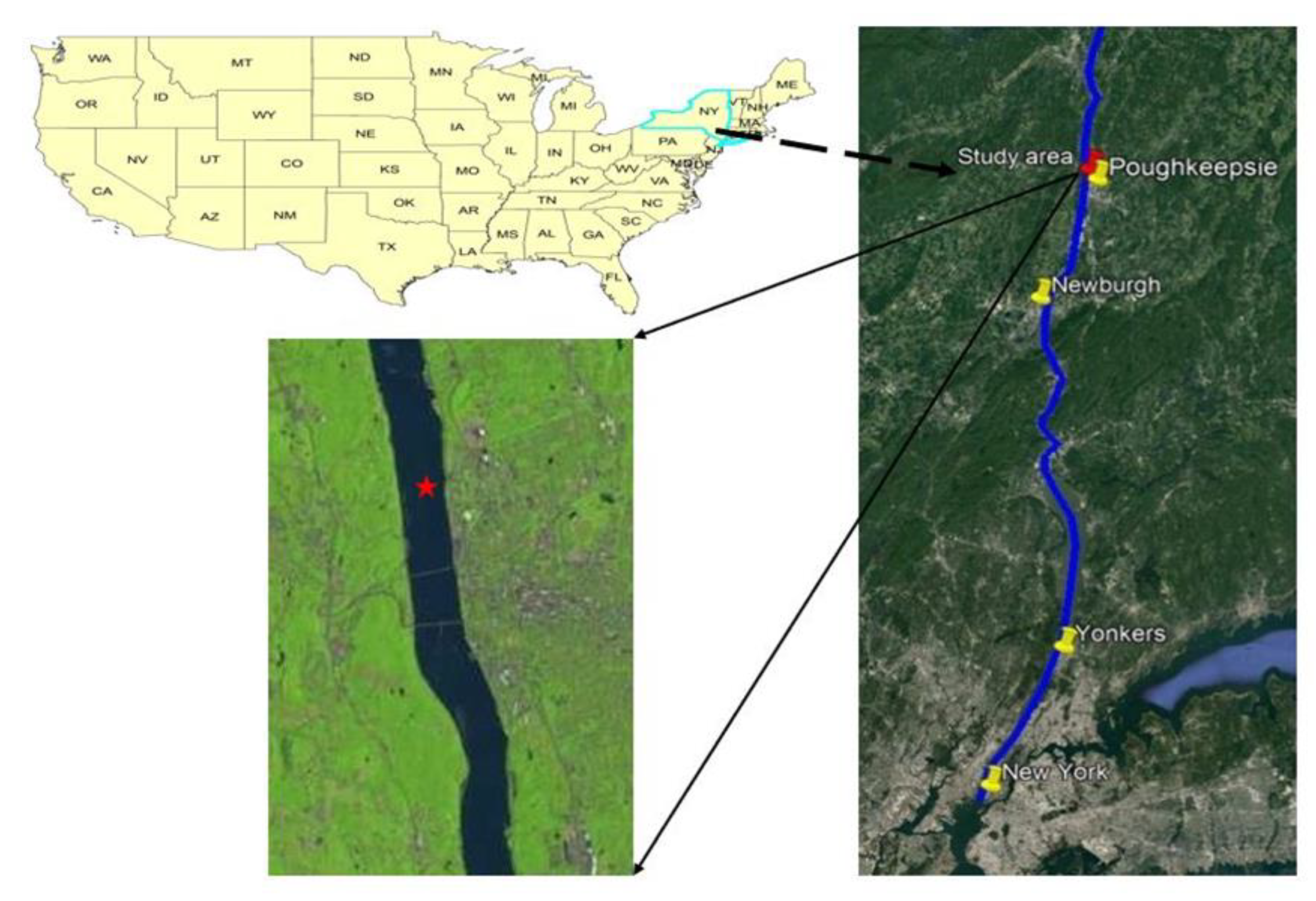
2. Overview of Case Study and Water Quality Data Description
3. Data Preparation and Methods
3.1. Preparation of Satellite Images
3.1.1. Conversion of Digital Number to Spectral Radiance
3.1.2. Conversion of Spectral Radiation to Spectral Reflectance
3.1.3. Separation of Water from Other Parts of Satellite Images
3.2. Correlation between Spectral Bands and WQPs
3.3. Correlation between WQPs and Spectral Indices
3.4. WQI Calculation
3.5. Definition of Statistical Indices
4. Implementation of Soft Computing Models
4.1. Model Tree
4.2. Multivariate Adaptive Regression Spline
4.3. Gene Expression Programming
4.4. Evolutionary Polynomial Regression
5. Results and Discussion
5.1. Statistical Performance of Soft Computing Techniques
5.2. Complexity of AI Model-Derived Expressions
5.3. Variation of WQI Values by AI Models
5.4. Comparisons of the Present Study with the Literature
6. Conclusions
- The correlation coefficients of WQP with single bands revealed that a considerable number of parameters were highly correlated with Landsat-8 bands 10 and 11;
- The correlation between spectral data and WQP improves when spectral indexes (RI and NDI) are utilized. In addition, the results showed that the use of spectral indices in some cases led to an increase in the value of R2 in MLR models;
- The WQI values were computed from the observed water quality data, which varied from 84.2 to 96.25 in the Hudson River. The observed WQI values given by CCME guidelines were indicative of good state of quality;
- The WQI values were predicted with AI models, for which four robust expressions were provided based on eight bands of Landsat-8 images. All the AI models were developed along with the optimum selection of the setting parameters;
- Statistical measures (i.e., IOA, RMSE, MAE, and SI) quantified the satisfying performance of non-linear multivariate expressions given by AI models (i.e., EPR, GEP, and MARS) and linear regression model (MT) in the prediction of WQI values for both training and testing stages. In addition, the results of the F-test and AUC approved the quantitative performance, and more importantly, the qualitative efficiency of AI models was statistically studied with violin graphs. Moreover, the uncertainty results of AI models performance indicated that EPR and MT had the lowest and highest degrees of uncertainty;
- AI models could efficiently detect both spatial and temporal variations of the WQI values for the studied reach of the Hudson River. Additionally, the comparisons of the present results with the literature were done in terms of the accuracy levels of AI models, the structural complexity of AI models, and the typical use of satellite images. According to R and RMSE criteria, the results of the present AI models (i.e., EPR, MT, GEP, and MARS) as white-box models were comparable with studies performed with SVM, RF, ANN, RT, and GBM models (introduced as black-box models).
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liyanage, C.; Yamada, K. Impact of Population Growth on the Water Quality of Natural Water Bodies. Sustainability 2017, 9, 1405. [Google Scholar] [CrossRef]
- Karn, S.K.; Harada, H. Surface Water Pollution in Three Urban Territories of Nepal, India, and Bangladesh. J. Environ. Manag. 2001, 28, 483–496. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Homaei, F.; Farhadi, H. Reliability assessment of water quality index based on guidelines of national sanitation foundation in natural streams: Integration of remote sensing and data-driven models. Artif. Intell. Rev. 2021, 54, 4619–4651. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, F.; Ding, J. Evaluation of water quality based on a machine learning algorithm and water quality index for the Ebinur Lake Watershed, China. Sci. Rep. 2017, 7, 12858. [Google Scholar] [CrossRef] [PubMed]
- Horton, R.K. An index number system for rating water quality. J. Water Pollut. Control Fed. 1965, 37, 300–306. [Google Scholar]
- Brown, R.M.; McClelland, N.I.; Deininger, R.A.; Tozer, R.G. A water quality index-do we dare? Water Sew. Work. 1970, 117, 339–343. [Google Scholar]
- Hassan, G.; Goher, M.E.; Shaheen, M.E.; Taie, S.A. Hybrid Predictive Model for Water Quality Monitoring Based on Sentinel-2A L1C Data. IEEE Access 2021, 9, 65730–65749. [Google Scholar] [CrossRef]
- Peterson, K.; Sidike, P.; Sloan, J.M. Deep learning-based water quality estimation and anomaly detection using Landsat-8/Sentinel-2 virtual constellation and cloud computing. GISci. Remote Sens. 2022, 57, 510–525. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote Sensing Techniques to Assess Water Quality. Photogramm. Eng. Remote Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef]
- Caballero, I.; Román, A.; Tovar-Sánchez, A.; Navarro, G. Water quality monitoring with Sentinel-2 and Landsat-8 satellites during the 2021 volcanic eruption in La Palma (Canary Islands). Sci. Total Environ. 2022, 822, 153433. [Google Scholar] [CrossRef]
- Pahlevan, N.; Smith, B.; Alikas, K.; Anstee, J.; Barbosa, C.; Binding, C.; Bresciani, M.; Cremella, B.; Giardino, C.; Gurlin, D.; et al. Simultaneous retrieval of selected optical water quality indicators from Landsat-8, Sentinel-2, and Sentinel-3. Remote Sens. Environ. 2022, 270, 112860. [Google Scholar] [CrossRef]
- Barrett, D.C.; Frazier, A.E. Automated Method for Monitoring Water Quality Using Landsat Imagery. Water 2016, 8, 257. [Google Scholar] [CrossRef]
- Niroumand-Jadidi, M.; Bovolo, F.; Bresciani, M.; Gege, P.; Giardino, C. Quality Retrieval from Landsat-9 (OLI-2) Imagery and Comparison to Sentinel-2. Remote Sens. 2022, 14, 4596. [Google Scholar] [CrossRef]
- Sagan, V.; Peterson, K.T.; Maimaitijiang, M.; Sidike, P.; Sloan, J.; Greeling, B.A.; Maalouf, S.; Adams, C. Monitoring inland water quality using remote sensing: Potential and limitations of spectral indices, bio-optical simulations, machine learning, and cloud computing. Earth Sci. Rev. 2020, 205, 103187. [Google Scholar] [CrossRef]
- Hou, X.; Feng, L.; Duan, H.; Chen, X.; Sun, D.; Shi, K. Fifteen-year monitoring of the turbidity dynamics in large lakes and reservoirs in the middle and lower basin of the Yangtze River, China. Remote Sens. Environ. 2017, 190, 107–121. [Google Scholar] [CrossRef]
- Su, T.C. A study of a matching pixel by pixel (MPP) algorithm to establish an empirical model of water quality mapping, as based on unmanned aerial vehicle (UAV) images. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 213–224. [Google Scholar] [CrossRef]
- Yang, Z.; Reiter, M.; Munyei, N. Estimation of chlorophyll—A concentrations in diverse water bodies using ratio-based NIR/Red indices. Remote Sens. Appl. Soc. Environ. 2017, 6, 52–58. [Google Scholar] [CrossRef]
- Shuchman, R.A.; Leshkevich, G.; Sayers, M.J.; Johengen, T.H.; Brooks, C.N.; Pozdnyakov, D. algorithm to retrieve chlorophyll, dissolved organic carbon, and suspended minerals from Great Lakes satellite data. J. Great Lakes Res. 2013, 39, 14–33. [Google Scholar] [CrossRef]
- Li, N.; Ning, Z.; Chen, M.; Wu, D.; Hao, C.; Zhang, D.; Bai, R.; Liu, H.; Chen, X.; Li, W.; et al. Satellite and Machine Learning Monitoring of Optically Inactive Water Quality Variability in a Tropical River. Remote Sens. 2022, 14, 5466. [Google Scholar] [CrossRef]
- Ahmed, M.; Mumtaz, R.; Anwar, Z.; Shaukat, A.; Arif, O.; Shafait, F. A Multi–Step Approach for Optically Active and Inactive Water Quality Parameter Estimation Using Deep Learning and Remote Sensing. Water 2022, 14, 2112. [Google Scholar] [CrossRef]
- Zhang, F.; Chan, N.W.; Liu, C.; Wang, X.; Shi, J.; Kung, H.T.; Li, X.; Guo, T.; Wang, W.; Cao, N. Water Quality Index (WQI) as a Potential Proxy for Remote Sensing Evaluation of Water Quality in Arid Areas. Water 2021, 13, 3250. [Google Scholar] [CrossRef]
- Chebud, Y.; Naja, G.M.; Rivero, R.G.; Melesse, A.M. Water Quality Monitoring Using Remote Sensing and an Artificial Neural Network. Water Air Soil Poll. 2012, 223, 4875–4887. [Google Scholar] [CrossRef]
- Chang, N.B.; Xuan, Z.; Yang, Y.J. Exploring spatiotemporal patterns of phosphorus concentrations in a coastal bay with MODIS images and machine learning models. Remote Sens. Environ. 2013, 134, 100–110. [Google Scholar] [CrossRef]
- Kim, Y.H.; Im, J.; Ha, H.K.; Choi, J.K.; Ha, S. Machine learning approaches to coastal water quality monitoring using GOCI satellite data. GISci. Remote Sens. 2014, 51, 158–174. [Google Scholar] [CrossRef]
- Sharaf El Din, E.; Zhang, Y.; Suliman, A. Mapping concentrations of surface water quality parameters using a novel remote sensing and artificial intelligence framework. Int. J. Remote Sens. 2017, 38, 1023–1042. [Google Scholar] [CrossRef]
- Arias-Rodriguez, L.F.; Duan, Z.; Díaz-Torres, J.D.J.; Basilio Hazas, M.; Huang, J.; Kumar, B.U.; Tuo, Y.; Disse, M. Integration of Remote Sensing and Mexican Water Quality Monitoring System Using an Extreme Learning Machine. Sensors 2021, 21, 4118. [Google Scholar] [CrossRef]
- Chen, P.; Wang, B.; Wu, Y.; Wang, Q.; Huang, Z.; Wang, C. Urban River water quality monitoring based on self-optimizing machine learning method using multi-source remote sensing data. Ecol. Indic. 2023, 146, 109750. [Google Scholar] [CrossRef]
- Alparslan, E.; Aydöner, C.; Tufekci, V.; Tüfekci, H. Water quality assessment at Ömerli Dam using remote sensing techniques. Environ. Monit. Assess. 2007, 135, 391–398. [Google Scholar] [CrossRef]
- Wei, Z.; Wei, L.; Yang, H.; Wang, Z.; Xiao, Z.; Li, Z.; Yang, Y.; Xu, G. Water Quality Grade Identification for Lakes in Middle Reaches of Yangtze River Using Landsat-8 Data with Deep Neural Networks (DNN) Model. Remote Sens. 2022, 14, 6238. [Google Scholar] [CrossRef]
- Brezonik, P.L.; Olmanson, L.G.; Finlay, J.C.; Bauer, M.E. Factors affecting the measurement of CDOM by remote sensing of optically complex inland waters. Remote Sens. Environ. 2015, 157, 199–215. [Google Scholar] [CrossRef]
- Sòria-Perpinyà, X.; Vicente, E.; Urrego, P.; Pereira-Sandoval, M.; Ruíz-Verdú, A.; Delegido, J.; Soria, J.M.; Moreno, J. Remote sensing of cyanobacterial blooms in a hypertrophic lagoon (Albufera of València, Eastern Iberian Peninsula) using multitemporal Sentinel-2 images. Sci. Total Environ. 2020, 698, 134305. [Google Scholar] [CrossRef] [PubMed]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Song, K. Water quality monitoring using Landsat Themate Mapper data with empirical algorithms in Chagan Lake, China. J. Appl. Remote Sens. 2011, 5, 053506. [Google Scholar] [CrossRef]
- Vincent, R.K.; Qin, X.M.; McKay, R.M.L.; Miner, J.; Czajkowski, K.; Savino, J.; Bridgeman, T. Phycocyanin detection from Landsat TM data for mapping cyanobacterial blooms in Lake Erie. Remote Sens. Environ. 2004, 89, 381–392. [Google Scholar] [CrossRef]
- Kachroud, M.; Trolard, F.; Kefi, M.; Jebari, S.; Bourrié, G. Water Quality Indices: Challenges and Application Limits in the Literature. Water 2019, 11, 361. [Google Scholar] [CrossRef]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Patricio-Valerio, L.; Schroeder, T.; Devlin, M.J.; Qin, Y.; Smithers, S. A Machine Learning Algorithm for Himawari-8 Total Suspended Solids Retrievals in the Great Barrier Reef. Remote Sens. 2022, 14, 3503. [Google Scholar] [CrossRef]
- Mehraein, M.; Mohanavelu, A.; Naganna, S.R.; Kulls, C.; Kisi, O. Monthly Streamflow Prediction by Metaheuristic Regression Approaches Considering Satellite Precipitation Data. Water 2022, 14, 3636. [Google Scholar] [CrossRef]
- Singh, V.K.; Singh, B.P.; Kisi, O.; Kushwaha, D.P. Spatial and multi-depth temporal soil temperature assessment by assimilating satellite imagery, artificial intelligence and regression based models in arid area. Comput. Electron. Agric. 2018, 150, 205–219. [Google Scholar] [CrossRef]
- Quinlan, J.R. Learning with Continuous Classes. In Proceedings of the 5th Australian Joint Conference on Artificial Intelligence, Hobart, Tasmania, Australia, 16–18 November 1992; pp. 343–348. [Google Scholar]
- Bayatvarkeshi, M.; Imteaz, M.; Kisi, O.; Zarei, M.; Yaseen, Z.M. Application of M5 model tree optimized with Excel Solver Platform for water quality parameter estimation. Environ. Sci. Pollut. Res. 2021, 28, 7347–7364. [Google Scholar] [CrossRef]
- Kim, S.; Alizamir, M.; Zounemat-Kermani, M.; Kisi, O.; Singh, V.P. Assessing the biochemical oxygen demand using neural networks and ensemble tree approaches in South Korea. J. Environ. Manag. 2020, 270, 110834. [Google Scholar] [CrossRef]
- Keshtegar, B.; Heddam, S.; Kisi, O.; Zhu, S.P. Modeling total dissolved gas (TDG) concentration at Columbia River basin dams: High-order response surface method (H-RSM) vs. M5Tree, LSSVM, and MARS. Arab. J. Geosci. 2019, 12, 544. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate Adaptive Regression Splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Shiau, J.; Lai, V.Q.; Keawsawasvong, S. Multivariate adaptive regression splines analysis for 3D slope stability in anisotropic and heterogenous clay. J. Rock Mech. Geotech. Eng. 2022, 15, 1052–1064. [Google Scholar] [CrossRef]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. Int. J. Complex Syst. 2001, 13, 87–129. Available online: https://www.gene-expression-programming.com/ (accessed on 11 August 2022).
- Borrelli, A.; De Falco, I.; Della Cioppa, A.; Nicodemi, M.; Trautteur, G. Performance of genetic programming to extract the trend in noisy data series. Phys. A Stat. Mech. Appl. 2006, 370, 104–108. [Google Scholar] [CrossRef]
- Najafzadeh, M.; Oliveto, G.; Saberi-Movahed, F. Estimation of Scour Propagation Rates around Pipelines While Considering Simultaneous Effects of Waves and Currents Conditions. Water 2022, 14, 1589. [Google Scholar] [CrossRef]
- Afrasiabian, B.; Eftekhari, M. Prediction of mode I fracture toughness of rock using linear multiple regression and gene expression programming. J. Rock Mech. Geotech. Eng. 2022, 14, 1421–1432. [Google Scholar] [CrossRef]
- Giustolisi, O.; Savic, D.A. A symbolic data-driven technique based on evolutionary polynomial regression. J. Hydroinformat. 2006, 8, 207–222. [Google Scholar] [CrossRef]
- Savic, D.; Giustolisi, O.; Berardi, L.; Shepherd, W.; Djordjevic, S.; Saul, A. Modelling sewer failure by evolutionary computing. Proc. Inst. Civ. Eng.-Water Manag. 2006, 159, 111–118. [Google Scholar] [CrossRef]
- Savic, D.A.; Giustolisi, O.; Laucelli, D. Asset deterioration analysis using multi-utility data and multi-objective data mining. J. Hydroinformat. 2009, 11, 211–224. [Google Scholar] [CrossRef]
- Fiore, A.; Marano, G.C.; Laucelli, D.; Monaco, P. Evolutionary Modeling to Evaluate the Shear Behavior of Circular Reinforced Concrete Columns. Adv. Civ. Eng. 2014, 2014, 684256. [Google Scholar] [CrossRef]
- Balacco, G.; Laucelli, D. Improved air valve design using evolutionary polynomial regression. Water Supply 2019, 19, 2036–2043. [Google Scholar] [CrossRef]
- Nahm, F.S. Receiver operating characteristic curve: Overview and practical use for clinicians. Korean J. Anesthesiol. 2022, 75, 25–36. [Google Scholar] [CrossRef]
- Fleiss, J.L. Statistical Methods for Rates and Proportions, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 1981; pp. 38–46. [Google Scholar]
- Ahmadianfar, I.; Jamei, M.; Karbasi, M.; Gharabaghi, B. A novel boosting ensemble committee-based model for local scour depth around non-uniformly spaced pile groups. Eng. Comput. 2022, 38, 3439–3461. [Google Scholar] [CrossRef]







| Parameter | Unit | Max | Min | Average | Standard Deviation |
|---|---|---|---|---|---|
| Tur | NTU | 28.69 | 1.12 | 16.67 | 6.3 |
| SO42− | mg/L | 16.7 | 9.02 | 11.66 | 2.34 |
| Na+ | mg/L | 31.4 | 14.1 | 20.64 | 5.02 |
| K+ | mg/L | 1.44 | 0.79 | 1.14 | 0.32 |
| pH | --- | 7.9 | 7.5 | 7.57 | 0.14 |
| NO3− | mg/L | 0.76 | 0.34 | 0.48 | 0.12 |
| Mg2+ | mg/L | 5.76 | 3.56 | 4.64 | 0.68 |
| Hardness | mg/L | 103 | 65 | 83.1 | 10.94 |
| F− | mg/L | 0.1 | 0.1 | 0.1 | 1.9 × 10−16 |
| Cl− | mg/L | 56.3 | 23.6 | 35.25 | 10.16 |
| AS | mg/L | 53 × 10−3 | 27 × 10−3 | 36 × 10−3 | 8.12 |
| Alk | mg/L | 76.7 | 52.4 | 65.7 | 6.88 |
| DO | mg/L | 14.1 | 7.5 | 10.9 | 2.18 |
| Bands | Wavelength (μm) | Resolution (m) |
|---|---|---|
| Band 1—Coastal aerosol | 0.43–0.45 | 30 |
| Band 2—Blue | 0.45–0.51 | 30 |
| Band 3—Green | 0.53–0.59 | 30 |
| Band 4—Red | 0.64–0.67 | 30 |
| Band 5—Near Infrared (NIR) | 0.85–0.88 | 30 |
| Band 6—SWIR 1 | 1.57–1.65 | 30 |
| Band 7—SWIR 2 | 2.11–2.29 | 30 |
| Band 8—Panchromatic | 0.50–0.68 | 15 |
| Band 9—Cirrus | 1.36–1.38 | 30 |
| Band 10—Thermal Infrared (TIRS) 1 | 10.6–11.19 | 100 |
| Band 11—Thermal Infrared (TIRS) 2 | 11.50–12.51 | 100 |
| Image Acquisition Date | Image ID | Range of Image Usage |
|---|---|---|
| 12 March 2021 | LC80130312021071LGN00 | 12 March 2021 |
| 13 April 2021 | LC80140312021110LGN00 | 13 March 2021–13 April 2021 |
| 20 April 2021 | LC80140312021126LGN00 | 14 April 2021–20 April 2021 |
| 6 May 2021 | LC80130312021135LGN00 | 21 April 2021–5 May 2021 |
| 15 May 2021 | LC80140312021158LGN00 | 7 May 2021–15 May 2021 |
| 7 June 2021 | LC80130312021167LGN00 | 16 May 2021–7 June 2021 |
| Parameters | Multivariate Linear Regression Equation | |
|---|---|---|
| Tur | 0.873 | |
| SO42− | 0.867 | |
| Na+ | 0.756 | |
| K+ | 0.849 | |
| pH | 0.939 | |
| NO3− | 0.868 | |
| Mg2+ | 0.888 | |
| Hardness | 0.801 | |
| F− | 0.937 | |
| Cl− | 0.954 | |
| AS | 0.936 | |
| Alk | 0.920 | |
| DO | 0.917 |
| Class | Threshold Value | Water Quality States |
|---|---|---|
| Ι | 95–100 | Excellent |
| ΙΙ | 80–94 | Good |
| ΙΙΙ | 60–79 | Fair |
| ΙV | 45–59 | Marginal |
| V | 0–44 | Poor |
| Parameter | Max | Min | Average | Standard Deviation |
|---|---|---|---|---|
| b1 | 0.107 | 0.034 | 0.055 | 0.02 |
| b2 | 0.09 | 0.037 | 0.055 | 0.02 |
| b3 | 0.072 | 0.029 | 0.048 | 0.012 |
| b4 | 0.09 | 0.029 | 0.057 | 0.021 |
| b5 | 0.052 | 0.025 | 0.034 | 0.007 |
| b6 | 0.038 | 0.016 | 0.027 | 0.007 |
| b7 | 0.053 | 0.011 | 0.026 | 0.011 |
| b8 | 0.171 | 0.036 | 0.064 | 0.012 |
| b9 | 0.004 | 0.0009 | 0.002 | 0.001 |
| b10 | 293.7 | 276.22 | 283.34 | 6.13 |
| b11 | 292.9 | 275.71 | 282.67 | 5.99 |
| WQI | 96.25 | 84.25 | 88.11 | 3.68 |
| Basis Function | Formulation |
|---|---|
| BF1 | |
| BF2 | |
| BF3 | |
| BF4 | |
| BF5 | |
| BF6 | |
| BF7 | |
| BF8 | |
| BF9 | |
| BF10 | |
| BF11 |
| Parameters | Values |
|---|---|
| Number of chromosomes | 30 |
| Linking function | + |
| Mutation | 0.00138 |
| Fixed-Root Mutation | 0.00068 |
| Gene-Recombination | 0.00068 |
| Gene-Transportation | 0.00277 |
| One-Point Recombination | 0.00277 |
| Best fitness function | 419.5948 |
| Stop condition | R-Square Threshold |
| Maximum depth of subtree | 7 |
| Mathematical operators and function | ±, ×,/, Ln(x), exp(x), Average (x1, x2) |
| Model. No | Formulation | MSE |
|---|---|---|
| 1 | 1.706 | |
| 2 | 1.588 | |
| 3 | 1.656 | |
| 4 | 1.585 | |
| 5 | 1.585 | |
| 6 | 1.521 | |
| 7 | 1.58 | |
| 8 | 1.499 | |
| 9 | 1.602 | |
| 10 | 1.562 | |
| 11 | 1.507 |
| Inner Function | Natural Logarithm |
|---|---|
| Range of exponents | [−2, −1.5, −1, −0.5, 0, 0.5, 1, 1.5, 2] |
| Number of terms | 6 |
| Expression structure | Sum(ai × x1× x2 × f (x1× x2)) + bias |
| Regression method | Non-negative least squares |
| Optimum number of Generation | [10 40] |
| Fitness function | Mean Square Error |
| AI Models | Training Phase | |||
|---|---|---|---|---|
| IOA | RMSE | MAE | SI | |
| MT | 0.969 | 1.287 | 0.0091 | 0.0146 |
| MARS | 0.992 | 0.64 | 0.0059 | 0.0073 |
| GEP | 0.964 | 1.383 | 0.0104 | 0.0157 |
| EPR | 0.973 | 1.194 | 0.0076 | 0.0135 |
| AI Models | Testing Phase | |||
| IOA | RMSE | MAE | SI | |
| MT | 0.978 | 1.085 | 0.0084 | 0.0146 |
| MARS | 0.975 | 1.165 | 0.0088 | 0.0129 |
| GEP | 0.978 | 1.052 | 0.0093 | 0.0109 |
| EPR | 0.977 | 1.123 | 0.0083 | 0.0135 |
| AI Models | SSR | SSE | MSR | MSE | F0 | Hypothesis States |
|---|---|---|---|---|---|---|
| GEP | 170.861 | 1213.8 | 13.143 | 14.985 | 0.877 | Accept |
| MARS | 60.549 | 1150.9 | 4.657 | 14.208 | 0.327 | Accept |
| EPR | 12462 | 13770 | 958.587 | 169.995 | 5.639 | Reject |
| M5MT | 308.959 | 1272.20 | 237.766 | 15.706 | 1.513 | Accept |
| AI Models | μe | Se | Uncertainty Band | ||
|---|---|---|---|---|---|
| GEP | 0.0710 | 0.8152 | 0.1419 | 0.0000003 | 0.1419 |
| MARS | 0.1732 | 1.5702 | 0.2755 | 0.0710 | 0.2046 |
| EPR | 0.2252 | 1.9852 | 0.2771 | 0.1732 | 0.1039 |
| M5MT | 0.2997 | 2.3734 | 0.3741 | 0.2252 | 0.1489 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najafzadeh, M.; Basirian, S. Evaluation of River Water Quality Index Using Remote Sensing and Artificial Intelligence Models. Remote Sens. 2023, 15, 2359. https://doi.org/10.3390/rs15092359
Najafzadeh M, Basirian S. Evaluation of River Water Quality Index Using Remote Sensing and Artificial Intelligence Models. Remote Sensing. 2023; 15(9):2359. https://doi.org/10.3390/rs15092359
Chicago/Turabian StyleNajafzadeh, Mohammad, and Sajad Basirian. 2023. "Evaluation of River Water Quality Index Using Remote Sensing and Artificial Intelligence Models" Remote Sensing 15, no. 9: 2359. https://doi.org/10.3390/rs15092359
APA StyleNajafzadeh, M., & Basirian, S. (2023). Evaluation of River Water Quality Index Using Remote Sensing and Artificial Intelligence Models. Remote Sensing, 15(9), 2359. https://doi.org/10.3390/rs15092359







