Wavelet Vegetation Index to Improve the Inversion Accuracy of Leaf V25cmax of Bamboo Forests
Abstract
:1. Introduction
2. Materials and Methods
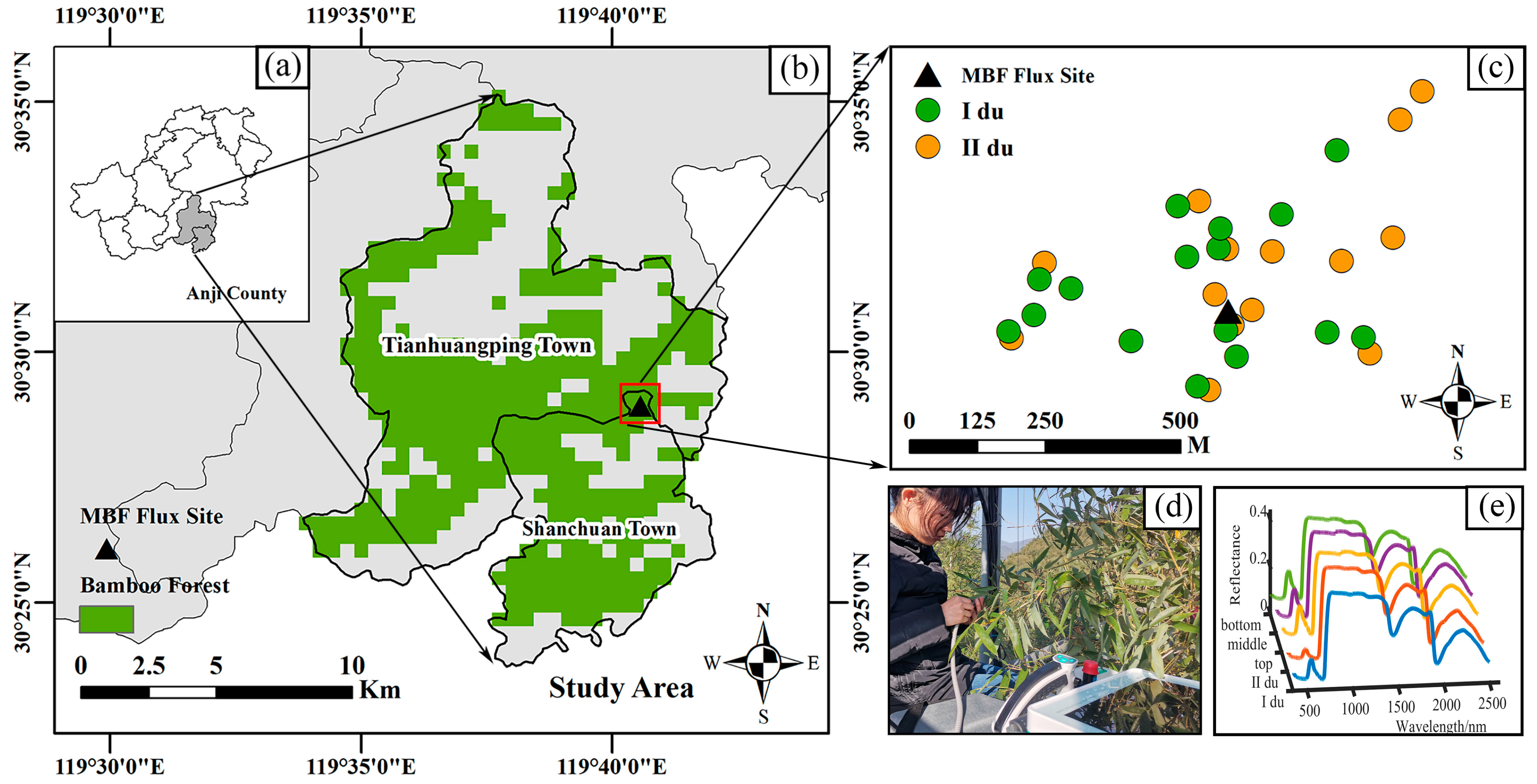
2.1. Study Area
2.2. Measurement of the A–Ci Curve and Hyperspectral Reflectance of Moso Bamboo Leaves
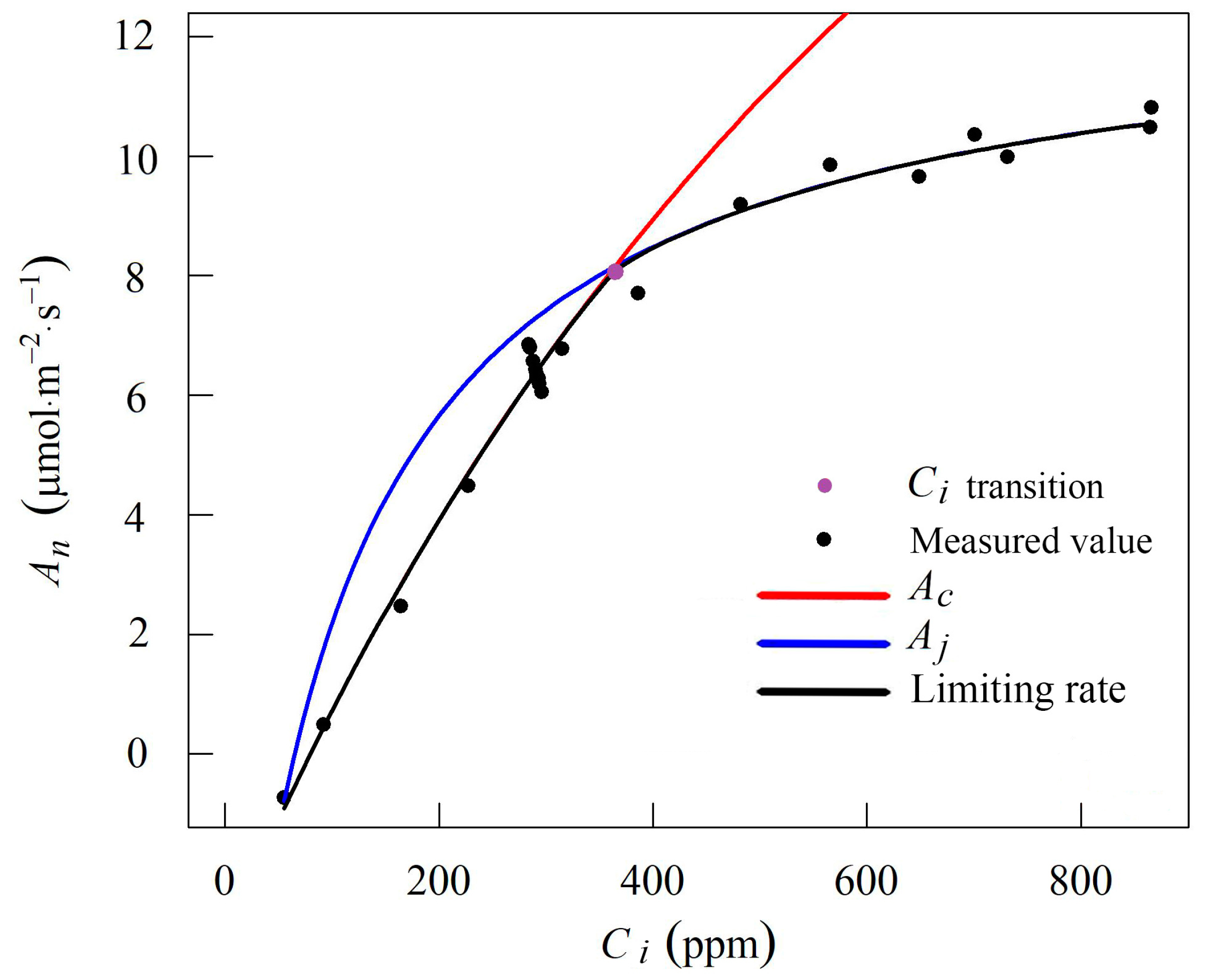
2.2.1. A–Ci Measurement
2.2.2. Hyperspectral Reflectance Measurement
2.3. V25cmax Calculation
2.4. Hyperspectral Vegetation Index
2.4.1. Hyperspectral Vegetation Index Calculation
2.4.2. Evaluation of the Correlation between HVI and V25cmax
2.5. Wavelet Transform and Wavelet Vegetation Index
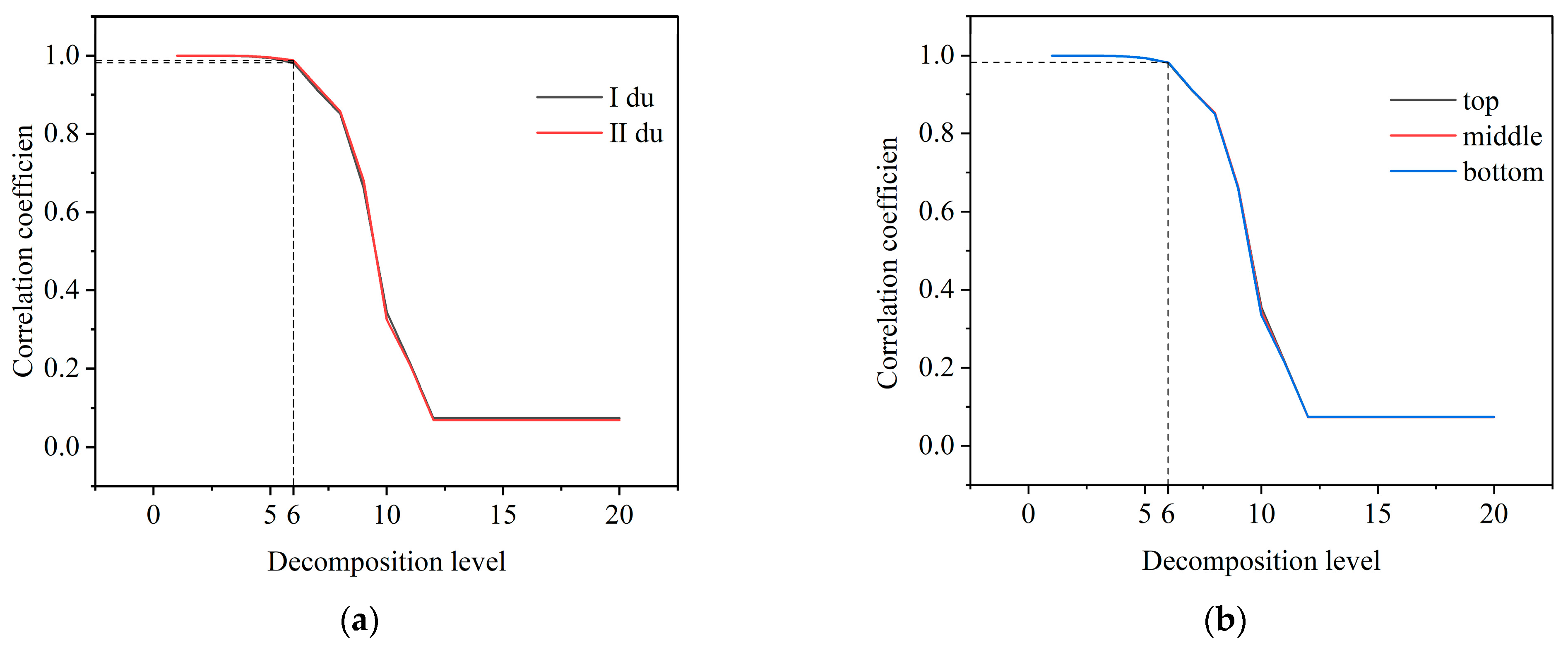
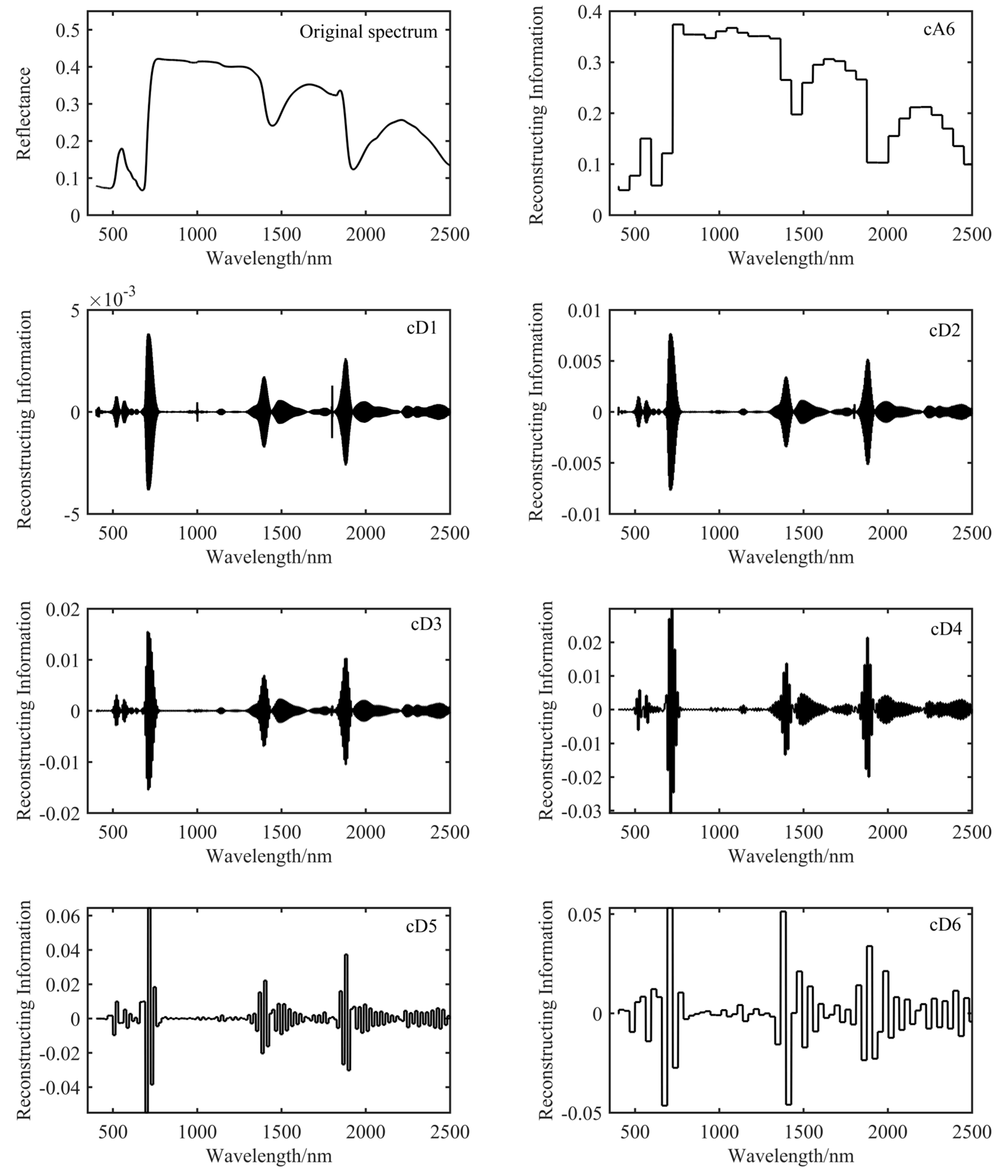
2.5.1. Wavelet Transform and Decomposition Level Selection of Hyperspectral Data
2.5.2. Construction and Screening of the Wavelet Vegetation Index
2.6. Construction of the V25cmax Inversion Model Based on the PLSR Model
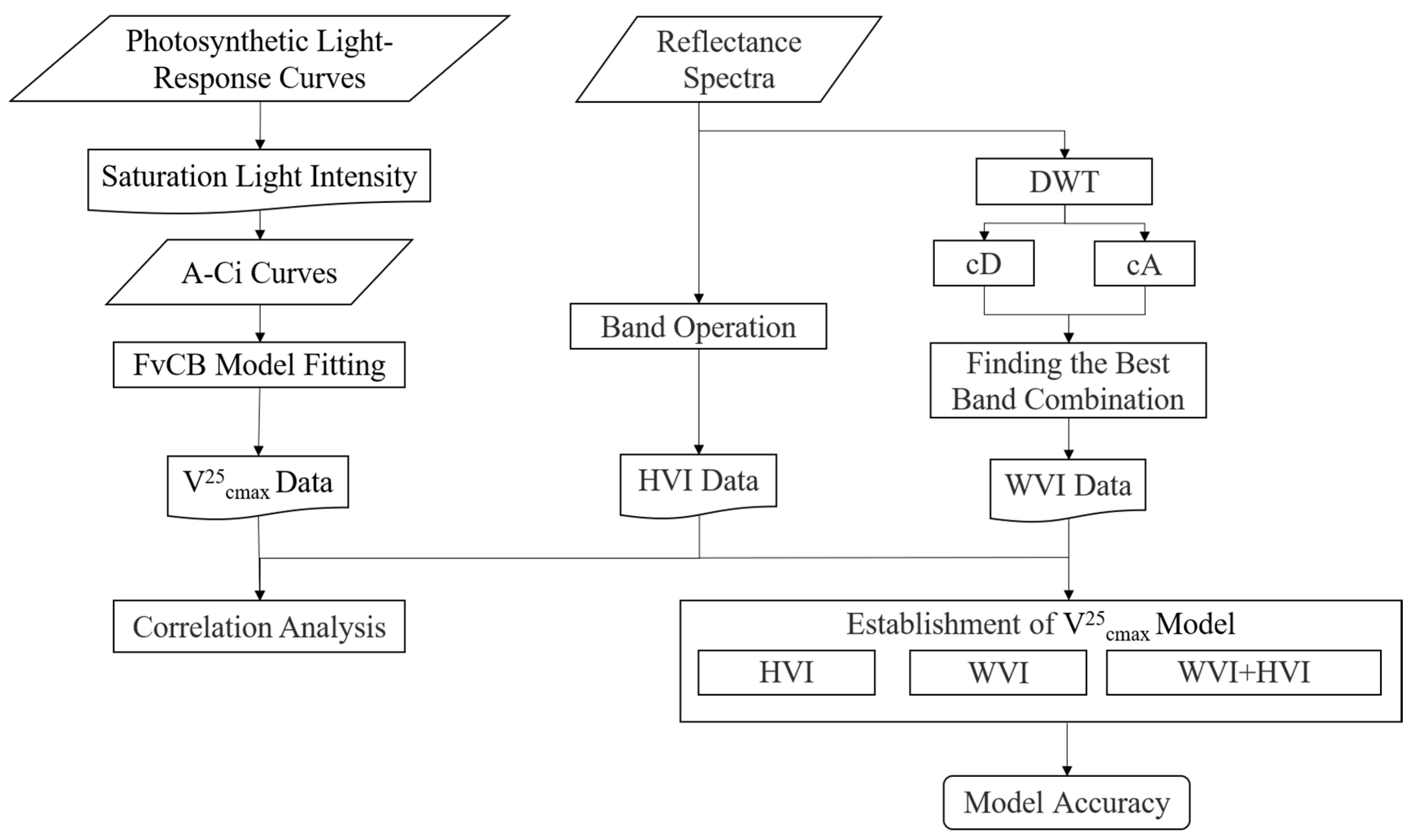
2.7. The Summary Scheme of Study
3. Results and Analysis
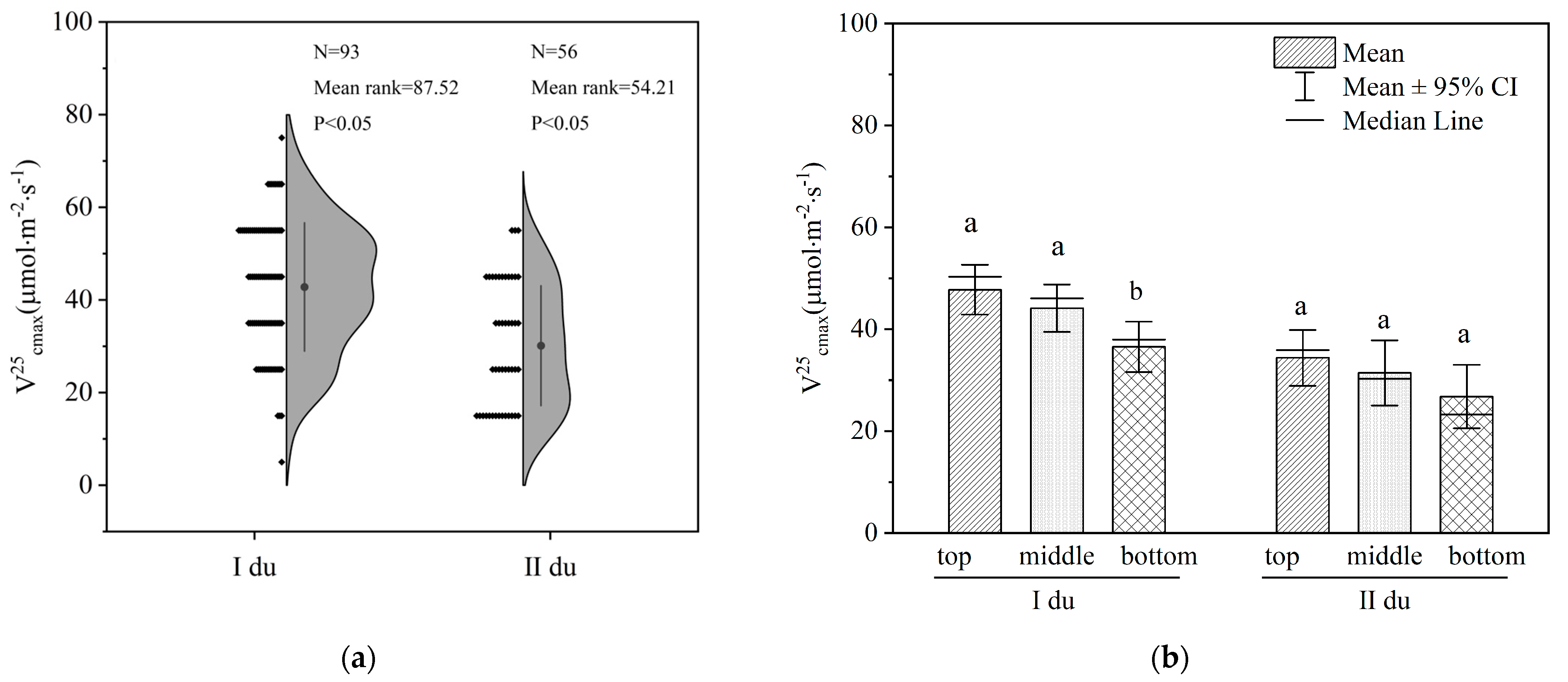
3.1. V25cmax Analysis of Moso Bamboo Leaves at the Different Ages and Canopy Positions
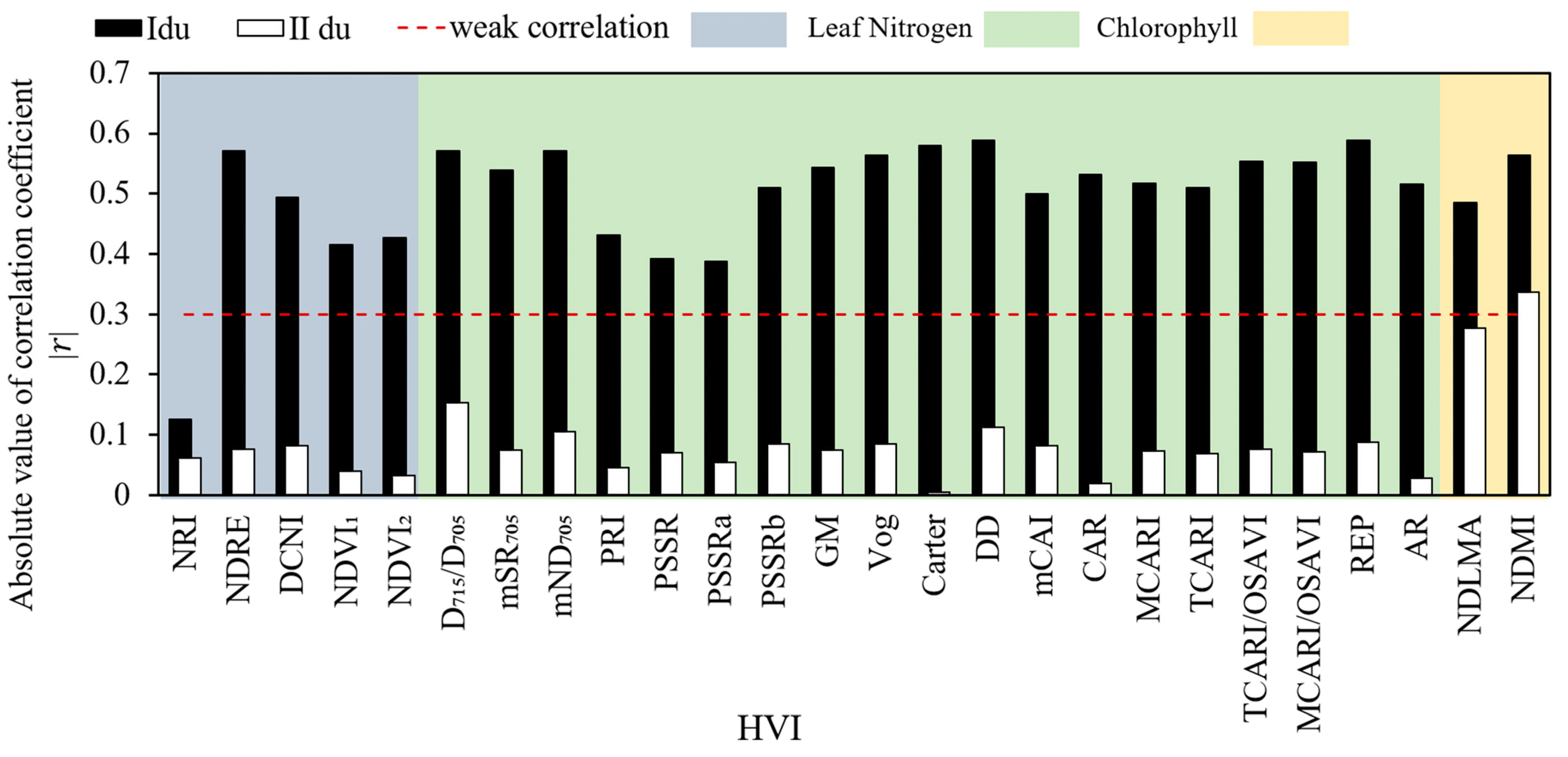
3.2. Correlation between the HVI and V25cmax of Moso Bamboo Leaves at the Different Ages
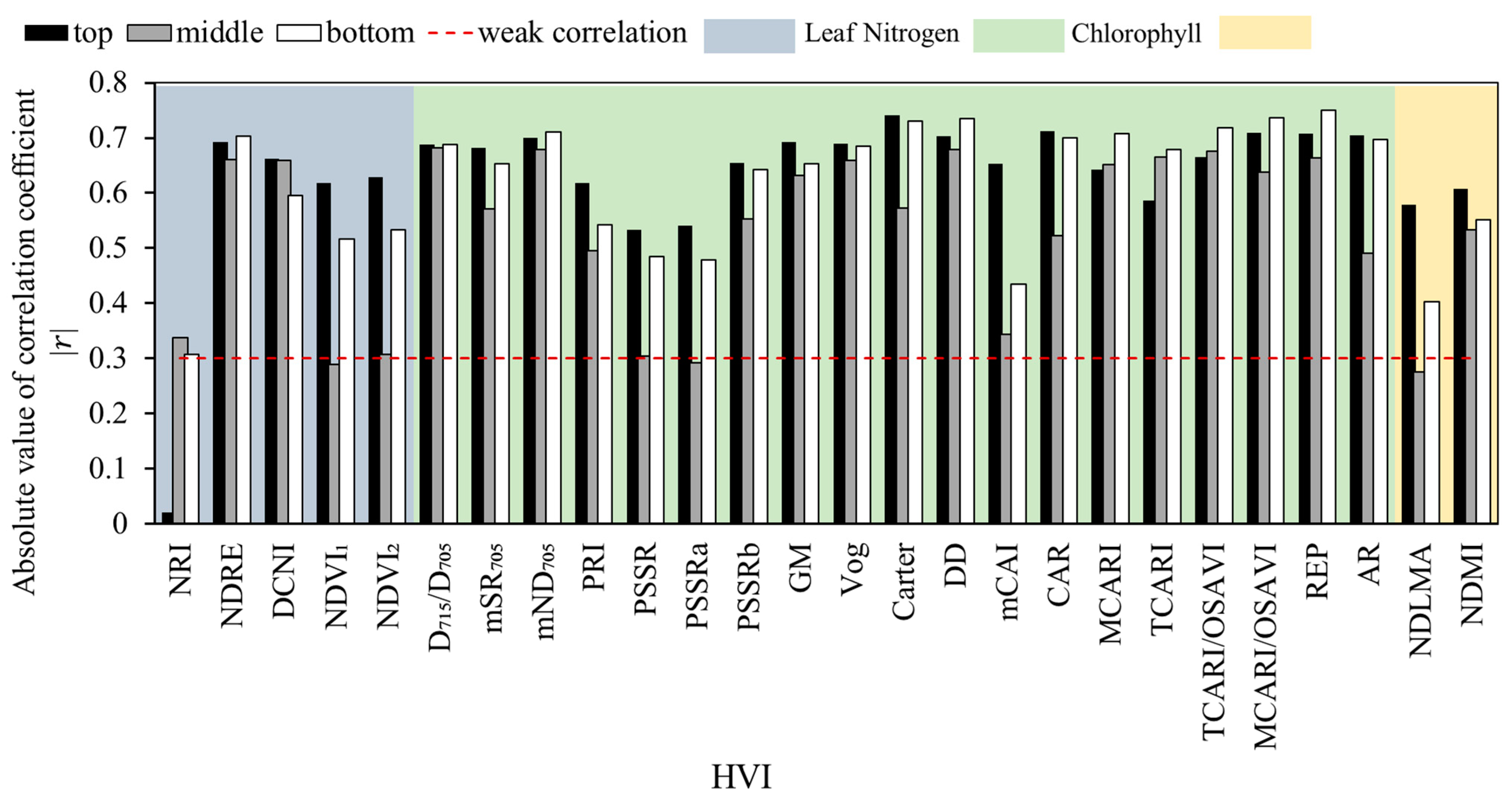
3.3. Correlation between the HVI and V25cmax of Moso Bamboo Leaves at the Different Canopy Positions
3.4. Correlation between the Wavelet Vegetation Index and V25cmax of Moso Bamboo Leaves
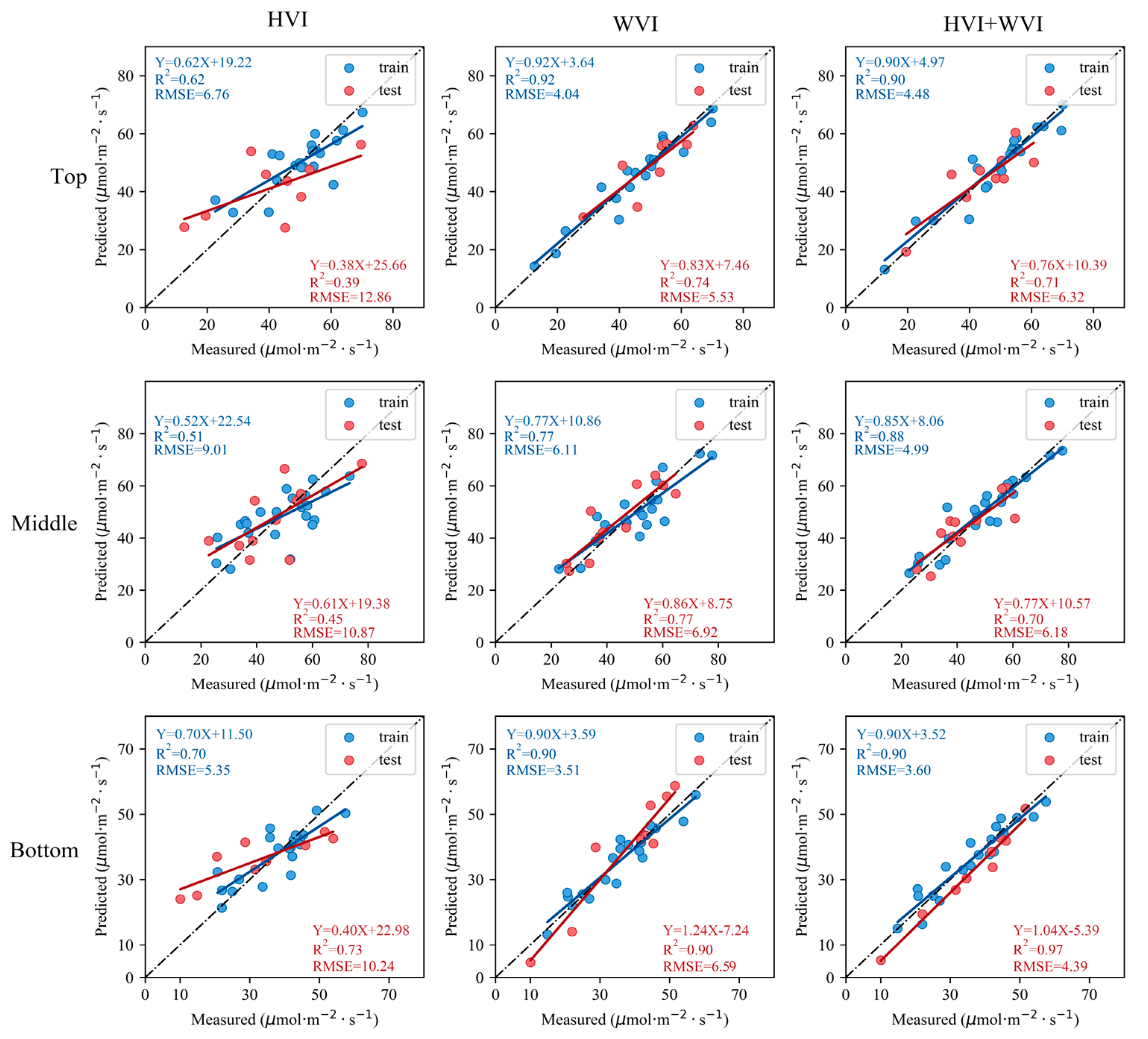
3.5. Inversion of V25cmax of Moso Bamboo Leaves
4. Discussion
4.1. The V25cmax Differences among the Different Bamboo Ages and Canopy Positions
4.2. The V25cmax of Leaves at the Different Ages Are Sensitive to Different Types of HVIs
4.3. The WVI Can Better Characterize V25cmax
4.4. The Model Constructed by the WVIs Improved the Accuracy of Inverting V25cmax
5. Conclusions
- The V25cmax differences between the different bamboo ages and canopy positions largely reflects the actual photosynthesis situation during the growth of bamboo leaves, which lays an important foundation for V25cmax retrieval from hyperspectral reflectance data.
- Most HVIs have not negligible correlation with the V25cmax of leaves of different ages and at different canopy positions, but their correlation is significantly lower than that between the WVI and V25cmax. The WVI comprising noise-free and detail-enhancing components can use information obtained from a wider range of bands and better reflect variation in V25cmax.
- The V25cmax inversion model constructed based on the WVI contains spectral features at different resolutions and levels and can be used to invert the V25cmax of moso bamboo leaves of different ages and at different canopy positions with high accuracy and few errors.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Farquhar, G.D.; von Caemmerer, S.; Berry, J.A. A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species. Planta 1980, 149, 78–90. [Google Scholar] [CrossRef] [PubMed]
- Kattge, J.; Knorr, W.; Raddatz, T.; Wirth, C. Quantifying photosynthetic capacity and its relationship to leaf nitrogen content for global-scale terrestrial biosphere models. Glob. Change Biol. 2009, 15, 976–991. [Google Scholar] [CrossRef]
- Dillen, S.Y.; de Beeck, M.O.; Hufkens, K.; Buonanduci, M.; Phillips, N.G. Seasonal patterns of foliar reflectance in relation to photosynthetic capacity and color index in two co-occurring tree species, Quercus rubra and Betula papyrifera. Agric. For. Meteorol. 2012, 160, 60–68. [Google Scholar] [CrossRef]
- Burnett, A.C.; Serbin, S.P.; Lamour, J.; Anderson, J.; Davidson, K.J.; Yang, D.; Rogers, A. Seasonal trends in photosynthesis and leaf traits in scarlet oak. Tree Physiol. 2021, 41, 1413–1424. [Google Scholar] [CrossRef] [PubMed]
- Rogers, A. The use and misuse of Vc,max in Earth System Models. Photosynth. Res. 2014, 119, 15–29. [Google Scholar] [CrossRef] [PubMed]
- Woodrow, I.; Berry, J. Enzymatic Regulation of Photosynthetic CO2, Fixation in C3 Plants. Annu. Rev. Plant Physiol. Plant Mol. Biol. 2003, 39, 533–594. [Google Scholar] [CrossRef]
- Song, G.; Wang, Q.; Jin, J. Exploring the instability of the relationship between maximum potential electron transport rate and maximum carboxylation rate in cool-temperate deciduous forests. Agric. For. Meteorol. 2021, 308-309, 108614. [Google Scholar] [CrossRef]
- Stinziano, J.R.; Morgan, P.B.; Lynch, D.J.; Saathoff, A.J.; McDermitt, D.K.; Hanson, D.T. The rapid A–Ci response: Photosynthesis in the phenomic era. Plant Cell Environ. 2017, 40, 1256–1262. [Google Scholar] [CrossRef]
- Rascher, U.; Alonso, L.; Burkart, A.; Cilia, C.; Cogliati, S.; Colombo, R.; Damm, A.; Drusch, M.; Guanter, L.; Hanus, J.; et al. Sun-induced fluorescence—A new probe of photosynthesis: First maps from the imaging spectrometer Hy Plant. Glob. Change Biol. 2015, 21, 4673–4684. [Google Scholar] [CrossRef]
- Croft, H.; Chen, J.M.; Luo, X.; Bartlett, P.; Chen, B.; Staebler, R.M. Leaf chlorophyll content as a proxy for leaf photosynthetic capacity. Glob. Change Biol. 2017, 23, 3513–3524. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, X.; Fan, W. Remote Sensing Inversion of Leaf Maximum Carboxylation Rate Based on a Mechanistic Photosynthetic Model. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Camino, C.; Gonzalez-Dugo, V.; Hernandez, P.; Zarco-Tejada, P.J. Radiative transfer Vcmax estimation from hyperspectral imagery and SIF retrievals to assess photosynthetic performance in rainfed and irrigated plant phenotyping trials. Remote Sens. Environ. 2019, 231, 111186. [Google Scholar] [CrossRef]
- Ji, J.; Li, X.; Du, H.; Mao, F.; Fan, W.; Xu, Y.; Huang, Z.; Wang, J.; Kang, F. Multiscale leaf area index assimilation for Moso bamboo forest based on Sentinel-2 and MODIS data. Int. J. Appl. Earth Obs. Geoinf. 2021, 104, 102519. [Google Scholar] [CrossRef]
- Gu, C.; Du, H.; Mao, F.; Han, N.; Zhou, G.; Xu, X.; Sun, S.; Gao, G. Global sensitivity analysis of PROSAIL model parameters when simulating Moso bamboo forest canopy reflectance. Int. J. Remote Sens. 2016, 37, 5270–5286. [Google Scholar] [CrossRef]
- Sun, S.B.; Du, H.Q.; Li, P.H.; Zhou, G.M.; Xu, X.J.; Gao, G.L.; Li, X.J. Retrieval of leaf net photosynthetic rate of moso bamboo forests using hyperspectral remote sensing based on wavelet transform. Chin. J. Appl. Ecol. 2016, 27, 49–58. [Google Scholar]
- Li, Y.; Zhou, G.; Gu, C.; Xu, X.; Sun, S.; Gao, G. Chlorophyll content in Phyllostachys violascens related to hyper-spectral vegetation indices and development of an inversion model. J. Zhejiang AF Univ. 2015, 32, 335–345. [Google Scholar]
- Cheng-Yan, G.U.; Hua-Qiang, D.U.; Zhou, G.M.; Han, N.; Xiao-Jun, X.U.; Zhao, X.; Sun, X.Y. Retrieval of leaf area index of Moso bamboo forest with Landsat Thematic Mapper image based on PROSAIL canopy radiative transfer model. Chin. J. Appl. Ecol. 2013, 24, 2248–2256. [Google Scholar]
- Du, H.-Q.; Ge, H.-L.; Fan, W.-Y.; Jin, W.; Zhou, Y.-F.; Li, J. Study on relationships between total chlorophyll with hyperspectral features for leaves of Pinus massoniana forest. Spectrosc. Spectr. Anal. 2009, 29, 3033–3037. [Google Scholar]
- Doughty, C.E.; Asner, G.P.; Martin, R.E. Predicting tropical plant physiology from leaf and canopy spectroscopy. Oecologia 2011, 165, 289–299. [Google Scholar] [CrossRef]
- Serbin, S.P.; Dillaway, D.N.; Kruger, E.L.; Townsend, P.A. Leaf optical properties reflect variation in photosynthetic metabolism and its sensitivity to temperature. J. Exp. Bot. 2012, 63, 489–502. [Google Scholar] [CrossRef]
- Ainsworth, E.A.; Serbin, S.P.; Skoneczka, J.A. Using leaf optical properties to detect ozone effects on foliar biochemistry. Photosynth. Res. 2014, 119, 65–76. [Google Scholar] [CrossRef]
- Yendrek, C.R.; Tomaz, T.; Montes, C.M.; Cao, Y.; Morse, A.M.; Brown, P.J.; McIntyre, L.M.; Leakey, A.D.B.; Ainsworth, E.A. High-Throughput Phenotyping of Maize Leaf Physiological and Biochemical Traits Using Hyperspectral Reflectance. Plant Physiol. 2016, 173, 614–626. [Google Scholar] [CrossRef]
- Silva-Perez, V.; Molero, G.; Serbin, S.P.; Condon, A.G.; Reynolds, M.P.; Furbank, R.T.; Evans, J.R. Hyperspectral reflectance as a tool to measure biochemical and physiological traits in wheat. J. Exp. Bot. 2017, 69, 483–496. [Google Scholar] [CrossRef] [PubMed]
- Barnes, M.L.; Breshears, D.D.; Law, D.J.; van Leeuwen, W.J.D.; Monson, R.K.; Fojtik, A.C.; Barron-Gafford, G.A.; Moore, D.J.P. Beyond greenness: Detecting temporal changes in photosynthetic capacity with hyperspectral reflectance data. PLoS ONE 2017, 12, e0189539. [Google Scholar] [CrossRef]
- Dechant, B.; Cuntz, M.; Vohland, M.; Schulz, E.; Doktor, D. Estimation of photosynthesis traits from leaf reflectance spectra: Correlation to nitrogen content as the dominant mechanism. Remote Sens. Environ. 2017, 196, 279–292. [Google Scholar] [CrossRef]
- Wu, J.; Rogers, A.; Albert, L.P.; Ely, K.; Prohaska, N.; Wolfe, B.T.; Oliveira Jr, R.C.; Saleska, S.R.; Serbin, S.P. Leaf reflectance spectroscopy captures variation in carboxylation capacity across species, canopy environment and leaf age in lowland moist tropical forests. New Phytol. 2019, 224, 663–674. [Google Scholar] [CrossRef] [PubMed]
- Fu, P.; Meacham-Hensold, K.; Guan, K.; Wu, J.; Bernacchi, C. Estimating photosynthetic traits from reflectance spectra: A synthesis of spectral indices, numerical inversion, and partial least square regression. Plant Cell Environ. 2020, 43, 1241–1258. [Google Scholar] [CrossRef] [PubMed]
- Fu, P.; Meacham-Hensold, K.; Guan, K.; Bernacchi, C.J. Hyperspectral Leaf Reflectance as Proxy for Photosynthetic Capacities: An Ensemble Approach Based on Multiple Machine Learning Algorithms. Front. Plant Sci. 2019, 10, 730. [Google Scholar] [CrossRef]
- Song, G.; Wang, Q. Including Leaf Traits Improves a Deep Neural Network Model for Predicting Photosynthetic Capacity from Reflectance. Remote Sens. 2021, 13, 4467. [Google Scholar] [CrossRef]
- Im, J.; Jensen, J.R.; Jensen, R.R.; Gladden, J.; Waugh, J.; Serrato, M. Vegetation Cover Analysis of Hazardous Waste Sites in Utah and Arizona Using Hyperspectral Remote Sensing. Remote Sens. 2012, 4, 327–353. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, T.; Guo, W.; Xu, X.; Qiao, H.; Xie, Y.; Ma, X. Leaf area index estimation model for UAV image hyperspectral data based on wavelength variable selection and machine learning methods. Plant Methods 2021, 17, 49. [Google Scholar] [CrossRef]
- Wang, Q.; Iio, A.; Kakubari, Y. Broadband simple ratio closely traced seasonal trajectory of canopy photosynthetic capacity. Geophys. Res. Lett. 2008, 35, L07401. [Google Scholar] [CrossRef]
- Jin, P.; Wang, Q.; Iio, A.; Tenhunen, J. Retrieval of seasonal variation in photosynthetic capacity from multi-source vegetation indices. Ecol. Inform. 2012, 7, 7–18. [Google Scholar] [CrossRef]
- Bruce, L.M.; Koger, C.H.; Jiang, L. Dimensionality reduction of hyperspectral data using discrete wavelet transform feature extraction. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2331–2338. [Google Scholar] [CrossRef]
- Blackburn, G.A.; Ferwerda, J.G. Retrieval of chlorophyll concentration from leaf reflectance spectra using wavelet analysis. Remote Sens. Environ. 2008, 112, 1614–1632. [Google Scholar] [CrossRef]
- Wang, J.; Chen, Y.; Chen, F.; Shi, T.; Wu, G. Wavelet-based coupling of leaf and canopy reflectance spectra to improve the estimation accuracy of foliar nitrogen concentration. Agric. For. Meteorol. 2018, 248, 306–315. [Google Scholar] [CrossRef]
- Li, F.; Wang, L.; Liu, J.; Wang, Y.; Chang, Q. Evaluation of Leaf N Concentration in Winter Wheat Based on Discrete Wavelet Transform Analysis. Remote Sens. 2019, 11, 1331. [Google Scholar] [CrossRef]
- Pu, R.; Gong, P. Wavelet transform applied to EO-1 hyperspectral data for forest LAI and crown closure mapping. Remote Sens. Environ. 2004, 91, 212–224. [Google Scholar] [CrossRef]
- Mao, F.; Li, P.; Zhou, G.; Du, H.; Xu, X.; Shi, Y.; Mo, L.; Zhou, Y.; Tu, G. Development of the BIOME-BGC model for the simulation of managed Moso bamboo forest ecosystems. J. Environ. Manag. 2016, 172, 29–39. [Google Scholar] [CrossRef] [PubMed]
- Mao, F.; Du, H.; Li, X.; Ge, H.; Cui, L.; Zhou, G. Spatiotemporal dynamics of bamboo forest net primary productivity with climate variations in Southeast China. Ecol. Indic. 2020, 116, 106505. [Google Scholar] [CrossRef]
- Kang, F.; Li, X.; Du, H.; Mao, F.; Zhou, G.; Xu, Y.; Huang, Z.; Ji, J.; Wang, J. Spatiotemporal Evolution of the Carbon Fluxes from Bamboo Forests and their Response to Climate Change Based on a BEPS Model in China. Remote Sens. 2022, 14, 366. [Google Scholar] [CrossRef]
- Ren, Y.; Yang, S.; Dongxiong, W.U.; Huang, C.; Guan, Y.; Miao, Y. Leaf senescence characteristics and the screen and identification of leaf senescence associated genes in moso bamboo. J. Fujian Agric. For. Univ. (Nat. Sci. Ed.) 2017, 46, 630–640. [Google Scholar]
- Wu, J.; Albert, L.P.; Lopes, A.P.; Restrepo-Coupe, N.; Hayek, M.; Wiedemann, K.T.; Guan, K.; Stark, S.C.; Christoffersen, B.; Prohaska, N.; et al. Leaf development and demography explain photosynthetic seasonality in Amazon evergreen forests. Science 2016, 351, 972–976. [Google Scholar] [CrossRef] [PubMed]
- Loren, P.A.; Jin, W.; Neill, P.; Plinio, B.d.C.; Travis, E.H.; Edgard, S.T.; Valeriy, Y.I.; Rafael, S.O.; Sabrina, G.; Marielle, N.S.; et al. Age-dependent leaf physiology and consequences for crown-scale carbon uptake during the dry season in an Amazon evergreen forest. New Phytol. 2018, 219, 870–884. [Google Scholar]
- Bielczynski, L.W.; Łącki, M.K.; Hoefnagels, I.; Gambin, A.; Croce, R. Leaf and Plant Age Affects Photosynthetic Performance and Photoprotective Capacity. Plant Physiol. 2017, 175, 1634–1648. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Song, C.; Song, J.; Wang, J.; Chen, S.; Yang, L.; Xiang, W.; Zhao, Z.; Jiang, J. Effects of leaf age and canopy structure on gross ecosystem production in a subtropical evergreen Chinese fir forest. Agric. For. Meteorol. 2021, 310, 108618. [Google Scholar] [CrossRef]
- Chen, G.-Y.; Yu, G.-L.; Chen, Y.; Xu, D.-Q. Exploring the observation methods of photosynthetic responses to light and carbon dioxide. Zhi Wu Sheng Li Yu Fen Zi Sheng Wu Xue Xue Bao J. Plant Physiol. Mol. Biol. 2006, 32, 691–696. [Google Scholar]
- Xia, N.; Yong-hui, C.; Ben-zhi, Z.; Xiao-zhen, L.; Yan, Z. Light Response of Phyllostachys edulis under Drought Stress: Based on 4 Models. For. Res. 2017, 30, 465–471. [Google Scholar]
- YE, Z.-P.; Yu, Q. Comparison of new and several classical models of photosynthesis in response to irradiance. Chin. J. Plant Ecol. 2008, 32, 1356. [Google Scholar]
- Liang, X.-Y.; Liu, S.-R. A review on the FvCB biochemical model of photosynthesis and the measurement of A-Ci curves. Chin. J. Plant Ecol. 2017, 41, 693–706. [Google Scholar]
- Sharkey, T.D.; Bernacchi, C.J.; Farquhar, G.D.; Singsaas, E.L. Fitting photosynthetic carbon dioxide response curves for C3 leaves. Plant Cell Environ. 2007, 30, 1035–1040. [Google Scholar] [CrossRef]
- Gu, L.; Pallardy, S.G.; Tu, K.P.; Law, B.E.; Wullschlrger, S.D. Reliable estimation of biochemical parameters from C3 leaf photosynthesis–intercellular carbon dioxide response curves. Plant Cell Environ. 2010, 33, 1852–1874. [Google Scholar] [CrossRef]
- Duursma, R.A. Plantecophys-An R Package for Analysing and Modelling Leaf Gas Exchange Data. PLoS ONE 2015, 10, e0143346. [Google Scholar] [CrossRef] [PubMed]
- Filella, I.; Serrano, L.; Serra, J.; Peñuelas, J. Evaluating Wheat Nitrogen Status with Canopy Reflectance Indices and Discriminant Analysis. Crop Sci. 1995, 35, 1400–1405. [Google Scholar] [CrossRef]
- Barnes, E.; Clarke, T.; Richards, S.; Colaizzi, P.; Haberland, J.; Kostrzewski, M.; Waller, P.; Choi, C.; Riley, E.; Thompson, T. Coincident detection of crop water stress, nitrogen status and canopy density using ground based multispectral data. Proceedings of 5th International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000; p. 6. [Google Scholar]
- Chen, P.; Haboudane, D.; Tremblay, N.; Wang, J.; Vigneault, P.; Li, B. New spectral indicator assessing the efficiency of crop nitrogen treatment in corn and wheat. Remote Sens. Environ. 2010, 114, 1987–1997. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Miller, J.R.; Mohammed, G.H.; Noland, T.L.; Sampson, P.H. Canopy optical indices from infinite reflectance and canopy reflectance models for forest condition monitoring: Application to hyperspectral CASI data. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium, IGARSS’99 (Cat. No.99CH36293), Hamburg, Germany, 28 June–2 July 1999; Volume 1873, pp. 1878–1881. [Google Scholar]
- Rouse Jr, J.W.; Haas, R.H.; Deering, D.W.; Schell, J.A.; Harlan, J.C. Monitoring the Vernal Advancement and Retrogradation (Green Wave Effect) of Natural Vegetation; RSC-1978-4; NASA Goddard Space Flight Center: Greenbelt, MD, USA, 1974.
- Vogelmann, J.E.; Rock, B.N.; Moss, D.M. Red edge spectral measurements from sugar maple leaves. Int. J. Remote Sens. 1993, 14, 1563–1575. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Relationships between leaf pigment content and spectral reflectance across a wide range of species, leaf structures and developmental stages. Remote Sens. Environ. 2002, 81, 337–354. [Google Scholar] [CrossRef]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ. 1992, 41, 35–44. [Google Scholar] [CrossRef]
- Blackburn, G.A. Spectral indices for estimating photosynthetic pigment concentrations: A test using senescent tree leaves. Int. J. Remote Sens. 1998, 19, 657–675. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Merzlyak, M.N. Remote estimation of chlorophyll content in higher plant leaves. Int. J. Remote Sens. 1997, 18, 2691–2697. [Google Scholar] [CrossRef]
- Carter, G.A. Ratios of leaf reflectances in narrow wavebands as indicators of plant stress. Int. J. Remote Sens. 1994, 15, 697–703. [Google Scholar] [CrossRef]
- le Maire, G.; François, C.; Dufrêne, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ. 2004, 89, 1–28. [Google Scholar] [CrossRef]
- Oppelt, N.; Mauser, W. The Chlorophyll Content of Maize (zea mays) Derived with the Airborne Imaging Spectrometer AVIS. In Proceedings of the Mesures physiques et signatures en télédétection, Aussois, France, 8–12 January 2001; pp. 407–412. [Google Scholar]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Daughtry, C.S.T.; Walthall, C.L.; Kim, M.S.; de Colstoun, E.B.; McMurtrey, J.E. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Miller, J.R.; Hare, E.W.; Wu, J. Quantitative characterization of the vegetation red edge reflectance 1. An inverted-Gaussian reflectance model. Int. J. Remote Sens. 1990, 11, 1755–1773. [Google Scholar] [CrossRef]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Wang, L.; Hunt, E.R.; Qu, J.J.; Hao, X.; Daughtry, C.S.T. Towards estimation of canopy foliar biomass with spectral reflectance measurements. Remote Sens. Environ. 2011, 115, 836–840. [Google Scholar] [CrossRef]
- Borovskaya, R.; Krivoguz, D.; Chernyi, S.; Kozhurin, E.; Khorosheltseva, V.; Zinchenko, E. Surface Water Salinity Evaluation and Identification for Using Remote Sensing Data and Machine Learning Approach. J. Mar. Sci. Eng. 2022, 10, 257. [Google Scholar] [CrossRef]
- Heckmann, D.; Schlüter, U.; Weber, A.P.M. Machine Learning Techniques for Predicting Crop Photosynthetic Capacity from Leaf Reflectance Spectra. Mol. Plant 2017, 10, 878–890. [Google Scholar] [CrossRef] [PubMed]
- Pantin, F.; Simonneau, T.; Muller, B. Coming of leaf age: Control of growth by hydraulics and metabolics during leaf ontogeny. New Phytol. 2012, 196, 349–366. [Google Scholar] [CrossRef]
- Peng, C.; Song, Y.; Li, C.; Mei, T.; Wu, Z.; Shi, Y.; Zhou, Y.; Zhou, G. Growing in Mixed Stands Increased Leaf Photosynthesis and Physiological Stress Resistance in Moso Bamboo and Mature Chinese Fir Plantations. Front. Plant Sci. 2021, 12, 649204. [Google Scholar] [CrossRef]
- Kenzo, T.; Ichie, T.; Watanabe, Y.; Yoneda, R.; Ninomiya, I.; Koike, T. Changes in photosynthesis and leaf characteristics with tree height in five dipterocarp species in a tropical rain forest. Tree Physiol. 2006, 26, 865–873. [Google Scholar] [CrossRef]
- Curran, P.J. Remote sensing of foliar chemistry. Remote Sens. Environ. 1989, 30, 271–278. [Google Scholar] [CrossRef]
- Zhou, Y.; Ju, W.; Sun, X.; Hu, Z.; Han, S.; Black, T.A.; Jassal, R.S.; Wu, X. Close relationship between spectral vegetation indices and Vcmax in deciduous and mixed forests. Tellus B Chem. Phys. Meteorol. 2014, 66, 23279. [Google Scholar] [CrossRef]
- McDonald, A.J.; Gemmell, F.M.; Lewis, P.E. Investigation of the Utility of Spectral Vegetation Indices for Determining Information on Coniferous Forests. Remote Sens. Environ. 1998, 66, 250–272. [Google Scholar] [CrossRef]
- Houborg, R.; Soegaard, H.; Boegh, E. Combining vegetation index and model inversion methods for the extraction of key vegetation biophysical parameters using Terra and Aqua MODIS reflectance data. Remote Sens. Environ. 2007, 106, 39–58. [Google Scholar] [CrossRef]
- Wang, X.; Cai, G.; Lu, X.; Yang, Z.; Zhang, X.; Zhang, Q. Inversion of Wheat Leaf Area Index by Multivariate Red-Edge Spectral Vegetation Index. Sustainability 2022, 14, 15875. [Google Scholar] [CrossRef]
- Du, H.; Zhou, G.; Mao, F.; Han, N. Quantitative Retrieval of Bamboo Forest Parameters by Multi-Source Remote Sensing; China Science Publishing & Media Ltd.: Beijing, China, 2022. [Google Scholar]
- Pu, R.; Gong, P. Hyperspectral Remote Sensing and Its Application; High Education Press: Beijing, China, 2000. [Google Scholar]
- Quebbeman, J.A.; Ramirez, J.A. Optimal allocation of leaf-level nitrogen: Implications for covariation of Vcmax and Jmax and photosynthetic downregulation. J. Geophys. Res. Biogeosciences 2016, 121, 2464–2475. [Google Scholar] [CrossRef]
- Jauregui, I.; Pozueta-Romero, J.; Córdoba, J.; Avice, J.-C.; Aparicio-Tejo, P.M.; Baroja-Fernández, E.; Aranjuelo, I. Unraveling the role of transient starch in the response of Arabidopsis to elevated CO2 under long-day conditions. Environ. Exp. Bot. 2018, 155, 158–164. [Google Scholar] [CrossRef]
- Du, H.; Zhou, G.; Ge, H.; Fan, W.; Xu, X.; Fan, W.; Shi, Y. Satellite-based carbon stock estimation for bamboo forest with a non-linear partial least square regression technique. Int. J. Remote Sens. 2012, 33, 1917–1933. [Google Scholar] [CrossRef]
- Jin, J.; Arief Pratama, B.; Wang, Q. Tracing Leaf Photosynthetic Parameters Using Hyperspectral Indices in an Alpine Deciduous Forest. Remote Sens. 2020, 12, 1124. [Google Scholar] [CrossRef]


| Type | HVI | Formula | Reference |
|---|---|---|---|
| Leaf Nitrogen | Nitrogen reflectance index (NRI) | (R570 − R670)/(R570 + R670) | Filella et al., 1995 [54] |
| Normalized difference red edge index (NDRE) | (R790 − R720)/(R790 + R720) | Barnes et al., 2000 [55] | |
| Double-peak canopy nitrogen index (DCNI) | Chen et al., 2010 [56] | ||
| Normalized difference vegetation index (NDVI1) | (R774 − R677)/(R774 + R677) | Zarco et al., 1999 [57] | |
| Normalized difference vegetation index (NDVI2) | (R800 − R670)/(R800 + R670) | Rouse et al., 1974 [58] | |
| Chlorophyll | Ratio of first derivative (D715/D705) | (R716 − R714)/(R706 − R704) | Vogelmann et al., 1993 [59] |
| Modified simple ratio (mSR705) | (R750 − R445)/(R705 + R445) | Sims et al., 2002 [60] | |
| Modified NDVI (mND705) | (R750 − R705)/(R750 + R705 − 2 ∗ R445) | Sims et al., 2002 [60] | |
| Physiological reflectance index (PRI) | (R570 − R539)/(R570 + R539) | Gamon et al., 1992 [61] | |
| Pigment specific simple ratio (PSSR) | R810/R674 | Zarco et al., 1999 [57] | |
| Pigment specific simple ratio Chla (PSSRa) | R800/R680 | Blackburn et al., 1998 [62] | |
| Pigment specific simple ratio Chlb (PSSRb) | R800/R635 | Blackburn et al., 1998 [62] | |
| Gitelson and Merzlyak index (GM) | R750/R700 | Gitelson et al.,1997 [63] | |
| Vogelmann index (Vog) | R740/R720 | Vogelmann et al., 1993 [59] | |
| Carter index (Carter) | R695/R760 | Carter et al., 1994 [64] | |
| Double difference index (DD) | (R750 − R720) − (R700 − R670) | le Mairet et al., 2004 [65] | |
| Modified chlorophyll absorption integral (mCAI) | Oppelt et al., 2001 [66] | ||
| Distance from the base line spanned by the green reflectance peak (CAR) | Broge et al., 2001 [67] | ||
| Modified chlorophyll absorption ratio index (MCARI) | Daughtry et al., 2000 [68] | ||
| Transformed chlorophyll absorption in reflectance index (TCARI) | Haboudane et al., 2002 [69] | ||
| TCARI/Optimized soil-adjusted vegetation index (TCARI/OSAVI) | TCARI/OSAVI | Haboudane et al., 2002 [69] | |
| MCARI/OSAVI | MCARI/OSAVI | Daughtry et al., 2000 [68] | |
| Red edge position (REP) | Miller et al., 1990 [70] | ||
| Integration of reflectivity at 450–680 nm (AR) | Zarco et al., 1999 [57] | ||
| Leaf Mass Area | Normalized dry leaf mass area index (NDLMA) | (R1368 − R1722)/(R1368 + R1722) | Feret et al., 2008 [71] |
| Normalized dry matter index (NDMI) | (R1649 − R1722)/(R1649 + R1722) | Wang et al., 2011 [72] |
| Absolute Value of Correlation, |R| | Interpretation |
|---|---|
| 0.00–0.30 | Negligible correlation |
| 0.30–0.50 | Weak correlation |
| 0.50–0.70 | Moderate correlation |
| 0.70–0.90 | Strong correlation |
| 0.90–1.00 | Very strong correlation |
| Leaf Nitrogen | Chlorophyll | Leaf Mass Area | |
|---|---|---|---|
| Top | NDRE (0.69) | Carter (0.74) | NDMI (0.61) |
| Middle | NDRE (0.66) | D715/D705 (0.68) | NDMI (0.53) |
| Bottom | NDRE (0.70) | REP (0.75) | NDMI (0.55) |
| Coefficients | I du | II du | ||
|---|---|---|---|---|
| WVI | |r| | WVI | |r| | |
| cA6 | wDVI692,820 | 0.61 | wDVI2292,1844 | 0.32 |
| wSR1460,2292 | 0.60 | wSR1652,1780 | 0.35 | |
| wNDVI2292,1460 | 0.60 | wNDVI1780,1652 | 0.35 | |
| cD1 | wDVI2185,2153 | 0.73 | wDVI1161,819 | 0.62 |
| wSR2148,2188 | 0.75 | wSR1684,2221 | 0.57 | |
| wNDVI2185,2147 | 0.74 | wNDVI2343,1714 | 0.59 | |
| cD2 | wDVI2178,2154 | 0.74 | wDVI2069,407 | 0.67 |
| wSR2154,2186 | 0.74 | wSR407,443 | 0.66 | |
| wNDVI2186,2154 | 0.74 | wNDVI2441,407 | 0.61 | |
| cD3 | wDVI2182,2158 | 0.71 | wDVI910,878 | 0.60 |
| wSR2158,2178 | 0.72 | wSR2362,2330 | 0.49 | |
| wNDVI2130,1418 | 0.71 | wNDVI2342,1154 | 0.54 | |
| cD4 | wDVI2176,2160 | 0.72 | wDVI2224,1696 | 0.51 |
| wSR2152,2184 | 0.73 | wSR1696,2224 | 0.54 | |
| wNDVI2184,2152 | 0.73 | wNDVI2312,1152 | 0.50 | |
| cD5 | wDVI2140,1628 | 0.72 | wDVI2396,1148 | 0.45 |
| wSR2156,2188 | 0.73 | wSR1516,2316 | 0.46 | |
| wNDVI2188,2156 | 0.73 | wNDVI2380,1148 | 0.48 | |
| cD6 | wDVI1604,836 | 0.60 | wDVI2372,1156 | 0.40 |
| wSR2084,740 | 0.60 | wSR1731,2372 | 0.40 | |
| wNDVI2084,740 | 0.60 | wNDVI2372,1124 | 0.46 |
| Coefficients | Top | Middle | Bottom | |||
|---|---|---|---|---|---|---|
| WVI | |r| | WVI | |r| | WVI | |r| | |
| cA6 | wDVI2420,1460 | 0.75 | wDVI820,756 | 0.66 | wDVI1076,564 | 0.76 |
| wSR692,820 | 0.73 | wSRC756,820 | 0.67 | wSR500,1908 | 0.75 | |
| wNDVI756,692 | 0.73 | wNDVI820,756 | 0.66 | wNDVI1908,500 | 0.74 | |
| cD1 | wDVI1827,490 | 0.84 | wDVI2153,1225 | 0.82 | wDVI2205,630 | 0.86 |
| wSR667,1667 | 0.84 | wSR1623,2153 | 0.82 | wSR2146,2183 | 0.87 | |
| wNDVI2234,1309 | 0.82 | wNDVI2153,1623 | 0.81 | wNDVI2196,2146 | 0.85 | |
| cD2 | wDVI2243,477 | 0.85 | wDVI1675,1291 | 0.80 | wDVI2205,631 | 0.86 |
| wSR629,1675 | 0.82 | wSR1359,1739 | 0.78 | wSR1995,719 | 0.85 | |
| wNDVI1665,479 | 0.83 | wNDVI1739,1359 | 0.78 | wNDVI1995,719 | 0.85 | |
| cD3 | wDVI2286,482 | 0.83 | wDVI2174,2156 | 0.78 | wDVI2186,2162 | 0.85 |
| wSR486,2062 | 0.82 | wSR2178,2156 | 0.78 | wSR2158,2186 | 0.85 | |
| wNDVI2062,486 | 0.81 | wNDVI2174,2156 | 0.76 | wNDVI1994,718 | 0.85 | |
| cD4 | wDVI2288,488 | 0.79 | wDVI2144,1632 | 0.75 | wDVI1424,640 | 0.86 |
| wSR504,1096 | 0.80 | wSR528,584 | 0.74 | wSR2160,2192 | 0.83 | |
| wNDVI2240,952 | 0.78 | wNDVI2144,1416 | 0.74 | wNDVI2000,728 | 0.83 | |
| cD5 | wDVI1820,732 | 0.76 | wDVI2140,1628 | 0.76 | wDVI1420,652 | 0.84 |
| wSR636,1068 | 0.79 | wSR2140,1420 | 0.76 | wSR2156,2188 | 0.82 | |
| wNDVI2092,732 | 0.79 | wNDVI2140,1420 | 0.76 | wNDVI2188,2156 | 0.83 | |
| cD6 | wDVI2044,804 | 0.74 | wDVI2148,836 | 0.71 | wDVI1892,516 | 0.82 |
| wSR484,2276 | 0.77 | wSR2148,740 | 0.74 | wSR516,1924 | 0.80 | |
| wNDVI2436,420 | 0.77 | wNDVI2148,740 | 0.74 | wNDVI1924,400 | 0.80 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, K.; Li, X.; Du, H.; Mao, F.; Ni, C.; Chen, Q.; Xu, Y.; Huang, Z. Wavelet Vegetation Index to Improve the Inversion Accuracy of Leaf V25cmax of Bamboo Forests. Remote Sens. 2023, 15, 2362. https://doi.org/10.3390/rs15092362
Guo K, Li X, Du H, Mao F, Ni C, Chen Q, Xu Y, Huang Z. Wavelet Vegetation Index to Improve the Inversion Accuracy of Leaf V25cmax of Bamboo Forests. Remote Sensing. 2023; 15(9):2362. https://doi.org/10.3390/rs15092362
Chicago/Turabian StyleGuo, Keruo, Xuejian Li, Huaqiang Du, Fangjie Mao, Chi Ni, Qi Chen, Yanxin Xu, and Zihao Huang. 2023. "Wavelet Vegetation Index to Improve the Inversion Accuracy of Leaf V25cmax of Bamboo Forests" Remote Sensing 15, no. 9: 2362. https://doi.org/10.3390/rs15092362







