Six Years of IKFS-2 Global Ozone Total Column Measurements
Abstract
1. Introduction
2. Materials and Methods
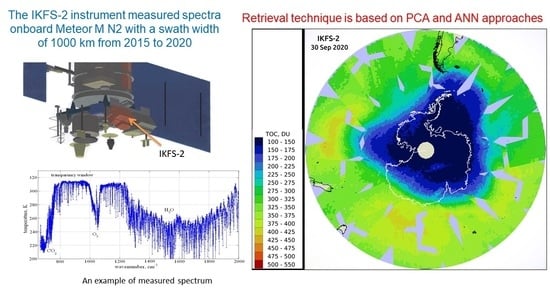
2.1. The IKFS-2 Instrument
2.2. Ozone Retrieval with the Updated ANN Algorithm
3. Results
3.1. Comparison versus Ground-Based Measurements
3.1.1. Comparison versus Hourly Dobson and Brewer Data
3.1.2. Comparison versus Daily Dobson and Brewer Data
- −
- Displacement of the intersection between the solar radiation trajectory and the layer of maximum ozone content from the location of the station due to the low Sun;
- −
- Greater ozone variability in polar latitudes, both in space and time, compared to the tropical regions;
- −
- An increase in IKFS-2 TOC retrieval errors that is associated with a possible decrease in the altitude gradient of the air temperature in the polar atmosphere and low surface temperature.
3.2. Comparison versus Satellite Data
3.2.1. Comparison versus OMI Data—Approximation Errors
3.2.2. Comparison versus TROPOMI
4. Discussion (Analysis of TOC Variability)
4.1. Comparison of Monthly Averaged Satellite Data
4.1.1. IKFS-2 and OMI
4.1.2. IKFS-2 and IASI
4.2. Analysis of IKFS-2 TOC Retrievals
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A






Appendix B
Appendix B.1. Retrieval Algorithm Detailed Description
Appendix B.1.1. Input Parameters
Appendix B.1.2. Algorithm Step by Step
| Spectral Region | Name | NPC | Spectral Point Numbers (Wavenumber, cm−1) | |
|---|---|---|---|---|
| First point k1 | Last point k2 | |||
| 660–1210 | Global | = 25 | 1 (660) | 1571 (1210) |
| 980–1080 | O3 band | = 50 | 915 (980) | 1200 (1080) |
| Parameter | Name | Input Vector |
|---|---|---|
| fraction of year (Day number/365 or 366) | f | |
| Pixel latitude, degrees | lat | |
| A zenith angle of satellite from pixel, degrees | Za | |
| PCs in the 600–1210 cm−1 spectral region | PCtotal | |
| PCs in the 980–1080 cm−1 spectral region | PCO3 |
| Name | Meaning | Type (Fortran) |
|---|---|---|
| f | Activation function | Character *4 |
| nl | Layers number, always 2 | Integer *4 |
| nx | Length of vector X | Integer *4 |
| nh | Number of hidden level neurons | Integer *4 |
| ny = 1 | Results number | Integer *4 |
| nz = 1 | Reserved | Integer *4 |
| Xmin | Xmin | Real *4 |
| Xmax | Xmax | Real *4 |
| Ymin | Ymin | Real *4 |
| Ymax | Ymax | Real *4 |
| b2 | ANN coefficien | Real *8 |
| W2 | ANN coefficiens | Real *8 |
| b1 | ANN coefficiens | Real *8 |
| W1 | ANN coefficiens | Real *8 |
| EOF total | ||
| nv | Number of spectral points = 1571 | Integer *4 |
| NPC | Number of EOF = 25 | Integer *4 |
| , EOF | Mean spectra and EOF | Real *8 |
| EOF O3 | ||
| Nv | Number of spectral points = 286 | Integer *4 |
| NPC | Number of EOF = 50 | Integer *4 |
| , EOF | Mean spectra and EOF | Real *8 |
References
- Farman, J.; Gardiner, B.; Shanklin, J. Large Losses of Total Ozone in Antarctica Reveal Seasonal ClOx/NOx Interaction. Nature 1985, 315, 207–210. [Google Scholar] [CrossRef]
- Chiodo, G.; Polvani, L.M.; Previdi, M. Large Increase in Incident Shortwave Radiation Due to the Ozone Hole Offset by High Climatological Albedo over Antarctica. J. Clim. 2017, 30, 4883–4890. [Google Scholar] [CrossRef]
- World Meteorological Organization (WMO). Executive Summary. Scientific Assessment of Ozone Depletion: 2022; GAW Report No. 278; WMO: Geneva, Switzerland, 2022; p. 56. Available online: https://ozone.unep.org/system/files/documents/Scientific-Assessment-of-Ozone-Depletion-2022-Executive-Summary.pdf (accessed on 5 March 2023).
- Bernhard, G.H.; Fioletov, V.E.; Groos, J.U.; Ialongo, I.; Johnsen, B.; Lakkala, K.; Svenby, T.; Muller, R.; Svendby, T. Record-Breaking Increases in Arctic Solar Ultraviolet Radiation Caused by Exceptionally Large Ozone Depletion in 2020. Geophys. Res. Lett. 2020, 47, e2020GL090844. [Google Scholar] [CrossRef]
- Manney, G.L.; Livesey, N.J.; Santee, M.L.; Froidevaux, L.; Lambert, A.; Lawrence, Z.D.; Millan, L.F.; Neu, J.L.; Read, W.G.; Schwartz, M.J.; et al. Record-Low Arctic Stratospheric Ozone in 2020: MLS Observations of Chemical Processes and Comparisons with Previous Extreme Winters. Geophys. Res. Lett. 2020, 47, e2020GL089063. [Google Scholar] [CrossRef]
- Lawrence, Z.D.; Perlwitz, J.; Butler, A.H.; Manney, G.L.; Newman, P.A.; Lee, S.H.; Nash, E.R. The Remarkably Strong Arctic Stratospheric Polar Vortex of Winter 2020: Links to Record-Breaking Arctic Oscillation and Ozone Loss. J. Geophys. Res. Atmos. 2020, 125, e2020JD033271. [Google Scholar] [CrossRef]
- Grooβ, J.-U.; Muller, R. Simulation of Record Arctic Stratospheric Ozone Depletion in 2020. J. Geophys. Res. 2021, 126, e2020JD033339. [Google Scholar] [CrossRef]
- Bernath, P.F. The Atmospheric Chemistry Experiment (ACE). J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 3–16. [Google Scholar] [CrossRef]
- Levelt, P.F.; Joiner, J.; Tamminen, J.; Veefkind, J.P.; Bhartia, P.K.; Zweers, D.C.S.; Duncan, B.N.; Streets, D.G.; Eskes, H.; van der A, R.; et al. The Ozone Monitoring Instrument: Overview of 14 Years in Space. Atmos. Chem. Phys. 2018, 18, 5699–5745. [Google Scholar] [CrossRef]
- Veefkind, J.P.; Aben, I.; McMullan, K.; Förster, H.; De Vries, J.; Otter, G.; Claas, J.; Eskes, H.J.; De Haan, J.F.; Kleipool, Q.; et al. TROPOMI on the ESA Sentinel-5 Precursor: A GMES Mission for Global Observations of the Atmospheric Composition for Climate, Air Quality and Ozone Layer Applications. Remote Sens. Environ. 2012, 120, 70–83. [Google Scholar] [CrossRef]
- Van Roozendael, M.; Loyola, D.; Spurr, R.; Balis, D.; Lambert, J.-C.; Livschitz, Y.; Valks, P.; Ruppert, T.; Kenter, P.; Fayt, C.; et al. TenYears of GOME/ERS-2 Total Ozone Data-The New GOME Data Processor (GDP) Version 4: 1. Algorithm Description. J. Geophys. Res. 2006, 111, D14311. [Google Scholar] [CrossRef]
- Seftor, C.J.; Jaross, G.; Kowitt, M.; Haken, M.; Li, J.; Flynn, L. Postlaunch Performance of the Suomi National Polar Orbiting Partnership Ozone Mapping and Profiler Suite (OMPS) Nadir Sensors. J. Geophys. Res. Atmos. 2014, 119, 4413–4428. [Google Scholar] [CrossRef]
- Aumann, H.H.; Chahine, M.T.; Gautier, C.; Goldberg, M.D.; Kalnay, E.; McMillin, L.M.; Revercomb, H.; Rosenkranz, P.W.; Smith, W.L.; Staelin, D.H.; et al. AIRS/AMSU/HSB on the Aqua Mission: Design, Science Objectives, Data Products, and Processing Systems. IEEE Geosci. Remote Sens. Lett. 2003, 41, 253–264. [Google Scholar] [CrossRef]
- Nassar, R.; Logan, J.; Worden, H.; Megretskaia, I.; Bowman, K.; Osterman, G.; Thompson, A.; Tarasick, D.W.; Austin, S.; Claude, H.; et al. Validation of Tropospheric Emission Spectrometer (TES) Nadir Ozone Profiles Using Ozonesonde Measurements. J. Geophys. Res. 2008, 113, D15S17. [Google Scholar] [CrossRef]
- Boynard, A.; Hurtmans, D.; Koukouli, M.E.; Goutail, F.; Bureau, J.; Safieddine, S.; Lerot, C.; Hadji-Lazaro, J.; Wespes, C.; Pommereau, J.-P.; et al. Seven years of IASI ozone retrievals from FORLI: Validation with independent total column and vertical profile measurements. Atmos. Meas. Technol. 2016, 9, 4327–4353. [Google Scholar] [CrossRef]
- Timofeyev, Y.M.; Uspensky, A.B.; Zavelevich, F.S.; Polyakov, A.V.; Virolainen, Y.A.; Rublev, A.N.; Kukharsky, A.V.; Kiseleva, J.V.; Kozlov, D.A.; Kozlov, I.A.; et al. Hyperspectral infrared atmospheric sounder IKFS-2 on “Meteor-M” No. 2—Four years in orbit. J. Quant. Spectrosc. Radiat. Transf. 2019, 238, 106579. [Google Scholar] [CrossRef]
- Froidevaux, L.Y.; Jiang, B.; Lambert, A.; Livesey, N.J.; Read, W.G.; Waters, J.W.; Browell, E.V.; Fuller, R.A.; Marcy, T.P.; Popp, P.J.; et al. Validation of Aura Microwave Limb Sounder Stratospheric Ozone Measurements. J. Geophys. Res. 2008, 113, D15S20. [Google Scholar] [CrossRef]
- McPeters, R.D.; Kroon, M.; Labow, G.; Brinksma, E.; Balis, D.; Petropavlovskikh, I.; Veefkind, J.P.; Bhartia, P.K.; Levelt, P.F. Validation of the Aura Ozone Monitoring Instrument Total Column Ozone Product. J. Geophys. Res. 2008, 113, D15S14. [Google Scholar] [CrossRef]
- McPeters, R.D.; Frith, S.; Labow, G.J. OMI Total Column Ozone: Extending the Long-Term Data Record. Atmos. Meas. Tech. 2015, 8, 4845–4850. [Google Scholar] [CrossRef]
- Kuttippurath, J.; Kumar, P.; Nair, P.J.; Chakraborty, A. Accuracy of Satellite Total Columnzone Measurements in Polar Vortex Conditions: Comparison with Ground-Based Observations in 1979–2013. Remote Sens. Environ. 2018, 209, 648–659. [Google Scholar] [CrossRef]
- Garane, K.; Koukouli, M.-E.; Verhoelst, T.; Lerot, C.; Heue, K.-P.; Fioletov, V.; Balis, D.; Bais, A.; Bazureau, A.; Dehn, A.; et al. TROPOMI/S5P total ozone column data: Global ground-based validation and consistency with other satellite missions. Atmos. Meas. Technol. 2019, 12, 5263–5287. [Google Scholar] [CrossRef]
- Viatte, C.; Schneider, M.; Redondas, A.; Hase, F.; Eremenko, M.; Chelin, P.; Flaud, J.-M.; Blumenstock, T.; Orphal, J. Comparison of Ground-based FTIR and Brewer O3 Total Column with Data from Two Different IASI Algorithms and from OMI and GOME-2 Satellite Instruments. Atmos. Meas. Technol. 2011, 4, 535–546. [Google Scholar] [CrossRef]
- Virolainen, Y.A.; Timofeyev, Y.M.; Poberovskii, A.V.; Polyakov, A.V.; Shalamyanskii, A.M. Empirical Assessment of Errors in Total Ozone Measurements with Different Instruments and Methods. Atmos. Ocean. Opt. 2017, 30, 382–388. [Google Scholar] [CrossRef]
- Garkusha, A.S.; Polyakov, A.V.; Timofeev, Y.M.; Virolainen, Y.A. Determination of the total ozone content from data of satellite IR Fourier-spectrometer. Izv. Atmos. Ocean. Phys. 2017, 53, 433–440. [Google Scholar] [CrossRef]
- Garkusha, A.S.; Polyakov, A.V.; Timofeev, Y.M.; Virolainen, Y.A.; Kukharsky, A.V. Determination of the Total Ozone Content in Cloudy Conditions based on Data from the IKFS-2 Spectrometer Onboard the Meteor-M no. 2 Satellite. Izv. Atmos. Ocean. Phys. 2018, 54, 1244–1248. [Google Scholar] [CrossRef]
- Polyakov, A.V.; Timofeyev, Y.M.; Virolainen, Y.A.; Kozlov, D.A. Atmospheric Ozone Monitoring with Russian Spectrometer IKFS-2. J. Appl. Spectrosc. 2019, 86, 650–654. [Google Scholar] [CrossRef]
- Virolainen, Y.A.; Timofeyev, Y.M.; Poberovsky, A.V. Intercomparison of Satellite and Ground-Based Ozone Total Column Measurements. Izv. Atmos. Ocean. Phys. 2013, 49, 993–1001. [Google Scholar] [CrossRef]
- Nerobelov, G.; Timofeyev, Y.; Virolainen, Y.; Polyakov, A.; Solomatnikova, A.; Poberovskii, A.; Kirner, O.; Al-Subari, O.; Smyshlyaev, S.; Rozanov, E. Measurements and Modelling of Total Ozone Columns near St. Petersburg, Russia. Remote Sens. 2022, 14, 3944. [Google Scholar] [CrossRef]
- Polyakov, A.; Virolainen, Y.; Nerobelov, G.; Timofeyev, Y.; Solomatnikova, A. Total ozone measurements using IKFS-2 spectrometer aboard MeteorM N2 satellite in 2019–2020. Int. J. Rem. Sens. 2021, 42, 8709–8733. [Google Scholar] [CrossRef]
- Golovin, Y.M.; Zavelevich, F.S.; Nikulin, A.G.; Kozlov, D.A.; Monakhov, D.O.; Kozlov, I.A.; Arkhipov, S.A.; Tselikov, V.A.; Romanovskii, A.S. Spaceborne Infrared Fourier-Transform Spectrometers for Temperature and Humidity Sounding of the Earth’s Atmosphere. Izv. Atmos. Ocean. Phys. 2014, 50, 1004–1015. [Google Scholar] [CrossRef]
- Timofeev, Y.M.; Nerobelov, G.M.; Polyakov, A.V.; Virolainen, Y.A. Satellite monitoring of the ozonosphere. Russ. Meteorol. Hydrol. 2021, 46, 849–855. [Google Scholar] [CrossRef]
- Balis, D.; Kroon, M.; Koukouli, M.E.; Brinksma, E.J.; Labow, G.; Veefkind, J.P.; McPeters, R.D. Validation of Ozone Monitoring Instrument Total Ozone Column Measurements Using Brewer and Dobson Spectrophotometer Ground-based Observations. J. Geogr. Res. 2007, 112, D24S46. [Google Scholar] [CrossRef]
- Kerr, J.B. New methodology for deriving total ozone and other atmospheric variables from Brewer spectrophotometer direct sun spectra. J. Geogr. Res. 2002, 107, ACH 22-1–ACH 22-17. [Google Scholar] [CrossRef]
- Boynard, A.; Hurtmans, D.; Garane, K.; Goutail, F.; Hadji-Lazaro, J.; Koukouli, M.E.; Wespes, C.; Vigouroux, C.; Keppens, A.; Pommereau, J.-P.; et al. Validation of the IASI FORLI/EUMETSAT ozone products using satellite (GOME-2), ground-based (Brewer–Dobson, SAOZ, FTIR) and ozonesonde measurements. Atmos. Meas. Technol. 2018, 11, 5125–5152. [Google Scholar] [CrossRef]
- Orfanoz-Cheuquelaf, A.; Rozanov, A.; Weber, M.; Arosio, C.; Ladstätter-Weißenmayer, A.; Burrows, J.P. Total ozone column from Ozone Mapping and Profiler Suite Nadir Mapper (OMPS-NM) measurements using the broadband weighting function fitting approach (WFFA). Atmos. Meas. Technol. 2021, 14, 5771–5789. [Google Scholar] [CrossRef]
- Verhoelst, T.; Granville, J.; Hendrick, F.; Köhler, U.; Lerot, C.; Pommereau, J.-P.; Redondas, A.; Van Roozendael, M.; Lambert, J.-C. Metrology of ground-based satellite validation: Co-location mismatch and smoothing issues of total ozone comparisons. Atmos. Meas. Technol. 2015, 8, 5039–5062. [Google Scholar] [CrossRef]
- Hurtmans, D.; Coheur, P.-F.; Wespes, C.; Clarisse, L.; Scharf, O.; Clerbaux, C.; Hadji-Lazaro, J.; George, M.; Turquety, S. FORLI radiative transfer and retrieval code for IASI. J. Quant. Spectrosc. Radiat. Transf. 2012, 113, 1391–1408. [Google Scholar] [CrossRef]
- Klekociuk, A.R.; Tully, M.B.; Krummel, P.B.; Henderson, S.I.; Smale, D.; Querel, R.; Nichol, S.; Alexander, S.P.; Fraser, P.J.; Nedoluha, G. The Antarctic ozone hole during 2020. J. S. Hemisph. Earth Syst. Sci. 2022, 72, 19–37. [Google Scholar] [CrossRef]
- Chubarova, N.E.; Timofeev, Y.M.; Virolainen, Y.A.; Polyakov, A.V. Estimates of UV Indices during the Periods of Reduced Ozone Content over Siberia in Winter–Spring 2016. Atmos. Ocean. Opt. 2019, 32, 177–179. [Google Scholar] [CrossRef]
- Petkov, B.; Vitale, V.; Di Carlo, P.; Mazzola, M.; Lupi, A.; Diémoz, H.; Fountoulakis, I.; Drofa, O.; Mastrangelo, D.; Casale, G.R.; et al. The 2020 Arctic ozone depletion and signs of its effect on the ozone column at lower latitudes. Bull. Atmos. Sci. Technol. 2021, 2, 8. [Google Scholar] [CrossRef]
- Solomon, S.; Haskins, J.; Ivy, D.; Min, F. Fundamental Differences Between Arctic and Antarctic Ozone Depletion. Proc. Natl. Acad. Sci. USA 2014, 111, 6220–6225. [Google Scholar] [CrossRef]
- Wohltmann, I.; von der Gathen, P.; Lehmann, R.; Maturilli, M.; Deckelmann, H.; Manney, G.L.; Davies, J.; Tarasick, D.; Jepsen, N.; Rivi, N.; et al. Near-Complete Local Reduction of Arctic Stratospheric Ozone by Severe Chemical Loss in Spring 2020. Geogr. Res. Lett. 2020, 47, e2020GL089547. [Google Scholar] [CrossRef]

















| Parameter | Requirement |
|---|---|
| spectral range | 5–15 μm (660–2000 cm−1) |
| non-apodized spectral resolution | 0.4 cm−1 |
| radiometric calibration error (λ = 11…12 μm, T = 280…300 K), no more than | 0.5 K |
| noise equivalent spectral radiance NESR, W/(m2 sr cm−1) | 3.5 × 10−4, λ = 6 μm 1.5 × 10−4, λ = 13 μm 4.5 × 10−4, λ = 15 μm |
| instantaneous field of view (IFOV) | 40 mrad (35 km) |
| swath width | 1000…2500 km |
| spatial step | 60…110 km |
| sampling period | 0.6 s |
| N | NPC total | NPC O3 | Nh | N Param. | Approximation Error, DU. | WOUDC | EUBREWNET | TROPOMI | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Bias, % | SD, % | Bias, % | SD, % | Bias, % | SD, % | ||||||
| 1 | 25 | 50 | 30 | 2401 | 8.36 | −0.23 | 2.9 | −0.40 | 2.7 | −1.2 | 3.1 |
| 2 | 30 | 60 | 50 | 4751 | 8.05 | −0.25 | 2.8 | −0.39 | 2.8 | −1.3 | 3.0 |
| N | I | Station | Latitude, Degrees | Longitude, Degrees | Altitude, m | Pairs Number | Bias, % | SDD, % |
|---|---|---|---|---|---|---|---|---|
| 1 | B | Eureka | 80.050 | −86.420 | 9 | 82,767 | −0.2 | 2.6 |
| 2 | B | Resolute | 74.700 | −94.970 | 68 | 11,979 | −0.6 | 2.1 |
| 3 | B | Churchill | 58.750 | −94.070 | 26 | 8360 | −1.6 | 3.0 |
| 4 | B | Obninsk | 55.100 | 36.610 | 100 | 1044 | −0.2 | 2.7 |
| 5 | B | Edmonton | 53.550 | −114.110 | 752 | 8496 | 1.0 | 3.1 |
| 6 | B | Goose Bay | 53.310 | −60.360 | 26 | 11,752 | 0.0 | 2.2 |
| 7 | B | Lindenberg | 52.209 | 14.121 | 127 | 9472 | −1.3 | 2.9 |
| 8 | B | De Bilt | 52.100 | 5.180 | 24 | 12,558 | −2.6 | 2.1 |
| 9 | D | Kyiv-Goloseyev | 50.364 | 30.497 | 206 | 3763 | −0.1 | 1.9 |
| 10 | B | Saturna Island | 48.770 | −123.130 | 202 | 7686 | 0.4 | 2.6 |
| 11 | B | Aosta | 45.740 | 7.360 | 570 | 1022 | 0.3 | 2.0 |
| 12 | B | Egbert | 44.230 | −79.780 | 264 | 7493 | −1.6 | 2.1 |
| 13 | D | Lannemezan | 44.129 | 0.370 | 590 | 131 | 2.4 | 2.0 |
| 14 | B | Toronto | 43.780 | −79.470 | 202 | 50,937 | −1.0 | 2.2 |
| 15 | B | Kislovodsk | 43.730 | 42.660 | 2070 | 3783 | 1.6 | 2.4 |
| 16 | B | Thessaloniki | 40.634 | 22.956 | 60 | 6959 | −1.0 | 2.2 |
| 17 | D | University of Tehran | 35.730 | 51.380 | 1419 | 674 | 1.1 | 2.0 |
| 18 | B | Mauna Loa (HI) | 19.540 | −155.580 | 3397 | 24,581 | 3.2 | 3.5 |
| 19 | B | Paramaribo | 5.806 | −55.210 | 16 | 10,880 | −0.5 | 2.1 |
| 20 | D | Natal | −5.835 | −35.207 | 49 | 32 | 0.5 | 1.2 |
| 21 | D | Cachoeira-Paulista | −22.69 | −46.200 | 574 | 26 | −3.5 | 1.6 |
| Total | 344,412 | −0.8 | 2.9 |
| N | Station | Latitude, Degrees | Longitude, Degrees | Altitude, m | Pairs Number | Bias, % | SDD, % |
|---|---|---|---|---|---|---|---|
| 1 | Sodankyla | 67.368 | 26.633 | 100 | 13,409 | 0.5 | 2.2 |
| 2 | Sondrestrom | 66.996 | −50.621 | 150 | 10,742 | −0.8 | 3.7 |
| 3 | Vindeln | 64.244 | 19.767 | 225 | 12,139 | −1.1 | 3.0 |
| 4 | Jokioinen | 60.814 | 23.499 | 106 | 1041 | −1.6 | 2.7 |
| 5 | Norrkoping | 58.580 | 16.150 | 43 | 16,162 | −0.9 | 2.1 |
| 6 | Obninsk | 55.099 | 36.607 | 100 | 616 | −3.0 | 2.7 |
| 7 | Manchester | 53.470 | −2.230 | 76 | 5871 | −2.5 | 2.3 |
| 8 | Warsaw | 52.246 | 20.940 | 120 | 4841 | −1.9 | 1.9 |
| 9 | Valentia | 51.930 | −10.250 | 14 | 5799 | −2.0 | 2.4 |
| 10 | Reading | 51.440 | −0.940 | 61 | 7958 | −2.7 | 2.7 |
| 11 | Arosa | 46.783 | 9.675 | 1840 | 14,249 | −0.3 | 2.0 |
| 12 | Aosta | 45.742 | 7.357 | 570 | 6823 | 0.5 | 2.6 |
| 13 | Zaragoza | 41.634 | −0.881 | 250 | 5843 | −2.0 | 3.3 |
| 14 | Thessaloniki | 40.634 | 22.956 | 60 | 7503 | −0.3 | 2.5 |
| 15 | Murcia | 38.028 | −1.169 | 69 | 4744 | −2.3 | 1.6 |
| 16 | El Arenosillo | 37.100 | −6.730 | 41 | 9662 | −1.1 | 2.1 |
| 17 | Lampedusa | 35.518 | 12.630 | 50 | 502 | −1.3 | 2.1 |
| 18 | Izana | 28.308 | −16.499 | 2370 | 27,809 | 2.3 | 1.6 |
| 19 | Abu Dhabi | 24.339 | 54.640 | 20 | 3682 | −1.4 | 3.3 |
| 20 | Tamanrasset | 22.790 | 5.529 | 1320 | 12,104 | −1.8 | 2.0 |
| 21 | Petaling Jaya | 3.100 | 101.650 | 46 | 4816 | −1.3 | 1.6 |
| 22 | Izobamba | −0.366 | −78.550 | 3058 | 167 | −1.2 | 2.4 |
| 23 | Nairobi | −1.301 | 36.759 | 1795 | 865 | 0.3 | 2.3 |
| 24 | Buenos Aires | −34.583 | −58.483 | 25 | 364 | −1.6 | 1.3 |
| 25 | Hobart | −42.904 | 147.327 | 20 | 12,462 | 0.0 | 2.7 |
| 26 | Rio Gallegos | −51.601 | −69.319 | 5 | 2390 | −1.0 | 3.6 |
| 27 | Punta Arenas | −53.137 | −70.880 | 22 | 3895 | 3.3 | 3.4 |
| 28 | San Marten | −68.130 | −67.106 | 30 | 126 | 2.2 | 3.6 |
| 29 | Princess lisabeth | −71.950 | 23.350 | 1390 | 345 | −0.8 | 3.0 |
| Total | 196,728 | −0.40 | 2.7 |
| Day | Night | |||
|---|---|---|---|---|
| Area | Bias, % | SDD, % | Bias, % | SDD, % |
| 90–60°N | −1.57 | 1.53 | −1.80 | 2.09 |
| 60–30°N | −0.79 | 1.67 | −0.85 | 1.51 |
| 30–0°N | −1.28 | 1.34 | −1.47 | 1.58 |
| 0–30°S | −1.10 | 1.17 | −1.37 | 1.46 |
| 30–60°S | −0.51 | 0.89 | −0.62 | 0.80 |
| 60–90°S | −5.36 | 3.33 | −7.57 | 2.75 |
| 90N–90°S | −0.92 | 1.65 | −1.08 | 1.68 |
| Latitude Range (Region) | |||||
|---|---|---|---|---|---|
| Year | 130°W–60°W (Canada) | 10°W–30°E (Northern and Central Europe) | 30°E–60°E (European Part of Russia) | 60°E–120°E (Western and Central Siberia) | 120°E–170°W (Eastern Siberia and Far East) |
| 2015 | 434.3 | 376.3 | 361.5 | 380.9 | 315.4 |
| 2016 | 429.6 | 358.9 | 358.3 | 354.6 | 314.7 |
| 2017 | 416.0 | 372.5 | 359.4 | 362.9 | 308.8 |
| 2018 | 440.0 | 429.4 | 416.6 | 399.6 | 314.0 |
| 2019 | 394.9 | 385.8 | 398.2 | 406.6 | 318.0 |
| 2020 | 340.8 | 396.6 | 399.0 | 388.8 | 298.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polyakov, A.; Virolainen, Y.; Nerobelov, G.; Kozlov, D.; Timofeyev, Y. Six Years of IKFS-2 Global Ozone Total Column Measurements. Remote Sens. 2023, 15, 2481. https://doi.org/10.3390/rs15092481
Polyakov A, Virolainen Y, Nerobelov G, Kozlov D, Timofeyev Y. Six Years of IKFS-2 Global Ozone Total Column Measurements. Remote Sensing. 2023; 15(9):2481. https://doi.org/10.3390/rs15092481
Chicago/Turabian StylePolyakov, Alexander, Yana Virolainen, Georgy Nerobelov, Dmitry Kozlov, and Yury Timofeyev. 2023. "Six Years of IKFS-2 Global Ozone Total Column Measurements" Remote Sensing 15, no. 9: 2481. https://doi.org/10.3390/rs15092481
APA StylePolyakov, A., Virolainen, Y., Nerobelov, G., Kozlov, D., & Timofeyev, Y. (2023). Six Years of IKFS-2 Global Ozone Total Column Measurements. Remote Sensing, 15(9), 2481. https://doi.org/10.3390/rs15092481