Next Article in Journal
Double-Factor Tensor Cascaded-Rank Decomposition for Hyperspectral Image Denoising
Next Article in Special Issue
Lunar Surface Resource Exploration: Tracing Lithium, 7 Li and Black Ice Using Spectral Libraries and Apollo Mission Samples
Previous Article in Journal
OEGR-DETR: A Novel Detection Transformer Based on Orientation Enhancement and Group Relations for SAR Object Detection
Previous Article in Special Issue
In-Situ Radar Observation of Shallow Lunar Regolith at the Chang’E-5 Landing Site: Research Progress and Perspectives
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 16
Issue 1
10.3390/rs16010107
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Constraints on the Fault Dip Angles of Lunar Graben and Their Significance for Lunar Thermal Evolution

by
Kai Zhu
1,2,
Jianzhong Liu
1,2,*,
Gregory Michael
1,
Danhong Lei
1 and
Xuejin Zeng
1
1
Center for Lunar and Planetary Science, Institute of Geochemistry, Chinese Academy of Sciences, Guiyang 550081, China
2
CAS Center for Excellence in Comparative Planetology, Chinese Academy of Sciences, Hefei 230026, China
*
Author to whom correspondence should be addressed.
Remote Sens. 2024, 16(1), 107; https://doi.org/10.3390/rs16010107
Submission received: 5 November 2023 / Revised: 15 December 2023 / Accepted: 16 December 2023 / Published: 26 December 2023
(This article belongs to the Special Issue Future of Lunar Exploration)
Browse Figures
Versions Notes

Abstract

:
Lunar grabens are the largest tensional linear structures on the Moon. In this paper, 17 grabens were selected to investigate the dips and displacement–length ratios (γ) of graben-bounding faults. Several topographic profiles were generated from selected grabens to measure their rim elevation, width and depth through SLDEM2015 (+LOLA) data. The differences in rim elevation (∆h) and width (∆W) between two topographic profiles on each graben were calculated, yielding 146 sets of data. We plotted ∆h vs. ∆W for each and calculated the dip angle (α) of graben-bounding faults. A dip of 39.9° was obtained using the standard linear regression method. In order to improve accuracy, large error data were removed based on error analysis. The results, 49.4° and 52.5°, were derived by the standard linear regression and average methods, respectively. Based on the depth and length of grabens, the γ value of the graben-bounding normal fault is also studied in this paper. The γ value is 3.6 × 10−3 for lunar normal faults according to the study of grabens and the Rupes Recta normal fault. After obtaining the values of α and γ, the increase in lunar radius indicated by the formation of grabens was estimated. We suggest that the lunar radius has increased by approximately 130 m after the formation of grabens. This study could aid in the understanding of normal fault growth and provide important constraints on the thermal evolution of the Moon.

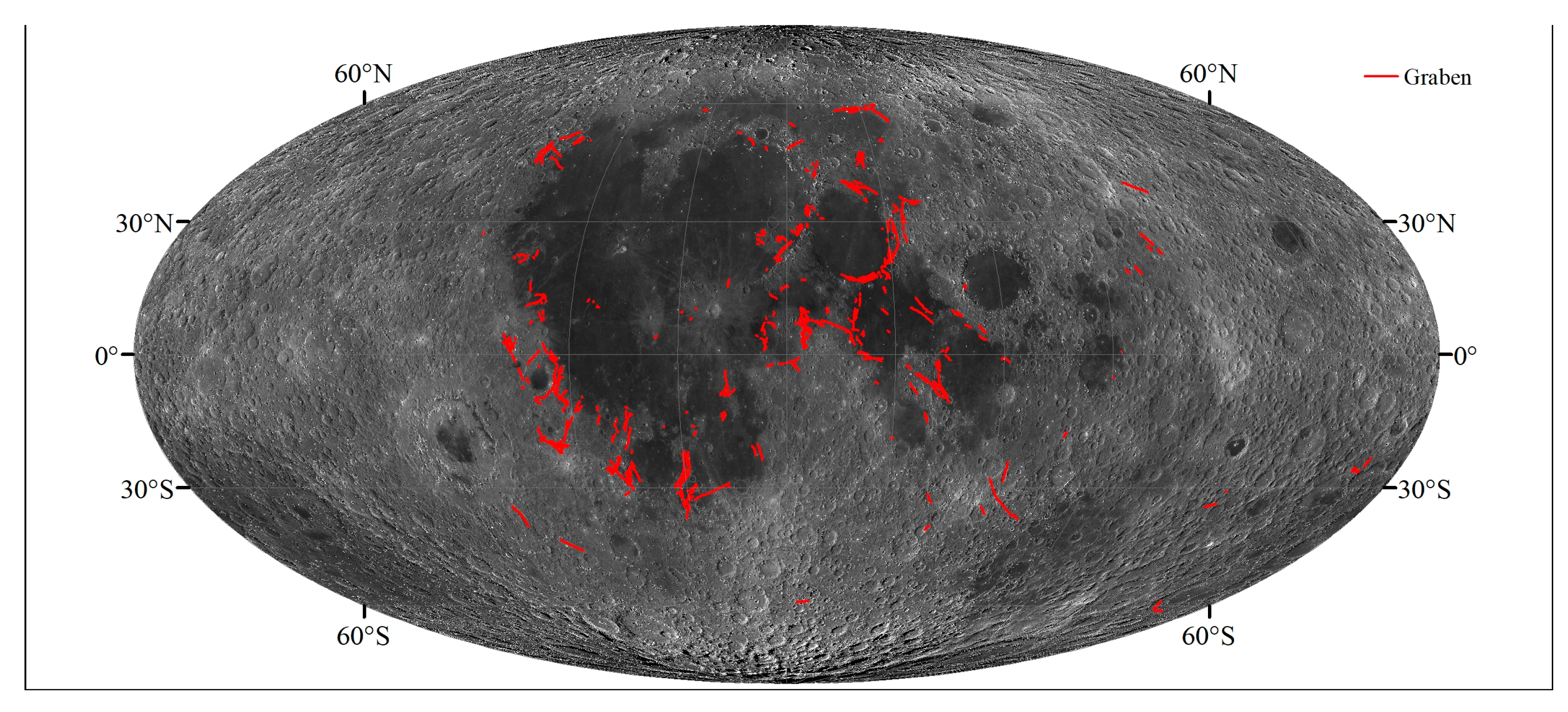
1. Introduction

Trenches in the lunar surface are collectively referred to as rilles [1,2,3,4]. Further research has shown that they have different origins (Figure 1). Sinuous rilles are formed by magmatic processes, and are also known as lava channels [4,5,6]. Straight and arcuate rilles, which are known as grabens, formed through tectonic processes or a combination of tectonic and magmatic processes [7,8,9,10,11]. Irregularly branching rilles in a crater floor are formed by the combined processes of impact and magma intrusion, also known as crater-floor fractures [12,13].
Lunar grabens are the largest tensional linear structures on the Moon (Figure 2) [14,15]. They extend in arcuate or linear patterns and appear as negative topographical features. They consist of a central down-dropped block bounded by two inward dipping normal faults (Figure 3). Lunar grabens are predominantly distributed around the margins of lunar mare basins. If magma were to flow on to the lunar surface through fissures, the fissures would be filled and buried by lava flows. Only when magma is emplaced near the shallow lunar crust in the form of a dike and triggers the extension of the lunar crust can grabens be formed and preserved [10,16,17,18,19]. The crust on the outer margin of basins is thick, preventing magma from rising to the surface and forming lava flows. Instead, magma is emplaced within the shallow surface in the form of a dike [10,20]. As a result, grabens tend to develop on the highland or old basaltic units.
Arcuate grabens, which are often aligned parallel to basin rims, may result from reactivation of circular impact structures. In contrast, straight grabens, while also often found near the basin rims, do not exhibit a clear association with the basin rims. They are more consistent with the lunar early grid–like structural system or radial impact fractures, which indicates that they may be the result of reactivation of more ancient fractures [21]. Grabens primarily formed between 3.7 and 3.4 Ga ago, with the peak period being ~3.6 Ga [21]. This age is slightly earlier than the peak period of basalt flooding on the Moon [21,22,23,24,25,26,27].
The study of lunar grabens can provide important constraints on the thermal evolution of the Moon [9,18,28,29,30]. The formation of grabens will result in an increase in the lunar surface area and radius. Constraints on the dip angle of graben-bounding normal faults serve as a crucial cornerstone of extensional strain studies. While the dip angles of graben-bounding normal faults can be directly measured through terrain data, these measurements are influenced by subsequent degradation and geological processes. As a result, the measured dip angles are typically approximately 20 degrees and generally do not exceed 30 degrees [9], which deviates significantly from the predicted 60° according to the Anderson Hypothesis [31].
Golombek (1979) [9] proposed that the increase in lunar radius is approximately 18 m indicated by the formation of grabens, which is much less than the radius variation (1 km) predicted by thermal studies [32,33]. This is primarily due to the lack of high-precision image and terrain data, resulting in a relatively small number of recognized lunar grabens.
In this paper, we present a study of lunar grabens. Utilizing the latest high-precision optical image and terrain topography data, the Displacement–length (D–L) ratios and dip angles of graben-bounding normal faults are calculated. We use the D–L ratios and dip angles as the basis to estimate the increase in the lunar surface area and radius indicated by the formation of the graben population. This research aims to provide constraints on thermal evolution during the formation of grabens.

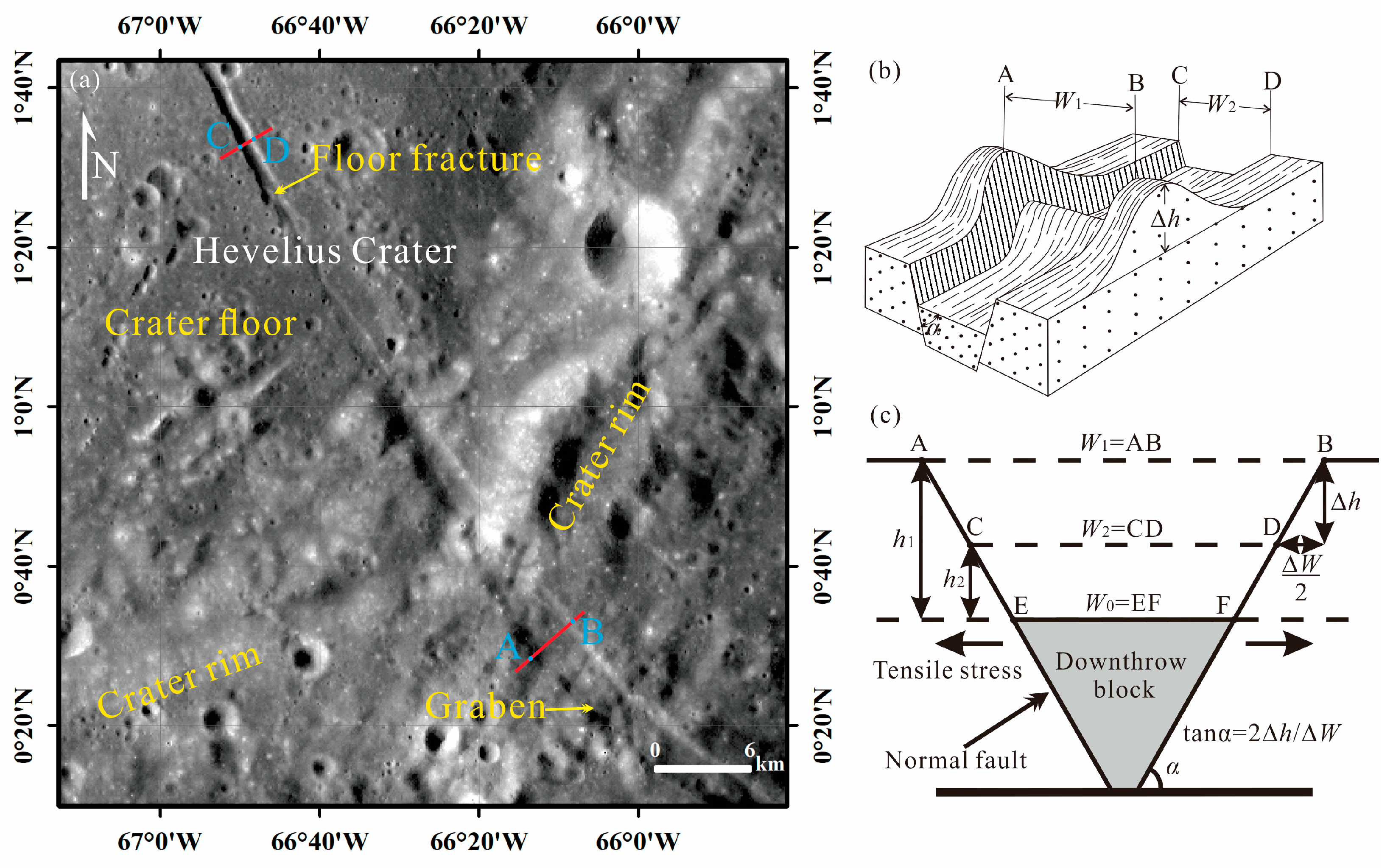
2. Materials and Methods

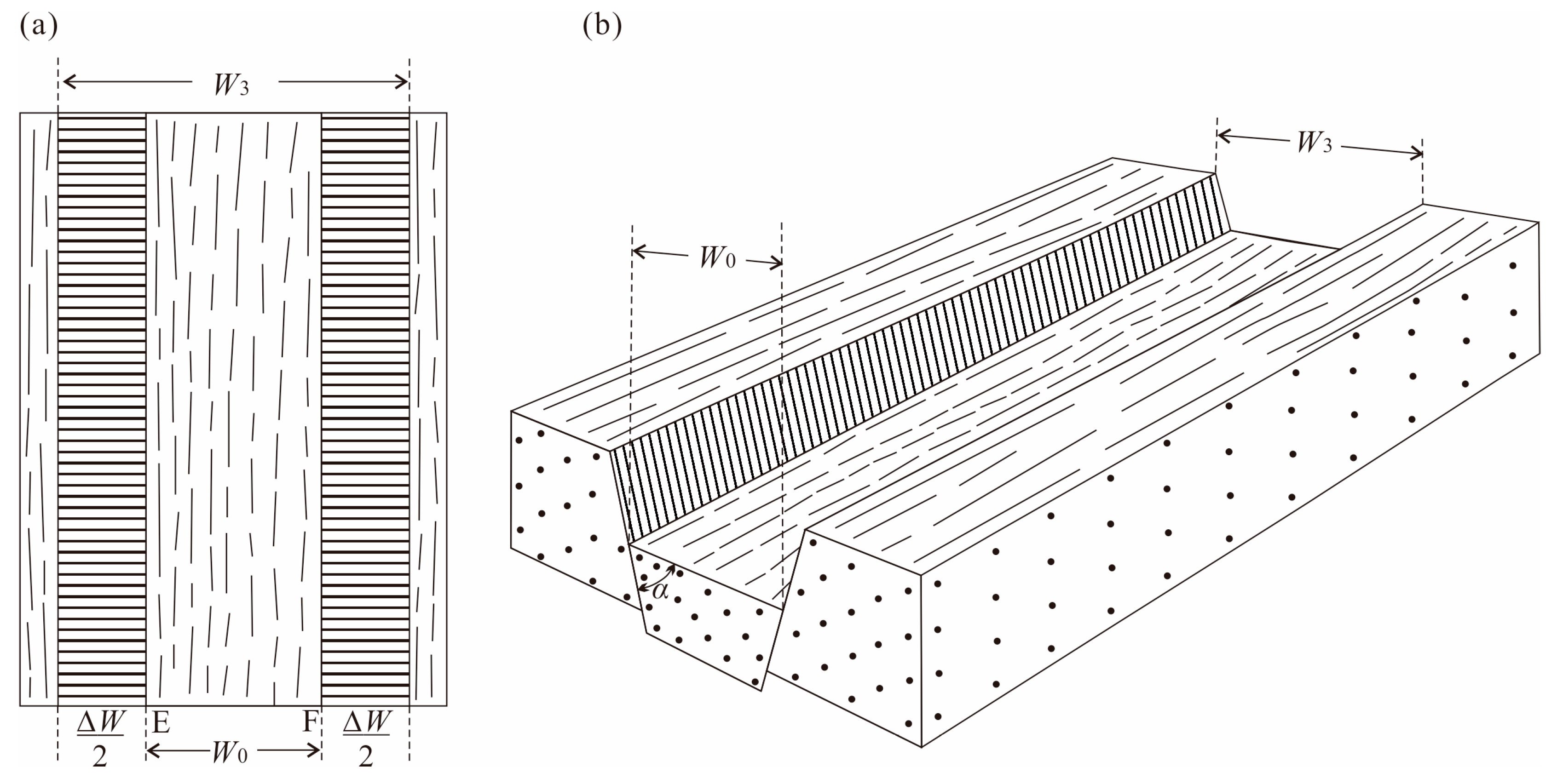
2.1. Calculation of Dips

McGill (1971) [8] discovered that the width of a graben changes with elevation. For a single lunar graben, higher elevations correspond to greater width. He proposed that this phenomenon occurs because the dip angles of the graben-bounding normal faults remain constant. As elevation increases, the distance between the fault planes on both sides of grabens becomes greater. Based on this observation, McGill (1971) [8] proposed a method for calculating fault dips (α) of grabens (Figure 3):
tanα = 2∆h/∆W,
where ∆h is the elevation difference, and ∆W is the width difference between the topographic high and low points, respectively.
∆h and ∆W can be calculated by the following equations:
∆W = W1 − W2 = (XB − XA) − (XD − XC),
∆ h = h 1 − h 2 = ( Y A + Y B ) − ( Y C + Y D ) 2 ,
where X is the horizontal distance from the point to the starting point of profile, and Y is elevation. Points A and B are the graben rim of the profile at the topographic high position along its length, with coordinates (XA, YA) and (XB, YB), respectively. Points C and D are the graben rim of the profile at the topographic low position, with coordinates (XC, YC) and (XD, YD), respectively (Figure 4a,b).
In total, 17 grabens were selected out of 812 identified for extracting topographic profiles (Table 1). Elevations were estimated by the SLDEM2015 (+LOLA) data created by the Lunar Orbiter Laser Altimeter (LOLA) and SELenological and Engineering Explorer (SELENE) Kaguya Teams [34]. The data cover latitudes within ±60°, at a horizontal resolution of ~59 m per pixel and a typical vertical accuracy from ~3 to 4 m.

2.2. Estimation of Area Growth

The formation of grabens results in an increase in the surface area of the Moon (Figure 5). The growth of area is calculated by below equation [35,36]:
∆ S = c o s α ∑ k = 1 n D k L k ,
By measuring the extension caused by the displacement of related faults in the lunar graben, the area growth indicated by the formation of the lunar graben can be calculated:
∆ S = ( W 3 − W 0 ) L ,
where ∆S is the increase in the area indicated by the formation of a graben with a length of L. W0 is the width of downthrow block (line segment EF in Figure 3c), and W3 is the width of graben.
(W3 − W0) can be calculated by:
(W3 − W0) = 2D × cosα,
Finally, for the area growth indicated by all grabens:
∆ S = 2 c o s   α ∑ k = 1 n D k L k ,
where α is the dip of graben-bounding fault, n is the total number of grabens.
Affected by collapse, W0 is difficult to be accurately measured. Previous studies [37] indicated that the maximum displacement (Dmax) and length (L) show a linear relation. A terrestrial fault population can be expressed using the following equation:
Dmax = γL,
where γ is a constant determined by rock type and tectonic setting [38].
Finally, ∆S is computed by:
∆ S = 2 γ c o s α ∑ k = 1 n L k 2
Using the Dmax to calculate the increase in area will result in an overestimated result. Instead, the average value of D was used for calculating γ.

3. Results

Based on image and topographic data, suitable grabens were selected from the 1:2,500,000-scale Lunar Geologic Map database for creating topographic profiles and calculating the dips of graben-bounding normal faults. The selection criteria for grabens state: (1) there are obvious terrain undulations along the extension of the graben; (2) topographic variations along the extension of graben should not have formed after the graben, such as uplift or subsidence due to later volcanic or tectonic activity; (3) the graben has clear, continuous, and straight boundaries; (4) the graben should not be filled by later lava flow.
At least two profiles are required to calculate the dip, but additional measurements can ensure accuracy of the calculation. Usually, there is at least one profile at high and low positions along the graben, respectively. Of course, for the sake of data diversity and richness, 2–8 profiles are set on a graben in appropriate positions (Figure 6a). A total of 69 profiles were generated. The information we need to obtain from the profile includes the graben depth (usually the minimum elevation on the profile), slope and the coordinates of the graben rim (e.g., points A and B in Figure 3c). Assuming that there are ‘n’ profiles on a single graben, the dip values can be calculated from the elevation and width differences between two profiles, resulting in a total of 1 + 2 + … + (n − 1) dip values for that graben. The number of profiles on each graben is presented in Table 1, yielding a total of 146 dip values. The α value calculated using the average method is 41.3°. The standard linear regression method has been applied to ∆W vs. ∆h plots for dip calculation. A total of 146 dip values yield a trend line with an equation of y = 0.4183x + 0.3811 (R2 = 0.5063), resulting in a α value of 39.9° (tanα = 0.4183 × 2, Figure 6b).

4. Discussion

4.1. Error Analysis

4.1.1. Degradation

Previous studies have shown that dips of fault planes exposed to the lunar surface have degraded to ~18° [9]. We also obtained similar results in this study. Based on the direct measurements from 17 grabens, the slopes of the graben-bounding normal faults are generally 5°–20° (Figure 4c,d and Table 1), and the steepest segments typically do not exceed 30°. This significant difference between the direct slope measurement (5°–20°) and the calculated ones (39.9°) primarily stems from subsequent degradation processes, notably collapse and burial effects.
Collapse, ejecta deposition and lava flow filling will reduce the depth of the lunar grabens (Figure 7a–c). However, their effects on the elevation and width of grabens are different. Subsequent collapse increases graben width and makes the fault slope become gentler [9]. Ejecta deposition and lava flow filling cause a decrease in width and depth, and increase in rim elevation. If a topographic profile passes through an area with a high degree of degradation, the error in measured dip will be greater. It is worth noting that there is a special situation: if collapse results in similar final slopes in both topographic high and low positions, the directly measured slopes will be significantly smaller than the true values, but the dips calculated using ∆W and ∆h can still have high accuracy. Collapse often occurs in areas with many fractures. Ejecta deposition is common in grabens, but is particularly evident in segments with large fresh impact craters nearby. Lava flow filling mainly occurs in graben segments that extend into a basin or crater floor.

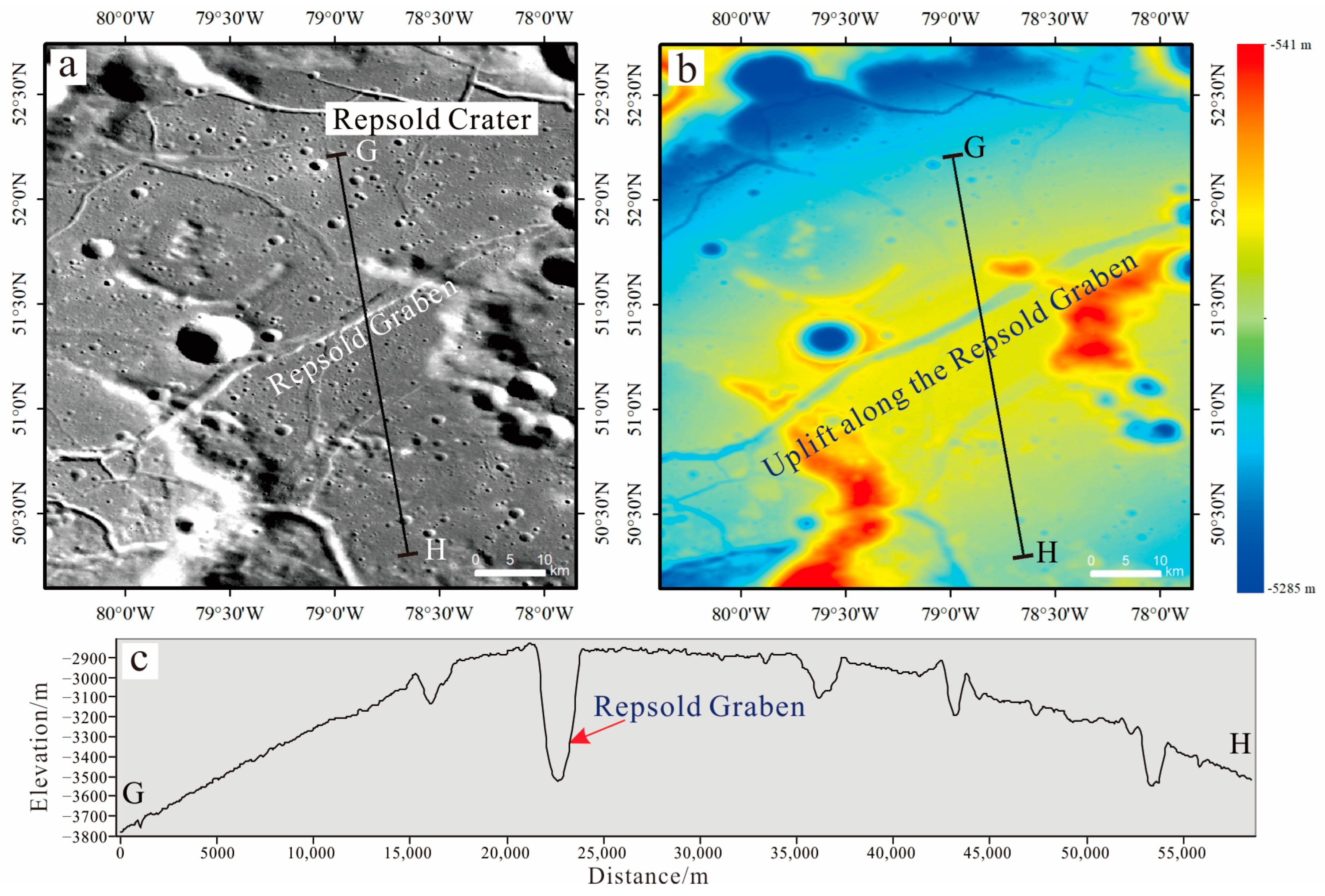
4.1.2. Uplift or Subsidence

Tectonic or volcanic activity may lead to changes in the elevation and width of graben (Figure 7d and Figure 8). These changes can introduce inaccuracies in the calculated results. If syn-tectonic or post-tectonic processes cause an uplift or subsidence along the graben extension, this will subsequently alter the ∆h between two profiles. Assuming that the graben width is not affected by uplift/subsidence, a decrease or increase in the ∆h would result in a smaller or larger calculated dip, respectively.
Uplift generally occurs on the crater-floor fractures at the center of craters (Figure 8). Some grabens are continuous with crater-floor fractures, which indicated that both of them are formed on the foundation of pre-existing fractures [21]. However, there are still certain differences in their formation mechanisms. Magma stalls beneath the crater floor, and is emplaced in the subsurface in the form of a laccolith, resulting in crater-floor fractures [13]. The crater floor is lifted up and fractured by magmatic intrusion during the formation of these crater-floor fractures. The emplacement of the laccolith not only causes surface uplift, but also causes angular rotation of bounding faults.
Sometimes, lunar surface uplift can be inferred from the anomaly of ∆W and ∆h between two profiles. The rim elevation at the crater center might be higher than that at the edge of crater floor, while the width of the crater-floor fracture at the crater center is narrower than that at the edge, resulting in a negative dip. This result contradicts the formation mechanism of the lunar graben, as it is expected that they consist of a central down-dropped block bounded by two inward dipping normal faults. The angular rotation of bounding faults caused by laccolith intrusion can be observed from the topographic profile, and the rotation angle generally does not exceed 5°. Only a few profiles passing through crater-floor fractures exhibit slight angular rotation. Thus, the angular rotation has little impact on the calculated results.

4.1.3. Elevation

Most factors that contribute to errors ultimately manifest as changes in elevation and width. Errors are more sensitive to changes in the elevation, because ∆h is generally much smaller than ∆W. Summarizing the above factors, anything that reduces the elevation difference will lead to a decrease in the calculated dip, and vice versa. If the ∆h between two profiles is small, fluctuations in elevation caused by degradation, manual recognition and other factors can be magnified which will result in large errors. This is particularly notable when the two profiles are close to each other, and the calculated dips might even be negative. This contradicts the fundamental theories and observed facts about graben formation. Thus, in order to minimize errors, it is important to select profiles with large ∆h for dip calculations.

4.2. Optimization of Calculation Results

According to the Anderson faulting model, the dip angle of normal faults is generally 60° [31]. Further deformation experiments on different types of rocks indicate that the dip angle have some variation (±10°) due to different materials [39,40,41]. Based on the study of Rima Hesiodus I, McGill (1971) [8] concluded that the dip of graben-bounding faults is 62°. Baldwin (1971) conducted a study on width and elevation changes for the Rima Goclenius II and calculated the dips of graben-bounding faults to be 46°. Golombek (1979) [9] obtained an average dip of 61° for 19 sets of data. The result of α = 39.9° calculated from all the data in this paper shows large errors (R2 = 0.5063) and differs greatly from other researchers’. The Rupes Recta fault, a normal fault younger than 3.2 Ga with clear contours and steep scarp [42], was used to constrain the original dip of the lunar normal fault. Fault growth models suggest that the fault often grows along the fault tips [35,43,44,45,46]. The middle segment of the fault has the maximum slip and the oldest exposure age. The slope profiles indicated that the maximum slope approaches 45° and 35° at the middle and edge of the Rupes Recta fault, respectively (Figure 9). Compared to the middle segment, the edge segment of the fault had undergone shorter weathering time. Thus, the original dip of the lunar normal fault may be between 45° and 70°. Based on the error analysis in the Section 4.1, it is possible to assess the accuracy of each calculation result. In order to improve computing accuracy, profiles and data with large errors are screened out and removed.
(1)
Removing the results calculated with small ∆h
The topographic profiles suggest that laccolith intrusion during the formation of crater-floor fractures will cause elevation to rise by tens to hundreds of meters, which will results in ∆h value with large error. A histogram of frequency versus α for 60 values calculated from data with ∆h < 200 m shows a maximum between −10° and 29°, and only eight values are in the range 30°–69° (Figure 10). The data with a small △h is obtained from grabens located in different regions. In addition, the dips calculated from small △h data vary widely, which excludes the possibility that the data with a small △h come from the same type of graben. It is observed that errors are generally greater when the ∆h is less than 200 m. Thus, the dips calculated from ∆h < 200 m (60 out of 146 values are removed) need to be removed, and then the remaining data were fitted to improve accuracy. The fitted result is tanα = 0.5367 × 2, α = 47.0°, R2 = 0.6338 (Figure 11a). To further enhance accuracy, negative dips were eliminated (14 out of 86 values are removed) before fitting, resulting in a higher precision (tanα = 0.5838 × 2, α = 49.4°, R2 = 0.7667; Figure 11b).
(2)
Assessment of each profile
An alternative approach to improve accuracy is to individually examine each profile from the grabens. Based on error analysis, profiles that always lead to large computation error have been identified. Those profiles are selectively included or excluded based on specific circumstances (Table 2). Then, the fault dip for each graben was calculated by the standard linear regression or average method. Finally, the average dip calculated from the 17 grabens is 52.5°.

4.3. Constraints on the Expansion Rate of the Moon

4.3.1. D–L Ratios for Graben-Bounding Faults

The γ value of fault populations on different planets has been studied in recent years [38,47,48,49,50]. However, previous research has primarily focused on the γ of thrust faults, while there had been less studies on the γ of normal faults on terrestrial planets.
On the Earth, the γ is typically between 8 × 10−3 and 5 × 10−2 over a range of tectonic settings, fault nature and rock types [38,51,52,53,54]. The γ is positively correlated with the planetary gravity [48]. Therefore, γ for the Martian fault population, as well as for Mercury thrust faults, is consistently approximately 5-fold smaller than that of the Earth [48]. The theoretical calculation for the Moon’s γ is only 1.0 × 10−3 owing to the relatively lower lunar gravity [48]. However, Watters and Johnson (2010) [49] found that the γ of small-scale thrust faults is approximately 1.2 × 10−2 based on the study of lobate scarps. After measuring the geometric features of wrinkle ridges within Mare Imbrium and Mare Serenitatis, Li et al. (2018) [50] discovered that the γ of associated thrust faults within these maria were 2.13 × 10−2 and 1.73 × 10−2, respectively. The above research suggests that fault scale might also be an important influencing factor γ value.
The physical simulations and field investigations indicate that the D/L ratio of normal faults on Earth is also inversely correlated with fault scale [38,51]. For normal faults with a length less than 200 m, the approximate γ is 1.1 × 10−2; and for a length greater than 600 m, the approximate γ is 8 × 10−3 [54]. Normal faults from the Martian northern plains, Tempe Terra and Alba Patera volcano show an γ value of 1 × 10−3, 6.7 × 10−3 and 6 × 10−3, respectively [47,55]. Martin and Watters (2022) had conducted a study on the γ value of the lunar grabens [56]. They concluded that the γ value is the maximum (6.3 × 10−3) for grabens developed in the highland, and grabens in the mare (4.9 × 10−3) and mixed terrains (3.0 × 10−3) have smaller γ values.
It is a challenging job to measure the γ of normal faults on terrestrial planets. The length of grabens can be measured by optical and terrain images. According to the theory, the fault displacement also can be calculated by the depth of newly formed graben. However, since the grabens have undergone degradation (e.g., collapse and filling effects) over the course of 3.6 billion years, the current depth measured through terrain data is not equivalent to the actual fault displacement. Sometimes, the impact of degradation is overlooked.
If the measured depth is directly used to calculate the γ, the obtained result would be smaller than the actual value. In order to improve the accuracy of γ, the graben depth reduced by degradation will be estimated. Shallow depressions on the Moon are estimated to fill in at a rate of 5 ± 3 cm per million years, as derived from the analysis of boulder tracks [57]. If grabens were filled in at a rate of ~5 cm per million years, the depth of graben has decreased by ~180 m in the past 3.6 Ga. Based on the above estimations, the existing measurement depth of grabens should be increased by another 180 m.
Utilizing the depths measured from 69 profiles to directly calculate the γ yield, an average value of 2.0 × 10−3 (for α = 52.5°). The γ value obtained by the standard linear regression method is 3.6 × 10−3 (y = 0.2743x + 56.042; Figure 12a). If degradation is considered and the depth is increased by 180 m, the calculation results obtained by the average method and the standard linear regression method are 3.8 × 10−3 and 3.2 × 10−3 (y = 0.3078x − 9.1666, R2 = 0.3568; Figure 12b), respectively. In addition, the Rupes Recta normal fault was also used to verify the results calculated from the profiles. A total of nine topographic profiles were carried out on this fault, yielding a γ value of 3.6 × 10−3. In summary, the γ value of the graben-bounding normal fault on the Moon is approximately 3.6 × 10−3.

4.3.2. Implications for Origin of Graben

Grabens are common on Earth, Mars, and the Moon, and there have been many studies and articles on the origin of grabens. Various models have been proposed for the origin of grabens, including formation by regional extension [9,58], dike intrusion [59], or a combination of tectonic processes and dike intrusion [10,17,18,19,60].
Although there are no plate tectonics on the Moon, the loading of basalt can also cause regional stress changes and produce various structures. It is believed that the loading of basalt and the release of magma to the surface producing voids to collapse below inside the basin can cause subsidence of the basin floor, resulting in regional tensile stress at the edge of the basin. Under the regional tensile stress field, tensile arcuate grabens are formed [58]. Based on the study of the geometric features of lunar grabens, Golombek (1979) [9] proposed a simple extension model to explain the origin of grabens.
Some studies on grabens on Earth and Mars indicate that dike intrusion can also form grabens. The dike intrusion hypothesis suggests that grabens are mainly formed by the extensional stress caused by the placement of dikes in the shallow crust [59]. Field investigation and geodetic data on Earth indicate that dike intrusion in volcanic rift zones typically results in normal faults and grabens [16]. The geometric features such as the morphology, peak spacing, and vertical displacement of grabens on Mars support the occurrence of dike intrusion [61,62]. Some selected lunar grabens in this study are connected to crater-floor fractures, indicating that they have similar origins. The crater-floor fractures are generally accompanied by many volcanos and pyroclastic rocks, and they originate from the emplacement of bedrock/laccolith in the shallow crust [13,63]. Traces of volcanic activity can also be observed along some lunar grabens, indicating the presence of underlying dikes [20]. The formation of grabens and volcanic activity may occur simultaneously, which is the result of stress fields generated by dikes approaching the surface from great depths [10,17,18,19,60].
The elastic model indicates that simple dike intrusion or the formation of normal faults will not cause significant subsidence of the overlying block. Only when the normal faults extend to the dike plane can this result in the observed displacement [16]. The terrain characteristics of the Martian graben are closest to the simulation results of normal fault formation combined dike intrusion, indicating that this type of structure likely originate from a combination of tectonic and magmatic process [61,64,65,66]. According to studies on terrain characteristics, some researchers believe that the formation of arcuate lunar grabens is mostly related to dike intrusion, while straight lunar grabens are mainly formed by simple tectonic movement with only a small portion having underlying dikes [11,66].
To sum up, a combination of tectonic and dike intrusion models is the preferred scenario. Loading of basalt within the basin results in a tensile stress field at the edge of the basin [58]. Fissures and magma intrusion occurred in this tensile stress field, resulting in the formation of grabens. The grabens on Earth, Mars and the Moon have similar geometric features. Field studies and experiments of graben on Earth indicate that dike intrusion plays an important role in the formation of grabens.

4.3.3. Implications for Lunar Thermal Evolution

According to thermal evolution models, in the Moon’s initial approximately 1 billion years, global expansion led to an increase in radius of approximately 2.7 to 3.7 km, and the fastest-growing rate occurred in the first 500 million years [32,33]. However, the currently observed lunar grabens mainly formed ~3.6 Ga [21]. It has not yet been discovered that grabens formed in the first 500 million years. This may be related to major geological events in the early stages of lunar evolution. During the magmatic ocean period (4.52–4.31 Ga), the lunar crust has strong plasticity, which is not conducive to the formation of faults [14,67]. The large-scale impact events that occurred between 4.3 billion and 3.8 billion years ago strongly altered the surface of the Moon. The current preserved lunar grabens are mainly formed during the period of basalt flooding. The accumulation of heat at the base of lunar mare regions drove the formation and ascent of magma, a process that resulted in the formation of lunar grabens [21]. All lunar grabens are restricted between 60°S and 60°N, and are concentrated in the nearside (Figure 2 and Table 3). The low latitude area (20°S~20°N) contains the largest number of grabens, and has the largest cumulative graben length. There are some grabens between 40°N and 60°N, but only one is located between 40°S and 60°S. These characteristics may be related to the distribution of basalt. The mare basalt extends northward from the equator to 60°N, while southward only extends to approximately 40°S. The consistency of time and spatial distribution further proves their genetic connection.
A total of 812 lunar grabens were identified on the 1:2,500,000-scale Lunar Geologic Map [14,15]. After further identification, 15 trenches formed by secondary impact were removed, and the remaining 797 grabens have a total length of approximately 22,000 km. Two scenarios were considered in the process of calculating the change in lunar radius. One is that the current lunar radius (~1737.1 km) is the result of expansion after graben formation. In this case, the increase in lunar radius indicated by grabens is ~130 m. Another scenario is that the Moon had contracted during the formation of later compression structures such as wrinkle ridges and lobate scarps. According to chronological studies, most wrinkle ridges are formed between 3.5 and 3.1 Ga [68], and the lobate scarps are generally younger than 0.8 Ga [69,70]. The wrinkle ridges and lobate scarps are products of lunar contraction after the formation of lunar grabens (~3.6 Ga) [21]. The lunar expansion model suggests that the change in lunar radius over the last 3.8 Ga is less than or equal to 1 km [32,33]. We assume that the lunar radius had decreased by 1 km during the formation of wrinkle ridges and lobate scarps, and the lunar radius was 1738.1 km after the formation of lunar grabens. Based on these assumptions, the lunar radius growth is calculated again and obtained a similar result. Thus, the increases in area and radius indicated by grabens are ~5671 km2 and ~130 m, respectively.
Golombek (1979) [9] proposed that the lunar radius has increased by ~18 m after the formation of the graben population. Thanks to the high-resolution images and terrain data, more lunar grabens were recognized, leading to a larger radius growth. Although our estimation suggested that the lunar radius has increased by 130 m, this is also much smaller than the value predicted by the model. This may be because many ancient lunar grabens are completely buried and destroyed by later geological events. In addition, crater-floor fractures were also the results of lunar expansion. Only a few crater-floor fractures that are continuous with the grabens have been included in the calculation in this study. Therefore, the total radius increase indicated by the formation of linear extension structures could be far more than 130 m.

5. Conclusions

(1)
Error analysis shows that various influencing factors are ultimately reflected in changes in elevation and graben width. Errors are more sensitive to changes in elevation.
(2)
The average and the standard linear regression methods were used to calculate the dips of the graben-bounding normal faults. A dip of 39.9° was obtained by the method of standard linear regression for all data. After removing large error data, the results of 49.4° and 52.5° were derived by the standard linear regression and average methods, respectively.
(3)
The D–L ratios calculated from the graben-bounding normal faults are between 2.0 × 10−3 and 3.8 × 10−3 (for α = 52.5°). The young Rupes Recta normal fault presents a D–L ratio of 3.6 × 10−3, which is basically consistent with the results calculated from the graben-bounding normal faults by the standard linear regression method. Thus, the D–L ratio of lunar normal fault is ~3.6 × 10−3.
(4)
The increase in lunar radius is estimated based on the dip and D–L ratio of the graben-bounding normal faults. The radius of the Moon expanded by approximately 130 m indicated by the formation of grabens.

Author Contributions

Conceptualization, K.Z. and J.L.; methodology, K.Z.; validation, G.M., D.L. and K.Z.; formal analysis, K.Z.; investigation, X.Z.; resources, K.Z. and J.L.; data curation, K.Z. and J.L.; writing—original draft preparation, K.Z.; writing—review and editing, G.M., D.L., K.Z., J.L. and X.Z.; visualization, K.Z.; project administration, K.Z. and J.L.; funding acquisition, K.Z. and J.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the National Key Research and Development Program of China (Grant No. 2022YFF0503100); the National Natural Science Foundation of China (Grant No. 42202264); Guizhou Provincial Science and Technology Projects (Grant NO. [QKHJC-ZK(2023)-478]); and the Key Research Program of the Chinese Academy of Sciences (Grant NO. KGFZD-145-23-15).

Data Availability Statement

The data presented in this study are available upon request from the corresponding author.

Acknowledgments

The authors would like to thank and acknowledge three reviewers for their thoughtful comments that helped to significantly improve our manuscript. We thank Ke Zhang and Li Zhang for their thoughtful suggestions which greatly helped us to improve the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Baldwin, R. The Measure of the Moon; University of Chicago Press: Chicago, IL, USA, 1963. [Google Scholar]
  2. Quaide, W. Rilles, ridges, and domes—Clues to maria history. Icarus 1965, 4, 374–389. [Google Scholar] [CrossRef]
  3. Ouyang, Z.Y. Introduction to Lunar Science; Chinese Aerospace Press: Beijing, China, 2005; pp. 1–362. (In Chinese) [Google Scholar]
  4. Hargitai, H. Rille. In Encyclopedia of Planetary Landforms; Springer: New York, NY, USA, 2014. [Google Scholar]
  5. Greeley, R. Lava tubes and channels in the lunar Marius Hills. Earth Moon Planets 1971, 3, 289–314. [Google Scholar] [CrossRef]
  6. Xiao, L.; Huang, J.; Zhao, J.; Zhao, J. Significance and preliminary proposal for exploring the lunar lava tubes. Sci. Sin. Phys. Mech. Astron. 2018, 48, 119602. (In Chinese) [Google Scholar] [CrossRef]
  7. Smith, G. A Comparison of Two Terrestrial Grabens with the Lunar Rilles Rima Ariadaeus and Rimae Hypatia I and II; USGS: Reston, VA, USA, 1966. [Google Scholar]
  8. McGill, G.E. Attitude of fractures bounding straight and arcuate lunar rilles. Icarus 1971, 14, 53–58. [Google Scholar] [CrossRef]
  9. Golombek, M.P. Structural analysis of lunar grabens and the shallow crustal structure of the Moon. J. Geophys. Res. 1979, 84, 4657–4666. [Google Scholar] [CrossRef]
  10. Head, J.W.; Wilson, L. Lunar graben formation due to near-surface deformation accompanying dike emplacement. Planet. Space Sci. 1993, 41, 719–727. [Google Scholar] [CrossRef]
  11. Nahm, A.L. Graben on the lunar nearside: Do dikes lie beneath? Acta Geol. Sin. Engl. Ed. 2016, 90, 175–176. [Google Scholar] [CrossRef]
  12. Schultz, P.H. Floor-fractured lunar craters. Moon 1976, 15, 241–273. [Google Scholar] [CrossRef]
  13. Jozwiak, L.M.; Head, J.W.; Wilson, L. Lunar floor-fractured craters as magmatic intrusions: Geometry, modes of emplacement, associated tectonic and volcanic features, and implications for gravity anomalies. Icarus 2015, 248, 424–447. [Google Scholar] [CrossRef]
  14. Lu, T.; Zhu, K.; Chen, S.; Liu, J.; Ling, Z.; Ding, X.; Han, K.; Chen, J.; Cheng, W.; Lei, D.; et al. The 1:2,500,000-scale global tectonic map of the Moon. Sci. Bull. 2022, 67, 1962–1966. [Google Scholar] [CrossRef]
  15. Ji, J.; Guo, D.; Liu, J. The 1:2,500,000-scale geologic map of the global Moon. Sci. Bull. 2022, 67, 1544–1548. [Google Scholar] [CrossRef] [PubMed]
  16. Rubin, A.M. Dike-induced faulting and graben subsidence in volcanic rift zones. J. Geophys. Res. 1992, 97, 1839–1858. [Google Scholar] [CrossRef]
  17. Rubin, A.M. Tensile fracture of rock at high confining pressure: Implications for dike propagation. J. Geophys. Res. 1993, 98, 15919–15935. [Google Scholar] [CrossRef]
  18. Wilson, L.; Head, J.W. Tharsis-radial graben system as the surface manifestation of plume-related dike intrusion complexes—Models and implications. J. Geophys. Res. 2002, 107, 5057. [Google Scholar] [CrossRef]
  19. Wilson, L.; Hawke, B.R.; Giguere, T.A.; Petrycki, E.R. An igneous origin for Rima Hyginus and Hyginus crater on the Moon. Icarus 2011, 215, 584–595. [Google Scholar] [CrossRef]
  20. Petrycki, J.A.; Wilson, L. Volcanic features and age relationships associated with lunar graben. In Proceedings of the Lunar and Planetary Science Conference, Houston, TX, USA, 15–19 March 1999; p. 1335. [Google Scholar]
  21. Lucchitta, B.K.; Watkins, J.A. Age of graben systems on the Moon. In Proceedings of the Ninth Lunar and Planetary Science Conference, Houston, TX, USA, 13–17 March 1978; pp. 3459–3472. [Google Scholar]
  22. Hiesinger, H.; Jaumann, R.; Neukum, G.; Head, J.W. Ages of mare basalts on the lunar nearside. J. Geophys. Res. Planets 2000, 105, 29239–29275. [Google Scholar] [CrossRef]
  23. Hiesinger, H.; Head, J.W.; Wolf, U.; Jaumann, R.; Neukum, G. Ages and stratigraphy of mare basalts in Oceanus Procellarum, Mare Nubium, Mare Cognitum, and Mare Insularum. J. Geophys. Res. 2000, 108, 5065. [Google Scholar] [CrossRef]
  24. Hiesinger, H.; Head, J.W.; Wolf, U.; Jaumann, R. Ages of lunar mare basalts in Mare Frigoris and other Nearside Maria. In Proceedings of the XXXIV Lunar & Planetary Science Conference, Houston, TX, USA, 17–21 March 2003; p. 1257. [Google Scholar]
  25. Hiesinger, H.; Head, J.W.; Wolf, U.; Jaumann, R.; Neukum, G. New ages for basalts in Mare Fecunditatis based on crater size-frequency measurements. In Proceedings of the XXXVII Lunar & Planetary Science Conference, Houston, TX, USA, 13–17 March 2006; p. 1151. [Google Scholar]
  26. Morota, T.; Haruyama, J.; Ohtake, M.; Matsunaga, T.; Honda, C.; Yokota, Y.; Kimura, J.; Ogawa, Y.; Hirata, N.; Demura, H.; et al. Timing and characteristics of the latest mare eruption on the Moon. Earth Planet. Sci. Lett. 2011, 302, 255–266. [Google Scholar] [CrossRef]
  27. Qian, Y.; She, Z.; He, Q.; Xiao, L.; Wang, Z.; Head, J.W.; Sun, L.; Wang, Y.; Wu, B.; Wu, X.; et al. Mineralogy and chronology of the young mare volcanism in the Procellarum-KREEP-Terrane. Nat. Astron. 2023, 7, 287–297. [Google Scholar] [CrossRef]
  28. Head, J.W.; Wilson, L. Lunar mare volcanism: Stratigraphy, eruption conditions, and evolution of secondary crust. Geochim. Cosmochim. Acta 1992, 56, 2155–2175. [Google Scholar] [CrossRef]
  29. Rubin, A.M.; Pollard, D.D. Origins of Blade-Like Dikes in Volcanic Rift Zones; Volcanism in Hawaii, USGS Project Paper; USGS: Reston, VA, USA, 1987; Volume 1350, pp. 1449–1470. [Google Scholar]
  30. Scott, R.; Wilson, L. The stress state of the lunar lithosphere and the volumes of intruded and erupted magmas. In Proceedings of the 32nd Annual Lunar and Planetary Science Conference, Houston, TX, USA, 12–16 March 2001; p. 1549. [Google Scholar]
  31. Anderson, E.M. The Dynamics of Faulting, 2nd ed.; Oliver and Boyd: London, UK, 1951; 206p. [Google Scholar]
  32. Solomon, S.C. The relationship between crustal tectonics and internal evolution in the Moon and Mercury. Phys. Earth Planet. Inter. 1977, 15, 135–145. [Google Scholar] [CrossRef]
  33. Solomon, S.C.; Chaiken, J. Thermal expansion and thermal stress in the moon and terrestrial planets: Clues to early thermal history. In Proceedings of the Lunar Science Conference, Houston, TX, USA, 15–19 March 1976; pp. 3229–3243. [Google Scholar]
  34. Barker, M.K.; Mazarico, E.; Neumann, G.A.; Zuber, M.T.; Haruyama, J.; Smith, D.E. A new lunar digital elevation model from the Lunar Orbiter Laser Altimeter and SELENE Terrain Camera. Icarus 2016, 273, 346–355. [Google Scholar] [CrossRef]
  35. Burgmann, R.; Pollard, D.D.; Martel, S.J. Slip distributions on faults: Effects of stress gradients, inelastic deformation, heterogeneous host-rock stiffness, and fault interaction. J. Struct. Geol. 1994, 16, 1675–1690. [Google Scholar] [CrossRef]
  36. Scholz, C.H.; Cowie, P.A. Determination of geologic strain from fault slip data. Nature 1990, 346, 837–839. [Google Scholar] [CrossRef]
  37. Cowie, P.A.; Scholz, C.H.; Edwards, M.; Malinverno, A. Fault strain and seismic coupling on mid-ocean ridges. J. Geophys. Res. 1993, 98, 17911–17920. [Google Scholar] [CrossRef]
  38. Cowie, P.A.; Scholz, C.H. Displacement-length scaling relationship for faults: Data synthesis and discussion. J. Struct. Geol. 1992, 14, 1149–1156. [Google Scholar] [CrossRef]
  39. Handin, J. Strength and ductility. In Handbook of Physical Constants; Geological Society of America Member: Boulder, CO, USA, 1966; Volume 97, pp. 223–289. [Google Scholar]
  40. Handin, J.; Hager, R.V., Jr. Experimental deformation of sedimentary rocks under confining pressure: Tests at room temperature on dry samples. Am. Assoc. Petrol. Geol. Bull. 1957, 41, 1–50. [Google Scholar]
  41. Handin, J.; Hager, R.V., Jr. Experimental deformation of sedimentary rocks under confining pressure: Tests at high temperature. Am. Assoc. Petrol. Geol. Bull. 1958, 42, 2892–2934. [Google Scholar]
  42. Nahm, A.L.; Schultz, R.A. Rupes Recta and the geological history of the Mare Nubium region of the Moon: Insights from forward mechanical modelling of the “Straight Wall”. Volcanism and Tectonism Across the Inner Solar System. Geol. Soc. Lond. Spec. Publ. 2015, 401, 377–394. [Google Scholar] [CrossRef]
  43. Pollard, D.D.; Segall, P. Theoretical displacements and stresses near fractures in rock: With applications to faults, joints, veins, dikes, and solution surfaces. In Fracture Mechanics of Rock; Atkinson, B.K., Ed.; Academic: San Diego, CA, USA, 1987; pp. 277–350. [Google Scholar]
  44. Walsh, J.J.; Waterson, J. Analysis of the relationship between displacements and dimensions of faults. J. Struct. Geol. 1988, 10, 239–247. [Google Scholar] [CrossRef]
  45. Cowie, P.A.; Scholz, C.H. Physical explanation for displacement-length relationship for faults using a post-yield fracture mechanics model. J. Struct. Geol. 1992, 14, 1133–1148. [Google Scholar] [CrossRef]
  46. Cowie, P.A.; Scholz, C.H. Growth of faults by accumulation of seismic slip. J. Geophys. Res. 1992, 97, 11085–11096. [Google Scholar] [CrossRef]
  47. Wilkins, S.J.; Schultz, R.A.; Anderson, R.C.; Dohm, J.M.; Dawers, N.H. Deformation rates from faulting at the Tempe Terra extensional province. Mars. Geophys. Res. Lett. 2002, 29, 1884. [Google Scholar] [CrossRef]
  48. Schultz, R.A.; Okubo, C.H.; Wilkins, S.J. Displacement-length scaling relations for faults on the terrestrial planets. J. Struct. Geol. 2006, 28, 2182–2193. [Google Scholar] [CrossRef]
  49. Watters, T.R.; Johnson, C.L. Lunar tectonics. In Planetary Tectonics; Watters, T.R., Schultz, R.A., Eds.; Cambridge University Press: Cambridge, UK, 2010; pp. 121–182. [Google Scholar]
  50. Li, B.; Ling, Z.; Zhang, J.; Chen, J.; Ni, Y.; Liu, C. Displacement-length ratios and contractional strains of lunar wrinkle ridges in mare serenitatis and mare tranquillitatis. J. Struct. Geol. 2018, 109, 27–37. [Google Scholar] [CrossRef]
  51. Dawers, N.H.; Anders, M.H. Displacement-length scaling and fault linkage. J. Struct. Geol. 1995, 17, 607–614. [Google Scholar] [CrossRef]
  52. Clark, R.; Cox, S. A modern regression approach to determining fault displacementlength scaling relationships. J. Struct. Geol. 1996, 18, 147–154. [Google Scholar] [CrossRef]
  53. Schultz, R.A.; Fossen, H. Displacement-length scaling in three dimensions: The importance of aspect ratio and application to deformation bands. J. Struct. Geol. 2002, 24, 1389–1411. [Google Scholar] [CrossRef]
  54. Dong, J.; Zhang, S.H.; Jiang, Y.B. The displacement-length relationship of faults and its significance. Earth Sci. Front. 2004, 11, 575–584. (In Chinese) [Google Scholar]
  55. Polit, A.T.; Schultz, R.A.; Soliva, R. Geometry, displacement-length scaling, and extensional strain of normal faults on mars with inferences on mechanical stratigraphy of the martian crust. J. Struct. Geol. 2009, 31, 662–673. [Google Scholar] [CrossRef]
  56. Martin, E.S.; Watters, T.R. Displacement-length scaling relations of nearside graben: Evidence of restricted normal faults on the Moon. Icarus 2022, 388, 115215. [Google Scholar] [CrossRef]
  57. Arvidson, R.; Drozd, R.J.; Hohenberg, C.M.; Morgan, C.J.; Poupeau, G. Horizontal transport of the regolith, modification of features, and erosion rates on the lunar surface. Moon 1975, 13, 67–79. [Google Scholar] [CrossRef]
  58. Solomon, S.; Head, J.W. Lunar mascon basins: Lava filling, tectonics, and evolution of the lithosphere Rev. Geophys. Space Phys. 1980, 18, 107–141. [Google Scholar] [CrossRef]
  59. Pollard, D.D.; Delaney, P.T.; Dutlield, W.A.; Endo, E.T.; Okanmra, A.T. Surface deformation in volcanic rift zones. Tectonophys 1983, 94, 541–584. [Google Scholar] [CrossRef]
  60. Mège, D.; Cook, A.C.; Garel, E.; Lagabrielle, Y.; Cormier, M.-H. Volcanic rifting at Marian graben. J. Geophys. Res. 2003, 108, 5044. [Google Scholar] [CrossRef]
  61. Schultz, R.A.; Okubo, C.H.; Goudy, C.L.; Wilkins, S.J. Igneous dikes on Mars revealed by Mars Orbiter Laser Altimeter topography. Geology 2004, 32, 889–892. [Google Scholar] [CrossRef]
  62. Schultz, R.A.; Moore, J.M.; Grosfils, E.B.; Tanaka, K.L.; Mege, D. The Canyonlands model for planetary grabens: Revised physical basis and implications. In The Geology of Mars: Evidence from Earth-Based Analogs; Chapman, M., Ed.; Cambridge University Press: Cambridge, UK, 2007; pp. 371–399. [Google Scholar]
  63. Wichman, R.W.; Schultz, P.H. Floor-fractured craters in Mare Smythii and west of Oceanus Procellarum: Implications of crater modification by viscous relaxation and igneous intrusion models. J. Geophys. Res. Planets 1995, 100, 21201–21218. [Google Scholar] [CrossRef]
  64. Klimczak, C. Igneous Dikes on the Moon: Evidence from Lunar Orbiter Laser Altimeter Topography. In Proceedings of the 44th Lunar and Planetary Science Conference, Houston, TX, USA, 18–22 March 2013. [Google Scholar]
  65. Klimczak, C. Geomorphology of lunar grabens requires igneous dikes at depth. Geology 2014, 42, 963–966. [Google Scholar] [CrossRef]
  66. Martin, E.S.; Watters, T.R. A tectonic origin for non-mascon related lunar graben. In Proceedings of the 49th Lunar and Planetary Science Conference, Woodlands, TX, USA, 19–23 March 2018; p. 2846. [Google Scholar]
  67. Guo, D.; Liu, J.; Head, J.; Zhang, F.; Ling, Z.; Chen, S.; Ding, X.; Ji, J.; Ouyang, Z. A Lunar Time Scale from the Perspective of the Moon’s Dynamic Evolution. Sci. China Earth Sci. 2023; accepted and in press. [Google Scholar]
  68. Yue, Z.; Michael, G.G.; Di, K.; Liu, J. Global survey of lunar wrinkle ridge formation times. Earth Planet. Sci. Lett. 2017, 477, 14–20. [Google Scholar] [CrossRef]
  69. Watters, T.R.; Robinson, M.S.; Beyer, R.A.; Banks, M.E.; Bell, J.F., III; Pritchard, M.E.; Hiesinger, H.; Van Der Bogert, C.H.; Thomas, P.C.; Turtle, E.P.; et al. Evidence of recent thrust faulting on the Moon revealed by the Lunar Reconnaissance Orbiter Camera. Science 2010, 329, 936–940. [Google Scholar] [CrossRef]
  70. Watters, T.R.; Robinson, M.S.; Collins, G.C.; Banks, M.E.; Daud, K.; Williams, N.R.; Selvans, M.M. Global thrust faulting on the Moon and the influence of tidal stresses. Geology 2015, 43, 851–854. [Google Scholar] [CrossRef]
Remotesensing 16 00107 g001
Figure 1. Lunar Reconnaissance Orbiter (LRO) Wide-Angle Camera (WAC) images of grabens (a,b), rilles (c) and crater-floor fractures (d).
Figure 1. Lunar Reconnaissance Orbiter (LRO) Wide-Angle Camera (WAC) images of grabens (a,b), rilles (c) and crater-floor fractures (d).
Remotesensing 16 00107 g001
Remotesensing 16 00107 g002
Figure 2. Distribution of lunar grabens. The base image is WAC mosaic.
Figure 2. Distribution of lunar grabens. The base image is WAC mosaic.
Remotesensing 16 00107 g002
Remotesensing 16 00107 g003
Figure 3. WAC image (a) and block sketch (b,c) of a lunar graben showing dependence of width on elevation; α may be calculated using Equation (1). (b) is modified from [8]. (c) shows the calculation principle of fault dip. AB and CD represent graben rim at the topographic high and low positions, respectively. The line segment EF in (c) indicate width of downthrow block.
Figure 3. WAC image (a) and block sketch (b,c) of a lunar graben showing dependence of width on elevation; α may be calculated using Equation (1). (b) is modified from [8]. (c) shows the calculation principle of fault dip. AB and CD represent graben rim at the topographic high and low positions, respectively. The line segment EF in (c) indicate width of downthrow block.
Remotesensing 16 00107 g003
Remotesensing 16 00107 g004
Figure 4. Topographic and slope profiles at the topographic high (a,c) and low (b,d) position. A, B, C, and D in Figure 4 equal to that in Figure 3a.
Figure 4. Topographic and slope profiles at the topographic high (a,c) and low (b,d) position. A, B, C, and D in Figure 4 equal to that in Figure 3a.
Remotesensing 16 00107 g004
Remotesensing 16 00107 g005
Figure 5. Vertical view (a) and sectional drawing (b) of a lunar graben.
Figure 5. Vertical view (a) and sectional drawing (b) of a lunar graben.
Remotesensing 16 00107 g005
Remotesensing 16 00107 g006
Figure 6. The eight profiles on Repsold Graben (a) and ∆W vs. ∆h plots for all the data (b). N is the number of measurements plotted in this figure.
Figure 6. The eight profiles on Repsold Graben (a) and ∆W vs. ∆h plots for all the data (b). N is the number of measurements plotted in this figure.
Remotesensing 16 00107 g006
Remotesensing 16 00107 g007
Figure 7. Various factors that affect the calculation results. (a) Basalt filling; (b) ejecta filling; (c) collapse; (d) reformed by later tectonic movements.
Figure 7. Various factors that affect the calculation results. (a) Basalt filling; (b) ejecta filling; (c) collapse; (d) reformed by later tectonic movements.
Remotesensing 16 00107 g007
Remotesensing 16 00107 g008
Figure 8. Uplift along the Repsold Graben. (a) is the WAC image of Repsold Graben, and (b) shows the topographic feature of Repsold Graben. (c) is the topographic profile in (a,b) (line segment GH).
Figure 8. Uplift along the Repsold Graben. (a) is the WAC image of Repsold Graben, and (b) shows the topographic feature of Repsold Graben. (c) is the topographic profile in (a,b) (line segment GH).
Remotesensing 16 00107 g008
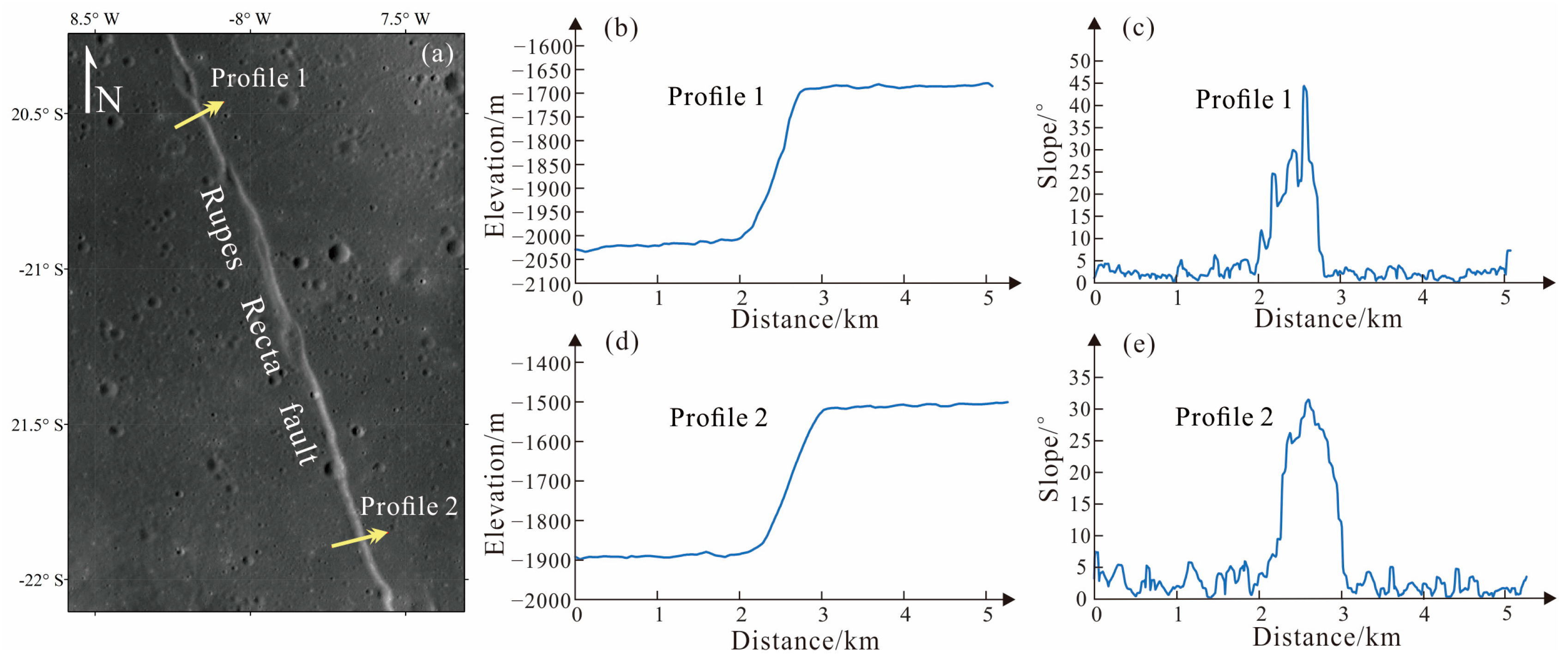
Remotesensing 16 00107 g009
Figure 9. Topographic and slope profiles at the edge (profile 1) and middle (profile 2) of the Rupes Recta fault. (a) is the WAC image of the Rupes Recta fault. (b,d) are topographic profiles. (c,e) are slope profiles.
Figure 9. Topographic and slope profiles at the edge (profile 1) and middle (profile 2) of the Rupes Recta fault. (a) is the WAC image of the Rupes Recta fault. (b,d) are topographic profiles. (c,e) are slope profiles.
Remotesensing 16 00107 g009
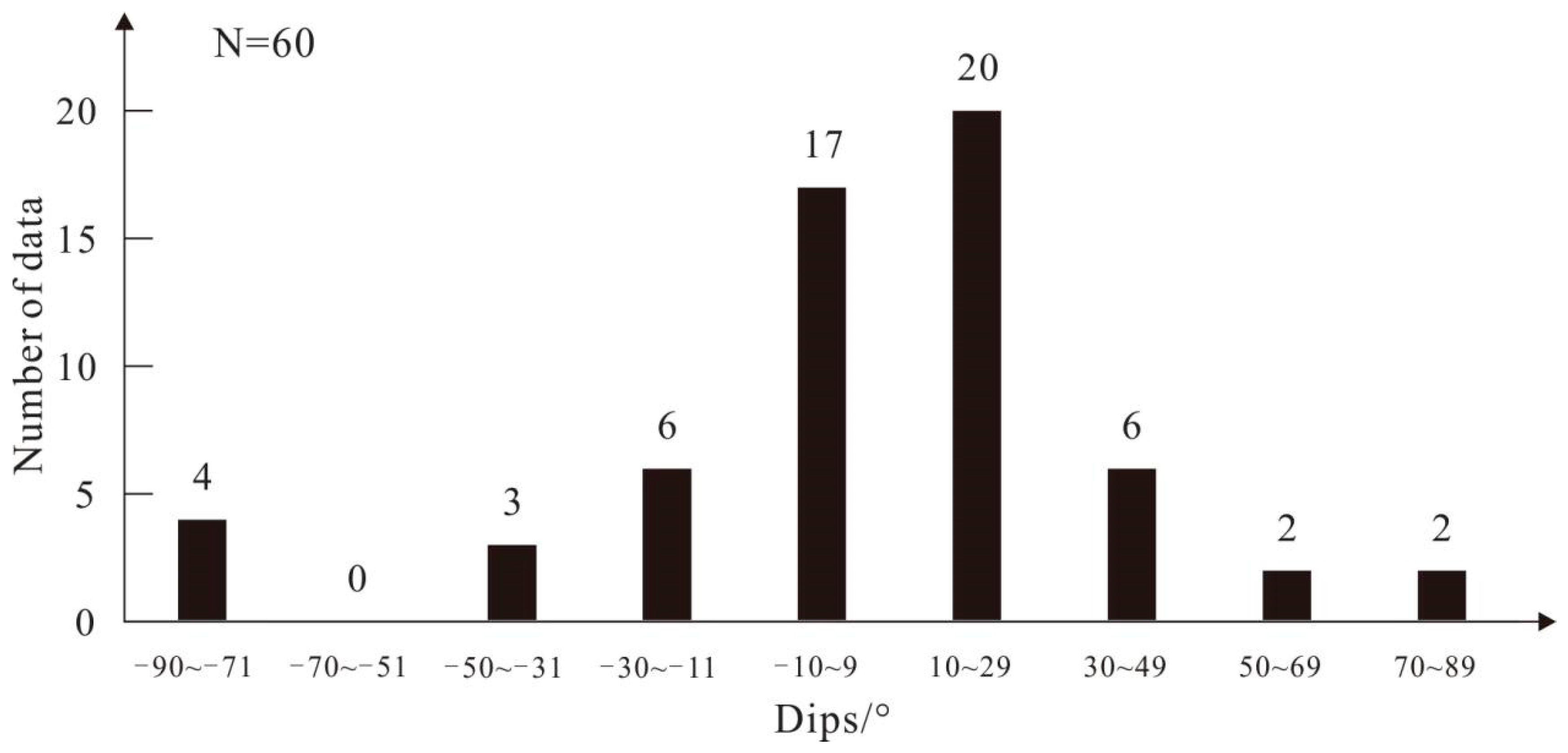
Remotesensing 16 00107 g010
Figure 10. Statistics of dips that were calculated from ∆h < 200 m data.
Figure 10. Statistics of dips that were calculated from ∆h < 200 m data.
Remotesensing 16 00107 g010
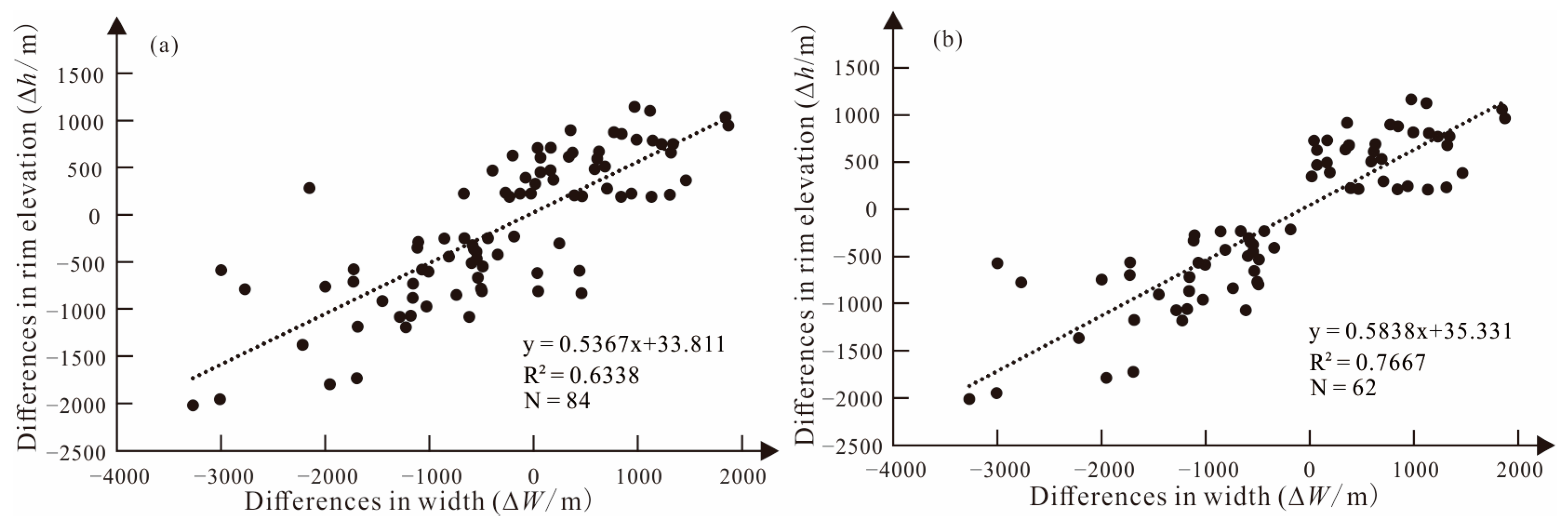
Remotesensing 16 00107 g011
Figure 11. ∆W vs. ∆h plots after removing ∆h < 200 m data (a) and negative values (b).
Figure 11. ∆W vs. ∆h plots after removing ∆h < 200 m data (a) and negative values (b).
Remotesensing 16 00107 g011
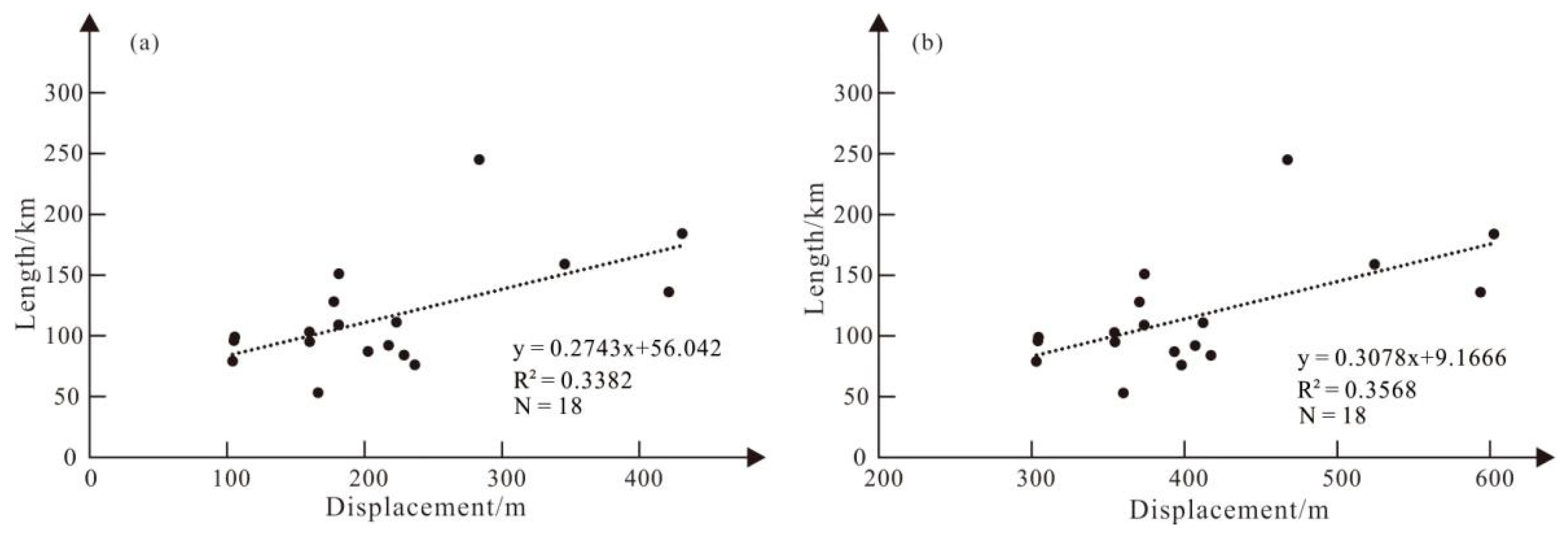
Remotesensing 16 00107 g012
Figure 12. The D–L plot of grabens. The D values in the (a) are calculated from depths, and the D values in the (b) include the depth reduction caused by degradation. The Graben Hippalus is split into two independent grabens for the purpose of the calculation. Therefore, 18 sets of data were obtained from 17 grabens.
Figure 12. The D–L plot of grabens. The D values in the (a) are calculated from depths, and the D values in the (b) include the depth reduction caused by degradation. The Graben Hippalus is split into two independent grabens for the purpose of the calculation. Therefore, 18 sets of data were obtained from 17 grabens.
Remotesensing 16 00107 g012
Table 1. Information of the selected 17 grabens.
Table 1. Information of the selected 17 grabens.
No.Graben NameLocationLength/kmDepth/mMaximum Measured Wall Slope/°Number of ProfilesNumber of Calculation ResultsDips/°
Starting/°
(X, Y)		End/°
(X, Y)
1/−67.33, 2.45 −64.74, −0.191111772961546.4
2/−74.00, −2.98−72.78, −5.6087161234647.8
3/−78.29, 4.58−76.42, 2.817612520334.0
4Gerard−84.61, 49.46−85.89, 47.1279831961561.6
5Repsold−82.72, 50.34−77.14, 51.881592743682852.3
6Sirsalis−61.99, −16.19−66.05, −20.971843424082841.5
7de Gasparis−48.32, −23.00−50.69, −25.86109144313316.1
8/−50.98, −25.64−48.76, −27.9492173304645.4
9/−46.78, −26.13−47.82, −29.1096832533−2.4
10Hippalus-1−30.20, −22.22−33.44, −29.24245225473326.6
11Hippalus-2−29.43, −25.69−31.14, −28.60998424213.3
12Hippalus-3−28.55, −23.57−28.77, −26.16951272121−3
13Hesiodus−27.53, −32.40−17.16, −28.942791422461513.3
14/9.62, 7.6514.41, 6.081362913451034.6
15Goclenius-141.39, −6.4043.88, −9.01103127233321.8
16Goclenius-243.89, −9.1145.22, −10.4353132213361.5
17/30.36, 30.2429.96, 27.4984182203368.5
Total 69146
Average 41.3
Table 2. Assessment of each profile.
Table 2. Assessment of each profile.
No.Length/kmNumber of ProfilesDips/°Reason for Removing ProfilesNumber of Remaining ProfilesNumber of Remaining Calculation ResultsCorrected Dips/°
1111646.4/61546.4
287447.8/4647.8
37634.0The graben where a profile passes through is filled with basalt. The other two are located too close to each other, resulting in small ∆h and large errors.00/
479661.6Two profiles are filled with ejecta, resulting in significant changes in rim elevation. 4661.0
5159852.3The graben passes through two craters, and the crater floor show significant uplift. All dips calculated from ∆h and ∆W have large errors. However, the dip calculated by standard linear regression is 52.3°.82852.3
6184841.5Multi-stage structures and ejecta filling are developed along the extension of the graben. All dips calculated from ∆h and ∆W have large errors. 82841.5
7109316.1One of profiles is influenced by collapse accumulations. This profile is removed. 2146.6
892445.4/4645.4
9963−2.4This graben is intersected by another graben, and its overall shape and boundaries are unclear.00/
10245326.6One of profiles is covered by ejecta, and this profile was removed.2156.4
119923.3Difference in elevation is small (~25 m), resulting in large error.00/
12952−3Difference in elevation is small (~12 m), resulting in large error.00/
13279613.3The elevation changes along the graben extension are not significant. In addition, many radiational patterns of ejecta cover this graben. 00/
14136534.6Two profiles have passed through areas with later uplift, and they are removed. Compared to these two profiles, only one profile has a significant elevation difference. Thus, two values calculated from large ∆h are selected for calculation.32(39 + 63.9)/2 = 51.5
15103321.8One profile has a significant elevation difference from the other two. Two values calculated from large ∆h are selected for dip calculation.32(46.8 + 67.4)/2 = 57.1
1653361.5One profile passed through the areas with later uplift, and it was removed.2159.2
1784368.5One profile has a significant elevation difference from the other two. Two values calculated from large ∆h are selected for dip calculation.32(63.2 + 67.1)/2 = 65.2
Total 69 98
Average 41.3 52.5
Table 3. Distribution of lunar grabens.
Table 3. Distribution of lunar grabens.
Latitude/°Number of GrabensTotal Length/km
60~401162739
40~201493460
20~02685778
0~−201545405
−20~−401094582
−40~−601272
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhu, K.; Liu, J.; Michael, G.; Lei, D.; Zeng, X. Constraints on the Fault Dip Angles of Lunar Graben and Their Significance for Lunar Thermal Evolution. Remote Sens. 2024, 16, 107. https://doi.org/10.3390/rs16010107

AMA Style

Zhu K, Liu J, Michael G, Lei D, Zeng X. Constraints on the Fault Dip Angles of Lunar Graben and Their Significance for Lunar Thermal Evolution. Remote Sensing. 2024; 16(1):107. https://doi.org/10.3390/rs16010107

Chicago/Turabian Style

Zhu, Kai, Jianzhong Liu, Gregory Michael, Danhong Lei, and Xuejin Zeng. 2024. "Constraints on the Fault Dip Angles of Lunar Graben and Their Significance for Lunar Thermal Evolution" Remote Sensing 16, no. 1: 107. https://doi.org/10.3390/rs16010107

APA Style

Zhu, K., Liu, J., Michael, G., Lei, D., & Zeng, X. (2024). Constraints on the Fault Dip Angles of Lunar Graben and Their Significance for Lunar Thermal Evolution. Remote Sensing, 16(1), 107. https://doi.org/10.3390/rs16010107

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop