Evaluation of IMERG Data over Open Ocean Using Observations of Tropical Cyclones

Abstract

The IMERG data product is an optimal combination of precipitation estimates from the Global Precipitation Mission (GPM), making use of a variety of data types, primarily data from various spaceborne passive instruments. Previous versions of the IMERG product have been extensively validated by comparisons with gauge data and ground-based radars over land. However, IMERG rain rates, especially sub-daily, over open ocean are less validated due to the scarcity of comparison data, particularly with the relatively new Version 07. To address this issue, we consider IMERG V07 30-min data acquired in tropical cyclones over open ocean. We perform two tasks. The first is a straightforward comparison between IMERG precipitation rates and those retrieved from the GPM Dual-frequency Precipitation Radar (DPR). From this, we find that IMERG and DPR are close at low rain rates, while, at high rain rates, IMERG tends to be lower than DPR. The second task is the assessment of IMERG’s ability to represent or detect structures commonly seen in tropical cyclones, including the annular structure and concentric eyewalls. For this, we operate on IMERG data with many machine learning algorithms and are able to achieve a 96% classification accuracy, indicating that IMERG does indeed contain TC structural information.

1. Introduction

The Integrated Multi-satellite Retrievals for the Global Precipitation Measurement (GPM) Mission (IMERG) is a global precipitation dataset with products covering various time scales (30 min, daily, and monthly) [1]. It is an integrated, or merged, product in that it uses a variety of sources based on the GPM mission [2], as will be described in more detail in Section 2. IMERG’s spatial and temporal coverage and sampling make it useful for many types of studies, from local weather events to climate. Because of its utility, it is important to thoroughly evaluate its accuracy. The review article by Pradhan et al. [3], which surveyed many articles that evaluate IMERG Versions 03–06, noted that studies of IMERG data quality over the ocean are much less common than over land. Our references [4,5] for ocean measurements are included in [3]. Besides these studies, we have identified a number of other studies that compare IMERG data over the ocean with other data sources [6,7,8,9,10]. These references describe comparisons with various in situ measurements, including shipborne gauges, gauges on islands, and measurements by buoys. Also reported are comparisons with various remotely sensed data. These include data from shipborne radars and similar rainfall products from spaceborne passive sensors. The comparison of IMERG with a reanalysis precipitation product is reported in [10].

A brief summary of [3,4,5,6,7,8,9,10] is that IMERG data can qualitatively represent the structure of rainfall systems, and rain rates can be either over- or underestimated, depending on the conditions (season, rain type and intensity, and product type and version). Also, the behavior of IMERG is less understood over open ocean [3] and especially at sub-daily timescales. To address these knowledge gaps, this study uses observations of rainfall in tropical cyclones over open ocean to evaluate the half-hourly IMERG V07 product. The choice of TCs for IMERG validation is made here due to their being long-lived, having a relatively large size, with heavy rainfall, and often possessing well-defined structures [11,12,13]. Such structures include concentric eyewalls, initially found in aircraft observations [14] and now routinely seen using satellite passive microwave data near a 90 GHz frequency [15,16]. This structure occurs during an eyewall replacement cycle (ERC), in which an outer eyewall forms around the existing eyewall. The old, inner eyewall decays as the new, outer eyewall strengthens and contracts, resulting in the eventual replacement of the old eyewall [13,14]. As such, they are transient, with both eyewalls visible for as little as a few hours. Likewise, annular TCs have relatively large eyes with essentially no spiral bands [17,18,19], showing a donut-like structure in satellite imagery. This structure seems to be stable, allowing annular TCs to remain annular, often with a moderate-to-high intensity, for several days. Beyond the annular structure and concentric eyewalls, more general TC structural characteristics (e.g., compact structure of intensifying TCs) have been known for years, as evidenced by work on the use of satellite data for TC intensity characterization, dating back to the pioneering work of Dvorak [20], and more recent work with both visible/IR and passive microwave data [21].

Because of the aforementioned characteristics, there are a number of IMERG-related publications dealing with the precipitation in TC. These typically focus on TCs nearing or making landfall, where surface radar and rain gauges are often readily available for comparison with IMERG, e.g., [22,23,24,25]. As with the studies mentioned above, these TC-based studies note both overestimation [22] and underestimation [24] at very high rain rates. Reference [26] evaluates IMERG for characterizing TCs and [27] compares the IMERG v06 TC rain rate measurements with those obtained from other satellite products, finding a significant overestimation of TC rain rate by IMERG.

To use TC data to address the gaps in the knowledge noted above, this study has two parts, using two distinct types of data. The first part considers a quantitative comparison of IMERG rain rates with those obtained from the Dual-frequency Precipitation Radar (DPR) onboard GPM [2]. Although IMERG makes some use of DPR measurements, it is dominated by passive microwave measurements. Persuasive arguments for the “approximate independence” of IMERG and DPR have been made in the literature and are thoroughly discussed in [28] and the references therein. The quantitative comparison in the first portion of the paper uses approximately co-incident and co-located IMERG and DPR TC measurements to evaluate the difference between these two sources. The second portion of the paper considers the ability of IMERG to distinguish between annular, concentric eyewall, and intensity/intensification features. The strategy for this task uses machine learning (ML); the goal is not to develop a practical machine learning algorithm but, rather, to use existing algorithms to test IMERG’s ability to distinguish the aforementioned structures in TCs. The next section describes the IMERG and DPR data used for the quantitative comparisons and the IMERG and ancillary data used for the classification study. The methods for both parts of the work are also described. Section 3 presents the results for the cases and for the full datasets for both parts of the work. The last two sections provide the discussion and conclusions.

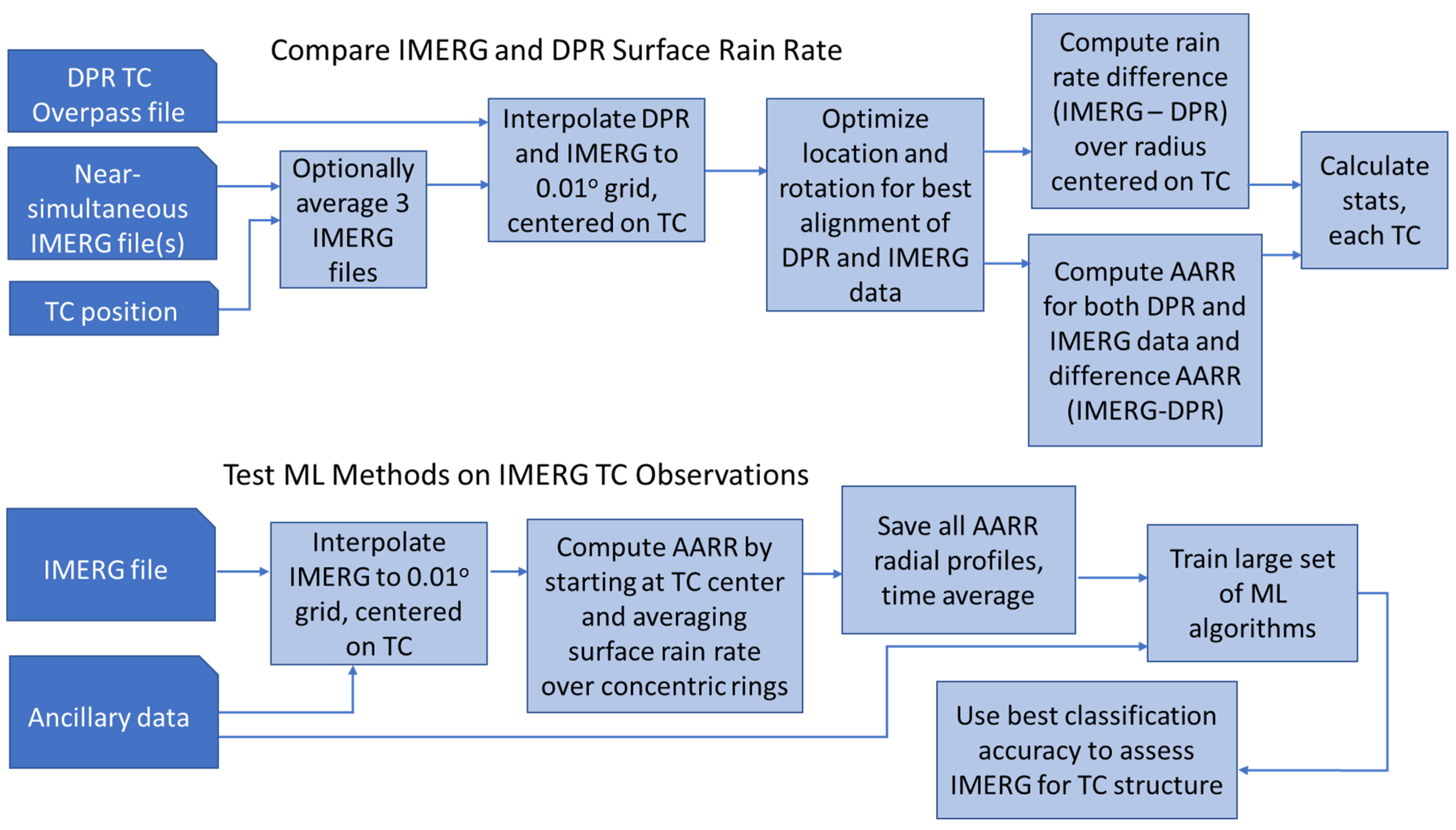
2. Data and Methods

2.1. Description of the Data Used

The IMERG data are described in [1]. The main precipitation-related input to IMERG is the brightness temperature measurements from multiple passive microwave instruments on various satellites, including the Global Precipitation Measurement (GPM) mission [2]. Additional inputs include passive infrared (IR) from various geostationary satellites, rain gauge data, and auxiliary information on the surface type, including snow coverage maps. The passive microwave brightness temperatures are intercalibrated and converted to surface rain rates. The resulting rain rates are gridded and adjusted via comparison with the Ku-band swath Combined Radar-Radiometer (CORRA) product from GPM, followed by adjustments for the known issues with CORRA [29]. This process ties the global passive microwave measurements with the GPM active/passive precipitation retrieval, while another step ties the precipitation estimates to satellite and gauge estimates from the Global Precipitation Climatology Project [30]. The adjusted, gridded rainfall estimates at half-hour time increments are then optimally combined with the other inputs by a Kalman filtering approach. The algorithm for the complete process is described in [31]. Reference [32] provides additional details on possible effects from using data from multiple sensors, specifically in relation to landfalling TC precipitation estimates. There are three IMERG output products. The one used here is Version 07 “Final” and is research quality; the half-hourly estimates have been further adjusted to match monthly satellite gauge data prior to product release.

The DPR data used here are the Level 2A DPR V07. This product contains profiles of the rain rate to the surface based on radar observations at the Ku- and Ka-bands [33]. While DPR is well calibrated and should provide accurate reflectivity measurements, there are likely still uncertainties and biases in the radar-retrieved rain rate [28]. The Level 2 DPR rain rates are instantaneous (with each cross-track scan taking less than one second) and are provided on the original DPR sampling grid covering a swath of about 220 km. The DPR spatial sampling and resolution are both about 5 km. In comparison, IMERG files provide surface rainfall in mm/h at 0.1° grid spacing. This corresponds to a spatial sample spacing of about 11 km; the effective spatial resolution of IMERG over the ocean is estimated at 10–20 km [34].

The IMERG and DPR data provide the data used in the quantitative rain rate comparisons. For the TC structure classification study, we use IMERG precipitation data and ancillary information about the TC structure. For the North Atlantic and Eastern North Pacific hurricanes, we rely on information provided in the National Hurricane Center (NHC) Tropical Cyclone Reports. These provide track and intensity information, as well comments on features, including concentric eyewalls and annular structure. For other ocean basins, location and intensity are available from the Joint Typhoon Warning Center best track data and from IBTrACS. However, these datasets do not include information on the storm structure. For TCs in these basins, the best data source for determining what structural features may have existed at different times within a given storm is the ARCHER TC product [35]. Wikipedia also has descriptions of TC structures that supplement the ARCHER results. Access to the IMERG, DPR, and all of the TC ancillary data is described in the section “Data Availability”.

A total of 72 TCs were chosen for this study. All reached at least Category 3 on the Saffir–Simpson scale at some point in their lifetime. However, additional criteria were added, depending on whether the TC is used for rain rate comparison, classification, or both. The simplest case is the quantitative comparison only. In this case, we compare a DPR “snapshot” of the TC with the IMERG product at the time closest to the DPR overpass. The challenge is finding cases in which the TC is covered by the rather narrow DPR swath. For this, we use the JAXA/EORC Tropical Cyclone Database (also listed in “Data Availability”). This site provides all GPM overpasses of global TCs and allows us to find radar overpasses that include the TC center. To find a moderate number of cases, the TC intensity at the time of the overpass, in some cases, is less than Category 3, although all storms were well organized, having a distinct center with the eye visible, especially in the DPR data. For each selected overpass, we download the DPR data product and the closest in time IMERG product; only these two files are needed. In practice, we also download the surrounding IMERG files, since we see moderate variability in the rain rates from one file to the next for the same TC. This allows testing the effects of averaging of the data in time.

More time-consuming is the selection of cases for the classification study. Using the various ancillary data mentioned above, we identify good candidates for various structures. TCs displaying various structures over their lifetimes are especially good candidates, since a single such TC generates training data for multiple classes. Such features are often correlated with the TC having at least Category 3 intensity. We then download the corresponding IMERG images (one per file) for the times in which various features occurred; for each selected TC, this is typically 100–200 IMERG files. Appendix A lists all the TCs used in this study, noting which are used for the DPR comparison, which are used for the classification study, and which are used for both. These are, respectively, labeled “D”, “C”, or “B” in the “Analysis” column in the TC table in Appendix A. This table also lists the start time for classification and the observation hours, which is one-half the number of 30-min files used for each TC.

2.2. Methods for Quantitative Comparison of the Rain Rates

This subsection describes how we compare DPR and IMERG data. Since the DPR sampling is irregular, roughly spaced at 0.05°, we create a grid with finer (0.01°) spacing. We then interpolate both the DPR data and the IMERG data to this same grid. In the process, we also convolve the DPR data with a smoothing function to degrade its resolution to approximately match IMERG. Based on [34], a resolution of 20 km is chosen for DPR. This is done to avoid artificially higher rates for DPR due to a better resolution, which would be an unfair comparison. Given the strong horizontal motion in TCs, even a few minutes of difference between the IMERG and DPR observations could cause a mismatch. Hence, additional alignment of the two datasets is performed by shifting and rotating the DPR data so as to minimize the root mean square difference in the rain rates. Once the IMERG and DPR data are aligned, we perform multiple surface rain rate comparisons.

First, we directly difference the two datasets over the 0.01° two-dimensional grid. From this, we compute the maximum, mean, standard deviation, and percentiles of the differences. Second, we compute the azimuth-averaged rain rate (AARR) as a function of the radius for each dataset by using concentric rings (annuli). The AARR is defined as the average DPR or IMERG rain rate in each ring out to a radius of about 180 km from the center. There are 80 radii sampled, with a spacing of 0.02° (2.2 km). The width of each ring is 0.035° or about 4 km. Hence, our sample interval in the radius is smaller than the radial resolution, implying that our rings overlap. Such is always desired for any type of sampling. The AARR is used in, for example, refs. [36,37]; the peak AARR, in most cases, is located near the TC center and is probably indicative of the average rain rate in the eyewall, since this is usually the location of the heaviest rain. Where the peak rain rate in the TC could be 100 mm/h in a very small area, azimuth averaging gives much lower maximum rain rates, e.g., 20 mm/h. Prior to computing the AARR, we manually inspect each dataset to find the best center relative to any azimuthally symmetric rain structures. This minimizes the variation within the rings used for the AARR. Once the AARR is calculated, we find the difference of the AARR at each radius. From this, we again compute the maximum, mean, standard deviation, and percentiles of the differences. In Section 3, Results, we illustrate these calculations on a single case and then provide statistics over all 50 TCs with simultaneous IMERG and DPR coverage. The methodology just described is summarized as the upper workflow in Figure 1.

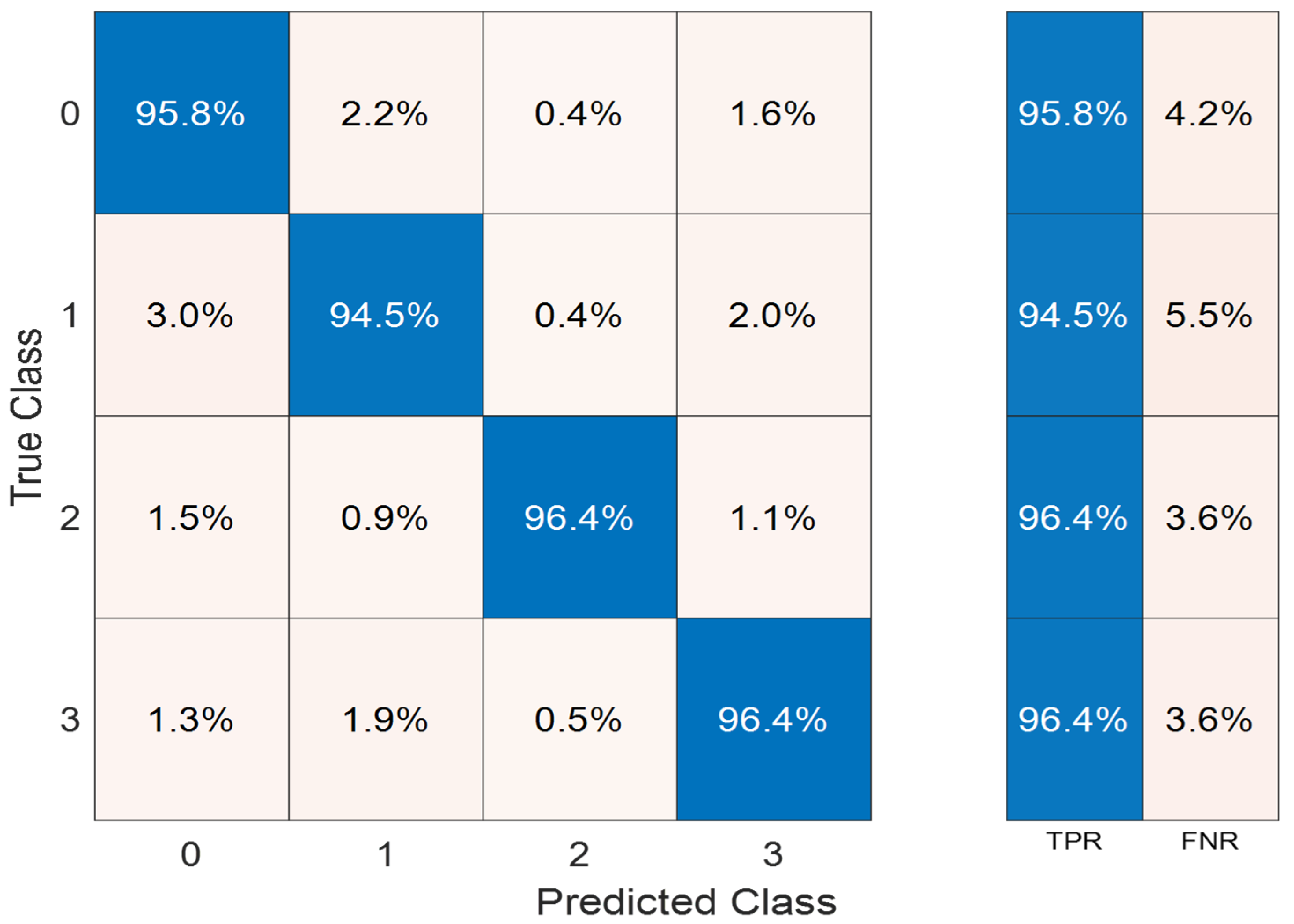
2.3. Methods for Evaluation of IMERG Feature Classification Ability

This subsection describes the methodology for assessing IMERG’s ability to detect various TC structures. We begin by describing the structures that we attempt to detect in IMERG data. These classes, or structures, are “nominal” (0), “concentric eyewalls” (1), “annular” (2), and “intensifying” (3). Class 0, or nominal, is essentially a null class in which none of the features characteristic of classes 1–3 are present. These would include TCs that have reached peak intensity or are weakening but still major TCs. Class 1, concentric eyewalls, is a transient feature but relatively common in higher-category TCs. Class 2, annular, is a much rarer occurrence, with only a small number occurring globally over a few years. The intensifying classification (3) is for TCs intensifying based on best track data. While TCs undergoing rapid intensification are of particular interest, we use the term “intensifying” to denote storms with rapid or moderate intensification, typically having a compact structure, with the most intense convection very close to the center [20]. Most cases for Class 3 are TCs intensifying to Category 4 or 5 on the Saffir–Simpson scale.

Figure 1, lower workflow, shows the steps in performing the assessment of the TC structural information available within the IMERG surface rain rate data. The first step in processing a particular TC, after downloading all the IMERG files, is to enter the best track 6-h locations in a database. The processing code uses these positions to find the center of the TC at each time over the period to be examined (typically, 1–4 days). These locations are then manually modified by stepping through the data for each storm and checking the reported position versus that visible in the corresponding IMERG images. Adjustments are performed to center any azimuthally symmetric rain structure. The 6-h positions are interpolated to obtain the estimate of the center at the time of the file being processed. The IMERG rain rates are interpolated to an 0.01° grid. The statistics of the rain rate are calculated within concentric annuli, or rings, around the TC center in the same manner and with the same parameters as for the DPR comparison. Using the ancillary data, we assign a classification of 0–3 at each 6-h TC position. For times between these 6-h values, we used the classification of the nearest neighbor in time. Optionally, averaging of radials over time can be performed. These steps for processing each TC require several hours, which is why only 35 TCs are chosen for the classification task. For this task, the more important number is the total number of TC observations—in this case, more than 3500.

The output of the preceding steps is a file for each TC containing the radial profiles of the rain rate for each IMERG file. With a radial resolution of 2 km, there are rain rates at each of 80 radii out to 180 km. The number of radial profiles for a given TC is the number of half-hourly IMERG files analyzed for that TC (chosen based on the duration of interesting features). Once the files for all TCs are generated, the analysis proceeds by merging them into a single array, which has 80 radii times the total number of IMERG files used for all TCs. This is because each radial profile corresponds to one 30-min IMERG file. The merged radials array also contains the class (0–3) for each radial profile. At this point, the time correlation between observations within the same storm is ignored. Each 80-element radial vector, with its class, becomes a training vector for a ML algorithm. To test IMERG’s ability to properly represent the aforementioned structures in TCs, we apply various statistical and ML-based supervised classification algorithms, seeing how well they can learn the TC structures (class) from the IMERG data.

The software used for exploring the relationships between the radial profiles and classification [38,39] has numerous ML classification methods, including K-nearest neighbor (KNN), linear discriminant analysis (LDA), support vector machine (SVM), and neural networks (NN). These methods are summarized in [38,39] and are further described in, e.g., [40,41]. The KNN classifier has a long history of use for these types of problems. Briefly, for a given input vector, KNN computes the distance from the input to each training vector. It then looks at the classes of the K neighbors with the smallest distances and assigns the class most represented in these neighbors. In the case of K = 1, it simply classifies the input as that of the closest neighbor. The LDA also has a long history; it is found as an optimization problem using classical statistical detection theory. Specifically, it finds the best linear filter that separates the class boundaries. The SVM is a kernel-based method; as such, it tries to map the LDA problem into a higher-dimensional space, where better class boundaries can be found. Neural networks are also nonlinear structures with many parameters. Since the goal here is to assess IMERG for use in sensing the TC structure, we are much more interested in the accuracy of the best technique; more details on the workings of the methods can be found in the references. Regarding training of the machine learning algorithm, there are various approaches. The main approach used here is a five-fold cross-validation. This is recommended for smaller datasets, since it makes use of all the data by partitioning it into five disjoint sets (folds) and training using four of the five folds, with the fifth fold being used for validation. This is repeated using each fold for validation, with the remaining four for training. The reason for such an approach is to prevent overfitting of the data (fitting to signal and noise). We also use a simpler method, called holdout validation, which trains with two-thirds of the supplied data and then tests on the remaining one-third.

3. Results

This section follows the order of Section 2, first describing the results from the DPR and IMERG comparison, then moving to the ML-based assessment of IMERG’s ability to capture TC structures. The results for each task are broken into two subsections, first showing examples or case studies, then describing results for the full sets of data for each task. Hence, we have the IMERG and DPR case studies in Section 3.1 and the overall statistics in Section 3.2. For the ML-based evaluation of IMERG, Section 3.3 examines example images and profiles, and Section 3.4 discusses the results using all TCs selected for the ML task.

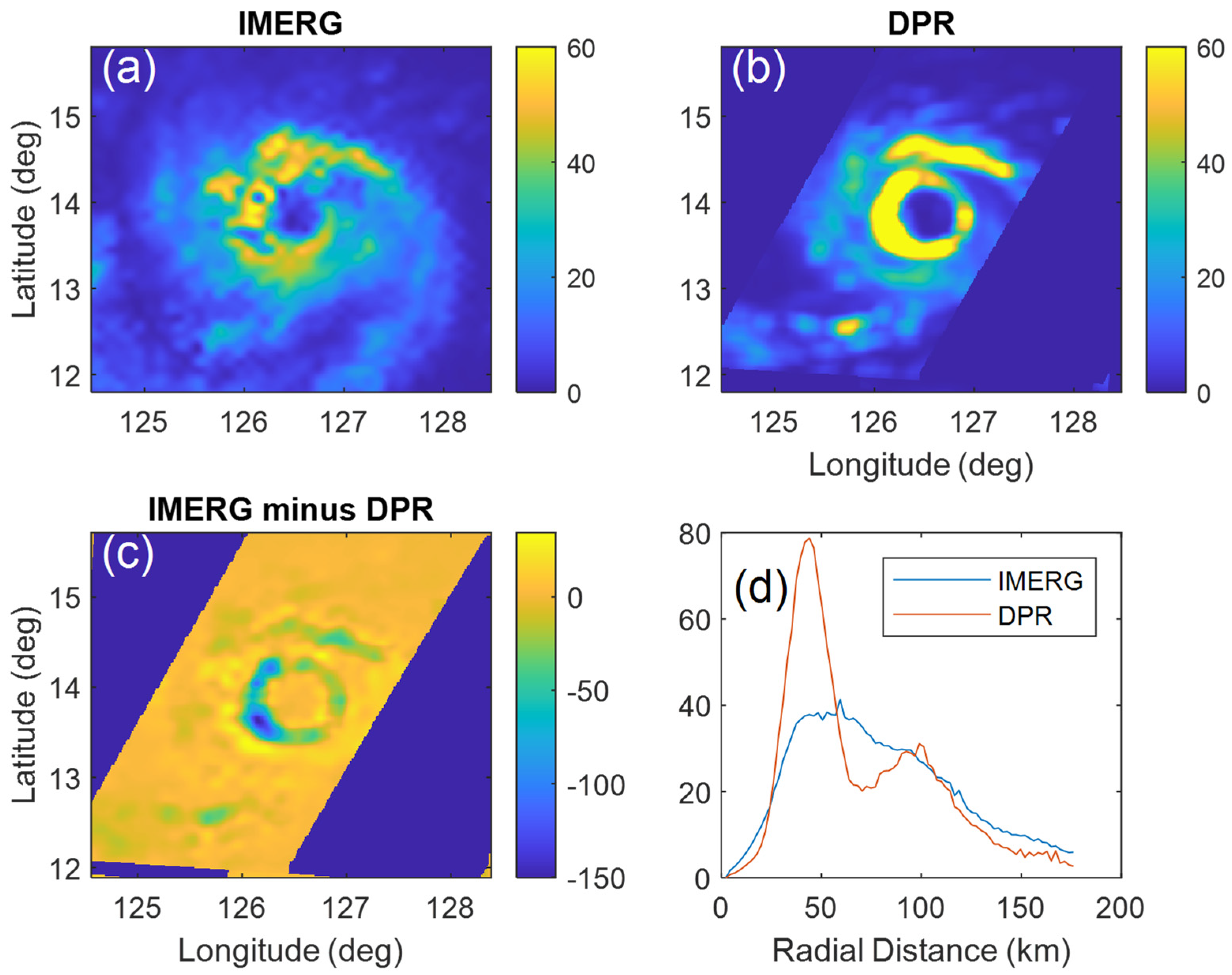
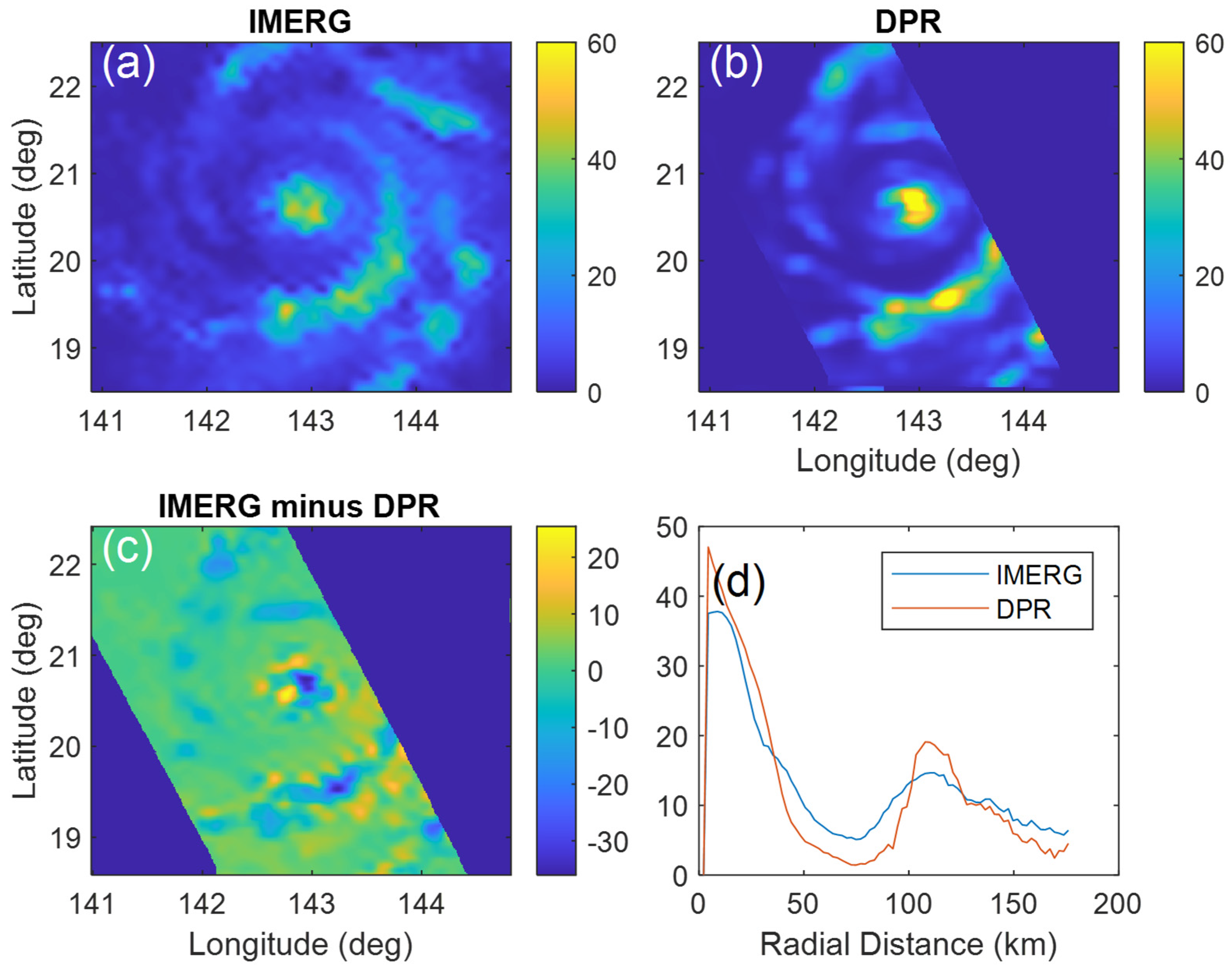
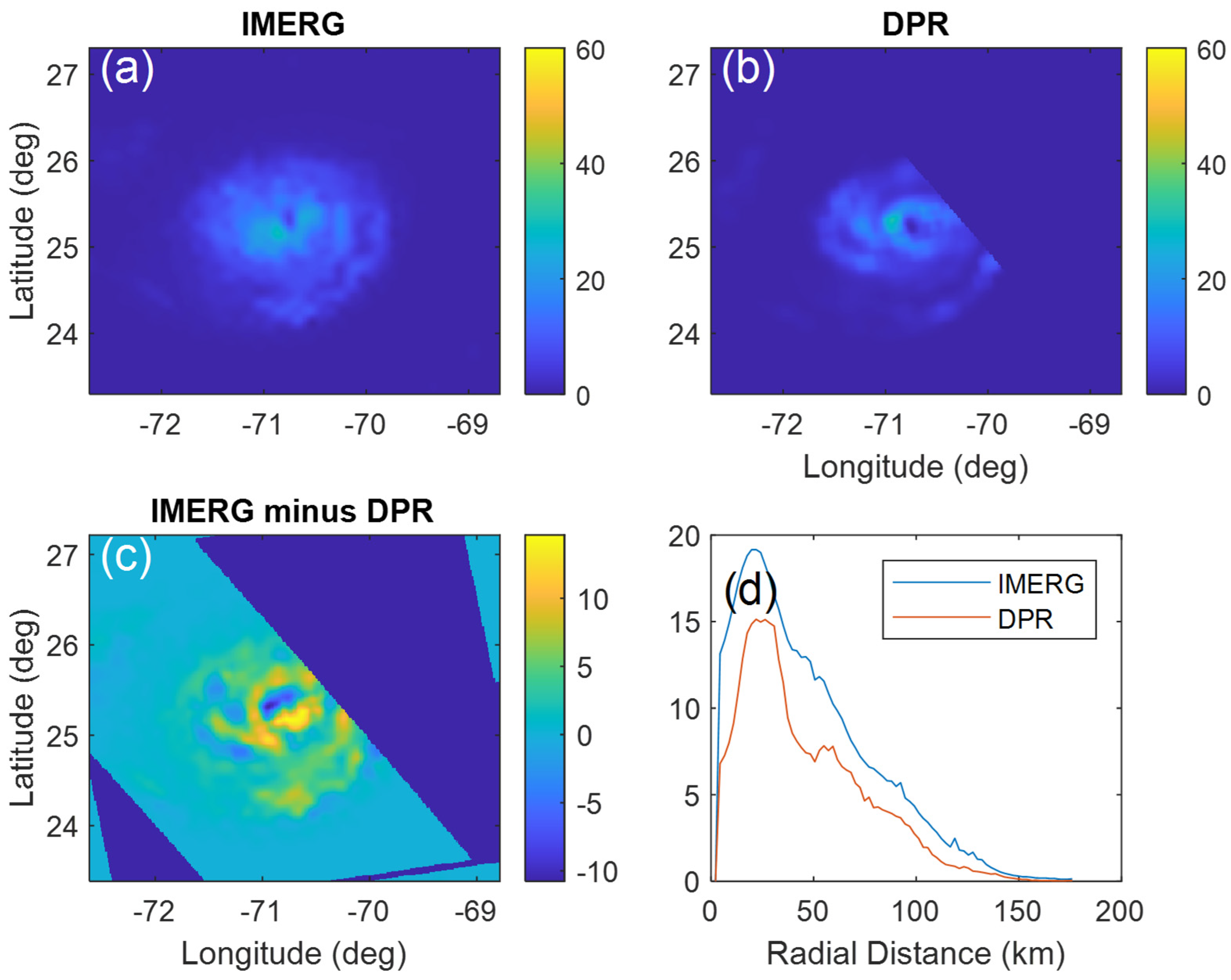
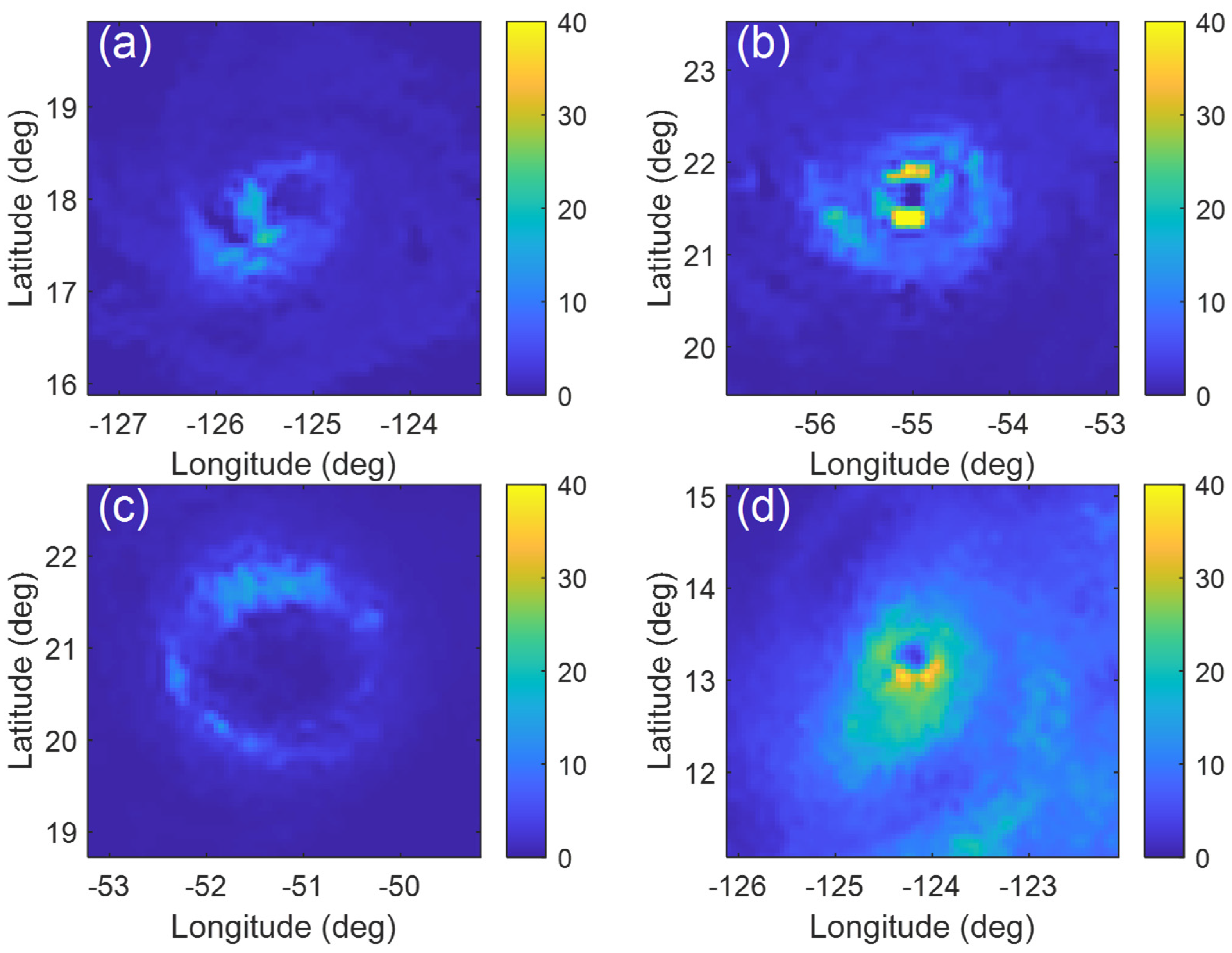
3.1. Case Comparisons of DPR and IMERG Data

The methodology for comparing DPR and IMERG data, described in Section 2, is applied to all 50 TCs chosen for this purpose. These are identified in Appendix A by the letter “D” or “B” in the “Analysis” column. This subsection reports comparisons for the three TCs. These cases are chosen as representative of IMERG rain rates seen over all of the DPR comparison TCs, namely, the severe underestimation of IMERG relative to DPR, small underestimation, and small-to-moderate overestimation. Figure 2 shows the first case, TC Surigae, with the IMERG and DPR surface rain rates shown in Figure 2a,b. Various statistics of TC Surigae and the other two TCs are listed in

Table 1. Rainfall statistics for the three example TCs. Values are rain rates in mm/h. RR indicates rain rate in the 2D data. AARR is the azimuthally averaged rain rate.

TC Name	IMERG RR Mean	DPR RR Mean	Std Dev RR Diff	IMERG RR Maximum	DPR RR Maximum	IMERG AARR Maximum	DPR AARR Maximum
Surigae	30.9	34.9	28.4	63.2	173.5	41.3	78.7
Bolaven	10.8	8.6	6.2	46.5	73.0	37.8	47.0
Dorian	10.4	7.5	3.6	29.6	30.7	19.2	15.1

. One can see that the DPR data show a much higher rain rate near the TC center than IMERG at the same location (Table 1, “Max RR IMERG” and “Max RR DPR”). The difference in the rain rates (IMERG-DPR) is shown in Figure 2c; there are both positive and negative differences distributed over the area, but the negative differenced are especially large in the dark ring surrounding the center. The intense rain near the TC center is evident in the AARR plots in Figure 2d, where IMERG is much smaller than DPR near a radial distance of 50 km. IMERG is then larger out to about a 90 km radius, with the two being very close beyond 90 km. When the 2D difference between IMERG and DPR is averaged over a disk with radius of about 180 km (1.6 degrees of latitude or longitude), the mean difference is about −4 mm/h (the mean IMERG is smaller than the mean DPR by 4 mm/h, as shown in the second and third columns of Table 1). It is clear that the IMERG/DPR difference does not approach a constant bias but depends on the location within the TC and probably the rainfall intensity. The standard deviation of the IMERG-DPR difference over the 2D domain provides an estimate of the fluctuation of the difference. If the difference was the same in all the pixels, the standard deviation would be zero. In the case of Surigae, it is 28 mm/h; normalized by the mean rain rate of 34.9, we get a ratio of 0.82, larger than that for the other two cases, to be discussed next.

Figure 3 provides the same information but for TC Bolaven. When comparing means over the 180-km radius disk, the IMERG rain rate actually exceeds that of DPR by 2 mm/h, as can be seen for TC Bolaven in Table 1. This is consistent with the difference image in Figure 3c; much of the TC has a small difference. The areas in which IMERG is lower (blue) show a somewhat axisymmetric pattern. Yellow areas, indicating IMERG is greater than DPR, are scattered over the storm, with notable areas at the eye and in a strong rain band to the south of the eye (between 19 and 20 latitude and near 143 longitude). That the differences are more uniform than Surigae is confirmed by the standard deviation; dividing Bolaven’s standard deviation by its mean gives a ratio of 0.72. Figure 3d shows that the AARR for both products have very similar radial patterns but with DPR higher near the TC center and the band out at radial distance 110 km, i.e., the regions with the heaviest precipitation. Figure 4 shows the case of TC Dorian, which represents an overestimation of the rain rate almost everywhere, except for a small area near the TC center (Figure 4c). The AARRs in Figure 4d show that IMERG is larger at all radii. When comparing means over the 180-km radius disk, the IMERG rain rate exceeds that of DPR by 4 mm/h. This TC has generally lower rain rates than either Surigae or Bolaven. Dorian has the smallest standard deviation normalized by the mean, namely 0.48.

3.2. Statistics of DPR and IMERG Comparison Data

Table 2. Comparison of the results on TC precipitation and results obtained here. AARR is the azimuthally averaged rainfall rate.

	Mean	Std Dev	10th%	50th%	90th%
2D RR difference stats:	−1.1	15.2	−5.5	−1.0	3.2
AARR difference stats:	0.1	6.4	−3.3	−0.1	3.5
AARR diff (r < 70 km):	−1.7	9.3	−14.0	0.1	6.8
AARR diff (r > 70 km):	1.2	4.2	−3.2	1.3	5.6

provides the results for all the TCs. The first column is the mean IMERG-DPR difference. Both the AARR and the 2D rain rate difference (“mean”) are negative by about 0.5 mm/h, indicating a relatively small negative bias of IMERG relative to DPR over the TC. However, both have rather large RMS differences, indicating that the difference of IMERG-DPR can have large fluctuations. The next three columns provide the statistics of the mean of each TC, e.g., using the first row, 10% of the TCs have mean differences less than −4.82 mm/h and 90% have means less than 3.98 mm/h. The second row provides the same statistics but on the AARR averaged over the radius. The last two rows show results for AARR over the radial distance, first for all radial distances less than 70 km and then for all radial distances greater than 70 km. These last two rows are useful in identifying where the differences occur. The larger underestimations by IMERG are at the smaller radii. We also checked the correlation between the DPR rain rate and measures of the IMERG-DPR difference. For the latter, we use both the signed difference in mm/h and the percentage difference, in which we divide the difference by the DPR rain rate and multiply by 100 to convert to percentage difference. In either case, we find that the DPR rain rate and the IMERG-DPR difference are negatively correlated at the p = 0.05 significance level, indicating larger underestimation in the IMERG product at higher DPR rain rates. This is true whether we use the 2D rain rate (RR) or the radial AARR data; the correlation coefficients are −0.7 for AARR and −0.8 for RR. While all of the above results are based on comparing the DPR data with a single IMERG file, we also tested whether averaging three IMERG files might improve the agreement with DPR. However, the results were essentially unchanged.

3.3. Examples of IMERG Data for Different TC Classes

The results here are based on the radial observations from all TCs chosen for this part of the study and listed in Appendix A (with “C” or “B” in the “Analysis” column). Before using ML algorithms, we examine several examples of the different TC classes described in Section 2 (classes 0–3). Figure 5 shows four IMERG images, corresponding to different classes. Figure 5a is TC Olivia, which did not show any of the features associated with classes 1–3 and so is classed as 0. Olivia had completed an eyewall replacement cycle on the day before the observation in Figure 5 but had not yet started intensifying. A radial plot of AARR for TC Olivia is shown in Figure 6a, along with plots for three other TCs, also classed as 0. Figure 5b shows TC Isabel, which was captured in the middle of an eyewall replacement. Concentric eyewalls are readily visible. The AARR for Isabel and three other TCs with concentric eyewalls are shown Figure 6b; the eyewalls are visible as maxima in the plots. These are particularly distinct in the plot for TC Frances. Figure 5c shows TC Larry, which had an annular structure (class 2) at the time of observation. As with the observations in vis/IR satellite imagery, the storm center is a large area of light or no rainfall. All four annular TCs in Figure 6c have similar radial profiles of AARR. Finally, the IMERG data for intensifying TCs (class 3) are shown in Figure 5d and Figure 6d. The image in Figure 5d has a small eye with relatively high rain rates around it. The plots in Figure 6d all show a steadily increasing rain rate toward the center, although the plot for TC Barbara peaks at radius 30 km, then drops and increases again toward the center.

3.4. IMERG Ability to Detect a TC Structure

The set of available ML-based classifiers, described in Section 2, we ran on all 3543 radial profiles of AARR, derived from the 35 TCs listed in Appendix A. Of this total number of profiles, the number for each class is (0) 1106, (1) 890, (2) 527, and (3) 1020. The results for all classifiers showed that the K-nearest neighbor (KNN) classifier with only one nearest neighbor (K = 1) has the highest classification accuracy. However, using KNN on radial profiles with no time averaging yielded a 66% accuracy. When averaging three samples, the accuracy jumps to 84%, and it increases to 89% with five samples. Using seven samples (i.e., averaging the data over 3 h) further improves the accuracy to 92%. The accuracy continues to improve with more averaging, plateauing at about 96% with 6 h averaging. More averaging can remove features and reduce accuracy. While the KNN method shows the best performance, the support vector machine (SVM) approach shows results with an accuracy of only a few percent lower than KNN. Figure 7 shows the classification accuracy matrix from the 6-h averaging run of KNN with K = 1. The left portion of the image shows the percentage of samples in each square of the matrix, where the horizontal axis is the predicted class of each column and the vertical axis is the true class for each row. Squares on the diagonal have the same predicted and true class, whereas all other squares are erroneous. The two-column matrix at the right is showing the true positive rate and false negative rate for each class; the former is the probability of correctly classifying a given observation, while the latter is the probability of an error. The accuracy just discussed is based on cross-validation, described in Section 2.3. The simpler holdout validation, using two-thirds of the data for training and one-third for testing, gave 95% accuracy on the test data versus the 96% found from cross-validation.

4. Discussion

The results in Section 3.1 and Section 3.2 can be summarized by the statement that the IMERG rain rates in TCs over the ocean can be smaller or larger than the nearly simultaneous and co-located rain rates retrieved from the DPR radar data. However, IMERG underestimation appears more common; furthermore, the correlation results indicate that it is more severe, both in absolute units and in percentage, at the highest DPR rain rates. As was briefly noted in the Introduction, both the overestimation and underestimation of very high rain rates have been reported. However, underestimation at very high rain rates appears more common in the literature [3] and is the finding here. We believe that the results here are the first reported for V07. Before concluding that all of the differences reported here are due to IMERG, we note that DPR has its own error sources, as described in [28]. We also note that DPR has a much higher spatial resolution than IMERG. We compensated by smoothing the DPR data to obtain a resolution that should be similar to IMERG. Nevertheless, it is possible that some of the differences seen here could be due to resolution differences, depending on which input data dominate the IMERG product at the time used [32].

The results in Section 3.3 and Section 3.4 show that radial profiles of AARR can detect various TC features or structures. The ML-based test results yielded a good classification accuracy of 96% overall, while the features detected in IMERG data are often better seen in other data, such as concentric eyewalls in 90 GHz radiometer data. However, IMERG has the advantage of being produced every 30 min and so may be useful for some TC studies.

5. Conclusions

We used knowledge of the structure and rain rate characteristics of tropical cyclones over open ocean to evaluate the GPM IMERG data product. To carry out this evaluation, we did comparisons with nearly simultaneous and co-located measurements by the GPM radar (DPR) and by applying machine learning to assess IMERG’s ability to detect known tropical cyclone (TC) structures. Based on these comparisons, we note the following:

• Comparisons with the surface rain rates from the GPM DPR show a tendency of IMERG to underestimate the rain rate relative to the radar. Furthermore, the tendency increases with the increasing rain rate.
• Concentric eyewalls, annular structure, and structure associated with intensifying TCs can be distinguished in the IMERG radial profiles of the azimuth mean rain rate but require temporal averaging over several hours.