A Side-Lobe Denoise Process for ISAR Imaging Applications: Combined Fast Clean and Spatial Focus Technique
Abstract
1. Introduction
- The acquisition of a large-scale set of measured echo data from non-cooperative targets remains unattainable;
- The construction of the output set proves to be challenging due to the angular sensitivity of ISAR image targets;
- Direct application of traditional networks to ISAR side-lobe noise reduction fails to yield satisfactory results due to substantial differences between ISAR and optical images.
- Based on the ISAR imaging model, we deduced the cause of side-lobe noise generation in imaging. Specifically, when the difference of each scattering amplitude is too large, the side-lobe of the sinc function cannot be completely eliminated, resulting in the appearance of side-lobe noise in the ISAR image. The above conclusion has been verified through simulation and measured data;
- To expedite the construction of the ISAR output dataset, we propose a fast clean algorithm. This method achieves rapid and effective side-lobe noise cancellation by implementing a high-pass filter on the range and Doppler bin;
- In the network design, we introduce a spatial attention layer and a loss function weight factor. By leveraging the sparsity of ISAR images, the noise reduction effect is enhanced, leading to a 2 dB improvement in the PSNR effect when comparing the image before and after optimization.
2. Problem Analysis and Sources of Ideas
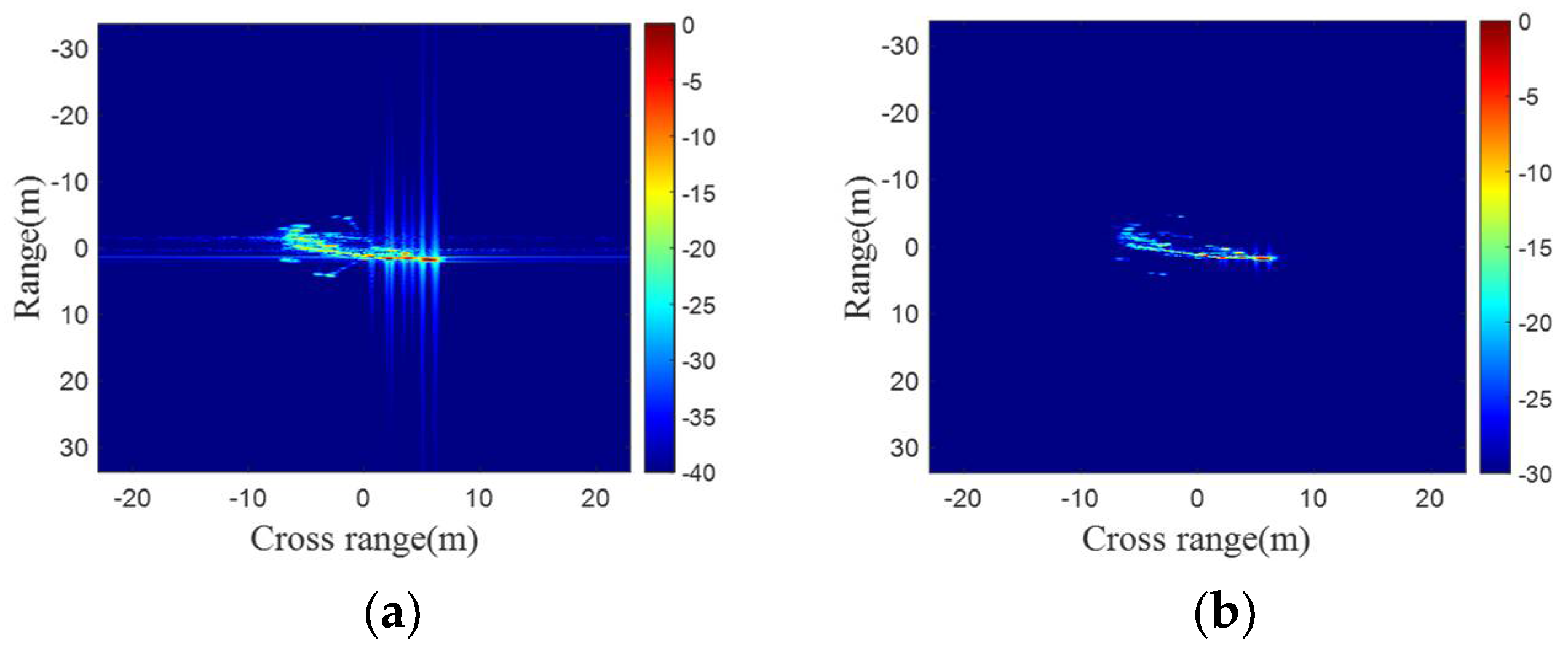
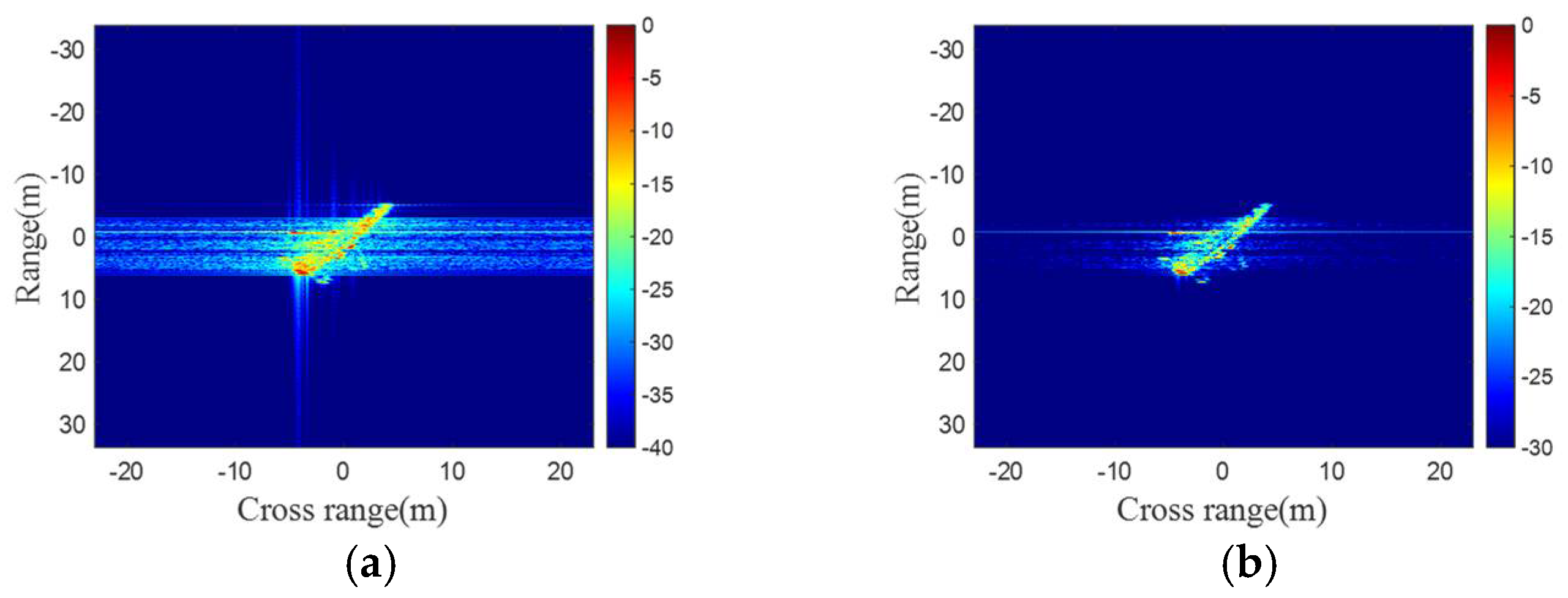
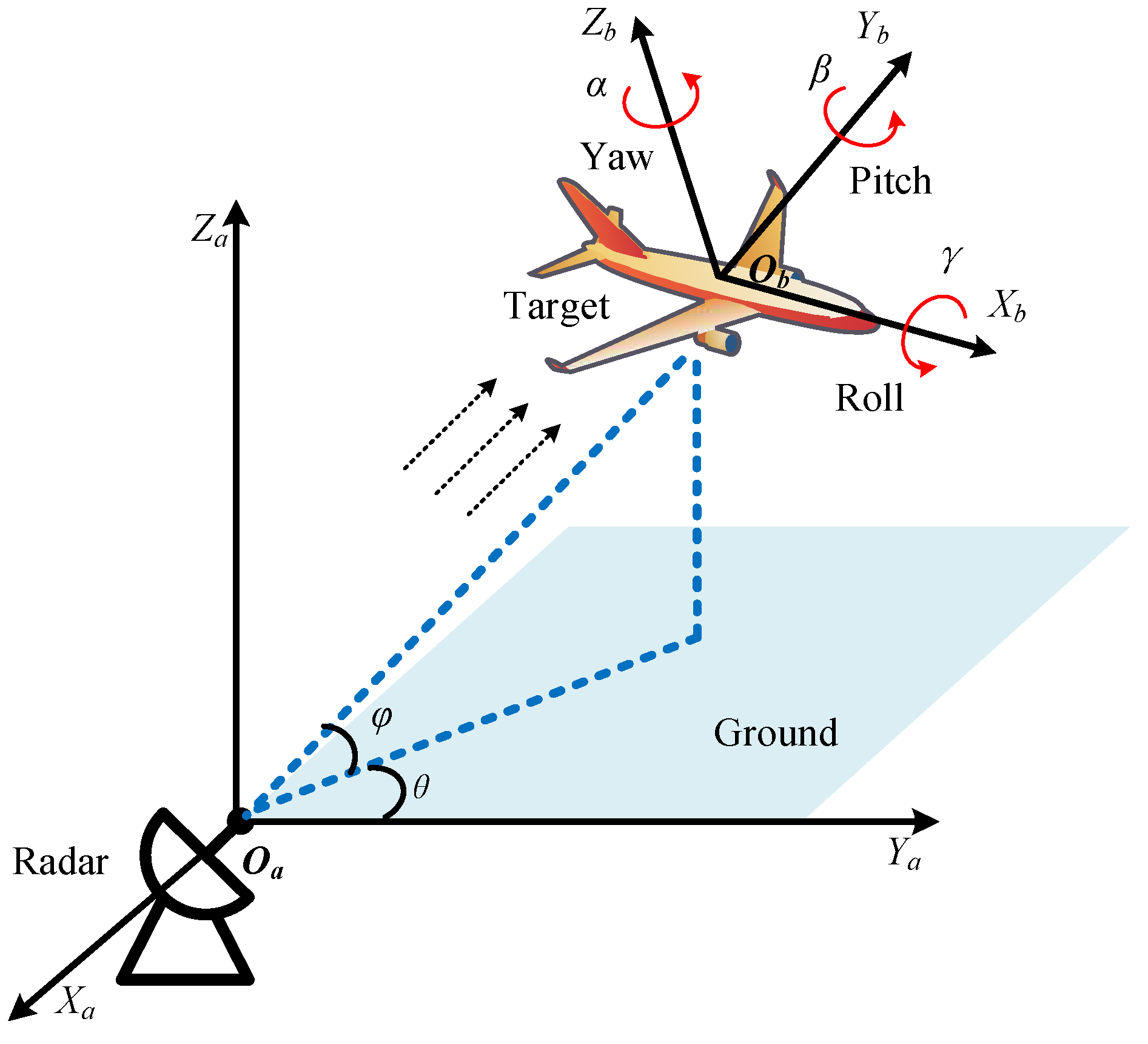
2.1. Problem Analysis
2.2. Sources of Ideas
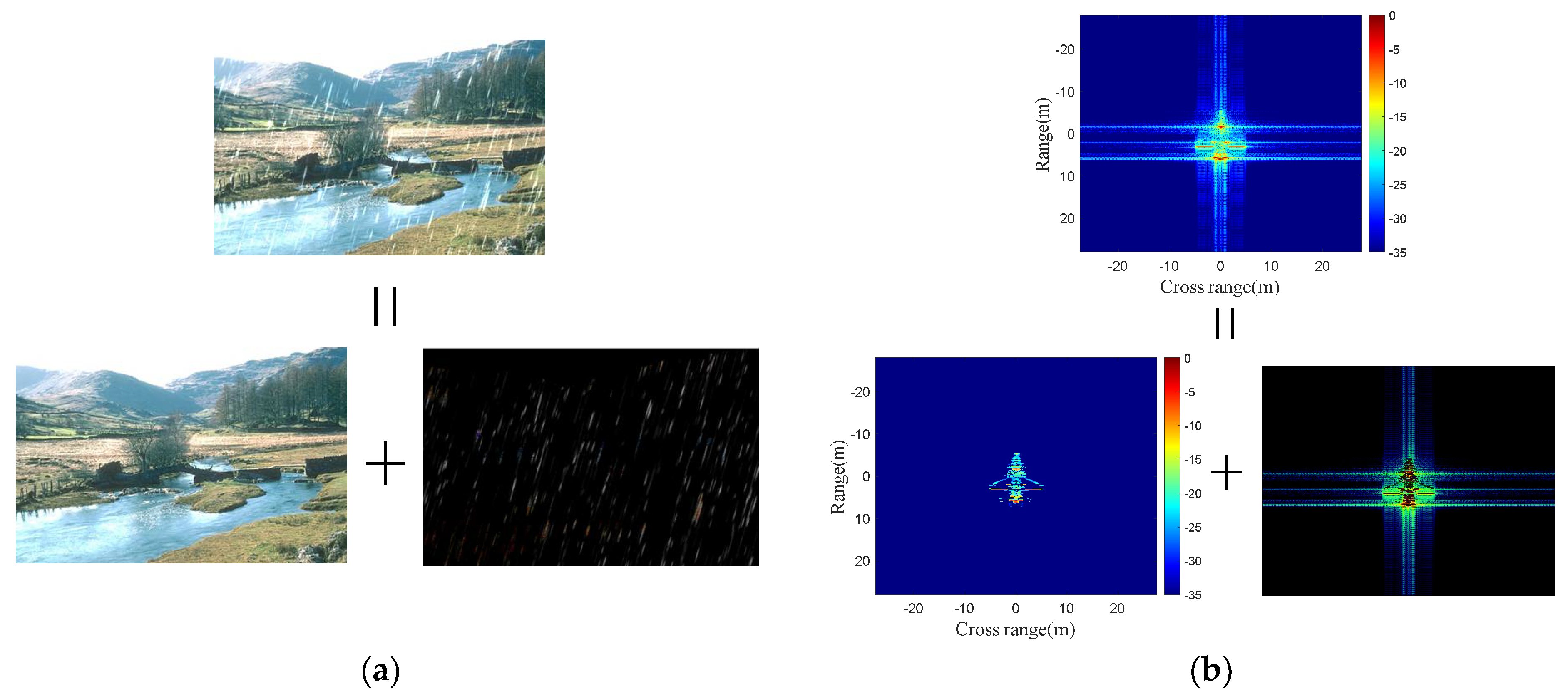
- Different causes. In optical imaging, rain noise occurs because light, with its long wavelength and weak bypass ability, cannot pass through raindrops, resulting in rain noise in the image. In radar images, as discussed in Section 2, the presence of the sinc function in the imaging result causes side-lobe noise higher than the weaker scattering points;
- Noise behavior. The performance of the noise differs as well. Rain noise in the image ‘covers’ the target image, while in radar images, the side-lobe noise and the target image are superimposed;
- Spatial distribution. The two types of noise manifest in different areas. Rain noise is distributed throughout the image, with a relatively fixed distribution position. On the other hand, side-lobe noise only appears near strong scattering points, and its position changes with the position of the strong scattering point.
- A novel spatial attention layer construction is applied in the network structure by our paper;
- An adaptive magnitude factor is designed to describe the loss function more accurately.
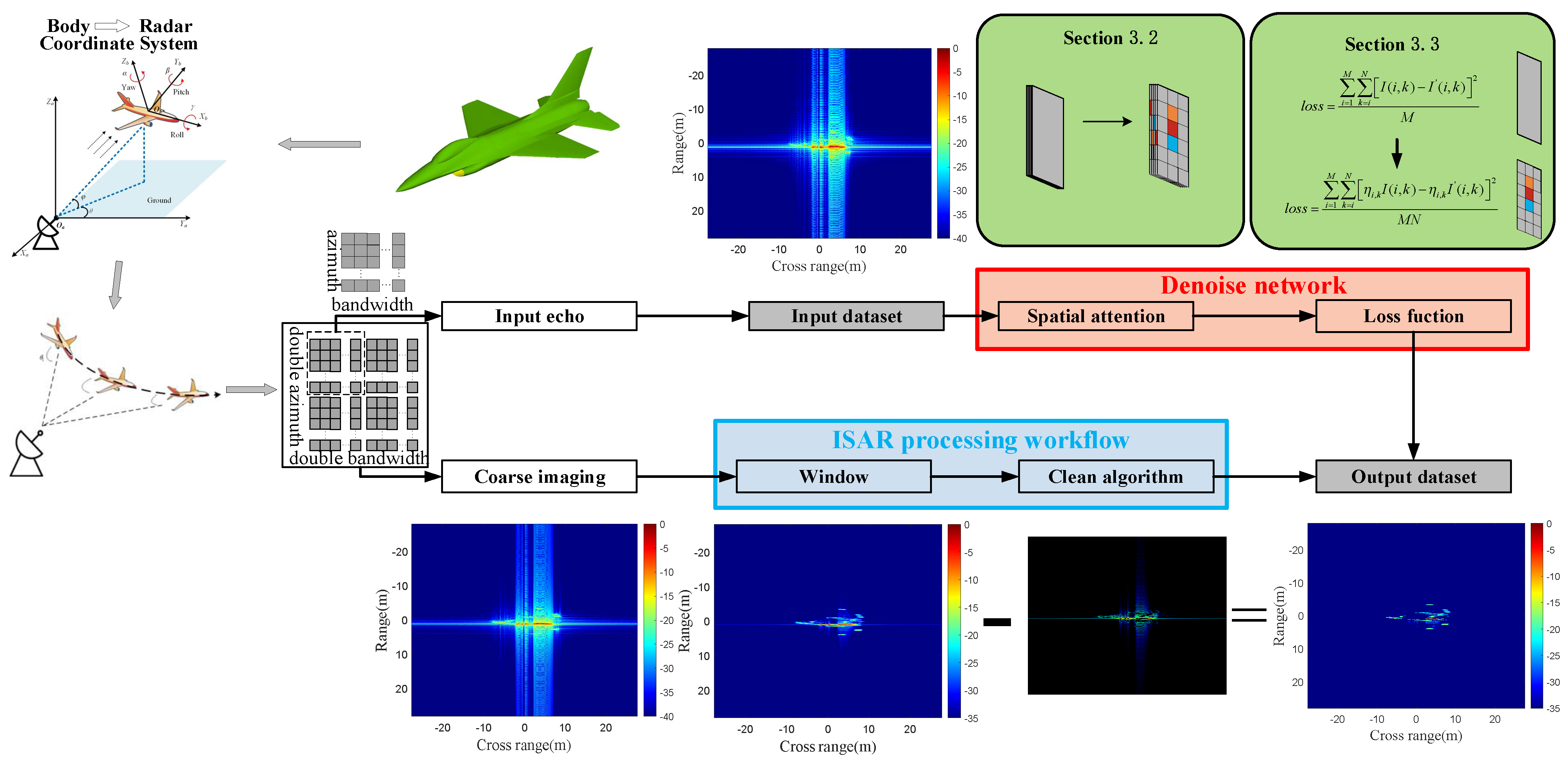
3. The Proposed Methods
3.1. The Fast Clean Technique
| Algorithm 1: The fast clean algorithm |
| Input: A signal matrix with side-lobe noise High-pass filtering threshold adjustment factor The function of the high-pass filter Output: A clean signal matrix |
| for i = 1 to H Calculate the high-pass filter threshold High-pass filtering for each range bin for j = 1 to W |
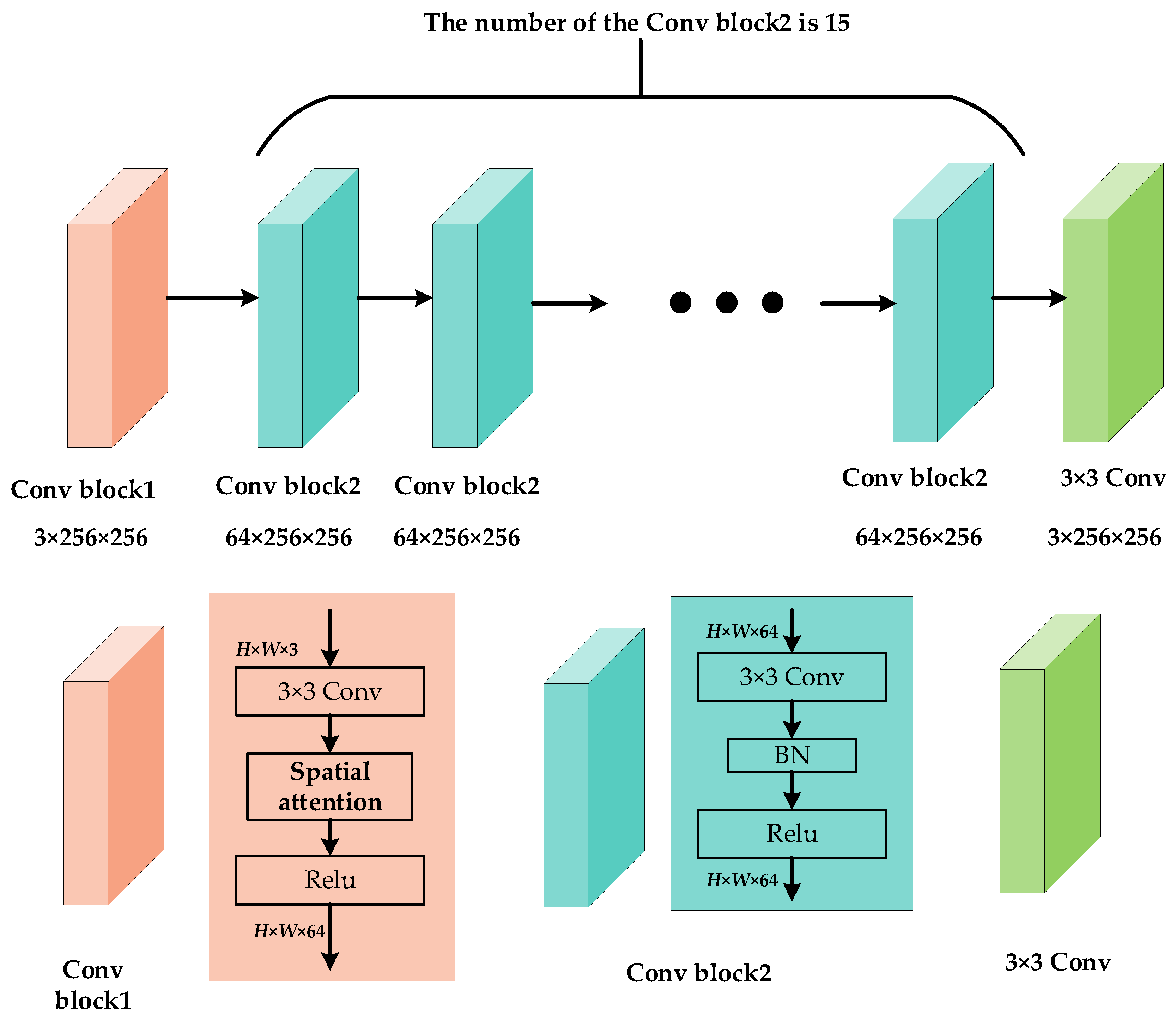
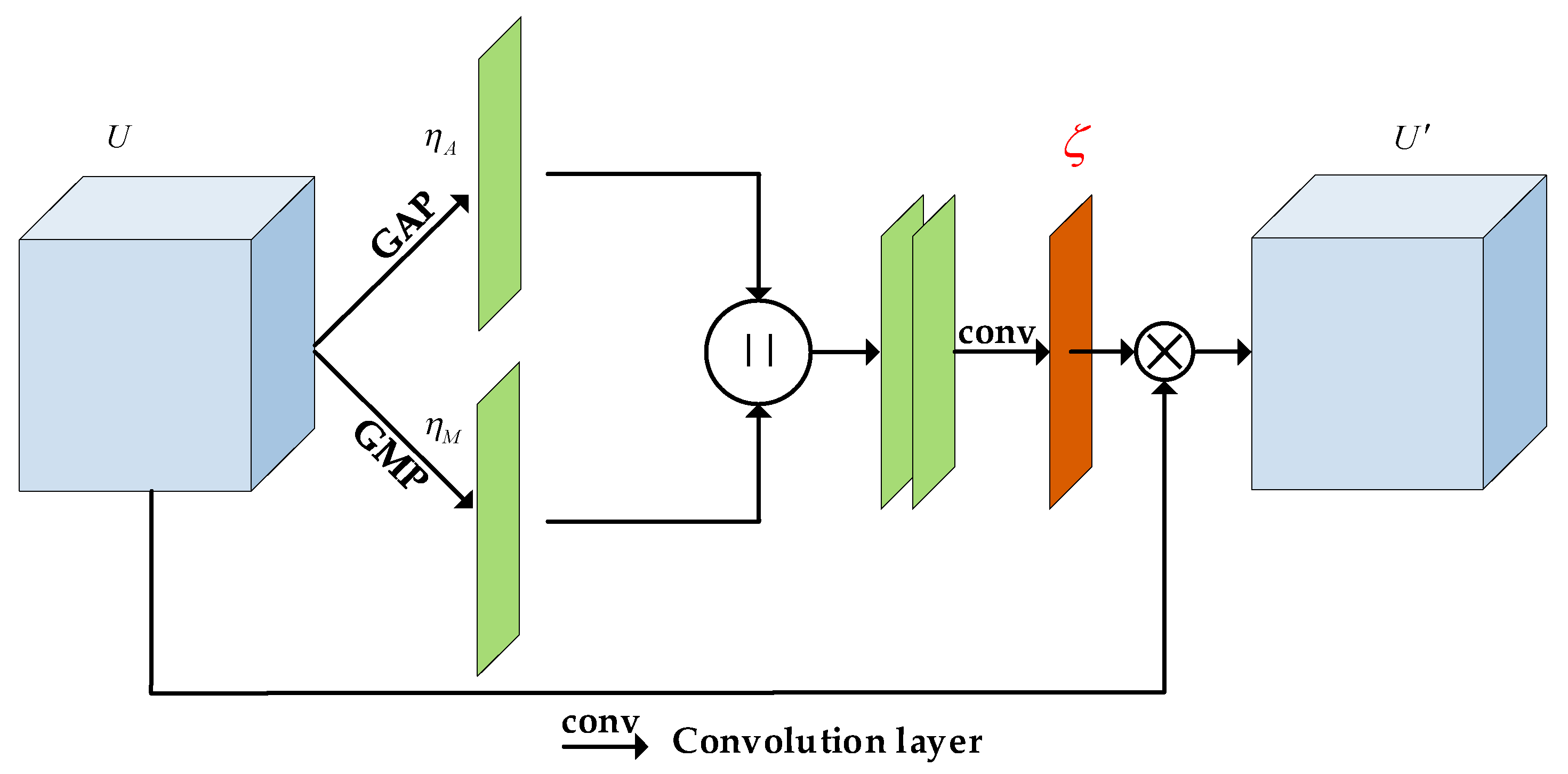
3.2. The Spatial Attention Block
3.3. Loss Function
4. The Dataset Construction
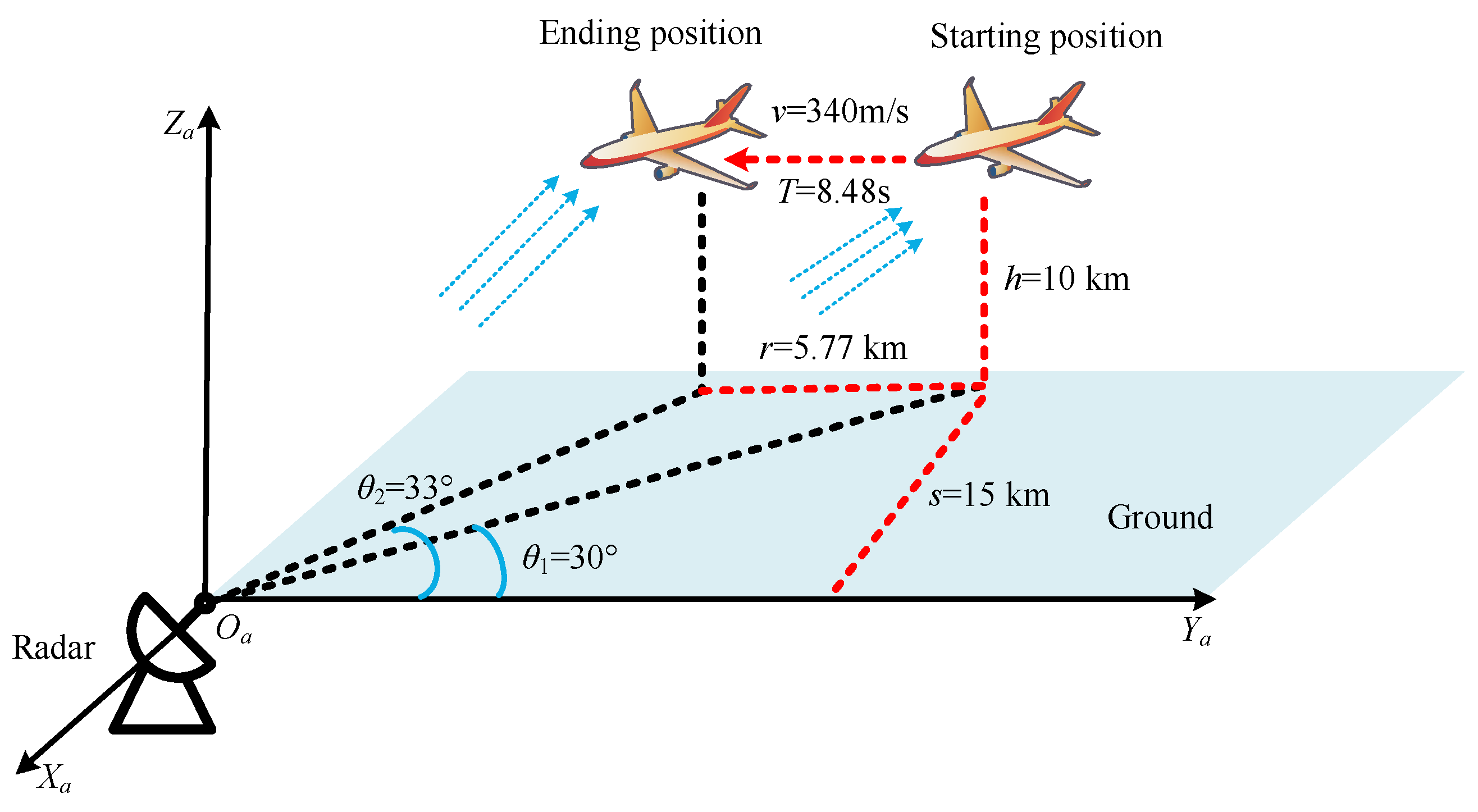
4.1. The Dataset Based on the GTD Model
4.2. The Dataset Based on the Electromagnetic Simulation Model
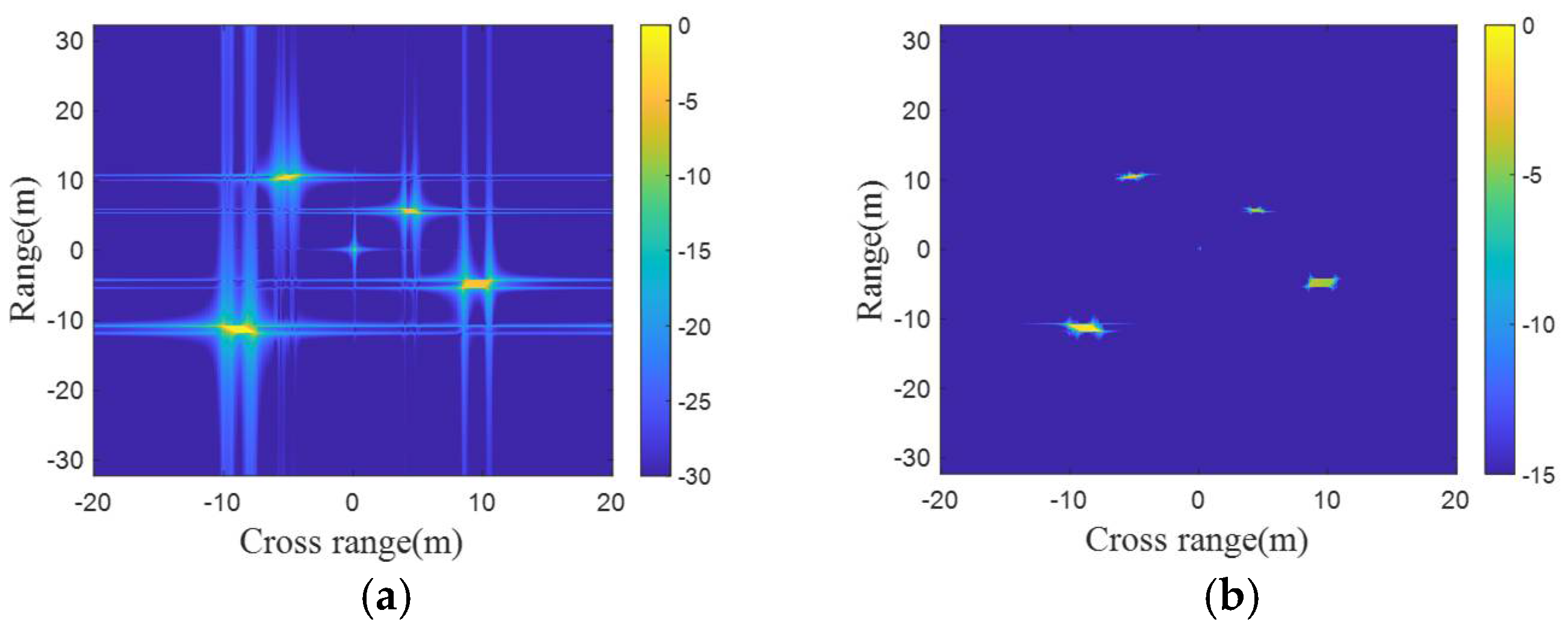
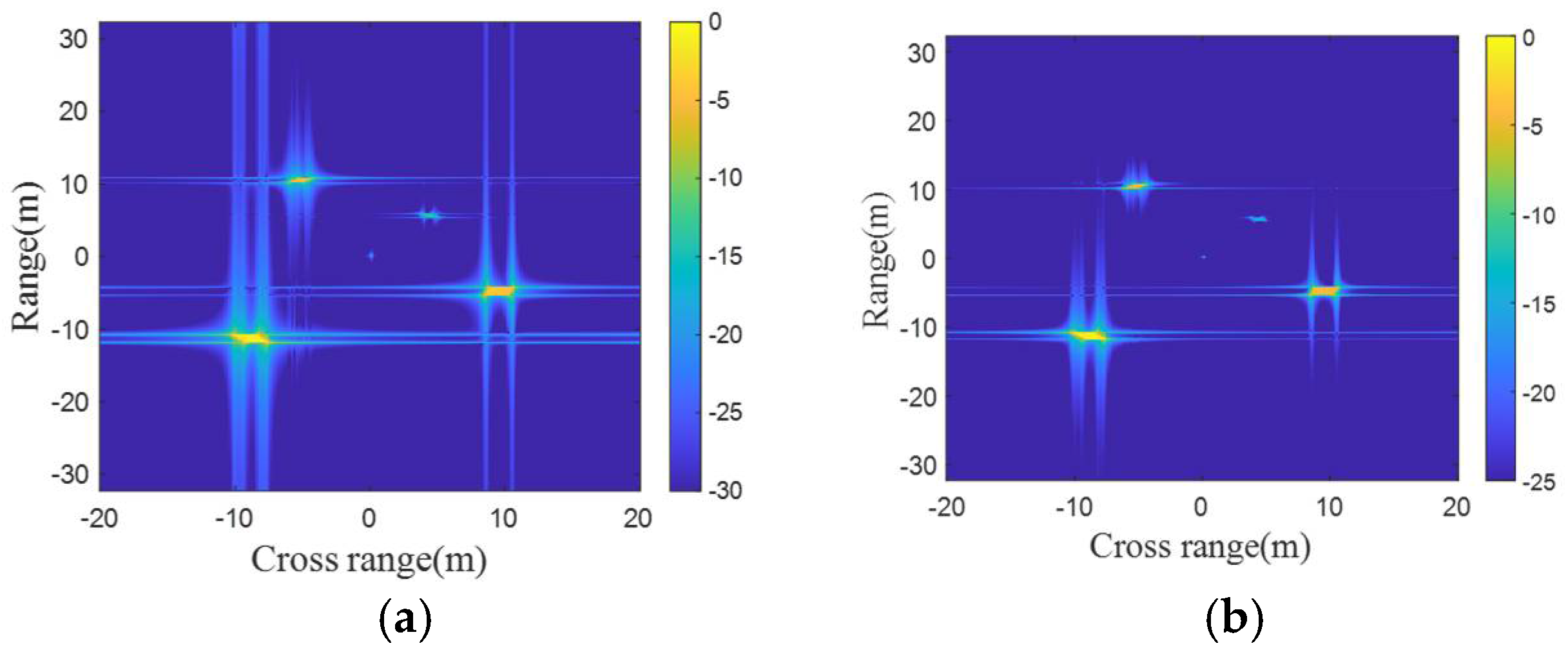
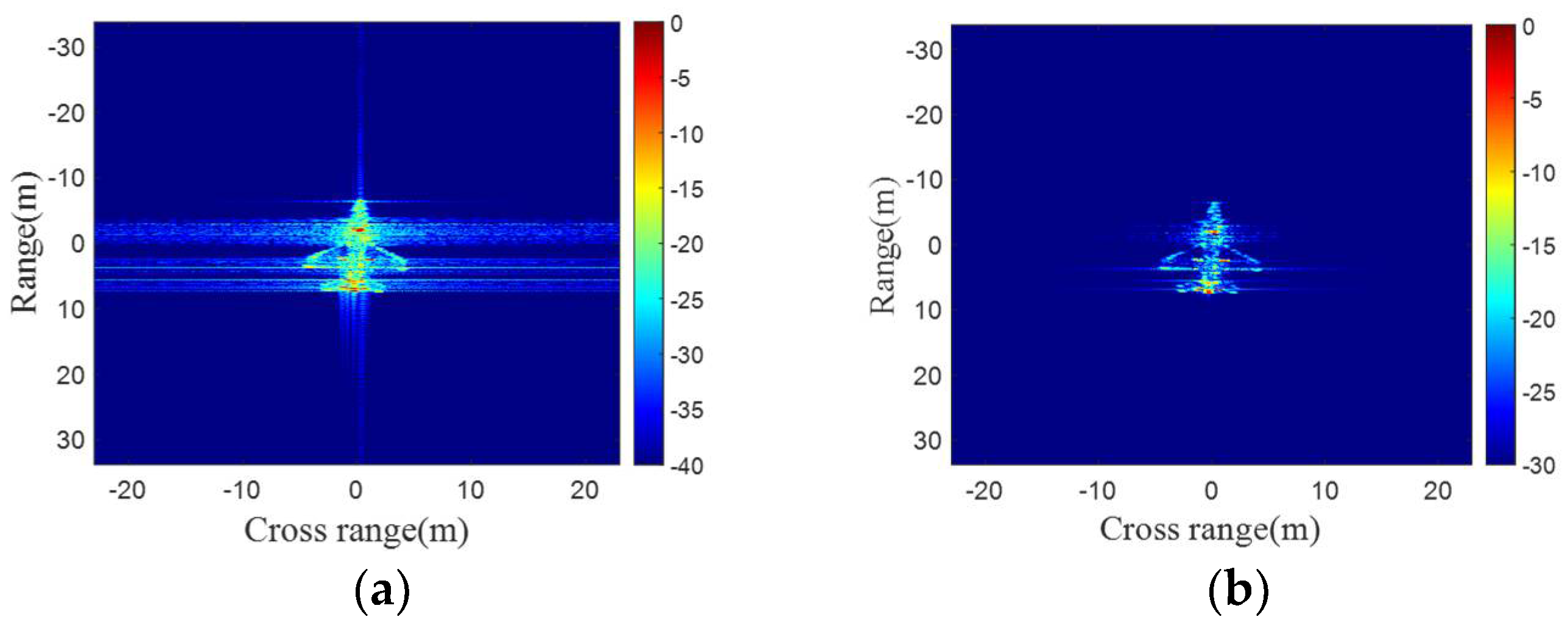
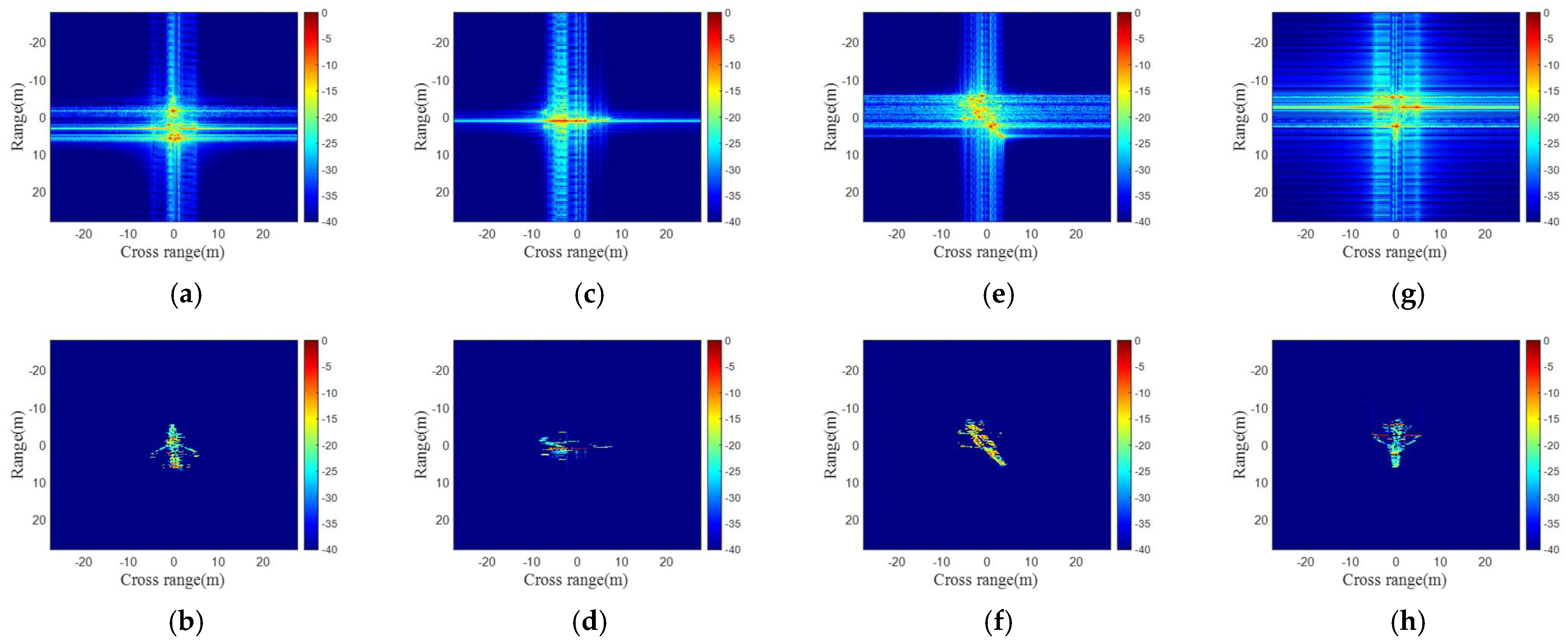
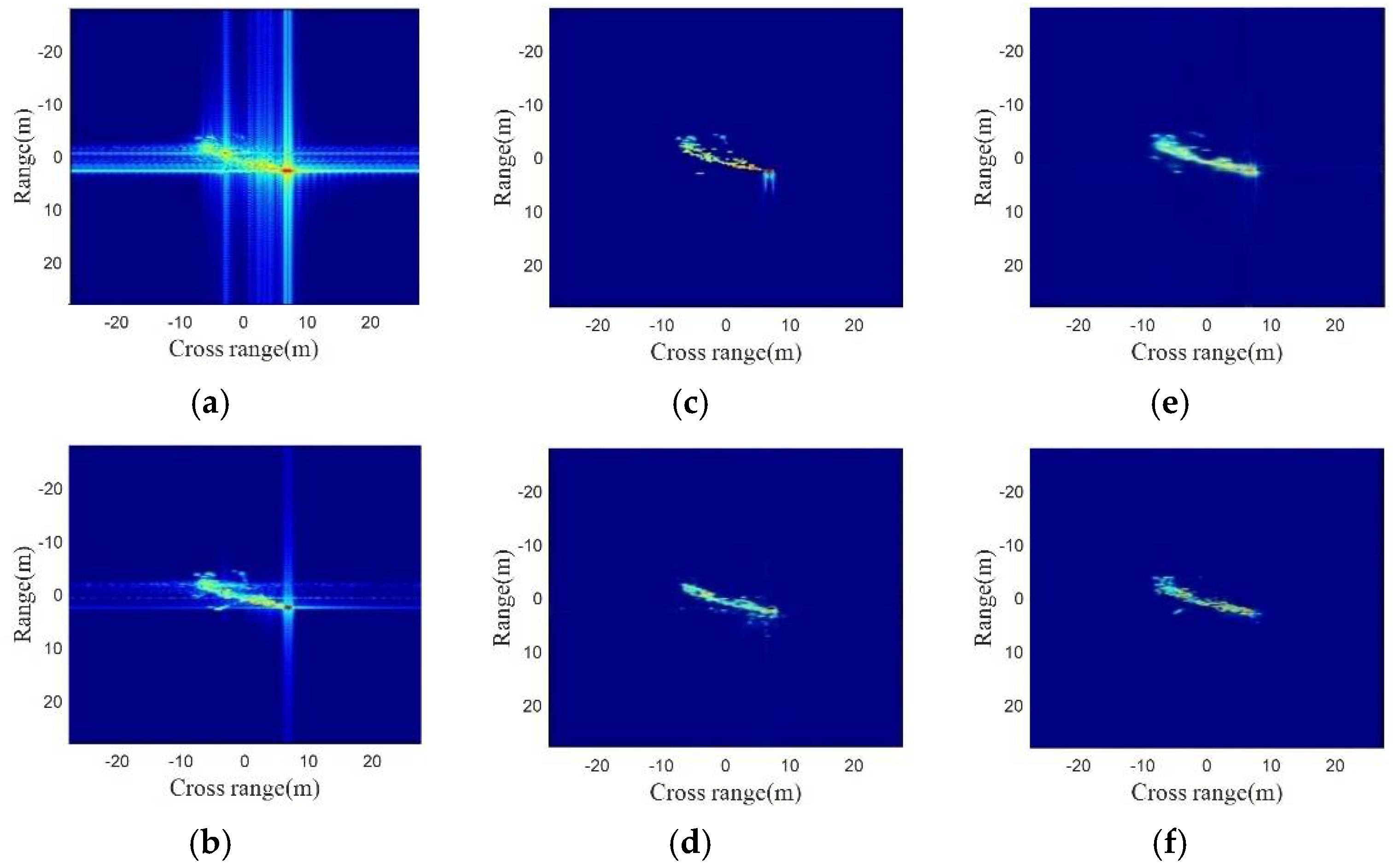
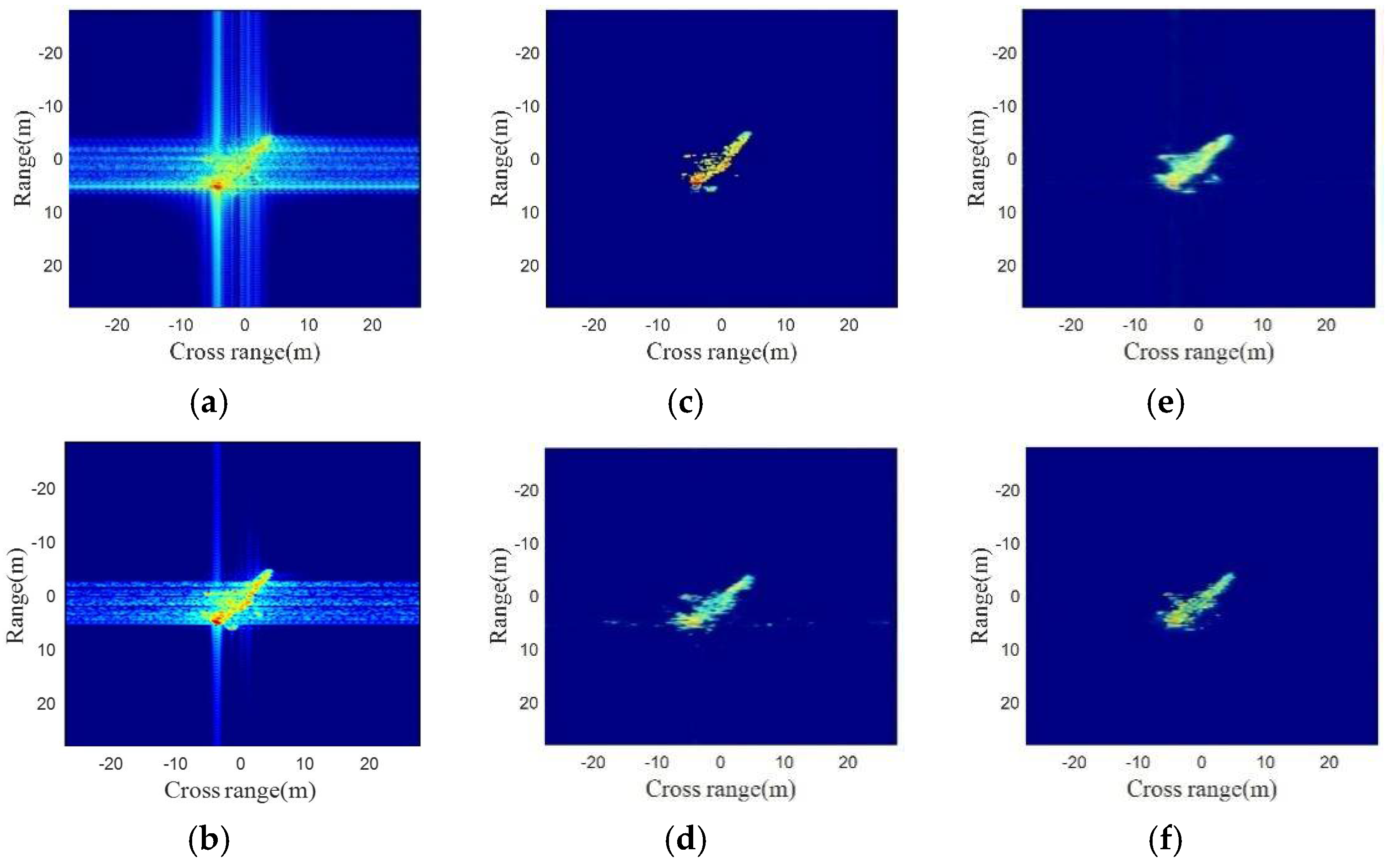
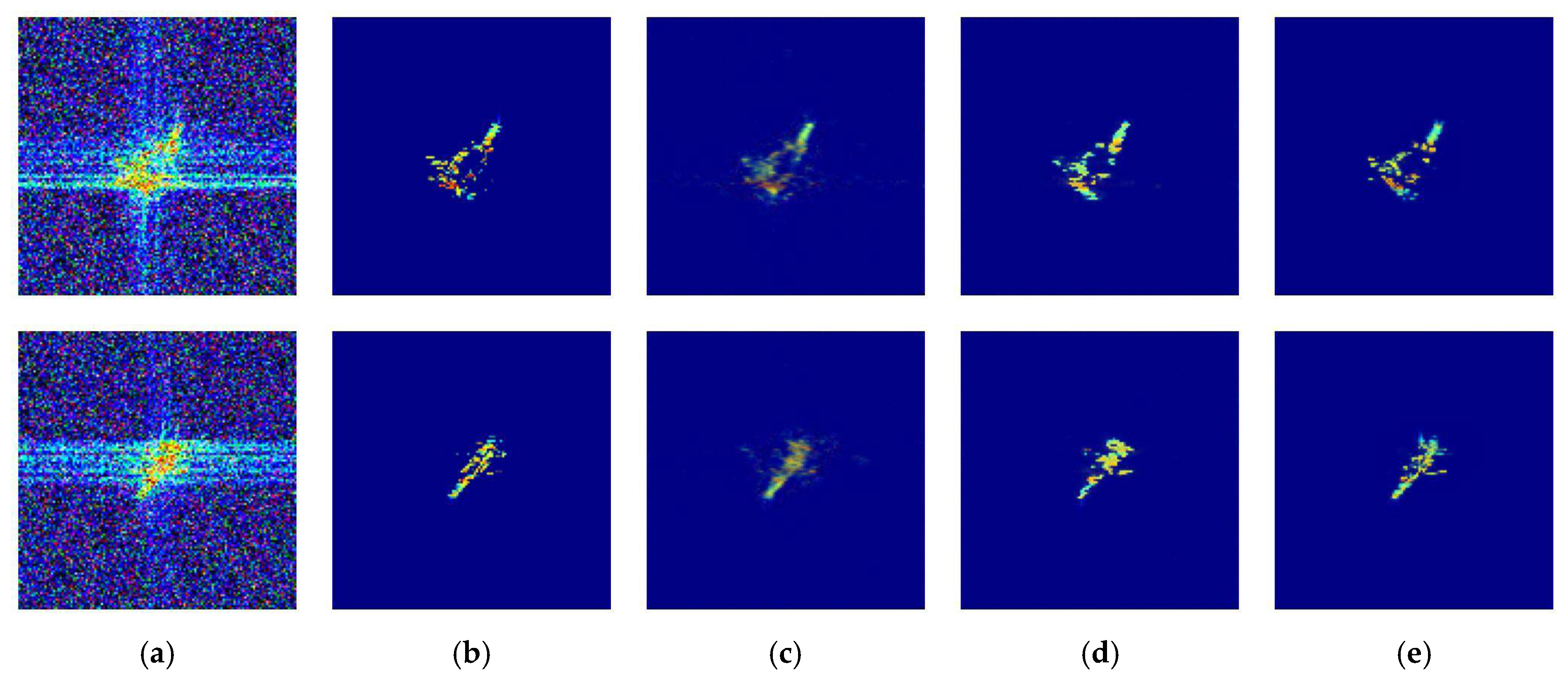
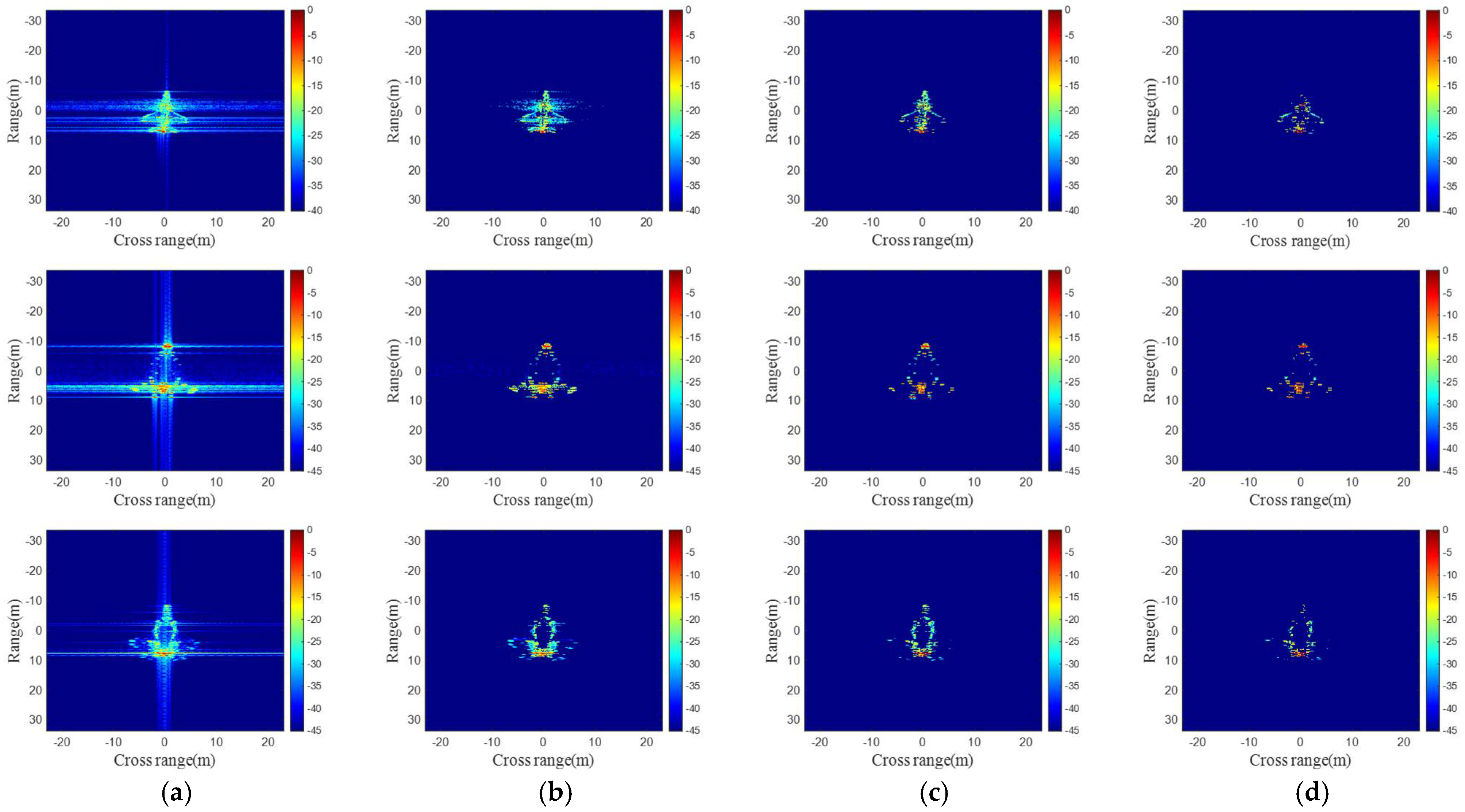
5. Simulation and Performance Evaluation
5.1. Introduction of the Datasets
5.2. Evaluation Criterions
5.3. Implementation Details
5.4. The Results of Training
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
 indicates concatenation.
indicates concatenation.

References
- Bhanu, B.; Dudgeon, D.E.; Zelnio, E.G.; Rosenfeld, A.; Casasent, D.; Reed, I.S. Guest editorial introduction to the special issue on automatic target detection and recognition. IEEE Trans. Image Process. 1997, 6, 1–6. [Google Scholar] [CrossRef]
- Meng, H.; Peng, Y.; Wang, W.; Cheng, P.; Li, Y.; Xiang, W. Spatio-Temporal-Frequency graph attention convolutional network for aircraft recognition based on heterogeneous radar network. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 5548–5559. [Google Scholar] [CrossRef]
- Gao, G. An improved scheme for target discrimination in high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 277–294. [Google Scholar] [CrossRef]
- Marchetti, E.; Stove, A.G.; Hoare, E.G.; Cherniakov, M.; Blacknell, D.; Gashinova, M. Space-based sub-THz ISAR for space situational awareness—Concept and design. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 1558–1573. [Google Scholar] [CrossRef]
- Berizzi, F.; Mese, E.D.; Diani, M.; Martorella, M. High-resolution ISAR imaging of maneuvering targets by means of the range instantaneous Doppler technique: Modeling and performance analysis. IEEE Trans. Image Process. 2001, 10, 1880–1890. [Google Scholar] [CrossRef] [PubMed]
- Wehner, D.R. High Resolution Radar; Artech House: Norwood, MA, USA, 1987. [Google Scholar]
- Jakowatz, C.V.; Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Thompson, P.A. Spotlight-Mode Synthetic Aperture Radar: A Signal Processing Approach; Kluwer: Boston, MA, USA, 1996. [Google Scholar]
- Harris, F.J. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Kulkarni, R.G. Polynomial Windows with fast decaying sidelobes for narrow-band signals. Signal Process. 2003, 83, 1145–1149. [Google Scholar] [CrossRef]
- Yoon, T.H.; Joo, E.K. A Flexible Window Function for Spectral Analysis [DSP Tips & Tricks]. IEEE Signal Process. Mag. 2010, 27, 139–142. [Google Scholar]
- Tsao, J.; Steinberg, B.D. Reduction of sidelobe and speckle artifacts in microwave imaging: The CLEAN technique. IEEE Trans. Antennas Propag. 1988, 36, 543–556. [Google Scholar] [CrossRef]
- Choi, I.-S.; Kim, H.-T. Two-dimensional evolutionary programming-based CLEAN. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 373–382. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian Denoiser: Residual Learning of Deep CNN for Image Denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Yan, Z.; Zhang, K.; Zuo, W.; Zhang, L. Toward Convolutional Blind Denoising of Real Photographs. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 1712–1722. [Google Scholar]
- Yu, K.; Wang, X.; Dong, C.; Tang, X.; Loy, C.C. Path-Restore: Learning Network Path Selection for Image Restoration. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 44, 7078–7092. [Google Scholar] [CrossRef] [PubMed]
- Mao, X.J.; Shen, C.H.; Yang, Y.B. Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections. In Proceedings of the 30th International Conference on Neural Information Processing Systems (NIPS), Barcelona, Spain, 5–10 December 2016; pp. 2802–2810. [Google Scholar]
- Jin, S.; Bae, Y.; Lee, S. ID-SAbRUNet: Deep Neural Network for Disturbance Suppression of Drone ISAR Images. IEEE Sens. J. 2024, 24, 15551–15565. [Google Scholar] [CrossRef]
- Walker, J.L. Range-Doppler Imaging of Rotating Objects. IEEE Trans. Aerosp. Electron. Syst. 1980, AES-16, 23–52. [Google Scholar] [CrossRef]
- Ausherman, D.A.; Kozma, A.; Walker, J.L.; Jones, H.M.; Poggio, E.C. Developments in Radar Imaging. IEEE Trans. Aerosp. Electron. Syst. 1984, AES-20, 363–400. [Google Scholar]
- Yu, X.; Wang, Z.; Du, X.; Jiang, L. Multipass Interferometric ISAR for Three-Dimensional Space Target Reconstruction. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5110317. [Google Scholar] [CrossRef]
- Chang, S.; Deng, Y.; Zhang, Y.; Zhao, Q.; Wang, R.; Zhang, K. An Advanced Scheme for Range Ambiguity Suppression of Spaceborne SAR Based on Blind Source Separation. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5230112. [Google Scholar] [CrossRef]
- Çulha, O.; Tanık, Y. Efficient Range Migration Compensation Method Based on Doppler Ambiguity Shift Transform. IEEE Sens. Lett. 2022, 6, 7000604. [Google Scholar] [CrossRef]
- Chen, C.-C.; Andrews, H.C. Target-Motion-Induced Radar Imaging. IEEE Trans. Aerosp. Electron. Syst. 1980, AES-16, 2–14. [Google Scholar] [CrossRef]
- Itoh, T.; Sueda, H.; Watanabe, Y. Motion compensation for ISAR via centroid tracking. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1191–1197. [Google Scholar] [CrossRef]
- Zhu, D.; Wang, L.; Yu, Y.; Tao, Q.; Zhu, Z. Robust ISAR Range Alignment via Minimizing the Entropy of the Average Range Profile. IEEE Geosci. Remote Sens. Lett. 2009, 6, 204–208. [Google Scholar]
- Wang, J.F.; Kasilingam, D. Global range alignment for ISAR. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 351–357. [Google Scholar] [CrossRef]
- Yang, J.G.; Huang, X.T.; Jin, T.; Xue, G.Y.; Zhou, Z.M. An Interpolated Phase Adjustment by Contrast Enhancement Algorithm for SAR. IEEE Geosci. Remote Sens. Lett. 2011, 8, 211–215. [Google Scholar]
- Perry, R.P.; DiPietro, R.C.; Fante, R.L. SAR imaging of moving targets. IEEE Trans. Aerosp. Electron. Syst. 1999, 35, 188–200. [Google Scholar] [CrossRef]
- Song, Y.; Pu, W.; Huo, J.; Wu, J.; Li, Z.; Yang, J. Deep Parametric Imaging for Bistatic SAR: Model, Property, and Approach. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5212416. [Google Scholar] [CrossRef]
- Xiao-Yu, X.; Huo, Y.; Hong-Cheng, C.-Y.Y. Performance Analysis for Two Parameter Estimation Methods of GTD Model. In Proceedings of the 2018 IEEE International Conference on Computational Electromagnetics (ICCEM), Chengdu, China, 26–28 March 2018; pp. 1–3. [Google Scholar]
- Potter, L.C.; Chiang, D.-M.; Carriere, R.; Gerry, M.J. A GTD-based parametric model for radar scattering. IEEE Trans. Antennas Propag. 1995, 43, 1058–1067. [Google Scholar] [CrossRef]
- Potter, L.C.; Moses, R.L. Attributed scattering centers for SAR ATR. IEEE Trans. Image Process. 1997, 6, 79–91. [Google Scholar] [CrossRef]
- Sketchfab 3D Resource. Available online: https://sketchfab.com/ (accessed on 24 November 2023).
- Wang, Z.; Fu, Y.; Liu, J.; Zhang, Y. LG-BPN: Local and Global Blind-Patch Network for Self-Supervised Real-World Denoising. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 18–22 June 2023; pp. 18156–18165. [Google Scholar]
- Zhang, Y.; Wang, R. A novel high-resolution and wide-swath SAR imaging mode. In Proceedings of the 13th European Conference on Synthetic Aperture Radar (EUSAR), Online, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Chen, X.; Wang, Z.J.; Mckeown, M. Joint blind source separation for neurophysiological data analysis: Multiset and multimodal methods. IEEE Signal Process. Mag. 2016, 33, 86–107. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, H.; Xu, Q.; Liu, J.; Liu, Y.; Wang, J. Practical Deep Raw Image Denoising on Mobile Devices. In 2020 European Conference on Computer Vision (ECCV); Springer: Cham, Switzerland, 2020; Volume 12351. [Google Scholar]
- Zhao, Y.; Jiang, Z.; Men, A.; Ju, G. Pyramid Real Image Denoising Network. In Proceedings of the 2019 IEEE Visual Communications and Image Processing (VCIP), Sydney, NSW, Australia, 1–4 December 2019; pp. 1–4. [Google Scholar]




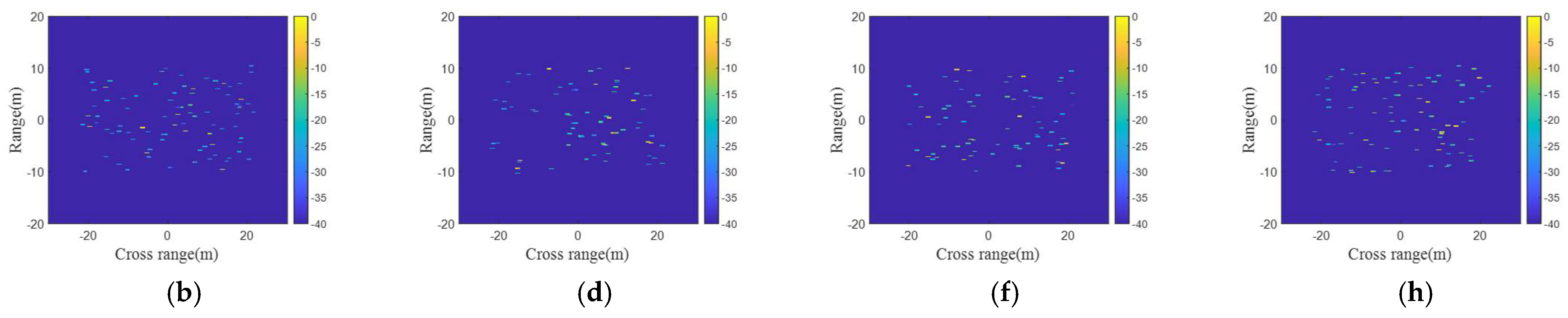



| Parameters | Value |
|---|---|
| Pulse repletion frequency (PRF) | 40 Hz |
| Bandwidth | 2 GHz |
| Pulse width | 25 μs |
| Carrier frequency | 10 GHz |
| Sampling frequency | 32 MHz |
| Observing time | 10 s |
| Scattering Centers | ||||
|---|---|---|---|---|
| Scattering center 1 | 0.1 | 0.1 | 0 | 1 |
| Scattering center 2 | 5 | 5 | 1 | 5 |
| Scattering center 3 | 10 | −5 | 0.5 | 8 |
| Scattering center 4 | −5 | 10 | −1 | 10 |
| Scattering center 5 | −10 | −10 | −0.5 | 20 |
| Scattering Centers | ||||
|---|---|---|---|---|
| Scattering center 1 | 0.1 | 0.1 | 0 | 1 |
| Scattering center 2 | 5 | 5 | 1 | 5 |
| Scattering center 3 | 10 | −5 | 0.5 | 50 |
| Scattering center 4 | −5 | 10 | −1 | 100 |
| Scattering center 5 | −10 | −10 | −0.5 | 200 |
| Configuration | Parameter |
|---|---|
| CPU | Intel(R) Xeon(R) Platinum 8270 32-Core Processor |
| GPU | NVIDIA Quadro RTX 8000 |
| Development tools | Python 3.10.8, Pytorch 1.13.1 |
| Network | PSNR | SSIM |
|---|---|---|
| Improved DNCNN | 29.20 | 0.9617 |
| Improved PMRID-Net | 30.01 | 0.9705 |
| Improved PRID-Net | 32.38 | 0.9784 |
| Network | 1st Experiment | 2nd Experiment | ||
|---|---|---|---|---|
| PSNR | Epoch | PSNR | Epoch | |
| Improved DNCNN | 25.15 | 200 | 27.76 | 50 |
| Improved PMRID-Net | 27.05 | 176 | 28.26 | 42 |
| Improved PRID-Net | 30.16 | 152 | 30.33 | 28 |
| Network | PSNR |
|---|---|
| Improved DNCNN | 29.20 |
| DNCNN | 27.26 |
| Improved PMRID-Net | 30.01 |
| PMRID-Net | 28.65 |
| Improved PRID-Net | 32.38 |
| PRID-Net | 31.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xv, J.-H.; Zhang, X.-K.; Zong, B.-f.; Zheng, S.-Y. A Side-Lobe Denoise Process for ISAR Imaging Applications: Combined Fast Clean and Spatial Focus Technique. Remote Sens. 2024, 16, 2279. https://doi.org/10.3390/rs16132279
Xv J-H, Zhang X-K, Zong B-f, Zheng S-Y. A Side-Lobe Denoise Process for ISAR Imaging Applications: Combined Fast Clean and Spatial Focus Technique. Remote Sensing. 2024; 16(13):2279. https://doi.org/10.3390/rs16132279
Chicago/Turabian StyleXv, Jia-Hua, Xiao-Kuan Zhang, Bin-feng Zong, and Shu-Yu Zheng. 2024. "A Side-Lobe Denoise Process for ISAR Imaging Applications: Combined Fast Clean and Spatial Focus Technique" Remote Sensing 16, no. 13: 2279. https://doi.org/10.3390/rs16132279
APA StyleXv, J.-H., Zhang, X.-K., Zong, B.-f., & Zheng, S.-Y. (2024). A Side-Lobe Denoise Process for ISAR Imaging Applications: Combined Fast Clean and Spatial Focus Technique. Remote Sensing, 16(13), 2279. https://doi.org/10.3390/rs16132279





