Unsupervised Characterization of Water Composition with UAV-Based Hyperspectral Imaging and Generative Topographic Mapping
Abstract
1. Introduction
2. Materials and Methods
2.1. Generative Topographic Mapping
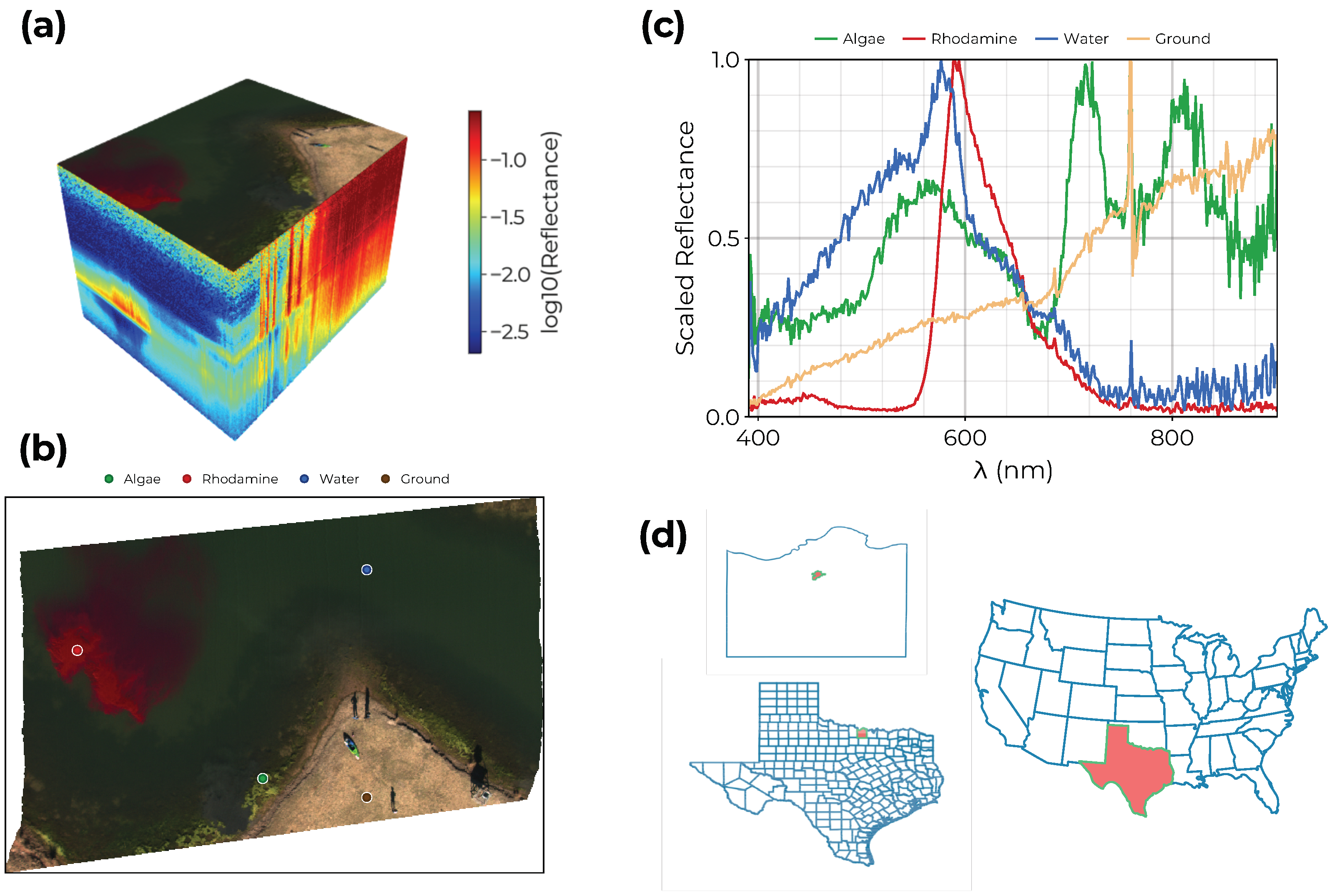
2.2. UAV-Based Hyperspectral Imaging
2.3. GTM Case Studies
3. Results
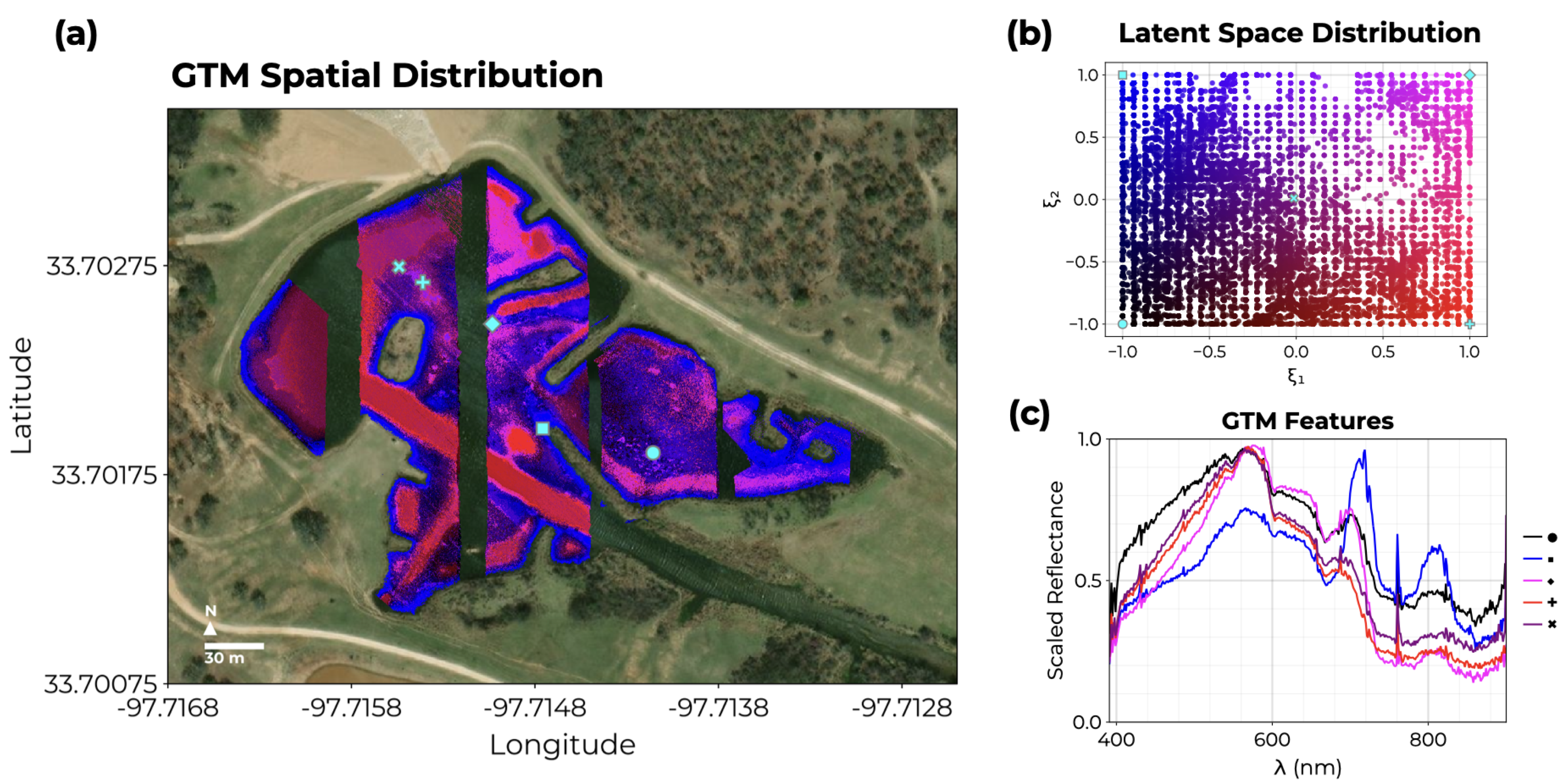
3.1. Water-Only Pixel Segmentation
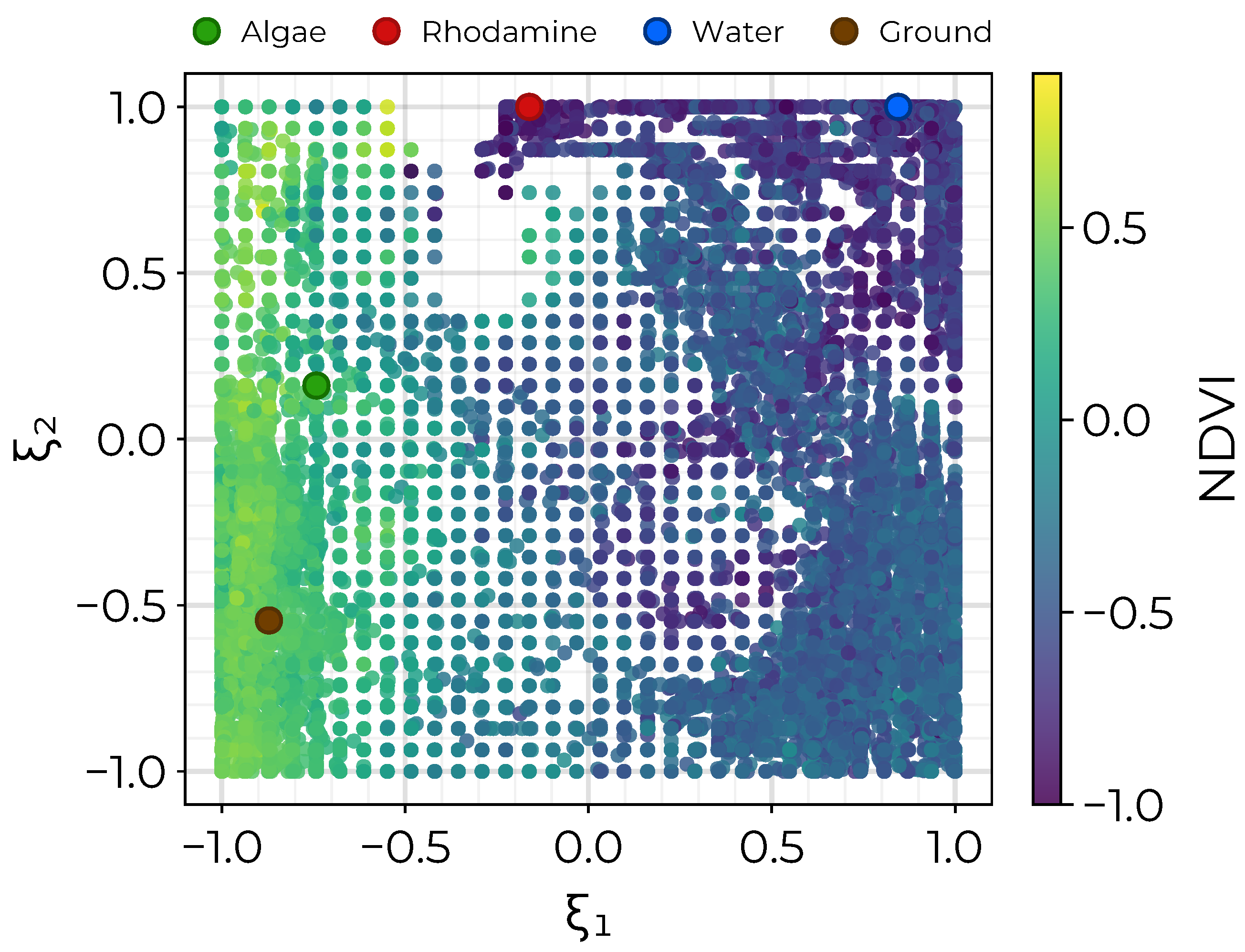
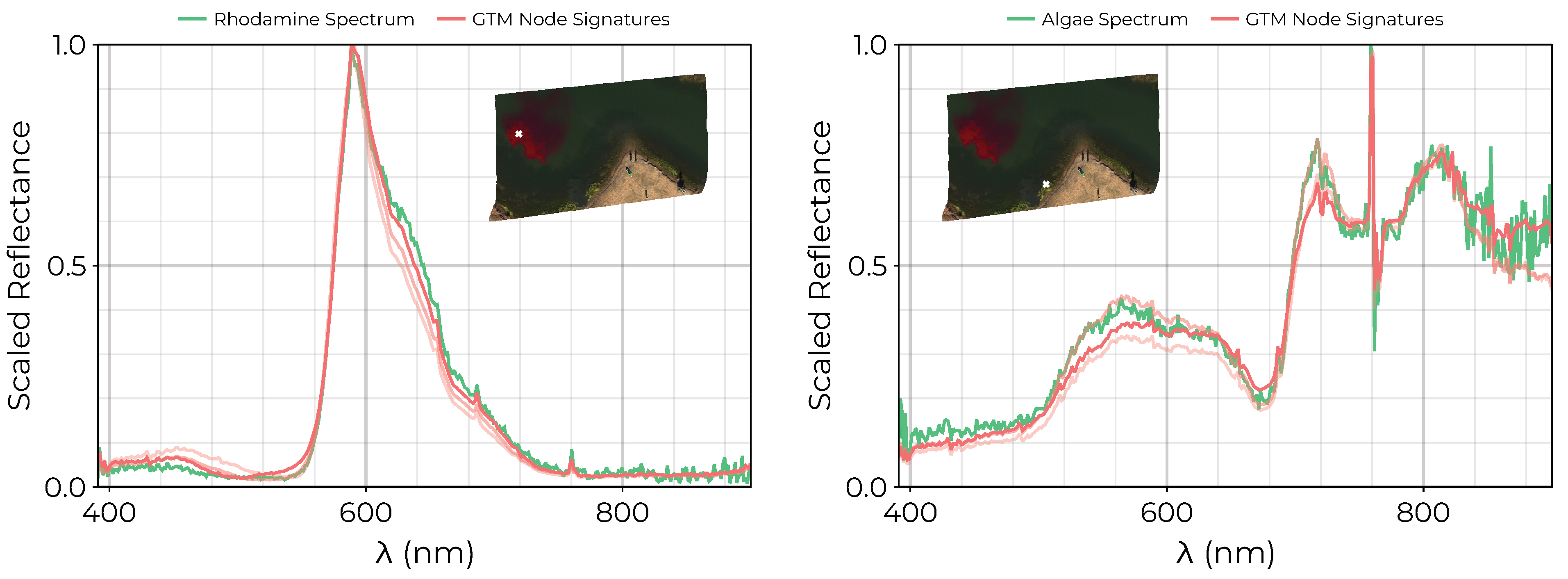
3.2. Endmember Extraction
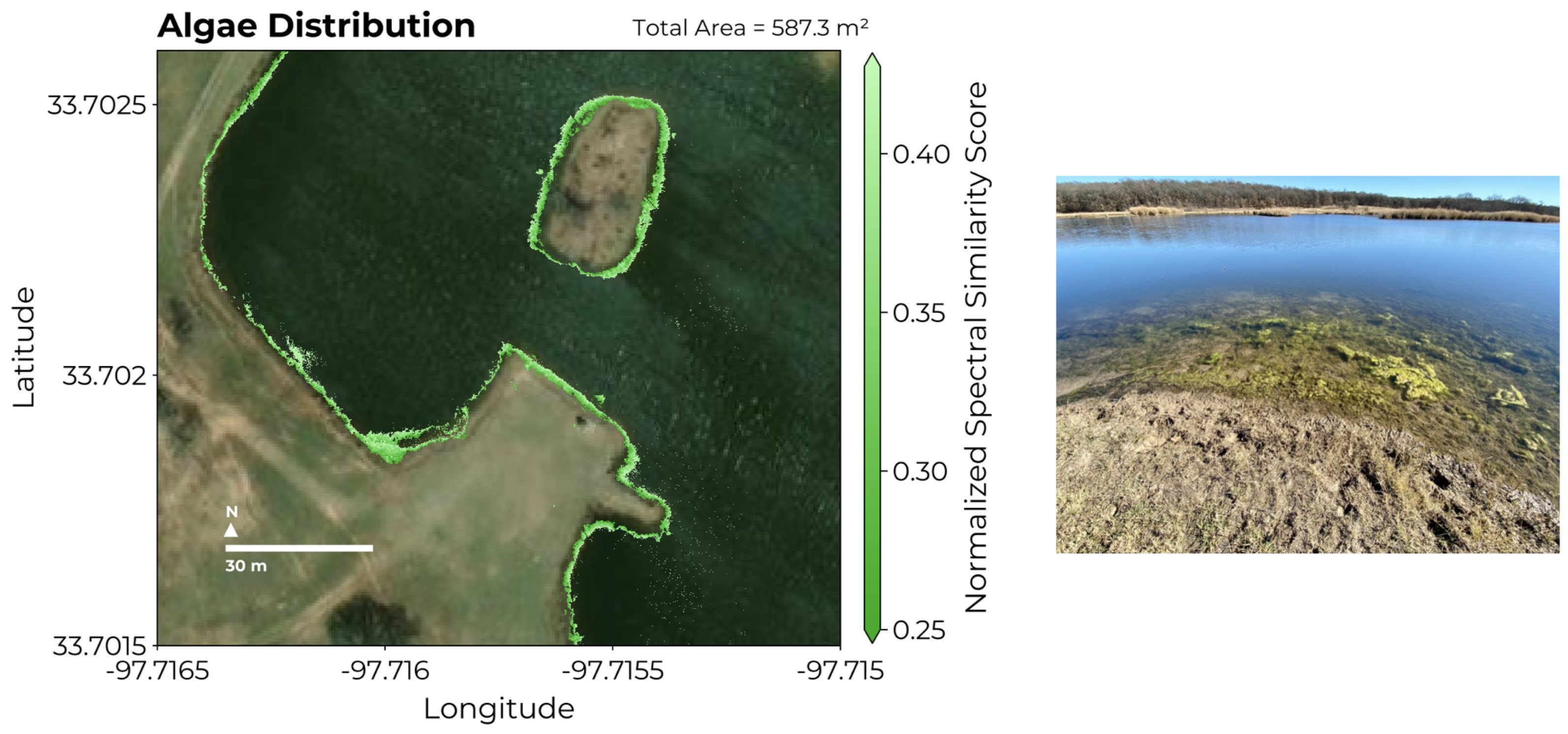
3.3. Abundance Mapping with NS3
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| GTM | Generative Topographic Mapping |
| SOM | Self Organizing Map |
| HSI | Hyperspectral Image |
| PCA | Principal Component Analysis |
| tSNE | t-Distributed Stochastic Neighbor Embedding |
| MLJ | Machine Learning in Julia |
| VNIR | Visible + Near-Infrared |
| NDWI | Normalized Difference Water Index |
| NS3 | Normalized Spectral Similarity Score |
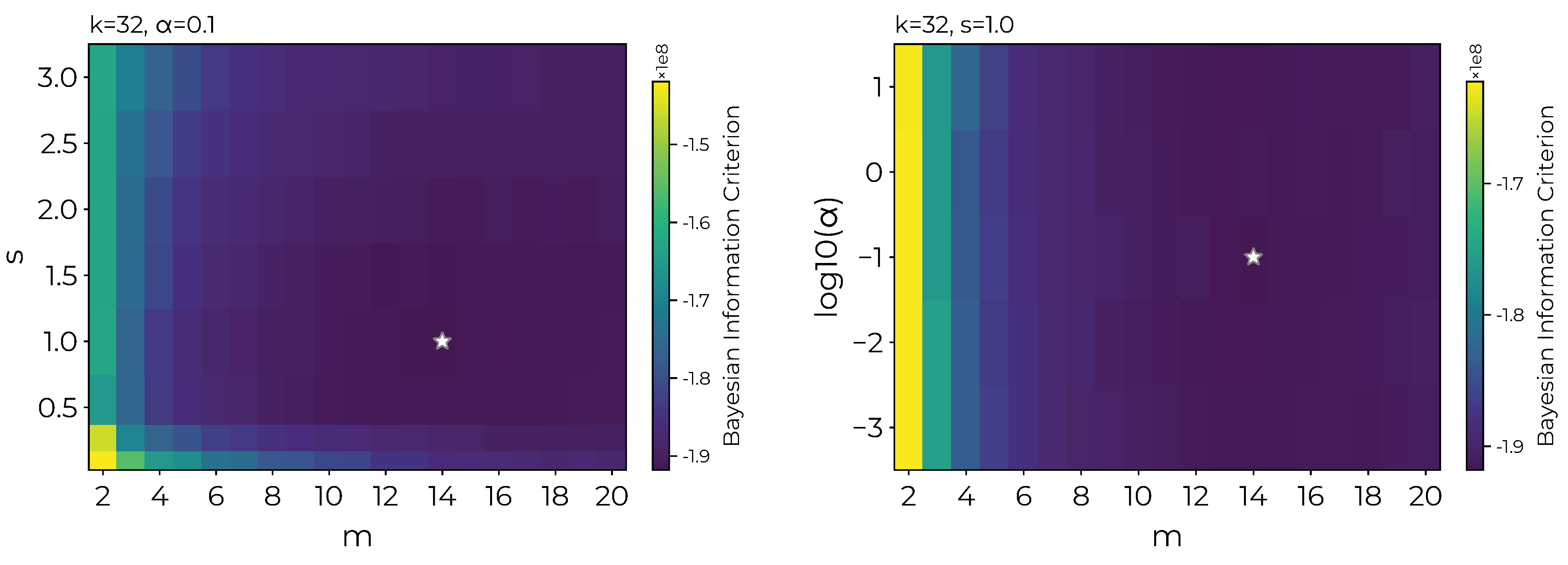
Appendix A. Hyperparameter Search Results
| m | s | k | BIC | AIC | |
|---|---|---|---|---|---|
| 14 | 0.1 | 1.0 | 32 | ||
| 13 | 0.01 | 1.0 | 32 | ||
| 16 | 0.01 | 1.5 | 32 | ||
| 14 | 10.0 | 1.0 | 32 | ||
| 16 | 0.001 | 1.5 | 32 | ||
| 13 | 1.0 | 1.0 | 32 | ||
| 13 | 10.0 | 1.0 | 32 | ||
| 14 | 0.001 | 1.5 | 32 | ||
| 13 | 0.1 | 1.0 | 32 | ||
| 14 | 0.01 | 1.0 | 32 | ||
| 15 | 0.01 | 1.5 | 32 | ||
| 14 | 0.01 | 1.5 | 32 | ||
| 15 | 1.0 | 1.0 | 32 | ||
| 18 | 0.01 | 1.5 | 32 | ||
| 12 | 0.01 | 1.0 | 32 | ||
| 15 | 0.01 | 0.5 | 32 | ||
| 17 | 1.0 | 1.0 | 32 | ||
| 16 | 0.1 | 1.0 | 32 | ||
| 18 | 0.001 | 1.5 | 32 | ||
| 13 | 0.001 | 1.0 | 32 | ||
| 12 | 1.0 | 1.0 | 32 | ||
| 17 | 0.001 | 1.5 | 32 | ||
| 15 | 0.001 | 1.5 | 32 | ||
| 15 | 10.0 | 1.0 | 32 | ||
| 12 | 0.1 | 1.5 | 32 |
References
- Koponen, S.; Pulliainen, J.; Kallio, K.; Hallikainen, M. Lake water quality classification with airborne hyperspectral spectrometer and simulated MERIS data. Remote. Sens. Environ. 2002, 79, 51–59. [Google Scholar] [CrossRef]
- Ritchie, J.C.; Zimba, P.V.; Everitt, J.H. Remote sensing techniques to assess water quality. Photogramm. Eng. Remote. Sens. 2003, 69, 695–704. [Google Scholar] [CrossRef]
- Adão, T.; Hruška, J.; Pádua, L.; Bessa, J.; Peres, E.; Morais, R.; Sousa, J.J. Hyperspectral imaging: A review on UAV-based sensors, data processing and applications for agriculture and forestry. Remote. Sens. 2017, 9, 1110. [Google Scholar] [CrossRef]
- Arroyo-Mora, J.P.; Kalacska, M.; Inamdar, D.; Soffer, R.; Lucanus, O.; Gorman, J.; Naprstek, T.; Schaaf, E.S.; Ifimov, G.; Elmer, K.; et al. Implementation of a UAV–hyperspectral pushbroom imager for ecological monitoring. Drones 2019, 3, 12. [Google Scholar] [CrossRef]
- Banerjee, B.P.; Raval, S.; Cullen, P. UAV-hyperspectral imaging of spectrally complex environments. Int. J. Remote. Sens. 2020, 41, 4136–4159. [Google Scholar] [CrossRef]
- Horstrand, P.; Guerra, R.; Rodríguez, A.; Díaz, M.; López, S.; López, J.F. A UAV platform based on a hyperspectral sensor for image capturing and on-board processing. IEEE Access 2019, 7, 66919–66938. [Google Scholar] [CrossRef]
- Vogt, M.C.; Vogt, M.E. Near-remote sensing of water turbidity using small unmanned aircraft systems. Environ. Pract. 2016, 18, 18–31. [Google Scholar] [CrossRef]
- Zhang, D.; Zeng, S.; He, W. Selection and quantification of best water quality indicators using UAV-mounted hyperspectral data: A case focusing on a local river network in Suzhou City, China. Sustainability 2022, 14, 16226. [Google Scholar] [CrossRef]
- Keller, S.; Maier, P.M.; Riese, F.M.; Norra, S.; Holbach, A.; Börsig, N.; Wilhelms, A.; Moldaenke, C.; Zaake, A.; Hinz, S. Hyperspectral data and machine learning for estimating CDOM, chlorophyll a, diatoms, green algae and turbidity. Int. J. Environ. Res. Public Health 2018, 15, 1881. [Google Scholar] [CrossRef]
- Lu, Q.; Si, W.; Wei, L.; Li, Z.; Xia, Z.; Ye, S.; Xia, Y. Retrieval of water quality from UAV-borne hyperspectral imagery: A comparative study of machine learning algorithms. Remote. Sens. 2021, 13, 3928. [Google Scholar] [CrossRef]
- Lary, D.J.; Schaefer, D.; Waczak, J.; Aker, A.; Barbosa, A.; Wijeratne, L.O.; Talebi, S.; Fernando, B.; Sadler, J.; Lary, T.; et al. Autonomous learning of new environments with a robotic team employing hyper-spectral remote sensing, comprehensive in-situ sensing and machine learning. Sensors 2021, 21, 2240. [Google Scholar] [CrossRef]
- Waczak, J.; Aker, A.; Wijeratne, L.O.; Talebi, S.; Fernando, B.; Hathurusinghe, P.; Iqbal, M.; Schaefer, D.; Lary, D.J. Characterizing Water Composition with an Autonomous Robotic Team Employing Comprehensive In-Situ Sensing, Hyperspectral Imaging, Machine Learning, and Conformal Prediction. Remote. Sens. 2024, 16, 996. [Google Scholar] [CrossRef]
- Parra, L.; Ahmad, A.; Sendra, S.; Lloret, J.; Lorenz, P. Combination of Machine Learning and RGB Sensors to Quantify and Classify Water Turbidity. Chemosensors 2024, 12, 34. [Google Scholar] [CrossRef]
- Chirchi, V.; Chirchi, E.; Khushi, E.C.; Bairavi, S.M.; Indu, K.S. Optical Sensor for Water Bacteria Detection using Machine Learning. In Proceedings of the 2024 11th International Conference on Computing for Sustainable Global Development (INDIACom), New Delhi, India, 28 February–1 March 2024; pp. 603–608. [Google Scholar] [CrossRef]
- Tyo, J.S.; Konsolakis, A.; Diersen, D.I.; Olsen, R.C. Principal-components-based display strategy for spectral imagery. IEEE Trans. Geosci. Remote. Sens. 2003, 41, 708–718. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, X. Hyperspectral image visualization using t-distributed stochastic neighbor embedding. In Proceedings of the MIPPR 2015: Remote Sensing Image Processing, Geographic Information Systems, and Other Applications, Enshi, China, 31 October–1 November 2015; Volume 9815, pp. 14–21. [Google Scholar]
- Heylen, R.; Parente, M.; Gader, P. A review of nonlinear hyperspectral unmixing methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2014, 7, 1844–1868. [Google Scholar] [CrossRef]
- Nascimento, J.M.; Dias, J.M. Vertex component analysis: A fast algorithm to unmix hyperspectral data. IEEE Trans. Geosci. Remote. Sens. 2005, 43, 898–910. [Google Scholar] [CrossRef]
- Feng, X.R.; Li, H.; Wang, R.; Du, Q.; Jia, X.; Plaza, A.J. Hyperspectral Unmixing Based on Nonnegative Matrix Factorization: A Comprehensive Review. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2022, 15, 4414–4436. [Google Scholar] [CrossRef]
- Cariou, C.; Chehdi, K. Unsupervised nearest neighbors clustering with application to hyperspectral images. IEEE J. Sel. Top. Signal Process. 2015, 9, 1105–1116. [Google Scholar] [CrossRef]
- Su, Y.; Li, J.; Plaza, A.; Marinoni, A.; Gamba, P.; Chakravortty, S. DAEN: Deep autoencoder networks for hyperspectral unmixing. IEEE Trans. Geosci. Remote. Sens. 2019, 57, 4309–4321. [Google Scholar] [CrossRef]
- Borsoi, R.A.; Imbiriba, T.; Bermudez, J.C.M. Deep generative endmember modeling: An application to unsupervised spectral unmixing. IEEE Trans. Comput. Imaging 2019, 6, 374–384. [Google Scholar] [CrossRef]
- Palsson, B.; Ulfarsson, M.O.; Sveinsson, J.R. Convolutional autoencoder for spectral–spatial hyperspectral unmixing. IEEE Trans. Geosci. Remote. Sens. 2020, 59, 535–549. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Cantero, M.; Perez, R.; Martinez, P.J.; Aguilar, P.; Plaza, J.; Plaza, A. Analysis of the behavior of a neural network model in the identification and quantification of hyperspectral signatures applied to the determination of water quality. In Proceedings of the Chemical and Biological Standoff Detection II SPIE, Philadelphia, PA, USA, 27–28 October 2004; Volume 5584, pp. 174–185. [Google Scholar]
- Duran, O.; Petrou, M. A time-efficient method for anomaly detection in hyperspectral images. IEEE Trans. Geosci. Remote. Sens. 2007, 45, 3894–3904. [Google Scholar] [CrossRef]
- Ceylan, O.; Kaya, G.T. Feature Selection Using Self Organizing Map Oriented Evolutionary Approach. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 4003–4006. [Google Scholar]
- Riese, F.M.; Keller, S.; Hinz, S. Supervised and semi-supervised self-organizing maps for regression and classification focusing on hyperspectral data. Remote. Sens. 2019, 12, 7. [Google Scholar] [CrossRef]
- Danielsen, A.S.; Johansen, T.A.; Garrett, J.L. Self-organizing maps for clustering hyperspectral images on-board a cubesat. Remote. Sens. 2021, 13, 4174. [Google Scholar] [CrossRef]
- Bishop, C.M.; Svensén, M.; Williams, C.K. GTM: The generative topographic mapping. Neural Comput. 1998, 10, 215–234. [Google Scholar] [CrossRef]
- Kireeva, N.; Baskin, I.; Gaspar, H.; Horvath, D.; Marcou, G.; Varnek, A. Generative topographic mapping (GTM): Universal tool for data visualization, structure-activity modeling and dataset comparison. Mol. Inform. 2012, 31, 301–312. [Google Scholar] [CrossRef]
- Gaspar, H.A.; Baskin, I.I.; Marcou, G.; Horvath, D.; Varnek, A. Chemical data visualization and analysis with incremental generative topographic mapping: Big data challenge. J. Chem. Inf. Model. 2015, 55, 84–94. [Google Scholar] [CrossRef]
- Horvath, D.; Marcou, G.; Varnek, A. Generative topographic mapping in drug design. Drug Discov. Today Technol. 2019, 32, 99–107. [Google Scholar] [CrossRef]
- Dempster, A.P.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–22. [Google Scholar] [CrossRef]
- Waczak, J. GenerativeTopographicMapping.jl. 2024. Available online: https://zenodo.org/records/11061258 (accessed on 24 April 2024).
- Bezanson, J.; Karpinski, S.; Shah, V.B.; Edelman, A. Julia: A fast dynamic language for technical computing. arXiv 2012, arXiv:1209.5145. [Google Scholar]
- Blaom, A.D.; Kiraly, F.; Lienart, T.; Simillides, Y.; Arenas, D.; Vollmer, S.J. MLJ: A Julia package for composable machine learning. arXiv 2020, arXiv:2007.12285. [Google Scholar] [CrossRef]
- Ruddick, K.G.; Voss, K.; Banks, A.C.; Boss, E.; Castagna, A.; Frouin, R.; Hieronymi, M.; Jamet, C.; Johnson, B.C.; Kuusk, J.; et al. A review of protocols for fiducial reference measurements of downwelling irradiance for the validation of satellite remote sensing data over water. Remote. Sens. 2019, 11, 1742. [Google Scholar] [CrossRef]
- Muller, R.; Lehner, M.; Muller, R.; Reinartz, P.; Schroeder, M.; Vollmer, B. A program for direct georeferencing of airborne and spaceborne line scanner images. Int. Arch. Photogramm. Remote. Sens. Spat. Inf. Sci. 2002, 34, 148–153. [Google Scholar]
- Bäumker, M.; Heimes, F. New calibration and computing method for direct georeferencing of image and scanner data using the position and angular data of an hybrid inertial navigation system. In Proceedings of the OEEPE Workshop, Integrated Sensor Orientation, Hannover, Germany, 17–18 September 2001; pp. 1–17. [Google Scholar]
- Mostafa, M.M.; Schwarz, K.P. A multi-sensor system for airborne image capture and georeferencing. Photogramm. Eng. Remote. Sens. 2000, 66, 1417–1424. [Google Scholar]
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote. Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- Nidamanuri, R.R.; Zbell, B. Normalized Spectral Similarity Score (NS3) as an Efficient Spectral Library Searching Method for Hyperspectral Image Classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2011, 4, 226–240. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Lyon, J.G.; Huete, A. Hyperspectral Indices and Image Classifications for Agriculture and Vegetation; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Alvarez-Vanhard, E.; Houet, T.; Mony, C.; Lecoq, L.; Corpetti, T. Can UAVs fill the gap between in situ surveys and satellites for habitat mapping? Remote. Sens. Environ. 2020, 243, 111780. [Google Scholar] [CrossRef]
- Gu, Y.; Huang, Y.; Liu, T. Intrinsic Decomposition Embedded Spectral Unmixing for Satellite Hyperspectral Images with Endmembers From UAV Platform. IEEE Trans. Geosci. Remote. Sens. 2023, 61, 5523012. [Google Scholar] [CrossRef]
- Balas, E. The prize collecting traveling salesman problem and its applications. In The Traveling Salesman Problem and Its Variations; Springer: Berlin/Heidelberg, Germany, 2007; pp. 663–695. [Google Scholar]
- Suryan, V.; Tokekar, P. Learning a spatial field in minimum time with a team of robots. IEEE Trans. Robot. 2020, 36, 1562–1576. [Google Scholar] [CrossRef]
- Han, T.; Goodenough, D.G. Investigation of nonlinearity in hyperspectral remotely sensed imagery—A nonlinear time series analysis approach. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 1556–1560. [Google Scholar] [CrossRef]
- Bishop, C.M.; Svensén, M.; Williams, C.K. Developments of the generative topographic mapping. Neurocomputing 1998, 21, 203–224. [Google Scholar] [CrossRef]
- Uddin, M.P.; Mamun, M.A.; Hossain, M.A. PCA-based feature reduction for hyperspectral remote sensing image classification. IETE Tech. Rev. 2021, 38, 377–396. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waczak, J.; Aker, A.; Wijeratne, L.O.H.; Talebi, S.; Fernando, A.; Dewage, P.M.H.; Iqbal, M.; Lary, M.; Schaefer, D.; Balagopal, G.; et al. Unsupervised Characterization of Water Composition with UAV-Based Hyperspectral Imaging and Generative Topographic Mapping. Remote Sens. 2024, 16, 2430. https://doi.org/10.3390/rs16132430
Waczak J, Aker A, Wijeratne LOH, Talebi S, Fernando A, Dewage PMH, Iqbal M, Lary M, Schaefer D, Balagopal G, et al. Unsupervised Characterization of Water Composition with UAV-Based Hyperspectral Imaging and Generative Topographic Mapping. Remote Sensing. 2024; 16(13):2430. https://doi.org/10.3390/rs16132430
Chicago/Turabian StyleWaczak, John, Adam Aker, Lakitha O. H. Wijeratne, Shawhin Talebi, Ashen Fernando, Prabuddha M. H. Dewage, Mazhar Iqbal, Matthew Lary, David Schaefer, Gokul Balagopal, and et al. 2024. "Unsupervised Characterization of Water Composition with UAV-Based Hyperspectral Imaging and Generative Topographic Mapping" Remote Sensing 16, no. 13: 2430. https://doi.org/10.3390/rs16132430
APA StyleWaczak, J., Aker, A., Wijeratne, L. O. H., Talebi, S., Fernando, A., Dewage, P. M. H., Iqbal, M., Lary, M., Schaefer, D., Balagopal, G., & Lary, D. J. (2024). Unsupervised Characterization of Water Composition with UAV-Based Hyperspectral Imaging and Generative Topographic Mapping. Remote Sensing, 16(13), 2430. https://doi.org/10.3390/rs16132430















