Simulation-Based Optimization of Path Planning for Camera-Equipped UAVs That Considers the Location and Time of Construction Activities
Abstract
:1. Introduction
2. Literature Review
2.1. Conventional Video Collection for Construction Monitoring
2.2. Data Collection Using UAV for Construction Monitoring
| Ref. | Sensor Type | Operation Environment | Waypoints Generation Method | Routing Algorithm | Schedule Considered | Application | Type of Target |
|---|---|---|---|---|---|---|---|
| [35] | Camera | Outdoor | Predefined | A* | No | Inspection | Constructed objects |
| [36] | n/a | Indoor | Predefined | A* | No | Inspection | Constructed objects |
| [37] | Camera | Outdoor/ Indoor | Sampling based on coverage | LKH and RRT* | No | 3D reconstruction and inspection | Constructed objects |
| [38] | Camera | Outdoor | Sampling based on coverage, sensor spec., and overlapping rate | DPSO and A* | No | 3D reconstruction and inspection | Constructed objects |
| [39] | Camera | Outdoor | Refining the nun-occluded sampled viewpoints to minimize the number of waypoints | A* | No | Inspection | Constructed objects |
| [40] | Laser scanner | Outdoor | Sampling based on coverage, sensor spec., overlapping rate, and criticality levels of different zones | GA and A* | No | Inspection | Constructed objects |
| [12] | Camera | Outdoor | Sampling | SVRP from ArcGIS | No | 3D reconstruction | Constructed objects |
| [41] | Camera | Outdoor | OABC Algorithm | No | 3D reconstruction | Constructed objects | |
| [11] | Camera | Outdoor/ Indoor | HEDAC | No | 3D reconstruction | Constructed objects | |
| [10] | Camera | Outdoor | Sampling based on 3D grid-based flight plan template and VL-MOGA | Yes | 3D reconstruction, progress monitoring | Constructed objects | |
| [42] | Camera | Outdoor | Sampling waypoints in the areas of interest | Improved ACO algorithm | No | Construction safety inspection | Safety risks on construction site |
| This paper | Camera | Outdoor | NSGA-II | A* and random-key GA | Yes | Activity monitoring | Construction activities |
2.3. Challenges in Applying Activity Recognition Techniques on Aerial Videos
3. Proposed Method
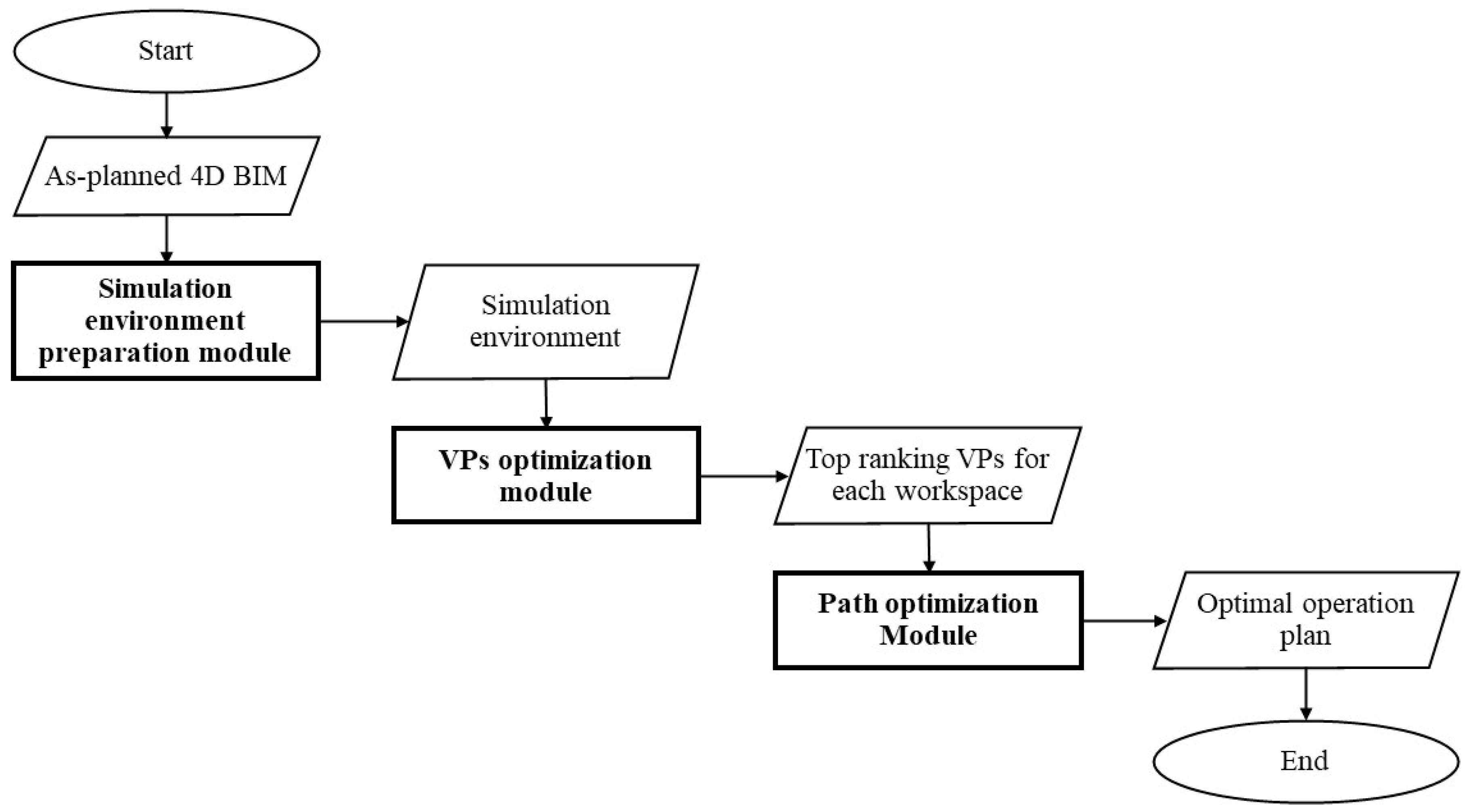
3.1. Method Overview
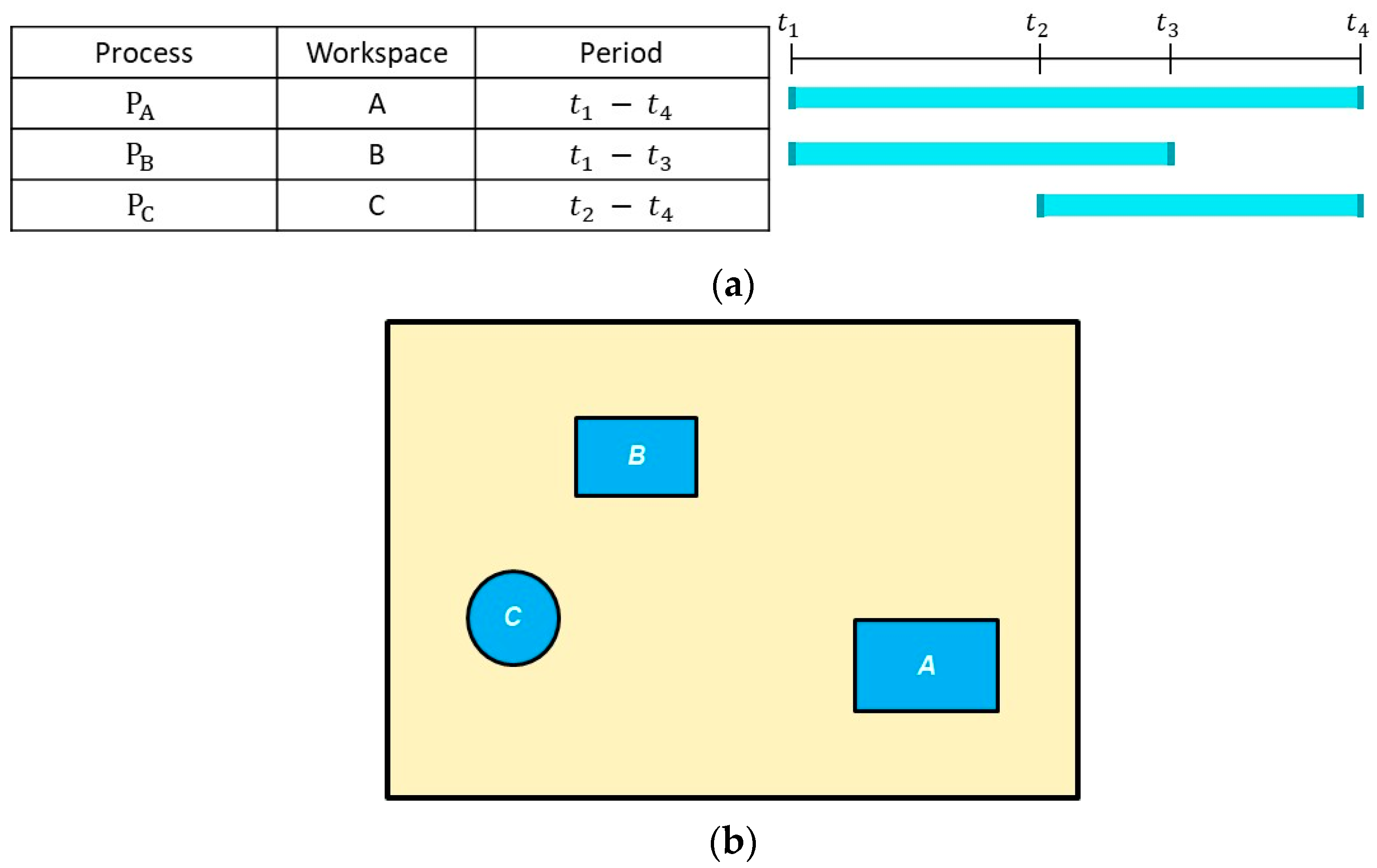
3.2. Simulation-Environment-Preparation Module
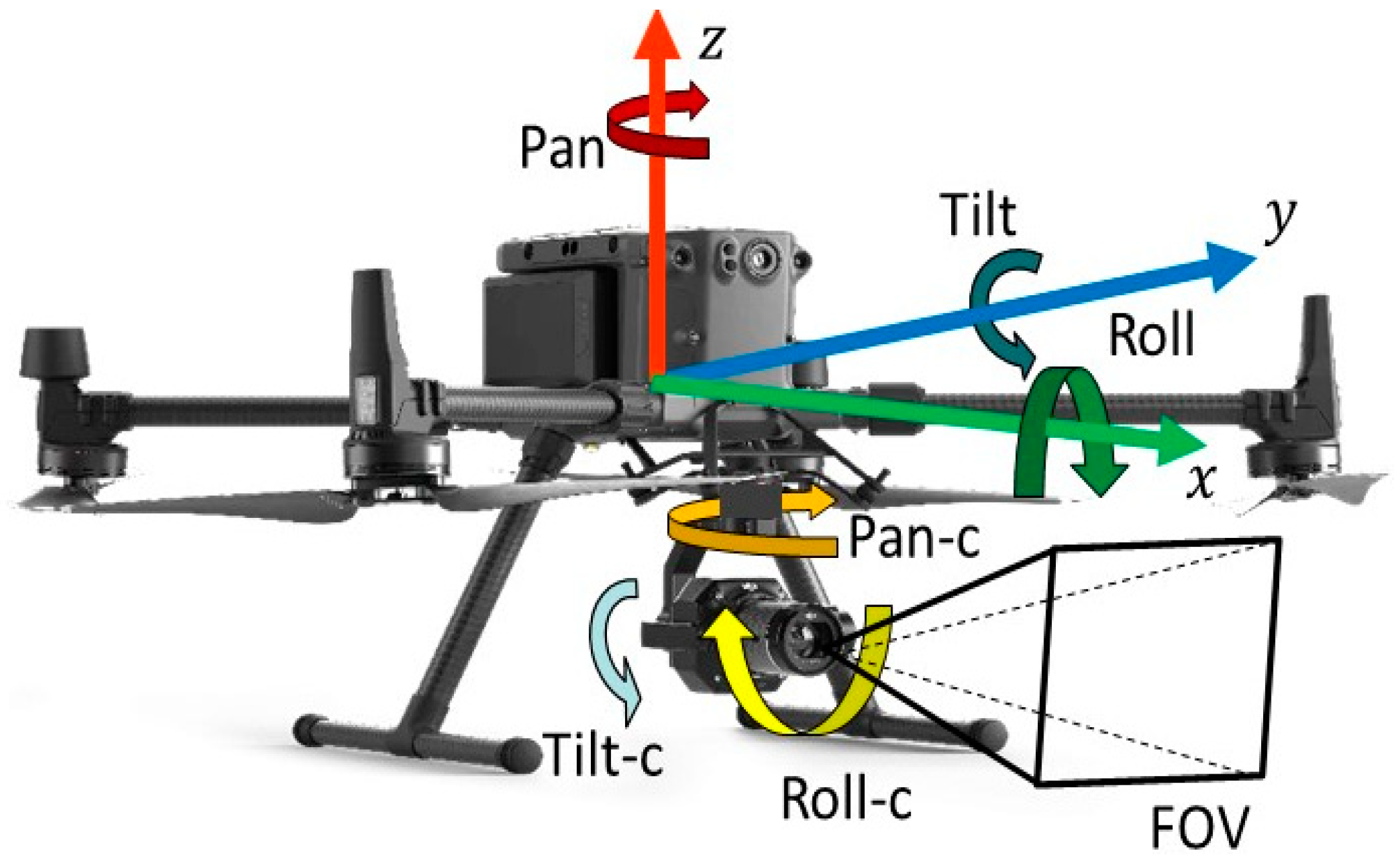
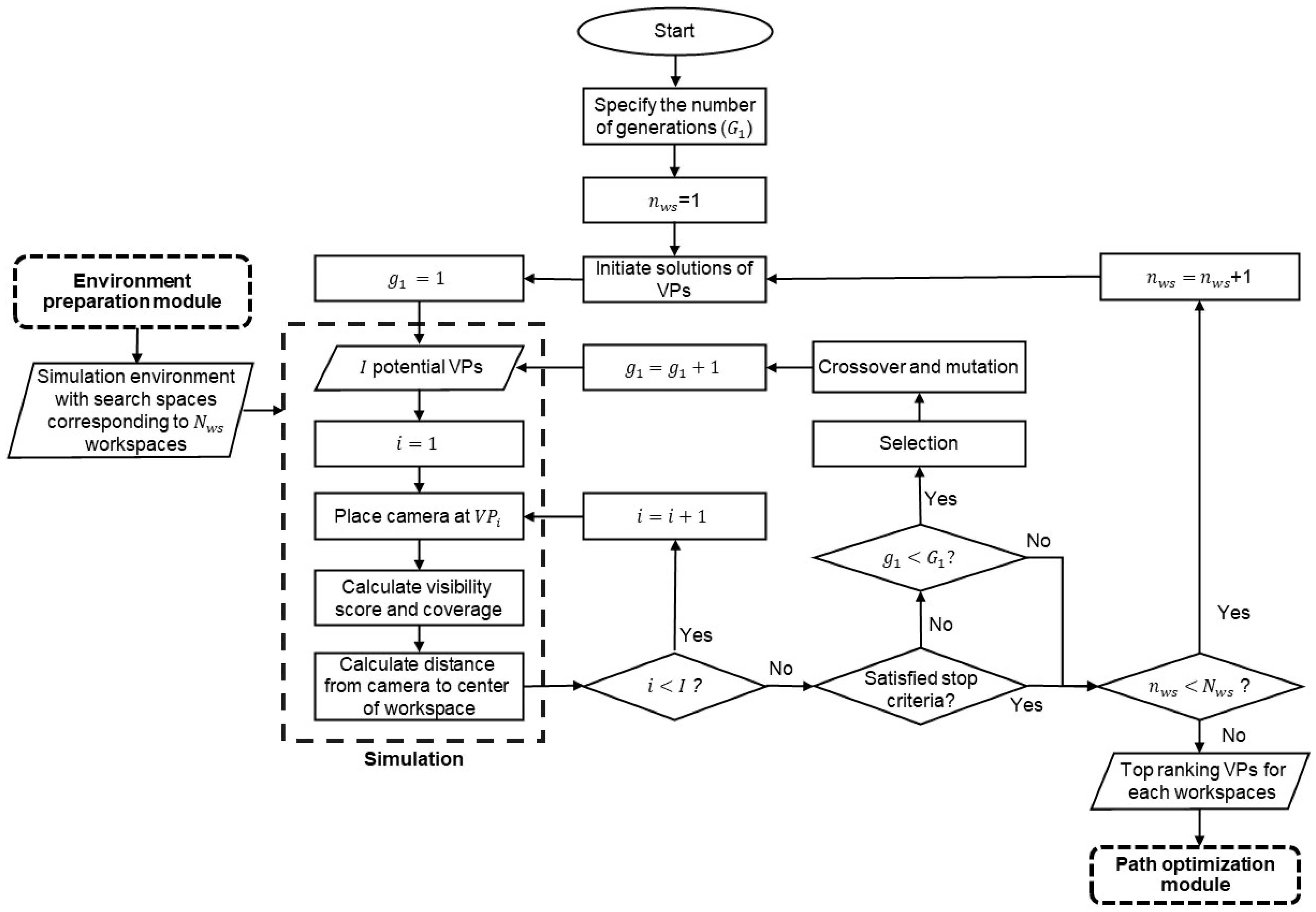
3.3. VPs-Optimization Module
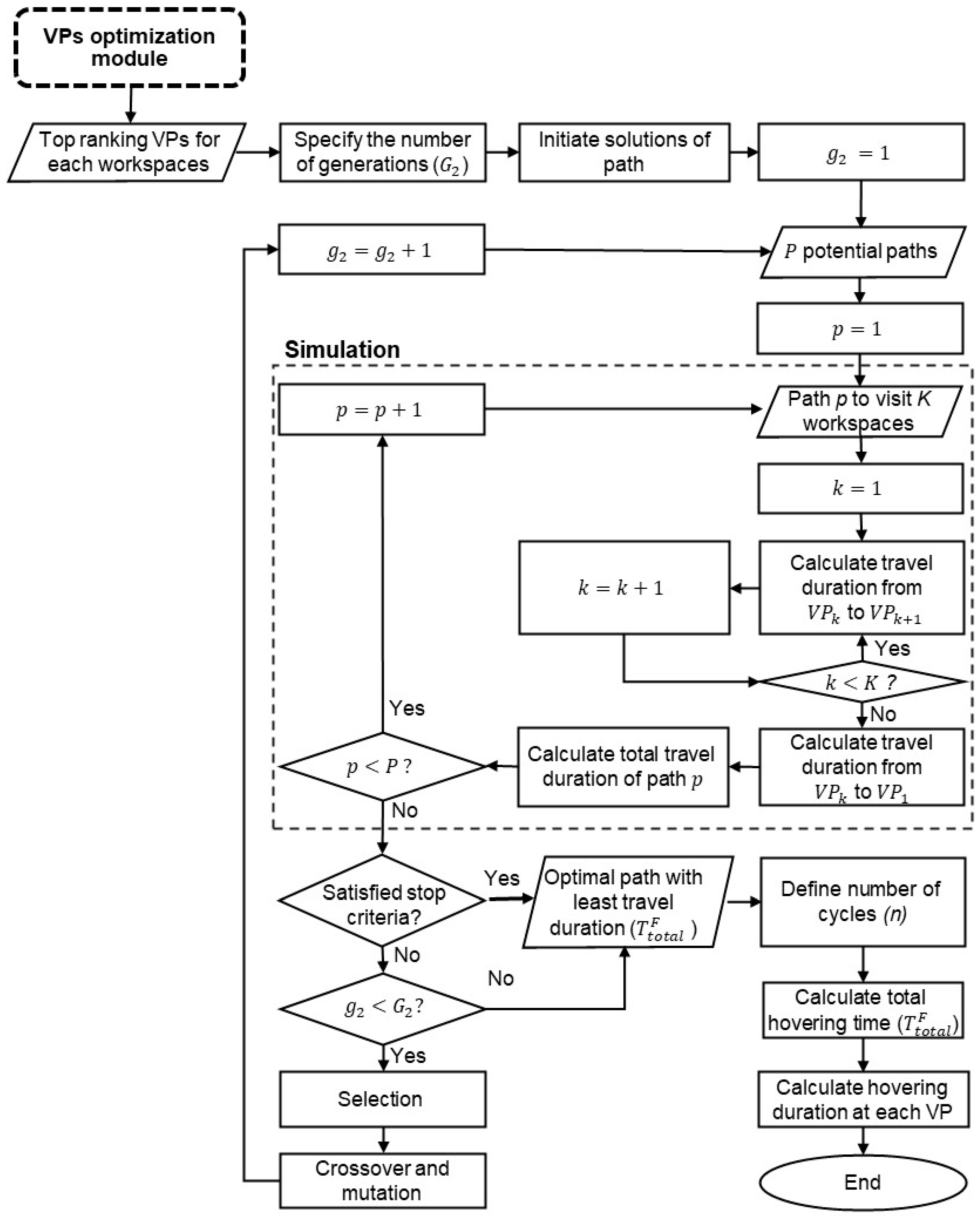
3.4. Path-Optimization Module
4. Implementation and Case Study
4.1. Implementation
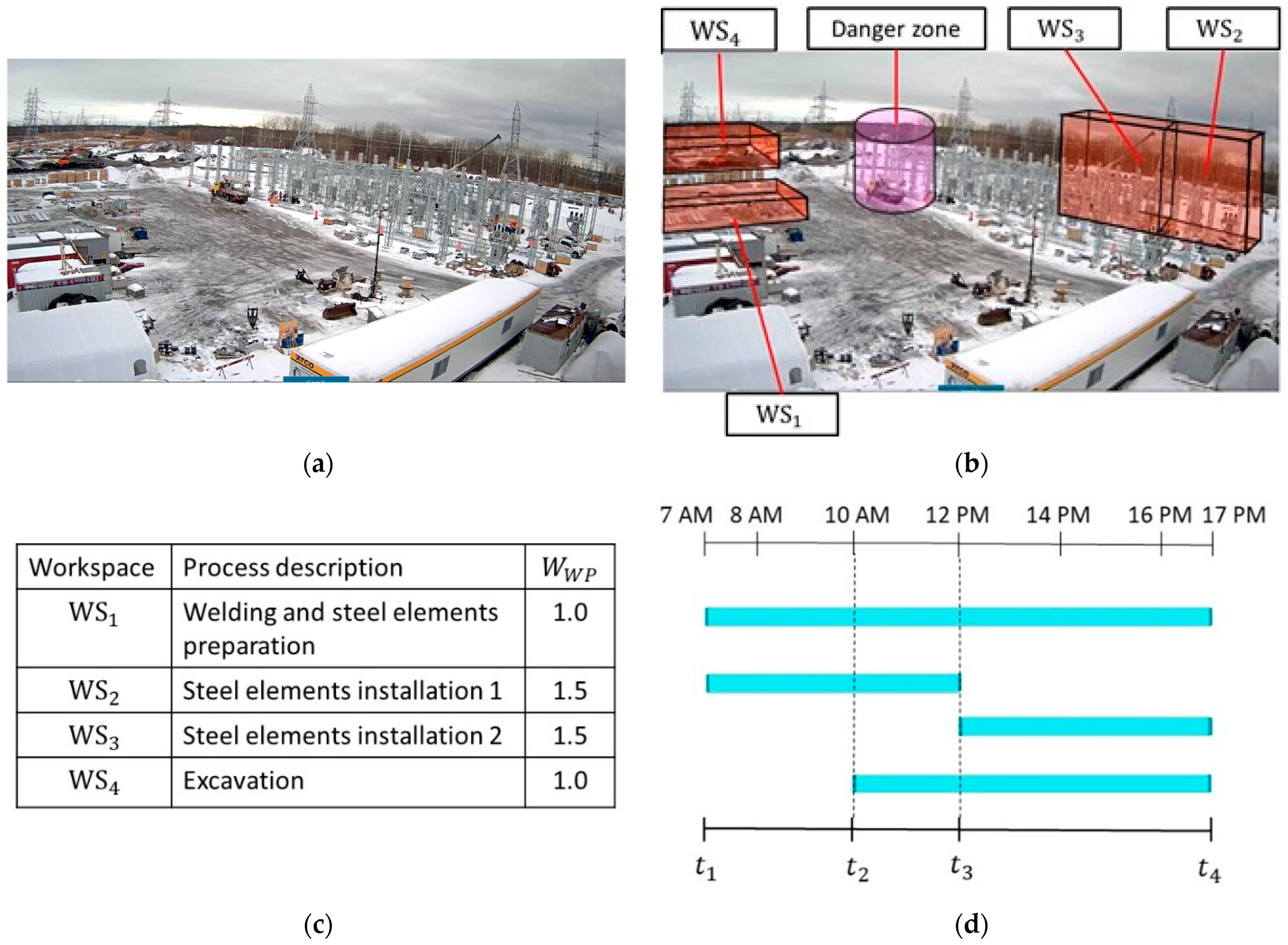
4.2. Case Study
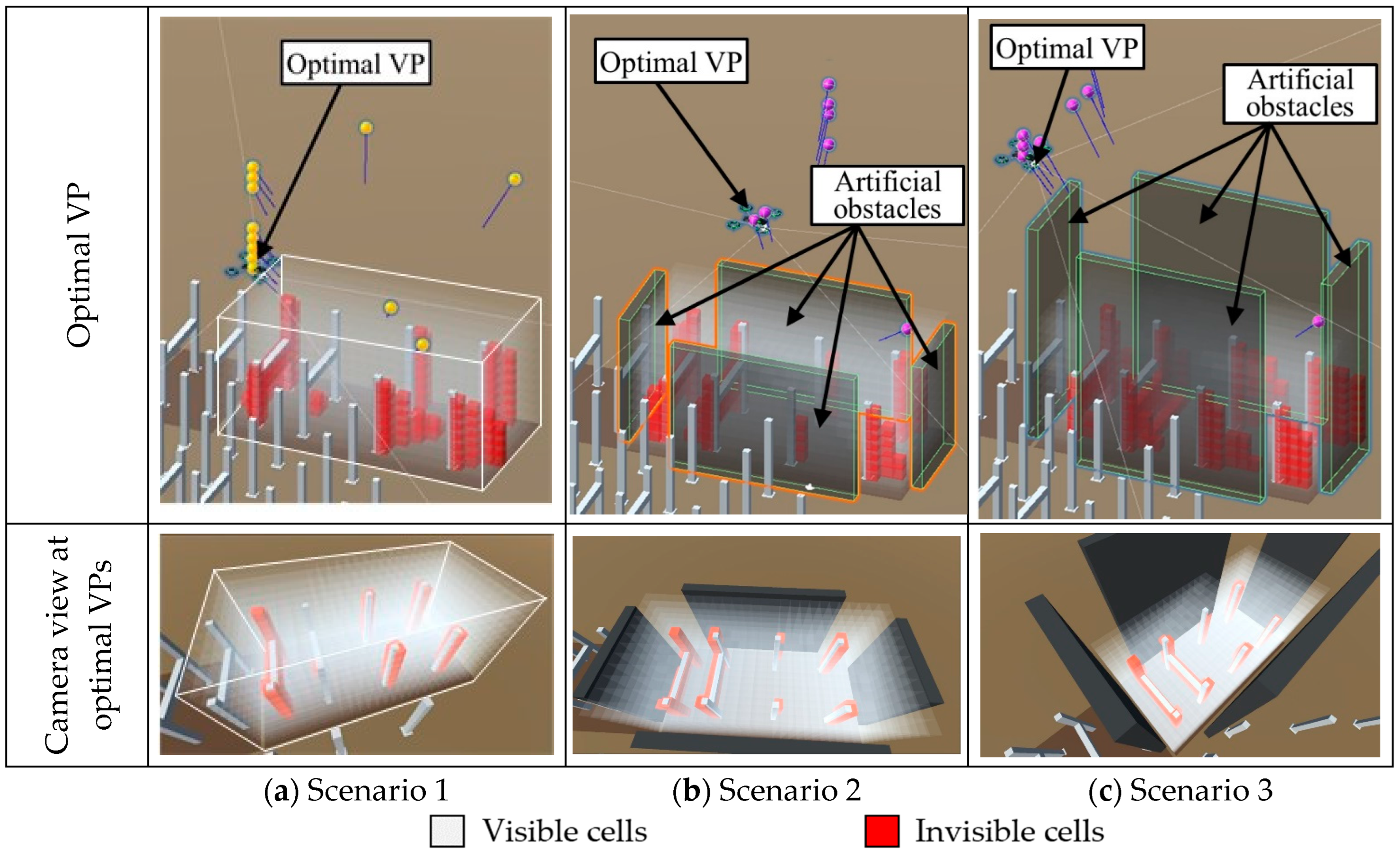
4.3. Pilot Test for Evaluating the VPs-Optimization Module
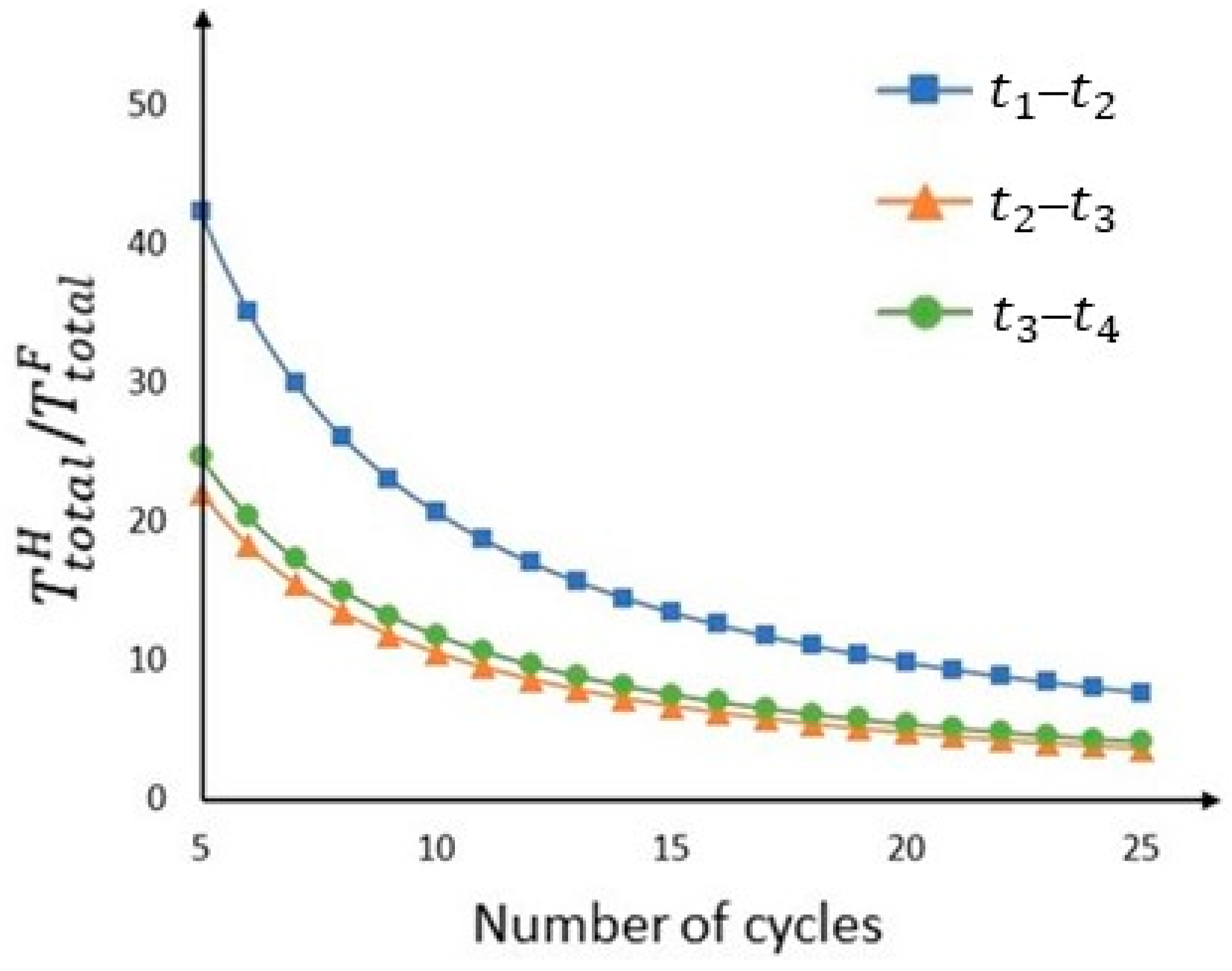
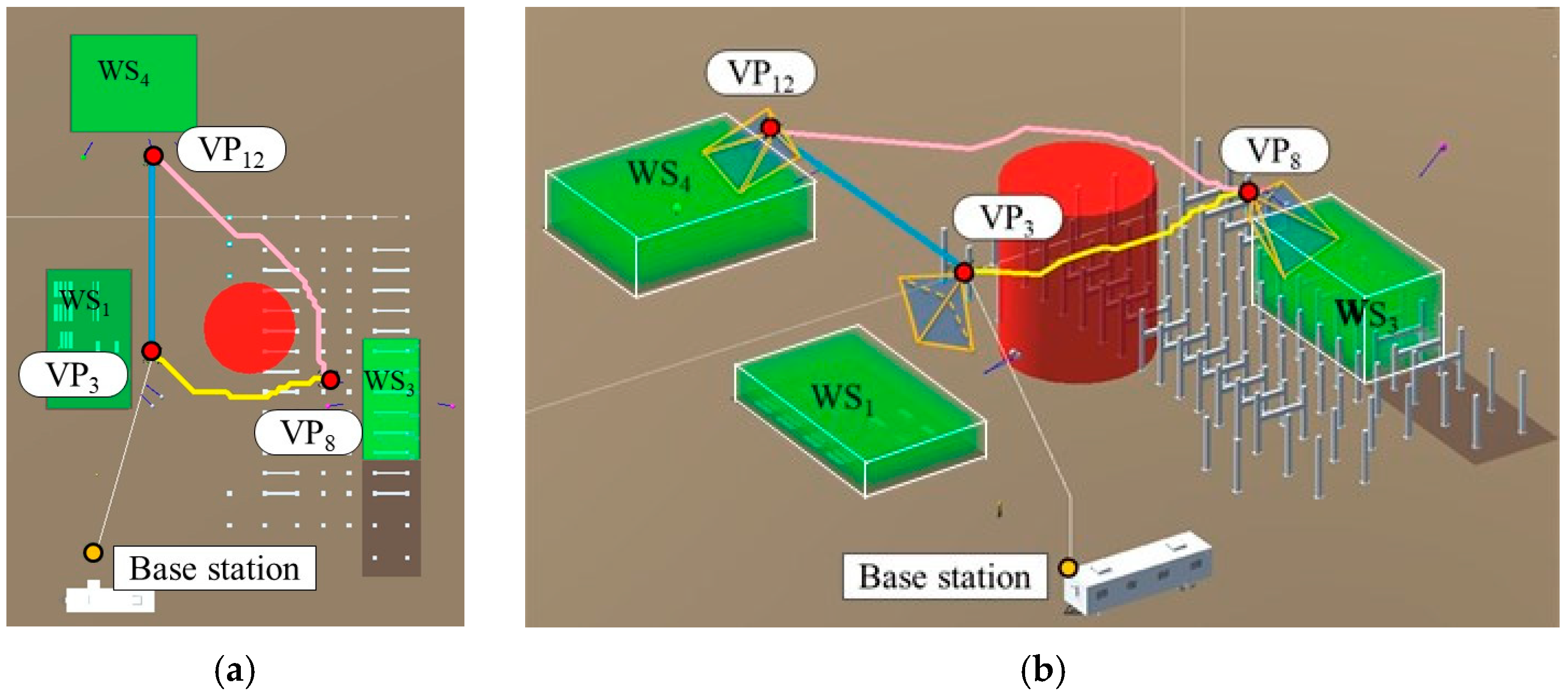
4.4. Results of the Case Study
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Alizadehsalehi, S.; Yitmen, I. The Impact of Field Data Capturing Technologies on Automated Construction Project Progress Monitoring. Procedia Eng. 2016, 161, 97–103. [Google Scholar] [CrossRef]
- Yang, J.; Park, M.-W.; Vela, P.A.; Golparvar-Fard, M. Construction Performance Monitoring via Still Images, Time-Lapse Photos, and Video Streams: Now, Tomorrow, and the Future. Adv. Eng. Inform. 2015, 29, 211–224. [Google Scholar] [CrossRef]
- Paneru, S.; Jeelani, I. Computer Vision Applications in Construction: Current State, Opportunities & Challenges. Autom. Constr. 2021, 132, 103940. [Google Scholar] [CrossRef]
- Xu, S.; Wang, J.; Shou, W.; Ngo, T.; Sadick, A.-M.; Wang, X. Computer Vision Techniques in Construction: A Critical Review. Arch. Comput. Methods Eng. 2021, 28, 3383–3397. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, Y.; Chen, H.; Ouyang, Y.; Luo, X.; Wu, X. BIM-Based Optimization of Camera Placement for Indoor Construction Monitoring Considering the Construction Schedule. Autom. Constr. 2021, 130, 103825. [Google Scholar] [CrossRef]
- Tran, S.V.-T.; Nguyen, T.L.; Chi, H.-L.; Lee, D.; Park, C. Generative Planning for Construction Safety Surveillance Camera Installation in 4D BIM Environment. Autom. Constr. 2022, 134, 104103. [Google Scholar] [CrossRef]
- Asadi, K.; Kalkunte Suresh, A.; Ender, A.; Gotad, S.; Maniyar, S.; Anand, S.; Noghabaei, M.; Han, K.; Lobaton, E.; Wu, T. An Integrated UGV-UAV System for Construction Site Data Collection. Autom. Constr. 2020, 112, 103068. [Google Scholar] [CrossRef]
- Ham, Y.; Han, K.K.; Lin, J.J.; Golparvar-Fard, M. Visual Monitoring of Civil Infrastructure Systems via Camera-Equipped Unmanned Aerial Vehicles (UAVs): A Review of Related Works. Vis. Eng. 2016, 4, 1. [Google Scholar] [CrossRef]
- Jeelani, I.; Gheisari, M. Safety Challenges of UAV Integration in Construction: Conceptual Analysis and Future Research Roadmap. Saf. Sci. 2021, 144, 105473. [Google Scholar] [CrossRef]
- Ibrahim, A.; Golparvar-Fard, M.; El-Rayes, K. Multiobjective Optimization of Reality Capture Plans for Computer Vision–Driven Construction Monitoring with Camera-Equipped UAVs. J. Comput. Civ. Eng. 2022, 36, 04022018. [Google Scholar] [CrossRef]
- Ivić, S.; Crnković, B.; Grbčić, L.; Matleković, L. Multi-UAV Trajectory Planning for 3D Visual Inspection of Complex Structures. Autom. Constr. 2023, 147, 104709. [Google Scholar] [CrossRef]
- Zheng, X.; Wang, F.; Li, Z. A Multi-UAV Cooperative Route Planning Methodology for 3D Fine-Resolution Building Model Reconstruction. ISPRS J. Photogramm. Remote Sens. 2018, 146, 483–494. [Google Scholar] [CrossRef]
- Huang, Y.; Amin, H. Simulation-Based Optimization of Path Planning for Camera-Equipped UAV Considering Construction Activities. In Proceedings of the Creative Construction Conference 2023, Keszthely, Hungary, 20–23 June 2023. [Google Scholar]
- Yang, J.; Shi, Z.; Wu, Z. Vision-Based Action Recognition of Construction Workers Using Dense Trajectories. Adv. Eng. Inform. 2016, 30, 327–336. [Google Scholar] [CrossRef]
- Roh, S.; Aziz, Z.; Peña-Mora, F. An Object-Based 3D Walk-through Model for Interior Construction Progress Monitoring. Autom. Constr. 2011, 20, 66–75. [Google Scholar] [CrossRef]
- Kropp, C.; Koch, C.; König, M. Interior Construction State Recognition with 4D BIM Registered Image Sequences. Autom. Constr. 2018, 86, 11–32. [Google Scholar] [CrossRef]
- Rebolj, D.; Pučko, Z.; Babič, N.Č.; Bizjak, M.; Mongus, D. Point Cloud Quality Requirements for Scan-vs-BIM Based Automated Construction Progress Monitoring. Autom. Constr. 2017, 84, 323–334. [Google Scholar] [CrossRef]
- Son, H.; Bosché, F.; Kim, C. As-Built Data Acquisition and Its Use in Production Monitoring and Automated Layout of Civil Infrastructure: A Survey. Adv. Eng. Inform. 2015, 29, 172–183. [Google Scholar] [CrossRef]
- Chen, C.; Zhu, Z.; Hammad, A. Automated Excavators Activity Recognition and Productivity Analysis from Construction Site Surveillance Videos. Autom. Constr. 2020, 110, 103045. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Q.; Yang, B.; Wu, T.; Lei, K.; Zhang, B.; Fang, T. Vision-Based Framework for Automatic Progress Monitoring of Precast Walls by Using Surveillance Videos during the Construction Phase. J. Comput. Civ. Eng. 2021, 35, 04020056. [Google Scholar] [CrossRef]
- Arif, F.; Khan, W.A. Smart Progress Monitoring Framework for Building Construction Elements Using Videography–MATLAB–BIM Integration. Int. J. Civ. Eng. 2021, 19, 717–732. [Google Scholar] [CrossRef]
- Soltani, M.M.; Zhu, Z.; Hammad, A. Framework for Location Data Fusion and Pose Estimation of Excavators Using Stereo Vision. J. Comput. Civ. Eng. 2018, 32, 04018045. [Google Scholar] [CrossRef]
- Bohn, J.S.; Teizer, J. Benefits and Barriers of Construction Project Monitoring Using High-Resolution Automated Cameras. J. Constr. Eng. Manag. 2010, 136, 632–640. [Google Scholar] [CrossRef]
- Fang, W.; Ding, L.; Luo, H.; Love, P.E.D. Falls from Heights: A Computer Vision-Based Approach for Safety Harness Detection. Autom. Constr. 2018, 91, 53–61. [Google Scholar] [CrossRef]
- Zhang, H.; Yan, X.; Li, H. Ergonomic Posture Recognition Using 3D View-Invariant Features from Single Ordinary Camera. Autom. Constr. 2018, 94, 1–10. [Google Scholar] [CrossRef]
- Bügler, M.; Borrmann, A.; Ogunmakin, G.; Vela, P.A.; Teizer, J. Fusion of Photogrammetry and Video Analysis for Productivity Assessment of Earthwork Processes. Comput.-Aided Civ. Infrastruct. Eng. 2017, 32, 107–123. [Google Scholar] [CrossRef]
- Luo, X.; Li, H.; Yang, X.; Yu, Y.; Cao, D. Capturing and Understanding Workers’ Activities in Far-Field Surveillance Videos with Deep Action Recognition and Bayesian Nonparametric Learning. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 333–351. [Google Scholar] [CrossRef]
- Torabi, G.; Hammad, A.; Bouguila, N. Two-Dimensional and Three-Dimensional CNN-Based Simultaneous Detection and Activity Classification of Construction Workers. J. Comput. Civ. Eng. 2022, 36, 04022009. [Google Scholar] [CrossRef]
- Park, M.-W.; Elsafty, N.; Zhu, Z. Hardhat-Wearing Detection for Enhancing On-Site Safety of Construction Workers. J. Constr. Eng. Manag. 2015, 141, 04015024. [Google Scholar] [CrossRef]
- Albahri, A.H.; Hammad, A. Simulation-Based Optimization of Surveillance Camera Types, Number, and Placement in Buildings Using BIM. J. Comput. Civ. Eng. 2017, 31, 04017055. [Google Scholar] [CrossRef]
- Kim, J.; Ham, Y.; Chung, Y.; Chi, S. Systematic Camera Placement Framework for Operation-Level Visual Monitoring on Construction Jobsites. J. Constr. Eng. Manag. 2019, 145, 04019019. [Google Scholar] [CrossRef]
- Yang, X.; Li, H.; Huang, T.; Zhai, X.; Wang, F.; Wang, C. Computer-Aided Optimization of Surveillance Cameras Placement on Construction Sites. Comput.-Aided Civ. Infrastruct. Eng. 2018, 33, 1110–1126. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, H.; Skitmore, M.; Li, Q.; Zhong, B. Optimal Camera Placement for Monitoring Safety in Metro Station Construction Work. J. Constr. Eng. Manag. 2019, 145, 04018118. [Google Scholar] [CrossRef]
- Maboudi, M.; Homaei, M.; Song, S.; Malihi, S.; Saadatseresht, M.; Gerke, M. A Review on Viewpoints and Path Planning for UAV-Based 3-D Reconstruction. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5026–5048. [Google Scholar] [CrossRef]
- Freimuth, H.; König, M. Planning and Executing Construction Inspections with Unmanned Aerial Vehicles. Autom. Constr. 2018, 96, 540–553. [Google Scholar] [CrossRef]
- Li, F.; Zlatanova, S.; Koopman, M.; Bai, X.; Diakité, A. Universal Path Planning for an Indoor Drone. Autom. Constr. 2018, 95, 275–283. [Google Scholar] [CrossRef]
- Bircher, A.; Kamel, M.; Alexis, K.; Burri, M.; Oettershagen, P.; Omari, S.; Mantel, T.; Siegwart, R. Three-Dimensional Coverage Path Planning via Viewpoint Resampling and Tour Optimization for Aerial Robots. Auton. Robots 2016, 40, 1059–1078. [Google Scholar] [CrossRef]
- Phung, M.D.; Quach, C.H.; Dinh, T.H.; Ha, Q. Enhanced Discrete Particle Swarm Optimization Path Planning for UAV Vision-Based Surface Inspection. Autom. Constr. 2017, 81, 25–33. [Google Scholar] [CrossRef]
- Huang, X.; Liu, Y.; Huang, L.; Stikbakke, S.; Onstein, E. BIM-Supported Drone Path Planning for Building Exterior Surface Inspection. Comput. Ind. 2023, 153, 104019. [Google Scholar] [CrossRef]
- Bolourian, N.; Hammad, A. LiDAR-Equipped UAV Path Planning Considering Potential Locations of Defects for Bridge Inspection. Autom. Constr. 2020, 117, 103250. [Google Scholar] [CrossRef]
- Chen, H.; Liang, Y.; Meng, X. A UAV Path Planning Method for Building Surface Information Acquisition Utilizing Opposition-Based Learning Artificial Bee Colony Algorithm. Remote Sens. 2023, 15, 4312. [Google Scholar] [CrossRef]
- Yu, L.; Huang, M.M.; Jiang, S.; Wang, C.; Wu, M. Unmanned Aircraft Path Planning for Construction Safety Inspections. Autom. Constr. 2023, 154, 105005. [Google Scholar] [CrossRef]
- Mliki, H.; Bouhlel, F.; Hammami, M. Human Activity Recognition from UAV-Captured Video Sequences. Pattern Recognit. 2020, 100, 107140. [Google Scholar] [CrossRef]
- Li, T.; Liu, J.; Zhang, W.; Ni, Y.; Wang, W.; Li, Z. UAV-Human: A Large Benchmark for Human Behavior Understanding with Unmanned Aerial Vehicles. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 16266–16275. [Google Scholar]
- Peng, H.; Razi, A. Fully Autonomous UAV-Based Action Recognition System Using Aerial Imagery. In Proceedings of the Advances in Visual Computing, San Diego, CA, USA, 5–7 October 2020; Bebis, G., Yin, Z., Kim, E., Bender, J., Subr, K., Kwon, B.C., Zhao, J., Kalkofen, D., Baciu, G., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 276–290. [Google Scholar]
- Aldahoul, N.; Karim, H.A.; Sabri, A.Q.M.; Tan, M.J.T.; Momo, M.A.; Fermin, J.L. A Comparison Between Various Human Detectors and CNN-Based Feature Extractors for Human Activity Recognition via Aerial Captured Video Sequences. IEEE Access 2022, 10, 63532–63553. [Google Scholar] [CrossRef]
- Gundu, S.; Syed, H. Vision-Based HAR in UAV Videos Using Histograms and Deep Learning Techniques. Sensors 2023, 23, 2569. [Google Scholar] [CrossRef]
- Othman, N.A.; Aydin, I. Challenges and Limitations in Human Action Recognition on Unmanned Aerial Vehicles: A Comprehensive Survey. Trait. Signal 2021, 38, 1403–1411. [Google Scholar] [CrossRef]
- Guévremont, M.; Hammad, A. Ontology for Linking Delay Claims with 4D Simulation to Analyze Effects-Causes and Responsibilities. J. Leg. Aff. Dispute Resolut. Eng. Constr. 2021, 13, 04521024. [Google Scholar] [CrossRef]
- Halpin, D.W.; Riggs, L.S. Planning and Analysis of Construction Operations; John Wiley & Sons: Hoboken, NJ, USA, 1992; ISBN 978-0-471-55510-0. [Google Scholar]
- Cho, J.-H.; Wang, Y.; Chen, I.-R.; Chan, K.S.; Swami, A. A Survey on Modeling and Optimizing Multi-Objective Systems. IEEE Commun. Surv. Tutor. 2017, 19, 1867–1901. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Snyder, L.V.; Daskin, M.S. A Random-Key Genetic Algorithm for the Generalized Traveling Salesman Problem. Eur. J. Oper. Res. 2006, 174, 38–53. [Google Scholar] [CrossRef]
- Matrice 100-Product Information-DJI. Available online: https://www.dji.com/ca/matrice100/info (accessed on 19 January 2024).
- Dewangan, R.K.; Shukla, A.; Godfrey, W.W. Three Dimensional Path Planning Using Grey Wolf Optimizer for UAVs. Appl. Intell. 2019, 49, 2201–2217. [Google Scholar] [CrossRef]
- Unity 2021.3. Available online: https://docs.unity3d.com/Manual/index.html (accessed on 10 April 2023).
- Python 3.11.3. Available online: https://docs.python.org/3/contents.html (accessed on 10 April 2023).
- Blank, J.; Deb, K. Pymoo: Multi-Objective Optimization in Python. IEEE Access 2020, 8, 89497–89509. [Google Scholar] [CrossRef]
- Ultimate A* Pathfinding Solution. Available online: https://assetstore.unity.com/packages/tools/ai/ultimate-a-pathfinding-solution-224082 (accessed on 29 May 2023).
- Deb, K.; Deb, D. Analysing Mutation Schemes for Real-Parameter Genetic Algorithms. Int. J. Artif. Intell. Soft Comput. 2014, 4, 1–28. [Google Scholar] [CrossRef]





| Ref. | Camera Type | Environment | Optimization Method | Simulation Platform | Schedule Considered? | Application |
|---|---|---|---|---|---|---|
| [30] | Fixed camera | Indoor | PICEA | 3D | No | General site monitoring |
| [32] | Fixed camera | Outdoor | NSGA-II | 2D | No | General site monitoring |
| [31] | Fixed camera | Outdoor | Semantic-Cost GA | 2D | No | General site monitoring |
| [33] | PTZ camera | Outdoor | Modified GA | 3D | No | Safety monitoring |
| [5] | Fixed camera | Indoor | PMGA | 2D | Yes | Activity monitoring |
| [6] | Fixed camera | Outdoor | NSGA-II | 3D | Yes | Safety monitoring |
| Workspace | Number of VPs | Range of Gene Value | Example Gene | Selected VP | Random Key | Visiting Order |
|---|---|---|---|---|---|---|
| A | 4 | [0, 4) | 3.83 | 0.83 | 3 | |
| B | 5 | [0, 5) | 3.25 | 0.25 | 1 | |
| C | 3 | [0, 3) | 1.77 | 0.77 | 2 |
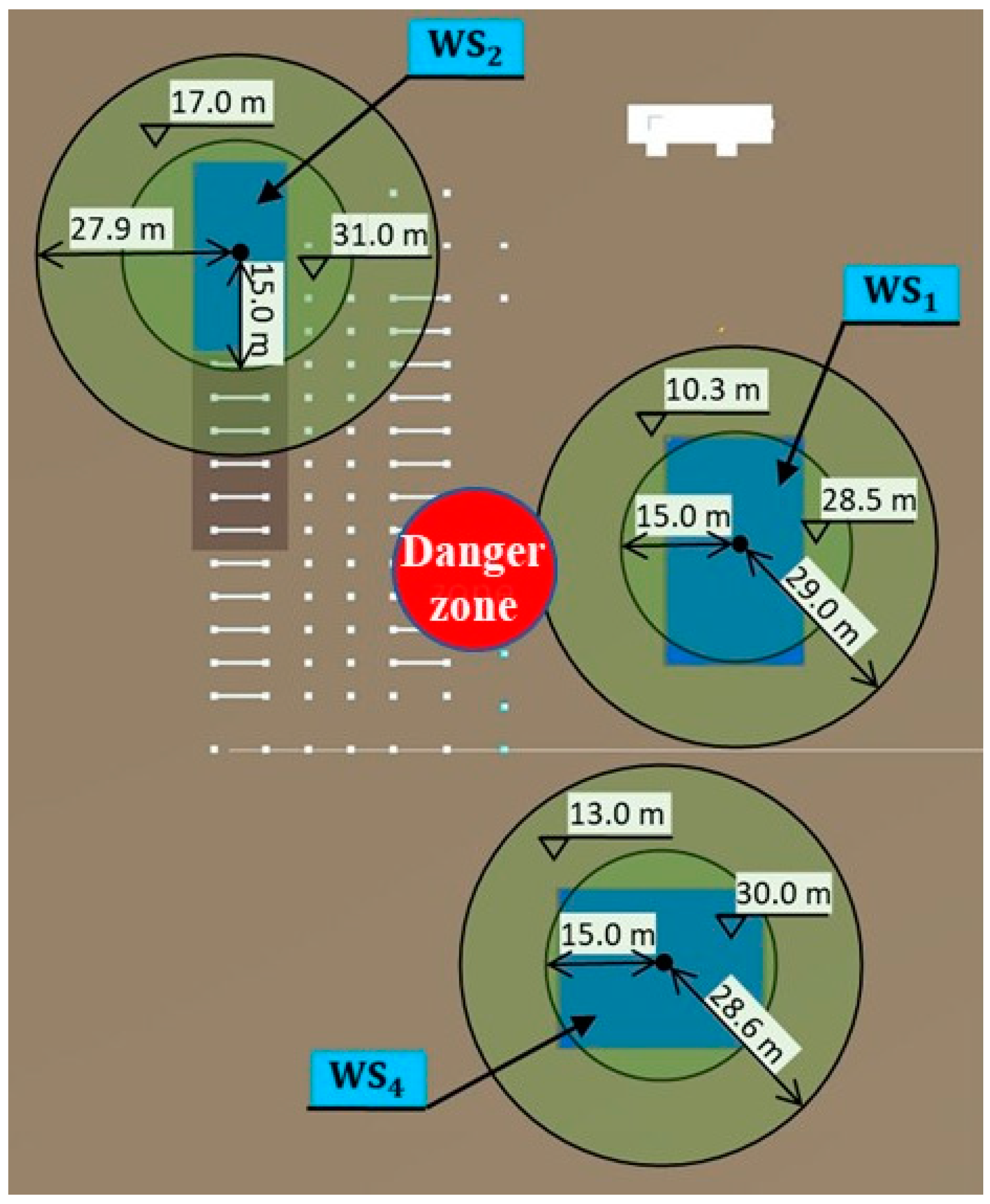
| ID | Center Point Coordinates and Height of Workspace | Range of Attribute Values of Each Search Space | ||||||
|---|---|---|---|---|---|---|---|---|
| (m) | (m) | h (m) | (m) | (m) | (m) | φ’ (°) | θ (°) | |
| WS1 | 67.0 | 26.0 | 5.0 | [38.0, 96.0] | [−3.0, 55.0] | [10.3, 28.5] | [−45, 45] | [15, 60] |
| WS2 | 1.0 | 66.0 | 12.0 | [−26.9, 28.9] | [38.1, 93.9] | [17.0, 31.0] | [−45, 45] | [15, 60] |
| WS3 | 1.0 | 40.0 | 12.0 | [−26.9, 28.9] | [12.1, 67.9] | [17.0, 31.0] | [−45, 45] | [15, 60] |
| WS4 | 57.0 | −29.0 | 8.0 | [28.4, 85.6] | [−57.6, −0.4] | [13.0, 30.0] | [−45, 45] | [15, 60] |
| VP ID | X (m) | Y (m) | Z (m) | (°) | (°) | Coverage (%) | Distance (m) | Fitness Value (%) | |
|---|---|---|---|---|---|---|---|---|---|
| Scenario 1 | 1 | 14 | 59 | 31 | 54 | −12 | 96.64 | 28.81 | 78.69 |
| 2 | 14 | 59 | 30 | 56 | −4 | 96.61 | 27.95 | 79.66 | |
| 3 | 14 | 59 | 29 | 56 | −22 | 96.44 | 27.09 | 80.51 | |
| 4 | 14 | 59 | 25 | 56 | −7 | 96.28 | 23.79 | 84.20 | |
| 5 | 14 | 59 | 24 | 51 | 0 | 96.25 | 23.00 | 85.09 | |
| 6 | 14 | 59 | 23 | 52 | 1 | 96.14 | 22.23 | 85.90 | |
| 7 | 14 | 59 | 22 | 51 | −6 | 96.06 | 21.47 | 86.71 | |
| 8 * | 14 | 59 | 21 | 50 | −6 | 95.72 | 20.74 | 87.29 | |
| 9 | −11 | 59 | 22 | 46 | 5 | 94.94 | 20.88 | 86.50 | |
| 10 | −11 | 73 | 20 | 44 | −7 | 92.50 | 20.10 | 85.45 | |
| 11 | 14 | 72 | 20 | 39 | 0 | 92.00 | 20.35 | 84.76 | |
| 12 | 14 | 75 | 17 | 37 | 4 | 90.78 | 19.75 | 84.48 | |
| Scenario 2 | 13 | −7 | 66 | 31 | 60 | −6 | 95.94 | 26.27 | 81.07 |
| 14 | −7 | 66 | 29 | 60 | −1 | 95.78 | 24.37 | 83.13 | |
| 15 | −7 | 66 | 28 | 60 | −3 | 95.69 | 23.43 | 84.15 | |
| 16 | 9 | 66 | 27 | 60 | 1 | 95.53 | 22.49 | 85.10 | |
| 17 * | 9 | 65 | 26 | 59 | −2 | 94.97 | 21.54 | 85.76 | |
| 18 | −7 | 66 | 25 | 60 | 0 | 93.39 | 20.64 | 85.53 | |
| 19 | 9 | 79 | 18 | 37 | 2 | 84.06 | 20.10 | 78.69 | |
| Scenario 3 | 20 | −6 | 52 | 31 | 59 | 9 | 95.25 | 29.03 | 77.32 |
| 21 | −6 | 52 | 30 | 59 | 7 | 94.81 | 28.18 | 77.95 | |
| 22 | 8 | 52 | 30 | 59 | −10 | 94.81 | 28.18 | 77.95 | |
| 23 | 8 | 52 | 29 | 59 | −4 | 94.72 | 27.33 | 78.86 | |
| 24 * | 8 | 52 | 28 | 59 | −19 | 94.64 | 26.50 | 79.76 | |
| 25 | −6 | 52 | 27 | 59 | −17 | 91.72 | 25.67 | 78.38 | |
| 26 | −5 | 51 | 26 | 56 | −9 | 91.31 | 25.14 | 78.67 | |
| 27 | 2 | 51 | 26 | 58 | 4 | 89.02 | 24.43 | 77.65 | |
| 28 | 8 | 79 | 18 | 41 | 9 | 80.44 | 19.72 | 76.23 |
| Workspace | VP ID | X (m) | Y (m) | Z (m) | (°) | (°) | Coverage (%) | Distance (m) | F (%) |
|---|---|---|---|---|---|---|---|---|---|
| WS1 | VP1 | 51 | 39 | 11 | 30 | −1 | 100.00 | 22.30 | 87.34 |
| VP2 | 53 | 12 | 13 | 39 | 12 | 100.00 | 22.41 | 87.23 | |
| VP3 | 53 | 30 | 20 | 57 | 2 | 100.00 | 22.77 | 86.89 | |
| WS2 | VP4 | 14 | 59 | 21 | 50 | −6 | 95.72 | 20.74 | 87.29 |
| VP5 | −11 | 59 | 22 | 46 | 5 | 94.94 | 20.88 | 86.50 | |
| VP6 | −11 | 73 | 20 | 44 | −7 | 92.50 | 20.10 | 85.45 | |
| WS3 | VP7 | −12 | 41 | 23 | 48 | 1 | 90.41 | 21.49 | 82.16 |
| VP8 | 15 | 35 | 22 | 48 | 0 | 90.40 | 21.63 | 82.00 | |
| VP9 | 15 | 41 | 25 | 47 | −1 | 92.01 | 23.69 | 80.91 | |
| WS4 | VP10 | 46 | −1 | 13 | 37 | 2 | 100.00 | 21.40 | 88.77 |
| VP11 | 68 | −13 | 14 | 39 | −4 | 100.00 | 21.84 | 88.32 | |
| VP12 | 53 | −14 | 20 | 50 | 0 | 100.00 | 22.29 | 87.86 |
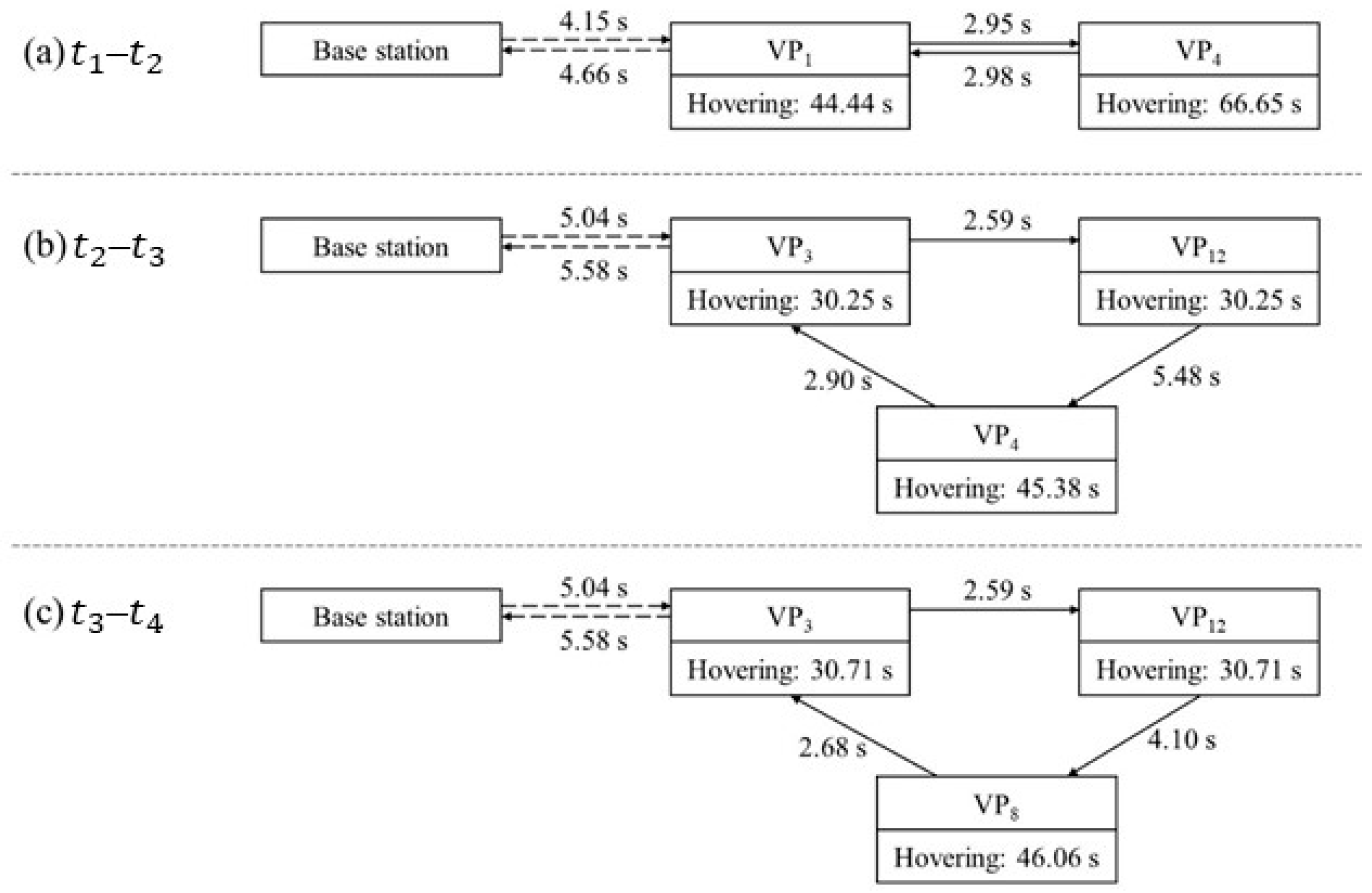
| Time Period | Path | (s) | (s) | (s) | (s) | (s) |
|---|---|---|---|---|---|---|
| VP1 –VP4 –VP1 | 4.15 | 4.66 | 5.93 | 111.09 | 117.02 | |
| VP3 –VP12 –VP4 –VP3 | 5.04 | 5.58 | 10.97 | 105.88 | 116.85 | |
| VP3 –VP12 –VP8 –VP3 | 5.04 | 5.58 | 9.37 | 107.48 | 116.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; Hammad, A. Simulation-Based Optimization of Path Planning for Camera-Equipped UAVs That Considers the Location and Time of Construction Activities. Remote Sens. 2024, 16, 2445. https://doi.org/10.3390/rs16132445
Huang Y, Hammad A. Simulation-Based Optimization of Path Planning for Camera-Equipped UAVs That Considers the Location and Time of Construction Activities. Remote Sensing. 2024; 16(13):2445. https://doi.org/10.3390/rs16132445
Chicago/Turabian StyleHuang, Yusheng, and Amin Hammad. 2024. "Simulation-Based Optimization of Path Planning for Camera-Equipped UAVs That Considers the Location and Time of Construction Activities" Remote Sensing 16, no. 13: 2445. https://doi.org/10.3390/rs16132445
APA StyleHuang, Y., & Hammad, A. (2024). Simulation-Based Optimization of Path Planning for Camera-Equipped UAVs That Considers the Location and Time of Construction Activities. Remote Sensing, 16(13), 2445. https://doi.org/10.3390/rs16132445





