Spreading Sea Clutter Suppression for High-Frequency Hybrid Sky-Surface Wave Radar Using Orthogonal Projection in Spatial–Temporal Domain
Abstract
:1. Introduction
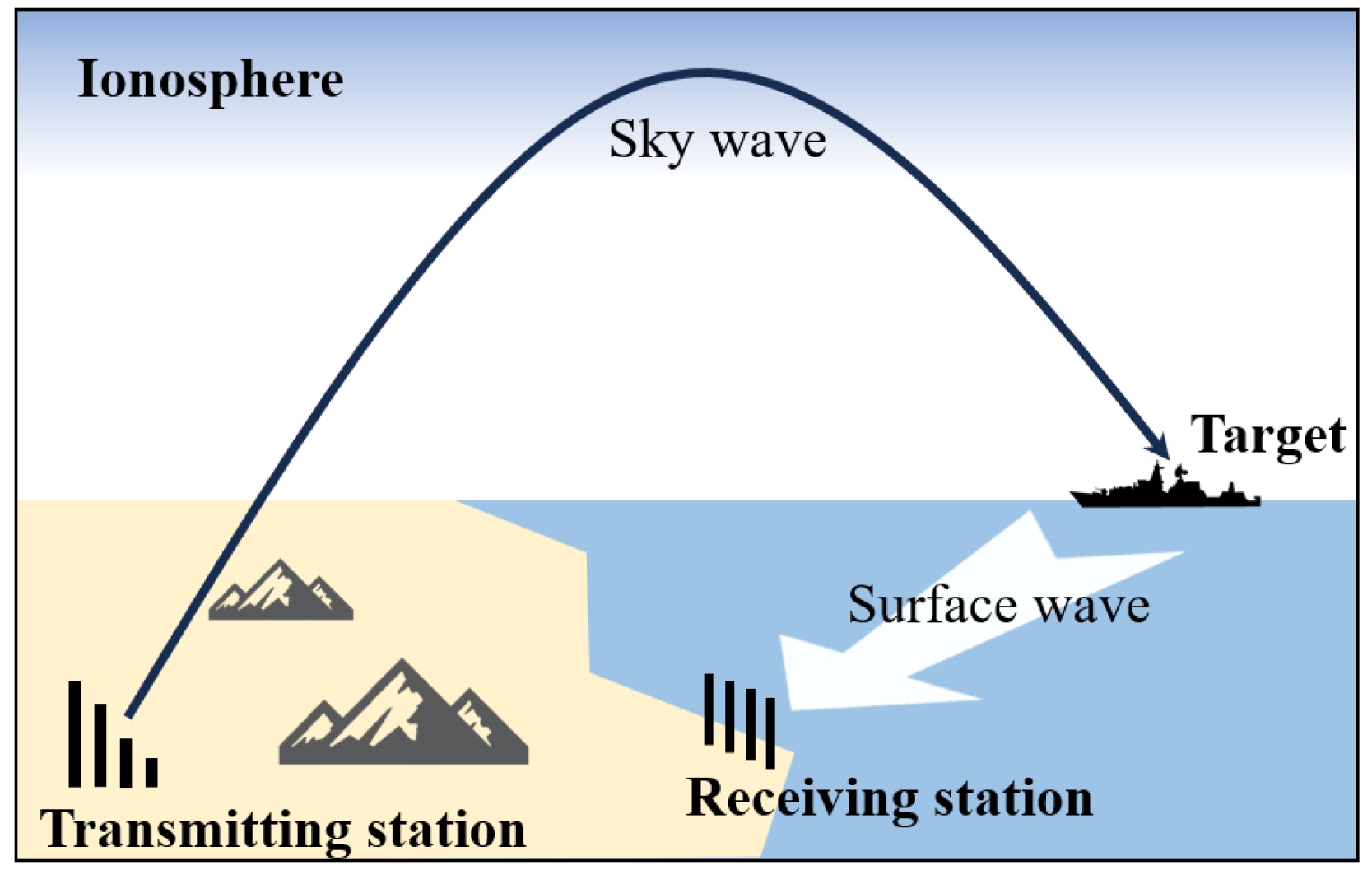
2. Model
2.1. Target Echo
2.2. Sea Clutter
2.3. Noise
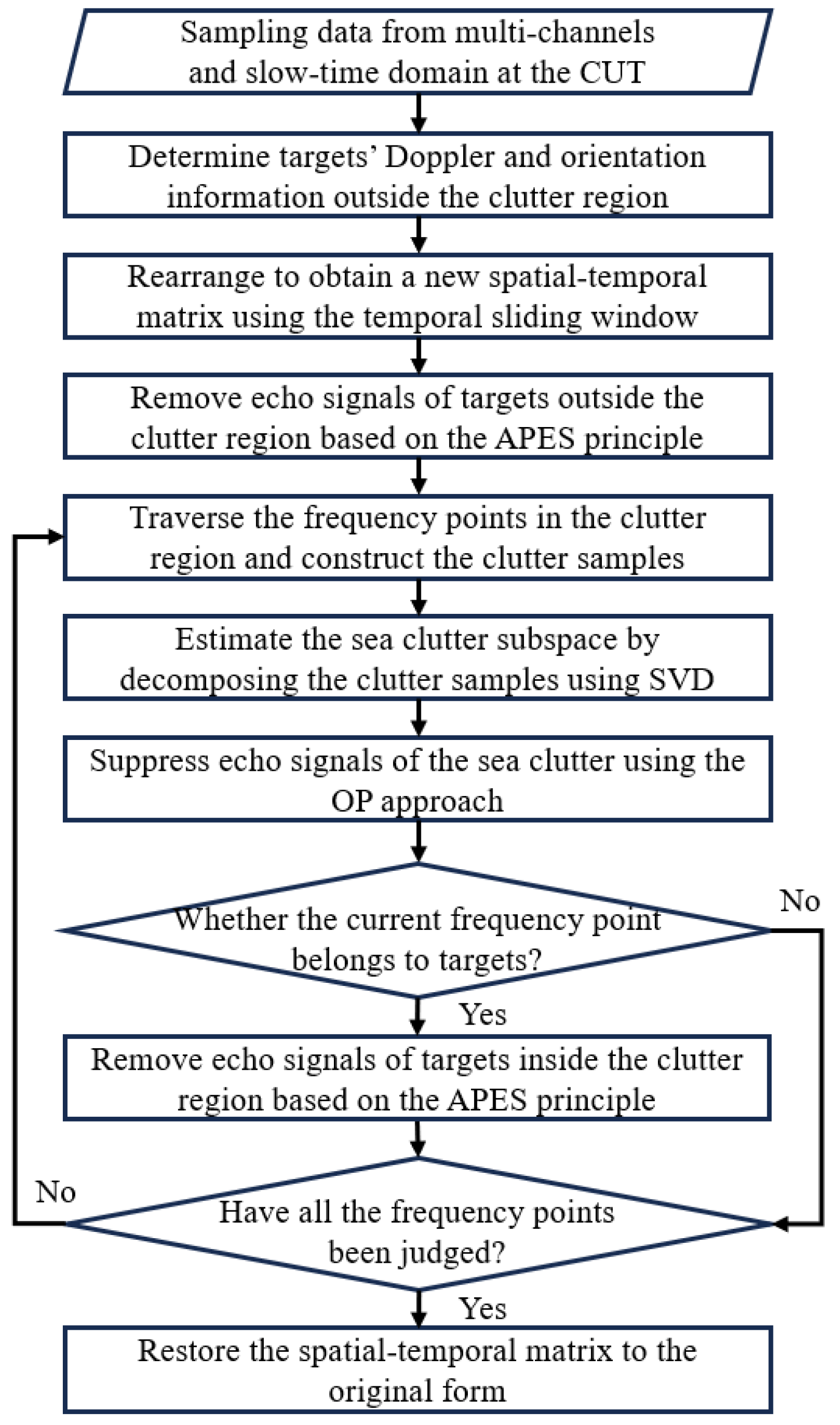
3. Methods
- Estimate the spatial–temporal spectrum (STS) using sampling data from multi-channels and slow-time domains at the CUT, divide the spectrum into clutter and non-clutter regions, and determine targets’ Doppler and orientation information outside the clutter region;
- Rearrange the data matrix from multi-channels and slow-time domains at the CUT into a new spatial–temporal matrix using the temporal sliding window and construct filters in the temporal domain to remove echo signals of targets outside the clutter region based on the APES principle;
- Traverse the frequency points in the clutter region and construct the clutter samples;
- Estimate the sea clutter subspace by decomposing the clutter samples using SVD;
- Suppress the sea clutter components by projecting the constructed spatial–temporal matrix into the orthogonal subspace concerning the sea clutter;
- Determine whether the current frequency point belongs to the target and update the clutter samples;
- Restore the spatial–temporal matrix to a matrix of multi-channels and slow-time domains at the CUT after all the frequency points in the clutter region are investigated.
3.1. Spectral Region Division
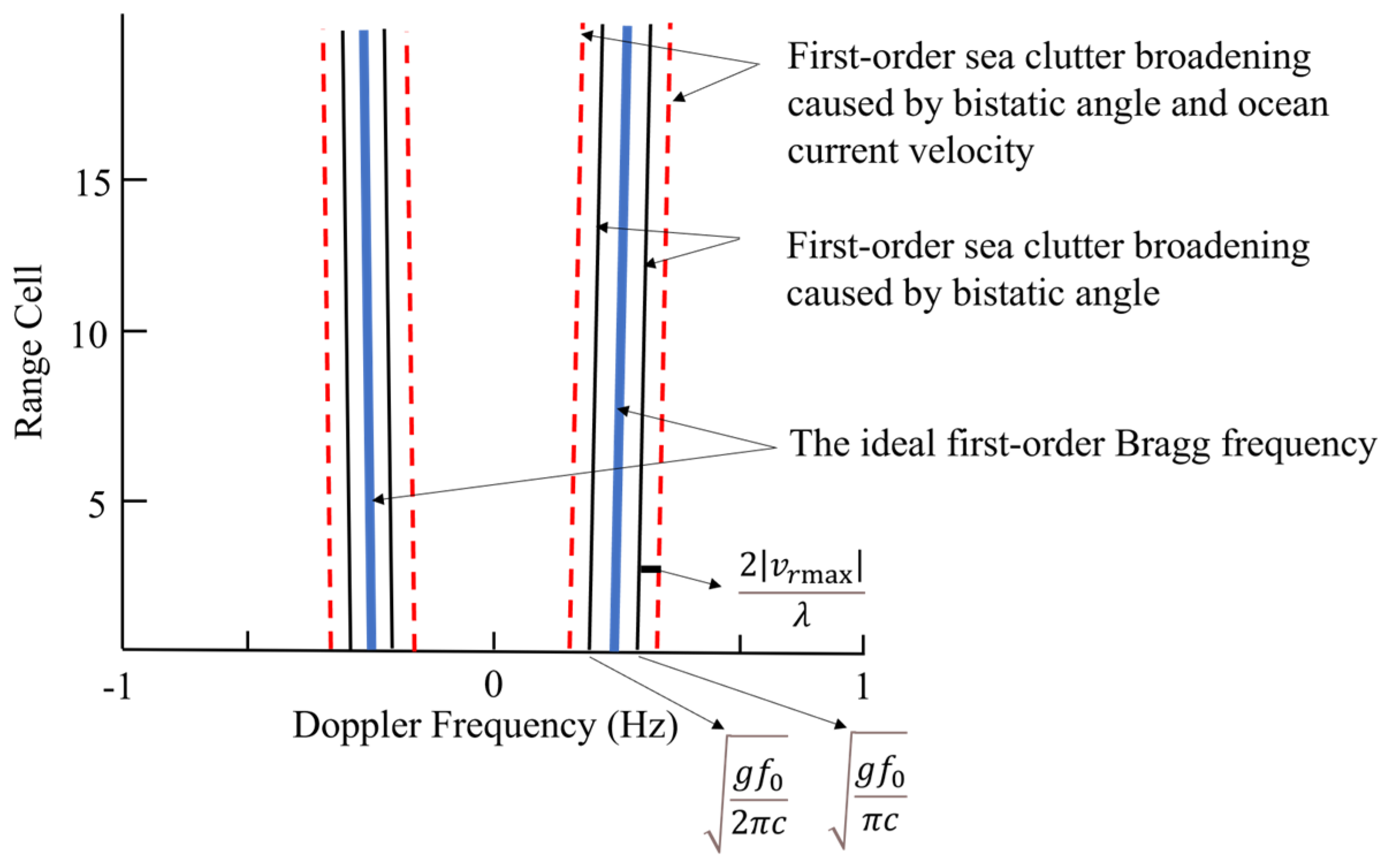
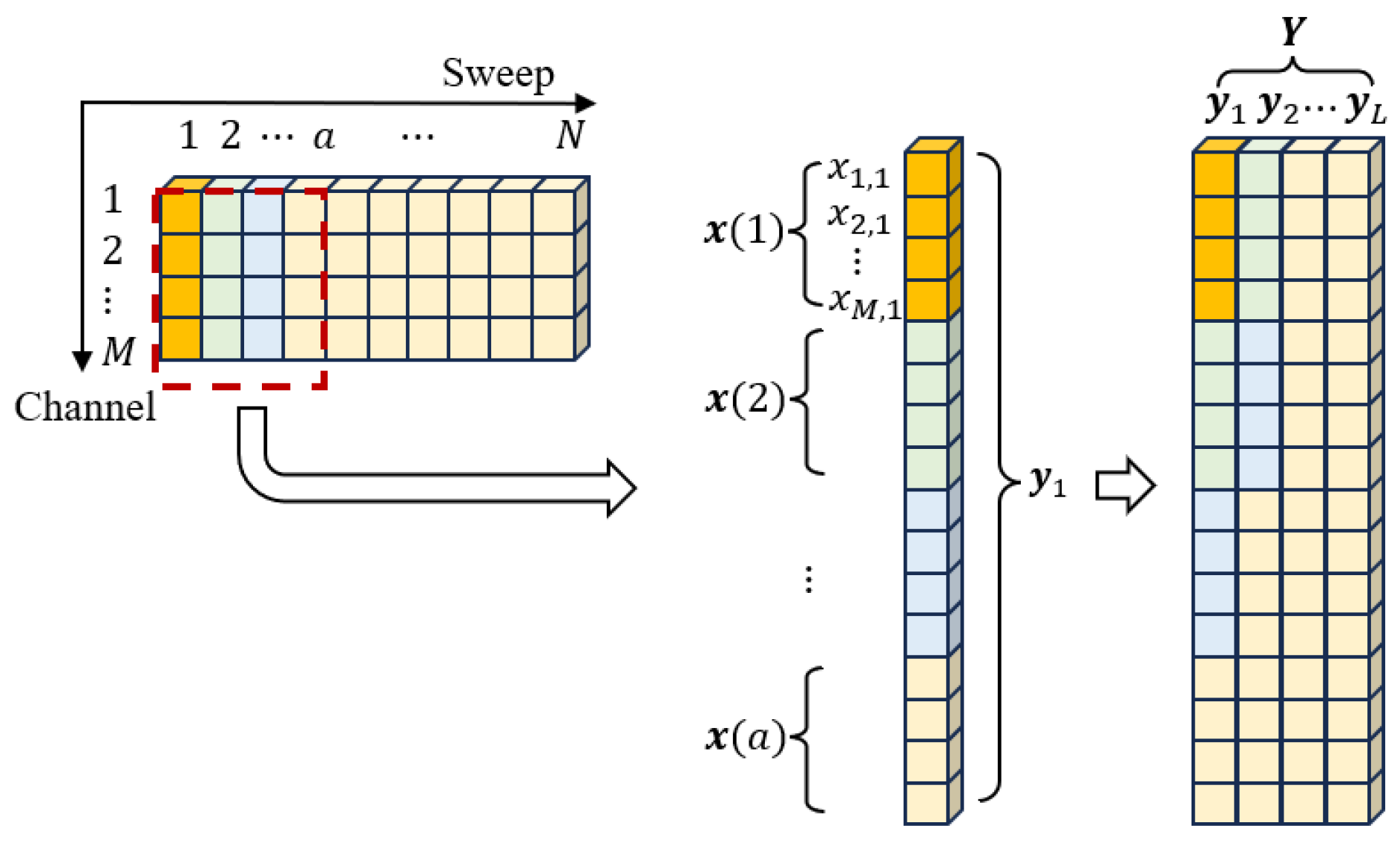
3.2. Clutter Sample Construction
3.3. Sea Clutter Suppression
4. Simulation
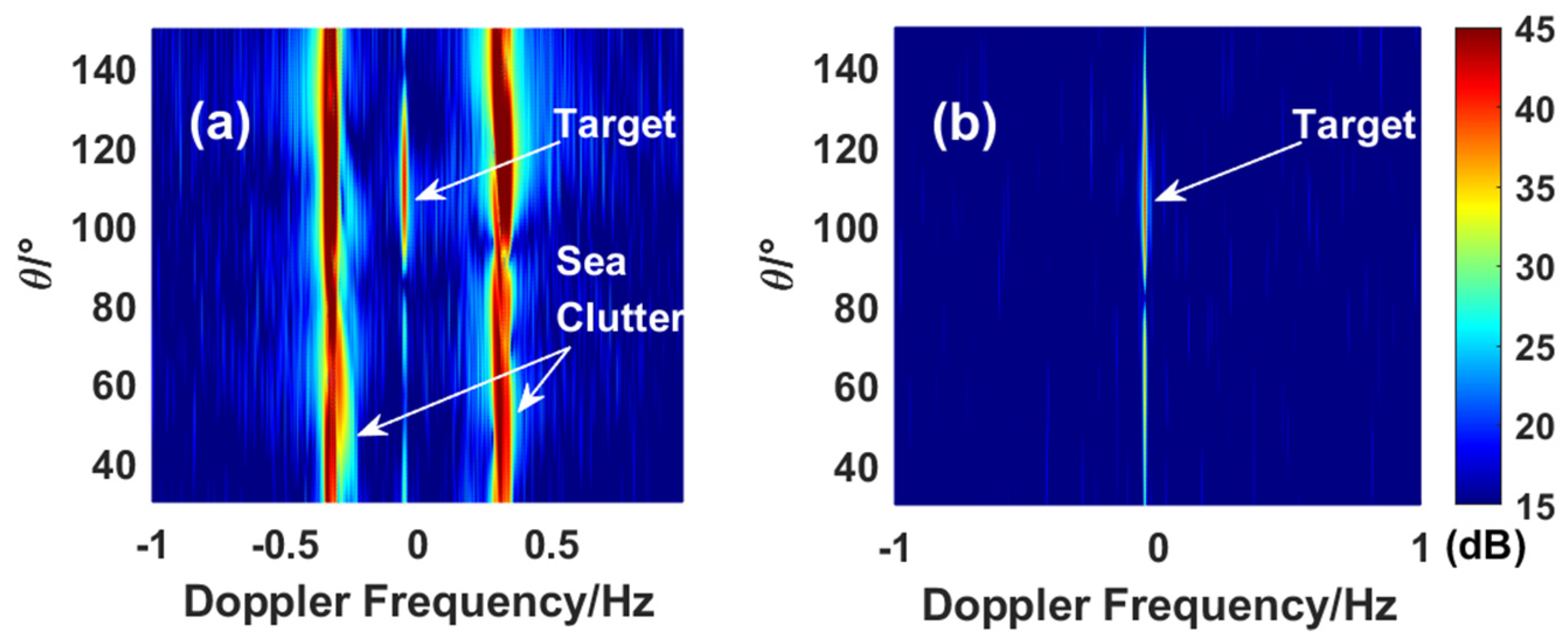
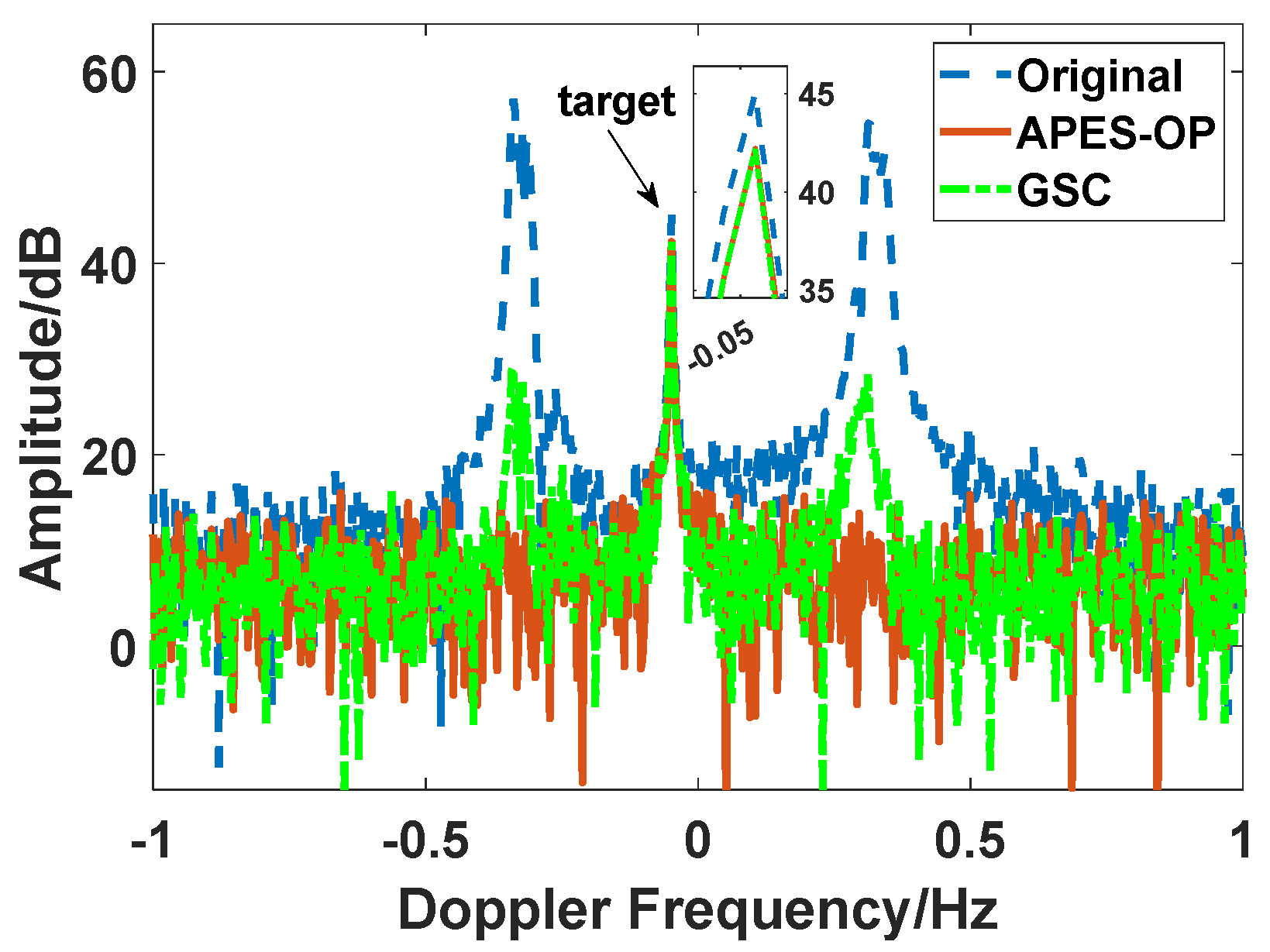
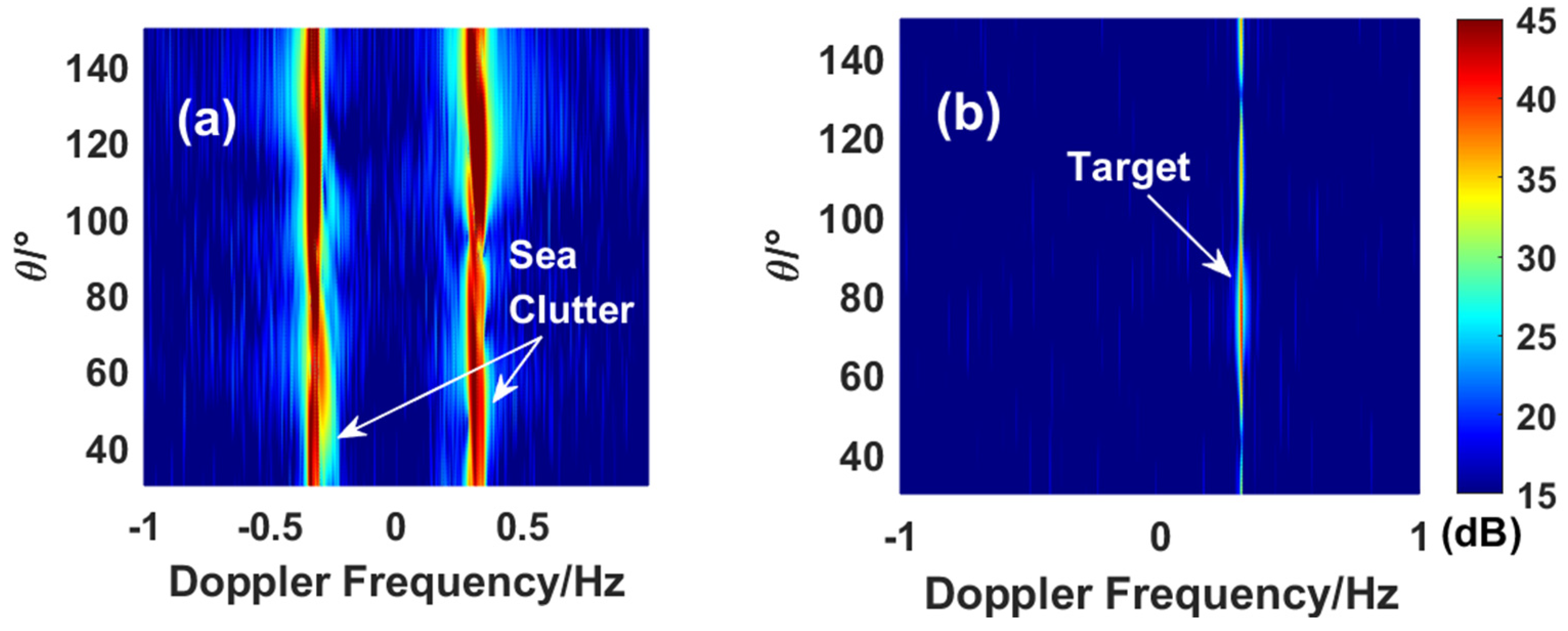
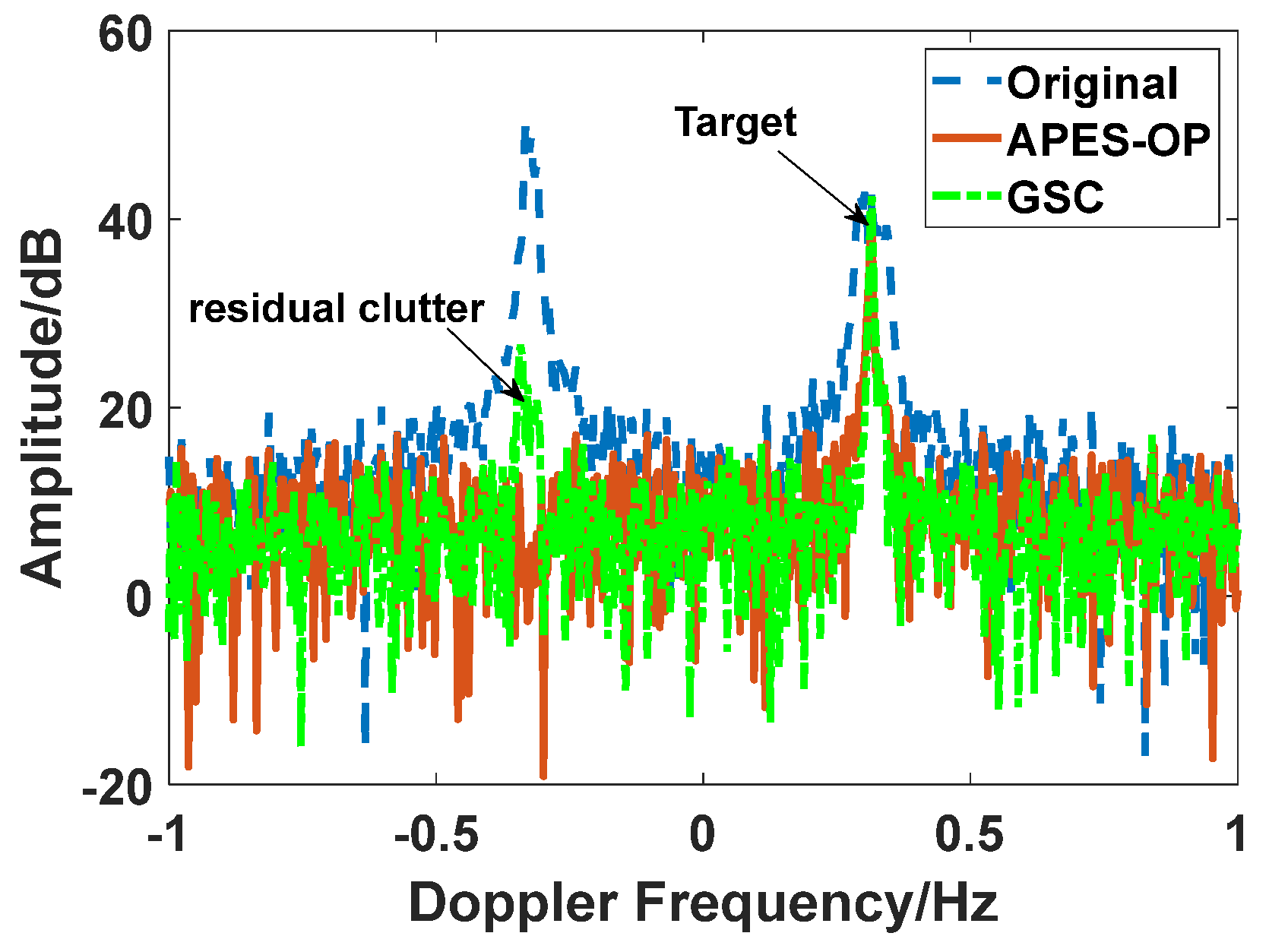
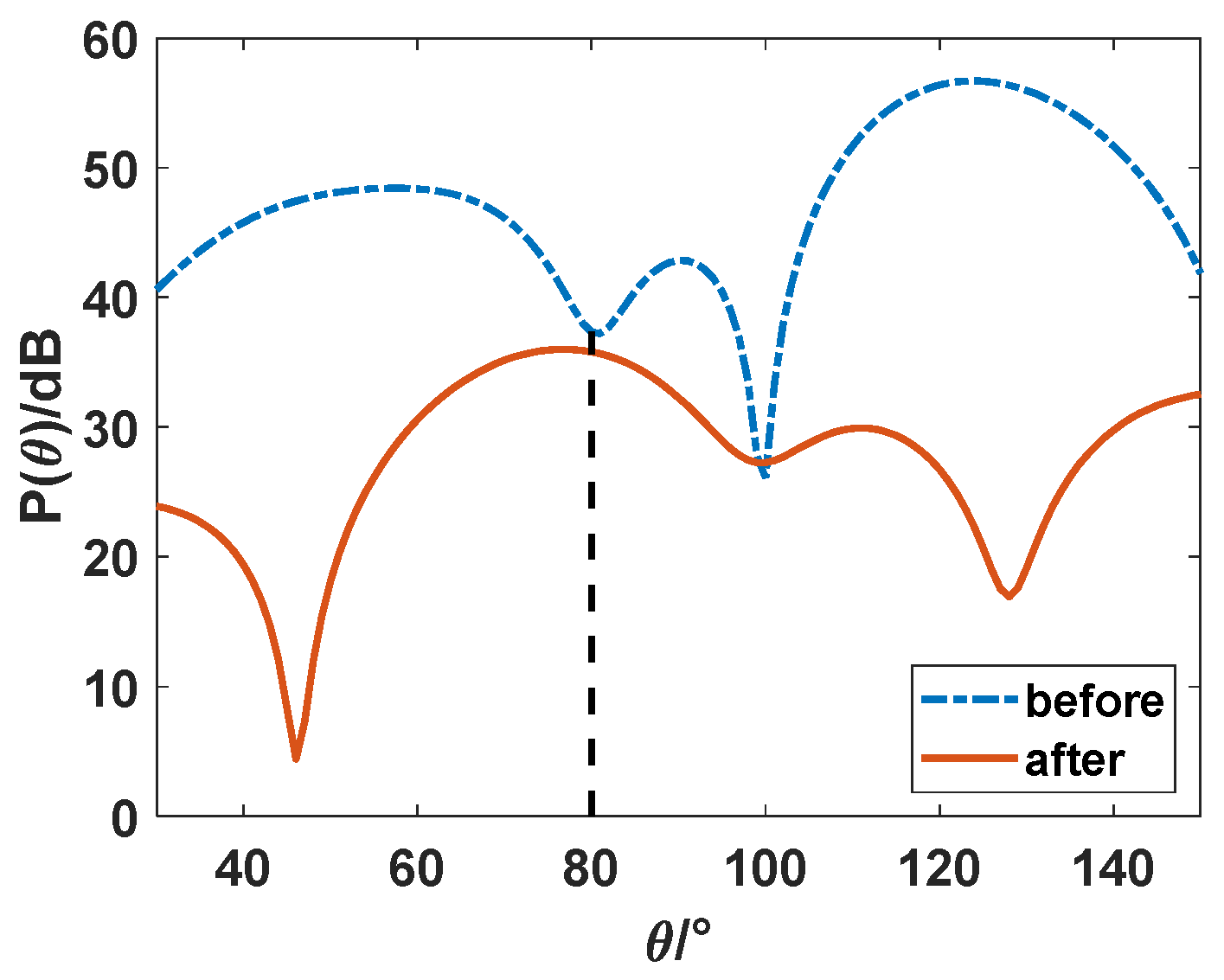
4.1. Target Outside the Clutter Region
4.2. Target Inside the Clutter Region
4.3. Target Inside the Clutter Region with Severe Ionospheric Disturbance
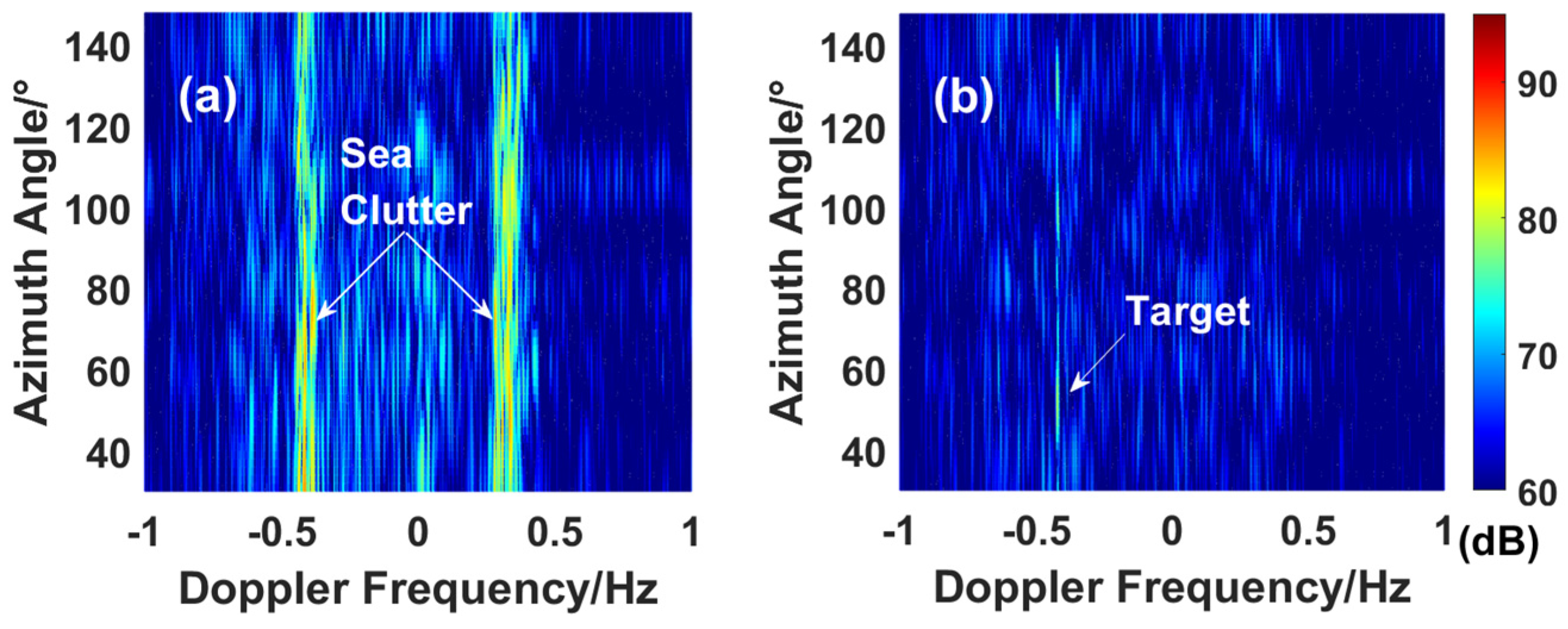
5. Experiment
5.1. System Layout
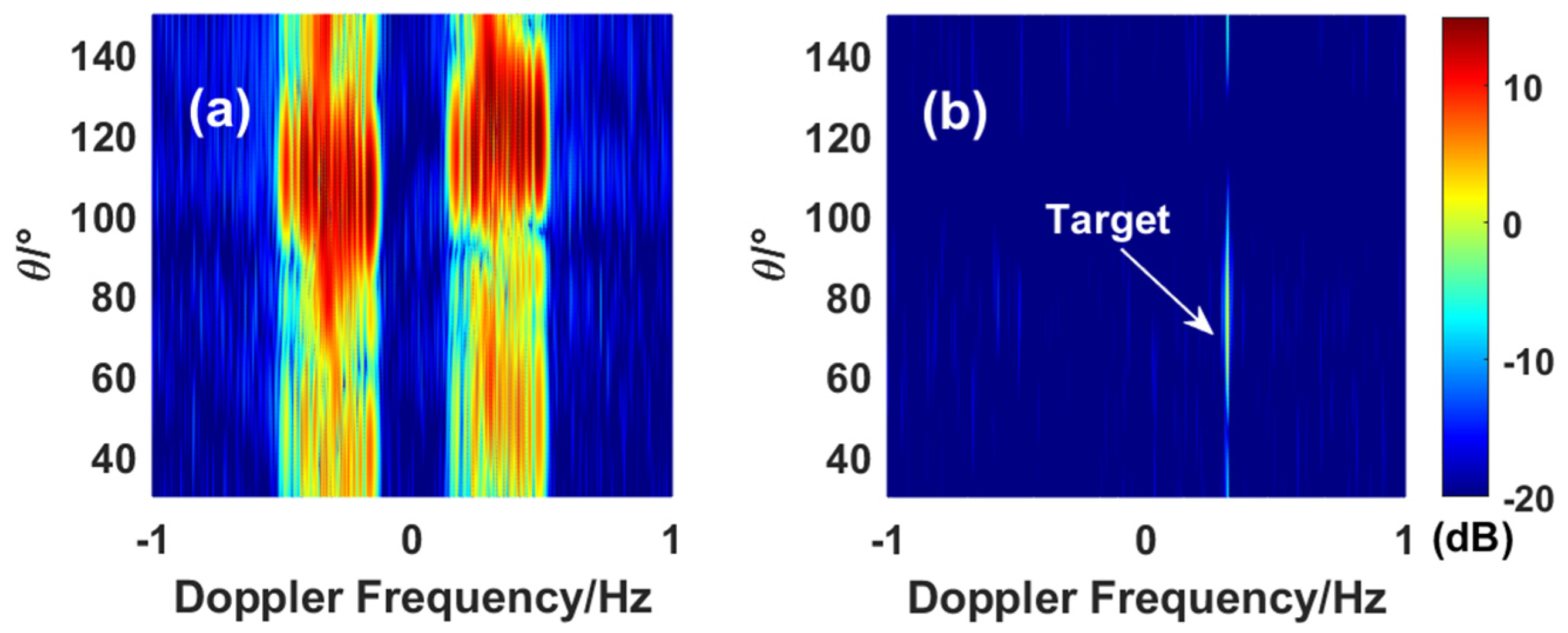
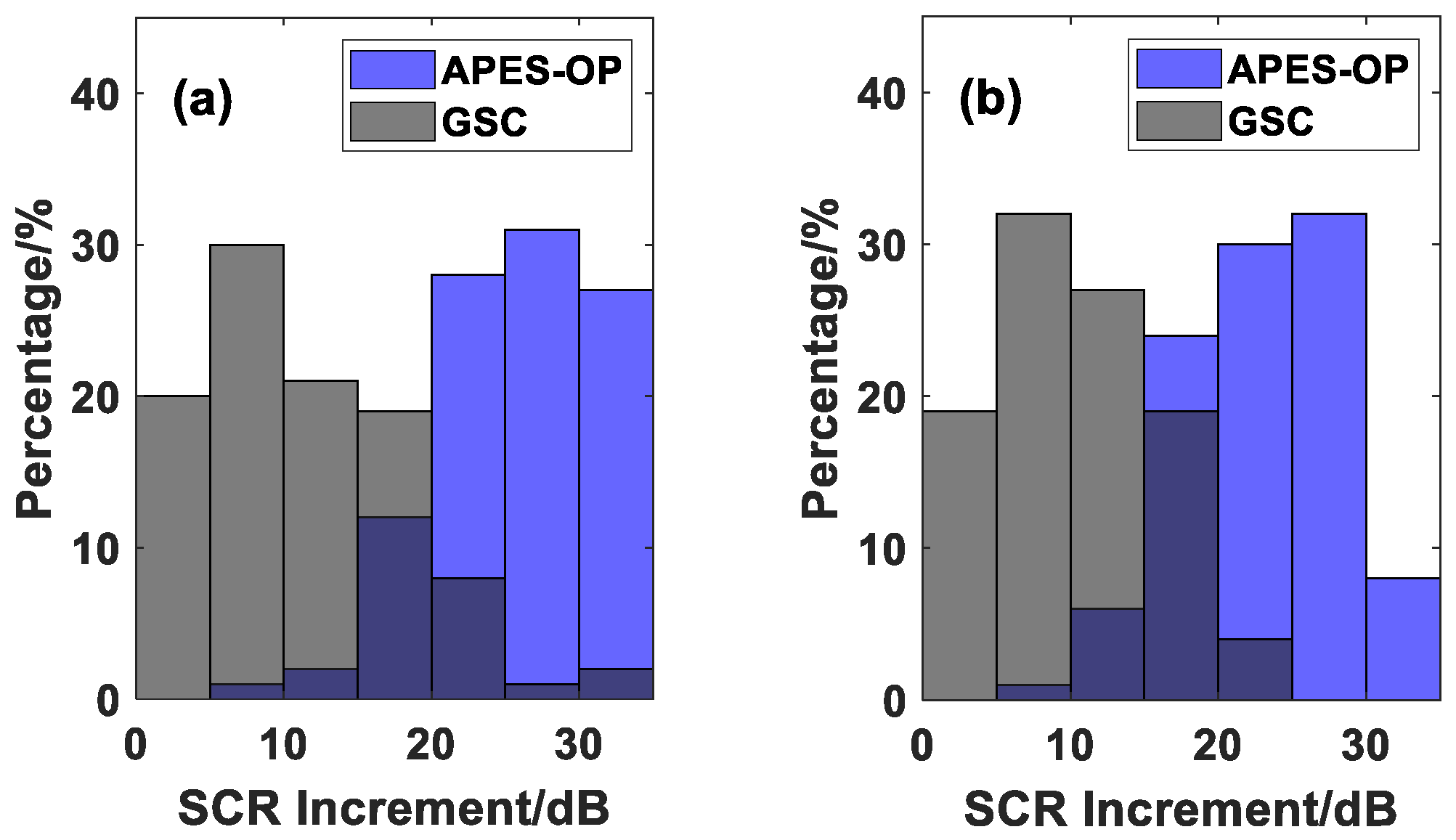
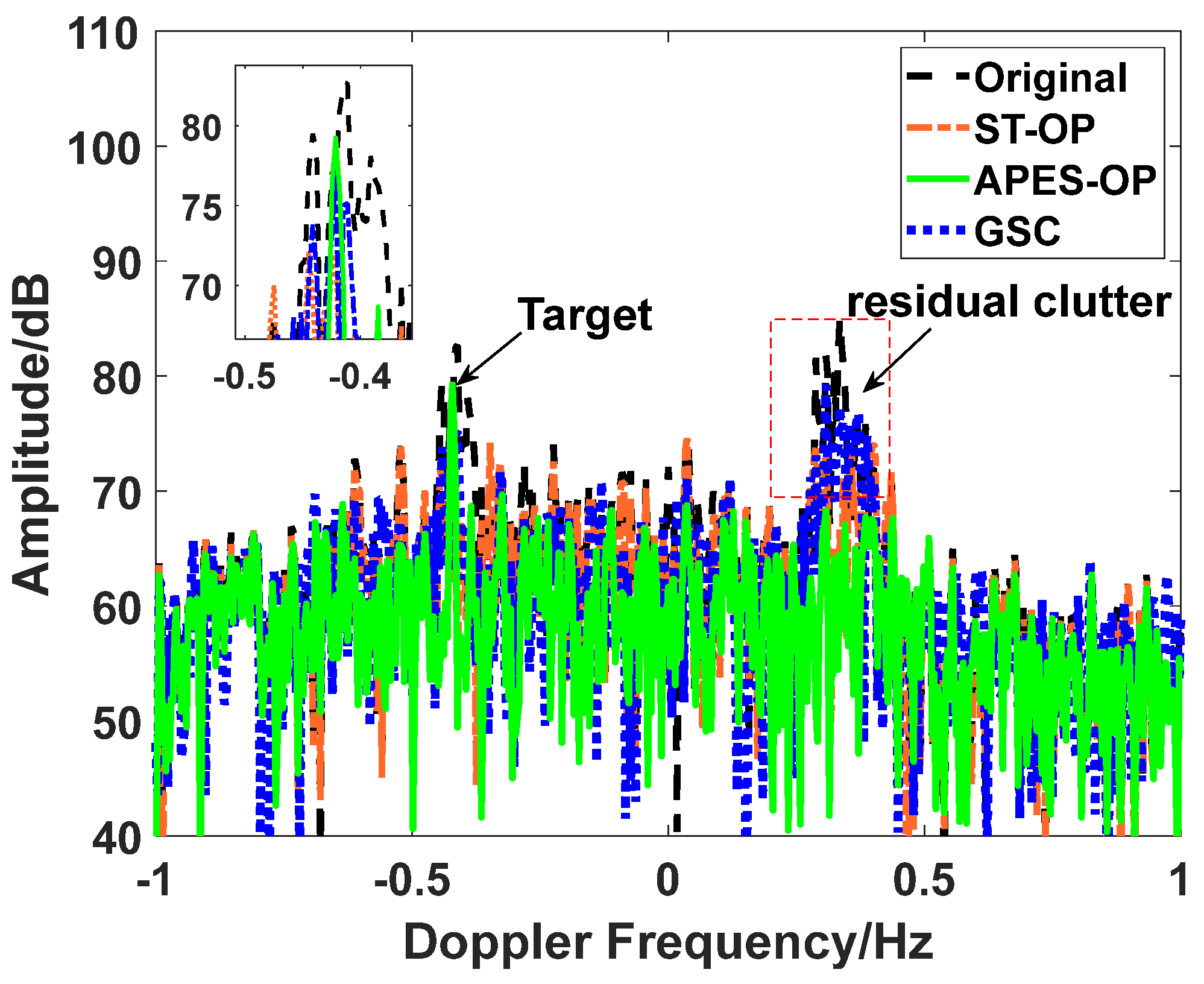
5.2. Single Target in Sea Clutter
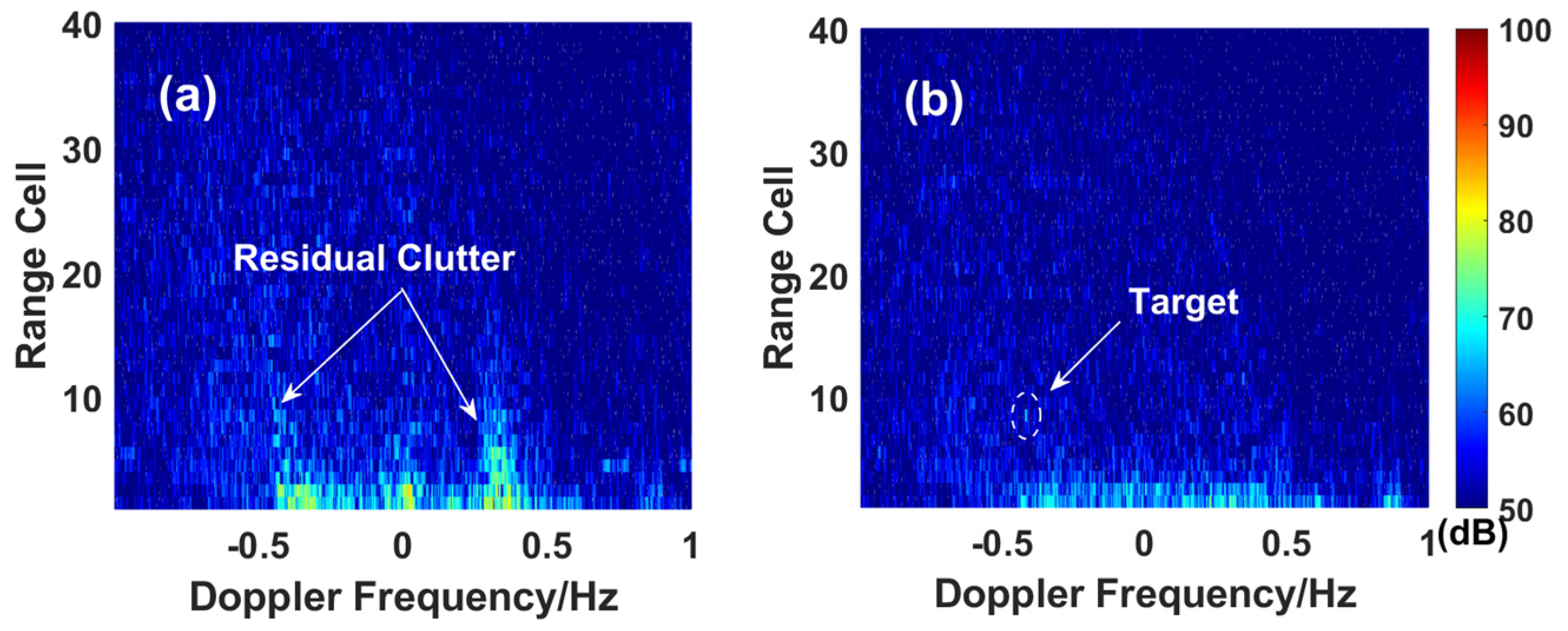
5.3. Multiple Targets in Sea Clutter
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Melyanovcky, P.A.; Turgenev, I.S. Bistatic HF radar for oceanography applications with the use of both ground and space waves. Telecommun. Radio Eng. 1997, 51, 2–3. [Google Scholar]
- Riddolls, R.J. Limits on the detection of low-Doppler targets by a high frequency hybrid sky-surface wave radar system. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 December 2008; pp. 1–4. [Google Scholar]
- Riddolls, R.J. Ship Detection Performance of a High Frequency Hybrid Sky-Surface Wave Radar; Defence R&D: Ottawa, Canada, 2007. [Google Scholar]
- Yang, L.; Fan, J.; Guo, L. Simulation analysis and experimental study on the echo characteristics of high-frequency hybrid sky–surface wave propagation mode. IEEE Trans. Antennas Propag. 2018, 66, 4821–4831. [Google Scholar] [CrossRef]
- Zhao, Z.; Wan, X.; Zhang, D. An experimental study of HF passive bistatic radar via hybrid sky-surface wave mode. IEEE Trans. Antennas Propag. 2012, 61, 415–424. [Google Scholar] [CrossRef]
- Li, M.; Zhang, L.; Wu, X. Ocean surface current extraction scheme with high-frequency distributed hybrid sky-surface wave radar system. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4678–4690. [Google Scholar] [CrossRef]
- Li, Y.; Wang, Z.; Xu, L. Spread sea clutter suppression via prior knowledge-based space time adaptive processing in high frequency hybrid sky-surface wave radar. IET Radar Sonar Nav. 2023, 17, 830–844. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Deng, W. Information geometric means-based STAP for nonhomogeneous clutter suppression in high frequency hybrid sky-surface wave radar. IEEE Sens. J. 2020, 21, 1787–1798. [Google Scholar] [CrossRef]
- Yuan, Z.; Tong, P.; Wei, Y. An augmented filtering method for shipborne HF hybrid sky-surface wave radar. In Proceedings of the International Conference on Radar Systems (RADAR 2022), Edinburgh, UK, 24–27 October 2022; pp. 488–493. [Google Scholar]
- Ji, Y.; Zhang, J.; Chu, X. Ocean surface current measurement with high-frequency hybrid sky–surface wave radar. Remote Sens. Lett. 2017, 8, 617–626. [Google Scholar] [CrossRef]
- Barrick, D. First-order theory and analysis of MF/HF/VHF scatter from the sea. IEEE Trans. Antennas Propag. 1972, 20, 2–10. [Google Scholar] [CrossRef]
- Khan, R.H. Ocean-clutter model for high-frequency radar. IEEE J. Ocean. Eng. 1991, 16, 181–188. [Google Scholar]
- Zhou, Q.; Yue, X.; Zhang, L.; Wu, X.; Wang, L. Correction of ionospheric distortion on HF hybrid sky-surface wave radar calibrated by direct wave. Radio Sci. 2019, 54, 380–396. [Google Scholar] [CrossRef]
- Li, Y.; Wei, Y.; Zhu, Y.; Guo, R.; Wang, Z.; Xu, R. Analysis and simulation for broadening first-order sea clutter spectrum in high frequency hybrid sky-surface wave propagation mode. IET Radar Sonar Nav. 2015, 9, 609–621. [Google Scholar]
- Hu, J.; Jian, C.; Li, H.; Xie, J. Knowledge-aided ocean clutter suppression method for sky-wave over-the-horizon radar. IEEE Geosci. Remote Sens. Lett. 2018, 15, 355–358. [Google Scholar] [CrossRef]
- Sekine, M. Log-Weibull distributed sea clutter. IEE Proc. F-Commun. Radar Signal Process. 1980, 3, 225–228. [Google Scholar] [CrossRef]
- Middleton, D. New physical-statistical methods and models for clutter and reverberation: The KA-distribution and related probability structures. IEEE J. Ocean. Eng. 1999, 24, 261–284. [Google Scholar] [CrossRef]
- Thayaparan, T.; Kennedy, S. Detection of a manoeuvring air target in sea-clutter using joint time–frequency analysis techniques. IEE Proc. Radar Sonar Navig. 2004, 151, 19–30. [Google Scholar] [CrossRef]
- Jangal, F.; Mandereau, F. HFSWR clutter mitigation: From wavelets to empirical mode decomposition. IEICE Proc. Ser. 2008, 35, 1–3. [Google Scholar]
- Jangal, F.; Saillant, S.; Hélier, M. Wavelet contribution to remote sensing of the sea and target detection for a high-frequency surface wave radar. IEEE Geosci. Remote Sens. Lett. 2008, 5, 552–556. [Google Scholar] [CrossRef]
- Yasotharan, A.; Thayaparan, T. Time-frequency method for detecting an accelerating target in sea clutter. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1289–1310. [Google Scholar] [CrossRef]
- Poon, M.W.Y.; Khan, R.H.; Le-Ngoc, S. A singular value decomposition (SVD) based method for suppressing ocean clutter in high frequency radar. IEEE Trans. Signal Process. 1993, 41, 1421–1425. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; He, C.; Xie, F. Using SVD-FRFT filtering to suppress first-order sea clutter in HFSWR. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1076–1080. [Google Scholar] [CrossRef]
- Lu, K.; Liu, X.; Liu, Y. Ionospheric decontamination and sea clutter suppression for HF skywave radars. IEEE J. Ocean. Eng. 2005, 30, 455–462. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Deng, W.; Guo, L.; Yang, Q. Low complexity single dataset STAP for nonstationary clutter suppression in HF mixed-mode surface wave radar. Remote Sens. Lett. 2021, 12, 1–10. [Google Scholar] [CrossRef]
- Tong, P.; Wei, Y.; Xu, R. APES based STAP for target detection in spread-Doppler clutter. In Proceedings of the 2016 IEEE 13th International Conference on Signal Processing (ICSP), Chengdu, China, 6–10 November 2016; pp. 1620–1623. [Google Scholar]
- Li, Y.; Wei, Y.; Xu, R.; Chu, T.; Wang, Z. Space-time characteristics and experimental analysis of broadening first-order sea clutter in HF hybrid sky-surface wave radar. Radioengineering 2014, 23, 831–841. [Google Scholar]
- Zhang, X.; Yang, Q.; Deng, W. Main-lobe cancellation of the space spread clutter for target detection in HFSWR. IEEE J. Sel. Top. Signal Process. 2015, 9, 1632–1638. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.; Zhao, C.; Ding, F. First-Order Sea Clutter Suppression for High-Frequency Surface Wave Radar Using Orthogonal Projection in Spatial–Temporal Domain. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Zhu, Y.; Wei, Y.; Yu, L. Ionospheric decontamination for HF hybrid sky-surface wave radar on a shipborne platform. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2162–2166. [Google Scholar] [CrossRef]
- Warrington, E.M.; Thomas, E.C.; Jones, T.B. Measurements on the wavefronts of ionospherically propagated HF radio waves made with a large aperture antenna array. IEE Proc. H Microw. Antennas Propag. IET Digit. Libr. 1990, 137, 25–30. [Google Scholar] [CrossRef]
- Fabrizio, G.A. Space-Time Characterisation and Adaptive Processing of Ionospherically-Propagated HF Signals. Ph.D. Thesis, Department of Electrical and Electronic Engineering, Adelaide, Australia, 2000. [Google Scholar]
- Stoica, P.; Li, H.; Li, J. A new derivation of the APES filter. IEEE Signal Process. Lett. 1999, 6, 205–206. [Google Scholar] [CrossRef]
- Aboutanios, E.; Mulgrew, B. A STAP algorithm for radar target detection in heterogeneous environments. In Proceedings of the IEEE/SP 13th Workshop on Statistical Signal Processing, Bordeaux, France, 17–20 July 2005; pp. 966–971. [Google Scholar]
- Degurse, J.F.; Savy, L.; Marcos, S. Reduced-rank STAP for target detection in heterogeneous environments. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1153–1162. [Google Scholar] [CrossRef]
- Walsh, J.; Gill, E.W.; Huang, W. On the development of a high-frequency radar cross section model for mixed path ionosphere–ocean propagation. IEEE Trans. Antennas Propag. 2015, 63, 2655–2664. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, L.; Li, M.; Wu, X.; Yue, X.; Yang, G. Floating-Platform High-Frequency Hybrid Sky-Surface Wave Radar: Simulations and Experiments. IEEE Trans. Antennas Propag. 2021, 70, 3112–3117. [Google Scholar] [CrossRef]
- Zhou, Q.; Tong, L.; Hong, H.; Wu, X.; Ding, C.; Zhu, X. Compensation of Ionospheric Phase Distortion in HF Hybrid Sky-Surface Wave Radar Using Piecewise Polynomial Phase Modeling Method. IEEE Trans. Geosci. Remote Sens. 2023, 62, 5100614. [Google Scholar] [CrossRef]
- Zhu, Y.; Wei, Y.; Tong, P. First order sea clutter cross section for bistatic shipborne HFSWR. J. Syst. Eng. Electron. 2017, 28, 681–689. [Google Scholar]
- Li, M.; Wu, X.; Yue, X.; Li, C.; Liu, J. A new algorithm for surface currents inversion with high-frequency over-the-horizon radar. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1303–1307. [Google Scholar] [CrossRef]
- Gorry, P.A. General least-squares smoothing and differentiation by the convolution (Savitzky-Golay) method. Anal. Chem. 1990, 62, 570–573. [Google Scholar] [CrossRef]
- Li, Y.; Yue, X.; Wu, X.; Zhang, L.; Zhou, Q.; Yi, X.; Liu, N. A higher-order singular value decomposition-based radio frequency interference mitigation method on high-frequency surface wave radar. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2770–2781. [Google Scholar] [CrossRef]
- Guo, X.; Sun, H.; Yeo, T.S. Transient interference excision in over-the-horizon radar using adaptive time-frequency analysis. IEEE Trans. Geosci. Remote Sens. 2005, 43, 722–735. [Google Scholar]
- Zhou, Q.; Zheng, H.; Wu, X.; Yue, X.; Cheng, Z.; Wang, Q. Fractional Fourier transform-based radio frequency interference suppression for high-frequency surface wave radar. Remote Sens. 2019, 12, 75. [Google Scholar] [CrossRef]
- Howland, P.E.; Cooper, D.C. Use of the Wigner-Ville distribution to compensate for ionospheric layer movement in high-frequency sky-wave radar systems. IEE Proc. F Radar Signal Process. 1993, 140, 29–36. [Google Scholar] [CrossRef]
- Buckley, K.; Griffiths, L. An adaptive generalized sidelobe canceller with derivative constraints. IEEE Trans. Antennas Propag. 1986, 34, 311–319. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Liu, J. A study on skywave-surface wave hybrid networking technique for HF oceanography radar. In Proceedings of the OCEANS 2014-TAIPEI, Taipei, Taiwan, 7–10 April 2014; pp. 1–4. [Google Scholar]


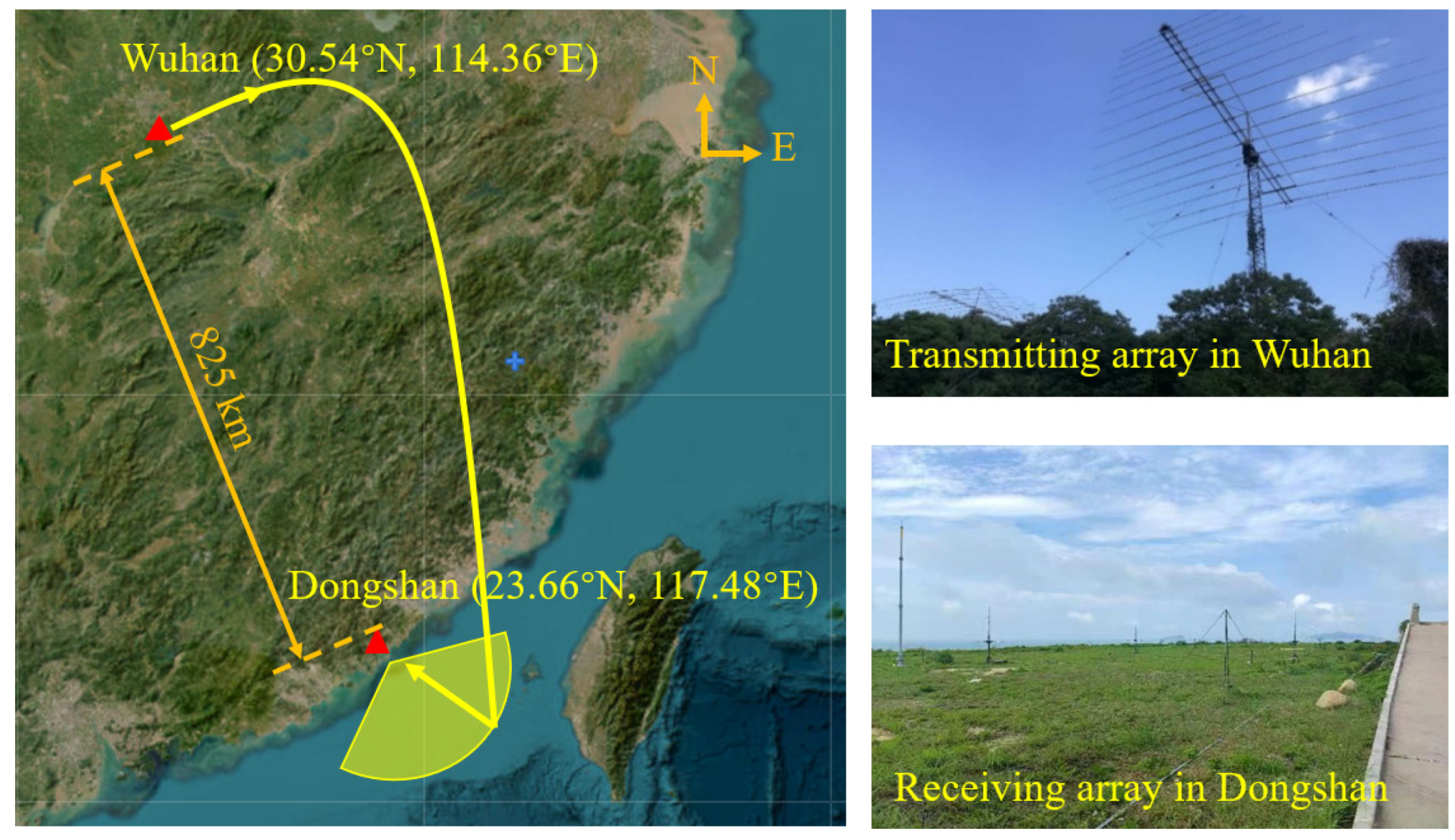




| The normal direction | 135° |
| of array | 825 km |
| Ionosphere height | 120 km |
| Wind direction | 225° |
| Wind speed | 20 knots |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Q.; Bai, Y.; Zhu, X.; Wu, X.; Hong, H.; Ding, C.; Zhao, H. Spreading Sea Clutter Suppression for High-Frequency Hybrid Sky-Surface Wave Radar Using Orthogonal Projection in Spatial–Temporal Domain. Remote Sens. 2024, 16, 2470. https://doi.org/10.3390/rs16132470
Zhou Q, Bai Y, Zhu X, Wu X, Hong H, Ding C, Zhao H. Spreading Sea Clutter Suppression for High-Frequency Hybrid Sky-Surface Wave Radar Using Orthogonal Projection in Spatial–Temporal Domain. Remote Sensing. 2024; 16(13):2470. https://doi.org/10.3390/rs16132470
Chicago/Turabian StyleZhou, Qing, Yufan Bai, Xiaohua Zhu, Xiongbin Wu, Hong Hong, Chuanwei Ding, and Heng Zhao. 2024. "Spreading Sea Clutter Suppression for High-Frequency Hybrid Sky-Surface Wave Radar Using Orthogonal Projection in Spatial–Temporal Domain" Remote Sensing 16, no. 13: 2470. https://doi.org/10.3390/rs16132470
APA StyleZhou, Q., Bai, Y., Zhu, X., Wu, X., Hong, H., Ding, C., & Zhao, H. (2024). Spreading Sea Clutter Suppression for High-Frequency Hybrid Sky-Surface Wave Radar Using Orthogonal Projection in Spatial–Temporal Domain. Remote Sensing, 16(13), 2470. https://doi.org/10.3390/rs16132470






