Improving the Estimation of Lake Ice Thickness with High-Resolution Radar Altimetry Data
Abstract
:1. Introduction
2. Lake Ice Thickness Signature in SAR Radar Echograms and Waveforms
3. Analytical Retrackers for the Estimation of LIT from High-Resolution SAR Data
3.1. SAR_LIT Waveform Model
3.2. FFSAR_LIT Waveform Model
3.3. Parameter Estimation
4. Target Lakes and Data
4.1. Target Lakes
4.2. Altimetry Data
4.2.1. High-Resolution Data
4.2.2. Low-Resolution Data
4.3. Lake Ice Model Simulations
5. Results and Discussion
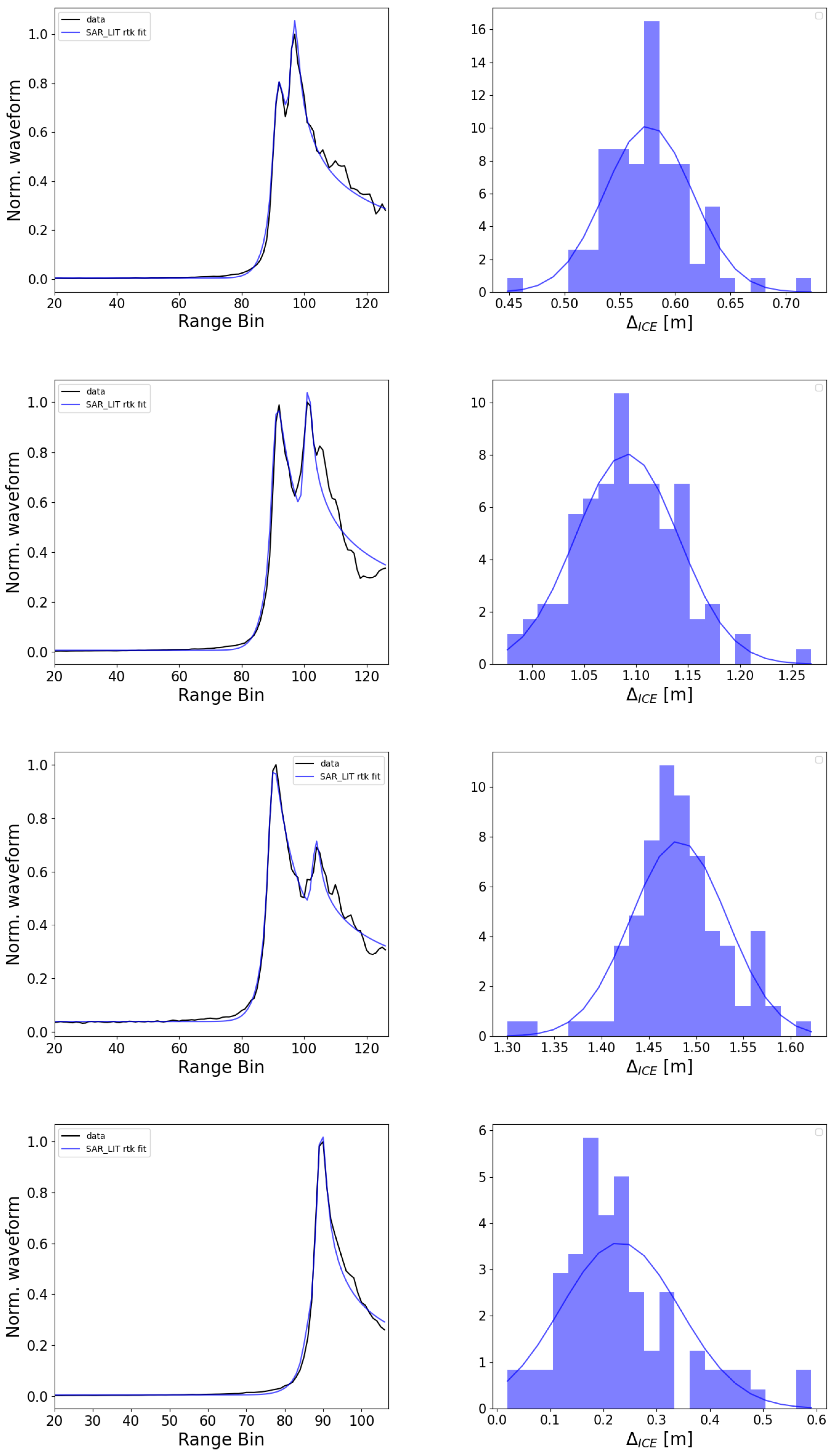
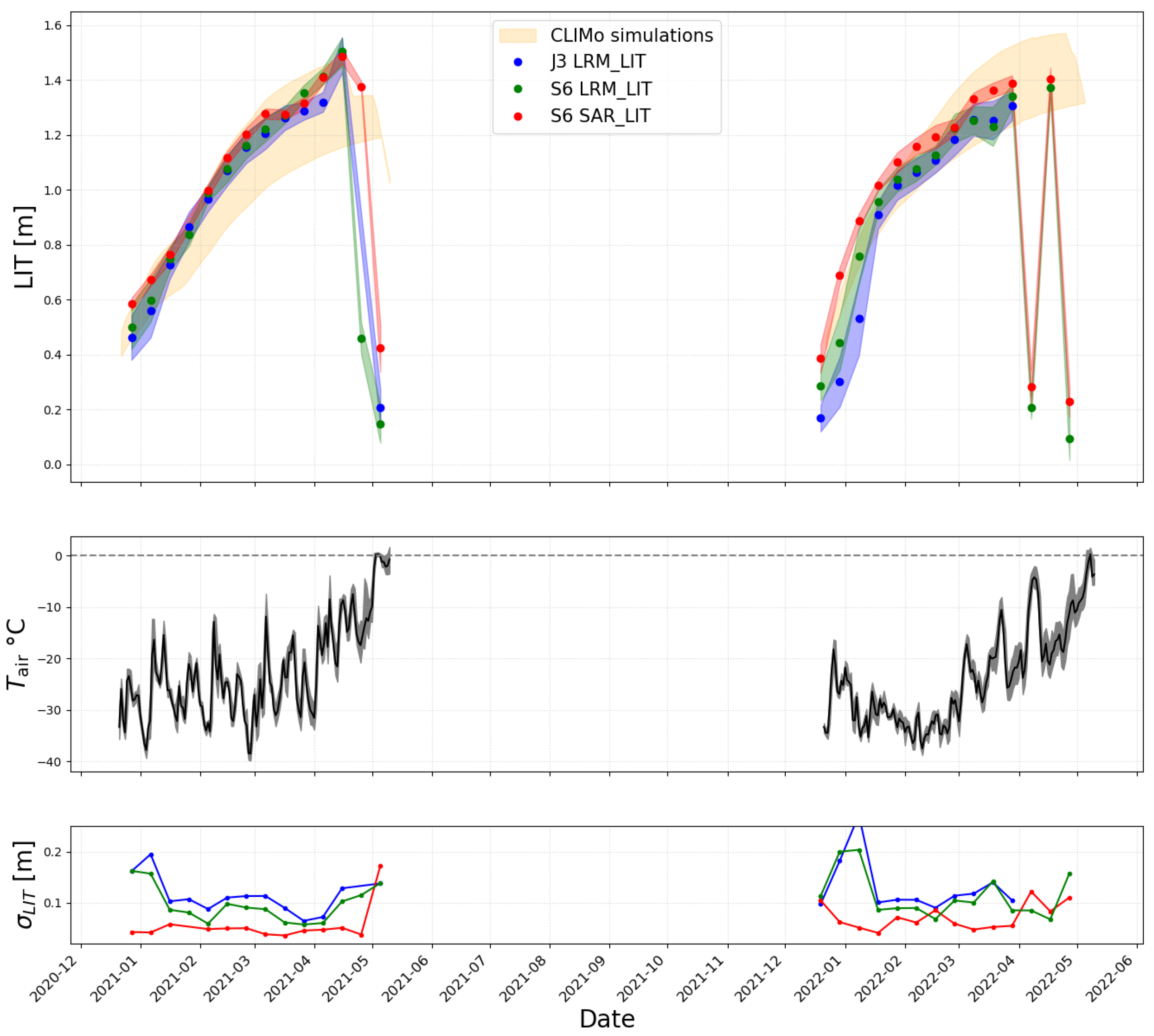
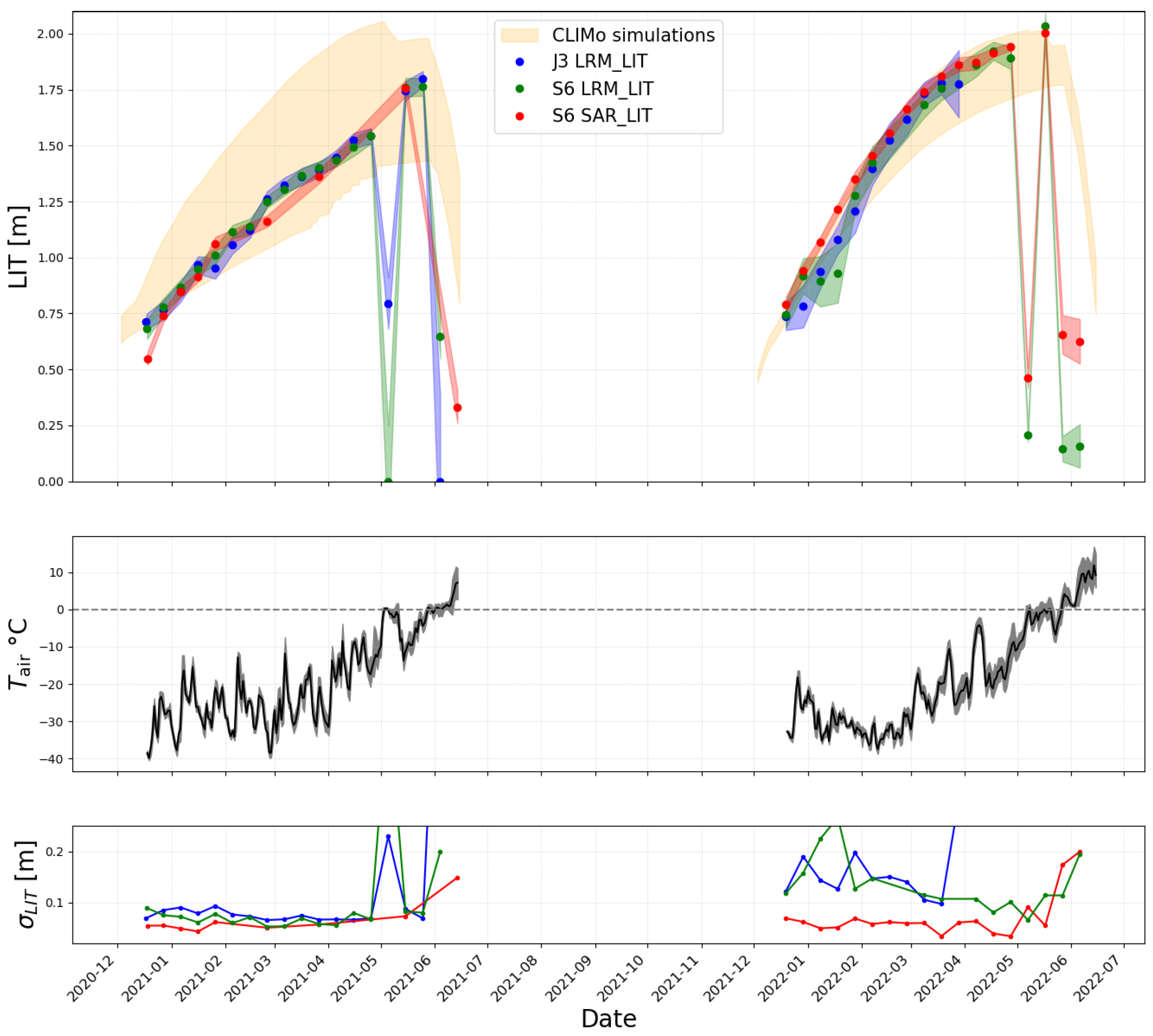
5.1. LIT Analysis of Sentinel-6 High-Resolution Data
5.2. Evaluation and Consistency
6. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Sentinel-6 System and Sensor Parameters
| Symbol | Description | Value |
|---|---|---|
| Central frequency | 13.575 GHz | |
| PTR time width | 0.8846 | |
| h | Nominal orbit height | 1347 km |
| Nominal satellite velocity | 6965 m/s | |
| Number of pulses per burst | 64 | |
| Pulse repetition frequency | 9175 Hz | |
| Half-power along track beam width | 1.33 deg | |
| Half-power across track beam width | 1.33 deg | |
| L | Total number of Doppler beams | 448 |
| B | Bandwidth | 320 MHz |
| Sampling frequency | 395 MHz |
References
- World Meteorological Organization. The 2022 GCOS ECVs Requirements (GCOS-245); World Meteorological Organization: Geneva, Switzerland, 2022; 244p. [Google Scholar]
- Ghiasi, Y.; Duguay, C.; Murfitt, J.; van der Sanden, J.; Thompson, A.; Drouin, H.; Prévost, C. Application of GNSS interferometric reflectometry for the estimation of lake ice thickness. Remote Sens. 2020, 12, 2721. [Google Scholar] [CrossRef]
- Brown, L.C.; Duguay, C.R. The fate of lake ice in the North American Arctic. Cryosphere Discuss. 2011, 5, 1775–1834. [Google Scholar] [CrossRef]
- Murfitt, J.; Duguay, C.R. 50 years of lake ice research from active microwave remote sensing: Progress and prospects. Remote Sens. Environ. 2021, 264, 112616. [Google Scholar] [CrossRef]
- Kang, K.K.; Duguay, C.R.; Howell, S.E.L.; Derksen, C.; Kelly, R. Sensitivity of AMSR-E brightness temperatures to the seasonal evolution of lake ice thickness. IEEE Geosci. Remote Sens. Lett. 2010, 7, 751–755. [Google Scholar] [CrossRef]
- Kang, K.K.; Duguay, C.; Lemmetyinen, J.; Gel, Y. Estimation of ice thickness on large northern lakes from AMSR-E brightness temperature measurements. Remote Sens. Environ. 2014, 150, 1–19. [Google Scholar] [CrossRef]
- Beckers, J.F.; Alec Casey, J.; Haas, C. Retrievals of lake ice thickness from Great Slave Lake and Great Bear Lake using CryoSat-2. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3708–3720. [Google Scholar] [CrossRef]
- Ye, H.; Jin, G.; Zhang, H.; Xiong, X.; Li, J.; Wang, J. Lake ice thickness retrieval method with ICESat-2-assisted CyroSat-2 echo peak selection. Remote Sens. 2024, 16, 546. [Google Scholar] [CrossRef]
- Shu, S.; Liu, H.; Beck, R.A.; Frappart, F.; Korhonen, J.; Xu, M.; Yang, B.; Hinkel, K.M.; Huang, Y.; Yu, B. Analysis of Sentinel-3 SAR altimetry waveform retracking algorithms for deriving temporally consistent water levels over ice-covered lakes. Remote Sens. Environ. 2020, 239, 111643. [Google Scholar] [CrossRef]
- Yang, Y.; Moore, P.; Li, Z.; Li, F. Lake level change from satellite altimetry over seasonally ice-covered lakes in the Mackenzie River Basin. IEEE Trans. Geosci. Remote Sens. 2021, 59, 8143–8152. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Huang, Q.; Zhao, F. The state and fate of lake ice thickness in the Northern Hemisphere. Sci. Bull. 2022, 67, 537–546. [Google Scholar] [CrossRef]
- Li, X.; Long, D.; Cui, Y.; Liu, T.; Lu, J.; Hamouda, M.A.; Mohamed, M.M. Ice thickness and water level estimation for ice-covered lakes with satellite altimetry waveforms and backscattering coefficients. Cryosphere 2023, 17, 349–369. [Google Scholar] [CrossRef]
- Mangilli, A.; Thibaut, P.; Duguay, C.R.; Murfitt, J. A New approach for the estimation of lake ice thickness from conventional radar altimetry. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4305515. [Google Scholar] [CrossRef]
- Raney, R. The delay/Doppler radar altimeter. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1578–1588. [Google Scholar] [CrossRef]
- Egido, A.; Smith, W.H.F. Fully focused SAR altimetry: Theory and applications. IEEE Trans. Geosci. Remote Sens. 2017, 55, 392–406. [Google Scholar] [CrossRef]
- Duguay, C.; Flato, G.; Jeffries, M.; Menard, P.; Morris, K.; Rouse, W. Ice cover variability on shallow lakes at high latitudes: Model simulations and observations. Hydrol. Process. 2003, 17, 3465–3483. [Google Scholar] [CrossRef]
- Gunn, G.; Duguay, C.; Brown, L.; King, J.; Atwood, D.; Kasurak, A. Freshwater lake ice thickness derived using surface-based X- and Ku-band FMCW scatterometers. Cold Reg. Sci. Technol. 2015, 120, 115–126. [Google Scholar] [CrossRef]
- Ray, C.; Martin-Puig, C.; Clarizia, M.P.; Ruffini, G.; Dinardo, S.; Gommenginger, C.; Benveniste, J. SAR altimeter backscattered waveform model. IEEE Trans. Geosci. Remote Sens. 2015, 53, 911–919. [Google Scholar] [CrossRef]
- Dinardo, S. Techniques and Applications for Satellite SAR Altimetry over Water, Land and Ice. Ph.D. Thesis, Technische Universität, Darmstadt, Germany, 2020. [Google Scholar] [CrossRef]
- Donlon, C.; Cullen, R.; Giulicchi, L.; Fornari, M.; Vuilleumier, P. Copernicus Sentinel-6 Michael Freilich satellite mission: Overview and preliminary in orbit results. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS, Brussels, Belgium, 11–16 July 2021; pp. 7732–7735. [Google Scholar] [CrossRef]
- Ehlers, F.; Schlembach, F.; Kleinherenbrink, M.; Slobbe, C. Validity assessment of SAMOSA retracking for fully-focused SAR altimeter waveforms. Adv. Space Res. 2023, 71, 1377–1396. [Google Scholar] [CrossRef]
- Ménard, P.; Duguay, C.R.; Flato, G.M.; Rouse, W.R. Simulation of ice phenology on Great Slave Lake, Northwest Territories, Canada. Hydrol. Process. 2002, 16, 3691–3706. [Google Scholar] [CrossRef]
- Rieu, P.; Amraoui, S.; Restano, M. SMAP (Standalone Multimission Altimetry Processor). 2021. Available online: https://github.com/cls-obsnadir-dev/SMAP-FFSAR (accessed on 24 June 2024).
- Murfitt, J.; Duguay, C.; Picard, G.; Gunn, G. Forward modelling of synthetic aperture radar backscatter from lake ice over Canadian Subarctic Lakes. Remote Sens. Environ. 2023, 286, 113424. [Google Scholar] [CrossRef]
- Surdu, C.M.; Duguay, C.R.; Brown, L.C.; Fernández Prieto, D. Response of ice cover on shallow lakes of the North Slope of Alaska to contemporary climate conditions (1950–2011): Radar remote-sensing and numerical modeling data analysis. Cryosphere 2014, 8, 167–180. [Google Scholar] [CrossRef]
- Kheyrollah Pour, H.; Duguay, C.R.; Scott, K.A.; Kang, K.K. Improvement of lake ice thickness retrieval from MODIS satellite data using a thermodynamic model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5956–5965. [Google Scholar] [CrossRef]
- Antonova, S.; Duguay, C.R.; Kääb, A.; Heim, B.; Langer, M.; Westermann, S.; Boike, J. Monitoring bedfast ice and ice phenology in lakes of the Lena River Delta using TerraSAR-X backscatter and coherence time series. Remote Sens. 2016, 8, 903. [Google Scholar] [CrossRef]
- Egido, A.; Dinardo, S.; Ray, C. The case for increasing the posting rate in delay/Doppler altimeters. Adv. Space Res. 2021, 68, 930–936. [Google Scholar] [CrossRef]
- Murfitt, J.; Duguay, C.R.; Picard, G.; Gunn, G.E. Investigating the effect of lake ice properties on multifrequency backscatter using the Snow Microwave Radiative Transfer Model. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4305623. [Google Scholar] [CrossRef]
- Kern, M.; Cullen, R.; Berruti, B.; Bouffard, J.; Casal, T.; Drinkwater, M.R.; Gabriele, A.; Lecuyot, A.; Ludwig, M.; Midthassel, R.; et al. The Copernicus Polar Ice and Snow Topography Altimeter (CRISTAL) high-priority candidate mission. Cryosphere 2020, 14, 2235–2251. [Google Scholar] [CrossRef]







| Data | [m] | [m] | MBE [m] | RMSE [m] | ||
|---|---|---|---|---|---|---|
| Great Slave Lake | S6 SAR 20 Hz | 15 April 2021 | - | - | ||
| S6 FF 140 Hz | 15 April 2021 | 0.041 | 0.045 | |||
| S6 SAR 140 Hz | 15 April 2021 | −0.028 | 0.037 | |||
| S6 LRM 20 Hz | 15 April 2021 | 0.017 | 0.033 | |||
| J3 LRM 20 Hz | 15 April 2021 | 0.04 | 0.04 | |||
| CLIMo-0 | 1.47 | 14 April 2021 | −0.07 | 0.08 | ||
| CLIMo-25 | 1.28 | 19 April 2021 | 0.10 | 0.10 | ||
| CLIMo-50 | 1.21 | 2 May 2021 | 0.20 | 0.20 | ||
| CLIMo-70 | 1.19 | 5 May 2021 | 0.23 | 0.23 | ||
| Baker Lake | S6 SAR 20 Hz | 17 May 2022 | - | - | ||
| S6 FF 140 Hz | 17 May 2022 | 0.004 | 0.036 | |||
| S6 SAR 140 Hz | 17 May 2022 | 0.014 | 0.045 | |||
| S6 LRM 20 Hz | 17 May 2022 | 0.023 | 0.032 | |||
| J3 LRM 20 Hz | - | - | 0.07 | 0.07 | ||
| CLIMo-0 | 2.05 | 07 May 2022 | −0.03 | 0.05 | ||
| CLIMo-25 | 1.88 | 14 May 2022 | 0.07 | 0.07 | ||
| CLIMo-50 | 1.82 | 27 May 2022 | 0.16 | 0.16 | ||
| CLIMo-70 | 1.77 | 27 May 2022 | 0.23 | 0.23 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mangilli, A.; Duguay, C.R.; Murfitt, J.; Moreau, T.; Amraoui, S.; Mugunthan, J.S.; Thibaut, P.; Donlon, C. Improving the Estimation of Lake Ice Thickness with High-Resolution Radar Altimetry Data. Remote Sens. 2024, 16, 2510. https://doi.org/10.3390/rs16142510
Mangilli A, Duguay CR, Murfitt J, Moreau T, Amraoui S, Mugunthan JS, Thibaut P, Donlon C. Improving the Estimation of Lake Ice Thickness with High-Resolution Radar Altimetry Data. Remote Sensing. 2024; 16(14):2510. https://doi.org/10.3390/rs16142510
Chicago/Turabian StyleMangilli, Anna, Claude R. Duguay, Justin Murfitt, Thomas Moreau, Samira Amraoui, Jaya Sree Mugunthan, Pierre Thibaut, and Craig Donlon. 2024. "Improving the Estimation of Lake Ice Thickness with High-Resolution Radar Altimetry Data" Remote Sensing 16, no. 14: 2510. https://doi.org/10.3390/rs16142510
APA StyleMangilli, A., Duguay, C. R., Murfitt, J., Moreau, T., Amraoui, S., Mugunthan, J. S., Thibaut, P., & Donlon, C. (2024). Improving the Estimation of Lake Ice Thickness with High-Resolution Radar Altimetry Data. Remote Sensing, 16(14), 2510. https://doi.org/10.3390/rs16142510









