Next Article in Journal
Assessing Forest Species Diversity in Ghana’s Tropical Forest Using PlanetScope Data
Previous Article in Journal
Three Decades of Oasis Transition and Its Driving Factors in Turpan–Hami Basin in Xinjiang, China: A Complex Network Approach
Previous Article in Special Issue
Long-Term Monitoring of Inland Water Quality Parameters Using Landsat Time-Series and Back-Propagated ANN: Assessment and Usability in a Real-Case Scenario
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 16
Issue 3
10.3390/rs16030464
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Estimation of the Biogeochemical and Physical Properties of Lakes Based on Remote Sensing and Artificial Intelligence Applications

by
Kaire Toming
1,2,*,
Hui Liu
3,
Tuuli Soomets
1,
Evelyn Uuemaa
4,
Tiina Nõges
2 and
Tiit Kutser
1
1
Estonian Marine Institute, University of Tartu, Mäealuse 14, EE-12618 Tallinn, Estonia
2
Chair of Hydrobiology and Fishery, Institute of Agricultural and Environmental Sciences, Estonian University of Life Sciences, Kreutzwaldi 5, EE-51006 Tartu, Estonia
3
Department of Forestry, Mississippi State University, Starkville, MS 39762, USA
4
Institute of Ecology and Earth Sciences, University of Tartu, Vanemuise 46, EE-51014 Tartu, Estonia
*
Author to whom correspondence should be addressed.
Remote Sens. 2024, 16(3), 464; https://doi.org/10.3390/rs16030464
Submission received: 17 December 2023 / Revised: 19 January 2024 / Accepted: 19 January 2024 / Published: 25 January 2024
(This article belongs to the Special Issue Remote Sensing and Artificial Intelligence in Inland Waters Monitoring)
Browse Figures
Versions Notes

Abstract

:
Lakes play a crucial role in the global biogeochemical cycles through the transport, storage, and transformation of different biogeochemical compounds. Their regulatory service appears to be disproportionately important relative to their small areal extent, necessitating continuous monitoring. This study leverages the potential of optical remote sensing sensors, specifically Sentinel-2 Multispectral Imagery (MSI), to monitor and predict water quality parameters in lakes. Optically active parameters, such as chlorophyll a (CHL), total suspended matter (TSM), and colored dissolved matter (CDOM), can be directly detected using optical remote sensing sensors. However, the challenge lies in detecting non-optically active substances, which lack direct spectral characteristics. The capabilities of artificial intelligence applications can be used in the identification of optically non-active compounds from remote sensing data. This study aims to employ a machine learning approach (combining the Genetic Algorithm (GA) and Extreme Gradient Boost (XGBoost)) and in situ and Sentinel-2 Multispectral Imagery data to construct inversion models for 16 physical and biogeochemical water quality parameters including CHL, CDOM, TSM, total nitrogen (TN), total phosphorus (TP), phosphate (PO4), sulphate, ammonium nitrogen, 5-day biochemical oxygen demand (BOD5), chemical oxygen demand (COD), and the biomasses of phytoplankton and cyanobacteria, pH, dissolved oxygen (O2), water temperature (WT) and transparency (SD). GA_XGBoost exhibited strong predictive capabilities and it was able to accurately predict 10 biogeochemical and 2 physical water quality parameters. Additionally, this study provides a practical demonstration of the developed inversion models, illustrating their applicability in estimating various water quality parameters simultaneously across multiple lakes on five different dates. The study highlights the need for ongoing research and refinement of machine learning methodologies in environmental monitoring, particularly in remote sensing applications for water quality assessment. Results emphasize the need for broader temporal scopes, longer-term datasets, and enhanced model selection strategies to improve the robustness and generalizability of these models. In general, the outcomes of this study provide the basis for a better understanding of the role of lakes in the biogeochemical cycle and will allow the formulation of reliable recommendations for various applications used in the studies of ecology, water quality, the climate, and the carbon cycle.

1. Introduction

There are more than 117 million lakes (>0.002 km2) on Earth [1]. They comprise only 4% of the Earth’s land surface but contain 85% of the global freshwater resource upon which society relies for drinking, agriculture, fisheries, energy, transport, recreation, and tourism [2]. Moreover, lakes offer diverse habitats, support high levels of biodiversity, provide ecosystem services [3], and play a crucial role in the global biogeochemical cycles through the transport, storage, and transformation of biogeochemical compounds [4,5,6]. They contribute to climate regulation and are recognized as valuable sentinels of global environmental change [7].
The wide ecological, environmental, and socio-economic importance of lakes demands continuous monitoring of the water quality of lakes. Therefore, the need for improved and innovative approaches and techniques to obtain the required high-quality information on biogeochemical and physical water quality parameters is continuously growing. However, traditional in situ data collection and analysis methods are labor-intensive and often expensive, leading to only a small fraction of lakes being regularly observed, typically at a single point, and providing only a snapshot in time [8,9]. It is difficult to detect spatial or temporal variations in water quality [10]. Remote sensing offers an alternative to these limitations, but it presents challenges due to the optical complexity of lake water, the lack of in situ data needed for validation, and the absence of satellite sensors specifically designed for remote sensing of lakes [11]. The available spatial, temporal, spectral, and radiometric resolutions of ocean and land surface remote sensors are often not sufficient for remote sensing of lake water quality [12,13,14,15,16,17]. The technical issues have been partly improved by the European Space Agency (ESA) with the launch of Multispectral Instruments (MSI) on board of Sentinel-2A and of Sentinel-2B. Although it was originally designed for land monitoring, Sentinel-2 MSI has proven suitable for estimating lake water quality [16,18,19,20,21]. Sentinel-2 MSI has a revisit time of two to five days and an acceptable radiometric resolution, and it allows data acquisition at 10 m, 20 m, and 60 m spatial resolutions. These capabilities enable the assessment of an unprecedented number of lakes on a global scale.
Water quality can be estimated based on different biogeochemical and physical parameters of the water. The optically active parameters of water, such as colored dissolved organic matter (CDOM), total suspended matter (TSM), and chlorophyll-a (CHL), can be directly detected using the optical remote sensing sensors, making them the most commonly used parameters in remote sensing studies and monitoring programs [22,23,24,25,26,27,28]. There are also some physical parameters of water, such as transparency (e.g., Secchi disk depth, SD) and water surface temperature (WT), that can be estimated directly from remote sensing data and have been widely used in inland water quality studies [29,30,31].
Estimating non-optically active biogeochemical and physical water quality parameters, such as dissolved organic carbon (DOC), total nitrogen (TN), total phosphorus (TP), ammonia nitrogen (NH3-N), ortho-phosphate (PO4), biochemical oxygen demand (BOD), chemical oxygen demand (COD), dissolved oxygen (O2), etc., that have no direct spectral characteristics, is much more challenging with optical remote sensing. However, the relationships between optically non-active and optically active lake water quality parameters allow the optical determination of non-active substances indirectly from remote sensing data [16,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61]. While the estimation of optically non-active parameters in water, which lack direct optical signatures and spectral characteristics, has been limited historically, pioneering studies trace back to the 1990s [14,62]. However, advancements in space science and increased computing capacity have fueled a notable and rapidly growing trend in estimating optically non-active water quality parameters through remote sensing [55,58,63,64].
Remote sensing-based water quality retrieval methods can be categorized into empirical, semi-empirical, analytical (physical), and semi-analytical methods [65,66,67,68]. Empirical techniques focus on statistical relationships between spectral bands or band combinations and observed water parameters, without considering the spectral characteristics of the water components or providing a physical justification for the association [69]. Semi-empirical approaches generate algorithms based on physical and spectral information, which are connected to the optical properties of the observed components [65,66,68]. Analytical methods use inherent and apparent optical properties to predict the reflectance of surface water and calculate the concentrations of water constituents, while semi-analytical methods employ simplified analytical models [70].
Empirical and semi-empirical approaches are usually restricted to a given location and time of calibration and they often have poor inversion precision and weak generalization in retrieving water quality parameters in optically complex waters with nonlinear relationships between the concentrations and optical signatures [71,72]. Machine learning, an application of artificial intelligence, can detect both linear and nonlinear interactions and improves the identification of complex relationships between independent and dependent variables through the model itself [72,73]. Different types of machine learning approaches, such as supervised (e.g., Decision Tree, Random Forest, Support Vector Machines, Extreme Gradient Boosting), unsupervised (e.g., K-Means Clustering), and reinforcement learning (e.g., Principal Component Analysis), have been used in previous studies of water quality remote sensing [55,72,74,75,76]. While machine learning does pose challenges, such as complex model parameters, broad generalizability, overfitting, and difficulty finding the best parameter combination through self-regulation [72,77], it is worth noting the positive aspects. For example, Extreme Gradient Boosting (XGBoost), which is known for its ensemble learning capabilities, offers distinct advantages such as the effective handling of complex relationships within the data, robustness against overfitting, and optimal performance even with limited samples [72,78]. The decision to utilize XGBoost is underpinned by its track record as one of the most successful machine learning techniques across various domains in recent years [79,80,81,82,83,84]. Notably, while widely acknowledged in broader applications, its potential in limnology, specifically in the realm of remote sensing of lakes, has been underexplored. The numerous tuning parameters in XGBoost significantly impact the model accuracy and performance, posing a challenge in manually tuning global parameters to achieve optimal results [72]. In addressing this, the Genetic Algorithm (GA), a search-based optimization method, has demonstrated success in optimizing parameter settings for machine learning models in various studies [72,85,86]. Together, XGBoost and GA form a synergistic pairing, well-suited to meet the challenges related to the remote sensing applications in lakes.
Considering all the above, this study aims to (1) use the GA_XGBoost machine learning algorithm along with in situ and Sentinel-2 MSI data to construct inversion models of 14 biogeochemical (TN, TP, PO4, sulfate (SO4), ammonium nitrogen (NH4N), 5 days BOD (BOD5), COD, CHL, CDOM, TSM, biomass of phytoplankton (FPBM), biomass of cyanobacteria (CYBM), pH, O2) and two physical (WT, SD) lake water quality parameters; and (2) provide a practical demonstration of the developed inversion models, illustrating their applicability in estimating various water quality parameters simultaneously across multiple lakes on five different dates. The results of this study will provide the basis for a better understanding of the role of lakes in the biogeochemical cycle and will facilitate reliable recommendations for various applications in the studies of ecology, water quality, the climate, and the carbon cycle. Additionally, the results will lead to the possibility to improve the cost-efficiency of lake monitoring and facilitate making detailed recommendations for decision-makers.

2. Materials and Methods

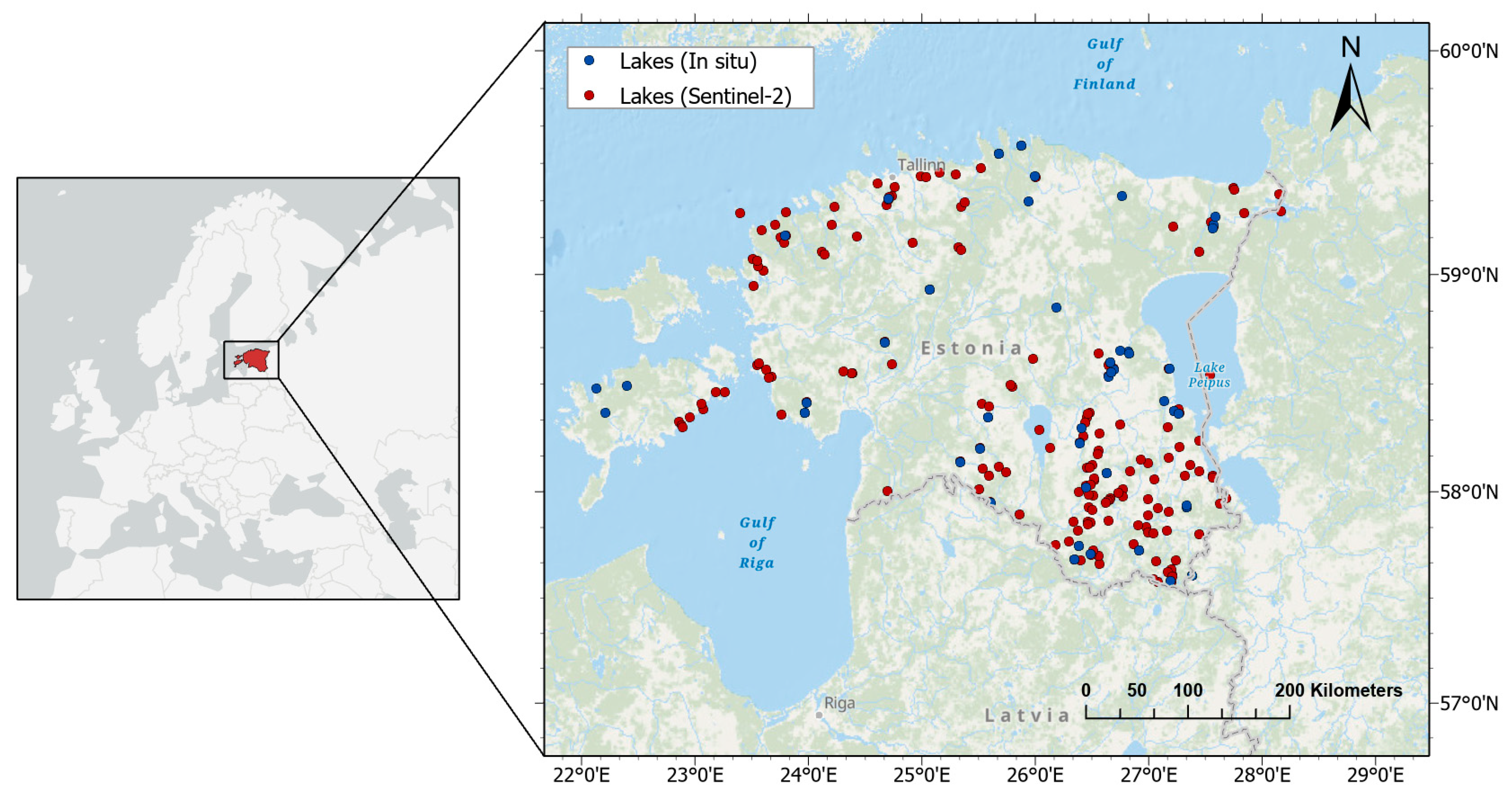
2.1. Study Sites

Biogeochemical and physical water quality parameters used as input data for the GA_XGBoost model in the current study were collected from the surface layer (0.5 m) of 45 Estonian lakes (Figure 1) from April to September in the years 2015 to 2020.
The surface areas of the in situ studied lakes are between 0.07 km2 to 27.4 km2 and the mean and the maximum depths vary from 0.3 m to 12 m, and from 1 m to 38 m, accordingly. These 45 lakes represent five different lake classes [87]: oligotrophic (3 lakes), mesotrophic (10 lakes), eutrophic/hypertrophic (25 lakes), semidystrophic/dystrophic (6 lakes), and acidotrophic (1 lake). Both soft-water and hard-water lakes were represented (see detailed information and sampling dates in Appendix A, Table A1). All lakes are included in the state monitoring program of Estonia and were sampled one to ten times during the study period. Data were collected by the Institute of Environmental and Agricultural Sciences of the Estonian University of Life Sciences and provided by the Environmental Monitoring Database (KESE) of the Estonian Environment Agency.
Based on the validated GA_XGBoost models, the biogeochemical and physical water quality parameters of 180 Estonian lakes with size >0.1 km2 (Figure 1) were retrieved from Sentinel-2 images on five different dates (19 April 2021; 10 May 2018; 18 June 2021; 18 July 2020; 17 August 2020) to demonstrate the implementation of the developed models. Although there are 354 lakes in Estonia that are larger than 0.1 km2, only 180 of them were cloudless on all five dates. An Analysis of Variance (ANOVA) test was used to analyze the differences among means of water quality parameters on different dates. Additionally, the Tukey’s Honest Significant Difference test (Tukey’s HSD), a post-hoc test based on the studentized range distribution, was employed to assess whether the biogeochemical and physical parameters on five different dates exhibited significant differences from each other.

2.2. Biogeochemical and Physical Water Quality Parameters

Most of the biogeochemical and physical parameters covered by the current study are optically non-active (13 parameters), while 3 parameters are optically active (Table 1).
The statistical information of the biogeochemical and physical water quality parameters of study lakes is summarized in the Table 2. Since the lakes with different trophic levels and different alkalinity from six different months were included in the study, a large variability of in situ data was expected. TP, PO4, NH4N, CHL, and CDOM showed the highest variability. Nevertheless, the skewness (showing the asymmetry of distribution) and kurtosis (showing whether the data are heavy-tailed or light-tailed relative to a normal distribution) values of in situ datasets remained mostly in the acceptable range (skewness was between −2 and 2 and kurtosis was between −7 and 7). However, some studied parameters were highly skewed, for example, TP, which followed log-normal distribution. In general, machine learning models (e.g., XGBoost) do not assume any normality and they also work well with non-normally distributed data. Despite this, log-transformed data were used in the case of highly skewed TP. In addition, CHL is known to be log-normally distributed, so log-transformed values are often used. Therefore, log-transformed data were also used for CHL in the current study.

2.3. Satellite Data

Copernicus Sentinel-2A and -2B MSI data were used to retrieve the biogeochemical and physical water quality parameters of lakes. The Sentinel-2 MSI is available in 13 spectral bands with different spatial resolutions. Band 1 to Band 8a were used in the current study. The spatial resolution of Band 2 (B2; central wavelength, CWL = 492.1 nm), Band 3 (B3; CWL = 559 nm), and Band 4 (B4; CWL = 665 nm) is 10 m. The spatial resolution of Band 5 (B5; CWL = 703.8 nm), Band 6 (B6; CWL = 739.1 nm), Band 7 (B7; CWL = 779.7 nm), and Band 8A (B8A; CWL = 864.80 nm) is 20 m. The spatial resolution of Band 1 (B1; CWL = 442.30 nm) is 60 m. Prior to the processing, all the Sentinel-2 images were resampled to 20 m spatial resolution. Sentinel-2 Level-1 data were processed using the ESTHub Processing Platform—Portal for Earth observation data processing (EstHub) provided by Land Board of Estonia and the Sentinel Application Platform (SNAP 8.0) and developed by Brockmann Consult (Hamburg, Germany), SkyWatch (Kitchener, UK), and C-S, Le Plessis Robinson (France). For atmospheric correction, Case 2 Regional CoastColour processor with C2X (v1.5.) neuronal nets [100] for S2 MSI (C2X) and the multisensor pixel identification tool (IdePix) were used. C2X was deliberately chosen for atmospheric correction due to its demonstrated effectiveness in previous studies, particularly in lakes with diverse optical properties within the same geographical region as in the present study [21,101]. To remove low quality or invalid pixels, following flags were used: IDEPIX_CLOUD, IDEPIX_CLOUD_AMBIGUOUS, IDEPIX_CLOUD_SURE, IDEPIX_CLOUD_BUFFER, IDEPIX_CLOUD_SHADOW, IDEPIX_COASTLINE, IDEPIX_LAND, IDEPIX_CIRRUS_SURE, IDEPIX_CIRRUS_AMBIGUOUS, IDEPIX_POTENTIAL_SHADOW, and IDEPIX_CLUSTERED_CLOUD_SHADOW.
The match-ups were extracted as the means of 3 × 3 pixels centered in the in situ sampling point. If the in situ sampling point was located too close to shoreline, the pixels of the center of the lake were extracted to minimize the adjacency effect. Match-ups were selected with up to 2 days difference between the Sentinel-2 image acquisition and the in situ measurement date. In this study, we obtained one (19 lakes), two (11 lakes), three (6 lakes), four (2 lakes), or 5–10 (6 lakes) matchups with Sentinel-2 data from April to September 2015–2020 (Appendix A, Table A1). The exact number of match-ups for each biogeochemical and physical water quality parameter is seen in Table 2.

2.4. Retrieval of Biogeochemical and Physical Water Quality Parameters

Fifteen different formulae based on 2- or 3-band or band ratios were used (Table 3). Every formula was tested with different band combinations.
A total of 3034 unique band combinations was generated. For each biogeochemical and physical water quality parameter, we initially employed all the input variables (single bands and band combinations), and then selected the best top ten inputs, and ultimately determined the optimal input combination within the top ten inputs range using a filter-based feature selection method. Subsequently, these selected combinations were employed in the GA_XGBoost model, and the best combinations for each parameter were determined based on model performance.

2.5. Extreme Gradient Boosting Model and Genetic Algorithm

The XGBoost modelling procedure starts with continuous iteration, when the tree will be added in each iteration to fit the residuals from the last fit, finally forming a robust estimator that integrates many tree models, thereby improving the model effect [72]. The predicted value in the gradient lifting regression tree is the weighted sum of the prediction results for all weak classifiers [72]. For XGBoost, each leaf node of a tree has a prediction score, i.e., the leaf weight, which is the regression value of all samples on that leaf node in that tree, and the sum of the leaf weights on all weak classifiers is the predicted value [72]. A more detailed description of XGBoost model can be found in [78].
GA was added to the XGBoost to optimize the tuning parameter selection process of the model (the model is continuously iterated until the optimal solution is reached). The GA_XGBoost algorithm successfully combines the advantages of small sample regression of XGBoost, controlling model complexity, and reducing model overfitting [72].
The parameter tuning of GA_XGBoost included the following (XGBoost Tutorials—xgboost 1.0.0-SNAPSHOT documentation [102]):
(1)
General parameters selection: Related to which booster to use for boosting. Gbtree booster that uses a tree-based model was selected;
(2)
Booster parameters:
  • Step size shrinkage used in the update to avoid overfitting (learning_rate). Range 0–1.
  • Maximum depth of a tree (max_depth). The higher the value the more complex the model and the probability of overfitting is higher. Range 0–∞.
  • Minimum sum of instance weight (hessian) required in a child (min_child_weight). The larger min_child_weight is, the more conservative the algorithm. Range 0–∞.
  • Subsample ratio of training instances (subsample). Setting it to 0.5 means that XGBoost will randomly sample half of the training data before trees grow, preventing overfitting. Subsampling occurs once in each boosting iteration. Range 0–1.
  • The subsample ratio of columns when building each tree (colsample_bytree). Subsampling is performed once for each tree constructed. Range 0–1.
(3)
Learning task parameters: specify the learning task and the consistent learning objective. Objective reg:squarederror (regression with squared loss) was applied.
Train/test/validation split was made prior to implementing the GA_XGBoost using 60% of the data for training, 20% of the data for validation, and 20% of the data for testing. The number of samples in each split varied by parameter because the initial set of samples was not the same per parameter. The training dataset was used for training the GA_XGBoost algorithm, while the test dataset was used for helping to adjust GA_XGBoost parameters to control the precision. The validation dataset was completely independent from the one that was used for testing the performance of the developed GA_XGBoost algorithm. The training, testing, and validation processes of the GA_XGBoost model were applied using the Scikit-learn Python modules and XGBoost Python package in Python 3.9.

2.6. Accuracy Evaluation

The ranking system based on different statistical metrics was used to find the best model for retrieval of the biogeochemical and physical water quality parameters from satellite data. A statistical metric, the coefficient of determination (R2), was scaled from 0 (minimum value) to 1 (maximum value) and a p-value < 0.001 was given 1, a p-value between 0.001 and 0.05 was given 0.5, and a p-value >0.05 was given 0. The root-mean-squared error (RMSE) and mean absolute percentage error (MAPE) were scaled from 0 (maximum value) to 1 (minimum value). Finally, all four values were summed and the model with the highest score was nominated as the best model for retrieval. Scikit-learn metrics module (sklearn.metrics, [103]) in Python 3.9 was used to calculate R2, RMSE, and MAPE. R2 denotes the squared correlation between the measured and predicted values.
With R2, a p-value was calculated. RMSE denotes the mean difference between the measured and predicted values. RMSE is calculated using Equation (1).
R M S E = 1 n ∑ i = 1 n y ^ i − y i 2
where y ^ i is the predicted value, y i is the measured value, and n is the number of measurements. MAPE denotes the mean absolute percentage error from the measured value and the predicted values divided by the measured value. MAPE is calculated using Equation (2).
M A P E = 100 % n ∑ i = 1 n y i − y ^ i y i
where y ^ i is the predicted value, y i is the measured value, and n is the number of measurements.

3. Results

3.1. Correlations between Optically Active and Optically Non-Active Parameters

Almost all the optically non-active parameters covered by the current study showed a statistically significant correlation (p-value < 0.05) with at least one of the optically active parameters (Figure 2). There were statistically significant positive correlations between CHL and TN, TP, BOD5, COD, FPBM, and CYBM. The same optically non-active water quality parameters gave negative correlations with SD. CDOM was positively correlated with TN, TP, PO4, NH4N, and COD, and was negatively correlated with pH. TSM showed positive correlations with SO4 and pH, and negative correlations with TP, PO4, and COD. O2 was the only parameter that did not show a statistically significant correlation with any optically active parameters. However, O2 was correlated with pH and BOD5, which correlated strongly with CDOM and CHL, respectively (Figure 2).
Given that various optically active substances exert an influence on different segments of the reflectance spectrum, the approach to non-optical substances involves seeking connections with the spectral regions affected by the correlated optical substances. Simultaneously, non-active substances are often associated with multiple optically active parameters. Therefore, our approach involved a thorough examination across various spectral bands to elucidate the rationale behind retrieving non-optically active parameter values through remote sensing methods.

3.2. Reflectance Spectra of Sentinel-2 MSI

The spectral characteristics of optically active substances varied among lakes with different trophic statuses, reflecting differences in their concentration and composition (Figure 3). Commonly, the mean reflectance spectra of oligotrophic lakes showed high values at shorter wavelengths and low values in the red part of the spectra. The mean reflectance spectra of mesotrophic and eutrophic lakes with turbid and productive waters showed typical peaks around 560 and 700–710 nm. The peak near 700–710 nm indicated a very high biomass in the water. Acidotrophic and dystrophic lakes were brown in color and were found mainly in forest and peatland areas. Their typical reflectance spectra were very similar and are combined into one class in Figure 3. In lakes with brown water, the water-leaving signal is usually very low in most parts of the spectrum due to a very high concentration of CDOM. However, the reflectance increased towards red wavelengths as CDOM absorption decreased exponentially with the increasing wavelength. As mentioned above, C2X was intentionally selected for atmospheric correction based on its established efficacy in prior studies, specifically in lakes exhibiting diverse optical properties within the identical geographical region as the current study [21,101], and the consistency of the reflectance spectra with the expected shapes reaffirms the reliability and robust performance of C2X, substantiating its effective application in waters characterized by diverse optical properties.

3.3. GA_XGBoost Model Performance and Evaluation

The best combinations of the two- or three-band or band ratio algorithms that outperformed other combinations from a total of 3034 algorithms were used in the GA_XGBoost model as an input variable (x) to predict one of the water quality parameters (y) (Table 4). Band 4 (665 nm) was used most frequently in the two or three bands or band ratio algorithms of the best models, followed by bands 2 (490 nm), 3 (560 nm), 5 (705 nm), and 6 (740 nm). Bands 1 (443 nm), 7 (783 nm) and 8a (865 nm) appeared somewhat less frequently. This was not surprising as the water leaving signal in the blue band (B1) was often negligible in our lakes due to the high concentration of CDOM and phytoplankton, both of which absorb blue light strongly. The water-leaving signal in NIR (Bands 7 and 8a) is usually negligible in aquatic environments due to the very high absorption of light by water molecules at those wavelengths. However, a very high biomass of phytoplankton (bloom) or a very high concentration of mineral particles results in non-negligible water reflectance in NIR [104,105,106]. The studied lakes usually did not have very high concentrations of mineral particles, while the high biomass was seen also in the 705 nm (B5) peak in the reflectance spectra of many lakes.
The scatter plots of training, test, and validation datasets produced using the best GA_XGBoost_model for deriving biogeochemical and physical water quality parameters from Sentinel-2 are shown in Figure 4. The performance metrics of the best GA_XGBoost models of different water quality parameters (Table 5) showed that the MAPE and RMSE increased and R2 decreased from the training stage to the testing stage (e.g., TN, SO4, O2, WT, COD, and SD). The change was generally smaller and rather minor when moving from the testing phase to the validation phase, with some exceptions (TP, TN, PO4, NH4, and SO4). Overall, GA_XGBoost models for optically active substances and parameters highly correlated with them (BOD5, FPBM, CYBM) performed significantly better than other models and showed high accuracy (R2 between 0.79 and 0.92). However, the MAPE exceeded the acceptable range (>50%) in the case of FPBM, CYBM, SO4, and NH4N. This was in contrast to TP, TN, PO4, O2, pH, WT, COD and SD, for which models had a somewhat lower R2, but MAPE remained <50%. The MAPE values for FPBM, CYBM, SO4, and NH4N surpassed the acceptable range, rendering it challenging to achieve accurate retrievals of the corresponding water quality parameters using these models. Thus, GA_XGBoost was able to predict 12 biogeochemical and physical water quality parameters with acceptable accuracy (TN, TP, PO4, BOD5, COD, CHL, CDOM, TSM, pH, O2, WT, SD). These 12 GA_XGBoost models were used to retrieve the biogeochemical and physical water quality parameters of 180 Estonian lakes >0.1 km2 from Sentinel-2 images simultaneously on five different dates (19 April 2021; 10 May 2018; 18 June 2021; 18 July 2020; 17 August 2020) to provide a practical demonstration of the developed inversion models.

3.4. A Practical Demonstration of the Developed Inversion Models

To demonstrate the practical utility of the developed models, the GA_XGBoost algorithms were employed to map biogeochemical and physical water quality parameters across 180 lakes on five distinct dates. We considered it important to choose dates when as many lakes as possible were cloud-free. Therefore, dates from different years are presented (Figure 5). However, we tried to ensure that all months from April to August were represented, regardless of the specific year. Furthermore, the aim was not to examine all 180 lakes in depth, but rather to provide a general demonstration of the developed models’ practical applicability.
In general, statistically significant differences were found between the mean values of biogeochemical and physical water quality parameters at different dates (ANOVA, p-value < 0.05). TP, TN, PO4, CHL, and CDOM were the highest on 19 April 2021 (0.05 mg/L, 0.98 mg/L, 0.011 mg/L, 12.9 µg/L, and 12.4 mg/L, respectively), and decreased in other months (Figure 5). The mean PO4 was significantly different from other dates on 19 April 2021 (Tukey’s HSD, p-value < 0.05), and the mean values of CDOM on 19 April 2021 and 10 May 2018 were significantly different from 18 July 2020 and 17 August 2020 (Tukey’s HSD, p-value < 0.05). The mean concentrations of TP, TN, TSM, and CHL differed most significantly on all five dates (Tukey’s HSD, p-value < 0.05). CHL reached its lowest values on 18 June 2021 (mean, 5.97 µg/L), TN and CDOM reached their lowest values on 18 July 2020 (the mean values were 0.76 mg/L and 8.74 mg/L, respectively), and TP and PO4 reached their lowest values on 17 August 2020 (the mean values were 0.02 mg/L and 0.007 mg/L, respectively). The concentrations of TSM were very variable in different lakes and the mean values showed no significant trend throughout the season. The average TN:TP ratio varied from 25 to 56 on different dates, having the highest mean values and being statistically distinct from the other dates in August 2020 (Tukey’s HSD, p-value < 0.05), indicating a high phosphorus limitation at that time of year at most of the lakes. The concentrations of BOD5 and COD decreased from April to July and increased slightly in August, similarly to CHL, with the mean values significantly different from others dates on 19 April 2021 (Tukey’s HSD, p-value < 0.05). Overall, the average BOD5 values were around 2 mg O2/L on all five dates and did not exceed 6 mg O2/L in any of the 180 lakes referring to clear or moderately polluted lakes. The mean value of COD ranged from 33.1 to 36.9 mg O2/L. The mean concentration of O2 was highest (8.53 mg/L) and the mean value of WT was lowest (17.4 °C) on 19 April 2021. The mean value of SD was also significantly lower (1.20 m) on 19 April 2021 compared to other dates (Tukey’s HSD, p-value < 0.05). Similarly to the mean concentration of CHL, the mean values of pH were somewhat higher on 19 April 2021 (8.09) and on 17 August 2020 (7.95).

4. Discussion

The correlation with optically active substances serves as a valuable consideration for the assessment of non-optically active water quality parameters using remote sensing. Furthermore, the goal is not merely to establish correlations but, more importantly, to determine causative relationships. This distinction underscores the significance of understanding the underlying mechanisms and interactions between optical and non-optical parameters for accurate remote sensing assessments of water quality. In our research, the statistical correlations between optically active substances and non-optically active water quality parameters can be considered causative. For example, TN, TP, BOD5, COD, FPBM, and CYBM were statistically significantly correlated with CHL. Nutrients influence CHL concentrations by inducing phytoplankton productivity and biomass growth [107]. Additionally, BOD5 shows the amount of the oxygen consumed by organisms and the readily decomposable organic matter in the water. The strong correlations between CHL and BOD5 revealed that phytoplankton and other aquatic plants are the primary sources of rapidly decaying organics [108], indicating an autochthonous carbon dominance in our study lakes. COD is a measure of oxygen used up during chemical oxidation. COD also refers to the amount of organic matter in water, but it also involves the refractory to decomposition allochthonous carbon, which is not reflected by BOD. Indeed, in our study, COD had a stronger correlation with CDOM than with CHL. CDOM also correlated well with nutrients, indicating their similar terrestrial origin [109]. The acidity of surface waters is affected by CDOM [110], which accounted for the significant negative correlation between pH and CDOM in our study. TSM and phosphorus in water have been demonstrated to be correlated [111,112,113,114], and were also correlated in this study. The particle size distribution, geographical variance, and percentage of phosphorous attached to particles all have an impact on the correlation between TP and TSM [114]. Moreover, in accordance with TSM concentrations, it may either absorb or desorb nutrients. Generally, 20% of the nutrients are present in particulate form in waters at TSM concentrations of 10 mg/L, 60% at TSM concentrations of 100 mg/L, and 80% at TSM concentrations of 1000 mg/L [114]. Recognizing the causative nature of these correlations improves remote sensing’s efficacy in assessing water quality, emphasizing the importance of taking into account both optical and non-optical parameters for a thorough understanding of environmental conditions in lakes.
As most optically non-active water quality parameters were impacted by several optical substances, no specific bands or band combinations were chosen, but rather as many various combinations as possible were tested to identify the most sensitive ones. The best results were obtained by combining different band combinations as GA XGBoost feature inputs. Similarly to us, Chen et al. [72] also obtained the best results for predicting CHL, TP, TN, NH3-N, and turbidity by combining multiple two- or three-band or band ratio algorithms in the GA_XGBoost model. Sentinel-2 MSI Band 4 (665 nm) was discovered to be the most applied band in the models. Band 4 or the bands near 665 nm of other sensors have previously been used as representative bands across the CHL, CDOM, and TSM two- or three-band or band ratio algorithms [16,18,115,116,117,118]. Utilizing diverse band combinations improves the robustness of predictive models, aligning with the broader trend of optimizing satellite-derived data for water quality assessment.
This study used the GA_XGBoost machine learning algorithm along with in situ and Sentinel-2 MSI data to construct the inversion models of 14 biogeochemical (TN, TP, PO4, SO4, NH4N, BOD5, COD, CHL, CDOM, TSM, FPBM, CYBM, pH, O2) and two physical (WT, SD) lake water quality parameters. XGBoost is a scalable end-to-end tree-boosting algorithm proposed by Chen et al. [78]. It has gained increasing attention in recent years due to its high efficiency and prediction accuracy. The most significant feature behind the effectiveness of XGBoost is its scalability in all setups due to several important systems and algorithmic optimizations [78]. XGBoost can be described as a novel tree-learning algorithm to handle sparse data and a theoretically based weighted quantile sketch method that enables the handling of instance weights in approximate tree learning [78]. Additionally, it has parallel and distributed computing and out-of-core computation accelerated learning, which enables faster model exploration and achieves a balance between model performance and computing speed inherent to XGBoost [78]. Adding regularization elements to the objective function controls the complexity of the model and supports feature sampling, which can prevent the overfitting of the model [78]. In our study, GA_XGBoost was able to predict ten biogeochemical (TN, TP, PO4, BOD5, COD, CHL, CDOM, TSM, pH, O2) and two physical water quality parameters (WT, SD). We have introduced performance scores to ensure the algorithm performs optimally across all three datasets (testing, training, validation). Upon examining the performance metrics in Table 5, it is noteworthy that there was an observed increase in MAPE and RMSE, accompanied by a decrease in R2 during the transition from the training to testing stages. Unfortunately, this pattern underscores the potential concern for overfitting, especially for certain parameters. The shift from testing to validation phases indicated a relatively smaller and more moderate change. However, it is advisable to employ a more effective approach for model selection, adjustments, and tuning in future studies to clearly avoid potential overfitting concerns. Additionally, the observed low accuracy in Table 5, particularly in the statistics for certain water quality parameters such as SO4, NH4N, FPBM, CYBM, and COD underline specific challenges faced by the GA_XGBoost machine learning algorithm. While our study achieved overall success, it is crucial to delve into the difficulties encountered, shedding light on the limitations of machine learning methods in environmental modelling using remote sensing. For example, COD, as an optically non-active parameter, presents inherent challenges due to the complexity of its determination. Unlike optically active substances, COD lacks direct spectral characteristics, making its estimation dependent on complicated relationships with other parameters. The difficulty lies in discerning these complex interactions accurately, contributing to variations in predictive performance. The complexities associated with the relationships between these substances and optically active parameters pose challenges that may not be fully addressed by machine learning algorithms alone. This challenge extends to other optically non-active parameters, such as SO4, NH4N, FPBM, and CYBM, as reflected in elevated performance metrics.
Moreover, the dataset size is an important aspect that might significantly influence the performance and generalizability of machine learning models. Unfortunately, the limitations in dataset size are inherent in remote sensing studies, particularly when dealing with match-ups between in situ measurements and satellite data. Given the constraints posed by the nature of remote sensing data and the relatively short study period, the choice of the XGBoost machine learning approach was deliberate. The XGBoost algorithm’s ability to handle smaller datasets efficiently played a crucial role in addressing the challenges set by the available data. This aligns with the established literature, including works by Chen et al. [72], which acknowledges the suitability of XGBoost for smaller datasets.
Furthermore, the dynamic nature of the biogeochemical and physical properties of lakes presents a challenge in ensuring the reliability of results produced using machine learning methods. Table 2 shows a diverse range of measured values for each water quality parameter, providing a snapshot of the variability in water quality conditions within the study area. While the dataset may not cover every conceivable scenario, it captures substantial variation that allowed the models to discern patterns and relationships. Additionally, our study incorporated data from different seasons to capture the temporal variability in these properties. However, it is essential to acknowledge that the dynamic nature of lakes introduces complexities that may impact the predictive accuracy of machine learning models. While we aimed to represent diverse seasonal conditions, the variability over time could present limitations, especially when attempting to generalize the models to broader contexts. Future studies could benefit from expanding the temporal scope and considering longer-term datasets to enhance the robustness of machine learning models in capturing the dynamic nature of lakes.
Even in light of these challenges, our results were in good consistency in terms of accuracy with the research of other authors who concentrated on individual lakes and only one or two parameters. In previous studies, XGBoost has been used to retrieve mostly CHL, TN, and TP, but also COD, electrical conductivity (EC), NH3-N, O2, pH, SD, SiO2, TSM, turbidity, and WT from mainly individual Chinese rivers, lakes, and reservoirs, primarily using Sentinel-2 MSI, Landsat 8 OLI, or an unmanned aerial vehicle (UAV) [72,74,119,120,121,122,123]. In these studies, XGBoost models demonstrated high accuracy in retrieving various water quality parameters in inland waters, outperforming other machine learning models such as Random Forest (RF), Support Vector Regressor (SVR), Deep Neural Network (DNN), Lasso, etc., as well as linear, quadratic polynomial, logarithmic, power, and exponential regression models (Appendix B, Table A2). While the developed machine learning models consistently yield reliable results in localized studies, it is important to acknowledge their potential limitations when applied to broader contexts. For instance, in large-scale water quality assessments, variations in geographical and environmental factors may necessitate adjustments, such as new band selection and parameter tuning, as highlighted by Guo et al. [46].
In general, the mean values and the variability of the estimated water quality parameters allowed us to demonstrate that it is possible to obtain reliable results for multiple lakes at the same time using the developed GA_XGBoost model and Sentinel-2 MSI data. Nutrient concentrations, and thus CHL, were greater in April and May. In spring, more light becomes available, the surface water gets warmer, the water column stratifies, and due to the inhibition of vertical mixing, phytoplankton and nutrients are compressed in the euphotic zone. As a result, an environment with relatively high nutrient and light levels is created, promoting fast phytoplankton development [124]. The mean concentrations of CHL were lower in June and July due to the decreasing nutrients in water. Nutrient depletion and increased zooplankton grazing often promote spring bloom collapse and maintain low phytoplankton biomass over summer [124]. A slight increase in CHL and TN concentrations in August revealed the presence of cyanobacteria in at least some lakes at that time as diazotrophic cyanobacteria may fix atmospheric nitrogen to meet their nitrogen needs [125]. The pH showed a similar seasonal trend as CHL, whose seasonal course is driven by primary production, which fixes inorganic carbon and therefore raises the pH during periods of intense growth [126]. In April and May, when the largest river discharge typically takes place [127], the mean concentration of CDOM was at its maximum. Water transparency (given as SD) was the lowest in April, which is typical of the spring months, confirming that CHL and CDOM concentrations have a strong impact on water clarity [128,129]. The mean water temperature was highest in June 2021, the same month that Estonia experienced the warmest June ever [130]. In April and May, the mean oxygen concentration was at its maximum. Firstly, oxygen dissolves better in cold water, and secondly, this is the peak period for primary production that produces oxygen as a by-product [131]. The high amount of CDOM in spring and the oxygen used in its decomposition may be the reason that the mean oxygen concentration did not reach saturation levels even in April [132]. The application of the GA_XGBoost model, combined with satellite data, indeed represents a powerful approach for remote sensing in the assessment of water quality across a diverse range of lakes. This method not only validates the efficiency of remote sensing, but also highlights its potential to provide comprehensive insights into spatiotemporal variations of numerous water quality parameters simultaneously across a large number of lakes.

5. Conclusions

This study aimed to use the GA_XGBoost machine learning algorithm along with in situ and Sentinel-2 MSI data to monitor and predict water quality parameters in lakes. We constructed inversion models of 16 physical and biogeochemical water quality parameters (TN, TP, PO4, SO4, NH4N, BOD5, COD, CHL, CDOM, TSM, FPBM, CYBM, pH, O2, WT, and SD) and provided a practical demonstration of the developed inversion models, illustrating their applicability in estimating various water quality parameters simultaneously across multiple lakes on five different dates.
  • GA_XGBoost exhibited strong predictive capabilities and it was able to accurately predict ten biogeochemical and two physical water quality parameters (TN, TP, PO4, BOD5, COD, CHL, CDOM, TSM, pH, O2, WT, and SD), showcasing its effectiveness in water quality and remote sensing applications.
  • The observed increase in MAPE and RMSE, accompanied by a decrease in R2 during the transition from training to testing stages, highlighted the potential concern for overfitting, especially for specific parameters. This emphasizes the need for careful model selection, adjustments, and tuning in future studies.
  • Despite the dynamic nature of lakes, our results demonstrated reliable estimates for multiple lakes simultaneously, considering the seasonal variations in water quality parameters.
While our findings contribute to the growing body of knowledge on remote sensing applications for water quality assessment, it is crucial to acknowledge certain limitations. Challenges linked to optically non-active parameters, the potential for overfitting, and the limitations of remote sensing datasets highlight the necessity for ongoing research and refinement of machine learning methodologies in environmental monitoring. Future investigations should delve into broader temporal scopes, incorporate longer-term datasets, and employ enhanced model selection strategies. These efforts are crucial for advancing the robustness and generalizability of remote sensing-based water quality models.

Author Contributions

T.K.: conceptualization, methodology, formal analysis, visualization, writing—original draft, writing—review and editing, funding acquisition. H.L.: methodology, formal analysis, writing—review and editing. T.S.: methodology, writing—review and editing. E.U.: formal analysis, writing—review and editing. K.T.: funding acquisition, writing—review and editing. T.N.: funding acquisition, writing—review and editing. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Estonian Research Council (under grants PRG302, PRG709, and PRG1764), the European Regional Developing Fund, and the program Mobilitas Pluss (grant number MOBTP106).

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://kese.envir.ee/ and https://dataspace.copernicus.eu/.

Acknowledgments

Estonian Environment Agency is acknowledged for providing biogeochemical and physical water quality parameters. The European Space Agency (ESA) and the European Union’s Earth observation program Copernicus are acknowledged for providing Sentinel-2 MSI data. The Estonian National Satellite Data Centre ESTHub is acknowledged for the possibility to search, download, and process the Copernicus program data. The three anonymous reviewers are acknowledged for their insightful comments and constructive feedback which significantly contributed to the improvement of this manuscript.

Conflicts of Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A

Table A1. Names, coordinates, maximum and mean depth, catchment area, and lake area of 45 Estonian lakes by sampling dates where in situ data of the current study were collected.
Table A1. Names, coordinates, maximum and mean depth, catchment area, and lake area of 45 Estonian lakes by sampling dates where in situ data of the current study were collected.
Lake NameLat (N)Lon (E)Max Depth, mMean Depth, mCatch. Area, km2Area, km2Trophic StateSampling Date
Aheru järv/Kandsi järv57.6884426.352837.43.452.42.34Eutrophic (hard water)12 September 2016
Elistvere järv58.5713926.707283.521711.29Eutrophic (macrophyte)9 May 2016
Elistvere järv58.5713926.707283.521711.29Eutrophic (macrophyte)15 September 2016
Endla järv58.8535726.196512.41.54332.84Mixotrophic (hard water)16 May 2018
Ermistu järv58.3692323.981462.91.332.34.49Eutrophic (macrophyte)30 May 2017
Hino järv57.5835727.2017710.43.12.121.99Oligotrophic6 May 2020
Hino järv57.5835727.2017710.43.12.121.99Oligotrophic12 August 2020
Hino järv57.5835727.2017710.43.12.121.99Oligotrophic7 September 2020
Jõemõisa järv58.6537226.828923.22.62160.72Mixotrophic (hard water)5 August 2015
Järise järv58.4941622.412621.40.711.10.96Eutrophic (macrophyte)22 August 2018
Kaiavere järv58.6038326.6748652.892.22.47Eutrophic (hard water)9 May 2016
Kaiavere järv58.6038326.6748652.892.22.47Eutrophic (hard water)20 July 2016
Kaiavere järv58.6038326.6748652.892.22.47Eutrophic (hard water)15 September 2016
Kaisma järv58.6931224.681322.11.25161.4Mixotrophic (hard water)20 May 2019
Kaisma järv58.6931224.681322.11.25161.4Mixotrophic (hard water)18 July 2019
Kaiu järv58.6420126.838932.62161.34Mixotrophic (hard water)5 August 2015
Kalli järv58.3769527.236231.41.182.81.99Eutrophic (macrophyte)9 May 2020
Karijärv58.2983126.4199314.55.711.10.82Eutrophic (hard water)14 September 2015
Karijärv58.2983126.4199314.55.711.10.82Eutrophic (hard water)3 July 2019
Karijärv58.2983126.4199314.55.711.10.82Eutrophic (hard water)4 September 2019
Kariste järv58.1416125.34847.23.31280.61Eutrophic (hard water)30 May 2017
Kariste järv58.1416125.34847.23.31280.61Eutrophic (hard water)25 September 2017
Karujärv58.3710222.216161.616.13.46Eutrophic (hard water)28 May 2018
Karujärv58.3710222.216161.616.13.46Eutrophic (hard water)22 August 2018
Konsu järv59.2265627.5805210.25.8271.39Mixotrophic (hard water)25 June 2019
Konsu järv59.2265627.5805210.25.8271.39Mixotrophic (hard water)22 April 2020
Kooru järv58.4836322.139461.20.338.70.85Eutrophic (halotrophic)16 August 2015
Kooru järv58.4836322.139461.20.338.70.85Eutrophic (halotrophic)27 September 2015
Kooru järv58.4836322.139461.20.338.70.85Eutrophic (halotrophic)28 September 2015
Kooru järv58.4836322.139461.20.338.70.85Eutrophic (halotrophic)29 May 2017
Kooru järv58.4836322.139461.20.338.70.85Eutrophic (halotrophic)28 May 2018
Kooru järv58.4836322.139461.20.338.70.85Eutrophic (halotrophic)28 July 2019
Kooru järv58.4836322.139461.20.338.70.85Eutrophic (halotrophic)29 August 2020
Koosa järv58.425727.144111.91.275.92.83Mixotrophic (macrophyte)20 July 2020
Käsmu järv59.5817525.883993.32.216.50.49Mixotrophic (soft water)12 August 2015
Käsmu järv59.5817525.883993.32.216.50.49Mixotrophic (soft water)12 August 2020
Köstrijärv57.7500926.394614.43.31.80.12Eutrophic (macrophyte)7 May 2018
Lahepera järv58.5737527.192744.22.428.90.1Eutrophic (macrophyte)11 May 2020
Lahepera järv58.5737527.192744.22.428.90.1Eutrophic (macrophyte)20 July 2020
Leegu järv58.3658727.2761410.65.60.86Eutrophic (macrophyte)20 July 2020
Lohja järv59.5482125.690923.72.212.30.56Mixotrophic (soft water)12 August 2015
Lohja järv59.5482125.690923.72.212.30.56Mixotrophic (soft water)8 July 2020
Lohja järv59.5482125.690923.72.212.30.56Mixotrophic (soft water)12 August 2020
Loosalu järv58.9333725.077753.71.60.35Dystrophic20 May 2018
Mustjärv (Nohipalo Mustjärv)57.9320127.342178.93.99.70.22Acidotrophic2 May 2016
Mustjärv (Nohipalo Mustjärv)57.9320127.342178.93.99.70.22Acidotrophic2 May 2017
Mustjärv (Nohipalo Mustjärv)57.9320127.342178.93.99.70.22Acidotrophic7 May 2020
Männiku järv59.3458324.7123995130.1Eutrophic (hard water)25 August 2015
Ohepalu järv59.3339525.951982.50.57.50.68Dystrophic23 July 2015
Ohepalu järv59.3339525.951982.50.57.50.68Dystrophic12 August 2020
Pabra järv57.6090127.395273.62.436.50.76Semidystrophic16 August 2017
Peenjärv59.2137927.57548---0.08Mixotrophic (hard water)25 June 2019
Pikkjärv (Viitna Pikkjärv)59.446526.010056.231.10.16Oligotrophic14 August 2017
Pikkjärv (Viitna Pikkjärv)59.446526.010056.231.10.16Oligotrophic15 May 2018
Pikkjärv (Viitna Pikkjärv)59.446526.010056.231.10.16Oligotrophic19 May 2020
Pikkjärv (Viitna Pikkjärv)59.446526.010056.231.10.16Oligotrophic17 August 2020
Pühajärv58.0240926.456678.54.3442.98Eutrophic (hard water)2 May 2016
Pühajärv58.0240926.456678.54.3442.98Eutrophic (hard water)2 May 2017
Pühajärv58.0240926.456678.54.3442.98Eutrophic (hard water)2 May 2018
Pühajärv58.0240926.456678.54.3442.98Eutrophic (hard water)7 August 2018
Pühajärv58.0240926.456678.54.3442.98Eutrophic (hard water)1 July 2019
Pühajärv58.0240926.456678.54.3442.98Eutrophic (hard water)2 September 2019
Pühajärv58.0240926.456678.54.3442.98Eutrophic (hard water)4 May 2020
Pühajärv58.0240926.456678.54.3442.98Eutrophic (hard water)7 May 2020
Saadjärv58.5368826.6577825831.97.23Eutrophic (hard water)9 May 2016
Saadjärv58.5368826.6577825831.97.23Eutrophic (hard water)14 July 2016
Saare järv58.6548926.76275.64.28.527.4Eutrophic (hard water)5 August 2015
Soitsjärv58.5566726.6816881.215.21.58Mixotrophic (macrophyte)9 May 2016
Suurjärv (Rouge Suurjärv)57.727526.92278381225.80.135Eutrophic (hard water)4 August 2015
Suurjärv (Rouge Suurjärv)57.727526.92278381225.80.135Eutrophic (hard water)4 May 2017
Suurjärv (Rouge Suurjärv)57.727526.92278381225.80.135Eutrophic (hard water)4 September 2019
Suurjärv (Rouge Suurjärv)57.727526.92278381225.80.135Eutrophic (hard water)5 May 2020
Suurjärv (Rouge Suurjärv)57.727526.92278381225.80.135Eutrophic (hard water)6 May 2020
Suurjärv (Rouge Suurjärv)57.727526.92278381225.80.135Eutrophic (hard water)7 September 2020
Tõhela järv58.4178523.996191.51.321.74.07Eutrophic (macrophyte)30 May 2017
Tõhela järv58.4178523.996191.51.321.74.07Eutrophic (macrophyte)25 July 2017
Tõhela järv58.4178523.996191.51.321.74.07Eutrophic (macrophyte)21 July 2020
Tänavjärv59.1789723.805632.51.84.71.39Semidystrophic17 August 2015
Tänavjärv59.1789723.805632.51.84.71.39Semidystrophic29 May 2016
Tänavjärv59.1789723.805632.51.84.71.39Semidystrophic30 August 2016
Tänavjärv59.1789723.805632.51.84.71.39Semidystrophic26 September 2016
Tänavjärv59.1789723.805632.51.84.71.39Semidystrophic27 September 2016
Tänavjärv59.1789723.805632.51.84.71.39Semidystrophic20 May 2019
Tänavjärv59.1789723.805632.51.84.71.39Semidystrophic24 May 2020
Tänavjärv59.1789723.805632.51.84.71.39Semidystrophic18 July 2020
Tänavjärv59.1789723.805632.51.84.71.39Semidystrophic16 August 2020
Tündre järv57.9507525.6188910.64.97.10.716Eutrophic (hard water)11 May 2016
Uljaste järv59.359426.773966.42.21.10.63Semidystrophic14 August 2017
Uljaste järv59.359426.773966.42.21.10.63Semidystrophic25 September 2017
Uljaste järv59.359426.773966.42.21.10.63Semidystrophic15 May 2019
Uljaste järv59.359426.773966.42.21.10.63Semidystrophic17 August 2020
Valgejärv (Kurtna Valgejärv)59.2634227.5971210.54.210.08Semidystrophic15 May 2019
Valgjärv58.0890326.640335.53.24.90.65Eutrophic (hard water)4 May 2017
Valgjärv58.0890326.640335.53.24.90.65Eutrophic (hard water)5 July 2017
Valgojärv (Nohipalo Valgojärv)57.941227.3466212.56.22.20.07Oligotrophic2 May 2017
Valgojärv (Nohipalo Valgojärv)57.941227.3466212.56.22.20.07Oligotrophic1 August 2017
Valgojärv (Nohipalo Valgojärv)57.941227.3466212.56.22.20.07Oligotrophic2 September 2019
Valgojärv (Nohipalo Valgojärv)57.941227.3466212.56.22.20.07Oligotrophic7 May 2020
Verevi järv58.2307426.40464113.61.10.12Hypertrophic8 August 2017
Verevi järv58.2307426.40464113.61.10.12Hypertrophic6 May 2020
Viljandi järv58.3502725.59324115.666.81.58Eutrophic (hard water)6 May 2020
Õisu järv58.2053225.520784.32.81991.93Eutrophic (hard water)8 July 2019
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)4 August 2015
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)11 May 2016
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)3 August 2016
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)12 September 2016
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)4 May 2017
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)7 May 2018
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)3 July 2019
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)4 September 2019
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)6 May 2020
Ähijärv57.7129726.496545.53.814.71.81Eutrophic (hard water)16 September 2020

Appendix B

Table A2. The performance metrics of different models for deriving biogeochemical and physical water quality parameters from remote sensing data. R2, R-squared; MAPE, mean absolute percentage error (%); RMSE, root-mean-square error; N, number of data.
Table A2. The performance metrics of different models for deriving biogeochemical and physical water quality parameters from remote sensing data. R2, R-squared; MAPE, mean absolute percentage error (%); RMSE, root-mean-square error; N, number of data.
Water Quality ParameterModelR2MAERMSEMAPERemote Sensing Platform/SensorSpatial ResolutionWaterbodyNReference
CHLGA_XGBoost0.860.020.05-UAV0.1Nanfei River67[72]
CHLXGBoost0.820.030.05-UAV0.1Nanfei River67[72]
CHLXGBoost-11.5014.7030.2Landsat 5 TM30 mLake Taihu163[119]
CHLXGBoost-7.2012.9034.8Landsat 7 ETM+30 mLake Taihu163[119]
CHLXGBoost-11.6015.7035.2Landsat 8 OLI30 mLake Taihu163[119]
CHLXGBoost0.421.522.07-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CHLXGBoost0.73-0.267.59Sentinel-2 MSI20 mQ reservoir96[74]
CHLXGBoost0.84-6.65-Zhuhai-No.1, CMOS30 mDushan Lake, Weishan Lake99[123]
CHLGA_RF0.800.030.05-UAV0.1Nanfei River67[72]
CHLRF0.740.040.06-UAV0.1Nanfei River67[72]
CHLRF-8.9014.4018.3Landsat 5 TM30 mLake Taihu163[119]
CHLRF-7.7013.8044.1Landsat 7 ETM+30 mLake Taihu163[119]
CHLRF-10.7014.9033.8Landsat 8 OLI30 mLake Taihu163[119]
CHLRF0.321.511.94-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CHLRF0.67-0.3013.13Sentinel-2 MSI20 mQ reservoir96[74]
CHLAdaBoost0.780.030.06-UAV0.1Nanfei River67[72]
CHLGA_AdaBoost0.830.030.05-UAV0.1Nanfei River67[72]
CHLSVR-13.4017.6046.5Landsat 5 TM30 mLake Taihu163[119]
CHLSVR-8.4018.7037.7Landsat 7 ETM+30 mLake Taihu163[119]
CHLSVR-13.1015.6032.2Landsat 8 OLI30 mLake Taihu163[119]
CHLSVR0.46-0.3614.3Sentinel-2 MSI20 mQ reservoir96[74]
CHLANN0.15-0.4517.94Sentinel-2 MSI20 mQ reservoir96[74]
CHLDNN0.810.030.05-UAV0.1Nanfei River67[72]
CHLBP0.121.572.21-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CHLLasso0.201.542.08-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CHLMLR0.101.602.24-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CODMnXGBoost0.110.790.86-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CODMnRF0.200.710.80-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CODMnBP0.220.690.80-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CODMnLasso0.070.700.83-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CODMnMLR0.060.710.83-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
CODMnML-MLR0.190.720.82-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
ECXGBoost0.27-1.23-Landsat 8 OLI30The Ganga River Basin, Cluster 0159[133]
ECXGBoost0.33-2.57-Landsat 8 OLI30The Ganga River Basin, Cluster 1159[133]
ECXGBoost0.21-2.85-Landsat 8 OLI30The Ganga River Basin, Cluster 2159[133]
ECXGBoost0.32-2.58-Landsat 8 OLI30The Ganga River Basin, Cluster 3159[133]
NH3-NGA_XGBoost0.690.140.16-UAV0.1Nanfei River67[72]
NH3-NXGBoost0.650.150.17-UAV0.1Nanfei River67[72]
NH3-NXGBoost0.82-0.1428.6Sentinel-2 MSI20 mQ reservoir96[74]
NH3-NGA_RF0.620.150.17-UAV0.1Nanfei River67[72]
NH3-NRF0.600.150.19-UAV0.1Nanfei River67[72]
NH3-NRF0.12-0.2273.53Sentinel-2 MSI20 mQ reservoir96[74]
NH3-NAdaBoost0.550.150.20-UAV0.1Nanfei River67[72]
NH3-NGA_AdaBoost0.670.150.17-UAV0.1Nanfei River67[72]
NH3-NSVR0.49-0.15118.45Sentinel-2 MSI20 mQ reservoir96[74]
NH3-NANN0.25-0.17107.43Sentinel-2 MSI20 mQ reservoir96[74]
NH3-NDNN0.630.150.18-UAV0.1Nanfei River67[72]
O2XGBoost0.97-0.01-Landsat 8 OLI30The Ganga River Basin, Cluster 0159[133]
O2XGBoost0.93-0.01-Landsat 8 OLI30The Ganga River Basin, Cluster 1159[133]
O2XGBoost0.90-0.01-Landsat 8 OLI30The Ganga River Basin, Cluster 2159[133]
O2XGBoost0.96-0.01-Landsat 8 OLI30The Ganga River Basin, Cluster 3159[133]
O2XGBoost0.90-0.140.07Sentinel-2 MSI20 mQ reservoir96[74]
O2RF0.77-0.343.43Sentinel-2 MSI20 mQ reservoir96[74]
O2SVR0.85-0.171.38Sentinel-2 MSI20 mQ reservoir96[74]
O2ANN0.79-0.202.04Sentinel-2 MSI20 mQ reservoir96[74]
pHXGBoost0.78-0.08-Landsat 8 OLI30The Ganga River Basin, Cluster 0159[133]
pHXGBoost0.74-0.19-Landsat 8 OLI30The Ganga River Basin, Cluster 1159[133]
pHXGBoost0.74-0.26-Landsat 8 OLI30The Ganga River Basin, Cluster 2159[133]
pHXGBoost0.76-0.09-Landsat 8 OLI30The Ganga River Basin, Cluster 3159[133]
SDXGBoost0.840.641.14-Landsat 5 TM30Different lake datasets from Europe, China, and America4099[123]
SDXGBoost0.760.891.87-Landsat 7 ETM+30Different lake datasets from Europe, China, and America2420[123]
SDXGBoost0.880.500.80-Landsat 8 OLI30Different lake datasets from Europe, China, and America1249[123]
SDXGBoost0.982.012.52-UAV0.185 mThe Shahu Port channel, The Xunsi River72[120]
SDRF0.971.982.81-UAV0.185 mThe Shahu Port channel, The Xunsi River72[120]
SDRF0.820.621.13-Landsat 5 TM30Different lake datasets from Europe, China, and America4099[123]
SDRF0.780.841.84-Landsat 7 ETM+30 mDifferent lake datasets from Europe, China, and America2420[123]
SDRF0.850.470.74-Landsat 8 OLI30 mDifferent lake datasets from Europe, China, and America1249[123]
SDAdaBoost0.982.002.55-UAV0.185 mThe Shahu Port channel, The Xunsi River72[120]
SDGBDT0.913.624.75-UAV0.185 mThe Shahu Port channel, The Xunsi River72[120]
SDExponential function0.45-12.48-UAV0.185 mThe Shahu Port channel, The Xunsi River72[120]
SDLinear function0.80-7.59-UAV0.185 mThe Shahu Port channel, The Xunsi River72[120]
SDLogarithmic function0.80-7.58-UAV0.185 mThe Shahu Port channel, The Xunsi River72[120]
SDPower function0.68-9.44-UAV0.185 mThe Shahu Port channel, The Xunsi River72[120]
SDQuadratic polynomial0.80-7.65-UAV0.185 mThe Shahu Port channel, The Xunsi River72[120]
SiO2XGBoost0.98-0.01-Landsat 8 OLI30The Ganga River Basin, Cluster 0159[133]
SiO2XGBoost0.96-0.01-Landsat 8 OLI30The Ganga River Basin, Cluster 1159[133]
SiO2XGBoost0.97-0.00-Landsat 8 OLI30The Ganga River Basin, Cluster 2159[133]
SiO2XGBoost0.97-0.00-Landsat 8 OLI30The Ganga River Basin, Cluster 3159[133]
TNGA_XGBoost0.790.741.09-UAV0.1Nanfei River67[72]
TNXGBoost0.700.811.28-UAV0.1Nanfei River67[72]
TNXGBoost0.711.031.33-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TNGA_RF0.670.911.35-UAV0.1Nanfei River67[72]
TNRF0.670.901.36-UAV0.1Nanfei River67[72]
TNRF0.701.131.50-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TNAdaBoost0.611.221.55-UAV0.1Nanfei River67[72]
TNGA_AdaBoost0.670.891.36-UAV0.1Nanfei River67[72]
TNDNN0.770.841.14-UAV0.1Nanfei River67[72]
TNBP0.820.841.27-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TNLasso0.641.281.45-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TNMLR0.641.271.46-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TNML-MLR0.820.871.28-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TPGA_XGBoost0.700.030.03-UAV0.1Nanfei River67[72]
TPXGBoost0.610.030.04-UAV0.1Nanfei River67[72]
TPXGBoost0.280.050.07-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TPGA_RF0.550.030.04-UAV0.1Nanfei River67[72]
TPRF0.460.030.05-UAV0.1Nanfei River67[72]
TPRF0.350.040.06-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TPAdaBoost0.610.030.04-UAV0.1Nanfei River67[72]
TPGA_AdaBoost0.640.030.04-UAV0.1Nanfei River67[72]
TPDNN0.560.030.04-UAV0.1Nanfei River67[72]
TPBP0.430.050.05-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TPLasso0.380.050.06-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TPMLR0.380.050.06-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TPML-MLR0.270.040.07-UAV1600 × 1300 pixelsThe Zhanghe River45[119]
TSMXGBoost0.18641.20751.90-Landsat 8 OLI30 mEbinur Lake, China102[121]
TSMXGBoost0.24798.85884.85-Sentinel-2 MSI20 mEbinur Lake, China102[121]
TSMRF0.68215.88256.92-Landsat 8 OLI30 mEbinur Lake, China102[121]
TSMRF0.73220.27222.69-Sentinel-2 MSI20 mEbinur Lake, China102[121]
TUBGA_XGBoost0.609.8210.13-UAV0.1Nanfei River67[72]
TUBXGBoost0.529.9711.47-UAV0.1Nanfei River67[72]
TUBGA_RF0.4510.2712.16-UAV0.1Nanfei River67[72]
TUBRF0.3710.5613.20-UAV0.1Nanfei River67[72]
TUBAdaBoost0.3910.3612.67-UAV0.1Nanfei River67[72]
TUBGA_AdaBoost0.4510.2812.26-UAV0.1Nanfei River67[72]
TUBDNN0.549.9211.03-UAV0.1Nanfei River67[72]
WTXGBoost0.73-0.15-Landsat 8 OLI30The Ganga River Basin, Cluster 0159[133]
WTXGBoost0.89-0.10-Landsat 8 OLI30The Ganga River Basin, Cluster 1159[133]
WTXGBoost0.89-0.08-Landsat 8 OLI30The Ganga River Basin, Cluster 2159[133]
WTXGBoost0.90-0.01-Landsat 8 OLI30The Ganga River Basin, Cluster 3159[133]

References

  1. Verpoorter, C.; Kutser, T.; Seekell, D.A.; Tranvik, L.J. A Global Inventory of Lakes Based on High-Resolution Satellite Imagery. Geophys. Res. Lett. 2014, 41, 6396–6402. [Google Scholar] [CrossRef]
  2. Postel, S.L. Entering an Era of Water Scarity: The Challeenges Ahead. Ecol. Appl. 2000, 10, 941–948. [Google Scholar] [CrossRef]
  3. Brönmark, C.; Hansson, L.A. Environmental Issues in Lakes and Ponds: Current State and Perspectives. Environ. Conserv. 2002, 29, 290–307. [Google Scholar] [CrossRef]
  4. Bastviken, D.; Tranvik, L.J.; Downing, J.A.; Crill, P.M.; Enrich-Prast, A. Freshwater Methane Emissions Offset the Continental Carbon Sink. Science 2011, 331, 50. [Google Scholar] [CrossRef]
  5. Tranvik, L.J.; Downing, J.A.; Cotner, J.B.; Loiselle, S.A.; Striegl, R.G.; Ballatore, T.J.; Dillon, P.; Finlay, K.; Fortino, K.; Knoll, L.B.; et al. Lakes and Reservoirs as Regulators of Carbon Cycling and Climate. Limnol. Ocean. 2009, 54, 2298–2314. [Google Scholar] [CrossRef]
  6. Tranvik, L.J.; Cole, J.J.; Prairie, Y.T. The Study of Carbon in Inland Waters-from Isolated Ecosystems to Players in the Global Carbon Cycle. Limnol. Ocean. Lett. 2018, 3, 41–48. [Google Scholar] [CrossRef]
  7. Adrian, R.; O’Reilly, C.M.; Zagarese, H.; Baines, S.B.; Hessen, D.O.; Keller, W.; Livingstone, D.M.; Sommaruga, R.; Straile, D.; van Donk, E.; et al. Lakes as Sentinels of Climate Change. Limnol. Ocean. 2009, 54, 2283–2297. [Google Scholar] [CrossRef]
  8. Papenfus, M.; Schaeffer, B.; Pollard, A.I.; Loftin, K. Exploring the Potential Value of Satellite Remote Sensing to Monitor Chlorophyll-a for US Lakes and Reservoirs. Environ. Monit. Assess. 2020, 192, 808. [Google Scholar] [CrossRef] [PubMed]
  9. Mumby, P.J.; Green, E.P.; Edwards, A.J.; Clark, C.D. The Cost-Effectiveness of Remote Sensing for Tropical Coastal Resources Assessment and Management. J. Environ. Manag. 1999, 55, 157–166. [Google Scholar] [CrossRef]
  10. Marcé, R.; George, G.; Buscarinu, P.; Deidda, M.; Dunalska, J.; de Eyto, E.; Flaim, G.; Grossart, H.P.; Istvanovics, V.; Lenhardt, M.; et al. Automatic High Frequency Monitoring for Improved Lake and Reservoir Management. Environ. Sci. Technol. 2016, 50, 10780–10794. [Google Scholar] [CrossRef] [PubMed]
  11. Palmer, S.C.J.; Kutser, T.; Hunter, P.D. Remote Sensing of Inland Waters: Challenges, Progress and Future Directions. Remote Sens. Environ. 2015, 157, 1–8. [Google Scholar] [CrossRef]
  12. Palmer, S.C.J.; Odermatt, D.; Hunter, P.D.; Brockmann, C.; Présing, M.; Balzter, H.; Tóth, V.R. Satellite Remote Sensing of Phytoplankton Phenology in Lake Balaton Using 10 years of MERIS Observations. Remote Sens. Environ. 2015, 158, 441–452. [Google Scholar] [CrossRef]
  13. Bresciani, M.; Vascellari, M.; Giardino, C.; Matta, E. Remote Sensing Supports the Definition of the Water Quality Status of Lake Omodeo (Italy). Eur. J. Remote Sens. 2012, 45, 349–360. [Google Scholar] [CrossRef]
  14. Dekker, A.G.; Peters, S.W.M. The Use of the Thematic Mapper for the Analysis of Eutrophic Lakes: A Case Study in the Netherlands. Int. J. Remote Sens. 1993, 14, 799–821. [Google Scholar] [CrossRef]
  15. Lee, Z.; Shang, S.; Qi, L.; Yan, J.; Lin, G. A Semi-Analytical Scheme to Estimate Secchi-Disk Depth from Landsat-8 Measurements. Remote Sens. Environ. 2016, 177, 101–106. [Google Scholar] [CrossRef]
  16. Toming, K.; Kutser, T.; Laas, A.; Sepp, M.; Paavel, B.; Nõges, T. First Experiences in Mapping Lakewater Quality Parameters with Sentinel-2 MSI Imagery. Remote Sens. 2016, 8, 640. [Google Scholar] [CrossRef]
  17. Kutser, T.; Paavel, B.; Verpoorter, C.; Ligi, M.; Soomets, T.; Toming, K.; Casal, G. Remote Sensing of Black Lakes and Using 810 Nm Reflectance Peak for Retrieving Water Quality Parameters of Optically Complex Waters. Remote Sens. 2016, 8, 497. [Google Scholar] [CrossRef]
  18. Chen, J.; Zhu, W.; Tian, Y.Q.; Yu, Q.; Zheng, Y.; Huang, L. Remote Estimation of Colored Dissolved Organic Matter and Chlorophyll-a in Lake Huron Using Sentinel-2 Measurements. J. Appl. Remote Sens. 2017, 11, 036007. [Google Scholar] [CrossRef]
  19. Liu, H.; Li, Q.; Shi, T.; Hu, S.; Wu, G.; Zhou, Q. Application of Sentinel 2 MSI Images to Retrieve Suspended Particulate Matter Concentrations in Poyang Lake. Remote Sens. 2017, 9, 761. [Google Scholar] [CrossRef]
  20. Ogashawara, I.; Kiel, C.; Jechow, A.; Kohnert, K.; Ruhtz, T.; Grossart, H.-P.; Hölker, F.; Nejstgaard, J.C.; Berger, S.A.; Wollrab, S. The Use of Sentinel-2 for Chlorophyll-a Spatial Dynamics Assessment: A Comparative Study on Different Lakes in Northern Germany. Remote Sens. 2021, 13, 1542. [Google Scholar] [CrossRef]
  21. Soomets, T.; Uudeberg, K.; Jakovels, D.; Brauns, A.; Zagars, M.; Kutser, T. Validation and Comparison of Water Quality Products in Baltic Lakes Using Sentinel-2 MSI and Sentinel-3 OLCI Data. Sensors 2020, 20, 742. [Google Scholar] [CrossRef]
  22. Ekstrand, S. Landsat TM Based Quantification of Chlorophyll-a during Algae Blooms in Coastal Waters. Int. J. Remote Sens. 1992, 13, 1913–1926. [Google Scholar] [CrossRef]
  23. Bresciani, M.; Stroppiana, D.; Odermatt, D.; Morabito, G.; Giardino, C. Assessing Remotely Sensed Chlorophyll-a for the Implementation of the Water Framework Directive in European Perialpine Lakes. Sci. Total Environ. 2011, 409, 3083–3091. [Google Scholar] [CrossRef] [PubMed]
  24. Chen, X.Y.; Zhang, J.; Tong, C.; Liu, R.J.; Mu, B.; Ding, J. Retrieval Algorithm of Chlorophyll-a Concentration in Turbid Waters from Satellite HY-1C Coastal Zone Imager Data. J. Coast. Res. 2019, 90, 146–155. [Google Scholar] [CrossRef]
  25. Kutser, T. Monitoring Long Time Trends in Lake Cdom Using Landsat Image Archive. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 389–392. [Google Scholar]
  26. Kutser, T.; Tranvik, L.; Pierson, D.C. Variations in Colored Dissolved Organic Matter between Boreal Lakes Studied by Satellite Remote Sensing. J. Appl. Remote Sens. 2009, 3, 033538. [Google Scholar] [CrossRef]
  27. Kutser, T.; Pierson, D.C.; Tranvik, L.; Reinart, A.; Sobek, S.; Kallio, K. Using Satellite Remote Sensing to Estimate the Colored Dissolved Organic Matter Absorption Coefficient in Lakes. Ecosystems 2005, 8, 709–720. [Google Scholar] [CrossRef]
  28. Knaeps, E.; Ruddick, K.G.; Doxaran, D.; Dogliotti, A.I.; Nechad, B.; Raymaekers, D.; Sterckx, S. A SWIR Based Algorithm to Retrieve Total Suspended Matter in Extremely Turbid Waters. Remote Sens. Environ. 2015, 168, 66–79. [Google Scholar] [CrossRef]
  29. Giardino, C.; Pepe, M.; Brivio, P.A.; Ghezzi, P.; Zilioli, E. Detecting Chlorophyll, Secchi Disk Depth and Surface Temperature in a Sub-Alpine Lake Using Landsat Imagery. Sci. Total Environ. 2001, 268, 19–29. [Google Scholar] [CrossRef] [PubMed]
  30. Wang, S.; Li, J.; Zhang, B.; Lee, Z.; Spyrakos, E.; Feng, L.; Liu, C.; Zhao, H.; Wu, Y.; Zhu, L.; et al. Changes of Water Clarity in Large Lakes and Reservoirs across China Observed from Long-Term MODIS. Remote Sens. Environ. 2020, 247, 111949. [Google Scholar] [CrossRef]
  31. Harrington, J.A.; Schiebe, F.R.; Nix, J.F. Remote Sensing of Lake Chicot, Arkansas: Monitoring Suspended Sediments, Turbidity, and Secchi Depth with Landsat MSS Data. Remote Sens. Environ. 1992, 39, 15–27. [Google Scholar] [CrossRef]
  32. Huang, C.; Yunmei, L.; Liu, G.; Guo, Y.; Yang, H.; Zhu, A.; Song, T.; Huang, T.; Zhang, M.; Shi, K. Tracing High Time-Resolution Fluctuations in Dissolved Organic Carbon Using Satellite and Buoy Observations: Case Study in Lake Taihu, China. Int. J. Appl. Earth Obs. Geoinf. 2017, 62, 174–182. [Google Scholar] [CrossRef]
  33. Li, S.; Toming, K.; Nõges, T.; Kutser, T. Integrating Remote Sensing of Hydrological Processes and Dissolved Organic Carbon Fluxes in Long-Term Lake Studies. J. Hydrol. 2022, 605, 127331. [Google Scholar] [CrossRef]
  34. Chen, J.; Zhu, W.; Tian, Y.Q.; Yu, Q. Monitoring Dissolved Organic Carbon by Combining Landsat-8 and Sentinel-2 Satellites: Case Study in Saginaw River Estuary, Lake Huron. Sci. Total Environ. 2020, 718, 137374. [Google Scholar] [CrossRef]
  35. Cao, F.; Tzortziou, M. Capturing Dissolved Organic Carbon Dynamics with Landsat-8 and Sentinel-2 in Tidally Influenced Wetland–Estuarine Systems. Sci. Total Environ. 2021, 777, 145910. [Google Scholar] [CrossRef]
  36. Arenz, R.F.; Lewis, W.M.; Saunders, J.F. Determination of Chlorophyll and Dissolved Organic Carbon from Reflectance Data for Colorado Reservoirs. Int. J. Remote Sens. 1996, 17, 1547–1565. [Google Scholar] [CrossRef]
  37. Shuchman, R.A.; Leshkevich, G.; Sayers, M.J.; Johengen, T.H.; Brooks, C.N.; Pozdnyakov, D. An Algorithm to Retrieve Chlorophyll, Dissolved Organic Carbon, and Suspended Minerals from Great Lakes Satellite Data. J. Great Lakes Res. 2013, 39, 14–33. [Google Scholar] [CrossRef]
  38. Winn, N.; Williamson, C.E.; Abbitt, R.; Rose, K.; Renwick, W.; Henry, M.; Saros, J. Modeling Dissolved Organic Carbon in Subalpine and Alpine Lakes with GIS and Remote Sensing. Landsc. Ecol. 2009, 24, 807–816. [Google Scholar] [CrossRef]
  39. Alcântara, E.; Bernardo, N.; Rodrigues, T.; Watanabe, F. Modeling the Spatio-Temporal Dissolved Organic Carbon Concentration in Barra Bonita Reservoir Using OLI/Landsat-8 Images. Model. Earth Syst. Environ. 2017, 3, 11. [Google Scholar] [CrossRef]
  40. Hirtle, H.; Rencz, A. The Relation between Spectral Reflectance and Dissolved Organic Carbon in Lake Water: Kejimkujik National Park, Nova Scotia, Canada. Int. J. Remote Sens. 2003, 24, 953–967. [Google Scholar] [CrossRef]
  41. Liu, D.; Yu, S.; Xiao, Q.; Qi, T.; Duan, H. Satellite Estimation of Dissolved Organic Carbon in Eutrophic Lake Taihu, China. Remote Sens. Environ. 2021, 264, 112572. [Google Scholar] [CrossRef]
  42. Jiang, G.; Ma, R.; Loiselle, S.A.; Duan, H. Optical Approaches to Examining the Dynamics of Dissolved Organic Carbon in Optically Complex Inland Waters. Environ. Res. Lett. 2012, 7, 034014. [Google Scholar] [CrossRef]
  43. Cai, X.; Li, Y.; Lei, S.; Zeng, S.; Zhao, Z.; Lyu, H.; Dong, X.; Li, J.; Wang, H.; Xu, J.; et al. A Hybrid Remote Sensing Approach for Estimating Chemical Oxygen Demand Concentration in Optically Complex Waters: A Case Study in Inland Lake Waters in Eastern China. Sci. Total Environ. 2023, 856, 158869. [Google Scholar] [CrossRef]
  44. Luo, J.; Pu, R.; Ma, R.; Wang, X.; Lai, X.; Mao, Z.; Zhang, L.; Peng, Z.; Sun, Z. Mapping Long-Term Spatiotemporal Dynamics of Pen Aquaculture in a Shallow Lake: Less Aquaculture Coming along Better Water Quality. Remote Sens. 2020, 12, 1866. [Google Scholar] [CrossRef]
  45. Cai, J.; Meng, L.; Liu, H.; Chen, J.; Xing, Q. Estimating Chemical Oxygen Demand in Estuarine Urban Rivers Using Unmanned Aerial Vehicle Hyperspectral Images. Ecol. Indic. 2022, 139, 108936. [Google Scholar] [CrossRef]
  46. Guo, H.; Huang, J.J.; Zhu, X.; Wang, B.; Tian, S.; Xu, W.; Mai, Y. A Generalized Machine Learning Approach for Dissolved Oxygen Estimation at Multiple Spatiotemporal Scales Using Remote Sensing. Environ. Pollut. 2021, 288, 117734. [Google Scholar] [CrossRef]
  47. Sharaf El Din, E.; Zhang, Y. Estimation of Both Optical and Nonoptical Surface Water Quality Parameters Using Landsat 8 OLI Imagery and Statistical Techniques. J. Appl. Remote Sens. 2017, 11, 1. [Google Scholar] [CrossRef]
  48. Elsayed, S.; Ibrahim, H.; Hussein, H.; Elsherbiny, O.; Elmetwalli, A.H.; Moghanm, F.S.; Ghoneim, A.M.; Danish, S.; Datta, R.; Gad, M. Assessment of Water Quality in Lake Qaroun Using Ground-Based Remote Sensing Data and Artificial Neural Networks. Water 2021, 13, 3094. [Google Scholar] [CrossRef]
  49. Ha, N.-T.; Nguyen, H.Q.; Truong, N.C.Q.; Le, T.L.; Thai, V.N.; Pham, T.L. Estimation of Nitrogen and Phosphorus Concentrations from Water Quality Surrogates Using Machine Learning in the Tri and Reservoir, Vietnam. Environ. Monit. Assess. 2020, 192, 789. [Google Scholar] [CrossRef] [PubMed]
  50. Dong, G.; Hu, Z.; Liu, X.; Fu, Y.; Zhang, W. Spatio-Temporal Variation of Total Nitrogen and Ammonia Nitrogen in the Water Source of the Middle Route of the South-To-North Water Diversion Project. Water 2020, 12, 2615. [Google Scholar] [CrossRef]
  51. Zhang, T.; Hu, H.; Ma, X.; Zhang, Y. Long-Term Spatiotemporal Variation and Environmental Driving Forces Analyses of Algal Blooms in Taihu Lake Based on Multi-Source Satellite and Land Observations. Water 2020, 12, 1035. [Google Scholar] [CrossRef]
  52. Yu, X.; Yi, H.; Liu, X.; Wang, Y.; Liu, X.; Zhang, H. Remote-Sensing Estimation of Dissolved Inorganic Nitrogen Concentration in the Bohai Sea Using Band Combinations Derived from MODIS Data. Int. J. Remote Sens. 2016, 37, 327–340. [Google Scholar] [CrossRef]
  53. Liu, C.; Zhang, F.; Ge, X.; Zhang, X.; Chan, N.W.; Qi, Y. Measurement of Total Nitrogen Concentration in Surface Water Using Hyperspectral Band Observation Method. Water 2020, 12, 1842. [Google Scholar] [CrossRef]
  54. Arango, J.G.; Nairn, R.W. Prediction of Optical and Non-Optical Water Quality Parameters in Oligotrophic and Eutrophic Aquatic Systems Using a Small Unmanned Aerial System. Drones 2019, 4, 1. [Google Scholar] [CrossRef]
  55. Yuan, X.; Wang, S.; Fan, F.; Dong, Y.; Li, Y.; Lin, W.; Zhou, C. Spatiotemporal Dynamics and Anthropologically Dominated Drivers of Chlorophyll-a, TN and TP Concentrations in the Pearl River Estuary Based on Retrieval Algorithm and Random Forest Regression. Environ. Res. 2022, 215, 114380. [Google Scholar] [CrossRef] [PubMed]
  56. Wang, X.; Gong, C.; Ji, T.; Hu, Y.; Li, L. Inland Water Quality Parameters Retrieval Based on the VIP-SPCA by Hyperspectral Remote Sensing. J. Appl. Remote Sens. 2021, 15, 042609. [Google Scholar] [CrossRef]
  57. Vakili, T.; Amanollahi, J. Determination of Optically Inactive Water Quality Variables Using Landsat 8 Data: A Case Study in Geshlagh Reservoir Affected by Agricultural Land Use. J. Clean. Prod. 2020, 247, 119134. [Google Scholar] [CrossRef]
  58. Soomets, T.; Toming, K.; Jefimova, J.; Jaanus, A.; Põllumäe, A.; Kutser, T. Deriving Nutrient Concentrations from Sentinel-3 OLCI Data in North-Eastern Baltic Sea. Remote Sens. 2022, 14, 1487. [Google Scholar] [CrossRef]
  59. Guo, H.; Tian, S.; Jeanne Huang, J.; Zhu, X.; Wang, B.; Zhang, Z. Performance of Deep Learning in Mapping Water Quality of Lake Simcoe with Long-Term Landsat Archive. ISPRS J. Photogramm. Remote Sens. 2022, 183, 451–469. [Google Scholar] [CrossRef]
  60. Isenstein, E.M.; Park, M.H. Assessment of Nutrient Distributions in Lake Champlain Using Satellite Remote Sensing. J. Environ. Sci. 2014, 26, 1831–1836. [Google Scholar] [CrossRef]
  61. Sun, D.; Qiu, Z.; Li, Y.; Shi, K.; Gong, S. Detection of Total Phosphorus Concentrations of Turbid Inland Waters Using a Remote Sensing Method. Water Air Soil. Pollut. 2014, 225, 1953. [Google Scholar] [CrossRef]
  62. Baban, S.M.J. Detecting Water Quality Parameters in the Norfolk Broads, U.K. Using Landsat Imagery. Int. J. Remote Sens. 1993, 14, 1247–1267. [Google Scholar] [CrossRef]
  63. Li, L.; Chen, X.; Zhang, M.; Zhang, W.; Wang, D.; Wang, H. The Spatial Variations of Water Quality and Effects of Water Landscape in Baiyangdian Lake, North China. Environ. Sci. Pollut. Res. 2022, 29, 16716–16726. [Google Scholar] [CrossRef]
  64. Gao, Y.; Gao, J.; Yin, H.; Liu, C.; Xia, T.; Wang, J.; Huang, Q. Remote Sensing Estimation of the Total Phosphorus Concentration in a Large Lake Using Band Combinations and Regional Multivariate Statistical Modeling Techniques. J. Environ. Manag. 2015, 151, 33–43. [Google Scholar] [CrossRef]
  65. Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A Comprehensive Review on Water Quality Parameters Estimation Using Remote Sensing Techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef]
  66. Mohseni, F.; Saba, F.; Mirmazloumi, S.M.; Amani, M.; Mokhtarzade, M.; Jamali, S.; Mahdavi, S. Ocean Water Quality Monitoring Using Remote Sensing Techniques: A Review. Mar. Environ. Res. 2022, 180, 105701. [Google Scholar] [CrossRef]
  67. Morel, A.Y.; Gordon, H.R. Report of the Working Group on Water Color. Bound. Layer. Meteorol. 1980, 18, 343–355. [Google Scholar] [CrossRef]
  68. Yang, H.; Kong, J.; Hu, H.; Du, Y.; Gao, M.; Chen, F. A Review of Remote Sensing for Water Quality Retrieval: Progress and Challenges. Remote Sens. 2022, 14, 1770. [Google Scholar] [CrossRef]
  69. Gordon, H.R.; Morel, A.Y. Remote Assessment of Ocean Color for Interpretation of Satellite Visible Imagery: A Review; Springer: New York, NY, USA, 1983; Volume 4. [Google Scholar] [CrossRef]
  70. Dekker, A.G.; Brando, V.E.; Anstee, J.M.; Pinnel, N.; Kutser, T.; Hoogenboom, E.J.; Peters, S.; Pasterkamp, R.; Vos, R.; Olbert, C.; et al. Imaging Spectrometry: Basic Principles and Prospective Applications; Springer: Berlin/Heidelberg, Germany, 2002; pp. 307–359. [Google Scholar] [CrossRef]
  71. Zhang, B.; Li, J.; Shen, Q.; Chen, D. A Bio-Optical Model Based Method of Estimating Total Suspended Matter of Lake Taihu from near-Infrared Remote Sensing Reflectance. Environ. Monit. Assess. 2008, 145, 339–347. [Google Scholar] [CrossRef] [PubMed]
  72. Chen, B.; Mu, X.; Chen, P.; Wang, B.; Choi, J.; Park, H.; Xu, S.; Wu, Y.; Yang, H. Machine Learning-Based Inversion of Water Quality Parameters in Typical Reach of the Urban River by UAV Multispectral Data. Ecol. Indic. 2021, 133, 108434. [Google Scholar] [CrossRef]
  73. Ruescas, A.; Hieronymi, M.; Mateo-Garcia, G.; Koponen, S.; Kallio, K.; Camps-Valls, G. Machine Learning Regression Approaches for Colored Dissolved Organic Matter (CDOM) Retrieval with S2-MSI and S3-OLCI Simulated Data. Remote Sens. 2018, 10, 786. [Google Scholar] [CrossRef]
  74. Tian, S.; Guo, H.; Xu, W.; Zhu, X.; Wang, B.; Zeng, Q.; Mai, Y.; Huang, J.J. Remote Sensing Retrieval of Inland Water Quality Parameters Using Sentinel-2 and Multiple Machine Learning Algorithms. Environ. Sci. Pollut. Res. 2022, 30, 18617–18630. [Google Scholar] [CrossRef]
  75. Xiao, Y.; Guo, Y.; Yin, G.; Zhang, X.; Shi, Y.; Hao, F.; Fu, Y. UAV Multispectral Image-Based Urban River Water Quality Monitoring Using Stacked Ensemble Machine Learning Algorithms—A Case Study of the Zhanghe River, China. Remote Sens. 2022, 14, 3272. [Google Scholar] [CrossRef]
  76. Zhang, F.; Wang, J.; Wang, X. Recognizing the Relationship between Spatial Patterns in Water Quality and Land-Use/Cover Types: A Case Study of the Jinghe Oasis in Xinjiang, China. Water 2018, 10, 646. [Google Scholar] [CrossRef]
  77. Hafeez, S.; Wong, M.S.; Ho, H.C.; Nazeer, M.; Nichol, J.; Abbas, S.; Tang, D.; Lee, K.H.; Pun, L. Comparison of Machine Learning Algorithms for Retrieval of Water Quality Indicators in Case-Ii Waters: A Case Study of Hong Kong. Remote Sens. 2019, 11, 617. [Google Scholar] [CrossRef]
  78. Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; Association for Computing Machinery: New York, NY, USA, 2016; pp. 785–794. [Google Scholar] [CrossRef]
  79. Ogunleye, A.; Wang, Q.-G. XGBoost Model for Chronic Kidney Disease Diagnosis. IEEE/ACM Trans. Comput. Biol. Bioinform. 2020, 17, 2131–2140. [Google Scholar] [CrossRef]
  80. Zamani Joharestani, M.; Cao, C.; Ni, X.; Bashir, B.; Talebiesfandarani, S. PM2.5 Prediction Based on Random Forest, XGBoost, and Deep Learning Using Multisource Remote Sensing Data. Atmosphere 2019, 10, 373. [Google Scholar] [CrossRef]
  81. Zhang, D.; Qian, L.; Mao, B.; Huang, C.; Huang, B.; Si, Y. A Data-Driven Design for Fault Detection of Wind Turbines Using Random Forests and XGboost. IEEE Access 2018, 6, 21020–21031. [Google Scholar] [CrossRef]
  82. Sheridan, R.P.; Wang, W.M.; Liaw, A.; Ma, J.; Gifford, E.M. Extreme Gradient Boosting as a Method for Quantitative Structure–Activity Relationships. J. Chem. Inf. Model. 2016, 56, 2353–2360. [Google Scholar] [CrossRef] [PubMed]
  83. Chen, X.; Huang, L.; Xie, D.; Zhao, Q. EGBMMDA: Extreme Gradient Boosting Machine for MiRNA-Disease Association Prediction. Cell Death Dis. 2018, 9, 3. [Google Scholar] [CrossRef]
  84. Fan, J.; Wang, X.; Wu, L.; Zhou, H.; Zhang, F.; Yu, X.; Lu, X.; Xiang, Y. Comparison of Support Vector Machine and Extreme Gradient Boosting for Predicting Daily Global Solar Radiation Using Temperature and Precipitation in Humid Subtropical Climates: A Case Study in China. Energy Convers. Manag. 2018, 164, 102–111. [Google Scholar] [CrossRef]
  85. Bhagat, S.K.; Tiyasha, T.; Awadh, S.M.; Tung, T.M.; Jawad, A.H.; Yaseen, Z.M. Prediction of Sediment Heavy Metal at the Australian Bays Using Newly Developed Hybrid Artificial Intelligence Models. Environ. Pollut. 2021, 268, 115663. [Google Scholar] [CrossRef]
  86. Chen, L.; Tan, C.H.; Kao, S.J.; Wang, T.S. Improvement of Remote Monitoring on Water Quality in a Subtropical Reservoir by Incorporating Grammatical Evolution with Parallel Genetic Algorithms into Satellite Imagery. Water Res. 2008, 42, 296–306. [Google Scholar] [CrossRef]
  87. Ott, I.; Kõiv, T. Estonian Small Lakes: Special Features and Changes; Estonian Environment Information Centre: Tallinn, Estonia, 1999. [Google Scholar]
  88. EVS-EN ISO 11905-1:2003; Water Quality—Determination of Nitrogen—Part 1: Method Using Oxidative Digestion with Peroxodisulfate. International Organization for Standardization: Geneva, Switzerland, 2003.
  89. EVS-EN ISO 15681-2:2018; Water Quality—Determination of Orthophosphate and Total Phosphorus Contents by Flow Analysis—Part 2: Method by Continuous Flow Analysis. International Organization for Standardization: Geneva, Switzerland, 2018.
  90. EVS-EN ISO 6878:2004; Water Quality—Determination of Phosphorus—Ammonium Molybdate Spectrometric Method. International Organization for Standardization: Geneva, Switzerland, 2004.
  91. ISO 10304-1:2007; Water Quality—Determination of Dissolved Anions by Liquid Chromatography of Ions—Part 1: Determination of Bromide, Chloride, Fluoride, Nitrate, Nitrite, Phosphate and Sulfate. International Organization for Standardization: Geneva, Switzerland, 2007.
  92. ISO 7150-1:1984; Water Quality—Determination of Ammonium—Part 1: Manual Spectrometric Method. International Organization for Standardization: Geneva, Switzerland, 1984.
  93. EVS-EN ISO 5815-1:2019; Water Quality—Determination of Biochemical Oxygen Demand after n Days (BODn)—Part 1: Dilution and Seeding Method with Allylthiourea Addition. International Organization for Standardization: Geneva, Switzerland, 2019.
  94. EVS-ISO 15705:2004; Water Quality—Determination of the Chemical Qxygen Demand Index (ST-COD)—Small-Scale Sealed-Tube Method. International Organization for Standardization: Geneva, Switzerland, 2004.
  95. EVS-EN 15204:2006; Water Quality—Guidance Standard on the Enumeration of Phytoplankton Using Inverted Microscopy (Utermöhl Technique). International Organization for Standardization: Geneva, Switzerland, 1992.
  96. EVS-EN ISO 10523:2012; Water Quality—Determination of pH. International Organization for Standardization: Geneva, Switzerland, 2012.
  97. EVS-EN ISO 5814:2012; Water Quality—Determination of Dissolved Oxygen—Electrochemical Probe Method. International Organization for Standardization: Geneva, Switzerland, 2012.
  98. Toming, K.; Kutser, T.; Tuvikene, L.; Viik, M.; Nõges, T. Dissolved Organic Carbon and Its Potential Predictors in Eutrophic Lakes. Water Res. 2016, 102, 32–40. [Google Scholar] [CrossRef] [PubMed]
  99. Hutchinson, G.E. A Treatise on Limnology: Geography, Physics, and Chemistry. In A Treatise on Limnology; John Wiley and Sons: New York, NY, USA, 1957. [Google Scholar]
  100. Brockmann, C.; Doerffer, R.; Marco, P.; Stelzer, K.; Embacher, S.; Ruescas, A. Evolution of the C2RCC Neural Network for Sentinel 2 and 3 for the Retrieval of Ocean. In Proceedings of the ‘Living Planet Symposium 2016’, (ESA SP-740, August 2016), Prague, Czech Republic, 9–13 May 2016; pp. 9–13. [Google Scholar]
  101. Uudeberg, K.; Ansko, I.; Põru, G.; Ansper, A.; Reinart, A. Using Opticalwater Types to Monitor Changes in Optically Complex Inland and Coastalwaters. Remote Sens. 2019, 11, 2297. [Google Scholar] [CrossRef]
  102. XGBoost Tutorials—Xgboost 1.0.0-SNAPSHOT Documentation. Available online: https://xgboost.readthedocs.io/en/stable/tutorials/index.html (accessed on 30 December 2022).
  103. Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2012, 12, 2825–2830. [Google Scholar]
  104. Doxaran, D.; Ruddick, K.; McKee, D.; Gentili, B.; Tailliez, D.; Chami, M.; Babin, M. Spectral Variations of Light Scattering by Marine Particles in Coastal Waters, from Visible to near Infrared. Limnol. Ocean. 2009, 54, 1257–1271. [Google Scholar] [CrossRef]
  105. Doxaran, D.; Froidefond, J.M.; Lavender, S.; Castaing, P. Spectral Signature of Highly Turbid Waters: Application with SPOT Data to Quantify Suspended Particulate Matter Concentrations. Remote Sens. Environ. 2002, 81, 149–161. [Google Scholar] [CrossRef]
  106. Kutser, T. Quantitative Detection of Chlorophyll in Cyanobacterial Blooms by Satellite Remote Sensing. Limnol. Ocean. 2004, 49, 2179–2189. [Google Scholar] [CrossRef]
  107. Smith, V.H. Eutrophication of Freshwater and Coastal Marine Ecosystems: A Global Problem. Environ. Sci. Pollut. Res. 2003, 10, 126–139. [Google Scholar] [CrossRef]
  108. Xu, Z.; Xu, Y.J. Rapid Field Estimation of Biochemical Oxygen Demand in a Subtropical Eutrophic Urban Lake with Chlorophyll a Fluorescence. Environ. Monit. Assess. 2015, 187, 4171. [Google Scholar] [CrossRef]
  109. Hébert, M.P.; Soued, C.; Fussmann, G.F.; Beisner, B.E. Dissolved Organic Matter Mediates the Effects of Warming and Inorganic Nutrients on a Lake Planktonic Food Web. Limnol. Ocean. 2022, 68, S23–S38. [Google Scholar] [CrossRef]
  110. Erlandsson, M.; Cory, N.; Köhler, S.; Bishop, K. Direct and Indirect Effects of Increasing Dissolved Organic Carbon Levels on PH in Lakes Recovering from Acidification. J. Geophys. Res. Biogeosci. 2010, 115, 1–8. [Google Scholar] [CrossRef]
  111. Grayson, R.B.; Finlayson, B.L.; Gippel, C.J.; Hart, B.T. The Potential of Field Turbidity Measurements for the Computation of Total Phosphorus and Suspended Solids Loads. J. Environ. Manag. 1996, 47, 257–267. [Google Scholar] [CrossRef]
  112. Jones, A.S.; Stevens, D.K.; Horsburgh, J.S.; Mesner, N.O. Surrogate Measures for Providing High Frequency Estimates of Total Suspended Solids and Total Phosphorus Concentrations. J. Am. Water Resour. Assoc. 2011, 47, 239–253. [Google Scholar] [CrossRef]
  113. Kusari, L. Turbidity as a Surrogate for the Determination of Total Phosphorus, Using Relationship Based on Sub-Sampling Techniques. Ecol. Eng. Environ. Technol. 2022, 23, 88–93. [Google Scholar] [CrossRef]
  114. Lannergård, E.E.; Ledesma, J.L.J.; Fölster, J.; Futter, M.N. An Evaluation of High Frequency Turbidity as a Proxy for Riverine Total Phosphorus Concentrations. Sci. Total Environ. 2019, 651, 103–113. [Google Scholar] [CrossRef]
  115. Viso-Vázquez, M.; Acuña-Alonso, C.; Rodríguez, J.L.; Álvarez, X. Remote Detection of Cyanobacterial Blooms and Chlorophyll-a Analysis in a Eutrophic Reservoir Using Sentinel-2. Sustainability 2021, 13, 8570. [Google Scholar] [CrossRef]
  116. Buma, W.G.; Lee, S.-I. Evaluation of Sentinel-2 and Landsat 8 Images for Estimating Chlorophyll-a Concentrations in Lake Chad, Africa. Remote Sens. 2020, 12, 2437. [Google Scholar] [CrossRef]
  117. Shang, Y.; Liu, G.; Wen, Z.; Jacinthe, P.A.; Song, K.; Zhang, B.; Lyu, L.; Li, S.; Wang, X.; Yu, X. Remote Estimates of CDOM Using Sentinel-2 Remote Sensing Data in Reservoirs with Different Trophic States across China. J. Environ. Manag. 2021, 286, 112275. [Google Scholar] [CrossRef]
  118. Kutser, T. The Possibility of Using the Landsat Image Archive for Monitoring Long Time Trends in Coloured Dissolved Organic Matter Concentration in Lake Waters. Remote Sens. Environ. 2012, 123, 334–338. [Google Scholar] [CrossRef]
  119. Cao, Z.; Ma, R.; Melack, J.M.; Duan, H.; Liu, M.; Kutser, T.; Xue, K.; Shen, M.; Qi, T.; Yuan, H. Landsat Observations of Chlorophyll-a Variations in Lake Taihu from 1984 to 2019. Int. J. Appl. Earth Obs. Geoinf. 2022, 106, 102642. [Google Scholar] [CrossRef]
  120. Wei, L.; Wang, Z.; Huang, C.; Zhang, Y.; Wang, Z.; Xia, H.; Cao, L. Transparency Estimation of Narrow Rivers by UAV-Borne Hyperspectral Remote Sensing Imagery. IEEE Access 2020, 8, 168137–168153. [Google Scholar] [CrossRef]
  121. Liu, C.; Duan, P.; Zhang, F.; Jim, C.Y.; Tan, M.L.; Chan, N.W. Feasibility of the Spatiotemporal Fusion Model in Monitoring Ebinur Lake’s Suspended Particulate Matter under the Missing-Data Scenario. Remote Sens. 2021, 13, 3952. [Google Scholar] [CrossRef]
  122. Wang, C.L.; Shi, K.Y.; Ming, X.; Cong, M.Q.; Liu, X.Y.; Guo, W.J. A Comparative Study of the COD Hyperspectral Inversion Models in Water Based on the Maching Learning. Spectrosc. Spectr. Anal. 2022, 42, 2353–2358. [Google Scholar] [CrossRef]
  123. Zhang, Y.; Shi, K.; Sun, X.; Zhang, Y.; Li, N.; Wang, W.; Zhou, Y.; Zhi, W.; Liu, M.; Li, Y.; et al. Improving Remote Sensing Estimation of Secchi Disk Depth for Global Lakes and Reservoirs Using Machine Learning Methods. GIScience Remote Sens. 2022, 59, 1367–1383. [Google Scholar] [CrossRef]
  124. Sommer, U.; Gliwicz, Z.M.; Lampert, W.; Duncan, A. The PEG-Model of Seasonal Succession of Planktonic Events in Fresh Waters. Arch. Hydrobiol. 1986, 106, 433–471. [Google Scholar] [CrossRef]
  125. Welch, E.B. Should Nitrogen Be Reduced to Manage Eutrophication If It Is Growth Limiting? Evidence from Moses Lake. Lake Reserv. Manag. 2009, 25, 401–409. [Google Scholar] [CrossRef]
  126. Schindler, D.W.; Fee, E.J. Diurnal Variation of Dissolved Inorganic Carbon and Its Use in Estimating Primary Production and CO2 Invasion in Lake 227. J. Fish. Res. Board Can. 2011, 30, 1501–1510. [Google Scholar] [CrossRef]
  127. Toming, K.; Tuvikene, L.; Vilbaste, S.; Agasild, H.; Viik, M.; Kisand, A.; Feldmann, T.; Martma, T.; Jones, R.I.; Nõges, T. Contributions of Autochthonous and Allochthonous Sources to Dissolved Organic Matter in a Large, Shallow, Eutrophic Lake with a Highly Calcareous Catchment. Limnol. Ocean. 2013, 58, 1259–1270. [Google Scholar] [CrossRef]
  128. Brezonik, P.; Menken, K.D.; Bauer, M. Landsat-Based Remote Sensing of Lake Water Quality Characteristics, Including Chlorophyll and Colored Dissolved Organic Matter (CDOM). Lake Reserv. Manag. 2005, 21, 373–382. [Google Scholar] [CrossRef]
  129. Tilzer, M.M. Secchi Disk—Chlorophyll Relationships in a Lake with Highly Variable Phytoplankton Biomass. Hydrobiologia 1988, 162, 163–171. [Google Scholar] [CrossRef]
  130. Suursaar, Ü. Summer 2021 Marine Heat Wave in the Gulf of Finland from the Perspective of Climate Warming. Est. J. Earth Sci. 2022, 71, 1. [Google Scholar] [CrossRef]
  131. Stefan, H.G.; Fang, X. Dissolved Oxygen Model for Regional Lake Analysis. Ecol. Model. 1994, 71, 37–68. [Google Scholar] [CrossRef]
  132. Zhang, Y.; Wu, Z.; Liu, M.; He, J.; Shi, K.; Zhou, Y.; Wang, M.; Liu, X. Dissolved Oxygen Stratification and Response to Thermal Structure and Long-Term Climate Change in a Large and Deep Subtropical Reservoir (Lake Qiandaohu, China). Water Res. 2015, 75, 249–258. [Google Scholar] [CrossRef]
  133. Krishnaraj, A.; Honnasiddaiah, R. Remote Sensing and Machine Learning Based Framework for the Assessment of Spatio-Temporal Water Quality in the Middle Ganga Basin. Environ. Sci. Pollut. Res. 2022, 29, 64939–64958. [Google Scholar] [CrossRef]
Remotesensing 16 00464 g001
Figure 1. Study area, 45 lakes of the input data for the GA_XGBoost model (Lakes (In situ), blue dots); and 180 Estonian lakes (>0.1 km2), whose biogeochemical and physical water quality parameters were retrieved using the GA_XGBoost models and Sentinel-2 data (Lakes (Sentinel-2), red dots).
Figure 1. Study area, 45 lakes of the input data for the GA_XGBoost model (Lakes (In situ), blue dots); and 180 Estonian lakes (>0.1 km2), whose biogeochemical and physical water quality parameters were retrieved using the GA_XGBoost models and Sentinel-2 data (Lakes (Sentinel-2), red dots).
Remotesensing 16 00464 g001
Remotesensing 16 00464 g002
Figure 2. Heatmap of Pearson correlations between biogeochemical and physical water quality parameters. Statistically significant correlations (p-value < 0.05) are colored either red (positive) or blue (negative), while correlations that were not significant (p > 0.05) are marked as grey.
Figure 2. Heatmap of Pearson correlations between biogeochemical and physical water quality parameters. Statistically significant correlations (p-value < 0.05) are colored either red (positive) or blue (negative), while correlations that were not significant (p > 0.05) are marked as grey.
Remotesensing 16 00464 g002
Remotesensing 16 00464 g003
Figure 3. The mean Sentinel-2 MSI atmospherically corrected reflectance spectra sorted by the trophic state of study lakes. Sentinel-2 data are derived from each match-up point. Thick lines show the mean value, and the semitransparent area shows the standard error (±) of the mean.
Figure 3. The mean Sentinel-2 MSI atmospherically corrected reflectance spectra sorted by the trophic state of study lakes. Sentinel-2 data are derived from each match-up point. Thick lines show the mean value, and the semitransparent area shows the standard error (±) of the mean.
Remotesensing 16 00464 g003
Remotesensing 16 00464 g004aRemotesensing 16 00464 g004b
Figure 4. Scatter plots of training, test, and validation datasets produced using the best GA_XGB_model for deriving biogeochemical and physical water quality parameters from Sentinel-2 data along with the ideal model (1:1 line). The figure starts on the previous page.
Figure 4. Scatter plots of training, test, and validation datasets produced using the best GA_XGB_model for deriving biogeochemical and physical water quality parameters from Sentinel-2 data along with the ideal model (1:1 line). The figure starts on the previous page.
Remotesensing 16 00464 g004aRemotesensing 16 00464 g004b
Remotesensing 16 00464 g005
Figure 5. The boxplots of the mean values of chlorophyll a (CHL, µg/L), colored dissolved organic matter (CDOM, mg/L), total suspended matter (TSM, mg/L), total nitrogen (TN, mg/L), total phosphorus (TP, mg/L), PO4 (mg/L), TN:TP ratio, BOD5 (mg O2/L), COD (mg O2/L), pH, Secchi depth (SD, m), water temperature (WT, C°), and O2 (mg/L) in 180 Estonian lakes > 0.1 km2 on five different dates using Sentinel-2 data. On the plots the line indicates the median, the circle is the mean, the box shows the interquartile range, and the upper and lower whiskers are the maximum and minimum, respectively.
Figure 5. The boxplots of the mean values of chlorophyll a (CHL, µg/L), colored dissolved organic matter (CDOM, mg/L), total suspended matter (TSM, mg/L), total nitrogen (TN, mg/L), total phosphorus (TP, mg/L), PO4 (mg/L), TN:TP ratio, BOD5 (mg O2/L), COD (mg O2/L), pH, Secchi depth (SD, m), water temperature (WT, C°), and O2 (mg/L) in 180 Estonian lakes > 0.1 km2 on five different dates using Sentinel-2 data. On the plots the line indicates the median, the circle is the mean, the box shows the interquartile range, and the upper and lower whiskers are the maximum and minimum, respectively.
Remotesensing 16 00464 g005
Table 1. Biogeochemical and physical parameters covered by the current study, their abbreviations, measurement units, and reference to measurement methodologies. Optically active parameters are underlined.
Table 1. Biogeochemical and physical parameters covered by the current study, their abbreviations, measurement units, and reference to measurement methodologies. Optically active parameters are underlined.
ParameterAbbreviationUnitReference/Standard
Total nitrogen TNmgN/LISO, 2003 [88]
Total phosphorus TPmgP/LISO, 2018 [89]
PhosphatePO4mg/LISO, 2004 [90]
SulfateSO4mg/LISO, 2007 [91]
Ammonium nitrogenNH4Nmg/LISO, 1984 [92]
5-day biochemical oxygen demand BOD5mgO₂/LISO, 2019 [93]
Dichromatic chemical oxygen demandCODmgO₂/LISO, 2004 [94]
Biomass of phytoplankton FPBMmg/LISO, 1992 [95]
Biomass of cyanobacteriaCYBMmg/LISO, 1992 [95]
pHpH ISO, 2012a [96]
Dissolved oxygen O2mg/LISO, 2012b [97]
Water temperatureWT°C[98]
Secchi disk depth SDm[99]
Chlorophyll a CHLµg/LISO, 1992 [95]
Colored dissolved organic matter CDOMmg/L[98]
Total suspended matterTSMmg/L[98]
Table 2. Means (mean), standard deviations (std), minimum (min) and maximum (max) values, 25th percentile, 50th percentile, 75th percentile, Kurtosis, and Skewness of biogeochemical and physical water quality parameters of study lakes (2015–2020). The names and units of the parameters are available in Table 1. Count shows the number of samples as well as the matchups with Sentinel-2 MSI data.
Table 2. Means (mean), standard deviations (std), minimum (min) and maximum (max) values, 25th percentile, 50th percentile, 75th percentile, Kurtosis, and Skewness of biogeochemical and physical water quality parameters of study lakes (2015–2020). The names and units of the parameters are available in Table 1. Count shows the number of samples as well as the matchups with Sentinel-2 MSI data.
CountMeanStdMin25%50%75%MaxSkewnessKurtosis
TN1020.900.610.150.510.731.103.902.236.77
TP1020.060.190.010.020.030.051.607.0250.4
PO4990.0080.0070.0020.0030.0060.010.052.9010.4
SO41007.707.280.101.704.6512.031.01.130.58
NH4N1020.0230.0210.010.010.020.0240.143.5715.9
BOD51022.151.390.701.301.702.687.501.773.45
COD8742.129.215.023.036.048.01601.994.20
CHL10213.614.91.003.458.3017.51002.6010.4
CDOM10210.915.90.853.105.5510.881.03.2210.7
TSM3815695.98.2399.11542233710.24−0.6
FPBM804.735.400.160.762.606.7821.71.360.82
CYBM581.813.240.000.030.332.0513.02.224.29
PH837.981.073.657.858.218.539.40−2.165.05
O2848.622.422.637.218.8010.115.6−0.060.41
WT8517.15.085.2013.718.020.626.9−0.40−0.35
SD981.881.240.250.701.752.605.000.67−0.37
Table 3. The basic formulae used in this study. B notes the atmospherically corrected angular dependent water-leaving reflectance and index a, b, or c denotes different Sentinel-2 bands (8 bands in different options).
Table 3. The basic formulae used in this study. B notes the atmospherically corrected angular dependent water-leaving reflectance and index a, b, or c denotes different Sentinel-2 bands (8 bands in different options).
Formula
1. Ba + Bb
2. Ba − Bb
3. Ba/Bb
4. Ba * Bb
5. Ba + Bb + Bc
6. Ba + Bb * Bc
7. (Ba + Bb) * Bc
8. (Ba − Bb) * Bc
9. (Ba + Bb)/Bc
10. Ba * Bb/Bc
11. (Ba − Bb)/(Ba + Bb)
12. (Ba/Bb) * (Ba/Bb)
13. Ba/Bb − Ba/Bc
14. Ba − (Bb + Bc)/2
15. Ba/(Bb + Bc)
Table 4. The two- or three-band or band ratio algorithms (selected using filter-based feature selection method) for deriving biogeochemical and physical water quality parameters (y) from Sentinel-2 MSI data that were used as input data (x) in the GA_XGBoost model. The full names and units of the parameters are available in Table 1 and the accuracy indices of the best models are shown in Table 5.
Table 4. The two- or three-band or band ratio algorithms (selected using filter-based feature selection method) for deriving biogeochemical and physical water quality parameters (y) from Sentinel-2 MSI data that were used as input data (x) in the GA_XGBoost model. The full names and units of the parameters are available in Table 1 and the accuracy indices of the best models are shown in Table 5.
Water Quality Parameter (y)x
TP‘B2 * B6’, ‘(B1 − B5) * B3’, ‘(B7/B3)*(B7/B3)’, ‘B4/B2-B4/B7’, ‘(B7 + B2)/B3’, ‘(B2 − B4)*B6’, ‘(B3 + B5) * B1’
TN‘B5 − (B4 + B3)/2’, ‘B7/(B2 + B4)’, ‘B7 − (B4 + B8A)/2’, ‘(B4 + B1)/B3’, ‘B1 − (B7 + B5)/2’, ‘(B1 + B8A)/B3’
PO4‘B2 * B6/B1’, ‘B3 * B6/B2’, ‘B7 * B3/B2’, ‘B2/(B7 + B6)’, ‘B2 − (B6 + B4)/2’, ‘B5 − (B2 + B3)/2’, ‘(B2 − B7) * B4’, ‘(B2 − B6)/(B2 − B6)’, ‘(B2/B6) * (B2/B6)’
NH4‘B2 − (B3 + B4)/2’, ‘B3 − (B6 + B1)/2’, ‘(B6 − B8A) * B5’, ‘B2/B4 − B2/B6’, ‘B2/B6 − B2/B4’, ‘B4/B8A − B4/B1’
SO4‘B3 * B8A/B4’, ‘B4 * B1/B7’, ‘B4/B2 − B4/B1’,’B1/(B7 + B2)’, ‘(B3 + B5)/B1’, ‘(B7 + B2)/B1’, ‘B1 − (B7 + B6)/2’, ‘(B1 − B3) * B5’, ‘(B8A − B7) * B6’
O2‘B5 * B2/B3’, ‘(B4 + B8A) * B3’, ‘B5 − (B4 + B8A)/2’, ‘(B1 − B8A) * B6) ‘
pH‘B2 − B1’, ‘(B6 + B8A)/B7’, ‘B2 − (B1 + B3)/2’, ‘B4 − (B3 + B5)/2’, ‘(B4 − B5) * B3’, ‘B4/B2 − B4/B1’
WT‘(B1 − B3) * B6’, ‘(B1 − B4) * B6’, ‘(B2 − B3) * B4’
COD‘B8A * B6/B1’, ‘B7 + B4 * B5’, ‘B7 + B5 * B4’, ‘B4 − (B5 + B8A)/2’, ‘(B5 − B6)/(B5 − B6)’, ‘B1/B3 − B1/B4’, ‘B1/B4 − B1/B3’
BOD5‘B4/B5’, ‘(B5 + B6)/B4’, ‘B6 − (B1 + B8A)/2’, ‘(B5/B4) * (B5/B4)’
SD‘B6 * B5/B4’, ‘(B1 − B2) * B6’, ‘(B2 − B1) * B6’, ‘(B2 − B5) * B6’
FPBM‘B6 * B2/B1’, ‘B7 + B3 * B2’, ‘(B7 + B6) * B8A’, ‘(B8A + B4) * B6’
CYBM‘B4 + B3 * B7’, ‘(B5 + B4) * B8A’, ‘(B8A + B4) * B7’
CHL‘(B2 + B4) * B8A’, ‘(B2/B6) * (B2/B6)’, ‘B4/B1 − B4/B5’
CDOM‘B2/B5 − B2/B6’, ‘B2/B6 − B2/B4’, ‘B4/B6 − B4/B5’, ‘B6/B7 − B6/B5’, ‘B7/B6 − B7/B5’
TSM‘B6-B2’, ‘B2-(B6 + B7)/2’, ‘(B3 − B4) * B1’, ‘(B4 − B3) * B1’, ‘(B5 − B4) * B8A’, ‘(B6 − B8A) * B7’
Table 5. The performance metrics of the best GA_XGBoost model for deriving biogeochemical and physical water quality parameters from Sentinel-2 data. n shows the number of match-ups between in situ and Sentinel-2 data; R2-is the coefficient of determination; MAPE is mean absolute percentage error (%); and RMSE is the root-mean-square error. Accuracy indices (R2, MAPE, RMSE) of the training, testing and validating phases are shown.
Table 5. The performance metrics of the best GA_XGBoost model for deriving biogeochemical and physical water quality parameters from Sentinel-2 data. n shows the number of match-ups between in situ and Sentinel-2 data; R2-is the coefficient of determination; MAPE is mean absolute percentage error (%); and RMSE is the root-mean-square error. Accuracy indices (R2, MAPE, RMSE) of the training, testing and validating phases are shown.
Water Quality Parameter TrainingTestingValidation
Total nnR2MAPE(%)RMSEnR2MAPE(%)RMSEnR2MAPE(%)RMSE
TP102600.990.160.00210.9036.50.02210.6034.40.02
TN102600.990.210.00210.6836.00.24210.4632.00.32
PO499590.997.240.0005200.8743.90.003200.4543.80.004
NH4102600.993.390.0008210.7975.50.02210.681610.19
SO4100600.990.890.03200.691683.26200.581235.20
O284500.991.980.21170.6215.21.31170.6246.14.54
pH83490.990.590.05170.727.020.64170.717.270.67
WT85510.991.370.78170.6314.13.08170.5817.33.96
COD87510.990.270.17180.4929.612.9180.4243.917.9
BOD5102600.990.030.0005210.9017.80.56210.8530.10.66
SD98580.997.700.12200.5837.90.86200.5738.70.81
FPBM80480.991.320.01160.791692.01160.791092.19
CYBM58340.994.940.0008120.856841.64120.885321.81
CHL102600.9617.33.41210.8071.59.87210.8248.84.78
CDOM102600.990.010.001210.9441.53.77210.9240.76.72
TSM38220.990.00070.00180.9420.322.380.8343.832.1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Toming, K.; Liu, H.; Soomets, T.; Uuemaa, E.; Nõges, T.; Kutser, T. Estimation of the Biogeochemical and Physical Properties of Lakes Based on Remote Sensing and Artificial Intelligence Applications. Remote Sens. 2024, 16, 464. https://doi.org/10.3390/rs16030464

AMA Style

Toming K, Liu H, Soomets T, Uuemaa E, Nõges T, Kutser T. Estimation of the Biogeochemical and Physical Properties of Lakes Based on Remote Sensing and Artificial Intelligence Applications. Remote Sensing. 2024; 16(3):464. https://doi.org/10.3390/rs16030464

Chicago/Turabian Style

Toming, Kaire, Hui Liu, Tuuli Soomets, Evelyn Uuemaa, Tiina Nõges, and Tiit Kutser. 2024. "Estimation of the Biogeochemical and Physical Properties of Lakes Based on Remote Sensing and Artificial Intelligence Applications" Remote Sensing 16, no. 3: 464. https://doi.org/10.3390/rs16030464

APA Style

Toming, K., Liu, H., Soomets, T., Uuemaa, E., Nõges, T., & Kutser, T. (2024). Estimation of the Biogeochemical and Physical Properties of Lakes Based on Remote Sensing and Artificial Intelligence Applications. Remote Sensing, 16(3), 464. https://doi.org/10.3390/rs16030464

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop