On the Importance of Precise Positioning in Robotised Agriculture
Abstract
:1. Introduction
- The innovative integration of visual odometry for enhanced accuracy. Through the integration of visual odometry with the GNSS, we effectively addressed short-term inaccuracies in GNSS readings, demonstrating the feasibility and efficacy of visual-odometry-based precision positioning systems in agricultural settings. Leveraging readily available hardware such as laptops with built-in cameras, our approach offers a cost-effective means to improve positioning accuracy in challenging agricultural environments.
- An empirical validation of budget-friendly GNSS solutions. Our study offers empirical evidence supporting the viability of cost-effective GNSS solutions in agricultural contexts. This validation underscores the practicality of affordable GNSS solutions for precision agriculture, especially for smaller farms facing budget constraints.
- The identification of challenges and potential solutions. Through both analysis of the literature and conclusions drawn from our experiments, this research identifies key challenges and proposes practical solutions for advancing positioning in agricultural robots. Additionally, we suggest potential applications of visual odometry in field robot navigation and autonomy, highlighting its role as a reliable backup system during adverse conditions for satellite-based positioning.
2. Advancing Precision Positioning in Agricultural Technology
2.1. The Role of Localisation in Crop Management
- Low accuracy (errors above one metre)—used for resource management, yield monitoring, and soil sampling;
- Medium accuracy (errors from twenty centimetres to one metre)—for tractor operator navigation with manual guidance;
- High accuracy (few centimetres of error)—for auto-guidance of tractors and machines performing precision operations.
2.2. Guidance Systems for Agricultural Machinery
2.3. Advantages of GNSS Localisation Systems
2.4. Precision in the Execution of Agro-Technical Treatments
2.5. Methods of Improving GNSS Positioning Accuracy
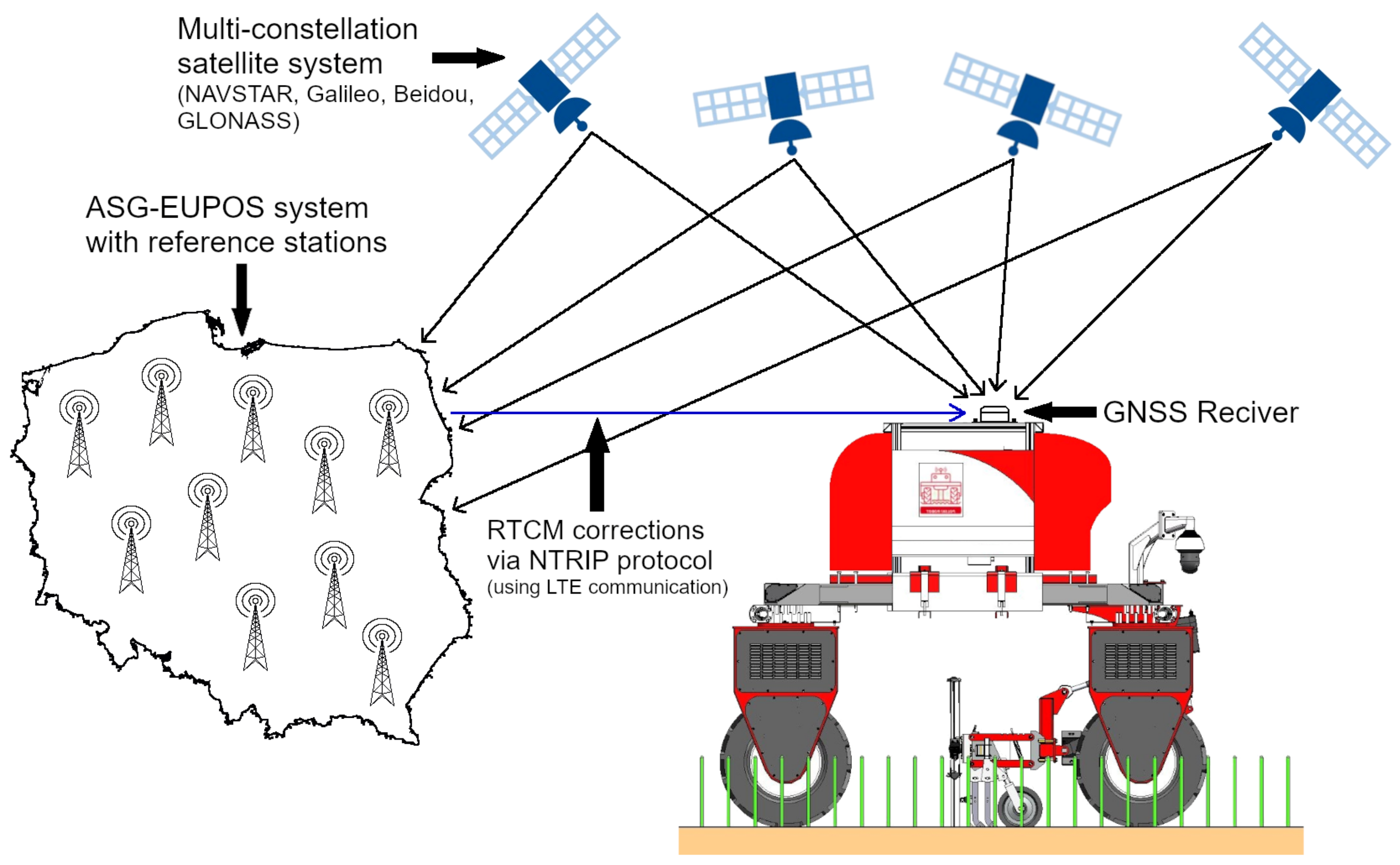
3. Experimental Evaluation of GNSS Localisation under Field Conditions
3.1. Motivation for the Experiment
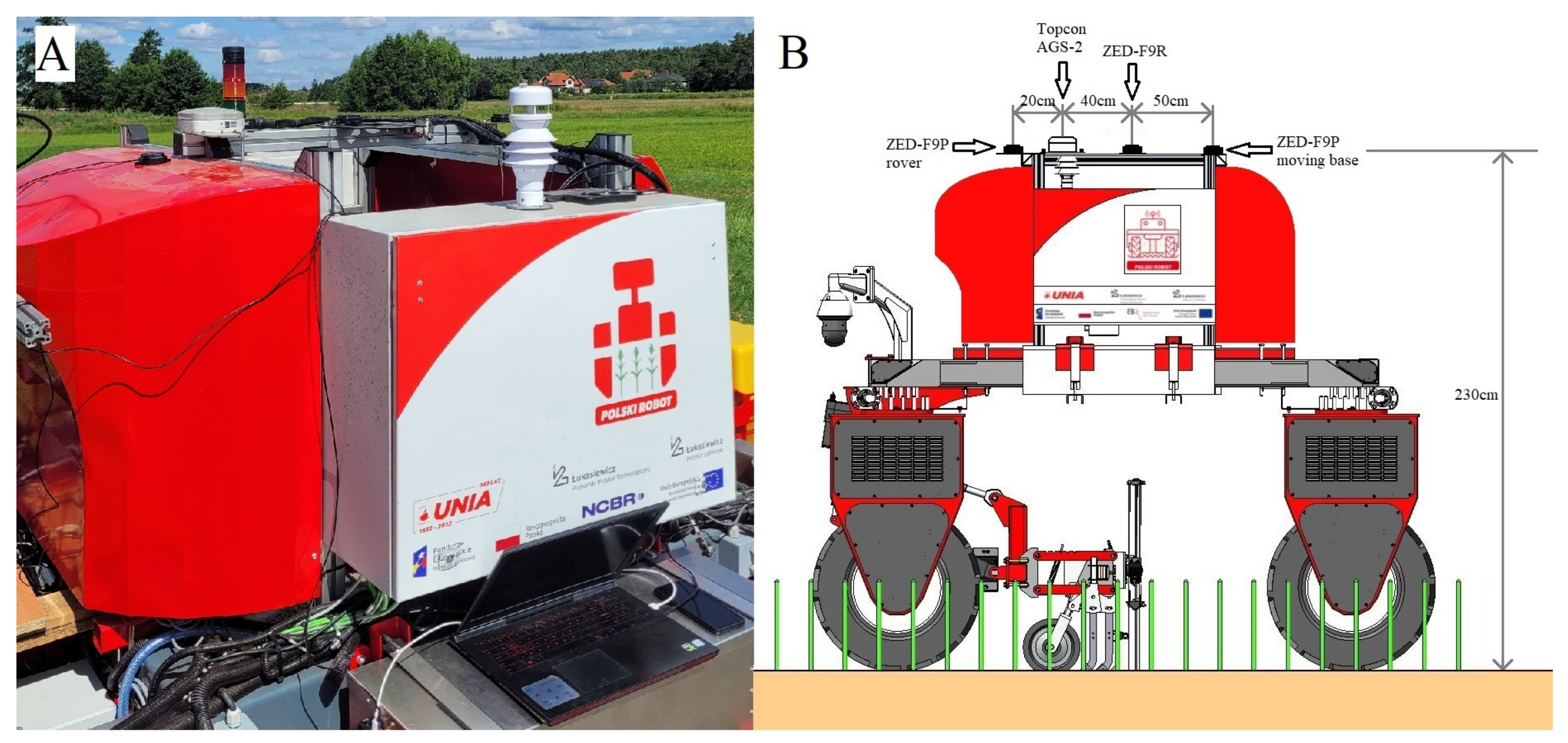
3.2. Experimental Setup and Environment
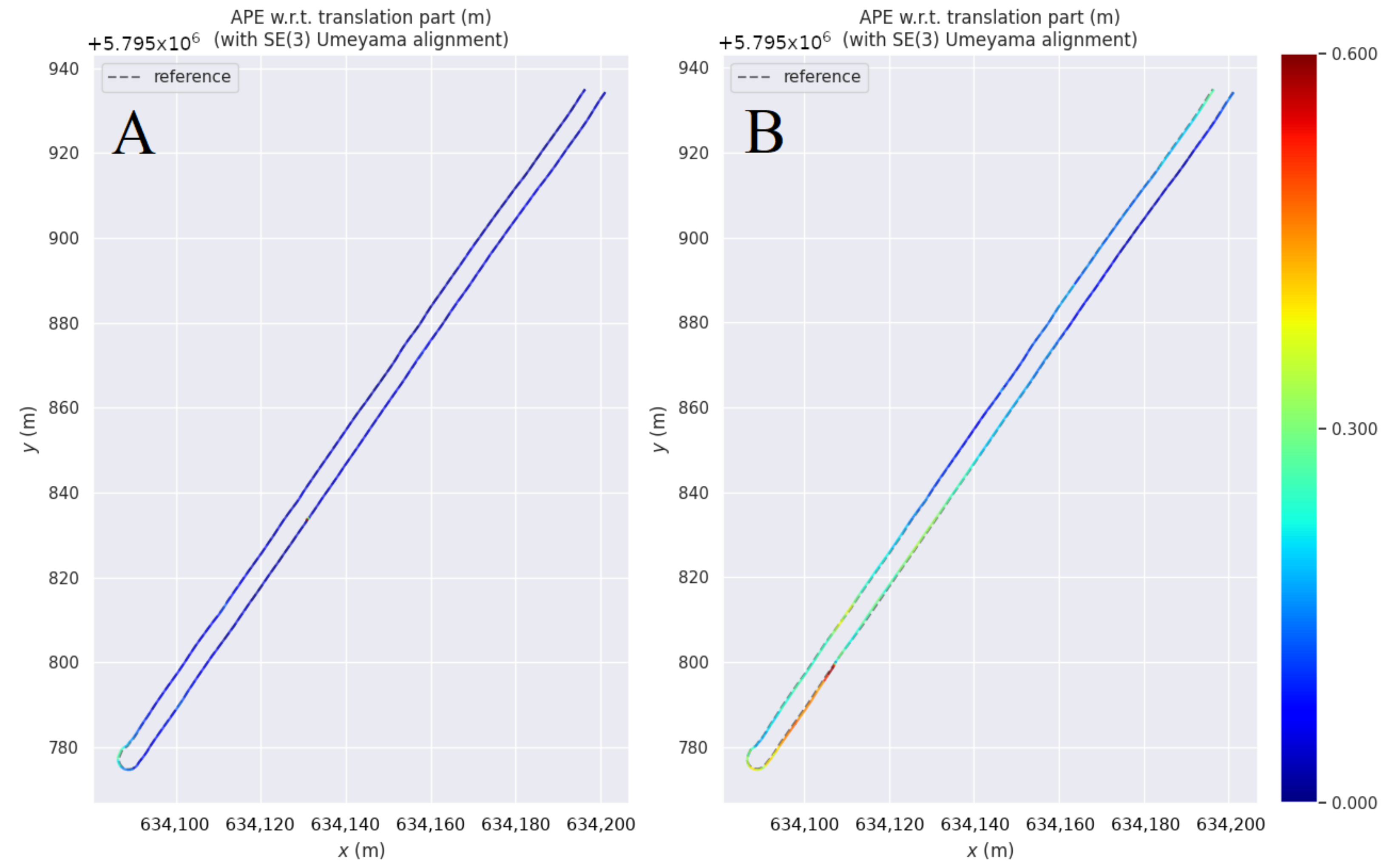
4. Results of GNSS-Based Localisation
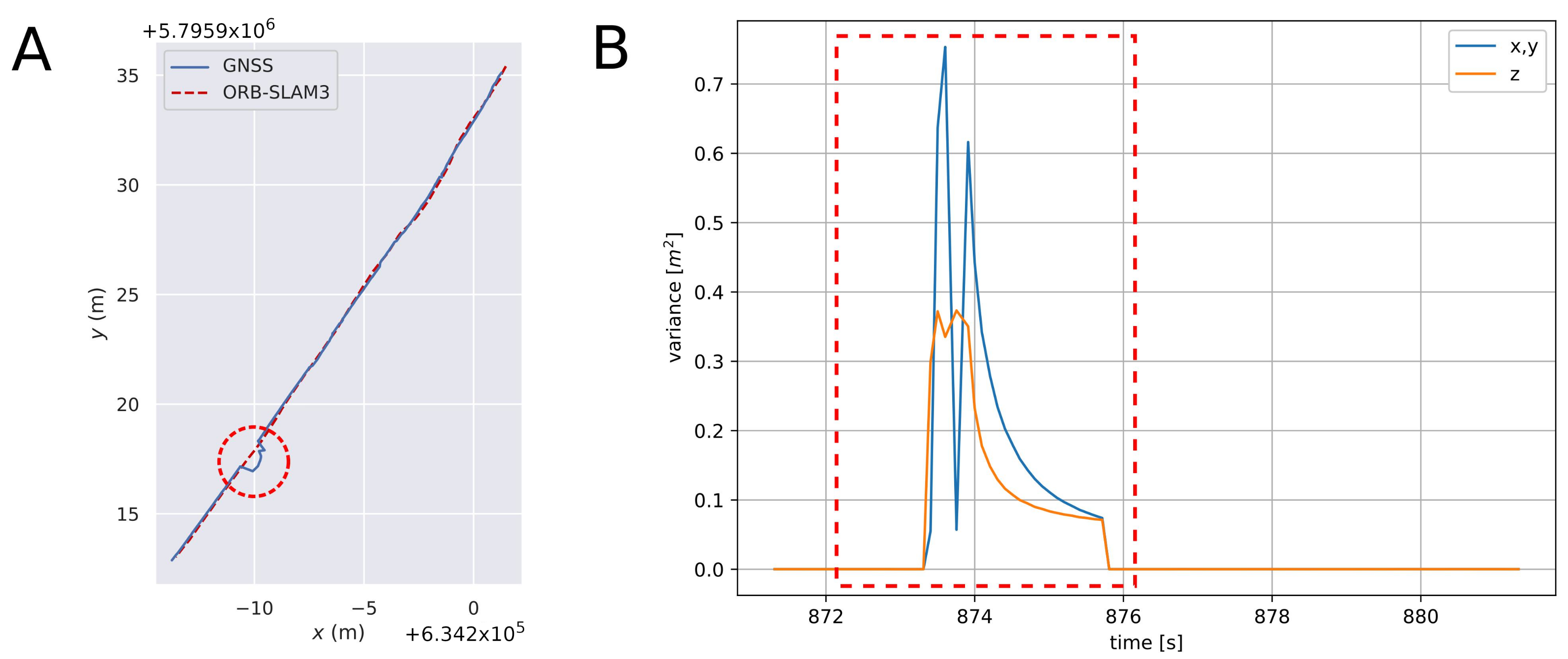
5. Correcting GNSS Trajectories with Visual Odometry
5.1. Low-Cost Visual Odometry as External Localisation Method
5.2. Integration Applying Factor Graph
5.3. Correction Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kulkarni, A.A.; Dhanush, P.; Chetan, B.S.; Gowda, T.; Shrivastava, P.K. Applications of Automation and Robotics in Agriculture Industries; A Review. In Proceedings of the International Conference on Mechanical and Energy Technologies (ICMET), Nanjing, China, 28–30 June 2019. [Google Scholar]
- Marinoudi, V.; Lampridi, M.; Kateris, D.; Pearson, S.; Sorensen, C.G.; Bochtis, D. The Future of Agricultural Jobs in View of Robotization. Sustainability 2021, 13, 12109. [Google Scholar] [CrossRef]
- Jurišić, M.; Plaščak, I.; Barač, Ž.; Radočaj, D.; Zimmer, D. Sensors and Their Application in Precision Agriculture. TehniČKI Glasnik 2021, 15, 529–533. [Google Scholar] [CrossRef]
- Paul, K.; Chatterjee, S.S.; Pai, P.; Varshney, A.; Juikar, S.; Prasad, V.; Bhadra, B.; Dasgupta, S. Viable smart sensors and their application in data driven agriculture. Comput. Electron. Agric. 2022, 198, 107096. [Google Scholar] [CrossRef]
- Vera, J.; Conejero, W.; Mira-García, A.B.; Conesa, M.R.; Ruiz-Sánchez, M.C. Towards irrigation automation based on dielectric soil sensors. J. Hortic. Sci. Biotechnol. 2021, 96, 696–707. [Google Scholar] [CrossRef]
- Guo, J.; Li, X.; Li, Z.; Hu, L.; Yang, G.; Zhao, C.; Fairbairn, D.; Watson, D.; Ge, M. Multi-GNSS precise point positioning for precision Agriculture. Precis. Agric. 2018, 19, 895–911. [Google Scholar] [CrossRef]
- Jha, K.; Doshi, A.; Patel, P.; Shah, M. A comprehensive review on automation in agriculture using artificial intelligence. Artif. Intell. Agric. 2019, 2, 1–12. [Google Scholar] [CrossRef]
- Alameen, A.A.; Al-Gaadi, K.A.; Tola, E. Development and performance evaluation of a control system for variable rate granular fertilizer application. Comput. Electron. Agric. 2019, 160, 31–39. [Google Scholar] [CrossRef]
- Chandel, N.S.; Mehta, C.R.; Tewari, V.K.; Nare, B. Digital map-based site-specific granular fertilizer application system. Curr. Sci. 2016, 111, 1208–1213. [Google Scholar] [CrossRef]
- Al-Gaadi, K.A.; Tola, E.; Alameen, A.A.; Madugundu, R.; Marey, S.A. Control and monitoring systems used in variable rate application of solid fertilizers: A review. J. King Saud Univ. Sci. 2023, 35, 102574. [Google Scholar] [CrossRef]
- Scarfone, A.; Picchio, R.; del Giudice, A.; Latterini, F.; Mattei, P.; Santangelo, E.; Assirelli, A. Semi-Automatic Guidance vs Manual Guidance in Agriculture: A Comparison Work Performance in Wheat Sowing. Electronics 2021, 10, 825. [Google Scholar] [CrossRef]
- Botta, A.; Cavallone, P.; Baglieri, L.; Colucci, G.; Tagliavini, L.; Quaglia, G. A Review of Robots, Perception, and Tasks in Precision Agriculture. Appl. Mech. 2022, 3, 830–854. [Google Scholar] [CrossRef]
- Cheng, C.; Fu, J.; Su, H.; Ren, L. Recent Advancements in Agriculture Robots: Benefits and Challenges. Machines 2023, 11, 48. [Google Scholar] [CrossRef]
- Mahmud, M.S.A.; Abidin, M.S.Z.; Emmanuel, A.A.; Hasan, H.S. Robotics and Automation in Agriculture: Present and Future Applications. Appl. Model. Simul. 2020, 4, 130–140. [Google Scholar]
- Mulla, D.; Khosla, R. Historical Evolution and Recent Advances in Precision Farming. In Soil-Specific Farming; Lal, R., Stewart, B.A., Eds.; CRC Press: Boca Raton, FL, USA, 2015; pp. 1–36. [Google Scholar]
- Radocaj, D.; Plascak, I.; Heffer, G.; Jurisic, M. A Low-Cost Global Navigation Satellite System Positioning Accuracy Assessment Method for Agricultural Machinery. Appl. Sci. 2022, 12, 693. [Google Scholar] [CrossRef]
- Si, J.; Niu, Y.; Lu, J.; Zhang, H. High-Precision Estimation of Steering Angle of Agricultural Tractors Using GPS and Low-Accuracy MEMS. IEEE Trans. Veh. Technol. 2019, 68, 11738–11745. [Google Scholar] [CrossRef]
- Perez-Ruiz, M.; Upadhyaya, S.K. GNSS in Precision Agricultural Operations. In New Approach of Indoor and Outdoor Localization Systems; Elbahhar, F.B., Rivenq, A., Eds.; IntechOpen: Rijeka, Croatia, 2012; Chapter 1. [Google Scholar]
- Nguyen, N.V.; Cho, W.; Hayashi, K. Performance evaluation of a typical low-cost multi-frequency multi-GNSS device for positioning and navigation in agriculture—Part 1: Static testing. Smart Agric. Technol. 2021, 1, 100004. [Google Scholar] [CrossRef]
- Catania, P.; Comparetti, A.; Febo, P.; Morelli, G.; Orlando, S.; Roma, E.; Vallone, M. Position Accuracy Comparision of GNSS Receivers Used for Mapping and Guidance of Agricultural Machines. Agronomy 2020, 10, 924. [Google Scholar] [CrossRef]
- Zawada, M.; Nijak, M.; Mac, J.; Szczepaniak, J.; Legutko, S.; Gościańska-Łowińska, J.; Szymczyk, S.; Kaźmierczak, M.; Zwierzyński, M.; Wojciechowski, J.; et al. Control and Measurement Systems Supporting the Production of Haylage in Baler-Wrapper Machines. Sensors 2023, 23, 2992. [Google Scholar] [CrossRef]
- Monteiro, A.; Santos, S.; Gonçalves, P. Precision Agriculture for Crop and Livestock Farming—Brief Review. Animals 2021, 11, 2345. [Google Scholar] [CrossRef]
- Winterhalter, W.; Fleckenstein, F.; Dornhege, C.; Burgard, W. Localization for precision navigation in agricultural fields—Beyond crop row following. J. Field Robot. 2021, 38, 429–451. [Google Scholar] [CrossRef]
- Šarauskis, E.; Kazlauskas, M.; Naujokienė, V.; Bručienė, I.; Steponavičius, D.; Romaneckas, K.; Jasinskas, A. Variable Rate Seeding in Precision Agriculture: Recent Advances and Future Perspectives. Agriculture 2022, 12, 305. [Google Scholar] [CrossRef]
- Perez-Ruiz, M.; Aguera, J.; Gil, J.; Slaughter, C. Optimization of agrochemical application in olive groves based on positioning sensor. Precis. Agric. 2011, 12, 564–575. [Google Scholar] [CrossRef]
- Gilson, E.; Just, J.; Pellenz, M.E.; de Paula Lima, L.J.; Chang, B.S.; Souza, R.D.; Montejo-Sanchez, S. UAV Path Optimization for Precision Agriculture Wireless Sensor Networks. Sensors 2020, 20, 6098. [Google Scholar]
- Zawada, M.; Legutko, S.; Gościańska-Łowińska, J.; Szymczyk, S.; Nijak, M.; Wojciechowski, J.; Zwierzyński, M. Mechanical Weed Control Systems: Methods and Effectiveness. Sustainability 2023, 15, 15206. [Google Scholar] [CrossRef]
- Gargano, G.; Licciardo, F.; Verrascina, M.; Zanetti, B. The Agroecological Approach as a Model for Multifunctional Agriculture and Farming towards the European Green Deal 2030—Some Evidence from the Italian Experience. Sustainability 2021, 13, 2215. [Google Scholar] [CrossRef]
- Perez-Ruiz, M.; Slaughter, D.C.; Gliever, C.J.; Upadhyaya, S.K. Automatic GPS-based intra-row weed knife control system for transplanted row crops. Comput. Electron. Agric. 2012, 80, 41–49. [Google Scholar] [CrossRef]
- Bogdan, K. Precision farming as an element of the 4.0 industry economy. Ann. Pol. Assoc. Agric. Agribus. Econ. 2020, 22, 119–128. [Google Scholar]
- D’Antonio, P.; Mehmeti, A.; Toscano, F.; Fiorentino, C. Operating performance of manual, semi-automatic, and automatic tractor guidance systems for precision farming. Res. Agric. Eng. 2023, 69, 179–188. [Google Scholar] [CrossRef]
- iTEC Pro. Available online: https://www.deere.com/en/technology-products/precision-ag-technology/guidance/itec-pro/ (accessed on 26 February 2024).
- Trimble Agriculture. Available online: https://agriculture.trimble.com/en/products/hardware/guidance-control/nav-900-guidance-controller (accessed on 10 June 2023).
- Tayebi, A.; Gomez, J.; Fernandez, M.; de Adana, F.; Gutierrez, O. Low-cost experimental application of real-time kinematic positioning for increasing the benefits in cereal crops. Int. J. Agric. Biol. Eng. 2021, 14, 175–181. [Google Scholar] [CrossRef]
- FieldBee. Available online: https://www.fieldbee.com/product/fieldbee-powersteer-basic/ (accessed on 10 June 2023).
- Agri Info Design. Available online: https://agri-info-design.com/en/agribus-navi/ (accessed on 10 June 2023).
- He, L. Variable Rate Technologies for Precision Agriculture. In Encyclopedia of Smart Agriculture Technologies; Springer International Publishing: Cham, Switzerland, 2022; pp. 1–9. [Google Scholar] [CrossRef]
- Trimble Agriculture. Available online: https://agriculture.trimble.com/en/products/hardware/displays/gfx-750-display (accessed on 10 June 2023).
- Topcon Positioning. Available online: https://www.topconpositioning.com/agriculture-gnss-and-guidance/gnss-receivers-and-controllers/ags-2 (accessed on 10 June 2023).
- John Deere Guidance Solutions. Available online: https://www.deere.com/en/technology-products/precision-ag-technology/guidance/ (accessed on 10 June 2023).
- FieldBee. Available online: https://www.fieldbee.com/blog/fieldbee-tractor-autosteer-versus-other-systems/ (accessed on 10 June 2023).
- Precision Agriculture: An Opportunity for EU Farmers-Potential Support with the CAP 2014–2020. Directorate-General for Internal Policies. Policy Department B. Structural and Cohesion Polices. European Parliamentary Research Service. Belgium. 2014. Available online: https://www.europarl.europa.eu/RegData/etudes/note/join/2014/529049/IPOL-AGRI_NT(2014)529049_EN.pdf (accessed on 10 June 2023).
- Kayacan, E.; Young, S.N.; Peschel, J.M.; Chowdhary, G. High-precision control of trcked field robots in the presence of unknown traction coefficients. Field Robot. 2018, 35, 1050–1062. [Google Scholar] [CrossRef]
- Gonzalez-de Santos, P.; Fernandez, R.; Sepulveda, D.; Navas, E.; Emmi, L.; Armada, M. Field Robots for Intelligent Farms—Inhering Features from Industry. Agronomy 2020, 10, 1638. [Google Scholar] [CrossRef]
- Thrun, S.; Burgard, W.; Fox, D. Probabilistic Robotics; Intelligent Robotics and Autonomous Agents; The MIT Press: Cambridge, MA, USA, 2005. [Google Scholar]
- Fountas, S.; Mylonas, N.; Malounas, I.; Rodias, E.; Santos, C.H.; Pekkeriet, E. Agricultural Robotics for Field Operations. Sensors 2020, 20, 2672. [Google Scholar] [CrossRef] [PubMed]
- Levoir, S.J.; Farley, P.A.; Sun, T.; Xu, C. High-Accuracy Adaptive Low-Cost Location Sensing Subsystems for Autonomous Rover in Precision Agriculture. Ind. Appl. 2020, 1, 74–94. [Google Scholar] [CrossRef]
- Guzman, L.E.S.; Acevedo, M.L.R.; Guevara, A.R. Weed-removal system based on artificial vision and movement planning by A* and RRT techniques. Acta Sci. Agron. 2019, 31, 42687. [Google Scholar] [CrossRef]
- Rivera, G.; Porras, R.; Florencia, R.; Sánchez-Solís, J.P. LiDAR applications in precision agriculture for cultivating crops: A review of recent advances. Comput. Electron. Agric. 2023, 207, 107737. [Google Scholar] [CrossRef]
- Ronen, A.; Agassi, E.; Yaron, O. Sensing with Polarized LIDAR in Degraded Visibility Conditions Due to Fog and Low Clouds. Sensors 2021, 21, 2510. [Google Scholar] [CrossRef]
- Pallottino, F.; Menesatti, P.; Figorilli, S.; Antonucci, F.; Tomasone, R.; Colantoni, A.; Costa, C. Machine Vision Retrofit System for Mechanical Weed Control in Precision Agriculture Applications. Sustainability 2018, 10, 2209. [Google Scholar] [CrossRef]
- Xu, B.; Chai, L.; Zhang, C. Research and application on corn crop identification and positioning method based on Machine vision. Inf. Process. Agric. 2023, 10, 106–113. [Google Scholar] [CrossRef]
- Mavridou, E.; Vrochidou, E.; Papakostas, G.A.; Pachidis, T.; Kaburlasos, V.G. Machine Vision Systems in Precision Agriculture for Crop Farming. J. Imaging 2019, 5, 89. [Google Scholar] [CrossRef]
- Li, J.; Tang, L. Crop recognition under weedy conditions based on 3D imaging for robotic weed control. Field Robotics 2018, 35, 596–611. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, Y.; Mu, D.; Bai, L.; Zhuang, H.; Li, H. YOLOX-based blue laser weeding robot in corn field. Plant Sci. 2022, 13, 1017803. [Google Scholar] [CrossRef]
- Supper, G.; Barta, N.; Gronauer, A.; Motsch, V. Localization accuracy of a robot platform using indoor positioning methods in a realistic outdoor setting. Die Bodenkult. J. Land Manag. Food Environ. 2021, 72, 133–139. [Google Scholar] [CrossRef]
- Jingyao, G.; Lie, T.; Brain, S. Plant Recognition through the Fusion of 2D and 3D Images for Robotic Weeding. In Proceedings of the ASABE Annual International Meeting, New Orleans, LA, USA, 26–29 July 2015. [Google Scholar]
- Weiss, U.; Biber, P.; Laible, S.; Bohlmann, K.; Zell, A. Plant Species Classification using a 3D LIDAR Sensor and Machine Lerning. In Proceedings of the 9th International Conference on Machine Learning and Applications, Washington, DC, USA, 12–14 December 2010. [Google Scholar]
- Fan, G.; Huang, J.; Yang, D.; Rao, L. Sampling visual SLAM with a wide-angle camera for legged mobile robots. IET Cyber-Syst. Robot. 2022, 4, 356–375. [Google Scholar] [CrossRef]
- Schmittmann, O.; Lammers, P.S. A True-Color Sensor and Suitable Evaluation Algorithm for Plant Recognition. Sensors 2017, 17, 1823. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.V.; Cho, W. Performance Evaluation of a Typical Low-Cost Multi-Frequency Multi-GNSS Device for Positioning and Navigation in Agriculture—Part 2: Dynamic Testing. AgriEngineering 2023, 5, 127–140. [Google Scholar] [CrossRef]
- Zhang, W.; Gong, L.; Huang, S.; Wu, S.; Liu, C. Factor graph-based high-precision visual positioning for agricultural robots with fiducial markers. Comput. Electron. Agric. 2022, 201, 107295. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, J. GNSS reveiver autonomous integrity monitoring (RAIM) algorithm based on robust estimation. Geod. Geodyn. 2016, 7, 117–123. [Google Scholar] [CrossRef]
- Blanch, J.; Walker, T.; Enge, P.; Lee, Y.; Pervan, B.; Rippl, M.; Spletter, A.; Kropp, V. Baseline Advanced RAIM User Algorithm and Possible Improvements. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 713–732. [Google Scholar] [CrossRef]
- Hewitson, S.; Wang, J. Extended Receiver Autonomous Integrity Monitoring (eRAIM) for GNSS/INS Integration. J. Surv. Eng. 2010, 136, 13–22. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Gebre-Egziaber, D. Kalman Filter-Based RAIM for GNSS Receivers. IEEE Trans. Aerosp. Electron. Syst. 2015, 51, 2444–2459. [Google Scholar] [CrossRef]
- Vieira, D.; Orjuela, R.; Spisser, M.; Basset, M. Positioning and Attitude determination for Precision Agriculture Robots based on IMU and Two RTK GPSs Sensor Fusion. IFAC PapersOnLine 2022, 55–32, 60–65. [Google Scholar] [CrossRef]
- Skrzypczyński, P. Mobile Robot Localization: Where We Are and What Are the Challenges? In Proceedings of the Automation 2017; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Eds.; Springer: Cham, Switzerland, 2017; pp. 249–267. [Google Scholar]
- Cao, M.; Zhang, J.; Chen, W. Visual-Inertial-Laser SLAM Based on ORB-SLAM3. Unmanned Syst. 2023, 12, 1–10. [Google Scholar] [CrossRef]
- He, X.; Gao, W.; Sheng, C.; Zhang, Z.; Pan, S.; Duan, L.; Zhang, H.; Lu, X. LiDAR-Visual-Inertial Odometry Based on Optimized Visual Point-Line Features. Remote Sens. 2022, 14, 622. [Google Scholar] [CrossRef]
- Cremona, J.; Comelli, R.; Pire, T. Experimental evaluation of Visual-Inertial Odometry systems for arable farming. J. Field Robot. 2022, 39, 1121–1135. [Google Scholar] [CrossRef]
- Skrzypczyński, P.; Ćwian, K. Localization of Agricultural Robots: Challenges, Solutions, and a New Approach. In Automation 2023: Key Challenges in Automation, Robotics and Measurement Techniques; Szewczyk, R., Zieliński, C., Kaliczyńska, M., Bučinskas, V., Eds.; Springer: Cham, Switzerland, 2023; pp. 118–128. [Google Scholar]
- Ampatzidis, Y.; De Bellis, L.; Luvisi, A. iPathology: Robotic Applications and Management of Plants and Plant Diseases. Sustainability 2017, 9, 1010. [Google Scholar] [CrossRef]
- Zaman, S.; Comba, L.; Biglia, A.; Ricauda Aimonino, D.; Barge, P.; Gay, P. Cost-effective visual odometry system for vehicle motion control in agricultural environments. Comput. Electron. Agric. 2019, 162, 82–94. [Google Scholar] [CrossRef]
- Geoportal Krajowy. Available online: https://mapy.geoportal.gov.pl/imap/Imgp_2.html?gpmap=gp0 (accessed on 30 September 2023).
- Google Maps Satellite View. Available online: https://www.google.pl/maps/dir//52.2965534,16.9670898/@52.2279691,16.625214,115569m/data=!3m1!1e3?entry=ttu (accessed on 30 September 2023).
- ASG-EUPOS Reference stations. Available online: https://www.asgeupos.pl/index.php?wpg_type=syst_descr&sub=ref_st (accessed on 30 September 2023).
- Grupp, M. evo: Python Package for the Evaluation of Odometry and SLAM. 2017. Available online: https://github.com/MichaelGrupp/evo (accessed on 30 September 2023).
- Sturm, J.; Engelhard, N.; Endres, F.; Burgard, W.; Cremers, D. A Benchmark for the Evaluation of RGB-D SLAM Systems. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vilamoura-Algarve, Portugal, 7–12 October 2012; pp. 573–580. [Google Scholar]
- Umeyama, S. Least-squares estimation of transformation parameters between two point patterns. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 376–380. [Google Scholar] [CrossRef]
- Liu, J.; Gao, W.; Hu, Z. Optimization-Based Visual-Inertial SLAM Tightly Coupled with Raw GNSS Measurements. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Xian, China, 30 May–5 June 2021; pp. 11612–11618. [Google Scholar]
- Chang, L.; Niu, X.; Liu, T.; Tang, J.; Qian, C. GNSS/INS/LiDAR-SLAM Integrated Navigation System Based on Graph Optimization. Remote Sens. 2019, 11, 1009. [Google Scholar] [CrossRef]
- Shu, F.; Lesur, P.; Xie, Y.; Pagani, A.; Stricker, D. SLAM in the Field: An Evaluation of Monocular Mapping and Localization on Challenging Dynamic Agricultural Environment. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, 5–9 January 2021; pp. 1760–1770. [Google Scholar]
- Scaramuzza, D.; Fraundorfer, F. Visual Odometry [Tutorial]. IEEE Robot. Autom. Mag. 2011, 18, 80–92. [Google Scholar] [CrossRef]
- Engel, J.; Schöps, T.; Cremers, D. LSD-SLAM: Large-Scale Direct Monocular SLAM. In Proceedings of the Computer Vision—ECCV 2014; Fleet, D., Pajdla, T., Schiele, B., Tuytelaars, T., Eds.; Springer International Publishing: Cham, Switzerland, 2014; pp. 834–849. [Google Scholar]
- Mur-Artal, R.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM: A Versatile and Accurate Monocular SLAM System. IEEE Trans. Robot. 2015, 31, 1147–1163. [Google Scholar] [CrossRef]
- Campos, C.; Elvira, R.; Rodríguez, J.J.G.; Montiel, J.M.M.; Tardós, J.D. ORB-SLAM3: An Accurate Open-Source Library for Visual, Visual–Inertial, and Multimap SLAM. IEEE Trans. Robot. 2021, 37, 1874–1890. [Google Scholar] [CrossRef]
- Ćwian, K.; Nowicki, M.R.; Skrzypczyński, P. GNSS-Augmented LiDAR SLAM for Accurate Vehicle Localization in Large Scale Urban Environments. In Proceedings of the 17th International Conference on Control, Automation, Robotics and Vision (ICARCV), Singapore, 11–13 December 2022. [Google Scholar]
- Grisetti, G.; Kümmerle, R.; Stachniss, C.; Burgard, W. A Tutorial on Graph-Based SLAM. IEEE Intell. Transp. Syst. Mag. 2010, 2, 31–43. [Google Scholar] [CrossRef]
- Kümmerle, R.; Grisetti, G.; Strasdat, H.; Konolige, K.; Burgard, W. g2o: A general framework for graph optimization. In Proceedings of the IEEE International Conference on Robotics and Automation, Shanghai, China, 9–13 May 2011; pp. 3607–3613. [Google Scholar]


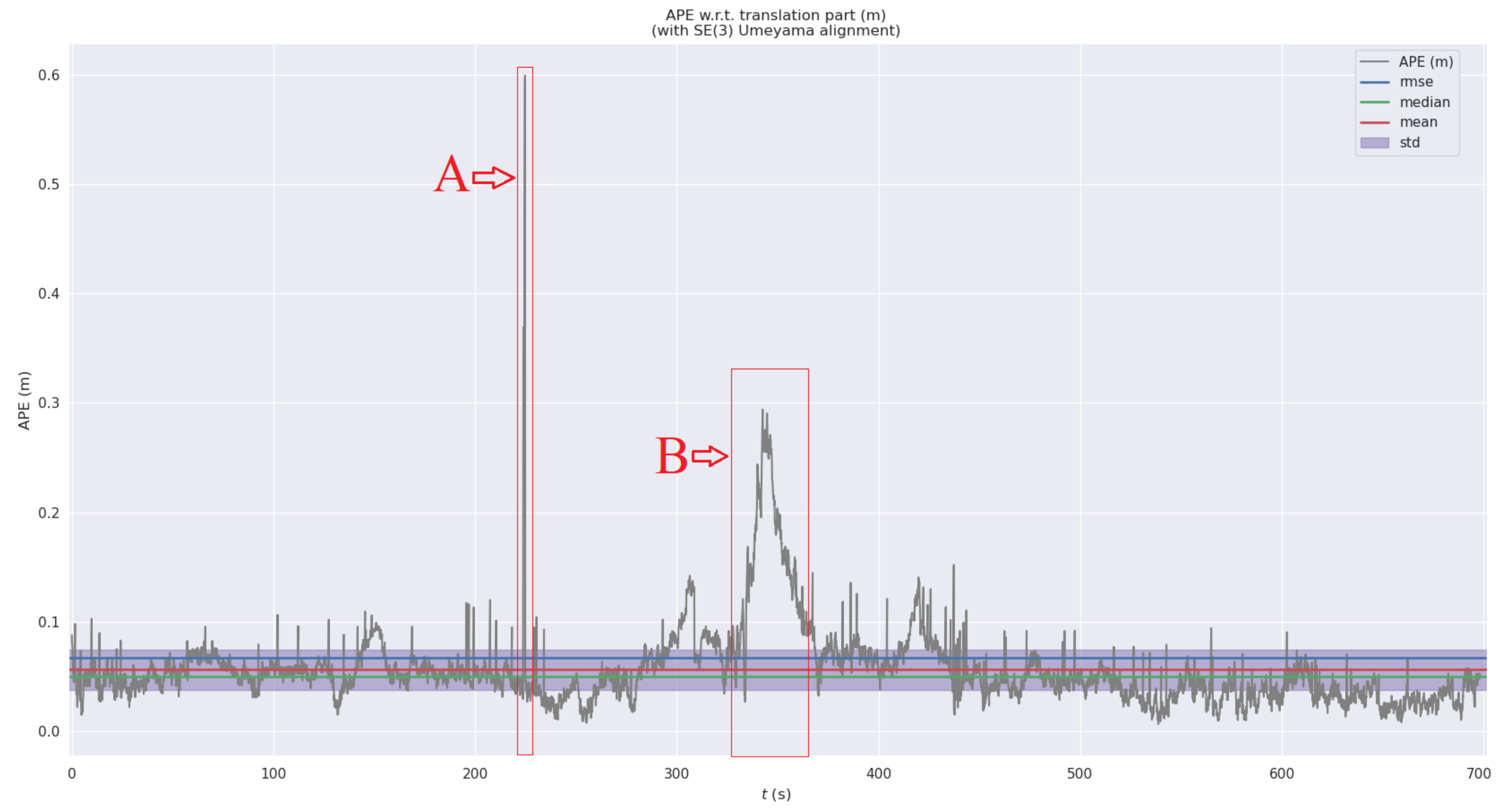
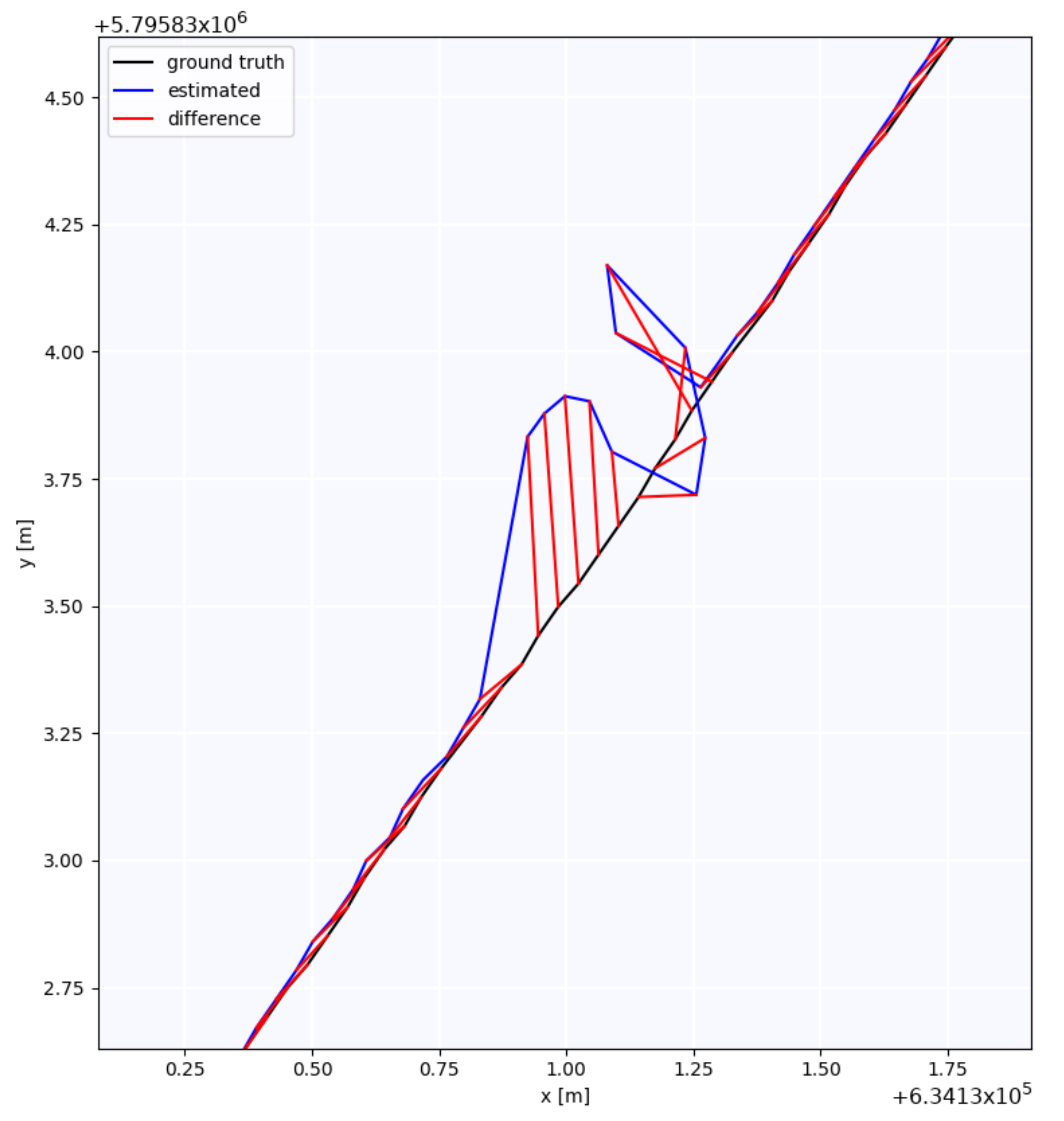
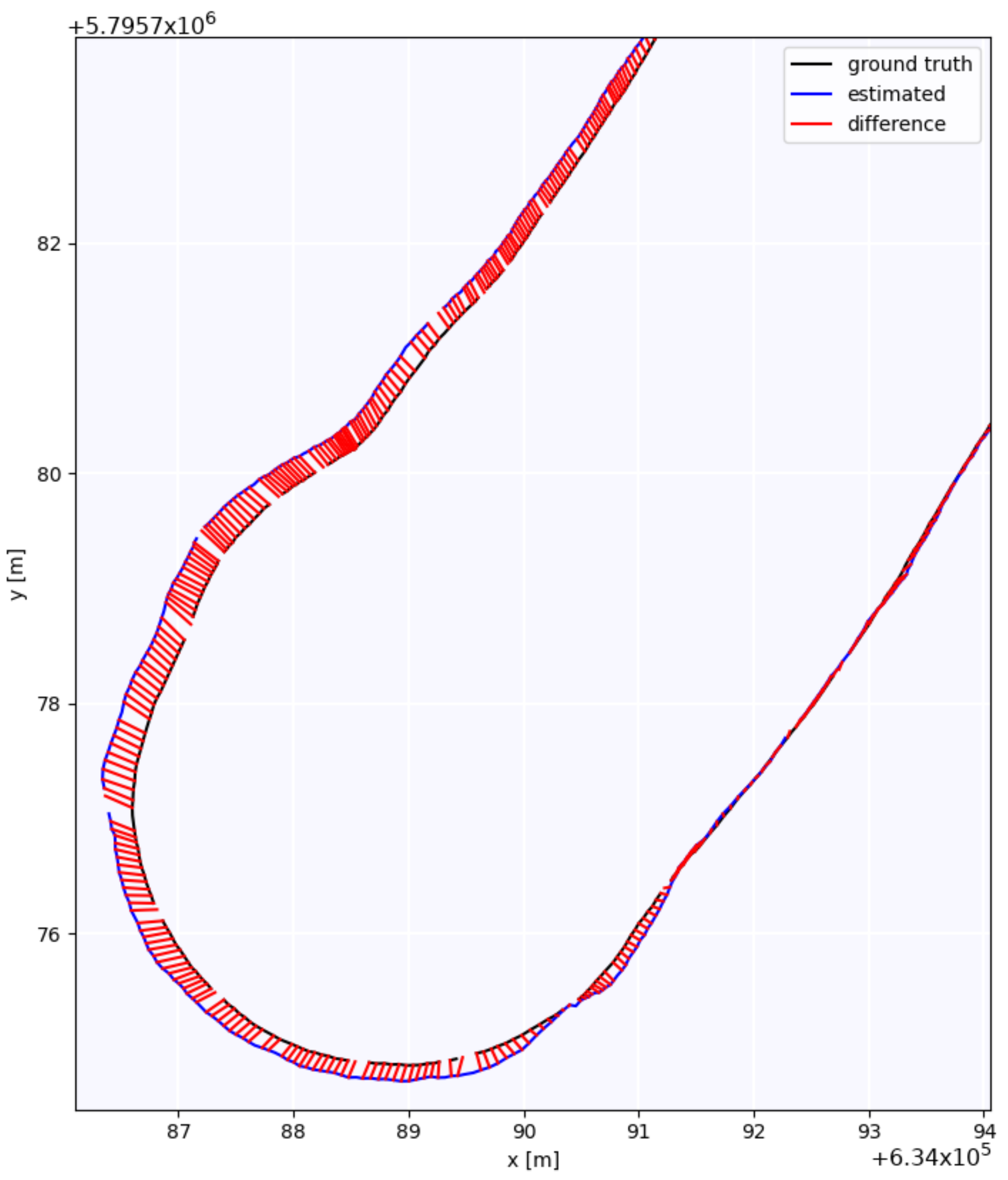
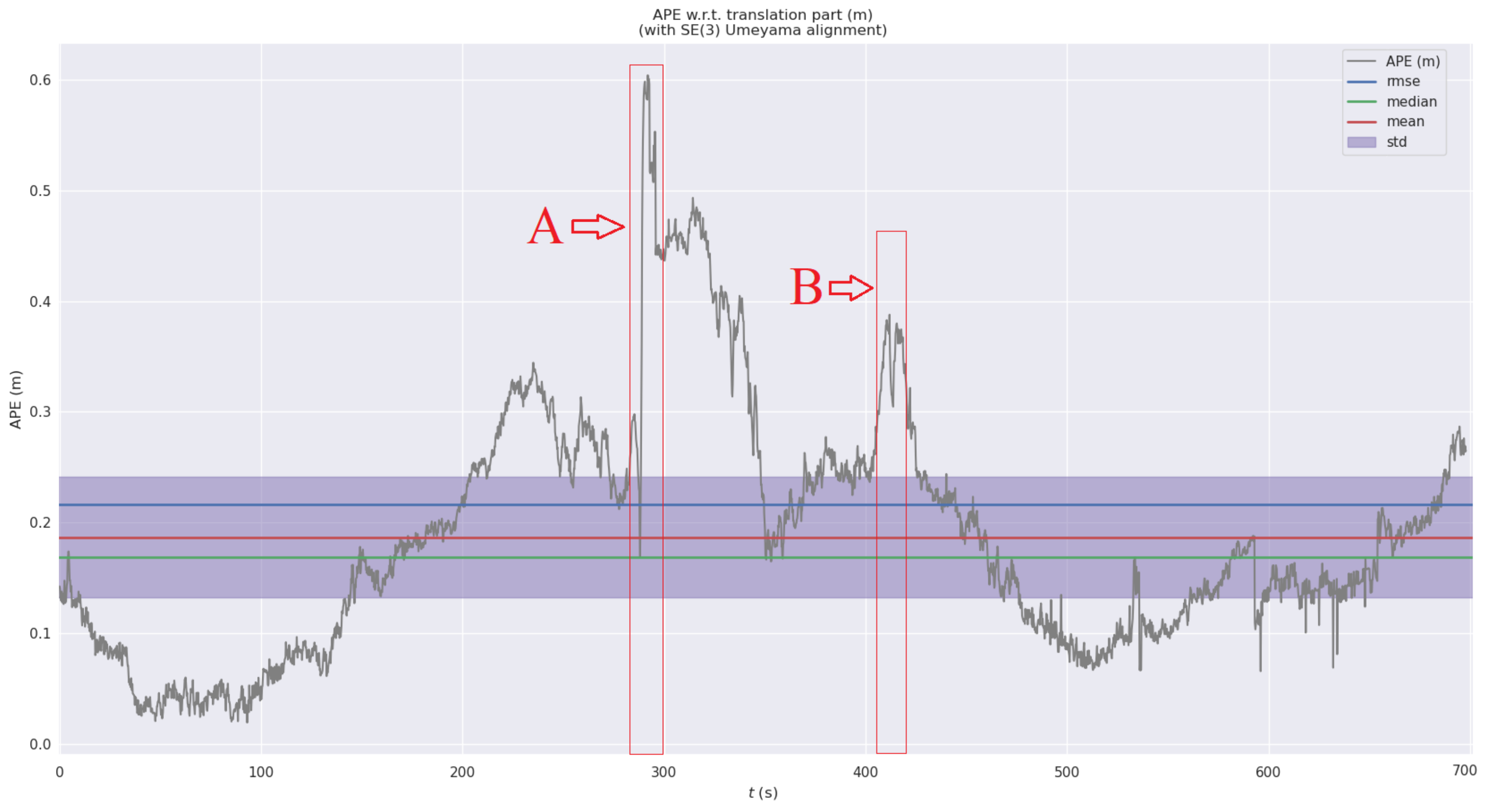
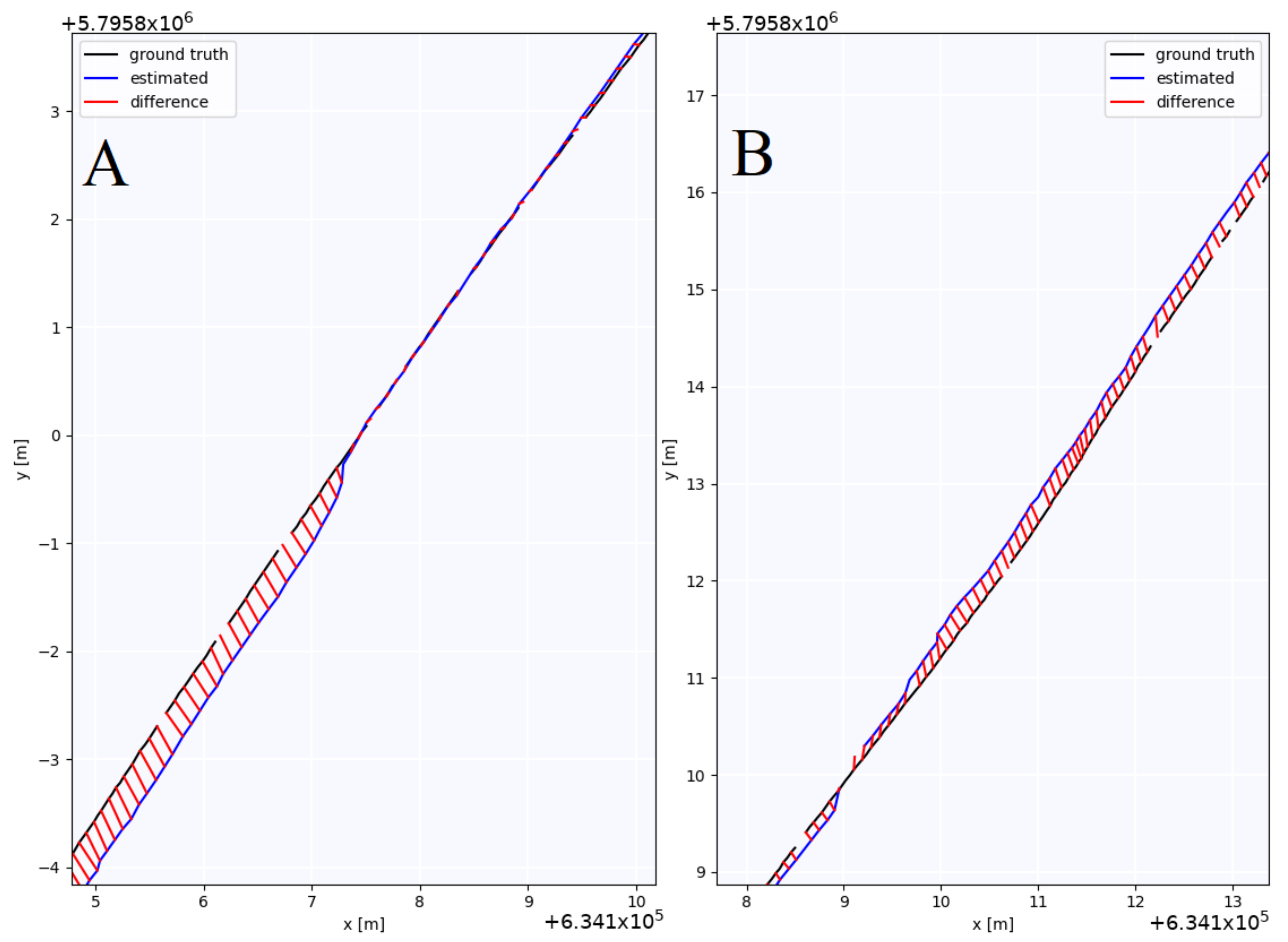

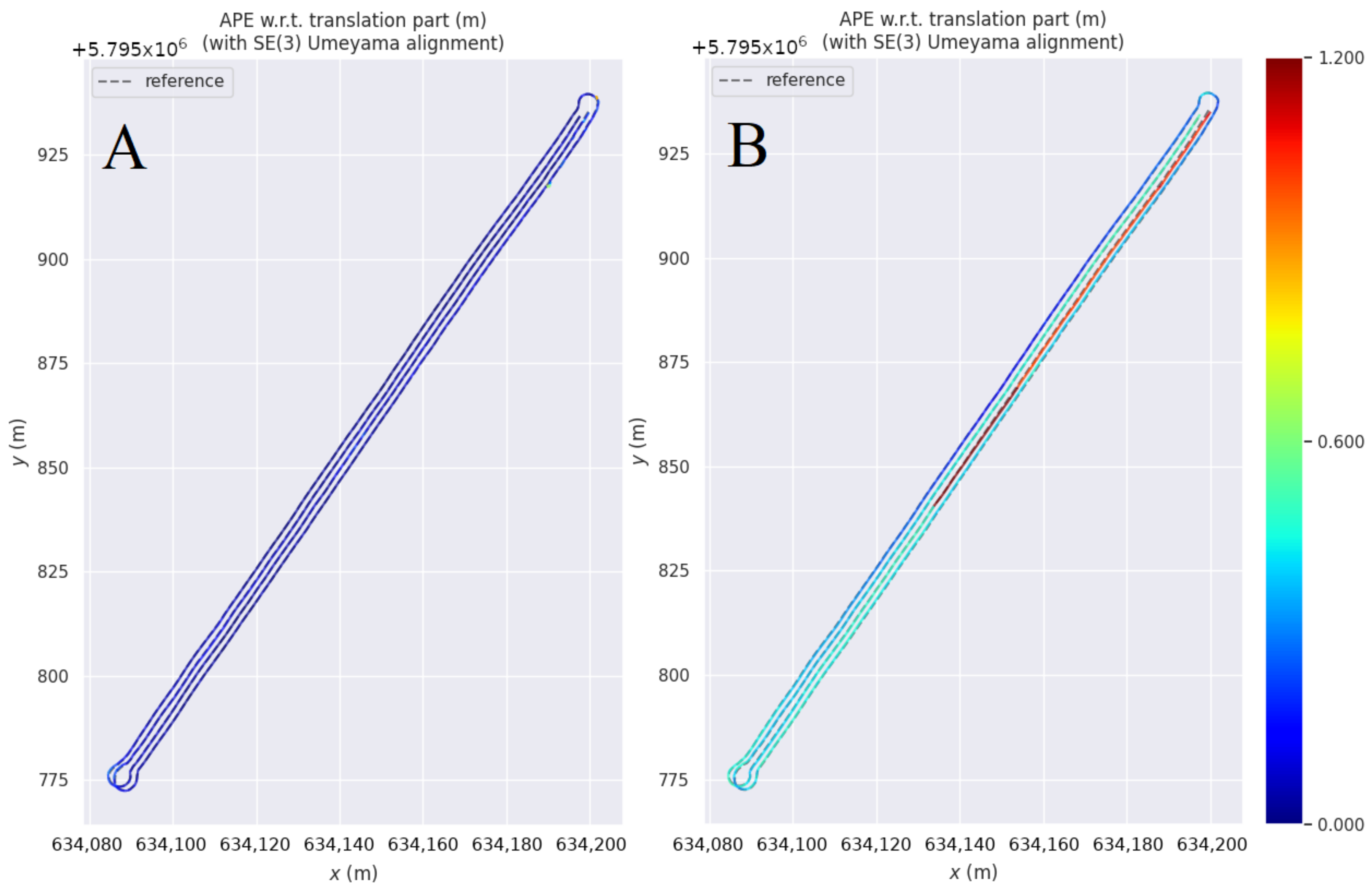

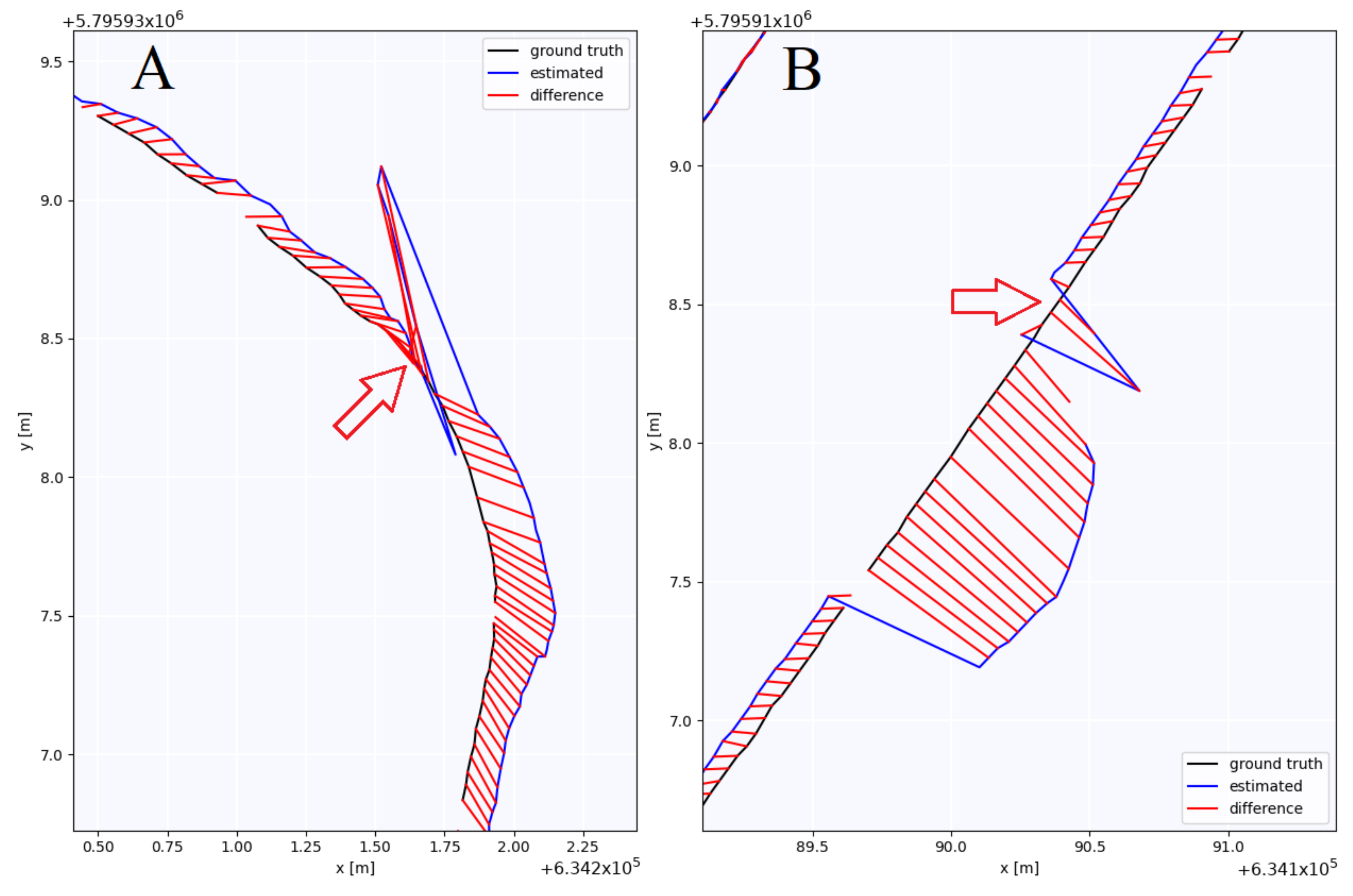
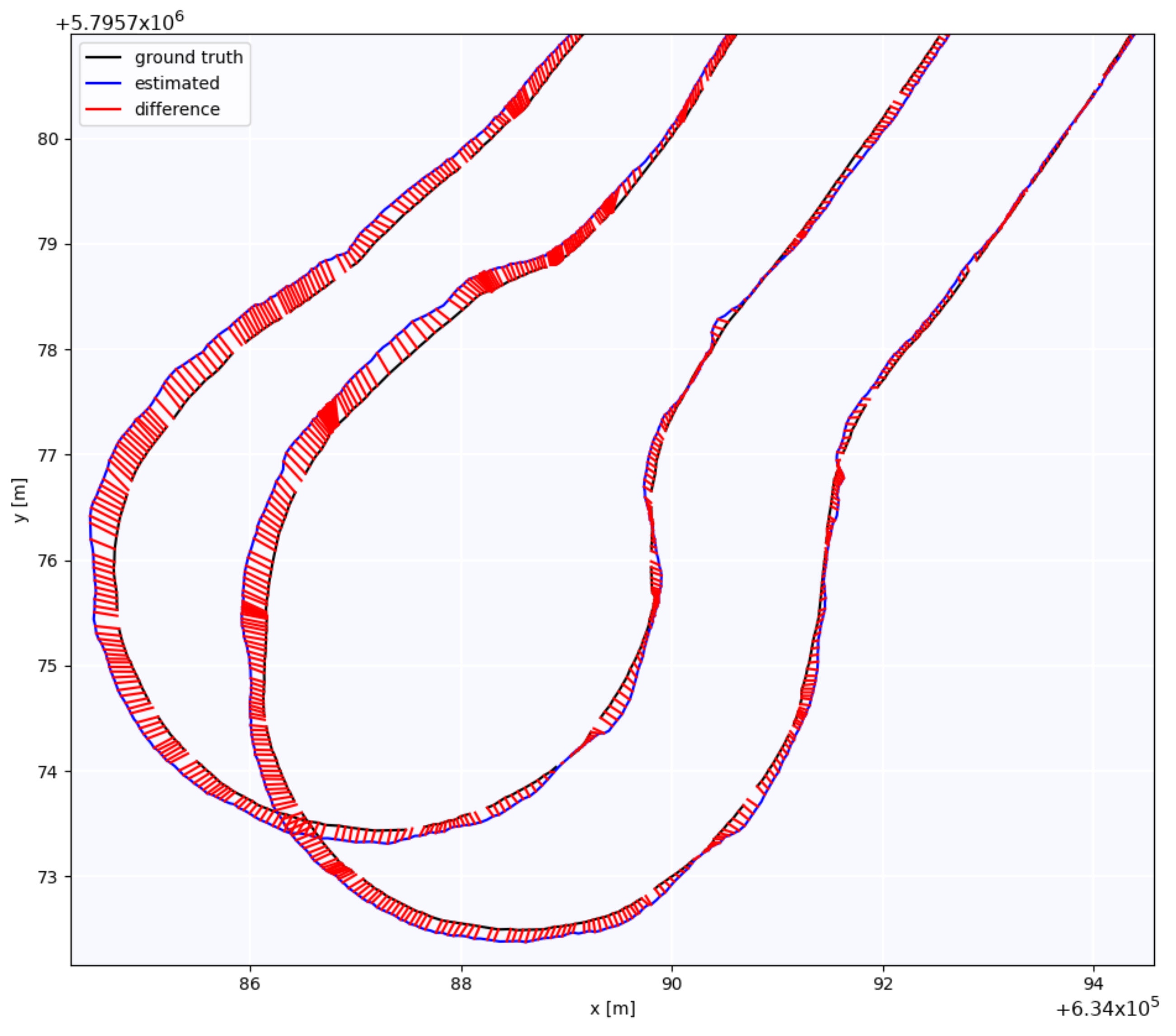
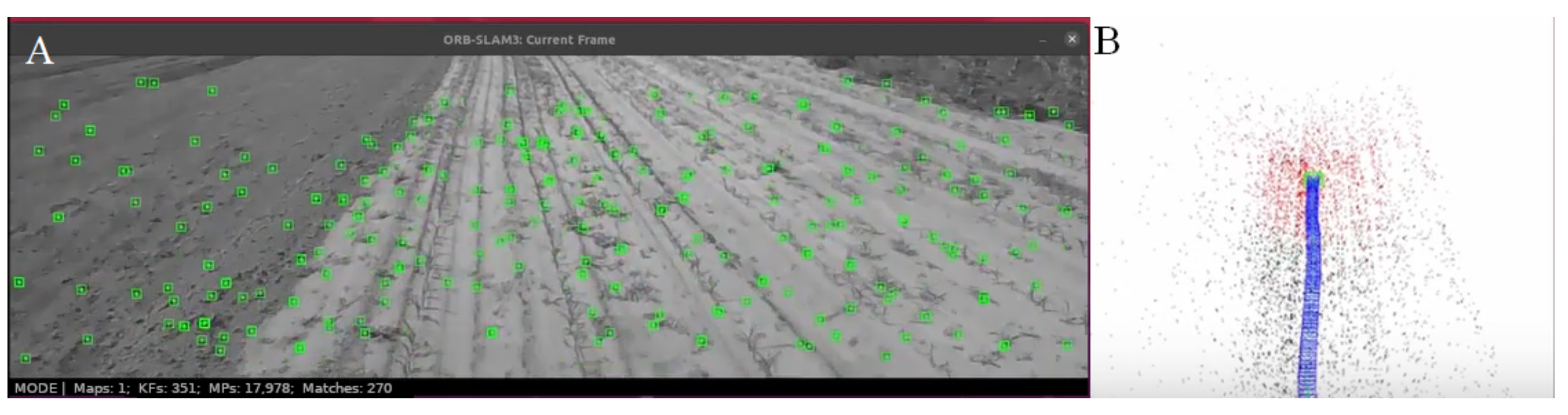


| Reciver | RMSE [m] | Mean [m] | Median [m] | std [m] | min [m] | max [m] | SSE [m] |
|---|---|---|---|---|---|---|---|
| ZED-F9R | 0.2165 | 0.1868 | 0.1685 | 0.1095 | 0.0192 | 0.6040 | 148.740 |
| ZED-F9P | 0.0671 | 0.0561 | 0.0497 | 0.0369 | 0.0064 | 0.5991 | 28.7672 |
| Reciver | RMSE [m] | Mean [m] | Median [m] | std [m] | min [m] | max [m] | SSE [m] |
|---|---|---|---|---|---|---|---|
| ZED-F9R | 0.5514 | 0.4757 | 0.4192 | 0.2787 | 0.1244 | 1.4379 | 2154.8667 |
| ZED-F9P | 0.0836 | 0.0682 | 0.0583 | 0.0483 | 0.0029 | 0.8706 | 99.3947 |
| Receiver | RMSE [m] | Mean [m] | Median [m] | std [m] | min [m] | max [m] | SSE [m] |
|---|---|---|---|---|---|---|---|
| ZED-F9P | 0.0660 | 0.0558 | 0.0497 | 0.0352 | 0.0062 | 0.4026 | 27.7628 |
| Receiver | RMSE [m] | Mean [m] | Median [m] | std [m] | min [m] | max [m] | SSE [m] |
|---|---|---|---|---|---|---|---|
| ZED-F9P | 0.0815 | 0.06787 | 0.0582 | 0.0451 | 0.0025 | 0.4261 | 94.4173 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nijak, M.; Skrzypczyński, P.; Ćwian, K.; Zawada, M.; Szymczyk, S.; Wojciechowski, J. On the Importance of Precise Positioning in Robotised Agriculture. Remote Sens. 2024, 16, 985. https://doi.org/10.3390/rs16060985
Nijak M, Skrzypczyński P, Ćwian K, Zawada M, Szymczyk S, Wojciechowski J. On the Importance of Precise Positioning in Robotised Agriculture. Remote Sensing. 2024; 16(6):985. https://doi.org/10.3390/rs16060985
Chicago/Turabian StyleNijak, Mateusz, Piotr Skrzypczyński, Krzysztof Ćwian, Michał Zawada, Sebastian Szymczyk, and Jacek Wojciechowski. 2024. "On the Importance of Precise Positioning in Robotised Agriculture" Remote Sensing 16, no. 6: 985. https://doi.org/10.3390/rs16060985
APA StyleNijak, M., Skrzypczyński, P., Ćwian, K., Zawada, M., Szymczyk, S., & Wojciechowski, J. (2024). On the Importance of Precise Positioning in Robotised Agriculture. Remote Sensing, 16(6), 985. https://doi.org/10.3390/rs16060985






