Practical Limitations of Using the Tilt Compensation Function of the GNSS/IMU Receiver
Abstract
:1. Introduction
2. Positioning Performance
- Availability. The absolute number of RTK fixed solutions during a certain period.
- Accuracy. The deviation of RTK fixed positions from ground truth with a higher degree of accuracy, where the ground truth can be determined by using a total station or by post-processing long-term GNSS data.
- Reliability. The percentage that the position error (with respect to ground truth) is less than three times the corresponding estimate of the coordinate quality (CQ) [12].
- (a)
- Predicted accuracy—the accuracy of position determination by the system relative to the actual values;
- (b)
- Repeatable accuracy—the level of accuracy that allows the user to return to the coordinates determined earlier by the same system;
- (c)
- Relative accuracy—the ability to measure (determine) the coordinates relative to a different user within the same system at the same time [13].
3. Methods of Testing GNSS Receivers
3.1. Aspects of Data Processing
3.2. Accuracy Aspects of GNSS/IMU
4. Results
4.1. The Previously Performed Experiment
4.2. The Accuracy of GNSS/IMU Receivers
5. Discussion
6. Conclusions
- For which tasks is the tilt compensation function most useful?
- What are the tasks that they cannot be used for?
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hofmann-Wellenhof, B.; Lichtenegger, H.; Wasle, E. GNSS—Global Navigation Satellite Systems: GPS, GLONASS, Galileo & More; Springer: Wien, Austria, 2008; 516p, ISBN 978-3-211-73012-6. [Google Scholar]
- Langley, R.B.; The Magnetic Compass and GPS. GPS World. 2003. Available online: http://gauss.gge.unb.ca/papers.pdf/gpsworld.september03.pdf (accessed on 5 November 2023).
- Luo, X.; Schaufler, S.; Richter, B. Leica GS18 T World’s Fastest GNSS RTK Rover; Leica Geosystems AG: Heerbrugg, Switzerland, 2018. [Google Scholar]
- Lin, H. High-precision RTK Positioning with Tilt, Compensation: Data Fusion Algorithm. In Proceedings of the 34th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2021), St. Louis, MO, USA, 20–24 September 2021; Wuhan University: Wuhan, China, 2021. [Google Scholar]
- Chen, Q.; Lin, H.; Guo, R.; Niu, X. Rapid and accurate initial alignment of the low-cost MEMS IMU chip dedicated for tilted RTK receiver. GPS Solut. 2020, 24, 119. [Google Scholar] [CrossRef]
- Luo, X.; Schaufler, S.; Carrera, M.; Celebi, I. High-precision RTK positioning with calibration-free tilt compensation. In Proceedings of the FIG Congress 2018, Istanbul, Turkey, 6–11 May 2018. [Google Scholar]
- Muhammad, S. GNSS/INS Integration in Urban Areas; Department of Electronics and Telecommunications; Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Luo, X.; Chen, J.; Richter, B. How Galileo benefits high-precision RTK—What to expect with the current constellation. GPS World 2017, 28, 22–28. [Google Scholar]
- NovAtel Customer Service. GPS Position Accuracy Measures. NovAtel Positioning Leadership, APN-029, Rev 1. 2003. Available online: http://www.gisresources.com/wp-content/uploads/2014/03/gps_book.pdf (accessed on 21 March 2024).
- An, X.; Meng, X.; Jiang, W. Multi-constellation GNSS precise point positioning with multi-frequency raw observations and dual-frequency observations of ionospheric-free linear combination. Satell. Navig. 2020, 1, 7. [Google Scholar] [CrossRef]
- Urke, T. Accuracy of Tilt-Compensated GNSS-Sensors Using Network-RTK; Fakultet for Ingeniørvitenskap Institutt for Vareproduksjon og Byggteknikk; Noregs Teknisk-Naturvitskaplege Universitet: Trondheim, Norway, 2021. [Google Scholar]
- González-Calvo, M.; Luo, X.; Aponte, J.A.; Richter, B. Improved high-precision RTK positioning through multipath reduction and interference mitigation. In Proceedings of the FIG Congress. Volunteering for the Future—Geospatial Excellence for a Better Living, Warsaw, Poland, 11–15 September 2022. [Google Scholar]
- Specht, C.; Szot, T.; Specht, M.; Dąbrowski, P. Selected aspects of testing the positioning accuracy of GNSS receivers used in sports and recreation by dynamic measurements Balt. J. Health Phys. Act. 2019, 11, 75–84. [Google Scholar] [CrossRef]
- Yang, N.; Freestone, J. High-performance GNSS antennas with phase-reversal quadrature feeding network and parasitic circular array. In Proceedings of the ION GNSS+ 2016, Portland, OR, USA, 12–16 September 2016; pp. 364–372. [Google Scholar]
- Bojorquez-Pacheco, N.; Romero-Andrade, R.; Trejo-Soto, M.E.; Hernández-Andrade, D.; Nayak, K.; Vidal-Vega, A.I.; Arana-Medina, A.I.; Sharma, G.; Acosta-Gonzalez, L.E.; Serrano-Agila, R. Ocena delovanja eno in dvofrekvenčnih nizkocenovnih spreje-mnikov GNSS v statičnem relativnem načinu|Performance evaluation of single and double-frequency low-cost GNSS receivers in static relative mode. Geod. Vestn. 2023, 67, 235–248. [Google Scholar] [CrossRef]
- El-Hattab, A.I. Influence of GPS antenna phase center variation on precise positioning. NRIAG J. Astron. Geophys. 2013, 2, 272–277. [Google Scholar] [CrossRef]
- Rocken, C.; Meertens, C.; Stephens, B.; Braun, J.; VanHove, T.; Perry, S.; Ruud, O.; McCallum, M.; Richardson, J.; UNAVCO Academic Research Infrastructure (ARI) Receiver and Antenna Test Report. UNAVCO Boulder Facility International Report. Available online: https://www.unavco.org/projects/project-support/development-testing/publications/ari_test.pdf (accessed on 5 December 2023).
- Zhou, R.; Hu, Z.; Zhao, Q.; Cai, H.; Liu, X.; Liu, C.; Wang, G.; Kan, H.; Chen, L. Consistency Analysis of the GNSS Antenna Phase Center Correction Models. Remote Sens. 2022, 14, 540. [Google Scholar] [CrossRef]
- Heister, H. The new ISO standard 17123-8 for checking GNSS field measuring systems. In Proceedings of the FIG Working Week, Stockholm, Sweden, 14–19 June 2008. [Google Scholar]
- ISO 17123-8:2015; Optics and Optical Instruments—Field Procedures for Testing Geodetic and Surveying Instruments, Part 8: GNSS Field Meas-urement Systems in Real-Time Kinematic (RTK). ISO: Geneva, Switzerland, 2015.
- Mader, G.L. GPS Antenna Calibration at the National Geodetic Survey. GPS Solut. 1999, 3, 50–58. [Google Scholar] [CrossRef]
- Prešeren, P.P.; Mencin, A.; Stopar, B. Analiza preizkusa instrumentarija gnss-rtk po navodilih standarda iso 17123-8.|Analysis of gnss-rtk instruments testing on the iso 17123-8 instructions. Geod. Vestn. 2010, 54, 607–626. [Google Scholar] [CrossRef]
- Ignjatović Stupar, D.; Ogrizović, V. Using single frequency receivers for future cubesat GPS-RO missions. In Proceedings of the 6th International Conference, Subotica, Serbia, 20 April 2018. [Google Scholar] [CrossRef]
- Li, J.; Li, F.; Liu, L.; Huang, L.; Zhou, L.; He, H. A CalibratedGPT3 (CGPT3) Model for the Site-Specific Zenith Hydrostatic Delay Estimation in the Chinese Mainland and Its Surrounding Areas. Remote Sens. 2022, 14, 6357. [Google Scholar] [CrossRef]
- Trimble Announces Calibration-Free Tilt Compensation for Their Flagship GNSS Rover. Available online: https://www.geospatialworld.net/blogs/trimble-announces-calibration-free-tilt-compensation-for-their-flagship-gnss-rover/ (accessed on 7 December 2023).
- Gučević, J.; Delčev, S.; Kuburić, M.; Trifković, M.; Ogrizović, V. Impact of Vial Bubble on the Accuracy of Positions in the GNSS-RTK Mode. Tech. Gaz. 2022, 29, 1230–1235. [Google Scholar] [CrossRef]
- Available online: http://www.registar.ats.rs/predmet/1323/ (accessed on 2 November 2023).
- Pravilnik o Primeni Tehnologije Globalnog Navigacionog Satelitskog Sistema u Oblastima Državnog Premera i Katastra, “Službeni Glasnik RS”, br. 72/2017. Available online: http://demo.paragraf.rs/demo/combined/Old/t/t2017_07/t07_0328.htm (accessed on 10 November 2023).
- AGROS. Available online: https://agros.rgz.gov.rs/ (accessed on 25 March 2024).
- Vekom Net. Available online: https://vekom.com/o-vekomnet-mrezi/ (accessed on 25 March 2024).
- GentooARS. Available online: http://www.geosolutions.co.rs/resenjeGeotaurNet.pdf (accessed on 25 March 2024).
- Gučević, J.; Vasović Šimšić, O.; Delčev, S.; Kuburić, M. Testing of Homogeneity of Coordinates of Various Permanent GNSS Reference Stations Networks of the Republic of Serbia According to the Common Requirements for Proving Competence. Sensors 2022, 22, 7867. [Google Scholar] [CrossRef] [PubMed]








| Accuracy Measures | Formula | Probability | Definition |
|---|---|---|---|
| DRMS | 65% | The square root of the average of the squared horizontal position errors. | |
| 2DRMS | 95% | Twice the DRMS of the horizontal position errors. | |
| MRSE | 61% | The radius of the sphere centered at the true position, containing the position estimate in 3D with a probability of 61%. |
| GNSS Receiver/ Software Support | Horizontal/ Vertical Accuracy | Tilt Compensation Accuracy (mm) | (mm) | (mm) |
|---|---|---|---|---|
| e-Survey E300pro/ SurPad 4.2 | 8 mm + 1 ppm/ 15 mm + 1 ppm | 30 | −0.04 ± 0.59 | 2.15 3.68 |
| SinoGNSS N3/ Survey Master | 8 mm + 0.5 ppm/ 15 mm + 0.5 ppm | 20 | −0.57 ± 0.86 | 5.00 5.57 |
| AlphaSurvey Alpha5i/ Alpha DiMap Pro | 8 mm + 1 ppm/ 15 mm + 1 ppm | 8 + 0.3·tilt | −2.64 ± 1.35 | 2.94 3.57 |
| AlphaSurvey Alpha4i/ Alpha DiMap Pro | 8 mm + 1 ppm/ 15 mm + 1 ppm | 8 + 0.3·tilt | 1.20 ± 0.78 | 2.97 2.37 |
| RUIDE RENO 1/ Surv X | 8 mm + 1 ppm/ 15 mm + 1 ppm | 10 + 0.7·tilt | 0.24 ± 0.55 | 1.43 2.57 |
| SOUTH G3/ Surv X | 8 mm + 0.5 ppm/ 15 mm + 0.5 ppm | 10 + 0.7·tilt | −1.61 ± 1.31 | 4.04 3.69 |
| RUIDE ROVA 1/ Surv X | 8 mm + 1 ppm/ 15 mm + 1 ppm | 10 + 0.7·tilt | −1.38 ± 0.67 | 1.67 2.67 |
| Deviation of Coordinates per Series | [mm] | [mm] | [mm] | [mm] | [mm] |
|---|---|---|---|---|---|
| GNSS receiver: | e-Survey E300pro | ||||
| x-axis | −2.87 | 8.33 | 13.73 | −11.87 | −7.07 |
| y-axis | 9.33 | −25.27 | 8.73 | 3.33 | −8.07 |
| GNSS receiver: | SinoGNSS N3 | ||||
| x-axis | 0.50 | −39.90 | 36.28 | −64.92 | −2.76 |
| y-axis | 10.32 | 49.48 | 18.26 | −26.88 | −48.02 |
| GNSS receiver: | AlphaSurvey Alpha 5i | ||||
| x-axis | 2.60 | −13.60 | −35.40 | −7.00 | −16.20 |
| y-axis | −3.60 | −3.40 | −9.20 | 0.20 | −4.20 |
| GNSS receiver: | AlphaSurvey Alpha 4i (for α = 45°) | ||||
| x-axis | 11.50 | 48.50 | −72.90 | −32.50 | 15.30 |
| y-axis | 10.50 | −121.30 | −79.90 | 65.50 | 14.10 |
| GNSS receiver: | RUIDE RENO 1 | ||||
| x-axis | −2.80 | 31.00 | 28.00 | −17.60 | 5.60 |
| y-axis | 29.53 | −22.87 | 19.53 | −21.87 | −22.07 |
| GNSS receiver: | SOUTH G3 | ||||
| x-axis | −22.07 | 4.73 | 13.73 | −25.07 | 8.73 |
| y-axis | 17.20 | −21.60 | 18.20 | 23.40 | 24.80 |
| GNSS receiver: | RUIDE ROVA 1 | ||||
| x-axis | 45.69 | 32.84 | 18.96 | −30.56 | −33.80 |
| y-axis | 25.36 | −8.16 | −51.89 | 37.29 | −51.40 |
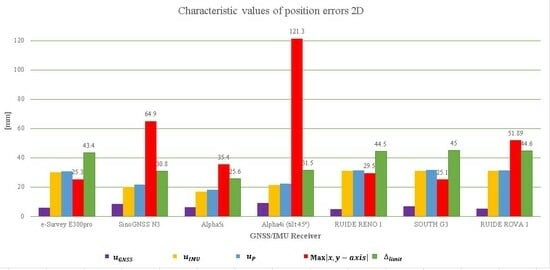
| GNSS/IMU Receiver | [mm] | [mm] | [mm] | Evaluation | ||
|---|---|---|---|---|---|---|
| e-Survey E300pro | 5.8 | 30 | 30.6 | 25.3 | 43.4 | “Satisfactory” |
| SinoGNSS N3 | 8.5 | 20 | 21.7 | 64.9 | 30.8 | “Unsatisfactory” |
| Alpha5i | 6.1 | 17 | 18.1 | 35.4 | 25.6 | “Unsatisfactory” |
| Alpha4i (tilt 45º) | 9.0 | 21.5 | 22.2 | 121.3 | 31.5 | “Unsatisfactory” |
| RUIDE RENO 1 | 5.0 | 31 | 31.4 | 29.5 | 44.5 | “Satisfactory” |
| SOUTH G3 | 6.8 | 31 | 31.7 | 25.1 | 45.0 | “Satisfactory” |
| RUIDE ROVA 1 | 5.1 | 31 | 31.4 | 51.89 | 44.6 | “Unsatisfactory” |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gučević, J.; Delčev, S.; Vasović Šimšić, O. Practical Limitations of Using the Tilt Compensation Function of the GNSS/IMU Receiver. Remote Sens. 2024, 16, 1327. https://doi.org/10.3390/rs16081327
Gučević J, Delčev S, Vasović Šimšić O. Practical Limitations of Using the Tilt Compensation Function of the GNSS/IMU Receiver. Remote Sensing. 2024; 16(8):1327. https://doi.org/10.3390/rs16081327
Chicago/Turabian StyleGučević, Jelena, Siniša Delčev, and Olivera Vasović Šimšić. 2024. "Practical Limitations of Using the Tilt Compensation Function of the GNSS/IMU Receiver" Remote Sensing 16, no. 8: 1327. https://doi.org/10.3390/rs16081327
APA StyleGučević, J., Delčev, S., & Vasović Šimšić, O. (2024). Practical Limitations of Using the Tilt Compensation Function of the GNSS/IMU Receiver. Remote Sensing, 16(8), 1327. https://doi.org/10.3390/rs16081327