Spatial Downscaling of ESA CCI Soil Moisture Data Based on Deep Learning with an Attention Mechanism
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.1.1. Study Area
2.1.2. ESA CCI SM Dataset
2.1.3. MODIS Products
2.1.4. Other Auxiliary Datasets
2.1.5. In Situ Soil Moisture Measurements
2.2. Method
2.2.1. Data Preprocessing
2.2.2. The SMNet Model with a CNN and Attention Mechanism
2.2.3. Hyperparameter Tuning
2.2.4. Model Training and Evaluation
3. Results
3.1. Feature Selection
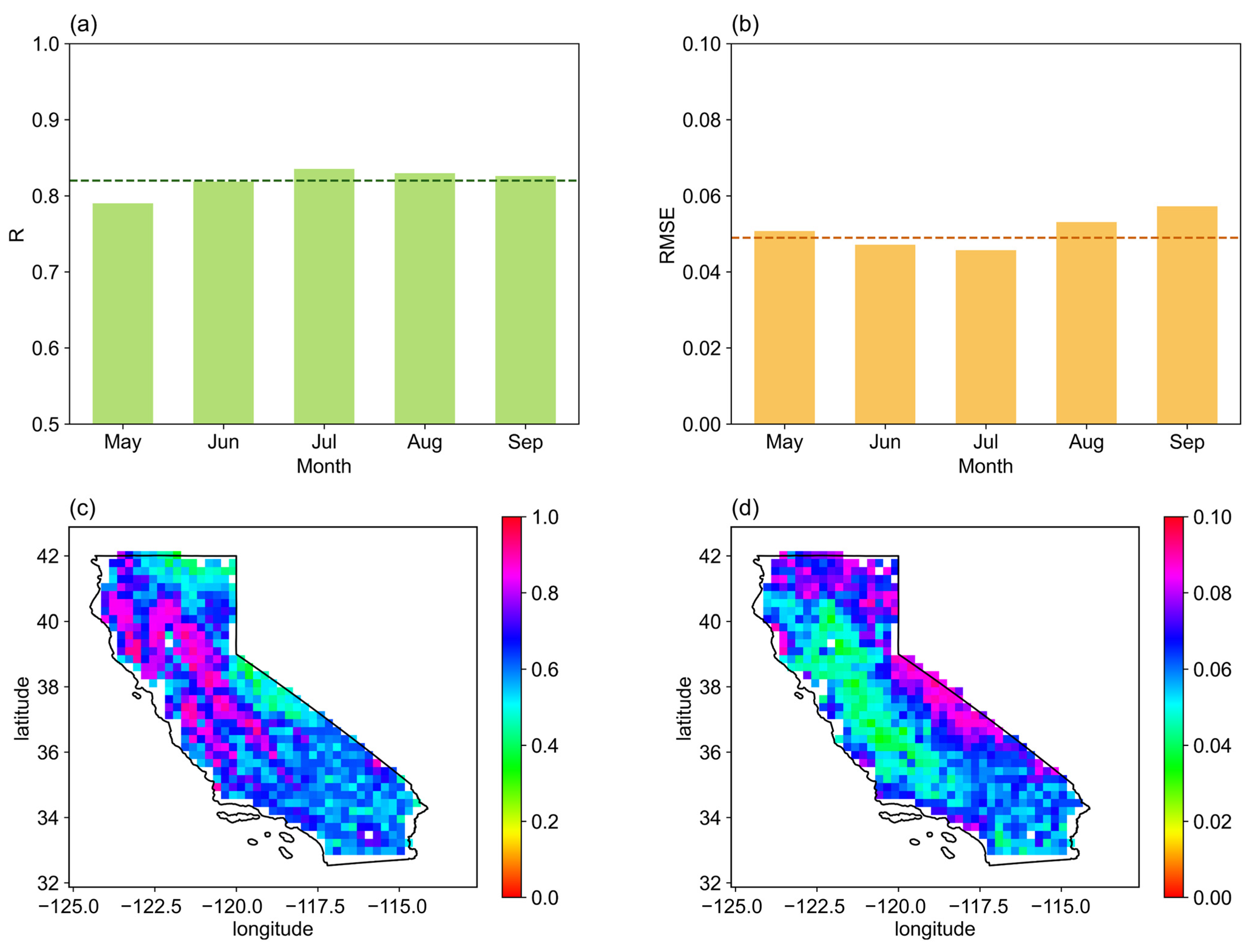
3.2. SMNet Model Performance Compared with the Original ESA CCI SM Data
3.3. Evaluation of the Downscaled SM Data with In Situ Measurements
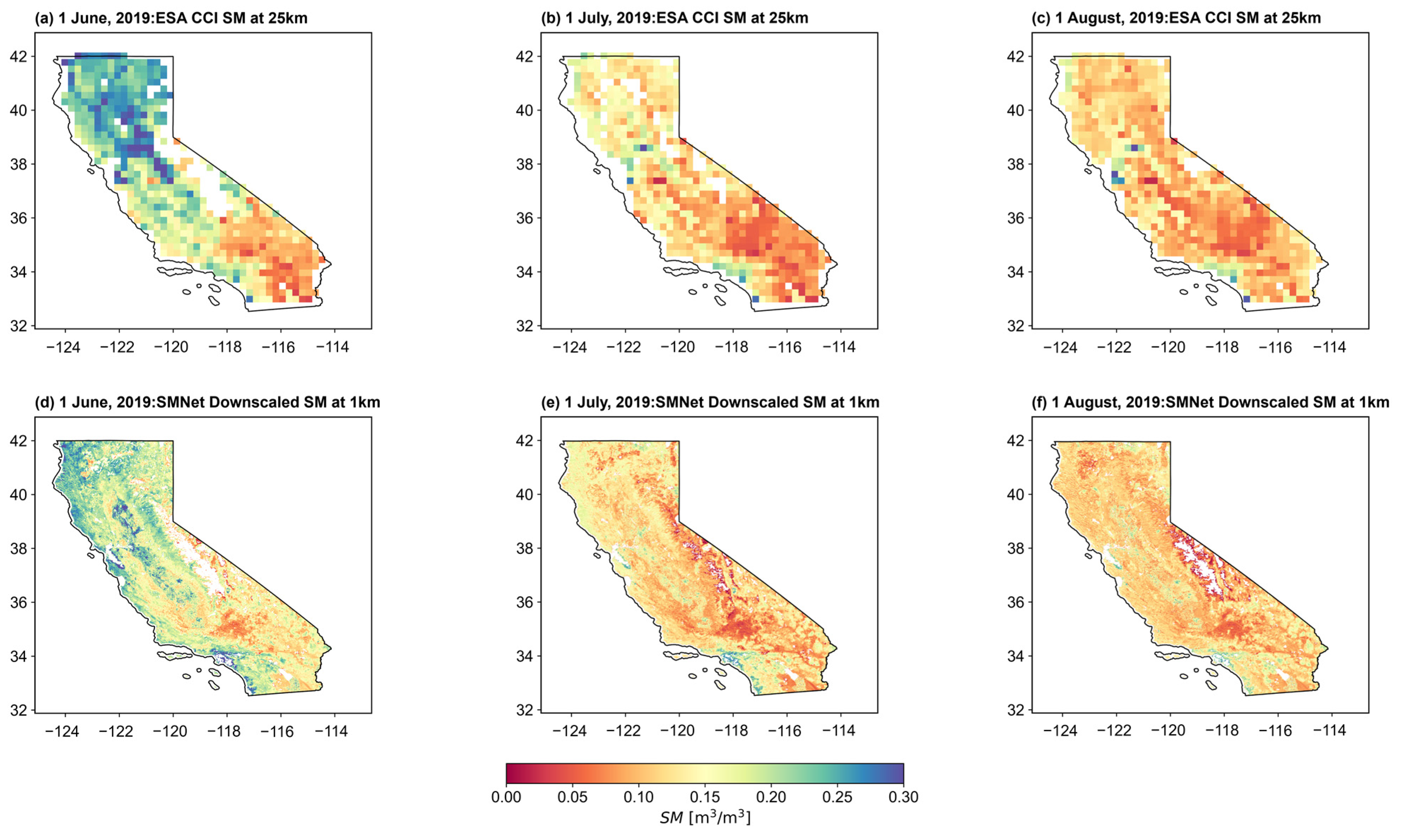
3.4. Spatial and Temporal Variation of the Downscaled ESA CCI SM Data
4. Discussion
4.1. Impact of the Input Datasets on Downscaling Efforts
4.2. The Impact of Different Methods in Downscaling Models
4.2.1. Comparison with Other Published Methods for Downscaling ESA CCI SM Data
4.2.2. The IMPACT of the Attention Mechanism in the Downscaling Model
4.3. Temporal Extrapolation of the Model
4.4. Uncertainty of the Downscaling Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| SCAN | ESA CCI SM | Downscaled SM | ||
|---|---|---|---|---|
| R | RMSE m3/m3 | R | RMSE m3/m3 | |
| Ash Valley | 0.79 | 0.138 | 0.83 | 0.085 |
| Bodie Hills | 0.73 | 0.076 | 0.73 | 0.064 |
| Cochora Ranch | 0.89 | 0.083 | 0.90 | 0.044 |
| Death Valley Jct | 0.72 | 0.085 | 0.75 | 0.062 |
| Deep Springs | 0.62 | 0.054 | 0.70 | 0.047 |
| Doe Ridge | 0.29 | 0.080 | 0.36 | 0.050 |
| Eagle Lake | 0.12 | 0.124 | 0.26 | 0.079 |
| Essex | 0.09 | 0.087 | 0.23 | 0.073 |
| Ford Dry Lake | 0.55 | 0.093 | 0.57 | 0.085 |
| French Gulch | 0.23 | 0.117 | 0.35 | 0.107 |
| Marble Creek | 0.57 | 0.100 | 0.67 | 0.110 |
| Monocline Ridge | 0.82 | 0.064 | 0.86 | 0.082 |
| Shadow Mtns | 0.68 | 0.080 | 0.65 | 0.124 |
| Stubblefield | 0.77 | 0.118 | 0.82 | 0.162 |
| SNOTEL | ESA CCI SM | Downscaled SM | ||
|---|---|---|---|---|
| R | RMSE m3/m3 | R | RMSE m3/m3 | |
| Blue Lakes | 0.57 | 0.096 | 0.44 | 0.068 |
| Burnside Lake | 0.74 | 0.096 | 0.82 | 0.077 |
| Carson Pass | 0.68 | 0.179 | 0.72 | 0.153 |
| Css Lab | 0.80 | 0.093 | 0.88 | 0.083 |
| Ebbetts Pass | 0.46 | 0.070 | 0.56 | 0.083 |
| Echo Peak | 0.66 | 0.073 | 0.67 | 0.077 |
| Fallen Leaf | 0.47 | 0.126 | 0.44 | 0.129 |
| Forestdale Creek | 0.79 | 0.144 | 0.78 | 0.129 |
| Hagans Meadow | 0.54 | 0.048 | 0.58 | 0.068 |
| Heavenly Valley | 0.39 | 0.327 | 0.34 | 0.252 |
| Horse Meadow | 0.73 | 0.088 | 0.70 | 0.073 |
| Independence Camp | 0.78 | 0.123 | 0.80 | 0.083 |
| Independence Creek | 0.86 | 0.086 | 0.87 | 0.063 |
| Independence Lake | 0.45 | 0.100 | 0.53 | 0.068 |
| Leavitt Lake | 0.52 | 0.100 | 0.63 | 0.100 |
| Leavitt Meadows | 0.68 | 0.054 | 0.71 | 0.067 |
| Lobdell Lake | 0.76 | 0.069 | 0.78 | 0.069 |
| Monitor Pass | 0.55 | 0.061 | 0.48 | 0.102 |
| Poison Flat | 0.52 | 0.205 | 0.55 | 0.157 |
| Rubicon #2 | 0.51 | 0.077 | 0.64 | 0.067 |
| Sonora Pass | 0.64 | 0.051 | 0.62 | 0.082 |
| Spratt Creek | 0.43 | 0.119 | 0.44 | 0.105 |
| State Line | 0.53 | 0.066 | 0.62 | 0.053 |
| Summit Meadow | 0.53 | 0.081 | 0.65 | 0.074 |
| Tahoe City Cross | 0.46 | 0.092 | 0.53 | 0.073 |
| Truckee #2 | 0.73 | 0.096 | 0.69 | 0.078 |
| VirginiaLakes Ridge | 0.49 | 0.079 | 0.64 | 0.057 |
| Ward Creek #3 | 0.45 | 0.112 | 0.48 | 0.109 |
| USCRN | ESA CCI SM | Downscaled SM | ||
|---|---|---|---|---|
| R | RMSE m3/m3 | R | RMSE m3/m3 | |
| 1 | 0.63 | 0.036 | 0.66 | 0.036 |
| 2 | 0.84 | 0.118 | 0.87 | 0.107 |
| 3 | 0.78 | 0.084 | 0.79 | 0.074 |
| 4 | 0.84 | 0.085 | 0.89 | 0.091 |
| 5 | 0.44 | 0.022 | 0.55 | 0.081 |

References
- Sun, H.; Cai, C.; Liu, H.; Yang, B. Microwave and Meteorological Fusion: A Method of Spatial Downscaling of Remotely Sensed Soil Moisture. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 1107–1119. [Google Scholar] [CrossRef]
- Idso, S.B.; Jackson, R.D.; Reginato, R.J.; Kimball, B.A.; Nakayama, F.S. The Dependence of Bare Soil Albedo on Soil Water Content. J. Appl. Meteorol. Climatol. 1975, 14, 109–113. [Google Scholar] [CrossRef]
- Merlin, O.; Walker, J.P.; Chehbouni, A.; Kerr, Y. Towards Deterministic Downscaling of SMOS Soil Moisture Using MODIS Derived Soil Evaporative Efficiency. Remote Sens. Environ. 2008, 112, 3935–3946. [Google Scholar] [CrossRef]
- Sánchez, N.; González-Zamora, Á.; Piles, M.; Martínez-Fernández, J. A New Soil Moisture Agricultural Drought Index (SMADI) Integrating MODIS and SMOS Products: A Case of Study over the Iberian Peninsula. Remote Sens. 2016, 8, 287. [Google Scholar] [CrossRef]
- Feng, S.; Huang, X.; Zhao, S.; Qin, Z.; Fan, J.; Zhao, S. Evaluation of Several Satellite-Based Soil Moisture Products in the Continental US. Sensors 2022, 22, 9977. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Zhang, R.; Pham, H.; Sharma, A. A Review of Satellite-Derived Soil Moisture and Its Usage for Flood Estimation. Remote Sens. Earth Syst. Sci. 2019, 2, 225–246. [Google Scholar] [CrossRef]
- Borodychev, V.V.; Lytov, M.N. Irrigation Management Model Based on Soil Moisture Distribution Profile. IOP Conf. Ser. Earth Environ. Sci. 2020, 577, 012022. [Google Scholar] [CrossRef]
- Doraiswamy, P.C.; Hatfield, J.L.; Jackson, T.J.; Akhmedov, B.; Prueger, J.; Stern, A. Crop Condition and Yield Simulations Using Landsat and MODIS. Remote Sens. Environ. 2004, 92, 548–559. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.P.; Yamada, T.J.; Balsamo, G.; Berg, A.A.; Boisserie, M.; Dirmeyer, P.A.; Doblas-Reyes, F.J.; Drewitt, G.; Gordon, C.T.; et al. Contribution of Land Surface Initialization to Subseasonal Forecast Skill: First Results from a Multi-Model Experiment. Geophys. Res. Lett. 2010, 37, L02402. [Google Scholar] [CrossRef]
- Gruber, A.; Dorigo, W.A.; Zwieback, S.; Xaver, A.; Wagner, W. Characterizing Coarse-Scale Representativeness of in Situ Soil Moisture Measurements from the International Soil Moisture Network. Vadose Zone J. 2013, 12, 1–16. [Google Scholar] [CrossRef]
- Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Dorigo, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Larson, K.M.; Njoku, E.G.; Small, E.E.; et al. State of the Art in Large-Scale Soil Moisture Monitoring. Soil. Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar] [CrossRef]
- Tavakol, A.; McDonough, K.R.; Rahmani, V.; Hutchinson, S.L.; Hutchinson, J.M.S. The Soil Moisture Data Bank: The Ground-Based, Model-Based, and Satellite-Based Soil Moisture Data. Remote Sens. Appl. Soc. Environ. 2021, 24, 100649. [Google Scholar] [CrossRef]
- Yuan, Q.; Shen, H.; Li, T.; Li, Z.; Li, S.; Jiang, Y.; Xu, H.; Tan, W.; Yang, Q.; Wang, J.; et al. Deep Learning in Environmental Remote Sensing: Achievements and Challenges. Remote Sens. Environ. 2020, 241, 111716. [Google Scholar] [CrossRef]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, Proximal, and Satellite Remote Sensing of Soil Moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial Soil Moisture Retrievals from the METOP-A Advanced Scatterometer (ASCAT). Geophys. Res. Lett. 2007, 34, L20401. [Google Scholar] [CrossRef]
- Yao, P.; Lu, H.; Shi, J.; Zhao, T.; Yang, K.; Cosh, M.H.; Gianotti, D.J.S.; Entekhabi, D. A Long Term Global Daily Soil Moisture Dataset Derived from AMSR-E and AMSR2 (2002–2019). Sci. Data 2021, 8, 143. [Google Scholar] [CrossRef]
- Gruber, A.; Scanlon, T.; van der Schalie, R.; Wagner, W.; Dorigo, W. Evolution of the ESA CCI Soil Moisture Climate Data Records and Their Underlying Merging Methodology. Earth Syst. Sci. Data 2019, 11, 717–739. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C. The SMOS Mission: New Tool for Monitoring Key Elements Ofthe Global Water Cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; O’neill, P.E.; Kellogg, K.H.; Crow, W.T.; Edelstein, W.N.; Entin, J.K.; Goodman, S.D.; Jackson, T.J.; Johnson, J. The Soil Moisture Active Passive (SMAP) Mission. Proc. IEEE 2010, 98, 704–716. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Martinuzzi, J.; Font, J.; Berger, M. Soil Moisture Retrieval from Space: The Soil Moisture and Ocean Salinity (SMOS) Mission. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1729–1735. [Google Scholar] [CrossRef]
- Das, N.N.; Entekhabi, D.; Dunbar, R.S.; Colliander, A.; Chen, F.; Crow, W.; Jackson, T.J.; Berg, A.; Bosch, D.D.; Caldwell, T.; et al. The SMAP Mission Combined Active-Passive Soil Moisture Product at 9 km and 3 km Spatial Resolutions. Remote Sens. Environ. 2018, 211, 204–217. [Google Scholar] [CrossRef]
- Piles, M.; Petropoulos, G.P.; Sánchez, N.; González-Zamora, Á.; Ireland, G. Towards Improved Spatio-Temporal Resolution Soil Moisture Retrievals from the Synergy of SMOS and MSG SEVIRI Spaceborne Observations. Remote Sens. Environ. 2016, 180, 403–417. [Google Scholar] [CrossRef]
- Sun, H.; Zhou, B.; Zhang, C.; Liu, H.; Yang, B. DSCALE_mod16: A Model for Disaggregating Microwave Satellite Soil Moisture with Land Surface Evapotranspiration Products and Gridded Meteorological Data. Remote Sens. 2020, 12, 980. [Google Scholar] [CrossRef]
- Leroux, D.J.; Das, N.N.; Entekhabi, D.; Colliander, A.; Njoku, E.; Jackson, T.J.; Yueh, S. Active–Passive Soil Moisture Retrievals during the SMAP Validation Experiment 2012. IEEE Geosci. Remote Sens. Lett. 2016, 13, 475–479. [Google Scholar] [CrossRef]
- Wu, X.; Walker, J.P.; Rüdiger, C.; Panciera, R.; Gao, Y. Intercomparison of Alternate Soil Moisture Downscaling Algorithms Using Active–Passive Microwave Observations. IEEE Geosci. Remote Sens. Lett. 2016, 14, 179–183. [Google Scholar] [CrossRef]
- Shangguan, Y.; Min, X.; Shi, Z. Inter-Comparison and Integration of Different Soil Moisture Downscaling Methods over the Qinghai-Tibet Plateau. J. Hydrol. 2023, 617, 129014. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Merlin, O.; Verhoest, N.E.C. A Review of Spatial Downscaling of Satellite Remotely Sensed Soil Moisture. Rev. Geophys. 2017, 55, 341–366. [Google Scholar] [CrossRef]
- Sabaghy, S.; Walker, J.P.; Renzullo, L.J.; Jackson, T.J. Spatially Enhanced Passive Microwave Derived Soil Moisture: Capabilities and Opportunities. Remote Sens. Environ. 2018, 209, 551–580. [Google Scholar] [CrossRef]
- Zhu, Z.; Bo, Y.; Sun, T. Spatial Downscaling of Satellite Soil Moisture Products Based on Apparent Thermal Inertia: Considering the Effect of Vegetation Condition. J. Hydrol. 2023, 616, 128824. [Google Scholar] [CrossRef]
- Zhao, W.; Wen, F.; Wang, Q.; Sanchez, N.; Piles, M. Seamless Downscaling of the ESA CCI Soil Moisture Data at the Daily Scale with MODIS Land Products. J. Hydrol. 2021, 603, 126930. [Google Scholar] [CrossRef]
- Song, P.; Huang, J.; Mansaray, L.R. An Improved Surface Soil Moisture Downscaling Approach over Cloudy Areas Based on Geographically Weighted Regression. Agric. For. Meteorol. 2019, 275, 146–158. [Google Scholar] [CrossRef]
- Kolassa, J.; Reichle, R.H.; Draper, C.S. Merging Active and Passive Microwave Observations in Soil Moisture Data Assimilation. Remote Sens. Environ. 2017, 191, 117–130. [Google Scholar] [CrossRef]
- Hu, F.; Wei, Z.; Zhang, W.; Dorjee, D.; Meng, L. A Spatial Downscaling Method for SMAP Soil Moisture through Visible and Shortwave-Infrared Remote Sensing Data. J. Hydrol. 2020, 590, 125360. [Google Scholar] [CrossRef]
- Wei, Z.; Meng, Y.; Zhang, W.; Peng, J.; Meng, L. Downscaling SMAP Soil Moisture Estimation with Gradient Boosting Decision Tree Regression over the Tibetan Plateau. Remote Sens. Environ. 2019, 225, 30–44. [Google Scholar] [CrossRef]
- Liu, Y.; Jing, W.; Wang, Q.; Xia, X. Generating High-Resolution Daily Soil Moisture by Using Spatial Downscaling Techniques: A Comparison of Six Machine Learning Algorithms. Adv. Water Resour. 2020, 141, 103601. [Google Scholar] [CrossRef]
- Zhao, H.; Li, J.; Yuan, Q.; Lin, L.; Yue, L.; Xu, H. Downscaling of Soil Moisture Products Using Deep Learning: Comparison and Analysis on Tibetan Plateau. J. Hydrol. 2022, 607, 127570. [Google Scholar] [CrossRef]
- Jiang, M.; Shen, H.; Li, J. Cycle GAN Based Heterogeneous Spatial-Spectral Fusion for Soil Moisture Downscaling. In Proceedings of the IGARSS 2022—2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 4819–4822. [Google Scholar]
- Sit, M.; Demiray, B.Z.; Demir, I. Spatial Downscaling of Streamflow Data with Attention Based Spatio-Temporal Graph Convolutional Networks [Preprint], EarthArXiv. Available online: https://eartharxiv.org/repository/view/5227/ (accessed on 4 September 2023). [CrossRef]
- Liu, G.; Zhang, R.; Hang, R.; Ge, L.; Shi, C.; Liu, Q. Statistical Downscaling of Temperature Distributions in Southwest China by Using Terrain-Guided Attention Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 1678–1690. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Y.; Ren, L.; Teuling, A.J.; Zhang, X.; Jiang, S.; Yang, X.; Wei, L.; Zhong, F.; Zheng, L. Reconstruction of ESA CCI Satellite-Derived Soil Moisture Using an Artificial Neural Network Technology. Sci. Total Environ. 2021, 782, 146602. [Google Scholar] [CrossRef]
- Dorigo, W.; Wagner, W.; Albergel, C.; Albrecht, F.; Balsamo, G.; Brocca, L.; Chung, D.; Ertl, M.; Forkel, M.; Gruber, A.; et al. ESA CCI Soil Moisture for Improved Earth System Understanding: State-of-the Art and Future Directions. Remote Sens. Environ. 2017, 203, 185–215. [Google Scholar] [CrossRef]
- Gensheimer, J.; Turner, A.J.; Köhler, P.; Frankenberg, C.; Chen, J. A Convolutional Neural Network for Spatial Downscaling of Satellite-Based Solar-Induced Chlorophyll Fluorescence (SIFnet). Biogeosciences 2022, 19, 1777–1793. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the Radiometric and Biophysical Performance of the MODIS Vegetation Indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Du, J.; Kimball, J.; Chan, S.; Colliander, A.; Carroll, M. Evaluation of Surface Fractional Water Impacts on SMAP Soil Moisture Retrieval. AGU Fall Meet. Abstr. 2021, 2021, H15W–1312. [Google Scholar]
- Koster, R.D.; Suarez, M.J.; Higgins, R.W.; Van den Dool, H.M. Observational Evidence That Soil Moisture Variations Affect Precipitation. Geophys. Res. Lett. 2003, 30, 1241. [Google Scholar] [CrossRef]
- Funk, C.; Peterson, P.; Landsfeld, M.; Pedreros, D.; Verdin, J.; Shukla, S.; Husak, G.; Rowland, J.; Harrison, L.; Hoell, A.; et al. The Climate Hazards Infrared Precipitation with Stations—A New Environmental Record for Monitoring Extremes. Sci. Data 2015, 2, 150066. [Google Scholar] [CrossRef] [PubMed]
- Arregocés, H.A.; Rojano, R.; Pérez, J. Validation of the CHIRPS Dataset in a Coastal Region with Extensive Plains and Complex Topography. Case Stud. Chem. Environ. Eng. 2023, 8, 100452. [Google Scholar] [CrossRef]
- Bai, L.; Shi, C.; Li, L.; Yang, Y.; Wu, J. Accuracy of CHIRPS Satellite-Rainfall Products over Mainland China. Remote Sens. 2018, 10, 362. [Google Scholar] [CrossRef]
- Nawaz, M.; Iqbal, M.F.; Mahmood, I. Validation of CHIRPS Satellite-Based Precipitation Dataset over Pakistan. Atmos. Res. 2021, 248, 105289. [Google Scholar] [CrossRef]
- Ocampo-Marulanda, C.; Fernández-Álvarez, C.; Cerón, W.L.; Canchala, T.; Carvajal-Escobar, Y.; Alfonso-Morales, W. A Spatiotemporal Assessment of the High-Resolution CHIRPS Rainfall Dataset in Southwestern Colombia Using Combined Principal Component Analysis. Ain Shams Eng. J. 2022, 13, 101739. [Google Scholar] [CrossRef]
- Crow, W.T.; Berg, A.A.; Cosh, M.H.; Loew, A.; Mohanty, B.P.; Panciera, R.; de Rosnay, P.; Ryu, D.; Walker, J.P. Upscaling Sparse Ground-Based Soil Moisture Observations for the Validation of Coarse-Resolution Satellite Soil Moisture Products. Rev. Geophys. 2012, 50, RG2002. [Google Scholar] [CrossRef]
- Coleman, M.L.; Niemann, J.D. Controls on Topographic Dependence and Temporal Instability in Catchment-Scale Soil Moisture Patterns. Water Resour. Res. 2013, 49, 1625–1642. [Google Scholar] [CrossRef]
- Ranney, K.J.; Niemann, J.D.; Lehman, B.M.; Green, T.R.; Jones, A.S. A Method to Downscale Soil Moisture to Fine Resolutions Using Topographic, Vegetation, and Soil Data. Adv. Water Resour. 2015, 76, 81–96. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Van Doninck, J.; Peters, J.; De Baets, B.; De Clercq, E.M.; Ducheyne, E.; Verhoest, N.E.C. The Potential of Multitemporal Aqua and Terra MODIS Apparent Thermal Inertia as a Soil Moisture Indicator. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 934–941. [Google Scholar] [CrossRef]
- Woo, S.; Park, J.; Lee, J.-Y.; Kweon, I.S. CBAM: Convolutional Block Attention Module. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 3–19. [Google Scholar]
- Liu, J.; Zhang, Y.; Liu, C.; Liu, X. Monitoring Impervious Surface Area Dynamics in Urban Areas Using Sentinel-2 Data and Improved Deeplabv3+ Model: A Case Study of Jinan City, China. Remote Sens. 2023, 15, 1976. [Google Scholar] [CrossRef]
- Ma, R.; Wang, J.; Zhao, W.; Guo, H.; Dai, D.; Yun, Y.; Li, L.; Hao, F.; Bai, J.; Ma, D. Identification of Maize Seed Varieties Using MobileNetV2 with Improved Attention Mechanism CBAM. Agriculture 2023, 13, 11. [Google Scholar] [CrossRef]
- Brunet, D.; Vrscay, E.R.; Wang, Z. On the Mathematical Properties of the Structural Similarity Index. IEEE Trans. Image Process. 2012, 21, 1488–1499. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C. Mean Squared Error: Love It or Leave It? A New Look at Signal Fidelity Measures. IEEE Signal Process. Mag. 2009, 26, 98–117. [Google Scholar] [CrossRef]
- Kang, S.-J. SSIM Preservation-Based Backlight Dimming. J. Disp. Technol. 2014, 10, 247–250. [Google Scholar] [CrossRef]
- Li, J.; Leng, G.; Peng, J. The Merit of Estimating High-Resolution Soil Moisture Using Combined Optical, Thermal, and Microwave Data. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.; Wang, S.; Zhang, H. A Robust Gap-Filling Approach for European Space Agency Climate Change Initiative (ESA CCI) Soil Moisture Integrating Satellite Observations, Model-Driven Knowledge, and Spatiotemporal Machine Learning. Hydrol. Earth Syst. Sci. 2023, 27, 577–598. [Google Scholar] [CrossRef]
- Roxy, M.S.; Sumithranand, V.B.; Renuka, G. Variability of Soil Moisture and Its Relationship with Surface Albedo and Soil Thermal Diffusivity at Astronomical Observatory, Thiruvananthapuram, South Kerala. J. Earth Syst. Sci. 2010, 119, 507–517. [Google Scholar] [CrossRef]
- Schnur, M.T.; Xie, H.; Wang, X. Estimating Root Zone Soil Moisture at Distant Sites Using MODIS NDVI and EVI in a Semi-Arid Region of Southwestern USA. Ecol. Inform. 2010, 5, 400–409. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A Simple Interpretation of the Surface Temperature/Vegetation Index Space for Assessment of Surface Moisture Status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Chen, L.; Xu, S.; Sun, H. A Machine Learning-Based Approach for Generating High-Resolution Soil Moisture from SMAP Products. Geocarto Int. 2022, 37, 16086–16107. [Google Scholar] [CrossRef]
- Dong, J.; Steele-Dunne, S.C.; Ochsner, T.E.; van de Giesen, N. Determining Soil Moisture and Soil Properties in Vegetated Areas by Assimilating Soil Temperatures. Water Resour. Res. 2016, 52, 4280–4300. [Google Scholar] [CrossRef]
- Ghahremanloo, M.; Mobasheri, M.R.; Amani, M. Soil Moisture Estimation Using Land Surface Temperature and Soil Temperature at 5 Cm Depth. Int. J. Remote Sens. 2019, 40, 104–117. [Google Scholar] [CrossRef]
- Merlin, O.; Rudiger, C.; Al Bitar, A.; Richaume, P.; Walker, J.P.; Kerr, Y.H. Disaggregation of SMOS Soil Moisture in Southeastern Australia. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1556–1571. [Google Scholar] [CrossRef]
- Zhan, X.; Houser, P.R.; Walker, J.P.; Crow, W.T. A Method for Retrieving High-Resolution Surface Soil Moisture from Hydros L-Band Radiometer and Radar Observations. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1534–1544. [Google Scholar] [CrossRef]
- Song, C.; Hu, G.; Wang, Y.; Qu, X. Downscaling ESA CCI Soil Moisture Based on Soil and Vegetation Component Temperatures Derived From MODIS Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2175–2184. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A.; Zhang, S.; Wang, J.; Niesel, J. Spatial Downscaling of Satellite Soil Moisture Data Using a Vegetation Temperature Condition Index. IEEE Trans. Geosci. Remote Sens. 2016, 54, 558–566. [Google Scholar] [CrossRef]
- Kovačević, J.; Cvijetinović, Ž.; Stančić, N.; Brodić, N.; Mihajlović, D. New Downscaling Approach Using ESA CCI SM Products for Obtaining High Resolution Surface Soil Moisture. Remote Sens. 2020, 12, 1119. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Jing, W.; Yue, X. Comparison of Different Machine Learning Approaches for Monthly Satellite-Based Soil Moisture Downscaling over Northeast China. Remote Sens. 2018, 10, 31. [Google Scholar] [CrossRef]
- Shangguan, Y.; Min, X.; Shi, Z. Gap Filling of the ESA CCI Soil Moisture Data Using a Spatiotemporal Attention-Based Residual Deep Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2023, 16, 5344–5354. [Google Scholar] [CrossRef]
- Xu, M.; Yao, N.; Yang, H.; Xu, J.; Hu, A.; Gustavo Goncalves de Goncalves, L.; Liu, G. Downscaling SMAP Soil Moisture Using a Wide & Deep Learning Method over the Continental United States. J. Hydrol. 2022, 609, 127784. [Google Scholar] [CrossRef]
- Kumar, B.; Atey, K.; Singh, B.B.; Chattopadhyay, R.; Acharya, N.; Singh, M.; Nanjundiah, R.S.; Rao, S.A. On the Modern Deep Learning Approaches for Precipitation Downscaling. Earth Sci. Inf. 2023, 16, 1459–1472. [Google Scholar] [CrossRef]
- Zhao, W.; Sánchez, N.; Lu, H.; Li, A. A Spatial Downscaling Approach for the SMAP Passive Surface Soil Moisture Product Using Random Forest Regression. J. Hydrol. 2018, 563, 1009–1024. [Google Scholar] [CrossRef]
- Long, D.; Bai, L.; Yan, L.; Zhang, C.; Yang, W.; Lei, H.; Quan, J.; Meng, X.; Shi, C. Generation of Spatially Complete and Daily Continuous Surface Soil Moisture of High Spatial Resolution. Remote Sens. Environ. 2019, 233, 111364. [Google Scholar] [CrossRef]
- Colliander, A.; Cosh, M.H.; Misra, S.; Jackson, T.J.; Crow, W.T.; Chan, S.; Bindlish, R.; Chae, C.; Holifield Collins, C.; Yueh, S.H. Validation and Scaling of Soil Moisture in a Semi-Arid Environment: SMAP Validation Experiment 2015 (SMAPVEX15). Remote Sens. Environ. 2017, 196, 101–112. [Google Scholar] [CrossRef]
- Ménard, C.B.; Essery, R.; Barr, A.; Bartlett, P.; Derry, J.; Dumont, M.; Fierz, C.; Kim, H.; Kontu, A.; Lejeune, Y.; et al. Meteorological and Evaluation Datasets for Snow Modelling at 10 Reference Sites: Description of in Situ and Bias-Corrected Reanalysis Data. Earth Syst. Sci. Data 2019, 11, 865–880. [Google Scholar] [CrossRef]
- Schmugge, T.J.; Jackson, T.J.; McKim, H.L. Survey of Methods for Soil Moisture Determination. Water Resour. Res. 1980, 16, 961–979. [Google Scholar] [CrossRef]
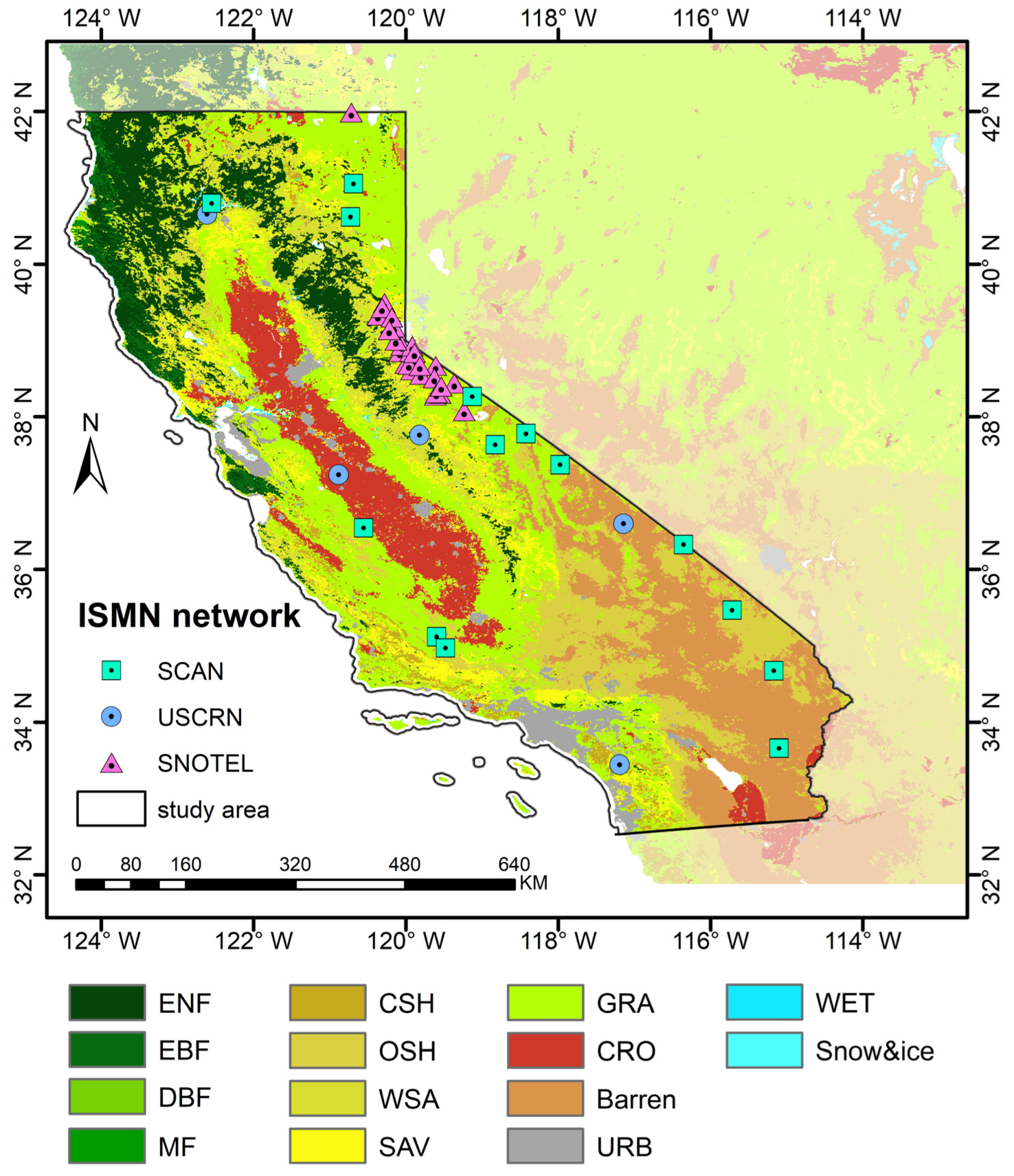

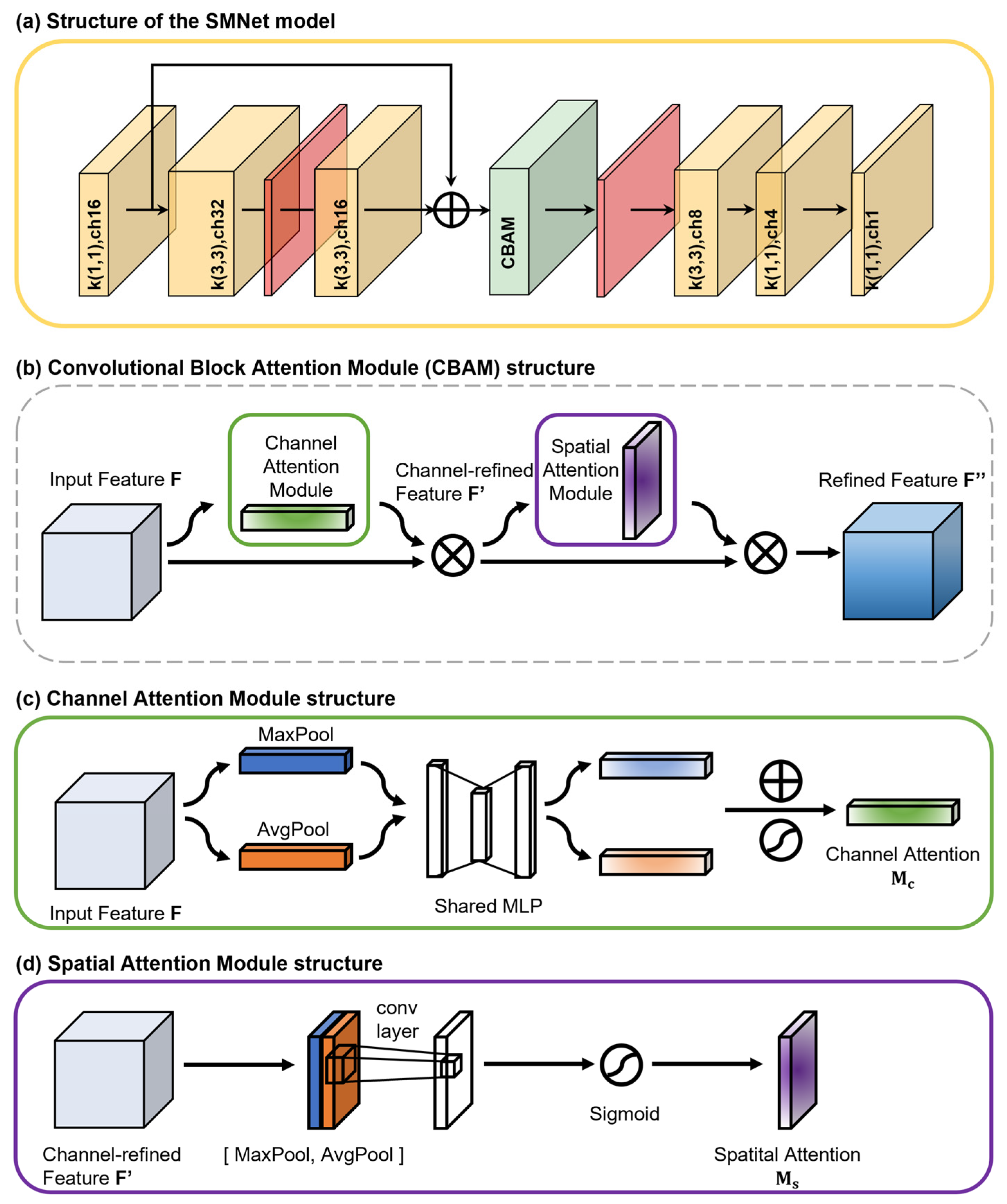
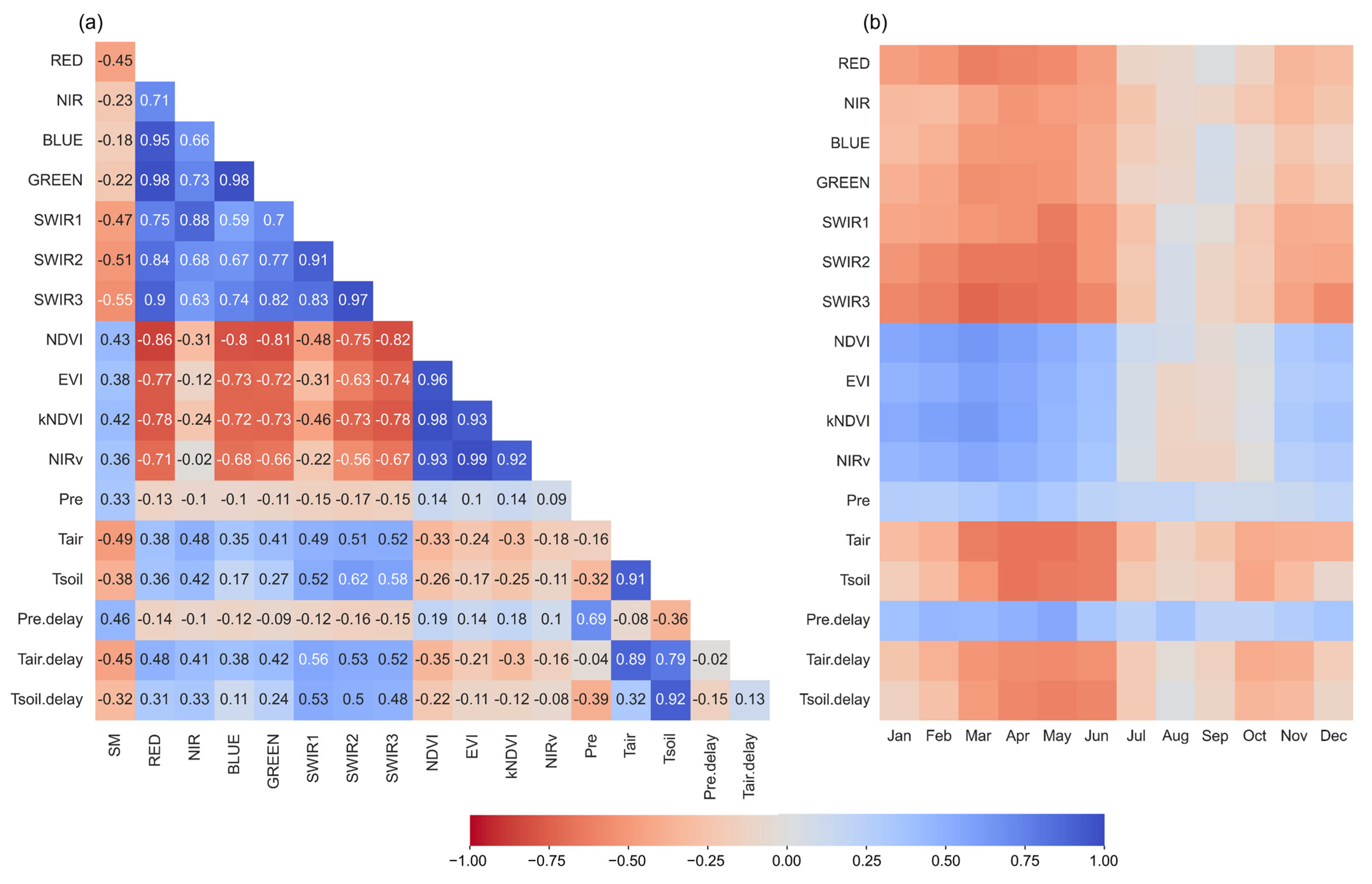
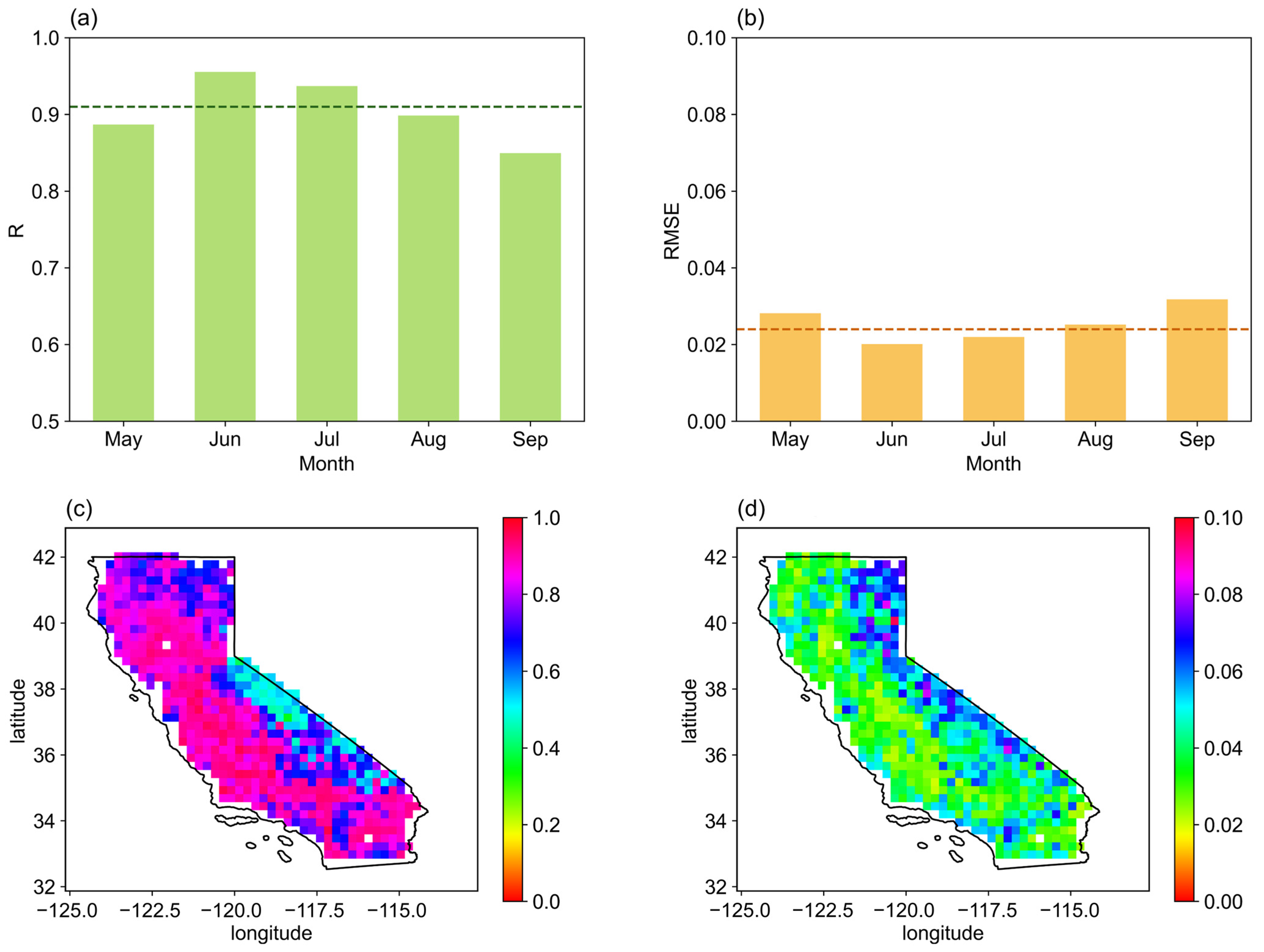



| Network | SCAN | USCRN | SNOTEL |
|---|---|---|---|
| Latitude | 33.65°N–41.05°N | 33.44°N–40.65°N | 38.07°N–41.98°N |
| Longitude | 122.55°W–115.10°W | 123.07°W–117.14°W | 120.71°W–119.23°W |
| Sampling Interval | 1 h | 1 h | 1 h |
| Depth(cm) Used | 0–5 | 0–5 | 0–5 |
| Site Used | 14 | 5 | 28 |
| Time Used | 2019–2021 | 2019–2021 | 2019–2021 |
| Type of Data | Variable (Notation) | Dataset | Spatial Resolution | |
|---|---|---|---|---|
| Target variable | SM | ESA CCI | 25 km | |
| Input variable | Surface reflectance | BLUE, GREEN, RED, NIR, SWIR1, SWIR2, and SWIR3 | MCD43A4 | 500 m |
| Vegetation indices | NDVI, EVI, kNDVI, and NIRv | MCD43A4 | 500 m | |
| Temperature | Mean air temperature (Tair) and mean air temperature delayed by one day (Tair.delay) | ERA5-Land | 0.1° | |
| Soil temperature | Mean soil temperature (Tsoil) and mean soil temperature delayed by one day (Tsoil.delay) | ERA5-Land | 0.1° | |
| Precipitation | Precipitation (Pre), and precipitation delayed by one day (Pre.delay) | CHIRPS | 0.05° | |
| Land cover | ENF, EBF, DBF, MF, CSH, OSH, WSA, SAV, GRA, CRO, URB, Barren, WET, and Snow&ice | MCD12Q1 | 500 m | |
| Topography | DEM | SRTM | 90 m | |
| Land mask | MOD44W | 250 m | ||
| Validation data | In situ SM | SCAN, USCRN, and SNOTEL | ISMN | |
| Parameter | Optimized Value |
|---|---|
| Batch size | 64 |
| Optimizer | Adam |
| Learning rate | 0.0073 |
| Weight decay | 2.0056 × 10−6 |
| Epoch | 464 |
| In Situ | ESA CCI SM | Downscaled SM | ||
|---|---|---|---|---|
| R | RMSE m3/m3 | R | RMSE m3/m3 | |
| SCAN | 0.56 | 0.093 | 0.62 | 0.077 |
| SNOTEL | 0.60 | 0.104 | 0.63 | 0.093 |
| USCRN | 0.71 | 0.070 | 0.75 | 0.078 |
| Approach | R | RMSE m3/m3 |
|---|---|---|
| SMNet | 0.91 | 0.024 |
| SMNet-surface reflectance | 0.81 | 0.043 |
| SMNet-VI | 0.83 | 0.039 |
| SMNet-Tair | 0.84 | 0.038 |
| SMNet-prep | 0.79 | 0.048 |
| SMNet-DEM | 0.75 | 0.052 |
| SMNet-LM | 0.86 | 0.031 |
| Source | Approaches | Study Area | Spatial Resolution | RMSE of In Situ Site Validation (m3/m3) |
|---|---|---|---|---|
| Zhao et al. [30] | Statistical model data fusion (GWR + ATPK) | Iberian Peninsula | 1 km | 0.091 |
| Song et al. [72] | Statistical model data fusion (TVDI + SVCT) | Nagqu, and Qinghai–Tibet Plateau | 1 km | 0.057 |
| Liu et al. [75] | CART, KNN, BAYE, and RF | Three northeastern provinces of China | 1 km | 0.076 0.074 0.075 0.073 |
| Peng et al. [73] | Statistical model (VTCI) | Yunnan Province, China, | 1 km | 0.078 |
| Shangguan et al. [76] | DL (CNN + Attention) | Qinghai–Tibet Plateau | 1 km | 0.099 |
| Kovačević et al. [74] | RF | California, USA | 1 km | 0.052 (PBO_H2O); 0.085 (SCAN); 0.090 (USCRN). |
| Our study | DL (CNN + Attention) | California, USA | 1 km | 0.077 (SCAN); 0.093 (SNOTEL); 0.078 (USCRN). |
| Experiments | Statistical Metrics | |
|---|---|---|
| R | RMSE m3/m3 | |
| (1) no attention module | 0.63 | 0.051 |
| (2) CBAM | 0.91 | 0.024 |
| (3) PSA | 0.88 | 0.029 |
| (4) DAN | 0.86 | 0.032 |
| (5) SENet | 0.84 | 0.034 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Lu, L.; Li, X.; Zhang, J.; Zhang, S.; Yang, S. Spatial Downscaling of ESA CCI Soil Moisture Data Based on Deep Learning with an Attention Mechanism. Remote Sens. 2024, 16, 1394. https://doi.org/10.3390/rs16081394
Zhang D, Lu L, Li X, Zhang J, Zhang S, Yang S. Spatial Downscaling of ESA CCI Soil Moisture Data Based on Deep Learning with an Attention Mechanism. Remote Sensing. 2024; 16(8):1394. https://doi.org/10.3390/rs16081394
Chicago/Turabian StyleZhang, Danwen, Linjun Lu, Xuan Li, Jiahua Zhang, Sha Zhang, and Shanshan Yang. 2024. "Spatial Downscaling of ESA CCI Soil Moisture Data Based on Deep Learning with an Attention Mechanism" Remote Sensing 16, no. 8: 1394. https://doi.org/10.3390/rs16081394
APA StyleZhang, D., Lu, L., Li, X., Zhang, J., Zhang, S., & Yang, S. (2024). Spatial Downscaling of ESA CCI Soil Moisture Data Based on Deep Learning with an Attention Mechanism. Remote Sensing, 16(8), 1394. https://doi.org/10.3390/rs16081394







