1. Introduction
Direction of arrival (DOA) estimation is a widely studied topic in the signal processing area, which performs a key role in wireless communications, astronomical observation, and radar applications [
1,
2,
3,
4,
5]. The conventional beamforming (CBF) method is a classical solution for DOA estimation. However, it suffers from Rayleigh limit. Subsequently, many traditional methods were proposed to meet the accuracy requirement and high resolution of DOA estimation, such as the minimum variance distortionless response (MVDR) beamformer (also referred to as the Capon beamformer) [
6], multiple signal classification method (MUSIC) algorithm [
7], estimation of signal parameters using rotational invariance techniques (ESPRIT) algorithm [
8] and their variants [
9,
10,
11,
12,
13]. However, the above-mentioned traditional methods require operations such as singular value decomposition and/or the inversion on the array covariance matrix of the received signal and/or spatial spectrum searching. As a result, their computational complexity is high, which makes it difficult for them to meet real-time requirements. Moreover, most of them have large estimation errors under harsh scenarios such as when the DOAs of source signals have small angular intervals or the signal-noise ratio (SNR) is low. To overcome the drawbacks of the traditional solutions, many studies use machine learning methods to solve the problem of DOA estimation, these methods first establish a training dataset with DOA labels, and then utilize existing machine learning techniques such as radial basis function (RBF) [
14] and support vector regression (SVR) [
15] to apply the derived mapping to the test data for DOA estimation. These methods require significant effort to learn the mapping during the training stage. However, once the mapping is learned and fixed after the training stage, they directly apply the mapping to process the testing data without labels to obtain DOA estimates. It is noted that the mapping only involves calculations of additions and multiplications, which avoids matrix inverse, decomposition, and spectrum searching. Thus, in the testing stage, they acquire higher computational efficiency compared to traditional methods [
16], but they heavily rely on the generalization characteristics of machine learning technology. That is, only when the training data and test data have almost the same distribution, satisfactory test results can be obtained.
In recent years, DOA estimation based on deep learning methods has gained great attention due to its high accuracy and high computational efficiency during the testing phase. In 2015, a single-layer neural network model based on classification was designed to implement DOA estimation [
17]. Since then, more and more improved neural networks aiming at solving DOA estimation have been proposed. In 2018, a deep neural network (DNN) was proposed, which contains a multitask auto-encoder and a set of parallel multi-layer classifiers, with the covariance vector of the array output as an input to the DNN, the auto-encoder decomposes the input vectors into sub-regions of space, then the classifiers output the spatial spectrum for DOA estimation [
18]. In 2019, a deep convolutional neural network (CNN) was developed for DOA estimation by mapping the initial sparse spatial spectrum obtained from the covariance matrix to the true sparse spatial spectrum [
19]. In 2020, a DeepMUSIC method was proposed for DOA estimation, by using multiple CNNs each of which is dedicated to learning the MUltiple SIgnal Classification (MUSIC) spectra of an angular sub-region [
20]. In 2021, a CNN with 2D filters was developed for DOA prediction in the low SNR [
21], by mapping the 2-D covariance matrix to the spatial spectrum labeled according to the true DOAs of source signals. In 2023, a DNN framework for DOA estimation in a uniform circular array was proposed, using transfer learning and multi-task techniques [
22]. The existing results show that deep learning frameworks provide better performance than traditional methods in harsh conditions such as low SNRs and small angle intervals between the DOAs of two source signals.
It is noted that all of the above-mentioned DNN-based DOA estimation methods choose to use the whole array covariance matrix of the received signal or its upper triangular elements or their transformation as the input of the network, which contains lots of redundant information when the array is uniformly linear. In addition, most of them try to match DOA estimation with the classification problem and thus use the spatial spectrum (labeled by the true DOAs of source signals or given by the existing traditional MUSIC method) as their output vector. Therefore, in the existing DNN-based DOA estimation approaches, the data redundancy in the input vector and the large size of the output vector lead to large sizes of hidden layers and make the DNN models complex overall, resulting in low computational efficiency.
There are a few works [
23,
24,
25] that use neural networks with regression for DOA estimation. In [
23], the neural network and a particle swarm optimization (PSO) were combined for DOA estimation, which might be trapped into a minimum solution. In [
24], a DNN with regression was developed to estimate the DOA of a single source signal, without considering the situation of multiple source signals. In [
25], a DNN with regression was designed for DOA estimation of multiple source signals. However, it does not consider the data redundancy in a uniform linear array (ULA).
In this paper, we consider a ULA, which is the most generally adopted array geometry for DOA estimation due to its regular structure and well-developed techniques according to the Nyquist sampling theorem [
26]. By exploring the property of the ULA, a lightweight DNN is proposed by designing an input vector with data redundancy removal and using the regression fashion for DOA estimation. The lightweight DNN significantly reduces the sizes of the input vector, hidden layers, and output vector, which leads to a reduction in the number of trainable parameters of the neural network and computational load. Meanwhile, the proposed lightweight DNN can preserve DOA estimation accuracy and performs better than the method in [
25]. It is noted that by considering that the array signal is different from the image signal and DOA information is hidden in each element of the input vector obtained from the covariance matrix of the array signal, we utilize a fully connected deep neuron network to obtain the mapping from the input vector to the DOAs of source signals.
Throughout this paper, *, T, H, and E represent the conjugate, transpose, conjugate transpose, and expectation operations, respectively.
2. Background
Assume that
K-independent far-field source signals
with a wavelength
and DOAs of
impinge on an
M-element uniform linear array (ULA) with an inter-element spacing
d. Moreover, it is assumed that the source signals and the array sensors are on the same plane. The received data of the array can be expressed as
where
n(
t) is an additive and zero-mean white Gaussian noise vector,
,
; In particular,
is an
M-dimensional steering vector, which is defined as
The array covariance matrix
R can be expressed as
where
,
is the noise power, and
is an identity matrix with a size of
. In practice, due to the finite snapshots, the covariance matrix
R can be estimated as
where
N is the number of snapshots, and
means the approximation of the quantity above which it appears.
Equation (
4) illustrates that
is a conjugate symmetric matrix. Utilizing this feature, many real-valued deep learning methods use the upper triangular elements as their input vectors [
18,
20]. Define the vector composed of the off-diagonal upper triangular elements of
by
, that is
It is noted that for a real-valued DNN network, the input vector needs to be real-valued. Therefore, by concatenating the real and imaginary parts of
, we obtain
below.
where
defines
norm.
and
represent the real and imaginary parts of a complex value, respectively.
In [
18], a fully connected DNN method with classification was developed for DOA estimation, and it utilizes the vector
as its input, named as the conventional DNN in this paper. Note that the input vector
contains data redundancy and costs the computational load without performance improvement. Moreover, since the conventional DNN is based on classification fashion, its output is equal to
, where
is the angle-searching range of the sources, and
is the grid; with
is equal to the smallest integer not smaller than
x. Therefore, the size of its output vector is much larger than the number of DOAs of sources, which further increases the computational load.
In the following, we analyze the data redundancy in the ULA and design a new input vector that removes data redundancy and retains DOA information. In a sequence, the lightweight DNN is proposed by using the newly designed input vector and employing the regression fashion for DOA estimation.
4. Lightweight DNN for DOA Estimation
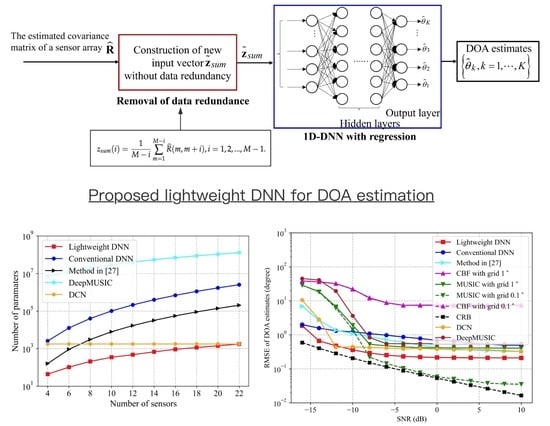
In this section, we propose a lightweight DNN for DOA estimation, which is illustrated in
Figure 1. As shown in
Figure 1, the proposed lightweight DNN model utilizes the newly developed input vector
as its input vector. Furthermore, different from the conventional DNN model with classification [
18,
19,
20,
21], the new DNN model is a regression model and has an output vector with a dimension equal to the number of sources, which approaches to the vector of true DOAs of sources in a regression fashion. It is noted that by considering the DOAs of sources are continuous values, the DNN model with regression can match the task of DOA estimation naturally. It is noted that in practice, prior to DOA estimation, the estimation of the number of sources can be accomplished by the classical methods such as the Minimum Description Length (MDL) and the Akaike Information Criterion (AIC) methods [
28]. In addition, by considering that the array signal is different from the image signal and DOA information is hidden in each element of the input vector which is obtained from the covariance matrix of the array signal, we select a fully connected deep neuron network to extract the mapping from the input vector to the DOAs of source signals.
As shown in
Figure 1, the proposed lightweight DNN is a fully connected network with regression and contains an input layer, several hidden layers with activation functions, and an output layer. Furthermore, each node of each layer in the network is connected to each node of the adjacent forward layer. The input data flows into the input layer, passes through the hidden layers, and turns into the output of the network, which gives DOA estimates. The detailed structure of the proposed lightweight DNN model and its construction of the training data set are given as follows. It is noted that both the proposed lightweight DNN method and the method in [
25] use regression for DOA estimation. The difference between the proposed lightweight DNN method and the one in [
25] is that the proposed lightweight DNN method removes the data redundancy and significantly reduces the trainable parameters, by analyzing the property of the covariance matrix of a ULA and the parameters of the network.
4.1. Detailed Structure of Lightweight DNN
The computations of hidden layers are feedforward as
where
L is the total number of the layers except for the input layer;
represent the output vector of the
l-th layer;
is the weight matrix between the (
l-1)-
th layer and
l-th layer;
is the bias vector of the
l-th layer;
is the activation function of the
l-th layer. The activation function is set as
, which is expressed as
where
is a real value. The output vector of the output layer is given as
In the training phase, the proposed DNN is performed in a supervised manner with the training data-label set, and the parameters of the DNN are adjusted to make the output vector approach to the label, which is composed of the DOAs of source signals. We define the number of input vectors by I. Then, the training data set can be expressed as with its label set , and are the i-th input vector and its label, respectively. is equal to generated in the i-th numerical experiment. is a K-dimensional vector composed of the true DOAs of sources in the i-th numerical experiment.
The set of all the trainable parameters in the lightweight DNN model can be collectively referred to as
. The update of
follows back-propagation towards minimizing the Mean Square Error(MSE) loss function as follows.
where
represents 2-norm, which measures the distance between the output vector of the network and the corresponding label,
represents the output vector of the network corresponding to the
i-th input vector. In the testing phase, the output vector of the output layer gives the estimated values of the DOAs of source signals explicitly.
For the lightweight DNN model, we define the size of the input vector by
. Note that with more layers and larger sizes of layers, the expressivity power of the network is increased during the training stage. However, the network tends to overfit the training data. As a result, in the testing stage, the performance is obviously degraded due to the lack of generalization. Furthermore, referring to [
18], for the balance between the expressivity power with deeper network and aggravation with more network parameters, we set the number of hidden layers to be 2 and their sizes are equal to
and
, respectively, where
is equal to the largest integer not larger than
x.
4.2. Construction of Training Data Set
Assuming that the searching angle range of the source signals is from to , the angular interval between two source signals in this range is defined as △, which is sampled from a set of , where , , and are the minimum angle interval between the DOAs of two source signals, the maximum angle interval, and an angle increment, respectively. In this way, any two source signals in this range that are spatially close to each other and those with large spacing can all be included in the training data set. Since the elements used as the input vector from the covariance matrix are not affected by the order of DOAs of source signals, with the DOA of the first source signal is sampled with a grid from to , and the DOA of the k-th source signal is . Furthermore, in order to adapt to the performance fluctuations in low SNRs, input vectors with multiple SNRs lower than 0dB are trained at the same time, making the lightweight DNN better adapted to unknown low and high SNRs during the testing phase.
4.3. Analysis of Number of Trainable Parameters
In this section, we present a comparative analysis of the proposed lightweight DNN, against the method in [
25], the conventional DNN in [
18], deep convolution network (DCN) in [
19], and DeepMUSIC in [
20], focusing on the number of trainable parameters. For the conventional DNN model in [
18], we follow the setting in [
18]. That is, for the autoencoder, we denote the size of each of the input and output layers as
, define the number of each encoder and decoder has one hidden layer with a size of
, and define the number of spatial subregion as
p. As a sequence, we obtain that for each of the multilayer classifiers after the autoencoder, the sizes of two hidden layers are equal to
and
, respectively. In addition, the size of output layer (denoted as
) for each multilayer classifier is equal to
Correspondingly, according to the analysis in
Section 3.1 for the proposed lightweight DNN, we have
. By following the above-mentioned definitions and the structure of the lightweight DNN, conventional DNN, and method in [
25], we can obtain the number of parameters in the three fully connected DNN models, as shown in
Table 1.
Table 2 shows the number of trainable parameters in DeepMUSIC and DCN by following the parameter settings in [
19,
20], which are mainly from the convolution layers and dense layers. For DeepMUSIC,
represents the number of input channels,
is the kernel size of the first two convolution layers, and
is the kernel size of convolution layer 3 and convolution layer 4.
is the number of filters.
and
represent the sizes of the first and second dense layers, respectively. For DCN,
,
,
and
represent the kernel size of the first till fourth convolution layers, of which the number of filters are
,
,
, and
, respectively. There is no dense layer.
When
,
,
,
,
,
,
,
,
,
,
,
,
,
,
=6,
,
,
,
, the total parameters of the above-mentioned five deep learning methods versus the number of sensors are shown in
Figure 2. From
Figure 2, we can see that the number of trainable parameters in the lightweight DNN is significantly reduced compared to those of the conventional DNN, method in [
25], and DeepMUSIC. In particular, when the number of sensors is 22, the number of parameters in the lightweight DNN is three orders, two orders, and five orders of magnitude less than that in the conventional DNN, the method in [
25], and DeepMUSIC, respectively. This fact contributes to fitting the DNN-based DOA estimation into the embedded system. In addition, the lightweight DNN method has fewer parameters than the DCN method when the number of sensors is less than 22. The DCN method remains constant regardless of the number of sensors. This is because the input of the DCN method is the spatial spectrum proxy, which has a fixed length equal to
. On the other hand, the inputs of other methods are all explicitly relevant to the dimension of the array covariance matrix. Thus, their parameters are related to the number of sensors.
4.4. Analysis of Computational Complexity
Analogous to the approach detailed in [
11], we quantify the primary computational complexity through the calculation of real-valued multiplications, as given in
Table 3. In this table,
L pertaining to the DCN denotes the length of the input vector, which is set as 120. In addition, we define
Note that when
and
, we have
[
11] and
. According to the settings in
Section 4.3, it is found from
Table 3 that the computational complexity of the CBF, MUSIC, DeepMUSIC, and DCN methods is significantly higher than that of the fully-connected DNN-based methods, which corresponds to the testing time in
Table 4 below.
6. Discussion
From the analysis above, it can be seen that the number of total parameters in the lightweight DNN model is significantly reduced compared to those DNN models that use the upper triangular elements of the covariance matrix as input. In particular, when the number of sensors is 22, it is 2 and 3 orders of magnitude less than that in the conventional DNN model and the method in [
25], respectively. This fact makes the proposed lightweight DNN suitable for real-time embedded applications. Furthermore, it is noted that the lightweight DNN can preserve high accuracy of DOA estimation and perform better than the conventional DNN and method in [
25]. In addition, it provides higher estimation accuracy and costs less trainable parameters and computational load than CNN-based methods such as DeepMUSIC and DCN. Also, it is illustrated that the lightweight DNN performs better than the spatial spectrum-based methods such as MUSIC and CBF method under harsh conditions such as low SNRs and/or closely spaced source signals and/or few snapshots. Moreover, its testing time is obviously shorter than that of the MUSIC and CBF method, due to the avoidance of spectrum searching and matrix decomposition. On the other hand, under good conditions such as high SNRs, the estimation accuracy of the lightweight DNN is lower than the MUSIC method with a grid of
. This is because the DNN-based methods are biased estimators while the MUSIC method can provide unbiased DOA estimation. It is noted that the MUSIC method with a grid of
provides higher estimation accuracy with a cost of a testing time of about 25 times more than that of the lightweight DNN. On the other hand, as shown in simulation results, the lightweight DNN can achieve high estimation accuracy such as
when the SNR is not extremely low (not lower than −6 dB) and the number of snapshots is not very small (not smaller than 100).