DRAF-Net: Dual-Branch Residual-Guided Multi-View Attention Fusion Network for Station-Level Numerical Weather Prediction Correction
Abstract
:1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Preliminaries
2.3. Methods
2.3.1. Overview of DRAF-Net
2.3.2. Multi-View Attention Fusion Mechanism
2.3.3. Dual-Branch Residual Structure
2.3.4. Overall Loss Function
3. Experiment
3.1. Experimental Setup
3.1.1. Comparative Experiments
3.1.2. Ablation Studies
3.1.3. Alternative Implementation Studies
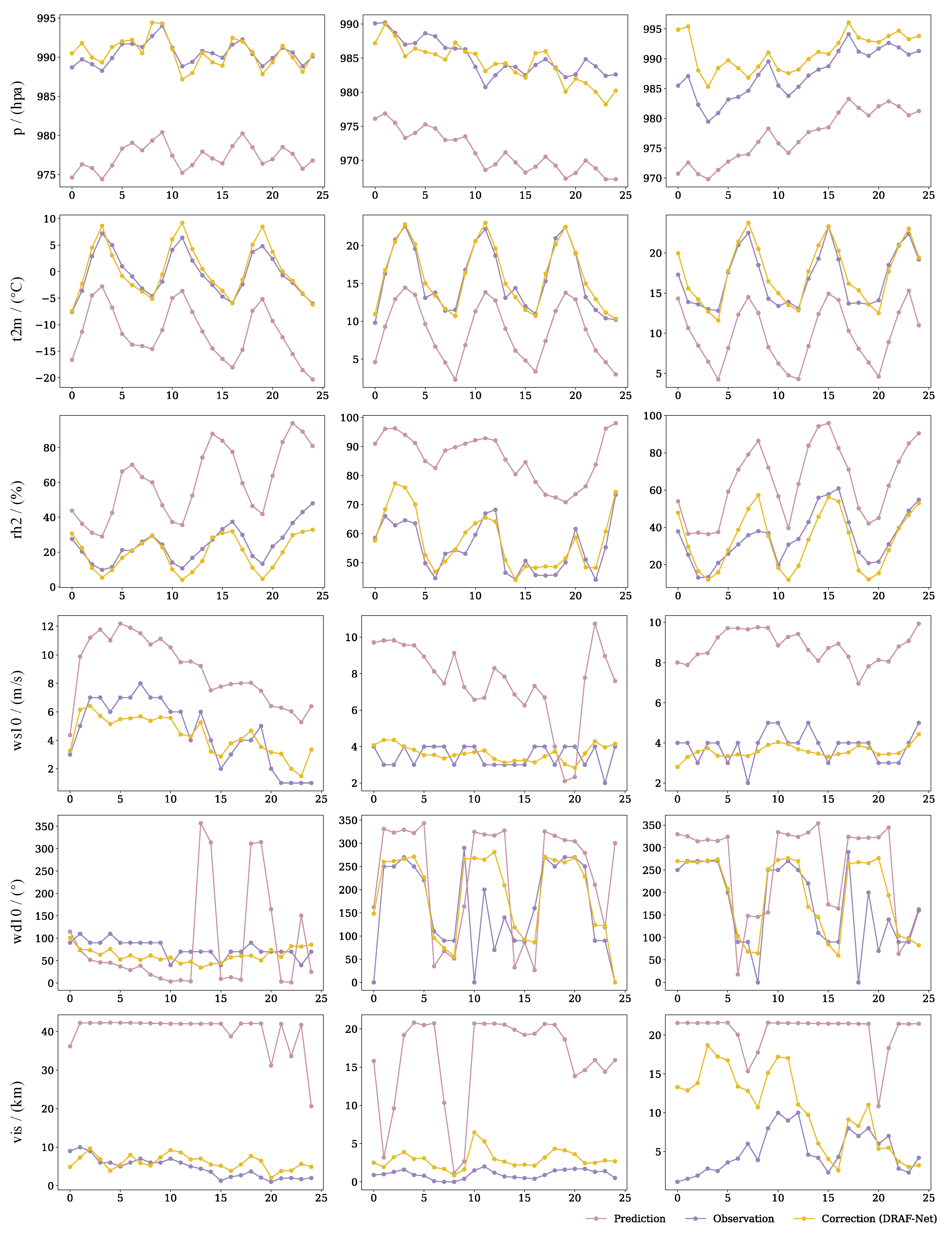
3.1.4. Visualization of Results
3.2. Implementation Details
3.3. Metrics
4. Results
4.1. Comparative Experiments
4.1.1. The First Dataset
4.1.2. The Second Dataset
| Input Format | Model | p (hpa) | t2m (°C) | rh2 (%) | ws10 (m/s) | wd10 (°) | vis (km) | Mean |
|---|---|---|---|---|---|---|---|---|
| - | Baseline | 28.80 | 3.46 | 15.87 | 1.91 | 120.66 | 12.04 | 30.46 |
| single-point (V) | LR | 24.93 | 2.84 | 13.80 | 1.60 | 103.04 | 8.49 | 25.79 |
| XGBoost | 20.19 | 2.42 | 12.45 | 1.43 | 97.62 | 7.60 | 23.62 | |
| LightGBM | 21.00 | 2.49 | 12.76 | 1.46 | 97.62 | 7.69 | 23.84 | |
| Temporal () | Transformer | 1.51 | 0.65 | 2.24 | 0.96 | 9.11 | 2.24 | 2.79 |
| Flashformer | 1.08 | 0.73 | 2.41 | 0.99 | 9.21 | 2.24 | 2.78 | |
| FlowFormer | 1.07 | 0.70 | 2.37 | 0.97 | 9.16 | 2.23 | 2.75 | |
| Informer | 1.77 | 0.87 | 2.63 | 1.10 | 9.68 | 2.47 | 3.09 | |
| Reformer | 1.03 | 0.59 | 2.18 | 0.94 | 9.08 | 2.20 | 2.67 | |
| iTransformer | 1.52 | 0.69 | 2.34 | 1.05 | 9.70 | 2.56 | 2.98 | |
| Spatiotemporal () | Transformer | 0.51 | 0.59 | 2.16 | 0.90 | 8.99 | 2.08 | 2.54 |
| Flashformer | 2.50 | 1.93 | 3.32 | 1.17 | 10.07 | 2.81 | 3.63 | |
| FlowFormer | 2.27 | 1.78 | 3.20 | 1.10 | 9.43 | 2.35 | 3.36 | |
| Informer | 2.38 | 1.91 | 3.22 | 1.14 | 9.92 | 2.66 | 3.54 | |
| Reformer | 0.64 | 1.03 | 3.10 | 1.11 | 9.52 | 2.38 | 2.96 | |
| iTransformer | 0.97 | 1.27 | 3.16 | 1.18 | 10.27 | 2.62 | 3.25 | |
| DRAF-Net | 0.24 | 0.49 | 2.03 | 0.88 | 8.90 | 2.00 | 2.42 |
| Input Format | Model | p (hpa) | t2m (°C) | rh2 (%) | ws10 (m/s) | wd10 (°) | vis (km) | Mean |
|---|---|---|---|---|---|---|---|---|
| - | Baseline | 15.22 | 2.68 | 11.93 | 1.36 | 80.19 | 9.48 | 20.14 |
| Single-point (V) | LR | 10.76 | 2.14 | 10.58 | 1.14 | 82.77 | 7.19 | 19.10 |
| XGBoost | 8.15 | 1.83 | 9.39 | 1.03 | 74.49 | 6.07 | 16.83 | |
| LightGBM | 8.95 | 1.88 | 9.66 | 1.05 | 75.04 | 6.23 | 17.14 | |
| Temporal () | Transformer | 0.56 | 0.48 | 1.61 | 0.68 | 6.65 | 1.67 | 1.94 |
| Flashformer | 0.56 | 0.55 | 1.75 | 0.71 | 6.80 | 1.68 | 2.01 | |
| FlowFormer | 0.42 | 0.52 | 1.71 | 0.69 | 6.68 | 1.64 | 1.94 | |
| Informer | 0.87 | 0.67 | 1.99 | 0.78 | 7.47 | 1.97 | 2.29 | |
| Reformer | 0.44 | 0.43 | 1.54 | 0.67 | 6.61 | 1.64 | 1.89 | |
| iTransformer | 0.60 | 0.51 | 1.72 | 0.74 | 7.28 | 2.01 | 2.14 | |
| Spatiotemporal () | Transformer | 0.40 | 0.44 | 1.55 | 0.65 | 6.46 | 1.49 | 1.83 |
| Flashformer | 1.62 | 1.38 | 4.10 | 0.82 | 8.48 | 1.89 | 3.05 | |
| FlowFormer | 1.20 | 1.60 | 3.34 | 0.86 | 8.06 | 1.75 | 2.80 | |
| Informer | 1.78 | 1.72 | 3.49 | 0.85 | 8.60 | 1.69 | 3.02 | |
| Reformer | 0.45 | 0.78 | 2.30 | 0.78 | 7.46 | 1.81 | 2.26 | |
| iTransformer | 0.76 | 0.97 | 2.45 | 0.84 | 7.34 | 1.84 | 2.37 | |
| DRAF-Net | 0.18 | 0.36 | 1.43 | 0.62 | 6.23 | 1.40 | 1.70 |
| Input Format | Model | p | t2m | rh2 | ws10 | wd10 | vis | Mean |
|---|---|---|---|---|---|---|---|---|
| - | Baseline | −7.37 | 0.01 | −9.49 | −0.91 | −132.23 | −13.82 | −27.30 |
| Single-point (V) | LR | −5.27 | 0.33 | −6.93 | −0.35 | −96.17 | −6.38 | -19.13 |
| XGBoost | −3.11 | 0.51 | −5.45 | −0.06 | −86.20 | −4.91 | −16.54 | |
| LightGBM | −3.45 | 0.48 | −5.77 | −0.12 | −86.22 | −5.05 | −16.69 | |
| Temporal () | Transformer | 0.98 | 0.97 | 0.79 | 0.52 | 0.24 | 0.49 | 0.67 |
| Flashformer | 0.99 | 0.96 | 0.76 | 0.49 | 0.22 | 0.49 | 0.65 | |
| FlowFormer | 0.99 | 0.96 | 0.77 | 0.51 | 0.23 | 0.49 | 0.66 | |
| Informer | 0.97 | 0.94 | 0.71 | 0.37 | 0.14 | 0.38 | 0.59 | |
| Reformer | 0.99 | 0.97 | 0.80 | 0.54 | 0.25 | 0.50 | 0.68 | |
| iTransformer | 0.98 | 0.96 | 0.77 | 0.43 | 0.14 | 0.33 | 0.60 | |
| Spatiotemporal () | Transformer | 0.99 | 0.97 | 0.81 | 0.57 | 0.26 | 0.56 | 0.69 |
| Flashformer | 0.94 | 0.69 | 0.54 | 0.29 | 0.07 | 0.20 | 0.46 | |
| FlowFormer | 0.95 | 0.74 | 0.57 | 0.37 | 0.19 | 0.44 | 0.54 | |
| Informer | 0.94 | 0.70 | 0.57 | 0.33 | 0.10 | 0.28 | 0.49 | |
| Reformer | 0.99 | 0.91 | 0.60 | 0.36 | 0.17 | 0.42 | 0.58 | |
| iTransformer | 0.99 | 0.87 | 0.58 | 0.27 | 0.03 | 0.30 | 0.51 | |
| DRAF-Net | 1.00 | 0.98 | 0.83 | 0.59 | 0.28 | 0.59 | 0.71 |
| Input Format | Model | p | t2m | rh2 | ws10 | wd10 | vis | Mean |
|---|---|---|---|---|---|---|---|---|
| - | Baseline | 0.91 | 0.90 | 0.74 | 0.52 | 0.32 | 0.14 | 0.59 |
| Single-point (V) | LR | 0.95 | 0.94 | 0.74 | 0.36 | 0.08 | 0.28 | 0.56 |
| XGBoost | 0.97 | 0.96 | 0.80 | 0.55 | 0.25 | 0.49 | 0.67 | |
| LightGBM | 0.97 | 0.96 | 0.78 | 0.49 | 0.23 | 0.46 | 0.65 | |
| Temporal () | Transformer | 0.97 | 0.98 | 0.87 | 0.64 | 0.33 | 0.59 | 0.73 |
| Flashformer | 0.97 | 0.95 | 0.81 | 0.61 | 0.29 | 0.71 | 0.72 | |
| FlowFormer | 0.97 | 0.97 | 0.85 | 0.62 | 0.32 | 0.74 | 0.75 | |
| Informer | 0.95 | 0.89 | 0.76 | 0.58 | 0.21 | 0.65 | 0.67 | |
| Reformer | 0.98 | 0.98 | 0.88 | 0.67 | 0.43 | 0.75 | 0.78 | |
| iTransformer | 0.96 | 0.95 | 0.82 | 0.60 | 0.22 | 0.64 | 0.70 | |
| Spatiotemporal () | Transformer | 0.98 | 0.98 | 0.89 | 0.71 | 0.50 | 0.77 | 0.81 |
| Flashformer | 0.89 | 0.80 | 0.71 | 0.56 | 0.35 | 0.61 | 0.65 | |
| FlowFormer | 0.92 | 0.85 | 0.73 | 0.58 | 0.38 | 0.69 | 0.69 | |
| Informer | 0.91 | 0.81 | 0.73 | 0.57 | 0.37 | 0.63 | 0.67 | |
| Reformer | 0.98 | 0.88 | 0.74 | 0.58 | 0.37 | 0.69 | 0.71 | |
| iTransformer | 0.98 | 0.87 | 0.74 | 0.56 | 0.31 | 0.64 | 0.68 | |
| DRAF-Net | 1.00 | 0.99 | 0.92 | 0.78 | 0.55 | 0.80 | 0.84 |
| Input Format | Model | Rain6 | Rain24 | ||||
|---|---|---|---|---|---|---|---|
| RMSE (mm) | MAE (mm) | Score (%) | RMSE (mm) | MAE (mm) | Score (%) | ||
| - | Baseline | 14.42 | 12.34 | 51.1 | 20.61 | 18.81 | 49.6 |
| Single-point (V) | LR | 12.84 | 11.92 | 62.4 | 17.57 | 16.93 | 60.1 |
| XGBoost | 12.50 | 10.27 | 65.7 | 16.56 | 15.54 | 63.2 | |
| LightGBM | 12.17 | 11.12 | 65.2 | 16.50 | 16.51 | 62.8 | |
| Temporal () | Transformer | 2.50 | 0.85 | 92.1 | 4.10 | 1.76 | 90.5 |
| Flashformer | 2.87 | 1.54 | 88.1 | 4.50 | 2.67 | 86.2 | |
| FlowFormer | 2.71 | 0.87 | 91.1 | 4.39 | 2.37 | 87.3 | |
| Informer | 2.82 | 1.38 | 89.2 | 4.27 | 2.00 | 88.9 | |
| Reformer | 2.79 | 1.10 | 90.1 | 4.43 | 2.64 | 87.1 | |
| iTransformer | 2.69 | 1.08 | 90.7 | 4.28 | 2.15 | 88.3 | |
| Spatiotemporal () | Transformer | 2.47 | 0.84 | 93.6 | 4.34 | 2.25 | 89.5 |
| Flashformer | 3.16 | 1.91 | 83.2 | 4.89 | 3.35 | 81.2 | |
| FlowFormer | 2.70 | 0.91 | 90.8 | 4.50 | 2.67 | 87.2 | |
| Informer | 2.92 | 1.73 | 87.9 | 4.63 | 2.89 | 85.6 | |
| Reformer | 2.88 | 1.26 | 89.0 | 4.51 | 2.70 | 86.4 | |
| iTransformer | 2.96 | 1.74 | 85.5 | 4.54 | 2.85 | 85.9 | |
| DRAF-Net | 2.30 | 0.52 | 98.6 | 3.85 | 1.09 | 93.9 | |
4.2. Ablation Studies
4.2.1. Ablation Study on the Dual-Branch Residual Structure
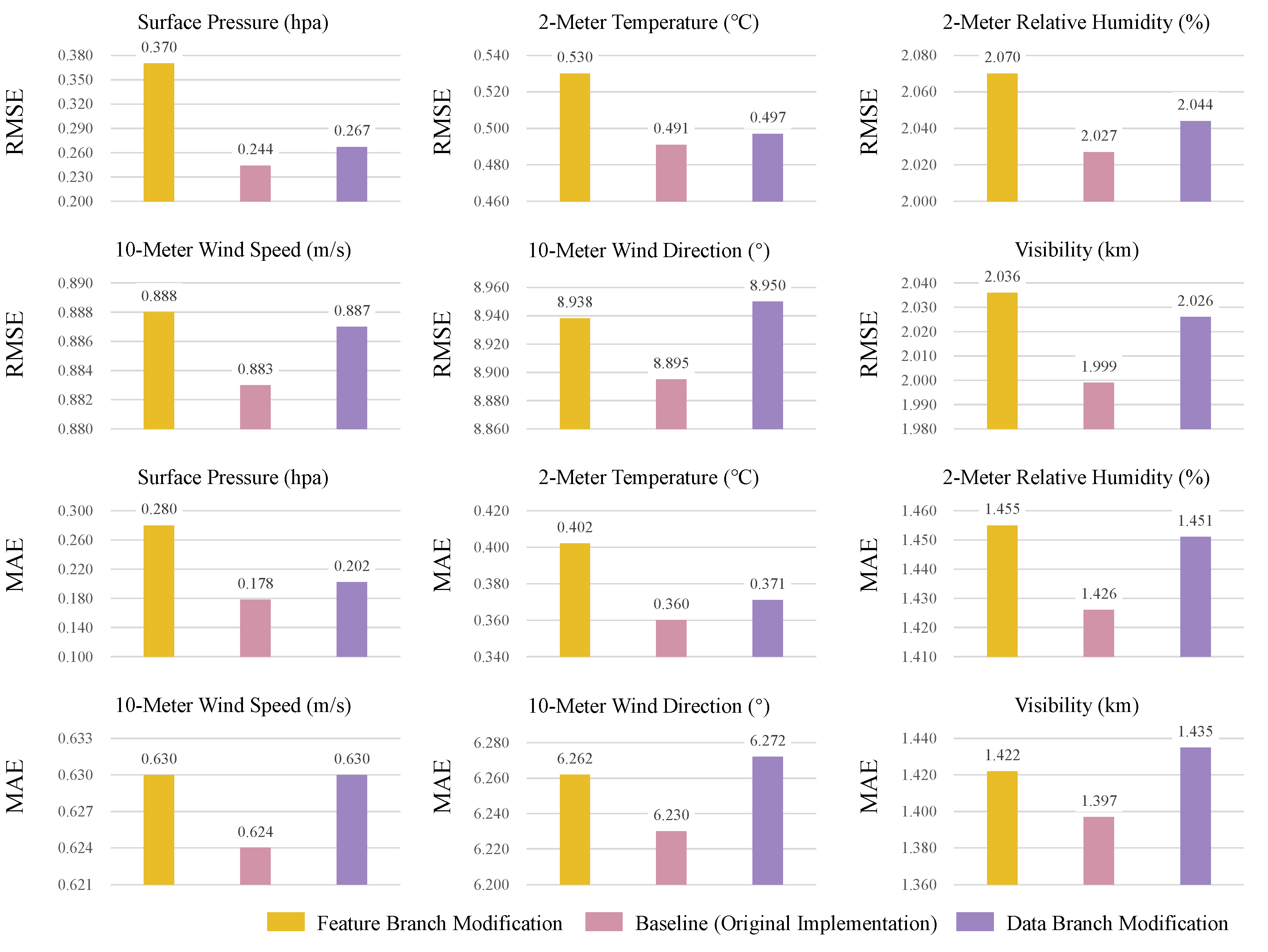
4.2.2. Ablation Study on the Multi-View Attention Fusion Mechanism
4.2.3. Ablation Study on the Variable-Weighted Combined Loss Function
4.3. Alternative Implementation Studies
4.4. Visualization of Results
5. Discussion
5.1. Analysis of Performance Differences Across Methods
5.2. Analysis of DRAF-Net’s Performance
5.3. Analysis of the Contribution of the Dual-Branch Residual Structure
5.4. Analysis of the Contribution of the Multi-View Attention Fusion Mechanism
5.5. Analysis of the Contribution of the Variable-Weighted Combined Loss Function
5.6. Limitations
5.7. Future Work
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Bauer, P.; Thorpe, A.; Brunet, G. The quiet revolution of numerical weather prediction. Nature 2015, 525, 47–55. [Google Scholar] [CrossRef] [PubMed]
- Kimura, R. Numerical weather prediction. J. Wind. Eng. Ind. Aerodyn. 2002, 90, 1403–1414. [Google Scholar] [CrossRef]
- Qin, Y.; Liu, Y.; Jiang, X.; Yang, L.; Xu, H.; Shi, Y.; Huo, Z. Grid-to-point deep-learning error correction for the surface weather forecasts of a fine-scale numerical weather prediction system. Atmosphere 2023, 14, 145. [Google Scholar] [CrossRef]
- Huo, J.; Bi, Y.; Wang, H.; Zhang, Z.; Song, Q.; Duan, M.; Han, C. A comparative study of cloud microphysics schemes in simulating a quasi-linear convective thunderstorm case. Remote Sens. 2024, 16, 3259. [Google Scholar] [CrossRef]
- Perera, L.P.; Soares, C.G. Weather routing and safe ship handling in the future of shipping. Ocean. Eng. 2017, 130, 684–695. [Google Scholar] [CrossRef]
- Rosillon, D.J.; Jago, A.; Huart, J.P.; Bogaert, P.; Journée, M.; Dandrifosse, S.; Planchon, V. Near real-time spatial interpolation of hourly air temperature and humidity for agricultural decision support systems. Comput. Electron. Agric. 2024, 223, 109093. [Google Scholar] [CrossRef]
- Chen, N.; Qian, Z.; Nabney, I.T.; Meng, X. Wind power forecasts using gaussian processes and numerical weather prediction. IEEE Trans. Power Syst. 2013, 29, 656–665. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Mu noz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The era5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, M.; Han, L.; Song, L.; Yang, L. Multi-element deep learning fusion correction method for numerical weather prediction. Acta Meteorol. Sin. 2022, 80, 153–167. [Google Scholar]
- Glahn, H.R.; Lowry, D.A. The use of model output statistics (mos) in objective weather forecasting. J. Appl. Meteorol. 1972, 11, 1203–1211. [Google Scholar] [CrossRef]
- Klein, W.H.; Lewis, B.M.; Enger, I. Objective prediction of five-day mean temperatures during winter. J. Atmos. Sci. 1959, 16, 672–682. [Google Scholar] [CrossRef]
- Monache, L.D.; Nipen, T.; Liu, Y.; Roux, G.; Stull, R. Kalman filter and analog schemes to postprocess numerical weather predictions. Mon. Weather. Rev. 2011, 139, 3554–3570. [Google Scholar] [CrossRef]
- Tan, J.; Chen, W.; Wang, S. Using a machine learning method for temperature forecast in hubei province. Adv. Meteorol. Sci. Technol. 2018, 8, 46–50. [Google Scholar]
- Ke, G.; Meng, Q.; Finley, T.; Wang, T.; Chen, W.; Ma, W.; Ye, Q.; Liu, T.-Y. Lightgbm: A highly efficient gradient boosting decision tree. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 3149–3157. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Guo, J.; Ren, G.; Liu, X.; Wang, X.; Lin, H. Research on numerical weather prediction wind speed correction based on stacking ensemble learning algorithm. E3S Web Conf. 2024, 520, 03005. [Google Scholar] [CrossRef]
- Sun, Q.; Jiao, R.; Xia, J.; Yan, Z.; Li, H.; Sun, J.; Wang, L.; Liang, Z. Adjusting Wind Speed Prediction of Numerical Weather Forecast Model Based on Machine Learning Methods. Meteorol. Sci. 2019, 45, 426–436. [Google Scholar]
- Nianfei, H.; Lu, Y.; Mingxuan, C.; Linye, S.; Weihua, C.; Lei, H. Machine learning correction of wind, temperature and humidity elements in beijing-tianjin-hebei region. J. Appl. Meteorol. Sci. 2022, 33, 489–500. [Google Scholar]
- Feng, H.; Lu, Y.; Chuxuan, Z.; Zhongliang, L. An experimental study of the short-time heavy rainfall event forecast based on ensemble learning and sounding data. J. Appl. Meteorol. Sci. 2021, 32, 188–199. [Google Scholar]
- Mao, K.; Zhao, C.; He, J. A research for 10m wind speed prediction based on XGBoost. J. Chengdu Univ. Inf. Technol. 2020, 35, 604–609. [Google Scholar]
- Zhang, C.; Liao, T.; Sun, Y.; Meng, X.; Zhang, C. Research on refined flow field simulation based on machine learning methods. J. Environ. Sci. 2022, 42, 318–331. [Google Scholar]
- Qiu, G.; Yu, B.; Tao, Y.; Yan, H.; Wang, Y. Forecasting of Extreme Wind Speed in Yanqing Competition Zone of the Winter Olympic Games Based on Ensemble Learning Algorithm. Meteorol. Mon. 2023, 49, 721–732. [Google Scholar]
- Li, H.; Yu, C.; Xia, J.; Wang, Y.; Zhu, J.; Zhang, P. A model output machine learning method for grid temperature forecasts in the beijing area. Adv. Atmos. Sci. 2019, 36, 1156–1170. [Google Scholar] [CrossRef]
- Whan, K.; Schmeits, M. Comparing area probability forecasts of (extreme) local precipitation using parametric and machine learning statistical postprocessing methods. Mon. Weather. Rev. 2018, 146, 3651–3673. [Google Scholar] [CrossRef]
- Bi, K.; Xie, L.; Zhang, H.; Chen, X.; Gu, X.; Tian, Q. Accurate medium-range global weather forecasting with 3d neural networks. Nature 2023, 619, 533–538. [Google Scholar] [CrossRef]
- Lam, R.; Sanchez-Gonzalez, A.; Willson, M.; Wirnsberger, P.; Fortunato, M.; Alet, F.; Ravuri, S.; Ewalds, T.; Eaton-Rosen, Z.; Hu, W.; et al. Learning skillful medium-range global weather forecasting. Science 2023, 382, 1416–1421. [Google Scholar] [CrossRef]
- Vaughan, A.; Markou, S.; Tebbutt, W.; Requeima, J.; Bruinsma, W.P.; Andersson, T.R.; Herzog, M.; Lane, N.D.; Chantry, M.; Hosking, J.S.; et al. Aardvark weather: End-to-end data-driven weather forecasting. arXiv 2024, arXiv:2404.00411. [Google Scholar]
- Wu, B.; Chen, W.; Wang, W.; Peng, B.; Sun, L.; Chen, L. Weathergnn: Exploiting meteo-and spatial-dependencies for local numerical weather prediction bias-correction. In Proceedings of the International Joint Conference on Artificial Intelligence, Jeju, Republic of Korea, 3–9 August 2024; pp. 2433–2441. [Google Scholar]
- Zeng, X.; Xue, F.; Zhao, R. Comparison study on several grid temperature rolling correction forecasting schemes. Meteor. Mon. 2019, 45, 1009–1018. [Google Scholar]
- Mouatadid, S.; Orenstein, P.; Flaspohler, G.; Cohen, J.; Oprescu, M.; Fraenkel, E.; Mackey, L. Adaptive bias correction for improved subseasonal forecasting. Nat. Commun. 2023, 14, 3482. [Google Scholar] [CrossRef]
- Vaswani, A. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 6000–6010. [Google Scholar]
- Ren, Y.; Ye, J.; Wang, X.; Xiao, F.; Liu, R. Sam-net: Spatio-temporal sequence typhoon cloud image prediction net with self-attention memory. Remote Sens. 2024, 16, 4213. [Google Scholar] [CrossRef]
- Liu, N.; Jiang, J.; Mao, D.; Fang, M.; Li, Y.; Han, B.; Ren, S. Artificial intelligence-based precipitation estimation method using fengyun-4b satellite data. Remote Sens. 2024, 16, 4076. [Google Scholar] [CrossRef]
- Gao, Z.; Tan, C.; Wu, L.; Li, S.Z. Simvp: Simpler yet better video prediction. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 19–24 June 2022; pp. 3170–3180. [Google Scholar]
- Tan, C.; Gao, Z.; Wu, L.; Xu, Y.; Xia, J.; Li, S.; Li, S.Z. Temporal attention unit: Towards efficient spatiotemporal predictive learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 18–22 June 2023; pp. 18770–18782. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.-Y.; Wong, W.-K.; Woo, W.-C. Convolutional lstm network: A machine learning approach for precipitation nowcasting. In Proceedings of the 29th Conference on Neural Information Processing Systems (NIPS 2015), Montreal, QC, Canada, 7–12 December 2015; pp. 802–810. [Google Scholar]
- Shi, B.; Ge, C.; Lin, H.; Xu, Y.; Tan, Q.; Peng, Y.; He, H. Sea surface temperature prediction using convlstm-based model with deformable attention. Remote Sens. 2024, 16, 4126. [Google Scholar] [CrossRef]
- Liang, Z.; Sun, R.; Duan, Q. Attribution of vegetation dynamics in the yellow river water conservation area based on the deep convlstm model. Remote Sens. 2024, 16, 3875. [Google Scholar] [CrossRef]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. Predrnn: Recurrent neural networks for predictive learning using spatiotemporal lstms. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA, 4–9 December 2017; pp. 679–888. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, J.; Philip, S.Y. Predrnn++: Towards a resolution of the deep-in-time dilemma in spatiotemporal predictive learning. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 5123–5132. [Google Scholar]
- Wang, S.; Chen, Y.; Yuan, Y.; Chen, X.; Tian, J.; Tian, X.; Cheng, H. Tsae-unet: A novel network for multi-scene and multi-temporal water body detection based on spatiotemporal feature extraction. Remote Sens. 2024, 16, 3829. [Google Scholar] [CrossRef]
- Tianzhi Cup Online Platform. Available online: https://tianzhibei.com/datasetDetailsPage?dataSetId=13 (accessed on 13 November 2024).
- Wu, H.; Wu, J.; Xu, J.; Wang, J.; Long, M. Flowformer: Linearizing transformers with conservation flows. arXiv 2022, arXiv:2202.06258. [Google Scholar]
- Kitaev, N.; Kaiser, Ł.; Levskaya, A. Reformer: The efficient transformer. arXiv 2020, arXiv:2001.04451. [Google Scholar]
- Dao, T.; Fu, D.; Ermon, S.; Rudra, A.; Ré, C. Flashattention: Fast and memory-efficient exact attention with io-awareness. Adv. Neural Inf. Process. Syst. 2022, 35, 16344–16359. [Google Scholar]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtually, 2–9 February 2021; Volume 5, pp. 11106–11115. [Google Scholar]
- Liu, Y.; Hu, T.; Zhang, H.; Wu, H.; Wang, S.; Ma, L.; Long, M. itransformer: Inverted transformers are effective for time series forecasting. arXiv 2023, arXiv:2310.06625. [Google Scholar]
- Loshchilov, I.; Hutter, F. Fixing weight decay regularization in Adam. arXiv 2017, arXiv:1711.05101. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Guo, Y.; Shao, C.; Su, A. Comparative evaluation of rainfall forecasts during the summer of 2020 over central east china. Atmosphere 2023, 14, 992. [Google Scholar] [CrossRef]
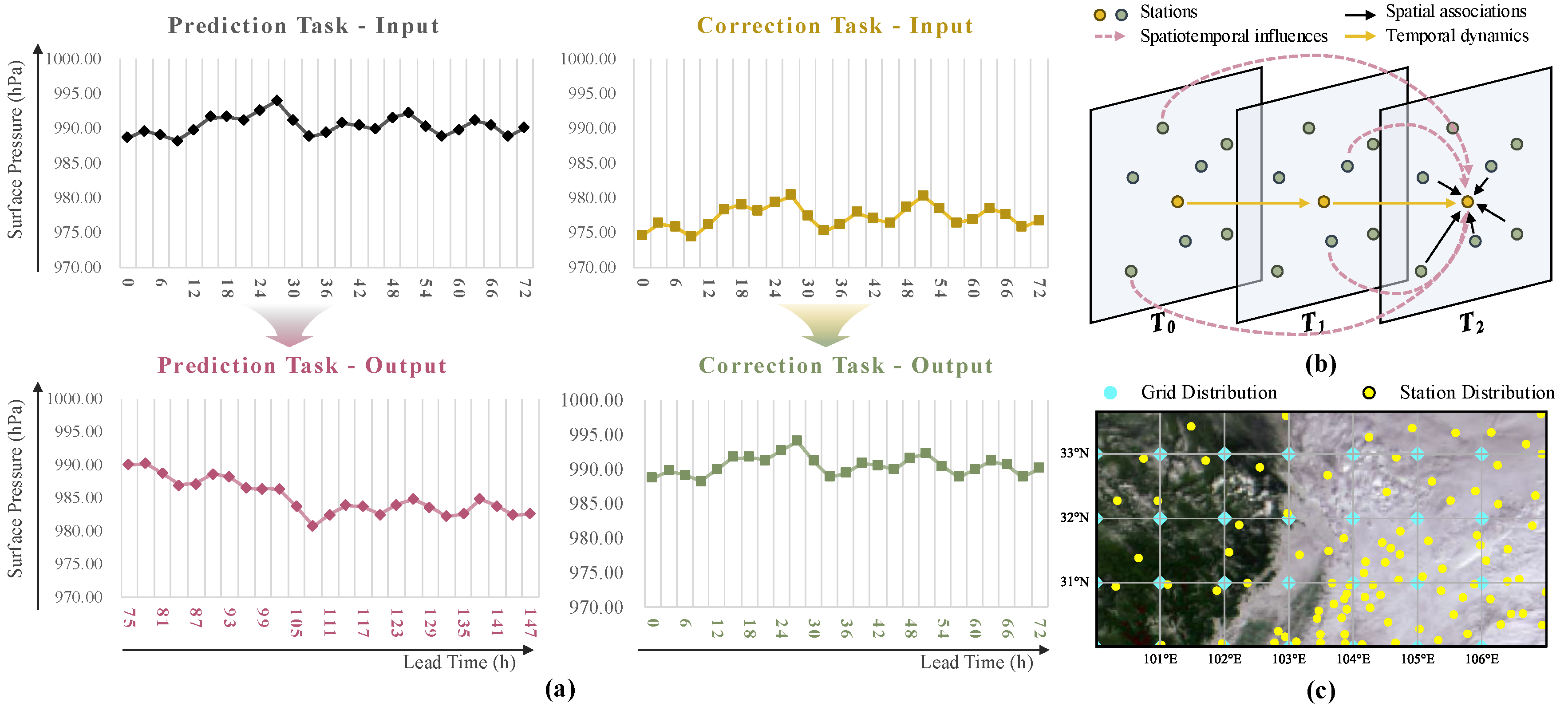
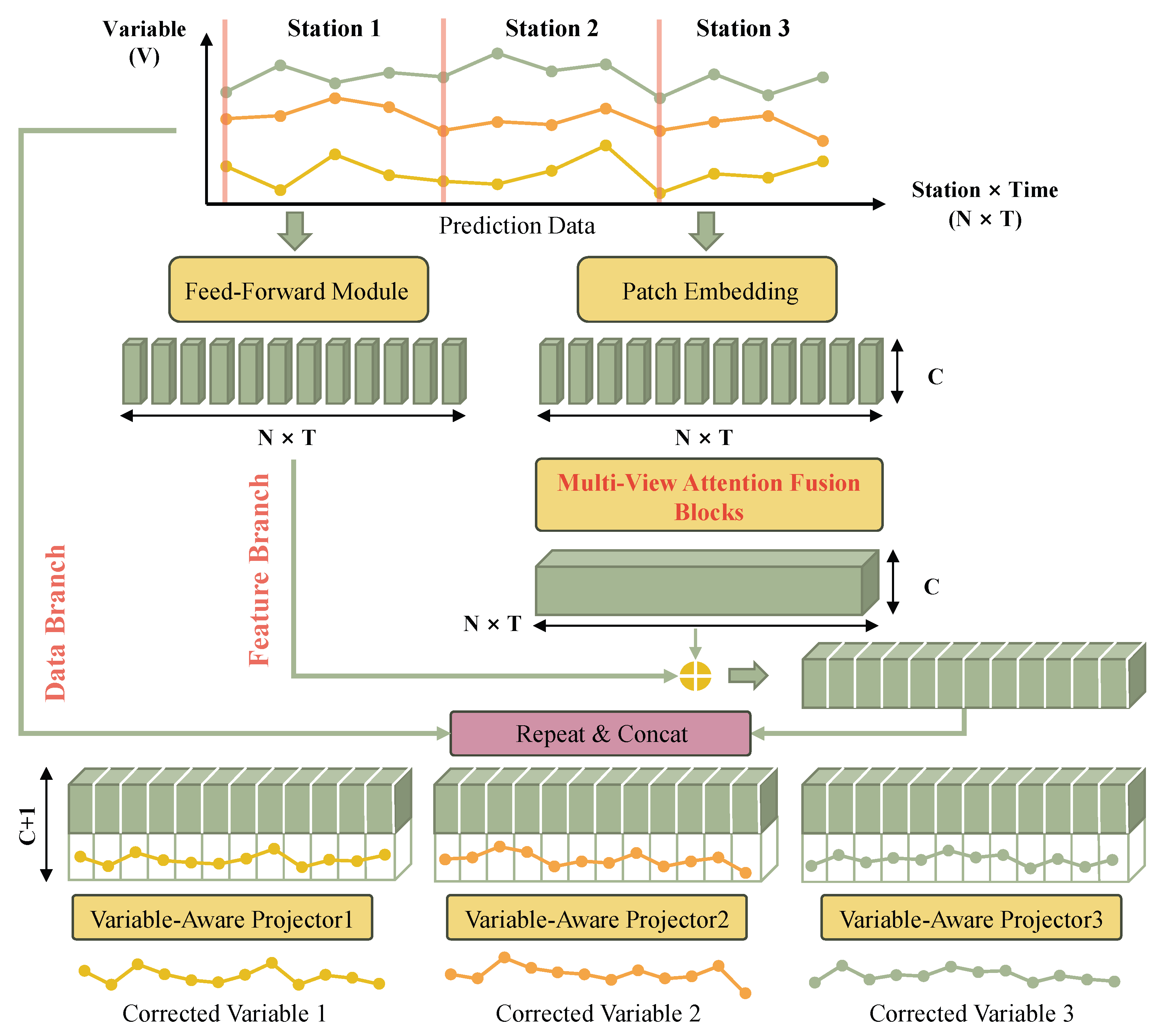
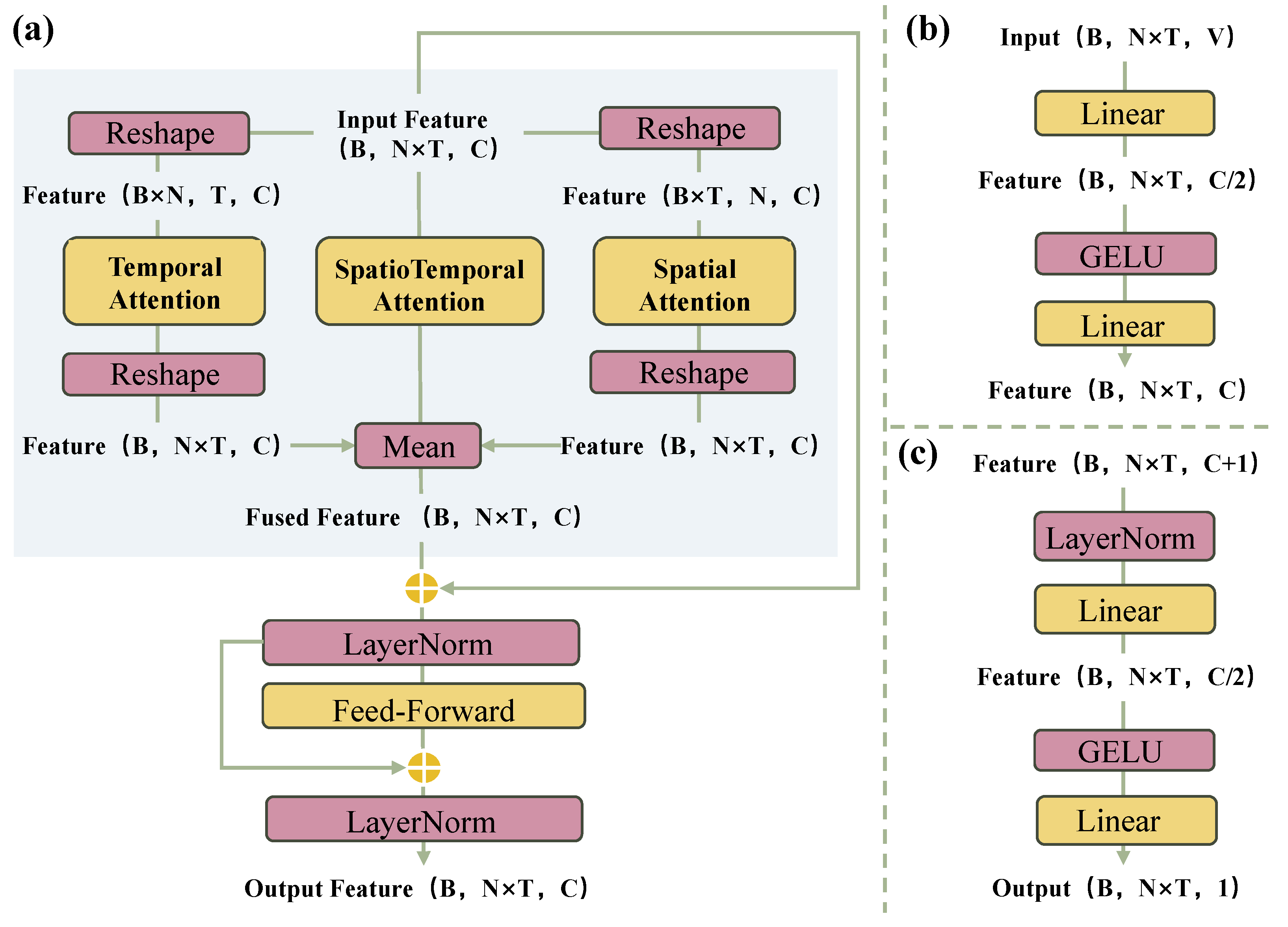
| Variable | Abbreviation | Unit | Valid Predictions | Valid Observations |
|---|---|---|---|---|
| Surface Pressure | p | hpa | 653,750 | 146,195 |
| Temperature at 2 m | t2m | °C | 653,750 | 146,522 |
| Relative Humidity at 2 m | rh2 | % | 653,750 | 138,415 |
| Wind Speed at 10 m | ws10 | m/s | 653,750 | 146,532 |
| Wind Direction at 10 m | wd10 | ° | 653,750 | 146,532 |
| Visibility | vis | km | 653,750 | 145,818 |
| Variable | Abbreviation | Unit | Valid Predictions | Valid Observations |
|---|---|---|---|---|
| 6-h accumulated precipitation | rain6 | mm | 329,800 | 142,368 |
| 24-h accumulated precipitation | rain24 | mm | 329,800 | 109,872 |
| Variables | Tiny | Light | Moderate | Heavy | Torrential |
|---|---|---|---|---|---|
| Rain6 (mm) | ≥10.0 | ||||
| Rain24 (mm) | ≥50.0 |
| Type | Tiny | Light | Middle | Heavy | Torrential |
|---|---|---|---|---|---|
| Tiny | 100 | 60 | 50 | 40 | 20 |
| Light | 60 | 100 | 75 | 60 | 30 |
| Middle | 50 | 75 | 100 | 80 | 40 |
| Heavy | 40 | 60 | 80 | 100 | 50 |
| Torrential | 20 | 30 | 40 | 50 | 100 |
| Feature Branch | Data Branch | RMSE | |||||
|---|---|---|---|---|---|---|---|
| p (hpa) | t2m (°C) | rh2 (%) | ws10 (m/s) | wd10 (°) | vis (km) | ||
| 0.465 | 0.565 | 2.068 | 0.889 | 8.925 | 2.031 | ||
| ✓ | 0.242 | 0.501 | 2.038 | 0.887 | 8.931 | 2.012 | |
| ✓ | 0.323 | 0.513 | 2.051 | 0.887 | 8.913 | 2.007 | |
| ✓ | ✓ | 0.244 | 0.491 | 2.027 | 0.883 | 8.895 | 1.999 |
| Feature Branch | Data Branch | MAE | |||||
| p (hpa) | t2m (°C) | rh2 (%) | ws10 (m/s) | wd10 (°) | vis (km) | ||
| 0.332 | 0.419 | 1.465 | 0.632 | 6.345 | 1.457 | ||
| ✓ | 0.178 | 0.367 | 1.446 | 0.631 | 6.251 | 1.413 | |
| ✓ | 0.239 | 0.378 | 1.436 | 0.630 | 6.241 | 1.404 | |
| ✓ | ✓ | 0.178 | 0.360 | 1.426 | 0.624 | 6.230 | 1.397 |
| Attention View | RMSE | |||||||
|---|---|---|---|---|---|---|---|---|
| S.T. | Temporal | Spatial | p (hpa) | t2m (°C) | rh2 (%) | ws10 (m/s) | wd10 (°) | vis (km) |
| ✓ | 0.329 | 0.520 | 2.096 | 0.898 | 8.938 | 2.076 | ||
| ✓ | 0.418 | 0.514 | 2.119 | 0.895 | 8.956 | 2.092 | ||
| ✓ | 0.289 | 0.529 | 2.073 | 0.895 | 9.011 | 2.052 | ||
| ✓ | ✓ | 0.327 | 0.505 | 2.079 | 0.892 | 8.925 | 2.048 | |
| ✓ | ✓ | 0.256 | 0.520 | 2.056 | 0.890 | 8.944 | 2.026 | |
| ✓ | ✓ | 0.265 | 0.500 | 2.062 | 0.889 | 8.931 | 2.040 | |
| ✓ | ✓ | ✓ | 0.244 | 0.491 | 2.027 | 0.883 | 8.895 | 1.999 |
| Attention View | MAE | |||||||
| S.T. | Temporal | Spatial | p (hpa) | t2m (°C) | rh2 (%) | ws10 (m/s) | wd10 (°) | vis (km) |
| ✓ | 0.226 | 0.388 | 1.490 | 0.646 | 6.335 | 1.479 | ||
| ✓ | 0.292 | 0.388 | 1.495 | 0.639 | 6.356 | 1.513 | ||
| ✓ | 0.190 | 0.409 | 1.460 | 0.637 | 6.387 | 1.435 | ||
| ✓ | ✓ | 0.200 | 0.378 | 1.451 | 0.634 | 6.251 | 1.463 | |
| ✓ | ✓ | 0.178 | 0.392 | 1.441 | 0.632 | 6.303 | 1.444 | |
| ✓ | ✓ | 0.184 | 0.364 | 1.436 | 0.631 | 6.272 | 1.451 | |
| ✓ | ✓ | ✓ | 0.178 | 0.360 | 1.426 | 0.624 | 6.230 | 1.397 |
| RMSE | ||||||||
|---|---|---|---|---|---|---|---|---|
| p (hpa) | t2m (°C) | rh2 (%) | ws10 (m/s) | wd10 (°) | vis (km) | |||
| ✓ | 0.248 | 0.568 | 2.073 | 0.908 | 9.385 | 2.081 | ||
| ✓ | 0.289 | 0.534 | 2.032 | 0.900 | 9.059 | 2.052 | ||
| ✓ | ✓ | 0.271 | 0.495 | 2.044 | 0.890 | 8.968 | 2.002 | |
| ✓ | ✓ | 0.265 | 0.495 | 2.050 | 0.894 | 8.956 | 2.026 | |
| ✓ | ✓ | ✓ | 0.244 | 0.491 | 2.027 | 0.883 | 8.895 | 1.999 |
| MAE | ||||||||
| p (hpa) | t2m (°C) | rh2 (%) | ws10 (m/s) | wd10 (°) | vis (km) | |||
| ✓ | 0.180 | 0.419 | 1.475 | 0.646 | 6.502 | 1.435 | ||
| ✓ | 0.186 | 0.433 | 1.451 | 0.639 | 6.387 | 1.429 | ||
| ✓ | ✓ | 0.181 | 0.388 | 1.446 | 0.636 | 6.303 | 1.416 | |
| ✓ | ✓ | 0.182 | 0.392 | 1.455 | 0.637 | 6.324 | 1.413 | |
| ✓ | ✓ | ✓ | 0.178 | 0.360 | 1.426 | 0.624 | 6.230 | 1.397 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Chen, J.; Xu, M.; Wu, M.; Zhang, C. DRAF-Net: Dual-Branch Residual-Guided Multi-View Attention Fusion Network for Station-Level Numerical Weather Prediction Correction. Remote Sens. 2025, 17, 206. https://doi.org/10.3390/rs17020206
Chen K, Chen J, Xu M, Wu M, Zhang C. DRAF-Net: Dual-Branch Residual-Guided Multi-View Attention Fusion Network for Station-Level Numerical Weather Prediction Correction. Remote Sensing. 2025; 17(2):206. https://doi.org/10.3390/rs17020206
Chicago/Turabian StyleChen, Kaixin, Jiaxin Chen, Mengqiu Xu, Ming Wu, and Chuang Zhang. 2025. "DRAF-Net: Dual-Branch Residual-Guided Multi-View Attention Fusion Network for Station-Level Numerical Weather Prediction Correction" Remote Sensing 17, no. 2: 206. https://doi.org/10.3390/rs17020206
APA StyleChen, K., Chen, J., Xu, M., Wu, M., & Zhang, C. (2025). DRAF-Net: Dual-Branch Residual-Guided Multi-View Attention Fusion Network for Station-Level Numerical Weather Prediction Correction. Remote Sensing, 17(2), 206. https://doi.org/10.3390/rs17020206






